Grid-like Vibration Measurements on Power Transformer Tank during Open-Circuit and Short-Circuit Tests
Abstract
1. Introduction
2. Theoretical Considerations
2.1. Propagation of Sound Waves in Solid Plates
2.2. Normal Modes and Natural Frequencies of a Plate
2.3. Analytical Determination of Sound Pressure in the Point Away from the Plane with Measured Vibration Velocity Distribution Considering Incoherent Plane Radiation
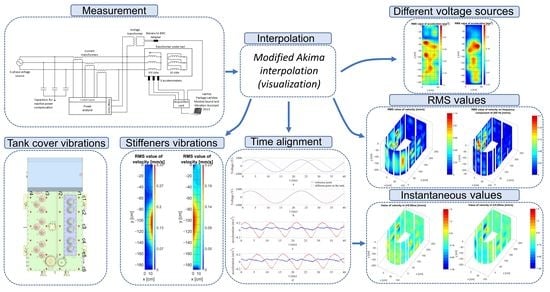
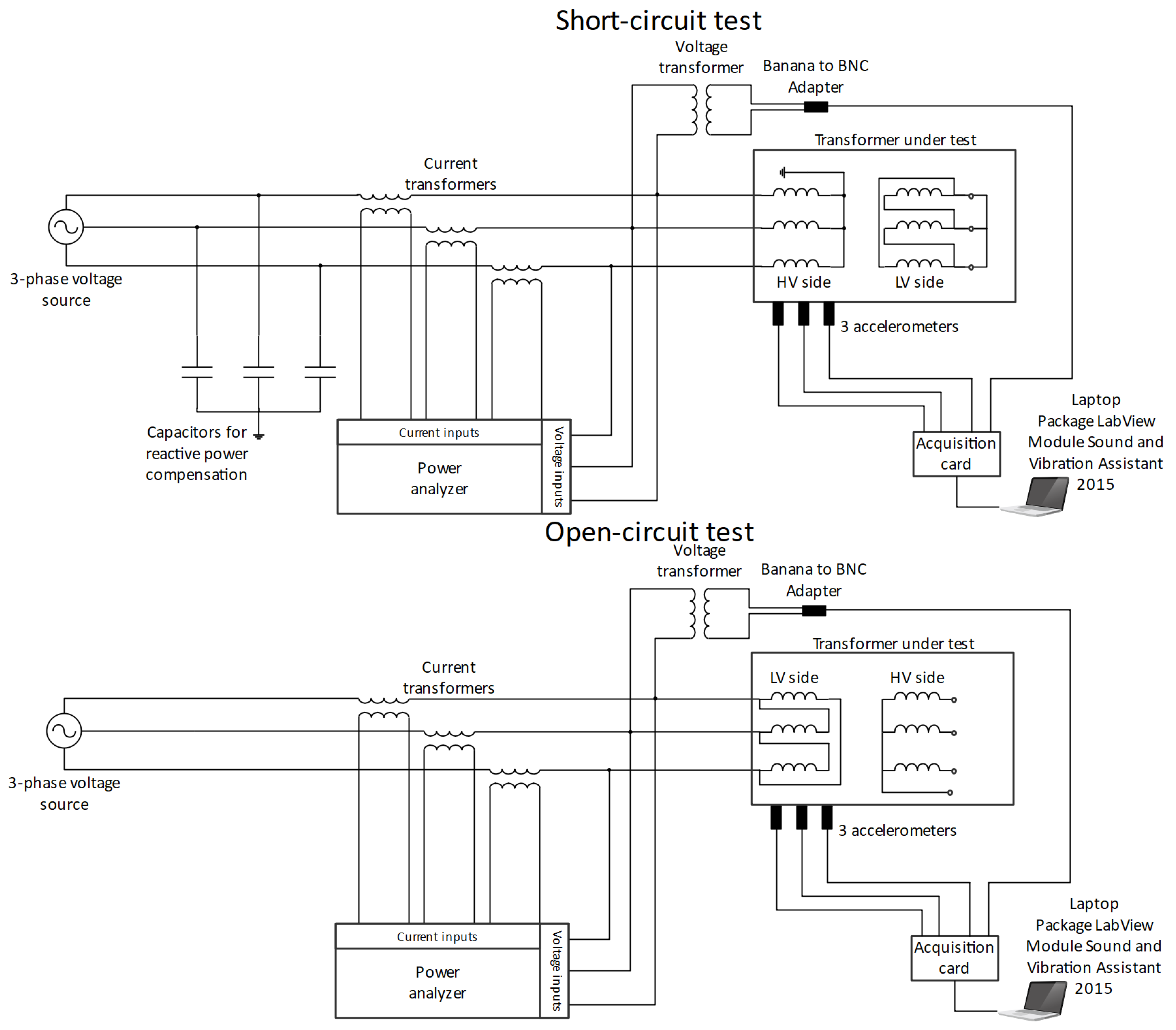
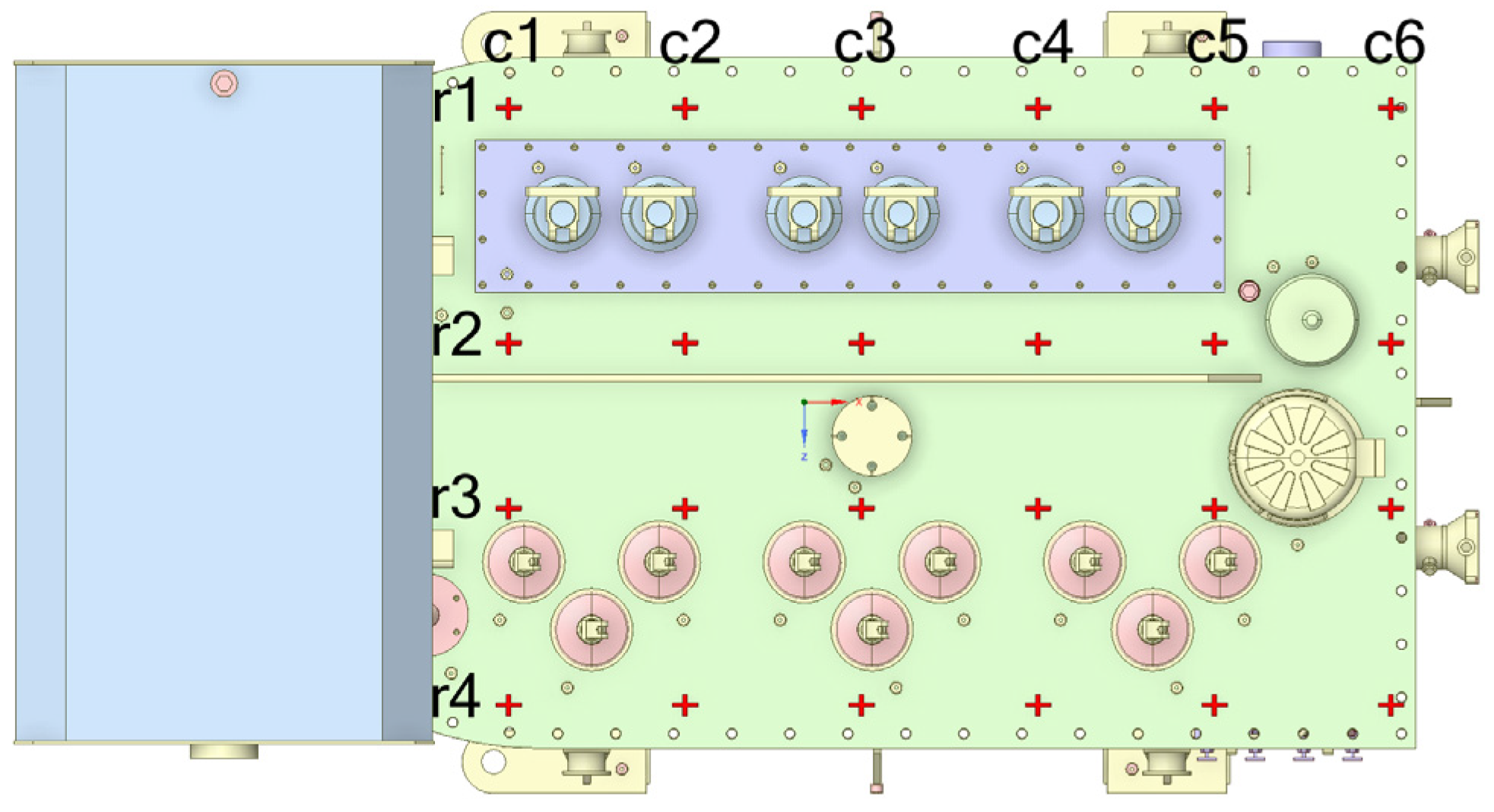
3. Measurement Setup
4. Results
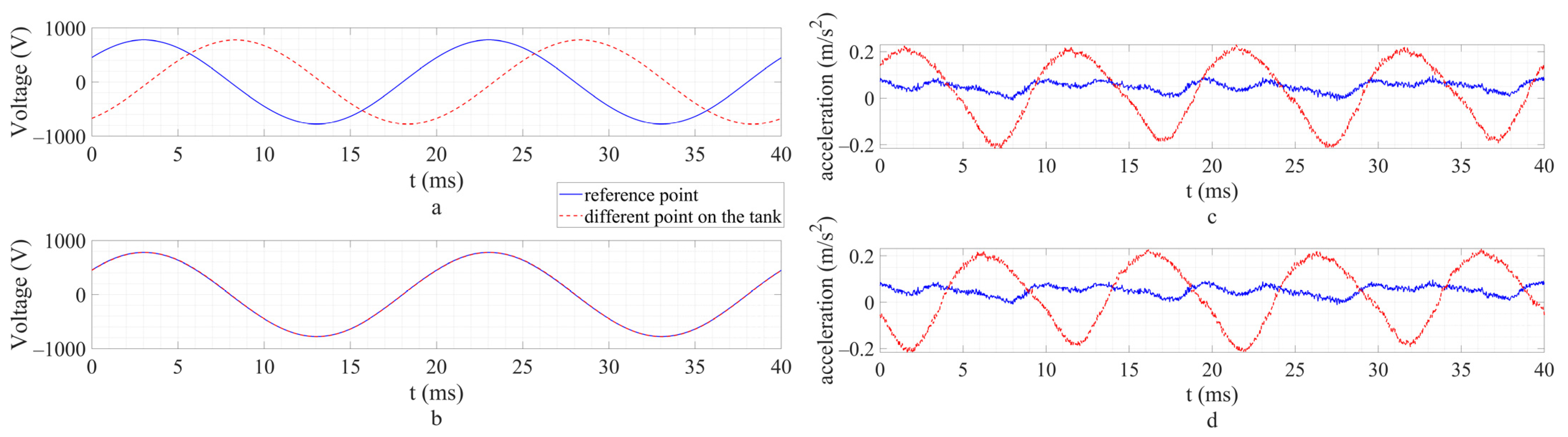
4.1. Comparison of the Vibration Measurements Using Two Different Voltage Sources
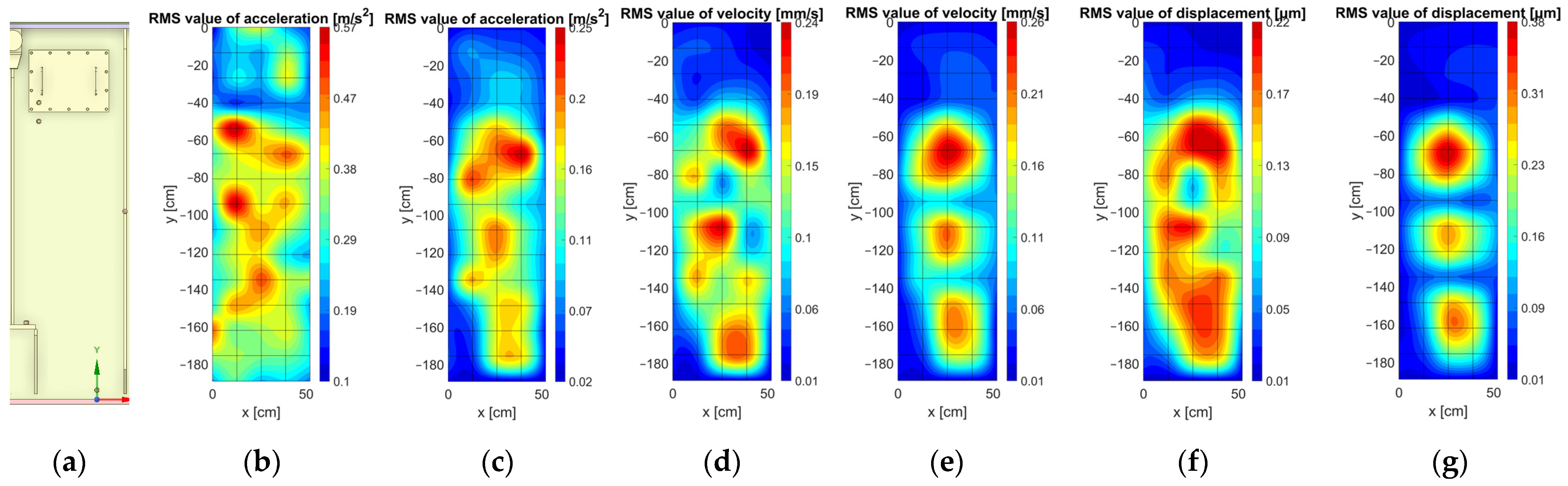
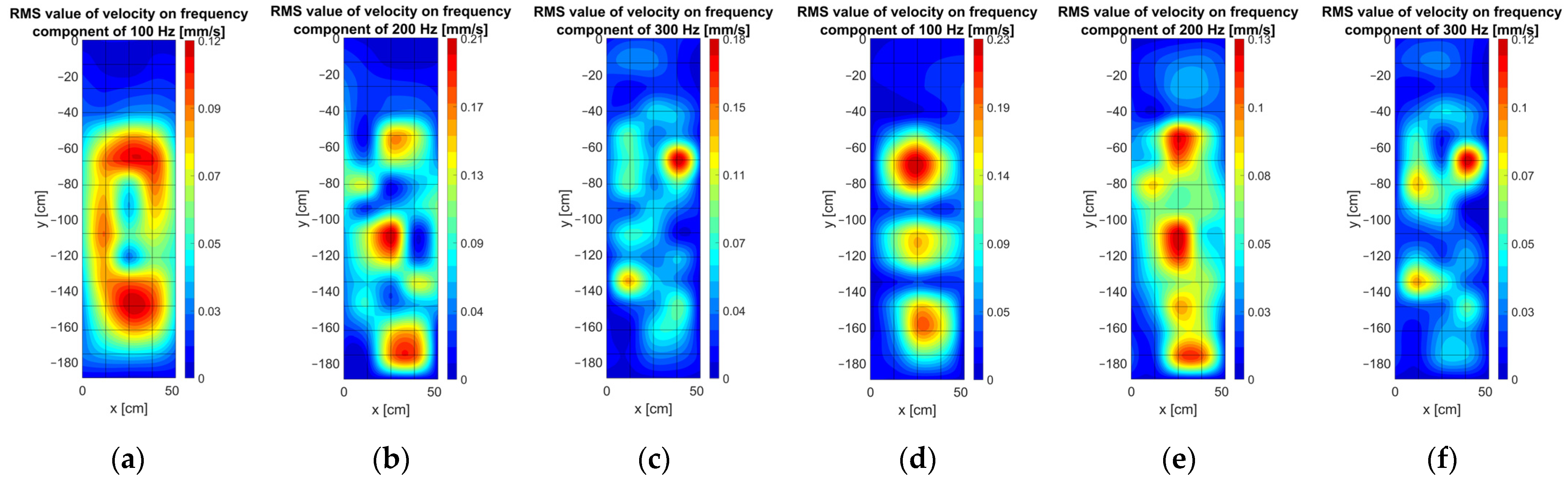
4.2. Visualization of the Measurement Results Using Matlab Interpolation Functions
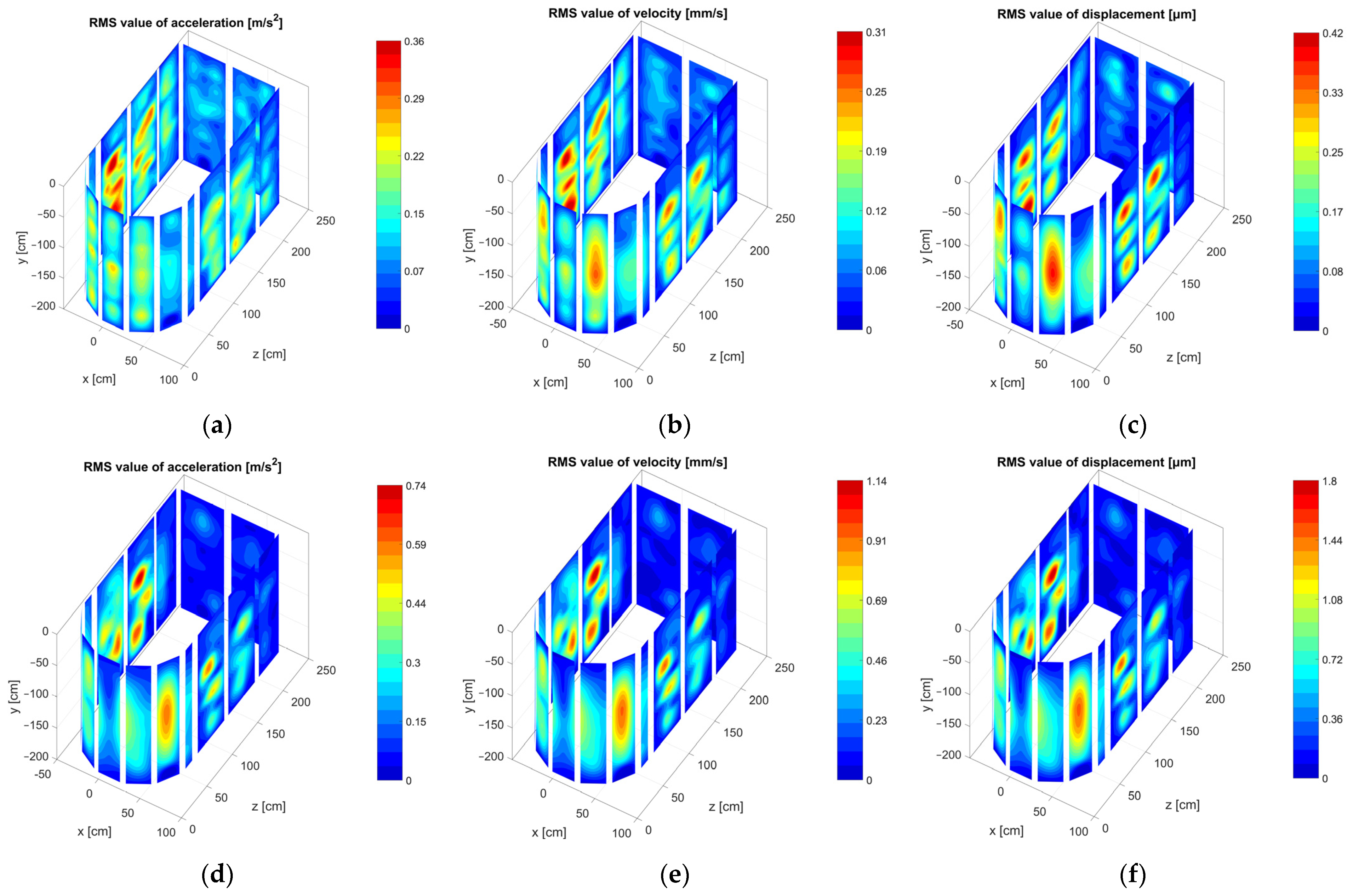
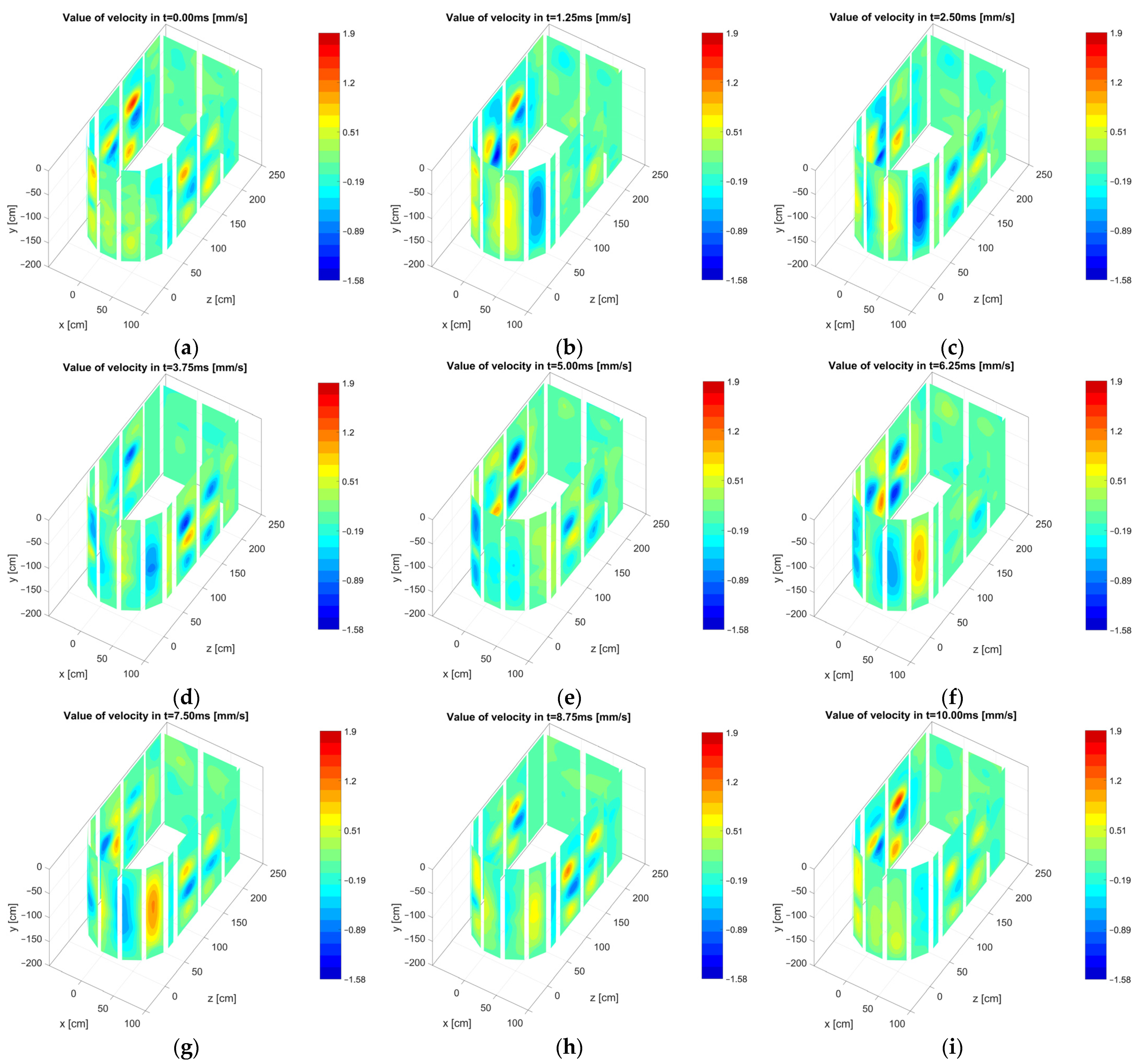
4.3. Visualization of the Tank Vibrations in 3D Space
4.4. Analytical Calculation of Critical, Crossover, and Resonant Frequencies of the Plate
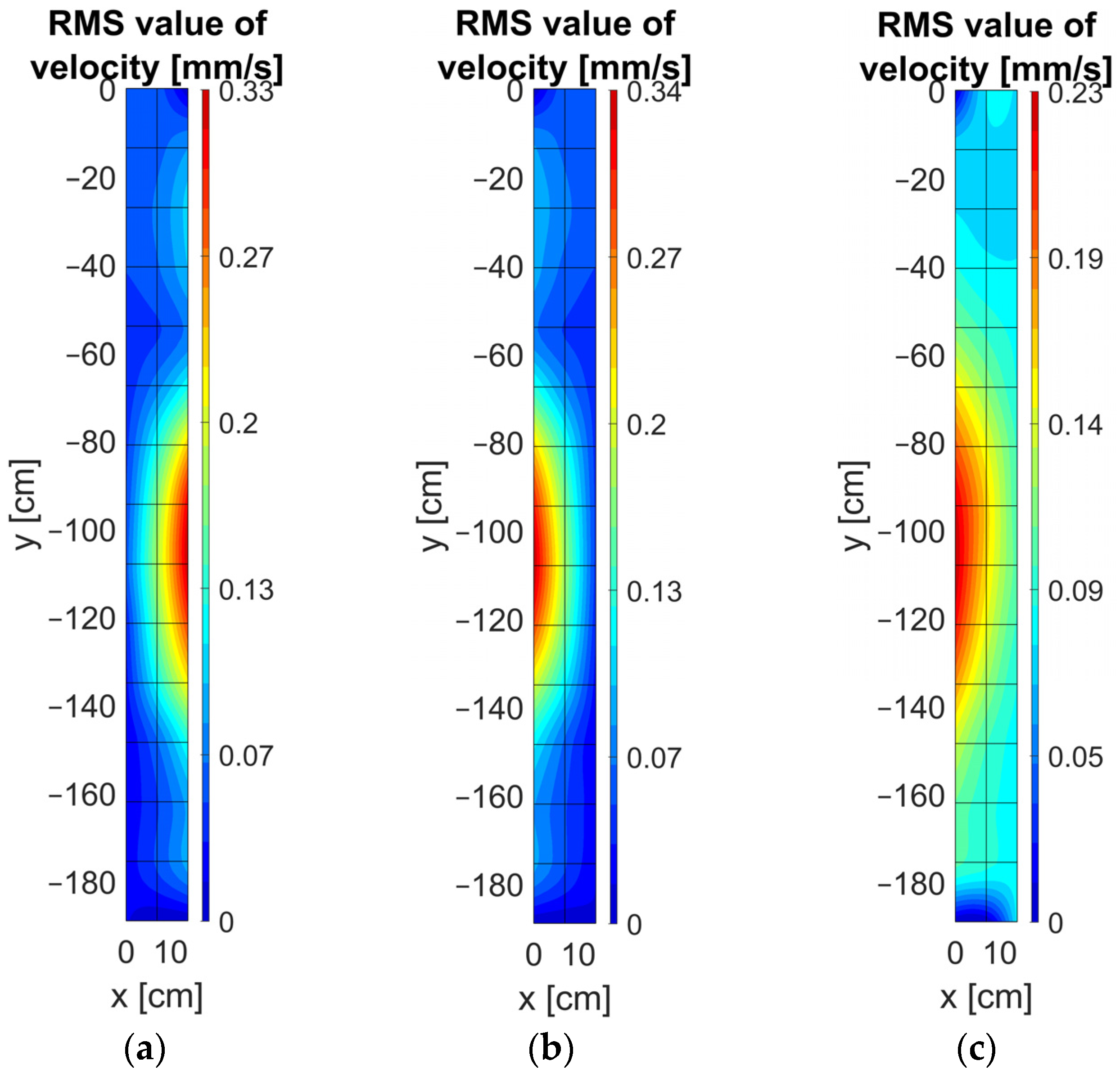
4.5. Vibrations of Tank Stiffeners and Cover
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Kulkarni, S.V.; Khaparde, S.A. Transformer Engineering: Design, Technology, and Diagnostics; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Oxfordshire, UK, 2013; ISBN 9781439854181. [Google Scholar]
- Jin, M.; Pan, J. Vibration Transmission from Internal Structures to the Tank of an Oil-Filled Power Transformer. Acoustics 2016, 113, 1–6. [Google Scholar] [CrossRef]
- IEC 60076-10; Power Transformers—Part 10: Determination of Sound Levels. International Electrotechnical Commission: Geneva, Switzerland, 2016.
- IEC 60076-10-1; Power Transformers—Part 10-1: Determination of Sound Levels—Application Guide. International Electrotechnical Commission: Geneva, Switzerland, 2016.
- Beltle, M.; Tenbohlen, S. Usability of Vibration Measurement for Power Transformer Diagnosis and Monitoring. In Proceedings of the 2012 IEEE International Conference on Condition Monitoring and Diagnosis, CMD 2012, Bali, Indonesia, 23–27 September 2012; pp. 281–284. [Google Scholar] [CrossRef]
- Jin, M.; Pan, J.; Huang, H.; Zhou, J. Transmission of Vibration of a Power Transformer from the Internal Structures to the Tank. In Proceedings of the Acoustics Fremantle 2012, Fremantle, Australia, 21–23 November 2012. [Google Scholar]
- Zhang, F.; Ji, S.; Shi, Y.; Zhan, C.; Zhu, L. Investigation on Vibration Source and Transmission Characteristics in Power Transformers. Appl. Acoust. 2019, 151, 99–112. [Google Scholar] [CrossRef]
- Hackl, A.; Hamberger, P. Investigation of Surface Velocity Pattern of Power Transformers Tanks. In Proceedings of the 19th International Conference on Electrical Machines, ICEM 2010, Rome, Italy, 6–8 September 2010. [Google Scholar] [CrossRef]
- Hrkac, M.; Kmita, G.; Kozupa, M.; Platek, R.; Sekula, R.; Zannol, R. Vibroacoustic Behavior of a Small Power Transformer. In Proceedings of the International Colloquium Transformer Research and Asset Management, Dubrovnik, Croatia, 16–18 May 2012; pp. 1–8. [Google Scholar]
- Lu, Z.; Zhang, C.; Wang, T.; Yu, H.; Wang, Z.; Li, C.; Liu, G. Measurement and Analysis of UHV Transformer Noise with Sound Intensity and Vibration Method. In Proceedings of the 2017 20th International Conference on Electrical Machines and Systems, ICEMS 2017, Sydney, Australia, 11–14 August 2017. [Google Scholar] [CrossRef]
- Wu, X.; Zhou, N.; Shi, Y.; Ji, S.; Fan, Z.; Lu, W.; Hu, S. Vibration Distribution Characteristics on Oil-Tank Surface of a Single-Phase Transformer. In Proceedings of the ICEMPE 2017—1st International Conference on Electrical Materials and Power Equipment, Xi’an, China, 14–17 May 2017; pp. 344–348. [Google Scholar] [CrossRef]
- Zhang, F.; Ji, S.; Shi, Y.; Zhu, L. Investigation on the Action of Eddy Current on Tank Vibration Characteristics in Dry-Type Transformer. IEEE Trans. Magn. 2019, 55, 8400908. [Google Scholar] [CrossRef]
- Shi, Y.; Ji, S.; Zhang, F.; Dang, Y.; Zhu, L. Application of Operating Deflection Shapes to the Vibration-Based Mechanical Condition Monitoring of Power Transformer Windings. IEEE Trans. Power Deliv. 2021, 36, 2164–2173. [Google Scholar] [CrossRef]
- Hu, Y.; Zheng, J.; Huang, H. Experimental Research on Power Transformer Vibration Distribution under Different Winding Defect Conditions. Electronics 2019, 8, 842. [Google Scholar] [CrossRef]
- Yang, F.; Ren, Z.; Zhang, D.; Li, L.; Fan, X.; Zhou, Y. Simulation Analysis and Experiment Validation of Vibration and Noise of Oil-Immersed Transformer. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems, ICEMS 2019, Harbin, China, 11–14 August 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Wang, Y.; Pan, J.; Jin, M. Finite Element Modelling of the Vibration of a Power Transformer. In Proceedings of the ACOUSTICS 2011, Gold Coast, Australia, 2–4 November 2011; Volume 34. [Google Scholar]
- Case, J. Numerical Analysis of the Vibration and Acoustic Characteristics of Large Power Transformers. Doctoral Dissertation, Queensland University of Technology, Brisbane, Australia, 2017. [Google Scholar]
- Yoshida, K.; Hoshino, T.; Murase, S.; Murakami, H.; Miyashita, T. Analysis of Load Noise Components in Small Core-Form Transformers. IEEE Trans. Power Deliv. 2021, 36, 2694–2704. [Google Scholar] [CrossRef]
- Hsu, C.H.; Lee, S.L.; Lin, C.C.; Liu, C.S.; Chang, S.Y.; Hsieh, M.F.; Huang, Y.M.; Fu, C.M. Reduction of Vibration and Sound-Level for a Single-Phase Power Transformer with Large Capacity. IEEE Trans. Magn. 2015, 51, 84032040. [Google Scholar] [CrossRef]
- Bouayed, K.; Mebarek, L.; Lanfranchi, V.; Chazot, J.D.; Marechal, R.; Hamdi, M.A. Noise and Vibration of a Power Transformer under an Electrical Excitation. Appl. Acoust. 2017, 128, 64–70. [Google Scholar] [CrossRef]
- Zhang, B.; Yan, N.; Du, J.; Han, F.; Wang, H. A Novel Approach to Investigate the Core Vibration in Power Transformers. IEEE Trans. Magn. 2018, 54, 8400804. [Google Scholar] [CrossRef]
- Holger Rindel, J. Sound Insulation in Buildings; CRC Press: Boca Raton, FL, USA, 2017; ISBN 9781498700429. [Google Scholar]
- Meyer, E.; Neumann, E.-G. Physical and Applied Acoustics: An Introduction; Academic Press: Cambridge, MA, USA, 1972; ISBN 978-0124931503. [Google Scholar]
- Takatsubo, J.; Ohno, S.; Suzuki, T. Calculation of the Sound Pressure Produced by Structural Vibration Using the Results of Vibration Analysis. Bull. JSME 1983, 26, 1970–1976. [Google Scholar] [CrossRef][Green Version]
- Bies, D.A.; Hansen, C.H. Engineering Noise Control: Theory and Practice, 4th ed.; Spon Press: London, UK, 2009; ISBN 9781482288704. [Google Scholar]
- Maidanik, G. Response of Ribbed Panels to Reverberant Acoustic Fields. J. Acoust. Soc. Am. 1962, 34, 809–826. [Google Scholar] [CrossRef]
- Wang, Y.; Jin, H.; Cai, X.; Gong, P.; Jiang, X. Study on the Sound Radiation Efficiency of a Typical Distribution Transformer. IEEE Access 2021, 9, 125151–125157. [Google Scholar] [CrossRef]
- Hohenwarter, D. Noise Radiation of (Rectangular) Plane Sources. Appl. Acoust. 1991, 33, 45–62. [Google Scholar] [CrossRef]
- Akima, H. A New Method of Interpolation and Smooth Curve Fitting Based on Local Procedures. J. ACM (JACM) 1970, 17, 589–602. [Google Scholar] [CrossRef]
- Akima, H. A Method of Bivariate Interpolation and Smooth Surface Fitting Based on Local Procedures. Commun. ACM 1974, 17, 18–20. [Google Scholar] [CrossRef]
- Interpolation for 2-D Gridded Data in Meshgrid Format—MATLAB Interp2. Available online: https://www.mathworks.com/help/matlab/ref/interp2.html (accessed on 8 June 2021).







| Sensitivity (±15%) | 10.2 mV/(m/s2) |
| Measurement Range | ±490 m/s2 |
| Frequency Range (±3 dB) | 0.5–10,000 Hz |
| Resonant Frequency | 22 kHz |
| Broadband Resolution | 3434 µm/s2 |
| Temperature Range | −54 °C to +121 °C |
| Enclosure Rating | IP68 |
| Spectral Noise (100 Hz) | 49.1 (µm/s2)/√Hz |
| Plate | Resonant Frequency [Hz] (Mode of Vibration) | |||||||
|---|---|---|---|---|---|---|---|---|
| 1, 2, 3, 14, 15 | 193 (1, 1) | 208 (1, 2) | 233 (1, 3) | 269 (1, 4) | 315 (1, 5) | 371 (1, 6) | 437 (1, 7) | 513 (1, 8) |
| 4, 13 | 312 (1, 1) | 327 (1, 2) | 352 (1, 3) | 388 (1, 4) | 434 (1, 5) | 490 (1, 6) | 556 (1, 7) | 632 (1, 8) |
| 5, 6, 11, 12 | 63 (1, 1) | 79 (1, 2) | 104 (1, 3) | 140 (1, 4) | 185 (1, 5) | 238 (2, 1) | 241 (1, 6) | 253 (2, 2) |
| 279 (2, 3) | 307 (1, 7) | 314 (2, 4) | 360 (2, 5) | 384 (1, 8) | 416 (2, 6) | 470 (1, 9) | 482 (2, 7) | |
| 7, 10 | 118 (1, 1) | 133 (1, 2) | 158 (1, 3) | 194 (1, 4) | 240 (1, 5) | 296 (1, 1) | 362 (1, 7) | 438 (1, 8) |
| 8, 9 | 62 (1, 1) | 77 (1, 2) | 102 (1, 3) | 138 (1, 4) | 184 (1, 5) | 232 (2, 1) | 240 (1, 6) | 247 (2, 2) |
| 273 (2, 3) | 306 (1, 7) | 308 (2, 4) | 354 (2, 5) | 382 (1, 8) | 410 (2, 6) | 469 (1, 9) | 476 (2, 7) | |
| y [cm] | RMS Velocity (OC) [mm/s] | RMS Velocity (SC) [mm/s] |
|---|---|---|
| 0 | 0.02 | 0.06 |
| −27 | 0.03 | 0.16 |
| −54 | 0.04 | 0.21 |
| −81 | 0.09 | 0.24 |
| −108 | 0.09 | 0.23 |
| −135 | 0.10 | 0.20 |
| −162 | 0.04 | 0.11 |
| −189 | 0.03 | 0.05 |
| RMS Velocity [mm/s] | c1 | c2 | c3 | c4 | c5 | c6 |
|---|---|---|---|---|---|---|
| OC | ||||||
| r1 | 0.01 | 0.02 | 0.01 | 0.02 | 0.03 | 0.02 |
| r2 | 0.06 | 0.06 | 0.04 | 0.03 | 0.09 | 0.02 |
| r3 | 0.06 | 0.08 | 0.09 | 0.10 | 0.06 | 0.02 |
| r4 | 0.01 | 0.02 | 0.02 | 0.01 | 0.01 | 0.02 |
| SC | ||||||
| r1 | 0.09 | 0.09 | 0.04 | 0.03 | 0.02 | 0.01 |
| r2 | 0.08 | 0.13 | 0.13 | 0.22 | 0.20 | 0.03 |
| r3 | 0.05 | 0.39 | 0.26 | 0.29 | 0.08 | 0.03 |
| r4 | 0.06 | 0.02 | 0.05 | 0.04 | 0.02 | 0.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petrović, K.; Petošić, A.; Župan, T. Grid-like Vibration Measurements on Power Transformer Tank during Open-Circuit and Short-Circuit Tests. Energies 2022, 15, 492. https://doi.org/10.3390/en15020492
Petrović K, Petošić A, Župan T. Grid-like Vibration Measurements on Power Transformer Tank during Open-Circuit and Short-Circuit Tests. Energies. 2022; 15(2):492. https://doi.org/10.3390/en15020492
Chicago/Turabian StylePetrović, Karlo, Antonio Petošić, and Tomislav Župan. 2022. "Grid-like Vibration Measurements on Power Transformer Tank during Open-Circuit and Short-Circuit Tests" Energies 15, no. 2: 492. https://doi.org/10.3390/en15020492
APA StylePetrović, K., Petošić, A., & Župan, T. (2022). Grid-like Vibration Measurements on Power Transformer Tank during Open-Circuit and Short-Circuit Tests. Energies, 15(2), 492. https://doi.org/10.3390/en15020492