Fractal Dimension of Digital 3D Rock Models with Different Pore Structures
Abstract
:1. Introduction
2. Methods
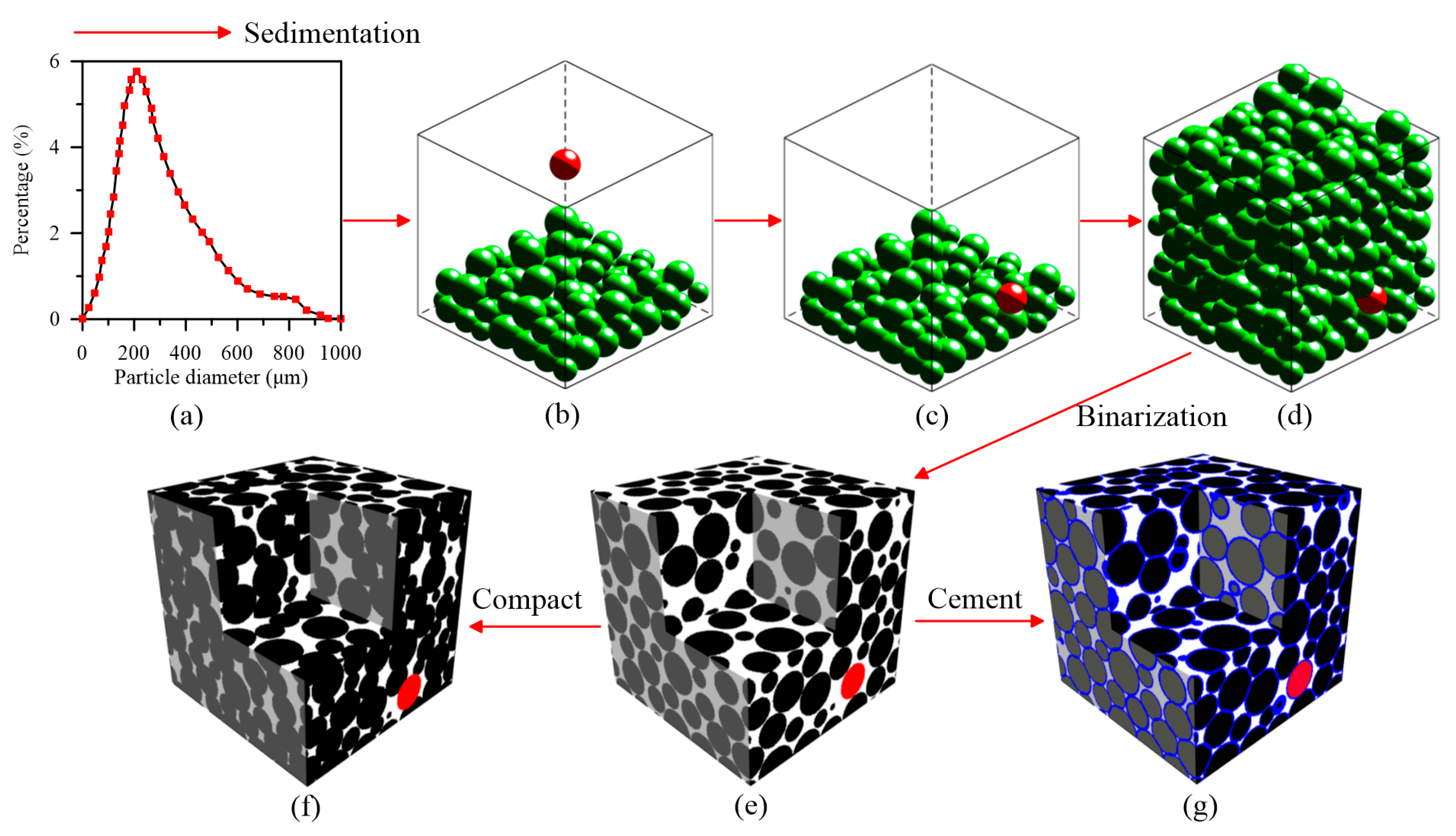
2.1. Process-Based Modeling
2.2. Calculation of Fractal Dimension
3. Digital Rock Model Material
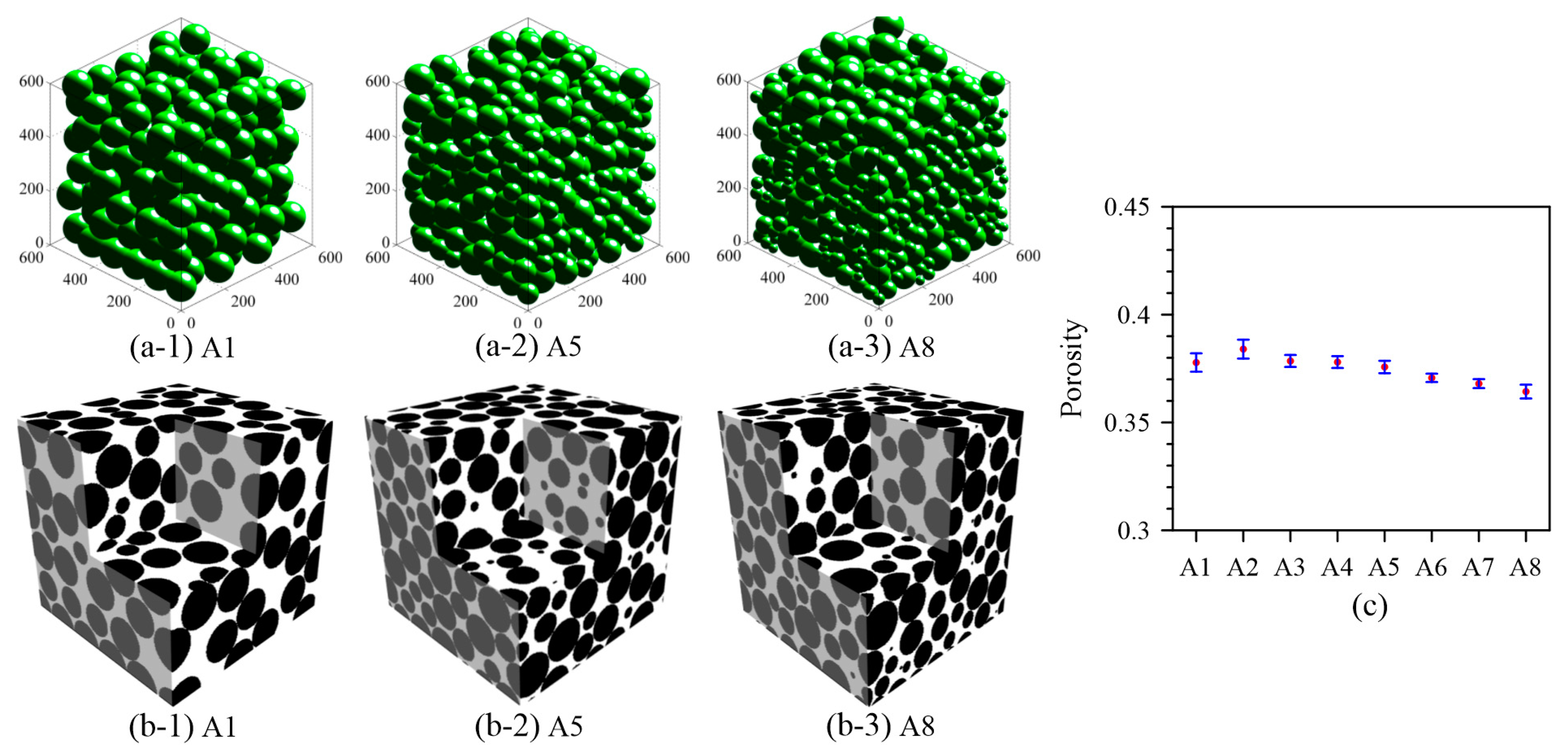
3.1. Sedimentation Model
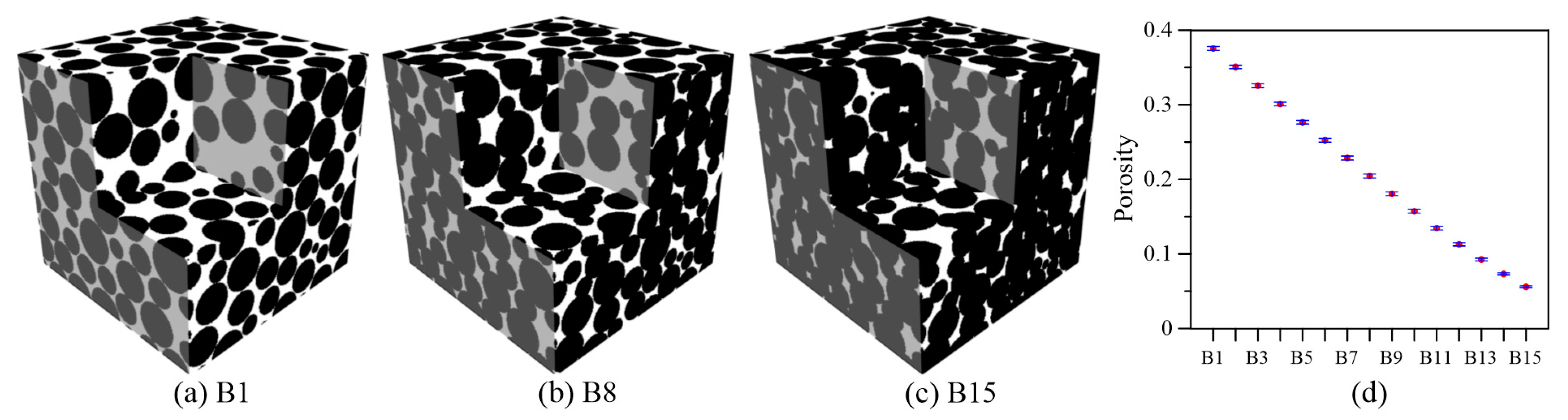
3.2. Compaction Model
3.3. Cementation Model
4. Results and Discussion
4.1. Fractal Dimension of Sedimentation Model
4.2. Fractal Dimension of Compaction Model
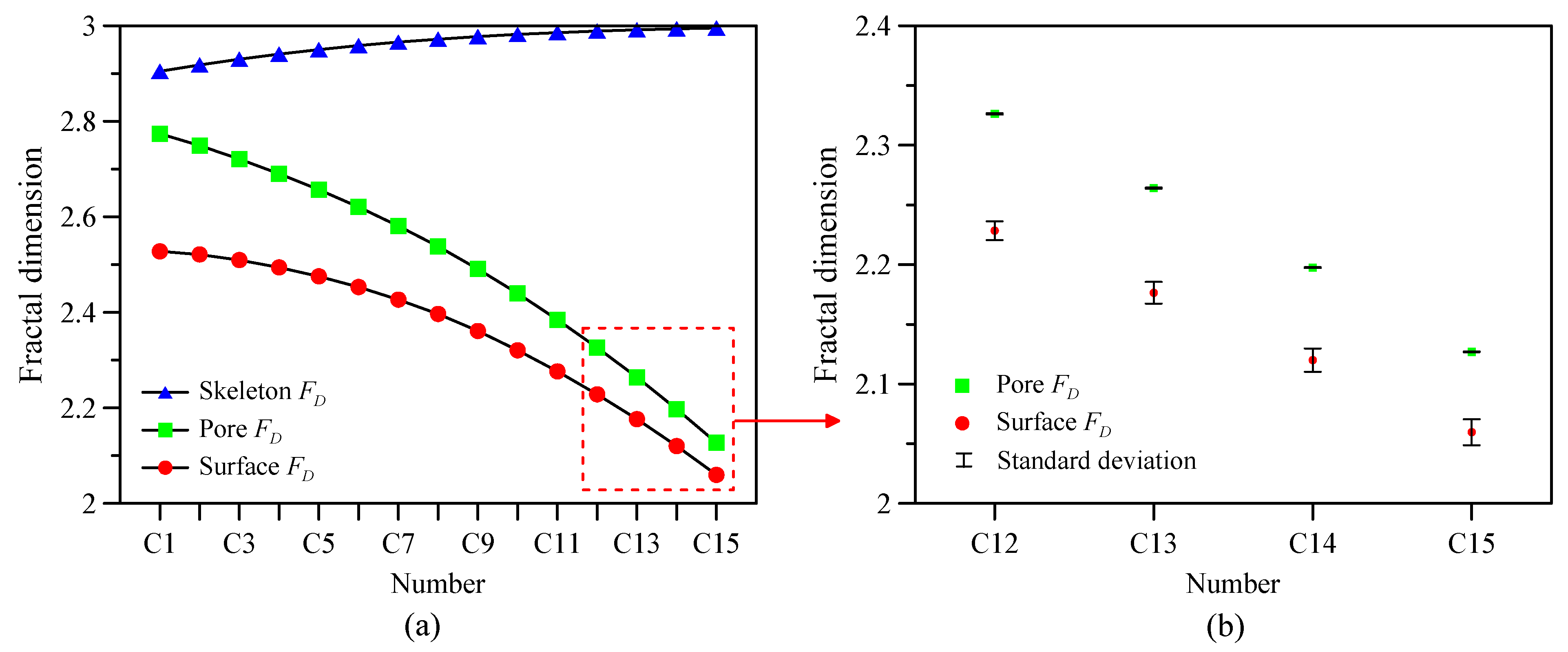
4.3. Fractal Dimension of Cementation Model
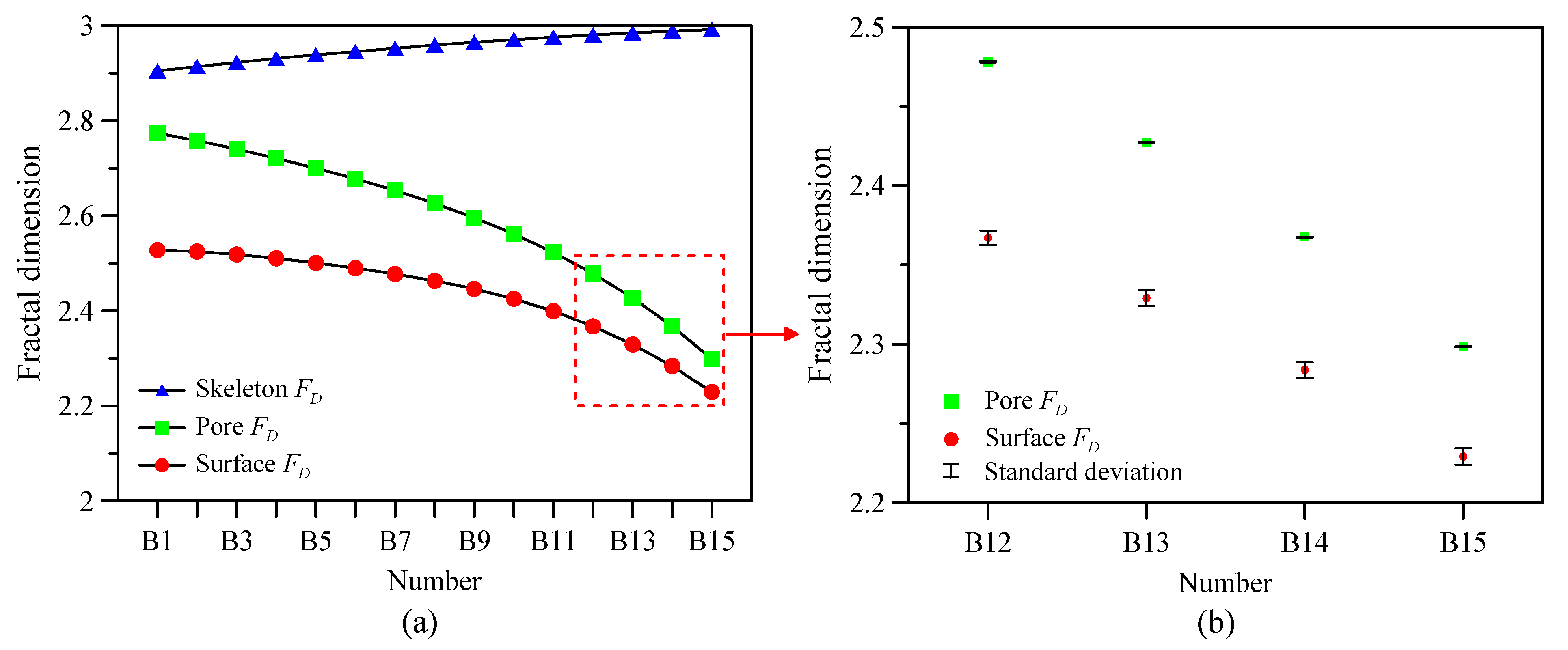
4.4. Quantitative Analysis of Fractal Dimension
5. Conclusions
- The surface fractal dimension is a useful parameter for characterizing and distinguishing the pore structure differences of the sedimentation model that has a slight change in porosity.
- The pore and surface fractal dimensions have significant responses, which proves that both pore and surface fractal dimensions can be utilized to characterize different pore structures in compaction and cementation models.
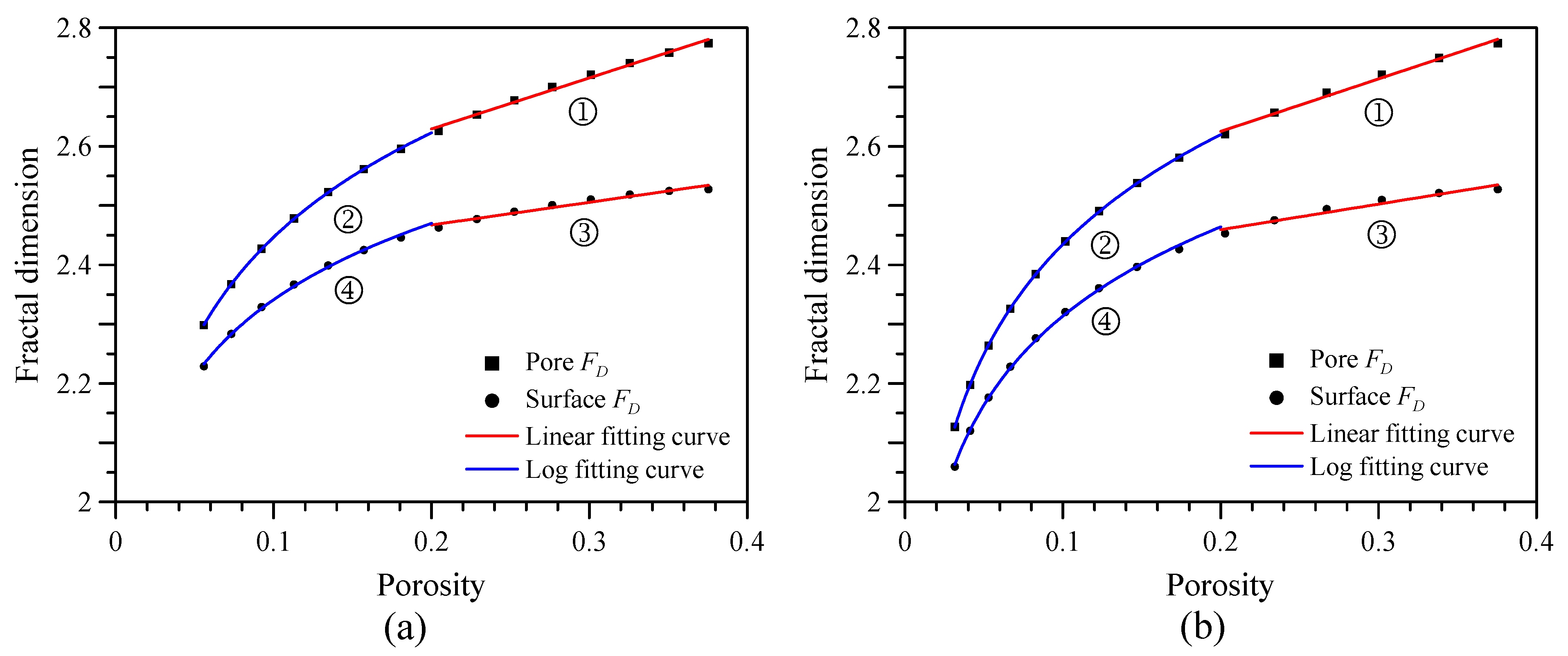
- The relations of porosity versus fractal dimension can be well fitted by the combination of linear and logarithmic equations in the compaction model and cementation model. In addition, the pore and surface fractal dimensions decrease more and more rapidly with the decrease in porosity.
- When the porosity is the same, the fractal dimension of the cementation model is smaller than that of the compaction model. The comparison of fractal dimensions reflects the difference in microscopic pore structures, indicating that the box-counting fractal dimension is an effective parameter for characterizing the pore structures of digital rocks.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Miller, K.; Vanorio, T.; Keehm, Y. Evolution of permeability and microstructure of tight carbonates due to numerical simulation of calcite dissolution. J. Geophys. Res. Solid Earth 2017, 122, 4460–4474. [Google Scholar] [CrossRef]
- Zhao, P.Q.; Wang, Z.L.; Sun, Z.C.; Cai, J.C.; Wang, L. Investigation on the pore structure and multifractal characteristics of tight oil reservoirs using NMR measurements: Permian Lucaogou Formation in Jimusaer Sag, Junggar Basin. Mar. Pet. Geol. 2017, 86, 1067–1081. [Google Scholar] [CrossRef]
- Andhumoudine, A.B.; Nie, X.; Zhou, Q.; Yu, J.; Kane, O.I.; Jin, L.; Djaroun, R.R. Investigation of coal elastic properties based on digital core technology and finite element method. Adv. Geo-Energy Res. 2021, 5, 53–63. [Google Scholar] [CrossRef]
- Zhu, L.Q.; Ma, Y.S.; Cai, J.C.; Zhang, C.M.; Wu, S.G.; Zhou, X.Q. Key factors of marine shale conductivity in southern China-Part II: The influence of pore system and the development direction of shale gas saturation models. J. Pet. Sci. Eng. 2022, 209, 109516. [Google Scholar] [CrossRef]
- Blunt, M.J.; Bijeljic, B.; Dong, H.; Gharbi, O.; Iglauer, S.; Mostaghimi, P.; Paluszny, A.; Pentland, C. Pore-scale imaging and modelling. Adv. Water Resour. 2013, 51, 197–216. [Google Scholar] [CrossRef] [Green Version]
- Wood, D.A. Techniques used to calculate shale fractal dimensions involve uncertainties and imprecisions that require more careful consideration. Adv. Geo-Energy Res. 2021, 5, 153–165. [Google Scholar] [CrossRef]
- Cai, J.C.; Lin, D.L.; Singh, H.; Wei, W.; Zhou, S.W. Shale gas transport model in 3D fractal porous media with variable pore sizes. Mar. Pet. Geol. 2018, 98, 437–447. [Google Scholar] [CrossRef]
- Xia, Y.X.; Cai, J.C.; Perfect, E.; Wei, W.; Zhang, Q.; Meng, Q.B. Fractal dimension, lacunarity and succolarity analyses on CT images of reservoir rocks for permeability prediction. J. Hydrol. 2019, 579, 124198. [Google Scholar] [CrossRef]
- Karimpouli, S.; Tahmasebi, P. Conditional reconstruction: An alternative strategy in digital rock physics. Geophysics 2016, 81, D465–D477. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, L.; Li, Y.; Liu, F.; Martyushev, D.A.; Yang, Y. Effects of microfractures on permeability in carbonate rocks based on digital core technology. Adv. Geo-Energy Res. 2022, 6, 86–90. [Google Scholar] [CrossRef]
- Thovert, J.F.; Adler, P.M. Grain reconstruction of porous media: Application to a Bentheim sandstone. Phys. Rev. E 2011, 83, 056116. [Google Scholar] [CrossRef] [PubMed]
- Lin, W.; Li, X.Z.; Yang, Z.M.; Wang, J.; Xiong, S.C.; Luo, Y.T.; Wu, G.M. Construction of dual pore 3-D digital cores with a hybrid method combined with physical experiment method and numerical reconstruction method. Transp. Porous Media 2017, 120, 227–238. [Google Scholar] [CrossRef]
- Arns, C.H.; Knackstedt, M.A.; Pinczewski, W.V.; Garboczi, E.J. Computation of linear elastic properties from microtomographic images: Methodology and agreement between theory and experiment. Geophysics 2002, 67, 1396–1405. [Google Scholar] [CrossRef]
- Fredrich, J.T.; Menendez, B.; Wong, T.F. Imaging the pore structure of geomaterials. Science 1995, 268, 276–279. [Google Scholar] [CrossRef] [PubMed]
- Vogel, H.J.; Roth, K. Quantitative morphology and network representation of soil pore structure. Adv. Water Resour. 2001, 24, 233–242. [Google Scholar] [CrossRef]
- Hazlett, R.D. Statistical characterization and stochastic modeling of pore networks in relation to fluid flow. Math. Geol. 1997, 29, 801–822. [Google Scholar] [CrossRef]
- Keehm, Y.; Mukerji, T.; Nur, A. Permeability prediction from thin sections: 3D reconstruction and Lattice-Boltzmann flow simulation. Geophys. Res. Lett. 2004, 31, L04606. [Google Scholar] [CrossRef]
- Okabe, H.; Blunt, M.J. Prediction of permeability for porous media reconstructed using multiple-point statistics. Phys. Rev. E 2004, 70, 066135. [Google Scholar] [CrossRef] [Green Version]
- Wu, K.J.; Nunan, N.; Crawford, J.W.; Young, I.M.; Ritz, K. An efficient Markov chain model for the simulation of heterogeneous soil structure. Soil Sci. So. Am. J. 2004, 68, 346–351. [Google Scholar] [CrossRef]
- Bakke, S.; Øren, P.E. 3-D pore-scale modelling of sandstones and flow simulations in the pore networks. SPE J. 1997, 2, 136–149. [Google Scholar] [CrossRef]
- Biswal, B.; Manwart, C.; Hilfer, R.; Bakke, S.; Øren, P.E. Quantitative analysis of experimental and synthetic microstructures for sedimentary rock. Phys. A 1999, 273, 452–475. [Google Scholar] [CrossRef] [Green Version]
- Jin, G.; Patzek, T.W.; Silin, D.B. Physics-based reconstruction of sedimentary rocks. In Proceedings of the SPE Western Regional/AAPG Pacific Section Joint Meeting, Long Beach, CA, USA, 19–24 May 2003; Society of Petroleum Engineers: Long Beach, CA, USA, 2003. [Google Scholar]
- Zhu, W.; Yu, W.H.; Chen, Y. Digital core modeling from irregular grains. J. Appl. Geophys. 2012, 85, 37–42. [Google Scholar] [CrossRef]
- Li, X.B.; Luo, M.; Liu, J.P. Fractal characteristics based on different statistical objects of process-based digital rock models. J. Pet. Sci. Eng. 2019, 179, 19–30. [Google Scholar] [CrossRef]
- Liu, X.F.; Sun, J.M.; Wang, H.T. Numerical simulation of rock electrical properties based on digital cores. Appl. Geophys. 2009, 6, 1–7. [Google Scholar] [CrossRef]
- Yao, J.; Wang, C.C.; Yang, Y.F.; Hu, R.R.; Wang, X. The construction of carbonate digital rock with hybrid superposition method. J. Pet. Sci. Eng. 2013, 110, 263–267. [Google Scholar] [CrossRef]
- Bryant, S.; Blunt, M. Prediction of relative permeability in simple porous media. Phys. Rev. A 1992, 46, 2004–2011. [Google Scholar] [CrossRef]
- Øren, P.E.; Bakke, S. Process based reconstruction of sandstones and prediction of transport properties. Transp. Porous Media 2002, 46, 311–343. [Google Scholar] [CrossRef]
- Radlinski, A.P.; Ioannidis, M.A.; Hinde, A.L.; Hainbuchner, M.; Baron, M.; Rauch, H.; Kline, S.R. Angstrom-to-millimeter characterization of sedimentary rock microstructure. J. Colloid Interf. Sci. 2004, 274, 607–612. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Les Objets Fractals: Forme, Hasard Et Dimension; Flammarion: Paris, France, 1975. [Google Scholar]
- Hansen, J.P.; Skjeltorp, A.T. Fractal pore space and rock permeability implications. Phys. Rev. B 1988, 38, 2635–2638. [Google Scholar] [CrossRef]
- Roy, A.; Perfect, E.; Dunne, W.M.; McKay, L.D. Fractal characterization of fracture networks: An improved box-counting technique. J. Geophys. Res. Solid Earth 2007, 112, B12201. [Google Scholar] [CrossRef]
- Wu, Z.H.; Zuo, Y.J.; Wang, S.Y.; Yi, T.S.; Chen, S.J.; Yu, Q.L.; Li, W.; Sunwen, J.B.; Xu, Y.F.; Wang, R.Y.; et al. Numerical simulation and fractal analysis of mesoscopic scale failure in shale using digital images. J. Pet. Sci. Eng. 2016, 145, 592–599. [Google Scholar] [CrossRef]
- Anovitz, L.M.; Cole, D.R.; Rother, G.; Allard, L.F.; Jackson, A.J.; Littrell, K.C. Diagenetic changes in macro- to nano-scale porosity in the St. Peter Sandstone: An (ultra) small angle neutron scattering and backscattered electron imaging analysis. Geochim. Cosmochim. Acta 2013, 102, 280–305. [Google Scholar] [CrossRef]
- Li, P.; Zheng, M.; Bi, H.; Wu, S.T.; Wang, X.R. Pore throat structure and fractal characteristics of tight oil sandstone: A case study in the Ordos Basin, China. J. Pet. Sci. Eng. 2017, 149, 665–674. [Google Scholar] [CrossRef]
- Krohn, C.E. Fractal measurements of sandstones, shales, and carbonates. J. Geophys. Res.: Solid Earth 1988, 93, 3297–3305. [Google Scholar] [CrossRef]
- Vega, S.; Jouini, M.S. 2D multifractal analysis and porosity scaling estimation in Lower Cretaceous carbonates. Geophysics 2015, 80, D575–D586. [Google Scholar] [CrossRef]
- Liu, K.Q.; Ostadhassan, M. Multi-scale fractal analysis of pores in shale rocks. J. Appl. Geophys. 2017, 140, 1–10. [Google Scholar] [CrossRef]
- Tao, G.L.; Zhang, J.R. Two categories of fractal models of rock and soil expressing volume and size-distribution of pores and grains. Chin. Sci. Bull. 2009, 54, 4458–4467. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.R.; Tao, G.L.; Huang, L.; Yuan, L. Porosity models for determining the pore-size distribution of rocks and soils and their applications. Chin. Sci. Bull. 2010, 55, 3960–3970. [Google Scholar] [CrossRef]
- Dathe, A.; Thullner, M. The relationship between fractal properties of solid matrix and pore space in porous media. Geoderma 2005, 129, 279–290. [Google Scholar] [CrossRef]
- Yu, B.M.; Cai, J.C.; Zou, M.Q. On the physical properties of apparent two-phase fractal porous media. Vadose Zone J. 2009, 8, 177–186. [Google Scholar] [CrossRef]
- Chen, X.J.; Yao, G.Q.; Cai, J.C.; Huang, Y.T.; Yuan, X.Q. Fractal and multifractal analysis of different hydraulic flow units based on micro-CT images. J. Nat. Gas Sci. Eng. 2017, 48, 145–156. [Google Scholar] [CrossRef]
- Liu, P.; Ju, Y.; Gao, F.; Ranjith, P.G.; Zhang, Q.B. CT identification and fractal characterization of 3-D propagation and distribution of hydrofracturing cracks in low-permeability heterogeneous rocks. J. Geophys. Res.: Solid Earth 2018, 123, 2156–2173. [Google Scholar] [CrossRef]
- Su, P.H.; Xia, Z.H.; Wang, P.; Ding, W.; Hu, Y.P.; Zhang, W.Q.; Peng, Y.J. Fractal and multifractal analysis of pore size distribution in low permeability reservoirs based on mercury intrusion porosimetry. Energies 2019, 12, 1337. [Google Scholar] [CrossRef] [Green Version]
- Cai, J.C.; Xia, Y.X.; Lu, C.; Bian, H.; Zou, S.M. Creeping microstructure and fractal permeability model of natural gas hydrate reservoir. Mar. Pet. Geol. 2020, 115, 104282. [Google Scholar] [CrossRef]
- Dou, W.C.; Liu, L.F.; Jia, L.B.; Xu, Z.J.; Wang, M.Y.; Du, C.J. Pore structure, fractal characteristics and permeability prediction of tight sandstones: A case study from Yanchang Formation, Ordos Basin, China. Mar. Pet. Geol. 2021, 123, 104737. [Google Scholar] [CrossRef]
- Li, X.B.; Wei, W.; Wang, L.; Ding, P.B.; Zhu, L.Q.; Cai, J.C. A new method for evaluating the pore structure complexity of digital rocks based on the relative value of fractal dimension. Mar. Pet. Geol. 2022, 141, 105694. [Google Scholar] [CrossRef]
- Rahner, M.S.; Halisch, M.; Fernandes, C.P.; Weller, A.; dos Santos, V.S.S. Fractal dimensions of pore spaces in unconventional reservoir rocks using X-ray nano- and micro-computed tomography. J. Nat. Gas Sci. Eng. 2018, 55, 298–311. [Google Scholar] [CrossRef]
- Lopes, R.; Betrouni, N. Fractal and multifractal analysis: A review. Med. Image Anal. 2009, 13, 634–649. [Google Scholar] [CrossRef]
- Bird, N.; Diaz, M.C.; Saa, A.; Tarquis, A.M. Fractal and multifractal analysis of pore-scale images of soil. J. Hydrol. 2006, 322, 211–219. [Google Scholar] [CrossRef]
- Tang, H.P.; Wang, J.Z.; Zhu, J.L.; Ao, Q.B.; Wang, J.Y.; Yang, B.J.; Li, Y.N. Fractal dimension of pore-structure of porous metal materials made by stainless steel powder. Powder Technol. 2012, 217, 383–387. [Google Scholar] [CrossRef]
- Lee, B.H.; Lee, S.K. Effects of specific surface area and porosity on cube counting fractal dimension, lacunarity, configurational entropy, and permeability of model porous networks: Random packing simulations and NMR micro-imaging study. J. Hydrol. 2013, 496, 122–141. [Google Scholar] [CrossRef]
- Dathe, A.; Eins, S.; Niemeyer, J.; Gerold, G. The surface fractal dimension of the soil-pore interface as measured by image analysis. Geoderma 2001, 103, 203–229. [Google Scholar] [CrossRef]
- Peng, R.D.; Yang, Y.C.; Ju, Y.; Mao, L.T.; Yang, Y.M. Computation of fractal dimension of rock pores based on gray CT images. Chin. Sci. Bull. 2011, 56, 3346–3357. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.M.; Liu, Y.; Song, Y.C.; Zhao, Y.C.; Zhao, J.F.; Wang, D.Y. Fractal analysis and its impact factors on pore structure of artificial cores based on the images obtained using magnetic resonance imaging. J. Appl. Geophys. 2012, 86, 70–81. [Google Scholar] [CrossRef]
- Perfect, E.; Donnelly, B. Bi-phase box counting an improved method for fractal analysis of binary images. Fractals 2015, 23, 1540010. [Google Scholar] [CrossRef] [Green Version]
- Luo, M.; Glover, P.W.J.; Zhao, P.Q.; Li, D. 3D digital rock modeling of the fractal properties of pore structures. Mar. Pet. Geol. 2020, 122, 104706. [Google Scholar] [CrossRef]
- Roberts, J.N.; Schwartz, L.M. Grain consolidation and electrical conductivity in porous media. Phys. Rev. B 1985, 31, 5990–5997. [Google Scholar] [CrossRef]
- Pentland, A.P. Fractal-based description of natural scenes. IEEE Trans. Pattern Anal. Mach. Intell. 1984, 6, 661–674. [Google Scholar] [CrossRef]
- Peitgen, H.O.; Jürgens, H.; Saupe, D.; Feigenbaum, M.J. Chaos And Fractals: New Frontiers of Science; Springer: New York, NY, USA, 1992. [Google Scholar]
- Li, J.; Du, Q.; Sun, C.X. An improved box-counting method for image fractal dimension estimation. Pattern Recogn. 2009, 42, 2460–2469. [Google Scholar] [CrossRef]
- So, G.B.; So, H.R.; Jin, G.G. Enhancement of the box-counting algorithm for fractal dimension estimation. Pattern Recogn. Lett. 2017, 98, 53–58. [Google Scholar] [CrossRef]
- Foroutan-pour, K.; Dutilleul, P.; Smith, D.L. Advances in the implementation of the box-counting method of fractal dimension estimation. Appl. Math. Comput. 1999, 105, 195–210. [Google Scholar] [CrossRef]




| Literature | Time | Material Object | Fractal Dimension | Influence Factor |
|---|---|---|---|---|
| [54] | 2001 | 2D image of soil | Surface | Image size and box size |
| [41] | 2005 | 2D image of porous structure | Matrix and pore | Mass fraction of matrix and pore |
| [42] | 2009 | 2D image of porous structure | Skeleton and pore | Porosity |
| [55] | 2011 | CT image of rock | Pore | Porosity |
| [56] | 2012 | MRI image of artificial core | Pore | Box size, threshold, resolution, and porosity |
| [53] | 2013 | 3D image of sand packing | Pore | Porosity and specific surface area |
| [57] | 2015 | 2D image of soil | Mass and pore | Mass fraction |
| [37] | 2015 | 2D image of carbonatite | Pore and multifractal | Porosity scaling |
| [24] | 2019 | Process-based model | Solid, pore, and interface | Porosity and complexity of pore structure |
| [58] | 2020 | Process-based model | Pore and interface | Porosity and specific surface area |
| Model A (Sedimentation) | Model B (Compaction) | Model C (Cementation) | ||||||
|---|---|---|---|---|---|---|---|---|
| No. | Particle Size (μm) | Porosity | No. | λ | Porosity | No. | β | Porosity |
| A1 | 100 | 0.3778 ± 0.0042 | B1 | 0 | 0.3755 ± 0.0029 | C1 | 0 | 0.3755 ± 0.0029 |
| A2 | 100,90 | 0.3840 ± 0.0044 | B2 | 0.02 | 0.3506 ± 0.0024 | C2 | 0.01 | 0.3382 ± 0.0027 |
| A3 | 100,90,80 | 0.3785 ± 0.0028 | B3 | 0.04 | 0.3257 ± 0.0025 | C3 | 0.02 | 0.3020 ± 0.0028 |
| A4 | 100,…,70 | 0.3780 ± 0.0028 | B4 | 0.06 | 0.3009 ± 0.0024 | C4 | 0.03 | 0.2672 ± 0.0028 |
| A5 | 100,…,60 | 0.3755 ± 0.0029 | B5 | 0.08 | 0.2764 ± 0.0025 | C5 | 0.04 | 0.2341 ± 0.0029 |
| A6 | 100,…,50 | 0.3707 ± 0.0019 | B6 | 0.10 | 0.2524 ± 0.0026 | C6 | 0.05 | 0.2028 ± 0.0029 |
| A7 | 100,…,40 | 0.3680 ± 0.0020 | B7 | 0.12 | 0.2287 ± 0.0027 | C7 | 0.06 | 0.1737 ± 0.0029 |
| A8 | 100,…,30 | 0.3643 ± 0.0032 | B8 | 0.14 | 0.2045 ± 0.0026 | C8 | 0.07 | 0.1470 ± 0.0028 |
| B9 | 0.16 | 0.1806 ± 0.0025 | C9 | 0.08 | 0.1229 ± 0.0027 | |||
| B10 | 0.18 | 0.1571 ± 0.0025 | C10 | 0.09 | 0.1016 ± 0.0026 | |||
| B11 | 0.20 | 0.1345 ± 0.0023 | C11 | 0.10 | 0.0829 ± 0.0024 | |||
| B12 | 0.22 | 0.1129 ± 0.0021 | C12 | 0.11 | 0.0667 ± 0.0023 | |||
| B13 | 0.24 | 0.0924 ± 0.0019 | C13 | 0.12 | 0.0529 ± 0.0021 | |||
| B14 | 0.26 | 0.0732 ± 0.0015 | C14 | 0.13 | 0.0412 ± 0.0017 | |||
| B15 | 0.28 | 0.0559 ± 0.0013 | C15 | 0.14 | 0.0315 ± 0.0014 | |||
| Model | Fractal Phase | Curve No. | Fitting Formula | R2 |
|---|---|---|---|---|
| Compaction | Pore | ➀ | FD = 0.8617 ϕn + 2.4569 | 0.9917 |
| ➁ | FD = 0.2541 ln(ϕn) + 3.0318 | 0.9999 | ||
| Surface | ➂ | FD = 0.3826 ϕn + 2.3908 | 0.9635 | |
| ➃ | FD = 0.1861 ln(ϕn) + 2.7697 | 0.9982 | ||
| Cementation | Pore | ➀ | FD = 0.8851 ϕn + 2.4483 | 0.9902 |
| ➁ | FD = 0.2671 ln(ϕn) + 3.0498 | 0.9999 | ||
| Surface | ➂ | FD = 0.4313 ϕn + 2.3732 | 0.9538 | |
| ➃ | FD = 0.2169 ln(ϕn) + 2.8132 | 0.9992 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Wei, W.; Wang, L.; Cai, J. Fractal Dimension of Digital 3D Rock Models with Different Pore Structures. Energies 2022, 15, 7461. https://doi.org/10.3390/en15207461
Li X, Wei W, Wang L, Cai J. Fractal Dimension of Digital 3D Rock Models with Different Pore Structures. Energies. 2022; 15(20):7461. https://doi.org/10.3390/en15207461
Chicago/Turabian StyleLi, Xiaobin, Wei Wei, Lei Wang, and Jianchao Cai. 2022. "Fractal Dimension of Digital 3D Rock Models with Different Pore Structures" Energies 15, no. 20: 7461. https://doi.org/10.3390/en15207461
APA StyleLi, X., Wei, W., Wang, L., & Cai, J. (2022). Fractal Dimension of Digital 3D Rock Models with Different Pore Structures. Energies, 15(20), 7461. https://doi.org/10.3390/en15207461







