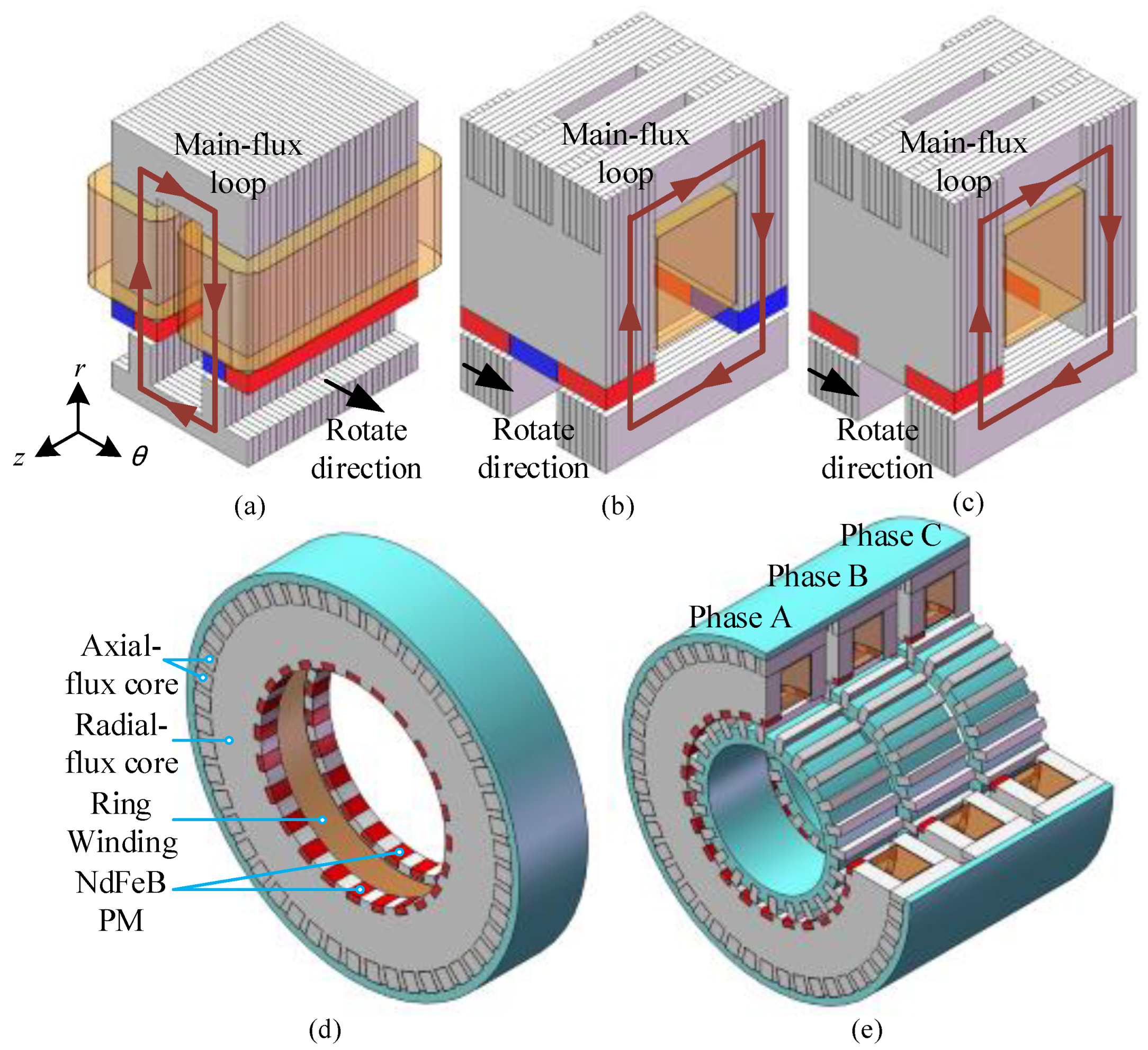
1. Introduction
The direct-drive motor is a transmission device that directly converts electrical energy into motion/rotation machinery without any intermediate conversion mechanism. Due to the use of “zero transmission”, it has obvious advantages compared to the traditional transmission method, such as simple structure, no contact, no wear, low noise, fast speed, high accuracy, etc. It has been considered as a suitable solution for many applications such as urban rail transit, electrical vehicles, and ocean-wind power-generation equipment [
1,
2,
3,
4]. The various motor topologies that have been investigated for direct-drive applications are divided into radial-flux motors and transverse-flux motors. Due to the direct competitive relationship between electrical load and magnetic load, it is difficult to further increase the torque density of radial-flux motors; thus, the transverse-flux motor becomes one of the most important research objects.
The main magnetic-flux path in transverse magnetic-flux motors is distributed in the plane that is perpendicular to the movement direction [
5]. This feature alleviates the opposition between the electric charge and the magnetic charge in the motor, making the transverse magnetic-flux motor have the advantages of high torque density and high-phase/multi-phase design feasibility [
6]. Several transverse-flux motor topologies have been proposed in the literature, such as the transverse-flux permanent-magnet synchronous motor (TFPM) [
7], the transverse-flux reluctance motor (TFRM) [
8] and the passive-rotor transverse-flux permanent-magnet motor [
9]. Nevertheless, the previous transverse-flux motors have always faced the problem of a high manufacturing cost, which is caused by the complex motor structure and the large amount of expensive high-performance rare-earth permanent magnets. For avoiding those shortcomings, a transverse-flux flux-reversal motor is proposed in [
10], which combines the technologies of the traditional flux-reversal motor [
11] and the transverse-flux motor. Both the stator and rotor of the TF-FRM can be fabricated using silicon steel sheet, which simplifies the manufacturing of the core; meanwhile, the total volume of the PMs used in the TF-FRM is less, while the provided torque density is considerable [
12].
In this paper, a transverse-flux flux-reversal motor with consequent-pole configuration (TF-CFRM) is proposed based on the foregoing TF-FRM, which can further reduce the volume of the PMs and provide high torque density. Firstly, the basic structure and running working principle are introduced. Secondly, the analytical expression of the electromagnetic torque is derived from a 3D-equivalent magnetic-circuit model. Then, the preliminary optimization of the key structural dimensions is done by the finite element method. Finally, the electromagnetic performances, e.g., torque performance, overload capability, and power factor, are analyzed by 3D FEM, and the results of the proposed TF-CFRM are compared with other transverse-flux motor topologies and a 2D flux-reversal motor.
3. Preliminary Analysis of TF-CFRM by 3D-Equivalent Magnetic-Circuit Model
A 3D-equivalent magnetic-circuit model is built for preliminary analysis of the TF-CFRM. Since the magnetic field of different phases of the TF-CFRM are decoupled, and the model has a periodicity along rotational direction, the magnetic-circuit model of the fundamental analysis unit, under two pole pitch, is built for simplifying the calculation.
The 3D-equivalent magnetic-circuit model of the TF-CFRM is shown in
Figure 3. There are two magneto-motive force (MMF) sources in the model:
Fm is the response to the MMF of the PM, and F
i is the response to the MMF of the armature winding.
Rδ1 and
Rδ2 are the air-gap reluctance under two poles;
Rm is the inner reluctance of the PMs;
Rst1-4 are the reluctances of the stator radial magnetic-flux cores, respectively;
Rsy is the reluctance of the stator axial magnetic-flux core;
Rr1 and
Rr2 are the reluctances of the rotor cores;
Rσs and
Rσc are the leakage flux reluctance of the stator radial magnetic-flux core and the leakage flux reluctance in the circumferential direction, respectively.
Then, the loop equations and node equations of the magnetic circuit can be obtained as follows:
where
Φm1 and
Φm2 are the total magnetic flux;
Φδ1 and
Φδ2 are the main magnetic flux of winding;
Φσc1 and
Φσc2 are the leakage flux along the circumferential direction.
Since the permeability of the core material is considerably larger than that of the air and PM when the cores are not in high-saturation status, the reluctances of the radial magnetic-flux core, axial magnetic-flux core, and rotor core can be neglected in calculation, for simplification.
As shown in
Figure 4, the red graphic area is the permanent-magnet reluctance, and the reluctance of the magnet is calculated as:
where
hm is the thickness of the PM,
μ0 is the vacuum permeability,
μr is the PM material’s relative permeability,
lpm is the circumferential length of the PM, and
lt is the axial length of the radial-flux core.
The narrow blank area between the rotor core and the PMs references the air-gap magnetoresistance,
Rδ1, which can be expressed as:
where
lrt is the circumferential length of the rotor core.
The quarter-arc section area references the air gap magnetoresistance,
Rδ2, which can be defined as:
where
τpm is the pole pitch of the motor.
Meanwhile, the leakage flux reluctance in the circumferential direction,
Rσc, can be defined as:
When there is non-pass current applied into the winding, the MMF of the armature winding,
Fi, is equal to zero, and the total main magnetic flux excited by the PM can be expressed as:
where
, and
.
As the reluctance of the air gap and the leakage flux reluctance are variables about the relative location between the rotor and stator, the value of the PM flux is a periodic variable, which can be written as:
where
Φ0 is the amplitude of PM main flux, which can be calculated when the reluctance is chosen as the values under the aligned position (where the center position of the PM is aligned to the center position of the rotor core), and ω = 2πf is the electrical angle.
According to Faraday’s law of electromagnetic induction, the expression of single-phase back EMF is:
where
j is the number of fundamental analysis unit along circumferential direction,
N is the number of turns for the winding, and
E0 is the root mean square (RMS) of the back EMF.
When a sinusoidal current is added into the winding under the control method of
id = 0, the single-phase electromagnetic torque can be expressed as:
where Ω is the mechanical rotate speed,
I is the RMS of the phase current, and
p is the pole-pair number.
Similarly, the electromagnetic torque of the other two phases can be obtained, and the total electromagnetic torque of the TF-CFRM can be divided as:
4. Influence of Key Dimensions on Torque Density of TF-CFRM
At present, there are two methods of analysis on the internal magnetic field of the motor: one is the analysis method (including the equivalent magnetic-circuit method, the magnetic-network method, etc.), and the other is the numerical method (the finite element method). Since the foregoing magnetic circuit of the TF-CFRM is built under several assumptions, the accuracy of the analysis method is comparatively low. In order to accurately calculate the performance of the motor, the finite element analysis of the transverse magnetic motor often adopts the three-dimensional finite element method. This method can consider the leakage flux of the magnet and the saturation of the iron core. In order to reduce the calculation time and increase the calculation speed of the finite element, the original model calculates the simulation of the three-dimensional finite element model with a basic analysis unit, and the calculation result of the entire motor can be obtained by adding the cycle-boundary condition. The basic dimensions and materials of the TF-CFRM used for analysis are shown in
Table 1.
The torque density is a key parameter to measure the characteristic of direct-drive motors. In this section, the influence of some dimensions on the torque density of the TF-CFRM is investigated. From the expression of electromagnetic torque, if the parameters of electrical load are selected, the value of torque is influenced by the reluctances of the main flux loop, the reluctances of the leakage flux loop, and the MMF of the PMs. Since the circumferential length of the PMs, lpm; the thickness of the PMs, hpm; and the circumferential length of rotor core, lrt, influence the reluctances and the MMF of the PM significantly, they are chosen as the object parameters to be investigated.
The influences of the PM dimensions on torque density are shown in
Figure 5. From the results, when the circumferential length of the PM is irrespective, and the thickness of the PM is variable, the torque density increases with the increasing of
hpm; when the value of
hpm is small, then it decreases with the increasing of
hpm. That is in accordance with the fact that the main flux loop’s reluctance is increased along with the PM’s MMF, when the thickness of the PM is added. The optimal value range of
hpm is 3–3.5 mm. Then, a ratio of
kpm =
lpm/
τpm is introduced, to correspond with the circumferential length of the PM, and the optimal value range of the ratio,
kpm, exists for a given ratio,
hpm, which generates the maximum torque density, with a range of 1.1–1.15.
Another factor affecting the gap magnetic resistance is the size of the rotor. Based on the optimization results of the stator PM dimensions, the influence of the circumferential length of the rotor core is analyzed when the PM dimensions are designed in the optimal range. Four typical combinations of PM dimensions are selected, e.g.,
hpm = 3.0 mm and
kpm = 1.10,
hpm = 3.0 mm and
kpm = 1.15,
hpm = 3.5 mm and
kpm = 1.10, and
hpm = 3.5 mm and
kpm = 1.15. A ratio,
krt =
lrt/
τpm, is also introduced to correspond with the circumferential length of the rotor core. As the results show in
Figure 6, when the ratio,
krt, is decreased from 1 to 0.4, the torque density is firstly increased and then decreased. The optimal values of
krt under different PM dimensions, to generate the maximum torque density, are all around 0.7. Then, the variable dimensions of the TF-CFRM are designed as
hpm = 3.5 mm,
kpm = 1.15, and
krt = 0.7 to achieve an optimal torque density.
5. Electromagnetic Performance Comparison among TF-CFRM, TF-FRM, and FRM
5.1. Torque Performance
The torque performance, such as the cogging torque, electromagnetic torque, and torque ripple of the TF-CFRM, are analyzed and compared with the TF-FRM and FRM by the finite element method. For fairness, all the models are designed to have the same stator outer diameter, rotor outer diameter, total axial length, and rated load current density for convenient comparison. Under the above comparison conditions, the rated load magnetic density distribution of the three types of motor-simulation models is shown in
Figure 7.
The torque waveforms of three motors are shown in
Figure 8: in the upper subfigure are the waveforms of cogging torques and in the lower subfigure are the waveforms of electromagnetic torques. The amplitude of cogging torque for the TF-CRFM is 0.77 N·m, which is 11.5% lower than that of the TF-FRM and 35.6% lower than that of the FRM. The average load torque of the TF-CFRM is 41.2 N·m, which is 4.8% larger than that of the TF-FRM and 5.9% higher than that of the FRM. Meanwhile, the torque ripple of the TF-CFRM under sinusoidal armature current is 3.6%, which is larger than the 3.1% of the FRM and the 2.4% of the TF-FRM. The larger total harmonic distortion of the TF-CFRM back EMF is what causes the bigger torque ripple.
The torque density per volume and force density per air-gap surface area of the TF-CFRM are also calculated and compared with some other transverse-flux motor topologies; the results are listed in
Table 2. As shown, the torque density per volume of the proposed TF-CFRM is 10.75 kN·m/m
3, which is 4.7% larger than that of the TF-FRM, 5.8% larger than that of the FRM, and 1.2% lower than that of the TFPM; the force density per air-gap surface area of the TF-CFRM is 1.35 N/cm
2, which is similar to the 1.29 N/cm
2 of the TF-FRM and the 1.27 N/cm
2 of the FRM, but 36.6% lower than that of the TFPM. However, the total volume of the PMs used in the TF-CFRM is only 67.3% of the TF-FRM, 23.1% of the TFPM, and 49.8% of the FRM, which shows a greater cost-to-performance ratio of the proposed TF-CFRM than that of those existing machines.
5.2. Overload Capability
Direct-drive motors are frequently operated in short-time high-overload operation mode, for example, startup, emergency acceleration and deceleration, etc. Therefore, this subsection presents a finite element analysis of the overload capability of the three types of stator permanent-magnet motors. The torque output capability of the TF-CFRM, TF-FRM, and FRM under an overload state are shown in
Figure 9.
When the armature current is small, the torque of all motors increases linearly with the current amplitude. Among the three kinds of motors, the torque of the TF-CFRM is slightly higher than that of the TF-FRM and FRM. Then, with the proportional increase in armature current, the TF-CFRM firstly falls into saturation, and its linear interval is shortest, while the TF-FRM and FRM can maintain a larger linear interval. When the armature current reaches three times the rated load, the torque of the TF-CFRM is 1.54 times that of the rated torque, while the TF-FRM and FRM are up to 2.25 and 2.38 times that of the rated torque, respectively.
The reason for this phenomenon is that only half of the equivalent air gap in the TF-CFRM is the sum of the permanent magnet and mechanical air gap, and the other half is only a mechanical air gap, which makes the comprehensive equivalent air gap of the TF-CFRM be thinner than that of the TF-FRM and FRM. Meanwhile, the armature-reaction magnetic field in the TF-CFRM is larger, and the armature magnetic flux directly path through the stator core into the rotor core. Thus, the cores of the TF-CFRM prefer to enter the saturation state easily, and the overload capability is limited.
In addition, the permanent magnet will be strongly demagnetized by the armature-reaction magnetic field under the overload state, so it is necessary to analyze the magnetic-density-distribution characteristics of the permanent magnet in the motor under an overload current. According to the material characteristic of NdFeB permanent magnet, when the motor is working under normal temperature (20 °C), the demagnetization curve and recovery line are both straight lines. The knee point for irreversible demagnetization is located in the third quadrant, and the permanent magnet is hardly dropped when in irreversible demagnetization danger. However, the overload current always leads to a larger copper loss and serious heating phenomenon, the permanent magnet may be worked under high temperature, and the knee point for irreversible demagnetization moves to the second quadrant [
14,
15,
16]. To roughly evaluate the antidemagnetization ability of the motors, the temperature is predicted as 100 °C, when the knee point is around 0.2 T, as shown in
Figure 10. In addition, the reference value of dangerous demagnetization is selected as 0.3 T, with few margins, during FEM analysis.
The magnetic density distributions of the permanent magnets in the TF-CFRM, TF-FRM, and FRM under three times the overload current are shown as
Figure 11. In the view of a single demagnetized permanent magnet, the volume of the dangerous area of the TF-CFRM, in which the magnetic density is lower than 0.3 T, accounts for nearly 26.71% of the total volume. This data is between the 16.71% of the TF-FRM and the 34.51% of the FRM.
It is obvious that the proportion of the dangerous regions in the demagnetized permanent magnets of the FRM is the highest. However, only a few permanent magnets in the FRM are severely demagnetized in the same moment, and the percentage of severely demagnetized permanent magnets in the TF-FRM and TF-CFRM is half. In general, the permanent magnet in the transverse-flux motor seems to face a higher risk of demagnetization, which means the transverse-flux motor is more suitable to be designed for applications with fewer overload working modes.
5.3. Power Factor (PF)
As is known, the transverse-flux motor owns the advantage of a high torque density and faces the disadvantage of a low PF. Therefore, the PF of three motors, TF-CFRM, TF-FRM, and FRM, was analyzed. Under the conditions of the same dimensions, the same current density, the same terminal voltage, and Id = 0 control, the PF of the TF-CFRM is only 0.30, which is 0.08 lower than that of the TF-FRM and 0.15 lower than that of the FRM. This shows that the PF of the TF-CFRM proposed in this article is only slightly lower than that of the TF-FRM, but the PF of those two types of transverse-flux motors is lower than that of the FRM and obviously lower than that of the typical PMSM and BLDC. It means that, when the same mechanical power is output, the TF-CFRM and TF-FRM will put forward higher requirements for the power level of the inverter hardware.
What should be mentioned here is that the PF discussed in this section is calculated with the Id = 0 method, according to the phasor schematic diagram of PF, which belongs to the machine itself, as the cosine value between the fundamental terminal-voltage wave and the standard sinusoidal phase-current wave. Since the motor can be driven by an inverter similar to a typical PMSM, with some advanced control algorithms, the total power factor presented to the grid side will be improved, which is one of the research priorities in our future work.
5.4. Efficiency
The output power of the proposed TF-CFRM, under different rotation speeds, is shown in
Figure 12; the rated power is designed as 2.2 kW.
For comparison, the loss and efficiencies of the three types of motors under the rated point are also analyzed by FEM. As shown in
Figure 13, the copper-loss value of the TF-CFRM and TF-FRM is 221.73 W, which is 32.2% lower than that of the FRM; the core loss value of the TF-CFRM is 98.27 W, which is 1.73 times that of the TF-FRM and similar to that of the FRM; the PM’s eddy loss of the TF-CFRM is 3.94 W, which is 81.74% of that of the TF-FRM and 13.14% of that of the FRM. When the mechanical loss is ignored, the efficiency of the TF-CFRM is 87.15%, and that of the other two machines is 87.83% and 81.92%, respectively. It can be seen that, under the designed rated point, the copper loss is the largest component among the three motors; although the core loss of the TF-CFRM is larger, the PM’s eddy loss and copper loss are lower. Meanwhile, the proposed TF-CFRM can provide an appreciable efficiency by using fewer permanent-magnet materials, when compared with the TF-FRM and typical FRM.
6. Conclusions
A transverse-flux flux-reversal motor with consequent-pole configuration is introduced in this paper. The expression of electromagnetic torque is derived from an equivalent magnetic-circuit model. The influences of the key dimensions on torque density are investigated by the finite element method; the optimal value of thickness of the PM, hpm; the ratio of the circumferential length of the PM to the pole pitch, kpm; and the ratio of the circumferential length of the rotor core to the pole pitch, krt, are 3.5 mm, 1.15, and 0.7, respectively, which provide useful information for the future design process. The torque performance of the proposed motor is analyzed and compared with the foregoing TF-FRM, FRM, and TFPM topologies in the literature. The torque density per volume of the TF-CFRM is 10.75 kN·m/m3 when the RMS current density is 5 A/mm2, which is similar to that of the TF-FRM and FRM. In addition, the efficiency of the proposed TF-CFRM is 87.15%, which is similar to that of the TF-FRM and a higher percentage than that of the FRM. Meanwhile, the total volume of the PMs used in the TF-CFRM is 67.3% of that of the TF-FRM and 49.8% of that of the FRM. Since most of the cost in permanent-magnet-motor manufacturing is occupied by the permanent magnet, it means that the TF-CFRM is a comprehensive solution that directly drives the motor, which can reduce budget costs and provide appreciable torque density and efficiency.
Aside from the low machine-manufacturing cost and high-torque-density advantages, the TF-CFRM faces several shortcomings, such as a weak torque-overload capacity (1.54 times the output torque with three times the overload current) and low power factor (0.30 in the example). These disadvantages will limit the application scenarios of the TF-CFRM, while slightly increasing the hardware cost of the supporting inverter control part. How to break through these shortcomings and expand the applicability and cost-effective advantage of the TF-CFRM will be key for research work in the future.