Shape Optimization of Oscillating Buoy Wave Energy Converter Based on the Mean Annual Power Prediction Model
Abstract
:1. Introduction
2. Methodology
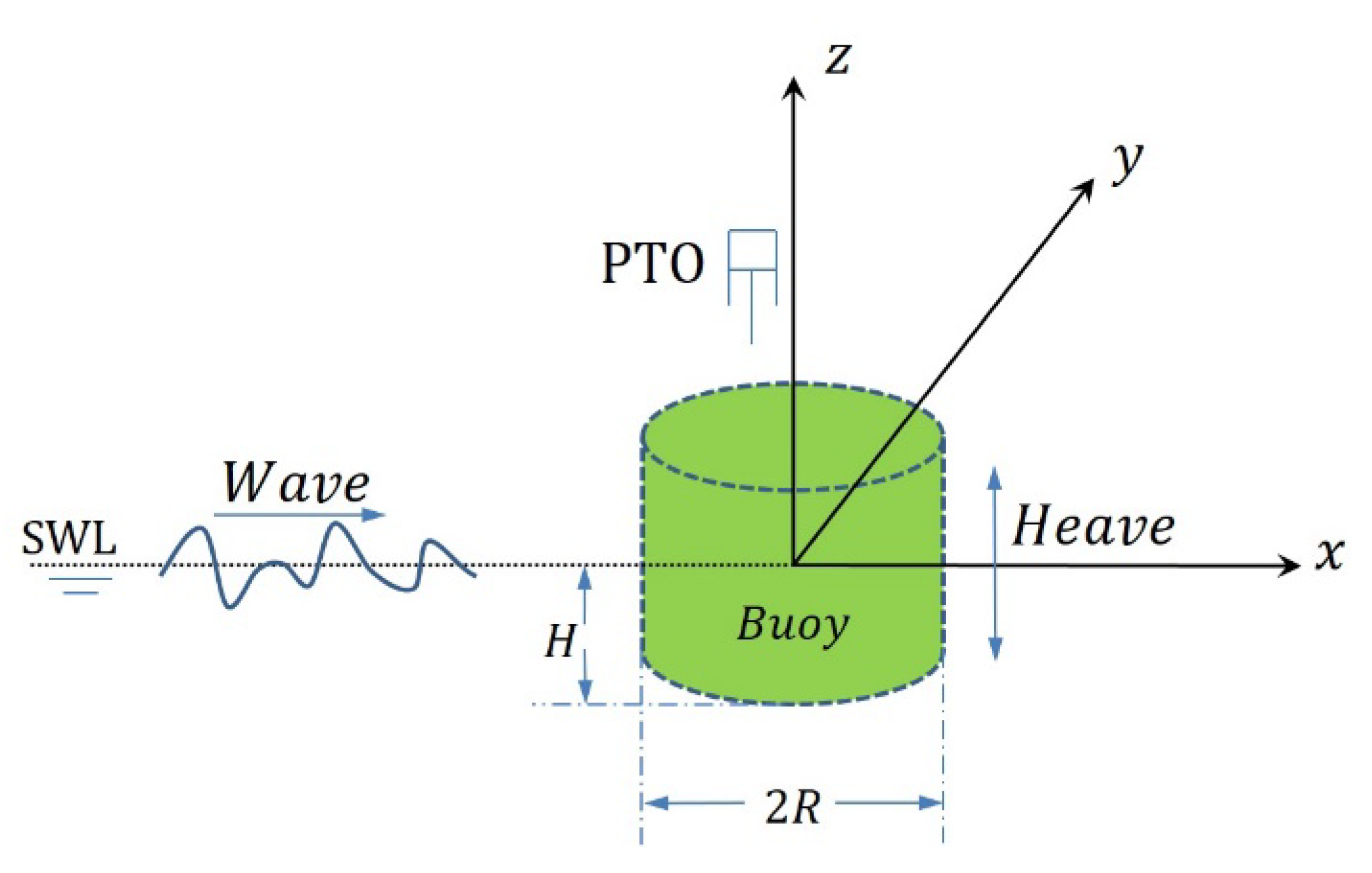
2.1. Geometric Model
2.2. Mean Annual Power
2.3. Prediction Model Method
2.3.1. Response Surface Method
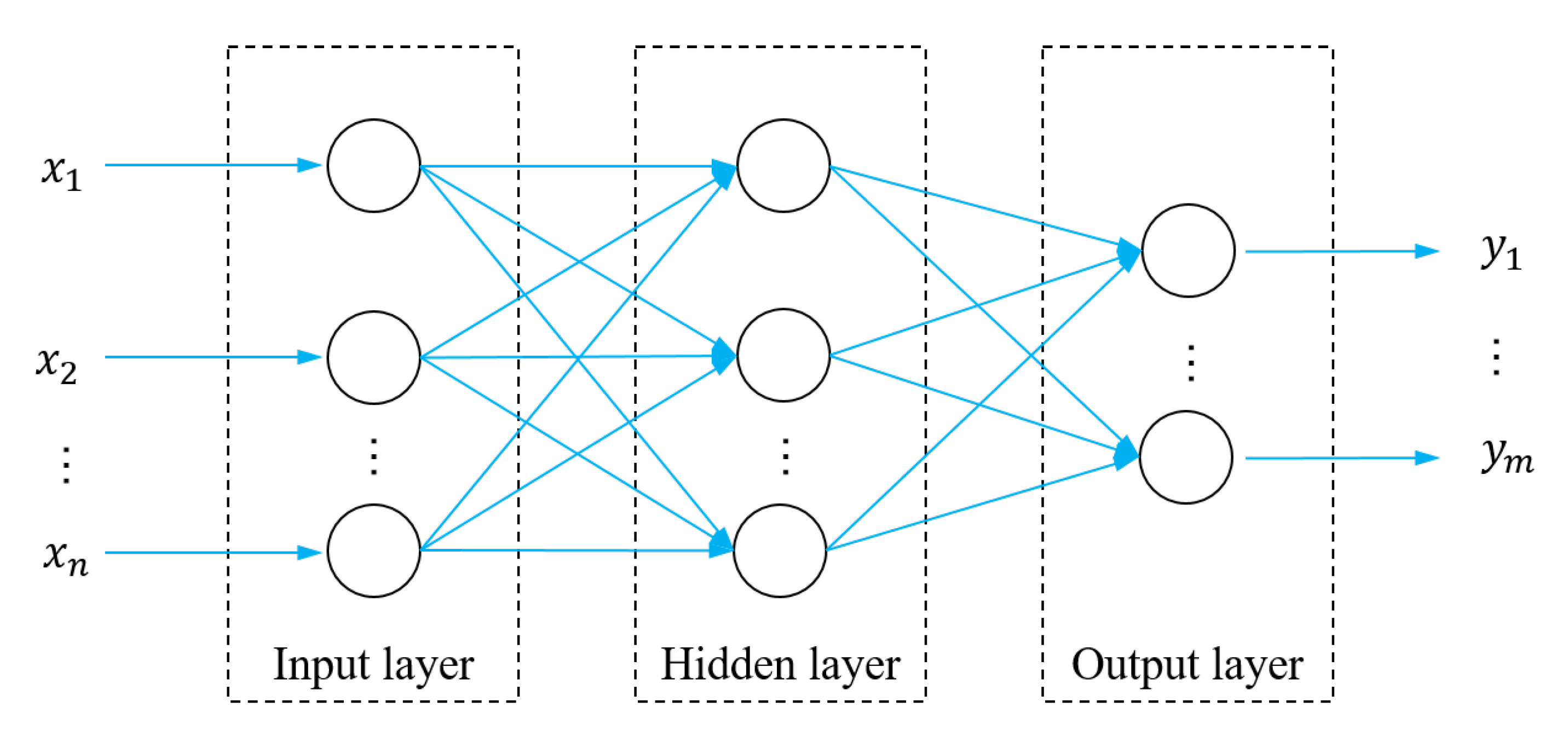
2.3.2. Radial Basis Functions Neural Network
2.3.3. Elliptical Basis Functions Neural Network
2.3.4. Error Analysis
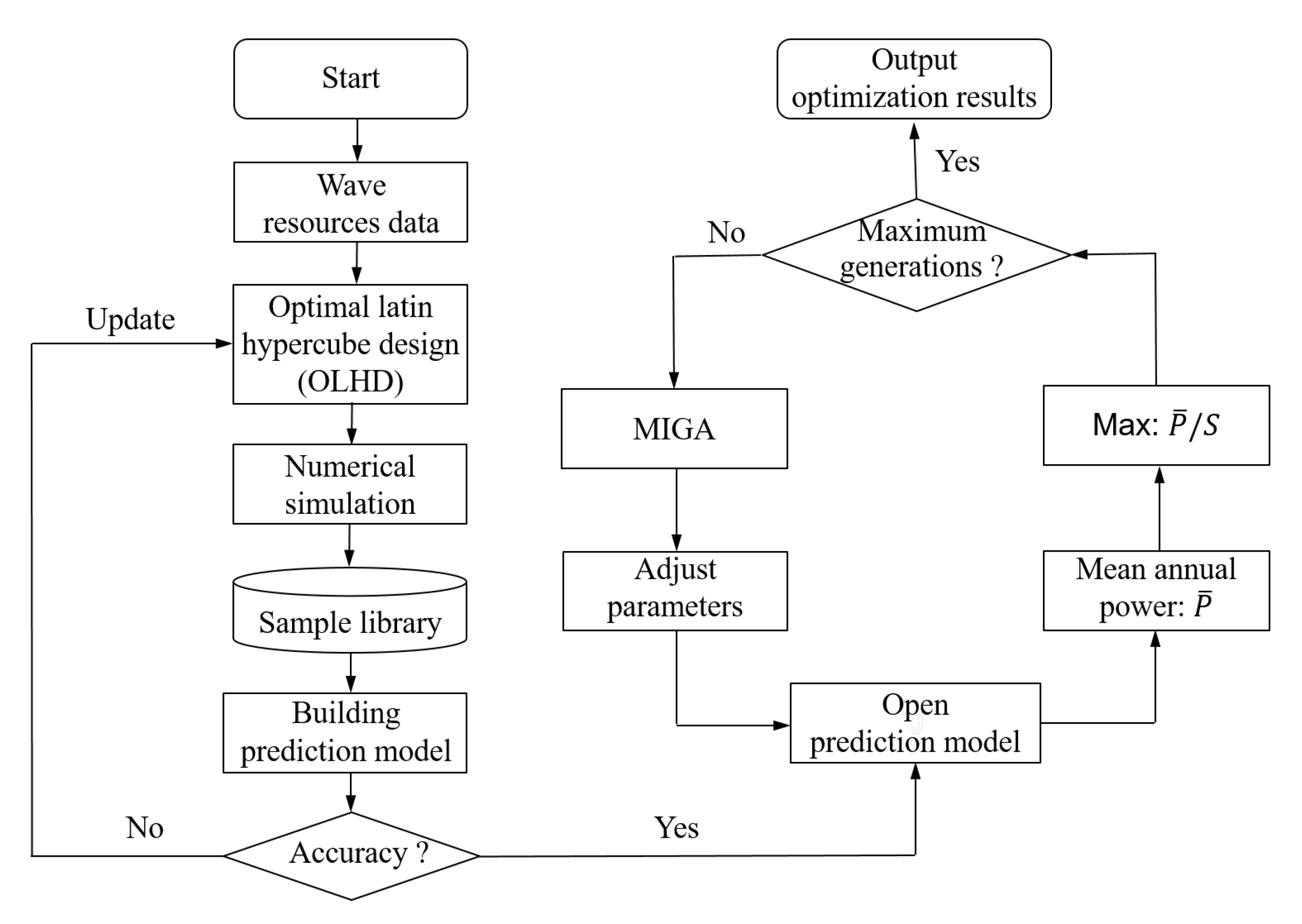
2.4. Optimization Algorithms and Processes
3. Building and Testing Prediction Models
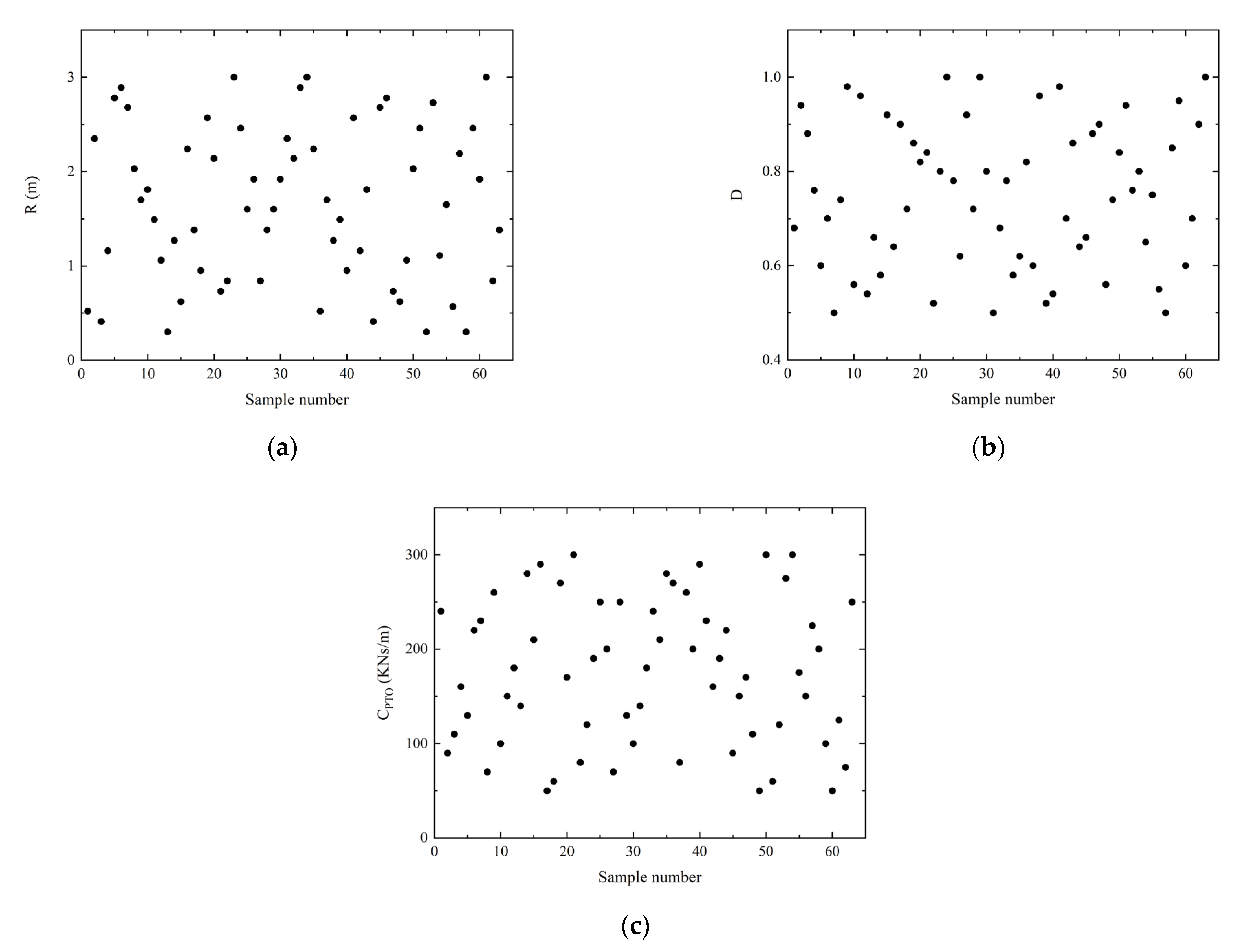
3.1. Sample Library
3.1.1. Determining the Design Space
- (1)
- The diameter of buoy is preferably 5–10% of the main wavelength [37]. Therefore, the value range of the buoy diameter can be expressed as follows:
- (2)
- In order to ensure the rationality of the buoy shape, the draft of the buoy is normalized, which is expressed as D = H/R. The value range of D can be expressed as follows:
- (3)
- The traditional design method for the PTO system damping is based on the spectral peak frequency resonance, which leads to low energy capturing efficiency [20]. Therefore, the global search method is used to find the optimal PTO system damping which matches the wave resources. The value range of CPTO can be expressed as follows:
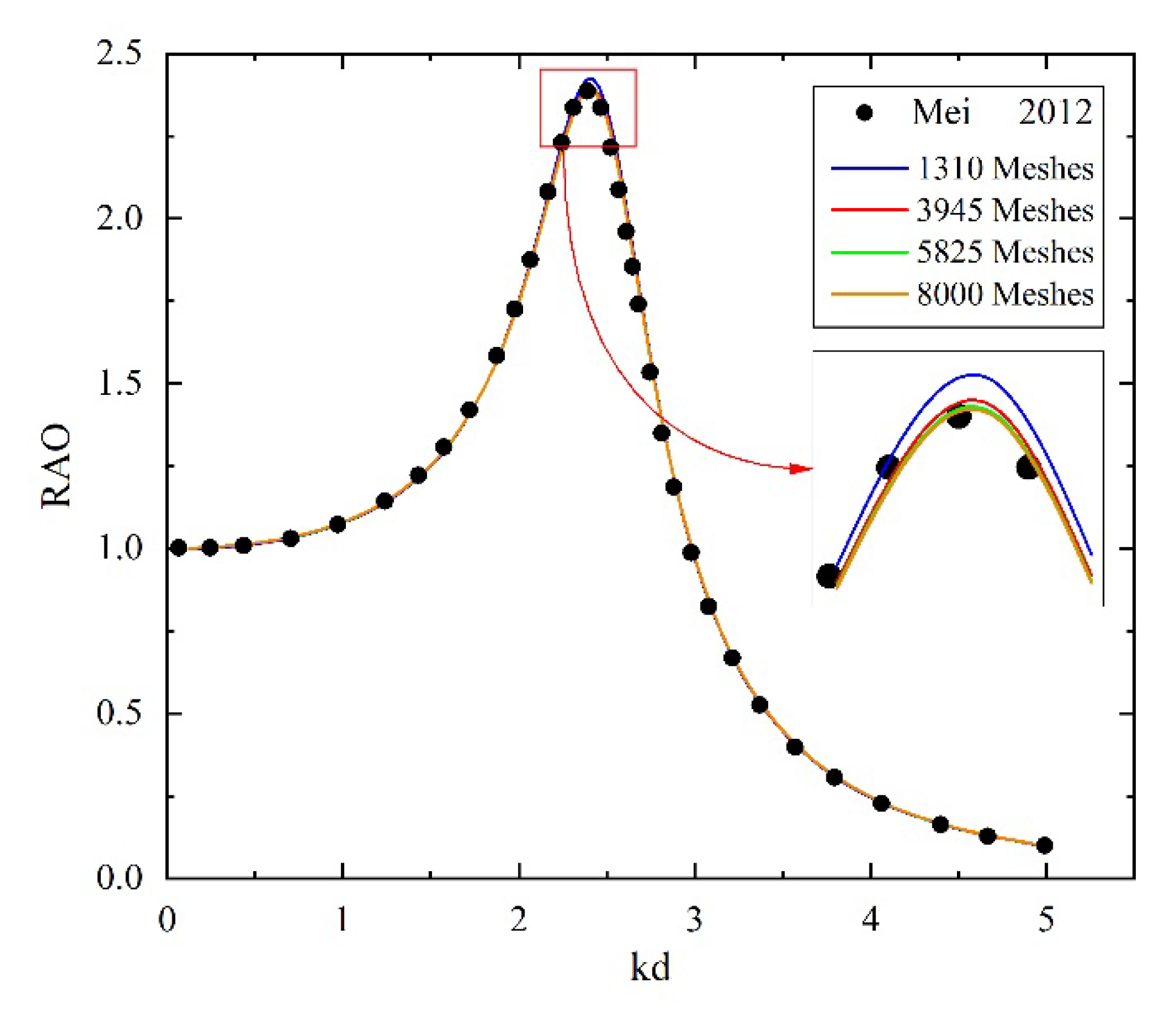
3.1.2. Hydrodynamic Calculation Verification
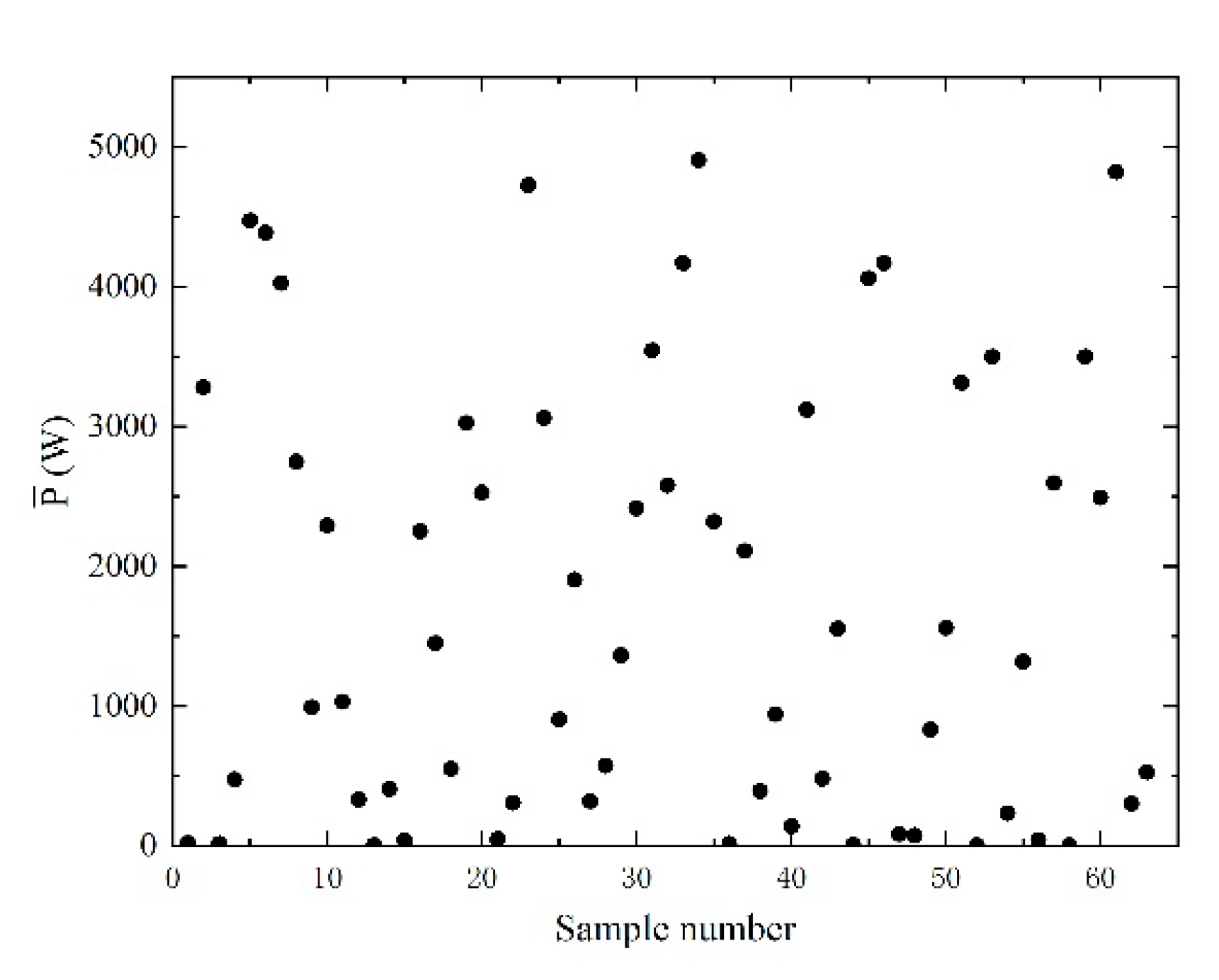
3.1.3. Calculating the Sample Points
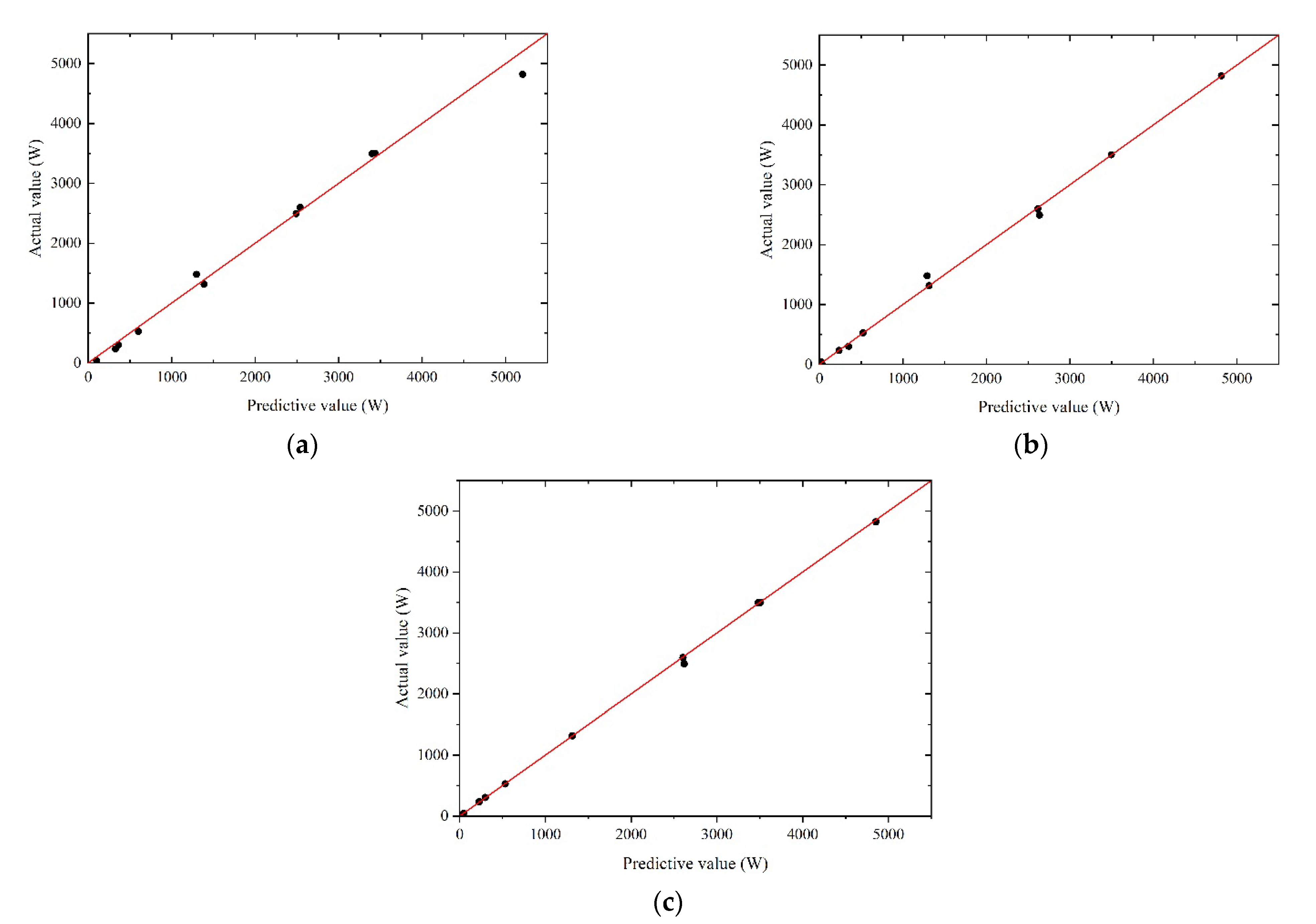
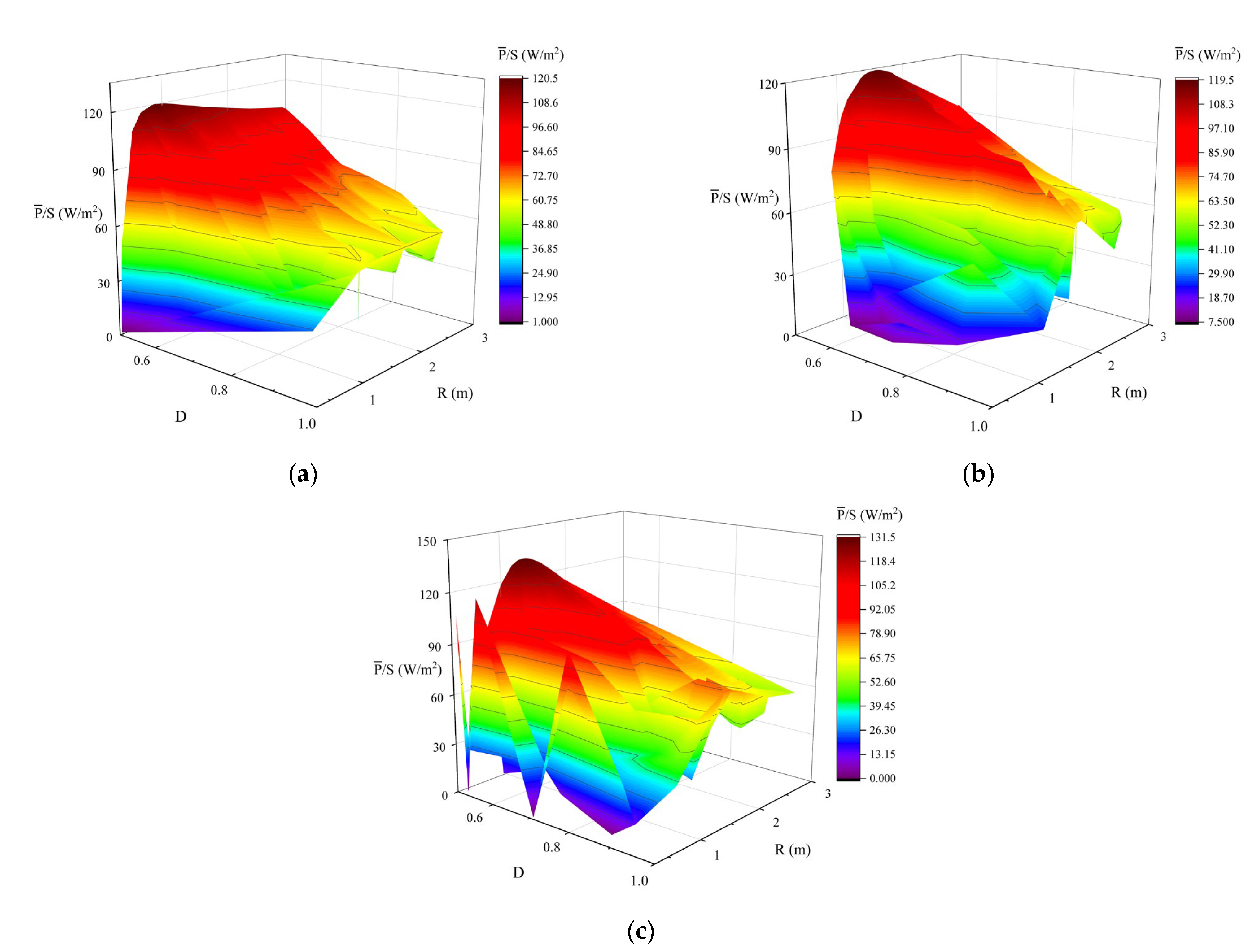
3.2. Training and Testing of the Prediction Model
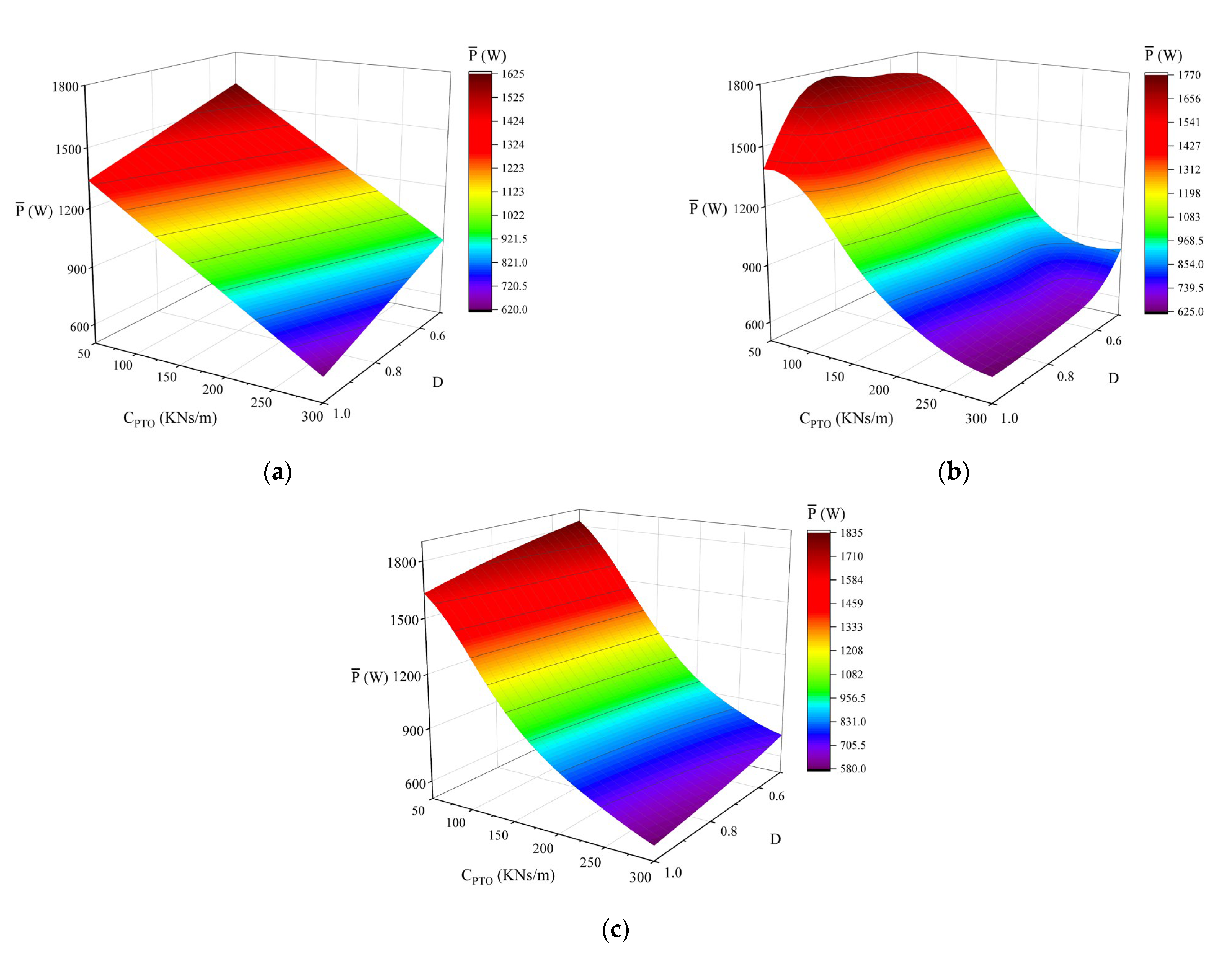
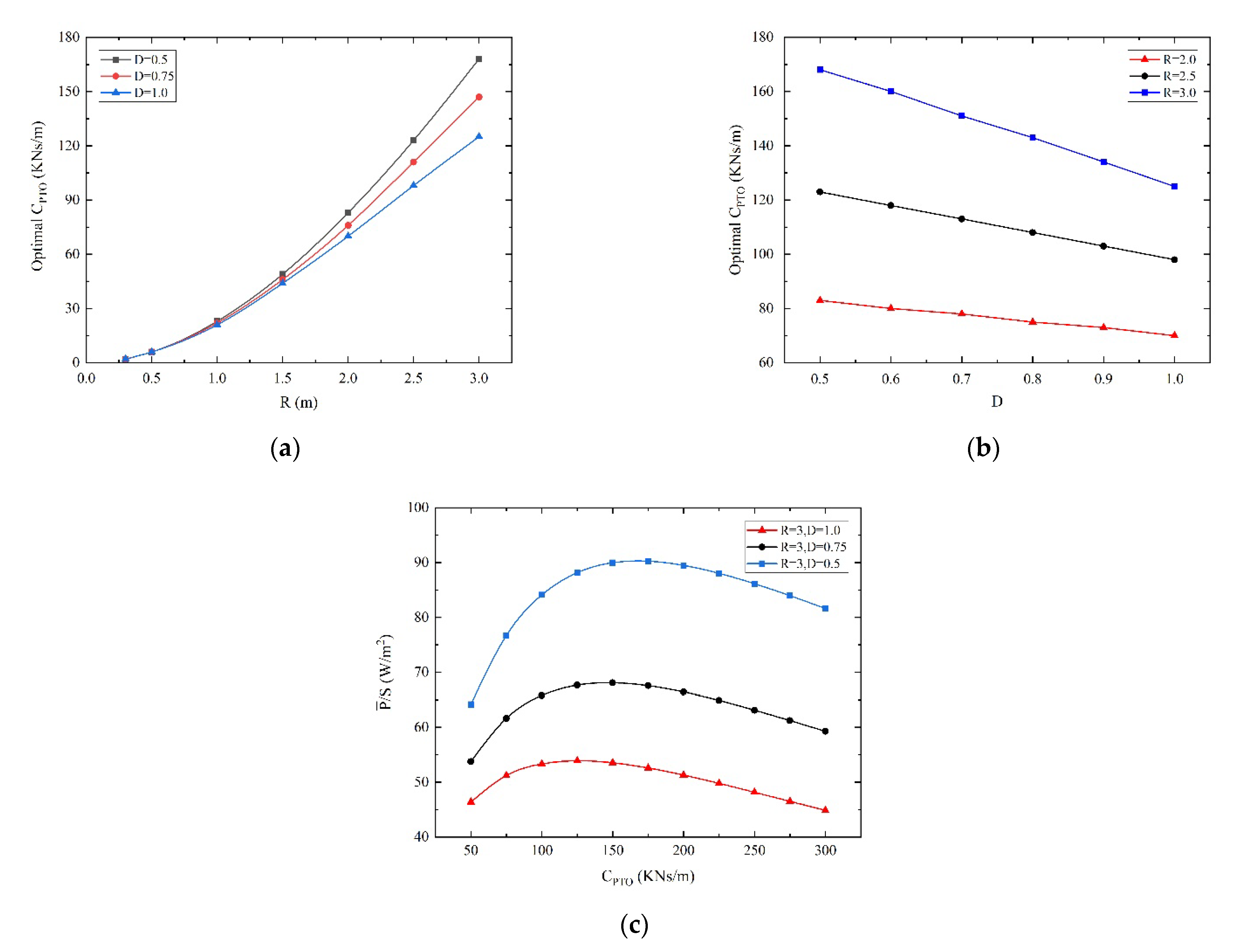
4. Optimization Results and Discussion
5. Conclusions
- (1)
- The comparison shows that the prediction model established by the RSM method has the worst accuracy, the prediction model trained by the RBFNN method has better accuracy, and the prediction model trained by the EBFNN method has the best accuracy. The mean annual power prediction model trained by the EBFNN method can more accurately reflect the mapping relationship between the input and output. According to the shape parameters of the buoy, the mean annual power can be accurately predicted.
- (2)
- Taking the wave statistics data of the Chengshantou sea area near Weihai City, Shandong Province, China, as an example, the method of combining MIGA and the mean annual prediction model is adopted to obtain a high-performance design scheme, which provides a reference for engineering design. In the optimization process, the mean annual power prediction model replaces the simulation calculation, which can reduce a lot of workload (i.e., repeated modeling, simulation, and calculation). Compared with optimization design based on simulation results, this method can save considerable time and cost, effectively shorten the optimization design cycle, and improve the optimization efficiency. This optimization method can also be extended to the optimal design of other sea areas or types of WECs. In the future, we will continue to explore WEC array optimization methods. In order to promote the development of WEC commercialization, WEC array optimization methods will be investigated in the future.
- (3)
- The three optimization parameters have a significant impact on the energy capture performance. When the buoy shape is determined, the /S first increases and then decreases with the increase of damping, and there is an optimal CPTO. The optimal CPTO is significantly affected by buoy radius and draft, which is positively correlated with the buoy radius and negatively correlated with the buoy draft. When CPTO is the optimal damping, the /S increases first and then decreases with the increase of radius and the /S decreases with the increase of draft.
Author Contributions
Funding
Conflicts of Interest
References
- Mathiesen, B.V.; Lund, H.; Karlsson, K. 100% Renewable energy systems, climate mitigation and economic growth. Appl. Energy 2011, 88, 488–501. [Google Scholar] [CrossRef]
- Panwar, N.L.; Kaushik, S.C.; Kothari, S. Role of renewable energy sources in environmental protection: A review. Renew. Sustain. Energy Rev. 2011, 15, 1513–1524. [Google Scholar] [CrossRef]
- Pecher, A.; Kofoed, J.P. Handbook of Ocean Wave Energy, 1st ed.; Springer Nature: Cham, Switzerland, 2017; pp. 19–34. [Google Scholar]
- Nguyen, H.P.; Wang, C.M.; Tay, Z.Y.; Luong, V.H. Wave Energy Converter and Large Floating Platform Integration: A Review. Ocean Eng. 2020, 213, 107768. [Google Scholar] [CrossRef]
- Zhao, C.Y.; Cao, F.F.; Shi, H.D. Optimisation of heaving buoy wave energy converter using a combined numerical model. Appl. Ocean Res. 2020, 102, 102208. [Google Scholar] [CrossRef]
- Hantoro, R.; Septyaningrum, E.; Hudaya, Y.R.; Utama, I. Stability analysis for trimaran pontoon array in wave energy converter–pendulum system (WEC-PS). Brodogradnja 2022, 73, 59–68. [Google Scholar] [CrossRef]
- Legaz, M.J.; Soares, C.G. Evaluation of various wave energy converters in the bay of Cádiz. Brodogradnja 2022, 73, 57–88. [Google Scholar] [CrossRef]
- Jin, S.; Greaves, D. Wave energy in the UK: Status review and future perspectives. Renew. Sustain. Energy Rev. 2021, 143, 110932. [Google Scholar] [CrossRef]
- Farkas, A.; Degiuli, N.; Martić, I. Assessment of Offshore Wave Energy Potential in the Croatian Part of the Adriatic Sea and Comparison with Wind Energy Potential. Energies 2019, 12, 2357. [Google Scholar] [CrossRef] [Green Version]
- Weber, J.; Mouwen, F.; Parish, A.; Robertson, D. Wavebob-Research & Development Network and Tools in the Context of Systems Engineering. In Proceedings of the 8th European Wave Tidal Energy Conference, London, UK, 15–16 November 2009; pp. 416–420. [Google Scholar]
- Falcão, A.F.O. Wave energy utilization: A review of the technologies. Renew. Sustain. Energy Rev. 2010, 14, 899–918. [Google Scholar] [CrossRef]
- Goggins, J.; Finnegan, W. Shape optimisation of floating wave energy converters for a specified wave energy spectrum. Renew. Energy 2014, 71, 208–220. [Google Scholar] [CrossRef]
- Shi, H.D.; Han, Z.H.; Zhao, C.Y. Numerical study on the optimization design of the conical bottom heaving buoy convertor. Ocean Eng. 2019, 173, 235–243. [Google Scholar] [CrossRef]
- Berenjkoob, M.N.; Ghiasi, M.; Soares, C.G. Influence of the shape of a buoy on the efficiency of its dual-motion wave energy conversion. Energy 2021, 214, 118998. [Google Scholar] [CrossRef]
- Shadman, M.; Estefen, S.F.; Rodriguez, C.A.; Nogueira, I.C.M. A geometrical optimization method applied to a heaving point absorber wave energy converter. Renew. Energy 2018, 115, 533–546. [Google Scholar] [CrossRef]
- Wu, J.M. Geometry Optimization of Heaving Axisymmetric Point Absorbers under Parametrical Constraints in Irregular Waves. J. Mar. Sci. Eng. 2021, 9, 1136. [Google Scholar] [CrossRef]
- McCabe, A.P.; Aggidis, G.A.; Widden, M.B. Optimizing the shape of a surge-and-pitch wave energy collector using a genetic algorithm. Renew. Energy 2010, 35, 2767–2775. [Google Scholar] [CrossRef]
- Garcia-Teruel, A.; DuPont, B.; Forehand, D.I.M. Hull geometry optimisation of wave energy converters: On the choice of the objective functions and the optimisation formulation. Appl. Energy 2021, 298, 117153. [Google Scholar] [CrossRef]
- Neshat, M.; Sergiienko, N.; Mirjalili, S.; Nezhad, M.M.; Piras, G.; Garcia, D.A. Multi-Mode Wave Energy Converter Design Optimisation Using an Improved Moth Flame Optimisation Algorithm. Energies 2021, 14, 3737. [Google Scholar] [CrossRef]
- Ji, T.; Cao, F.F.; Dong, X.C.; Li, D.M.; Shi, H.D. Optimized design of 3-DOF buoy wave energy converters under a specified wave energy spectrum. Appl. Ocean Res. 2021, 116, 102885. [Google Scholar] [CrossRef]
- Koh, H.J.; Ruy, W.S.; Cho, I.H.; Kweon, H.M. Multi-objective optimum design of a buoy for the resonant-type wave energy converter. J. Mar. Sci. Technol. 2015, 20, 53–63. [Google Scholar] [CrossRef]
- Colby, M.K.; Nasroullahi, E.M.; Tumer, K. Optimizing Ballast Design of Wave Energy Converters Using Evolutionary Algorithms. In Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation, Dublin, Ireland, 12–16 July 2011; pp. 1739–1746. [Google Scholar]
- Avila, D.; Marichal, G.N.; Quiza, R.; Luis, F.S. Prediction of Wave Energy Transformation Capability in Isolated Islands by Using the Monte Carlo Method. J. Marine Sci. Eng. 2021, 9, 980. [Google Scholar] [CrossRef]
- Avila, D.; Marichal, G.N.; Padrón, I.; Quiza, R.; Hernández, A. Forecasting of wave energy in Canary Islands based on artificial intelligence. Appl. Ocean Res. 2020, 101, 102–189. [Google Scholar] [CrossRef]
- Wang, W.; Liu, Y.J.; Bai, F.G.; Xue, G. Capture Power Prediction of the Frustum of a Cone Shaped Floating Body Based on BP Neural Network. J. Marine Sci. Eng. 2021, 9, 656. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Hua, X. Prediction and optimization of oscillating wave surge converter using machine learning techniques. Energy Convers. Manag. 2020, 210, 112677. [Google Scholar] [CrossRef]
- Perez, T. Ship Motion Control: Course Keeping and Roll Stabilisation Using Rudder and Fins; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- McCabe, A. Constrained optimization of the shape of a wave energy collector by genetic algorithm. Renew. Energy 2013, 51, 274–284. [Google Scholar] [CrossRef]
- Kavuri, S.N.; Venkatasubramanian, V. Using fuzzy clustering with ellipsoidal units in neural networks for robust fault classification. Comput. Chem. Eng. 1993, 17, 765–784. [Google Scholar] [CrossRef]
- Wang, J.; Pang, Y.J.; Cheng, Y.X.; Yang, Z.Y.; Liu, W. Application of prediction models to optimize the design of the non-uniform ring-frames pressure shell. J. Ship Mech. 2014, 18, 1331–1338. [Google Scholar] [CrossRef]
- Eiben, A.E.; Smith, J.E. Introduction to Evolutionary Computing, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 37–69. [Google Scholar]
- Miki, M.; Hiroyasu, T.; Kaneko, M.; Hatanaka, K. A Parallel Genetic Algorithm with Distributed Environment Scheme. In Proceedings of the 1999 IEEE International Conference on Systems, Man, and Cybernetics, Tokyo, Japan, 12–15 October 1999; pp. 695–700. [Google Scholar]
- Zhang, W.W.; Qi, H.; Yu, Z.Q.; He, M.J.; Ren, Y.T.; Li, Y. Optimization configuration of selective solar absorber using multi-island genetic algorithm. Sol. Energy 2021, 224, 947–955. [Google Scholar] [CrossRef]
- ECMWF. Available online: https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era5 (accessed on 13 December 2021).
- Bhatta, D.D.; Rahman, M. On scattering and radiation problem for a cylinder in water of finite depth. Int. J. Eng. Sci. 2003, 41, 931–967. [Google Scholar] [CrossRef]
- Chen, Z.F.; Zhou, B.Z.; Zhang, L.; Sun, L.; Zhang, X.W. Performance evaluation of a dual resonance wave-energy convertor in irregular waves. Appl. Ocean Res. 2018, 77, 77–88. [Google Scholar] [CrossRef]
- Falnes, J.; Perlin, M. Ocean waves and oscillating systems: Linear interactions including wave-energy extraction. Appl. Mech. Rev. 2003, 56, B3. [Google Scholar] [CrossRef]
- Garcia-Teruel, A.; Forehand, D.I.M. A review of geometry optimisation of wave energy converters. Renew. Sustain. Energy Rev. 2021, 139, 110593. [Google Scholar] [CrossRef]
- Mei, C.C. Hydrodynamic principles of wave power extraction. Phil. Trans. R. Soc. A 2012, 370, 208–234. [Google Scholar] [CrossRef]
- Chen, W.; Jin, R.C.; Sudjianto, A. Analytical Global Sensitivity Analysis and Uncertainty Propagation for Robust Design. J. Qual. Technol. 2006, 38, 333–348. [Google Scholar] [CrossRef]


| Hs (m) | Tav (s) | Total | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2.5 | 3.5 | 4.5 | 5.5 | 6.5 | 7.5 | 8.5 | 9.5 | 10.5 | 11.5 | ||
| 0.25 | 3.25 | 14.00 | 7.37 | 2.64 | 0.77 | 0.16 | 0.07 | 0.03 | 0.01 | 0.00 | 28.30% |
| 0.75 | 0.10 | 15.56 | 18.28 | 5.19 | 1.63 | 0.67 | 0.32 | 0.19 | 0.04 | 0.02 | 42.00% |
| 1.25 | 0.00 | 0.54 | 10.88 | 3.37 | 0.46 | 0.14 | 0.08 | 0.02 | 0.02 | 0.02 | 15.53% |
| 1.75 | 0.00 | 0.00 | 1.64 | 5.24 | 0.31 | 0.07 | 0.00 | 0.00 | 0.00 | 0.01 | 7.27% |
| 2.25 | 0.00 | 0.00 | 0.02 | 2.76 | 0.89 | 0.03 | 0.00 | 0.00 | 0.00 | 0.00 | 3.70% |
| 2.75 | 0.00 | 0.00 | 0.00 | 0.39 | 1.62 | 0.03 | 0.00 | 0.00 | 0.00 | 0.00 | 2.04% |
| 3.25 | 0.00 | 0.00 | 0.00 | 0.01 | 0.79 | 0.08 | 0.00 | 0.00 | 0.00 | 0.00 | 0.88% |
| 3.75 | 0.00 | 0.00 | 0.00 | 0.00 | 0.11 | 0.11 | 0.01 | 0.00 | 0.00 | 0.00 | 0.23% |
| 4.25 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.05% |
| 4.75 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00% |
| Total | 3.35% | 30.10% | 38.19% | 19.60% | 6.58% | 1.34% | 0.48% | 0.24% | 0.07% | 0.05% | 100% |
| Run# | R | D | CPTO | Run# | R | D | CPTO |
|---|---|---|---|---|---|---|---|
| 1 | 0.52 | 0.68 | 240 | 33 | 2.89 | 0.78 | 240 |
| 2 | 2.35 | 0.94 | 90 | 34 | 3 | 0.58 | 210 |
| 3 | 0.41 | 0.88 | 110 | 35 | 2.24 | 0.62 | 280 |
| 4 | 1.16 | 0.76 | 160 | 36 | 0.52 | 0.82 | 270 |
| 5 | 2.78 | 0.6 | 130 | 37 | 1.7 | 0.6 | 80 |
| 6 | 2.89 | 0.7 | 220 | 38 | 1.27 | 0.96 | 260 |
| 7 | 2.68 | 0.5 | 230 | 39 | 1.49 | 0.52 | 200 |
| 8 | 2.03 | 0.74 | 70 | 40 | 0.95 | 0.54 | 290 |
| 9 | 1.7 | 0.98 | 260 | 41 | 2.57 | 0.98 | 230 |
| 10 | 1.81 | 0.56 | 100 | 42 | 1.16 | 0.7 | 160 |
| 11 | 1.49 | 0.96 | 150 | 43 | 1.81 | 0.86 | 190 |
| 12 | 1.06 | 0.54 | 180 | 44 | 0.41 | 0.64 | 220 |
| 13 | 0.3 | 0.66 | 140 | 45 | 2.68 | 0.66 | 90 |
| 14 | 1.27 | 0.58 | 280 | 46 | 2.78 | 0.88 | 150 |
| 15 | 0.62 | 0.92 | 210 | 47 | 0.73 | 0.9 | 170 |
| 16 | 2.24 | 0.64 | 290 | 48 | 0.62 | 0.56 | 110 |
| 17 | 1.38 | 0.9 | 50 | 49 | 1.06 | 0.74 | 50 |
| 18 | 0.95 | 0.72 | 60 | 50 | 2.03 | 0.84 | 300 |
| 19 | 2.57 | 0.86 | 270 | 51 | 2.46 | 0.94 | 60 |
| 20 | 2.14 | 0.82 | 170 | 52 | 0.3 | 0.76 | 120 |
| 21 | 0.73 | 0.84 | 300 | 53 | 2.73 | 0.8 | 275 |
| 22 | 0.84 | 0.52 | 80 | 54 | 1.11 | 0.65 | 300 |
| 23 | 3 | 0.8 | 120 | 55 | 1.65 | 0.75 | 175 |
| 24 | 2.46 | 1 | 190 | 56 | 0.57 | 0.55 | 150 |
| 25 | 1.6 | 0.78 | 250 | 57 | 2.19 | 0.5 | 225 |
| 26 | 1.92 | 0.62 | 200 | 58 | 0.3 | 0.85 | 200 |
| 27 | 0.84 | 0.92 | 70 | 59 | 2.46 | 0.95 | 100 |
| 28 | 1.38 | 0.72 | 250 | 60 | 1.92 | 0.6 | 50 |
| 29 | 1.6 | 1 | 130 | 61 | 3 | 0.7 | 125 |
| 30 | 1.92 | 0.8 | 100 | 62 | 0.84 | 0.9 | 75 |
| 31 | 2.35 | 0.5 | 140 | 63 | 1.38 | 1 | 250 |
| 32 | 2.14 | 0.68 | 180 |
| Prediction Model | R (m) | D (m/m) | CPTO (KNs/m) | /S (W/m2) | Simulation Result | Error |
|---|---|---|---|---|---|---|
| RSM | 0.91 | 0.5 | 50 | 120.18 | 109.80 | 9.45% |
| RBFNN | 1.56 | 0.5 | 50 | 119.10 | 126.08 | 5.54% |
| EBFNN | 1.34 | 0.5 | 50 | 131.46 | 131.63 | 0.13% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, T.; Liu, Y.; Huang, S.; Xue, G. Shape Optimization of Oscillating Buoy Wave Energy Converter Based on the Mean Annual Power Prediction Model. Energies 2022, 15, 7470. https://doi.org/10.3390/en15207470
Liu T, Liu Y, Huang S, Xue G. Shape Optimization of Oscillating Buoy Wave Energy Converter Based on the Mean Annual Power Prediction Model. Energies. 2022; 15(20):7470. https://doi.org/10.3390/en15207470
Chicago/Turabian StyleLiu, Tiesheng, Yanjun Liu, Shuting Huang, and Gang Xue. 2022. "Shape Optimization of Oscillating Buoy Wave Energy Converter Based on the Mean Annual Power Prediction Model" Energies 15, no. 20: 7470. https://doi.org/10.3390/en15207470






