Simulation Studies of Energy Recovery in a BLDC Motor-Based Kinetic Energy Storage
Abstract
:1. Introduction
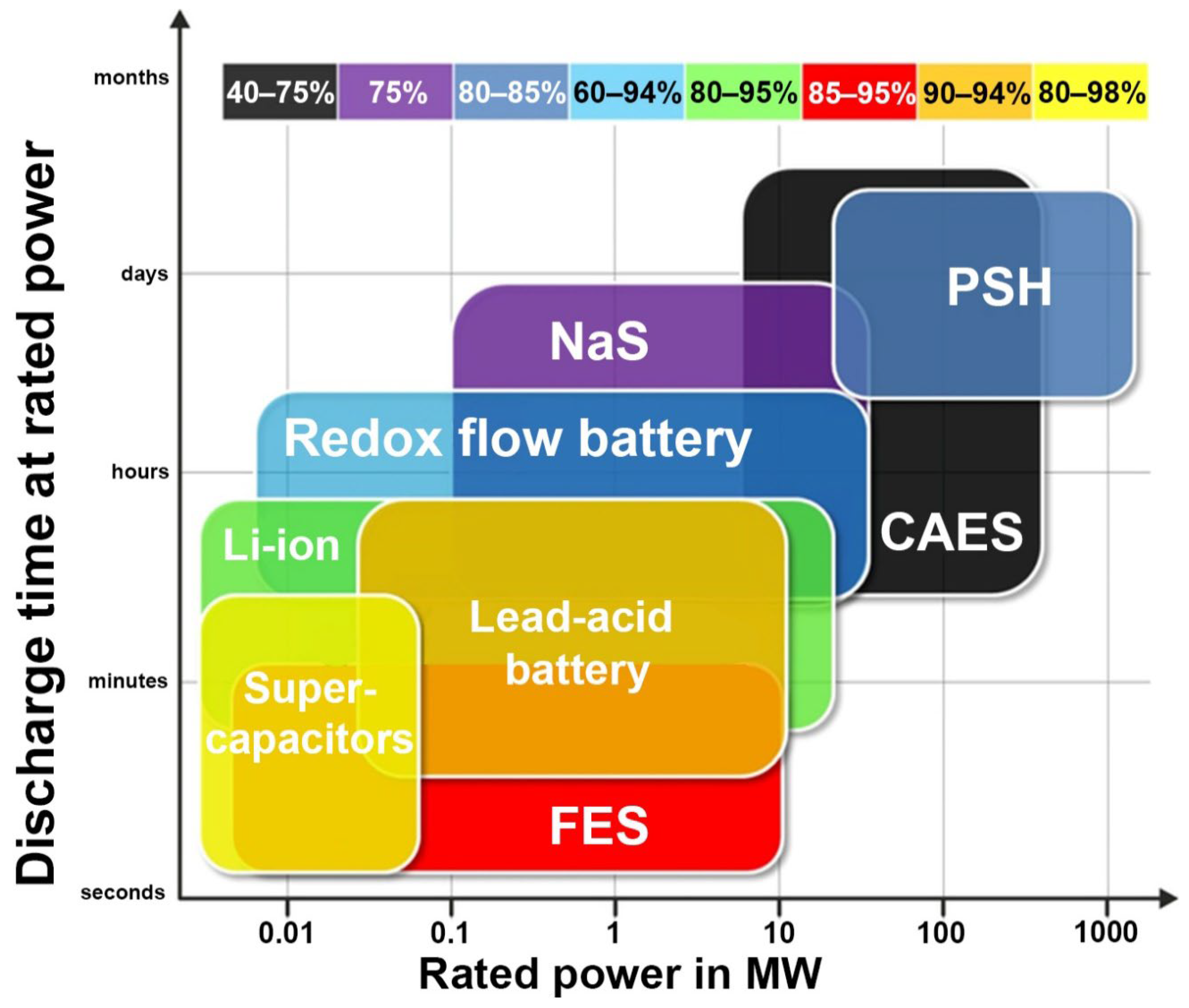
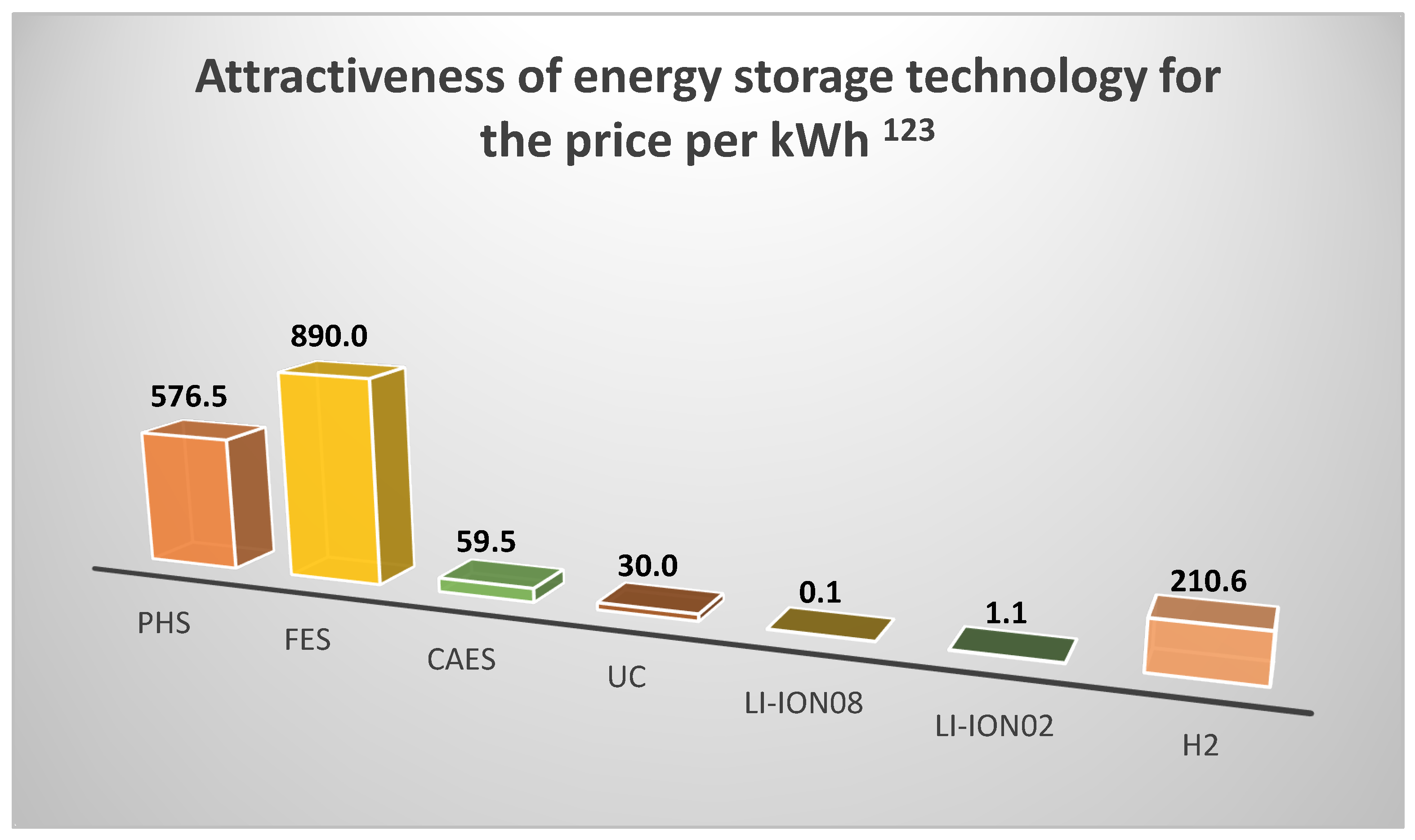
Kinetic Energy Storage
- improved efficiency of power generation,
- improved management efficiency of energy production and transmission systems,
- improved power quality,
- better use of renewable energy sources [9],
- reliability of power supply (sources of additional energy, amount of stored energy),
- reducing costs of power outages,
- ensuring electricity supply.
- duration of energy storage,
- amount of stored energy,
- speed of energy storage and recovery,
- type of technology used,
- number of cycles and depth of discharge,
- efficiency of the storage technology.
| Type of Battery | Current Parameters | Targets for 2020–2030 | Target for 2050 |
|---|---|---|---|
| Li-ion for high-power applications |
|
|
|
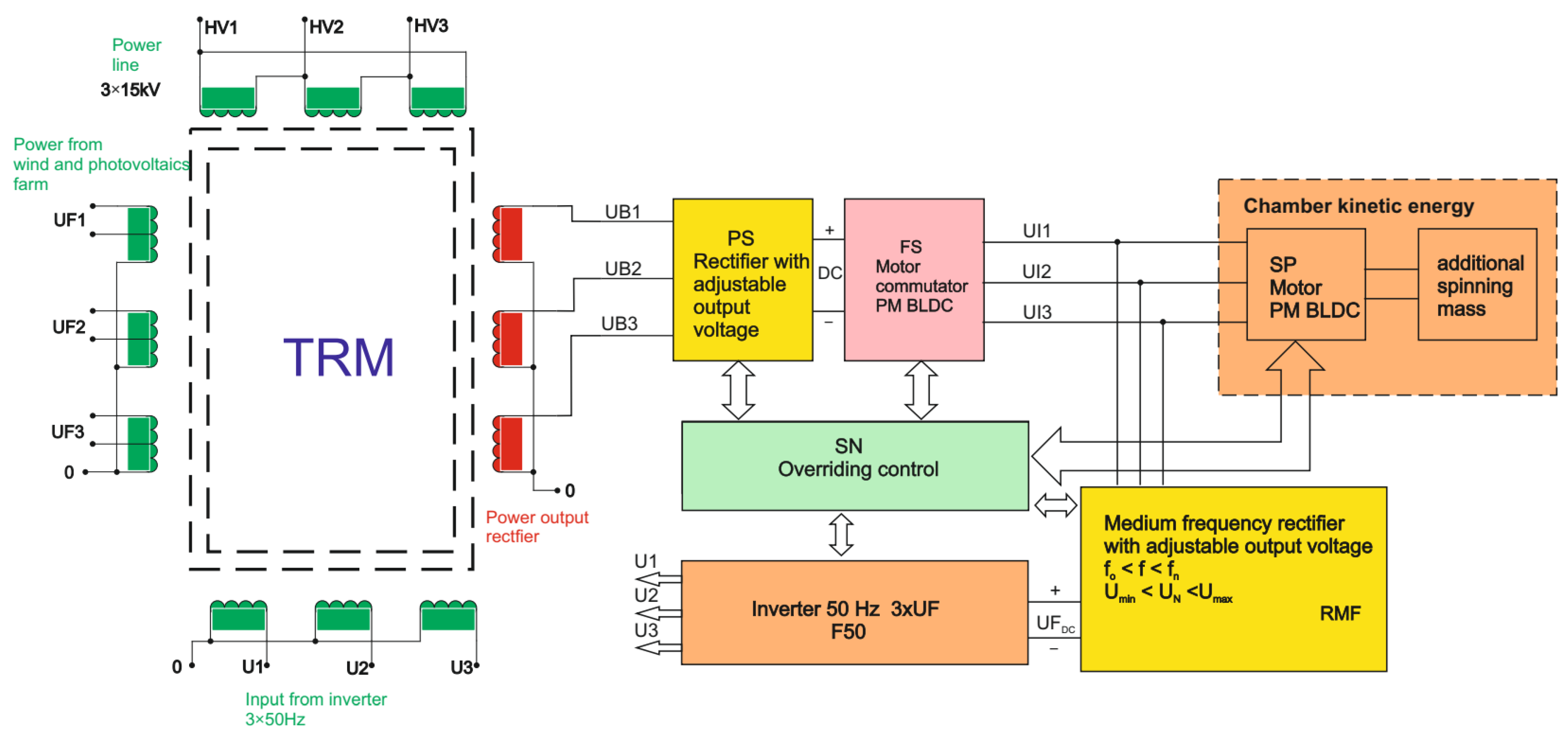
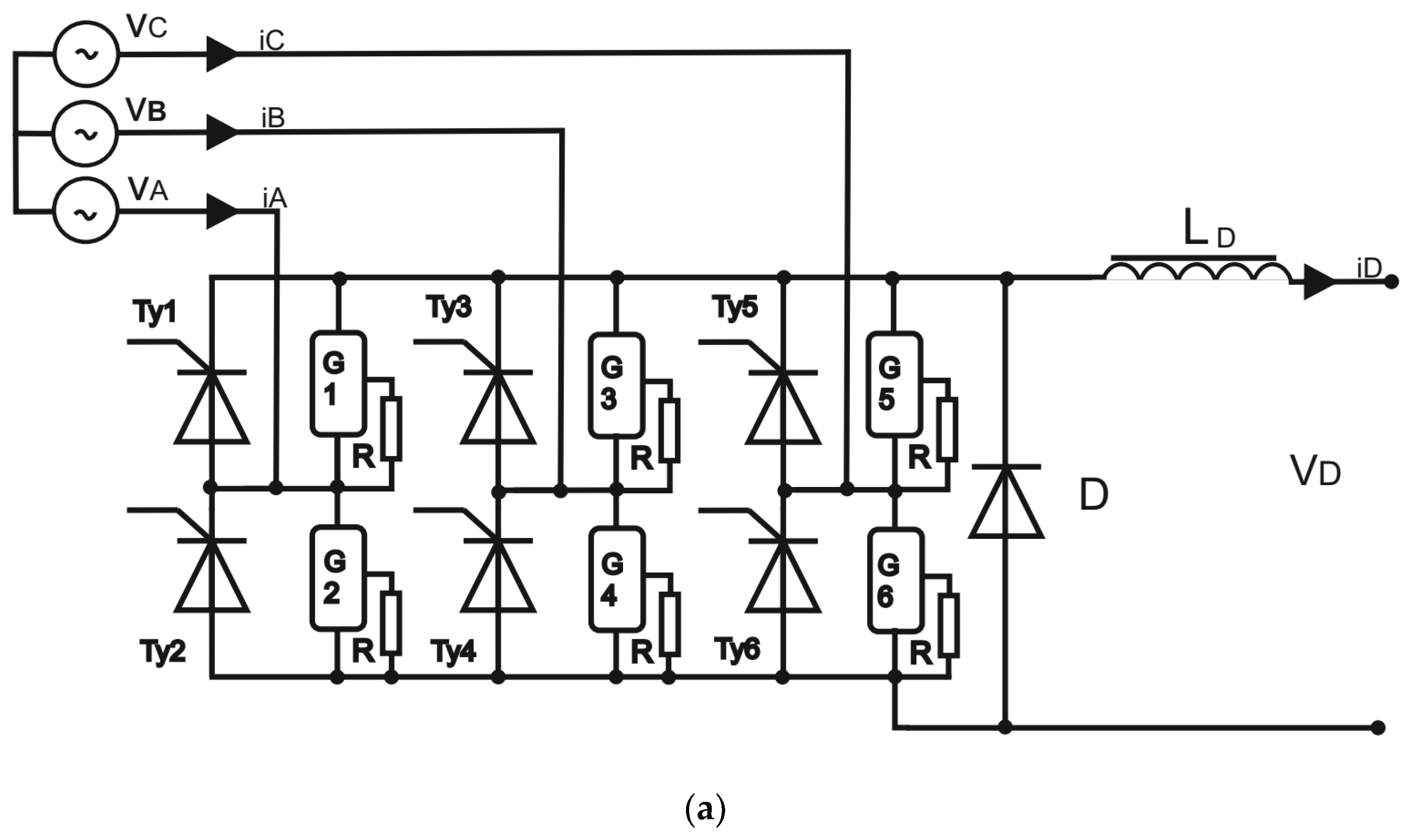
2. Energy Recovery Circuit of the Kinetic Storage with 6T Rectifier
- Vinp-p—input phase-to-phase voltage of the bridge;
- iout—output current of the RMF bridge;
- α—thyristors’ firing angle;
- f—input voltage frequency;
- LDC—DC output circuit inductance.
- ▪ proportional,
- ▪ integral,
- ▪ derivative,
3. Simulation Research
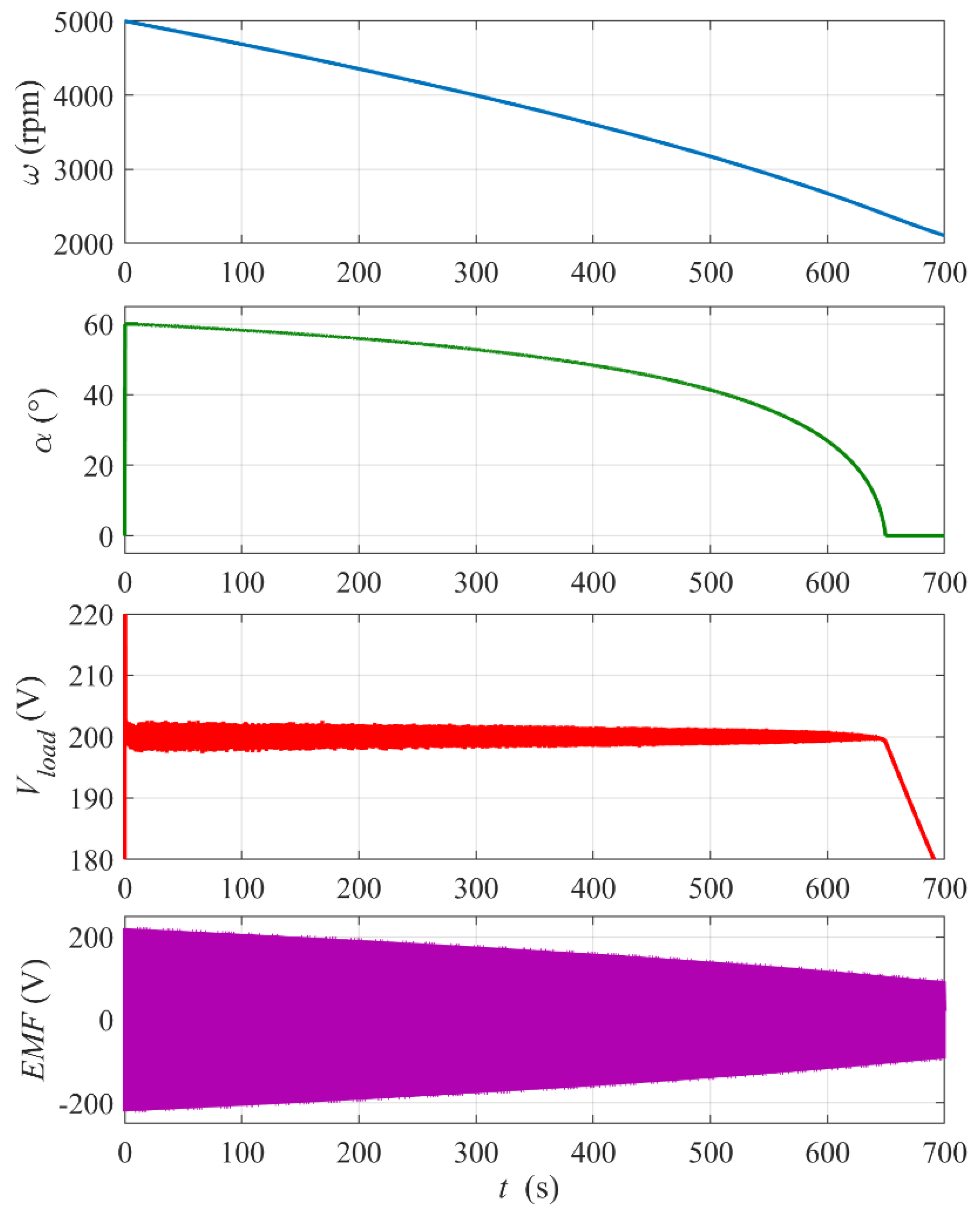
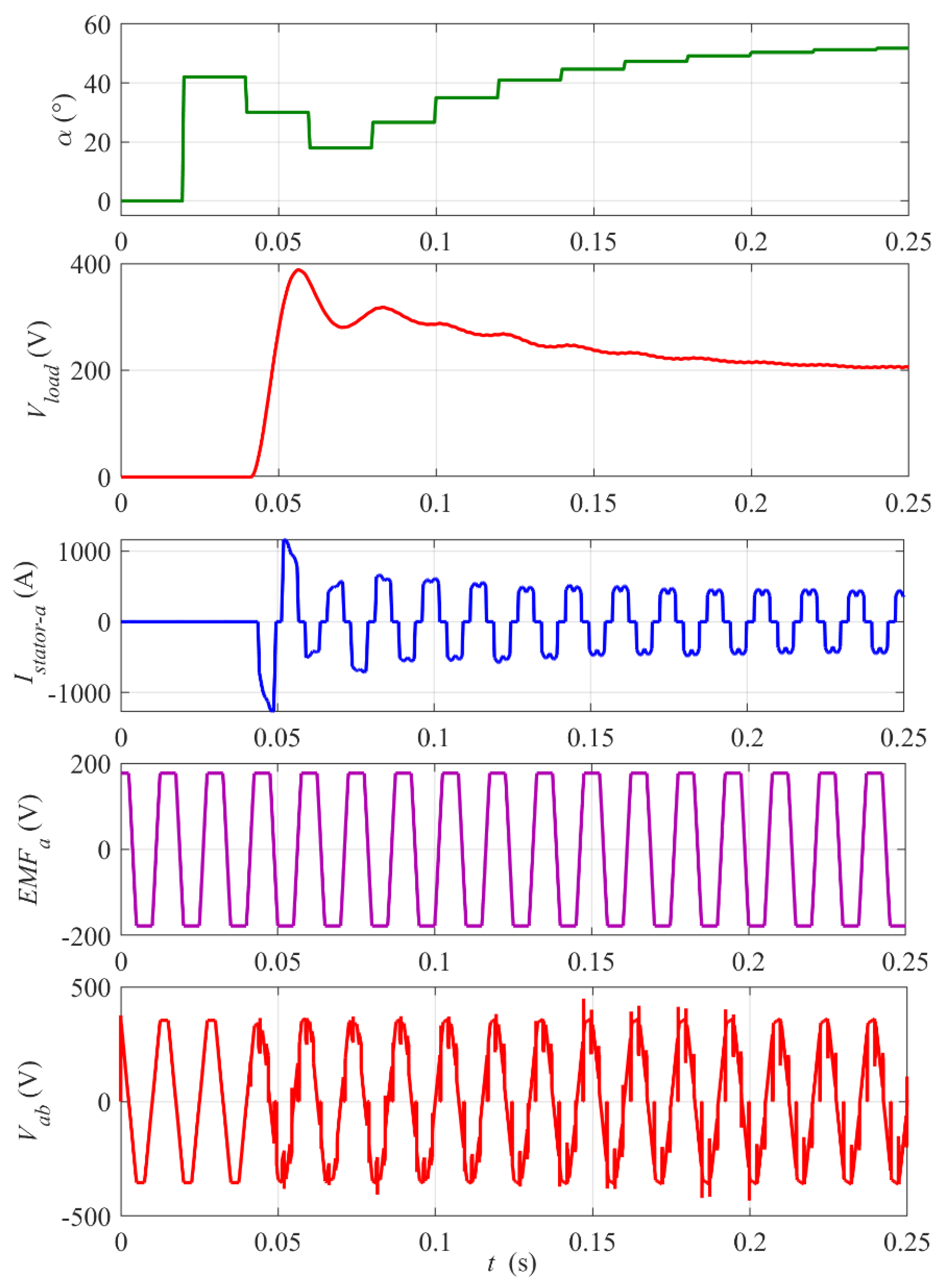
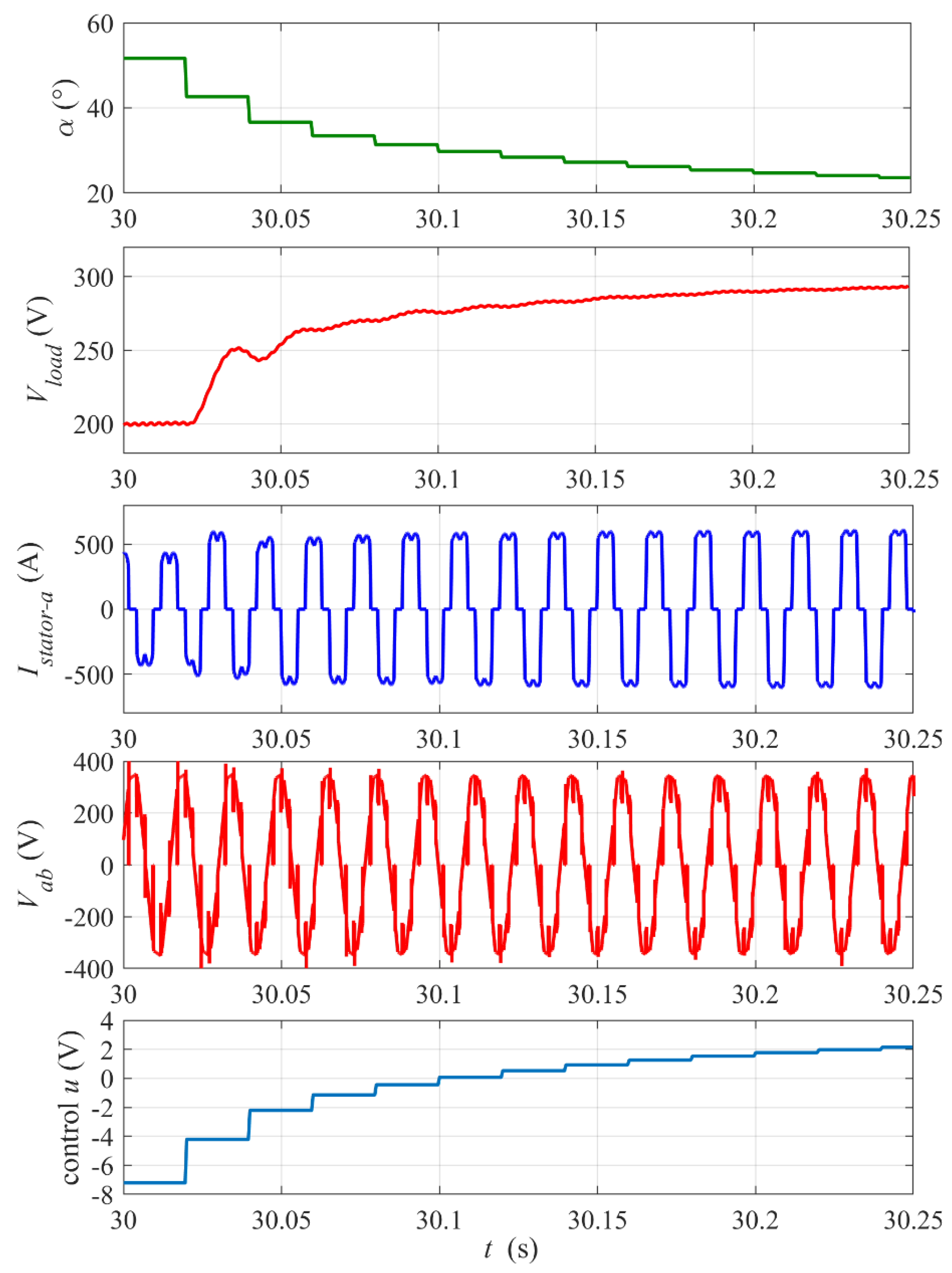
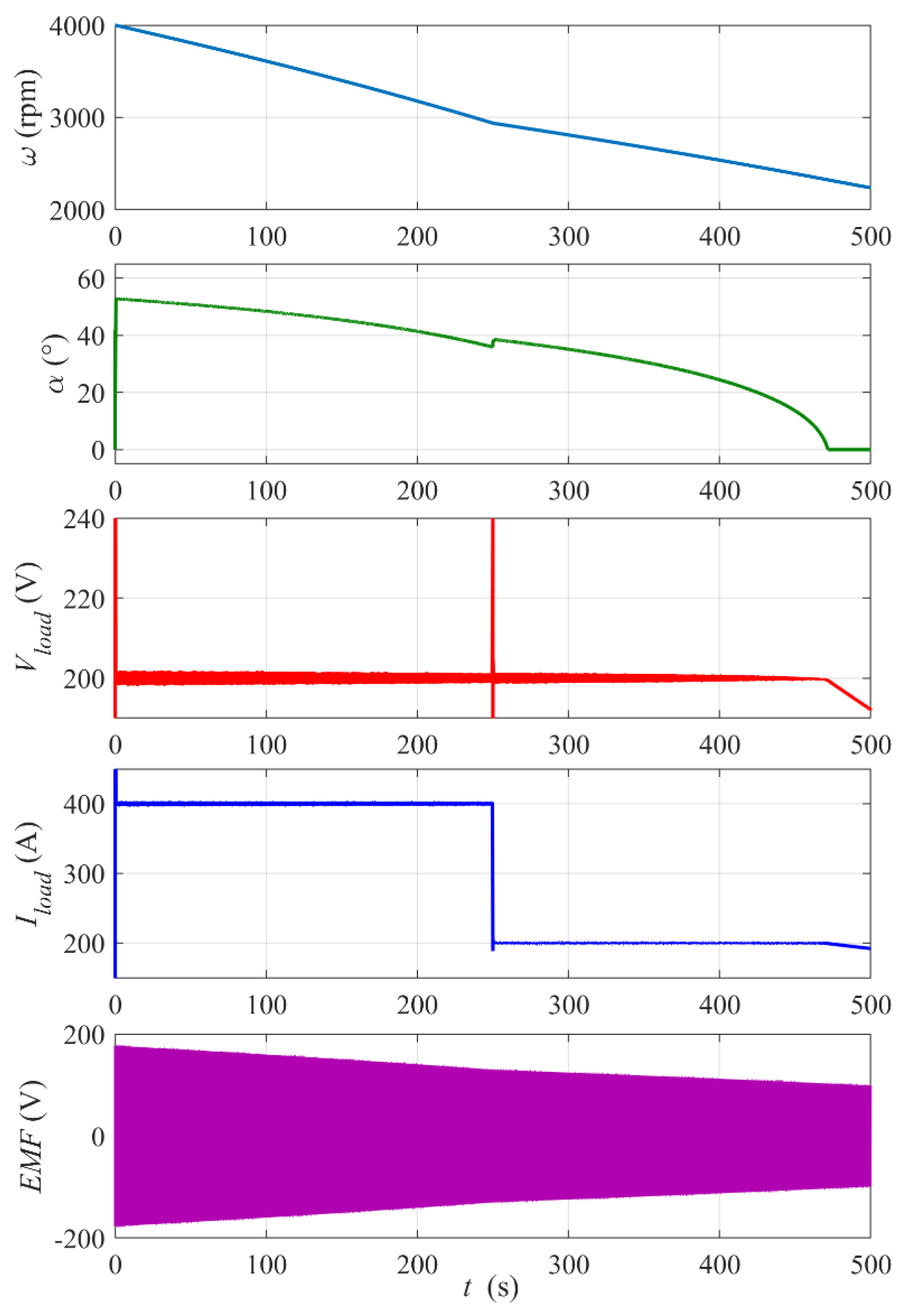
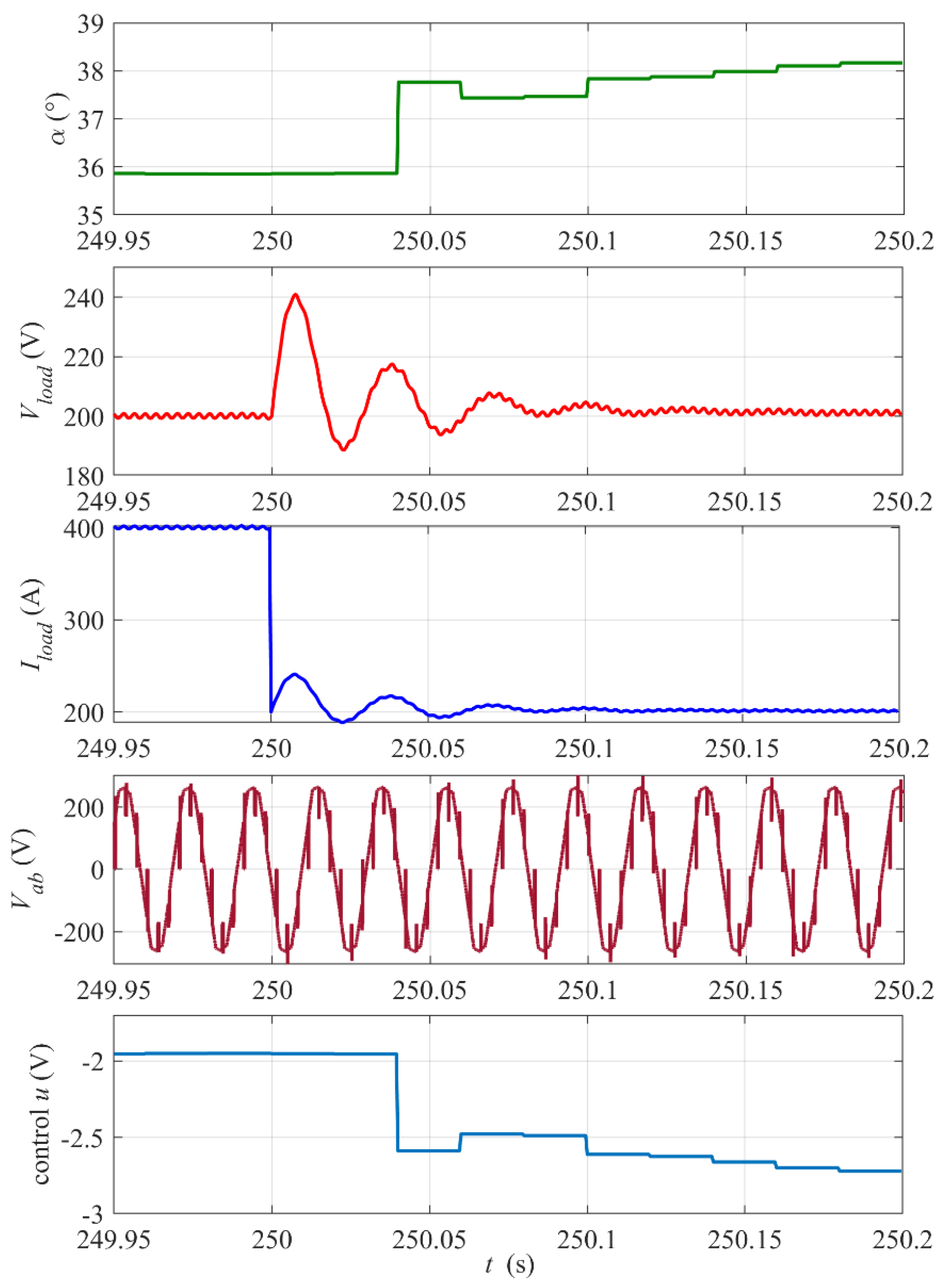
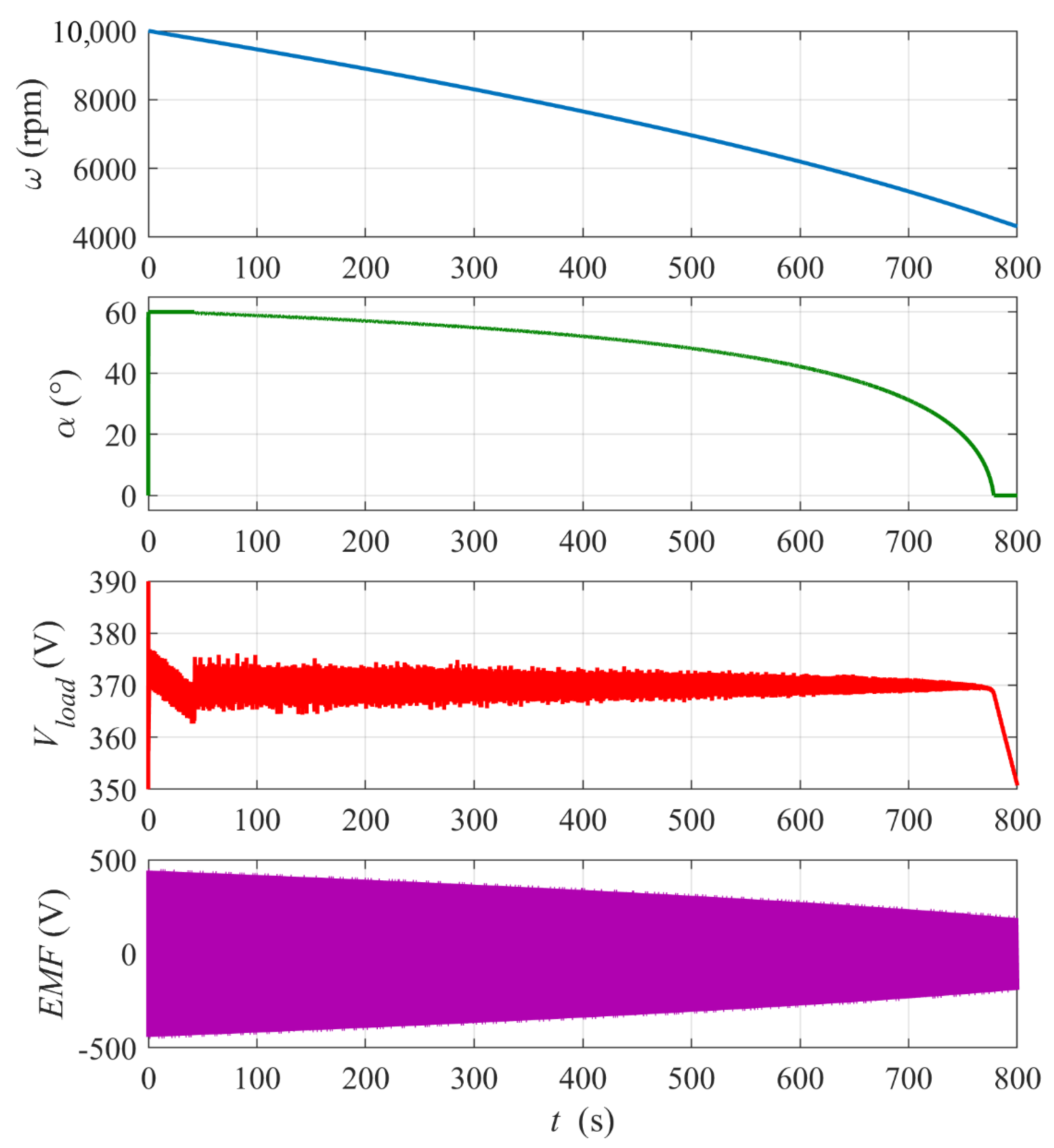
- how long the flywheel storage can stabilize the output DC voltage for a constant load power (time of changing the thyristors’ firing angle α from 60° to 0°) starting from a given initial rotational speed of the flywheel,
- percentage of the initial kinetic energy E0kin converted into electric energy Eload supplied to the load during the period of the load power stabilization,
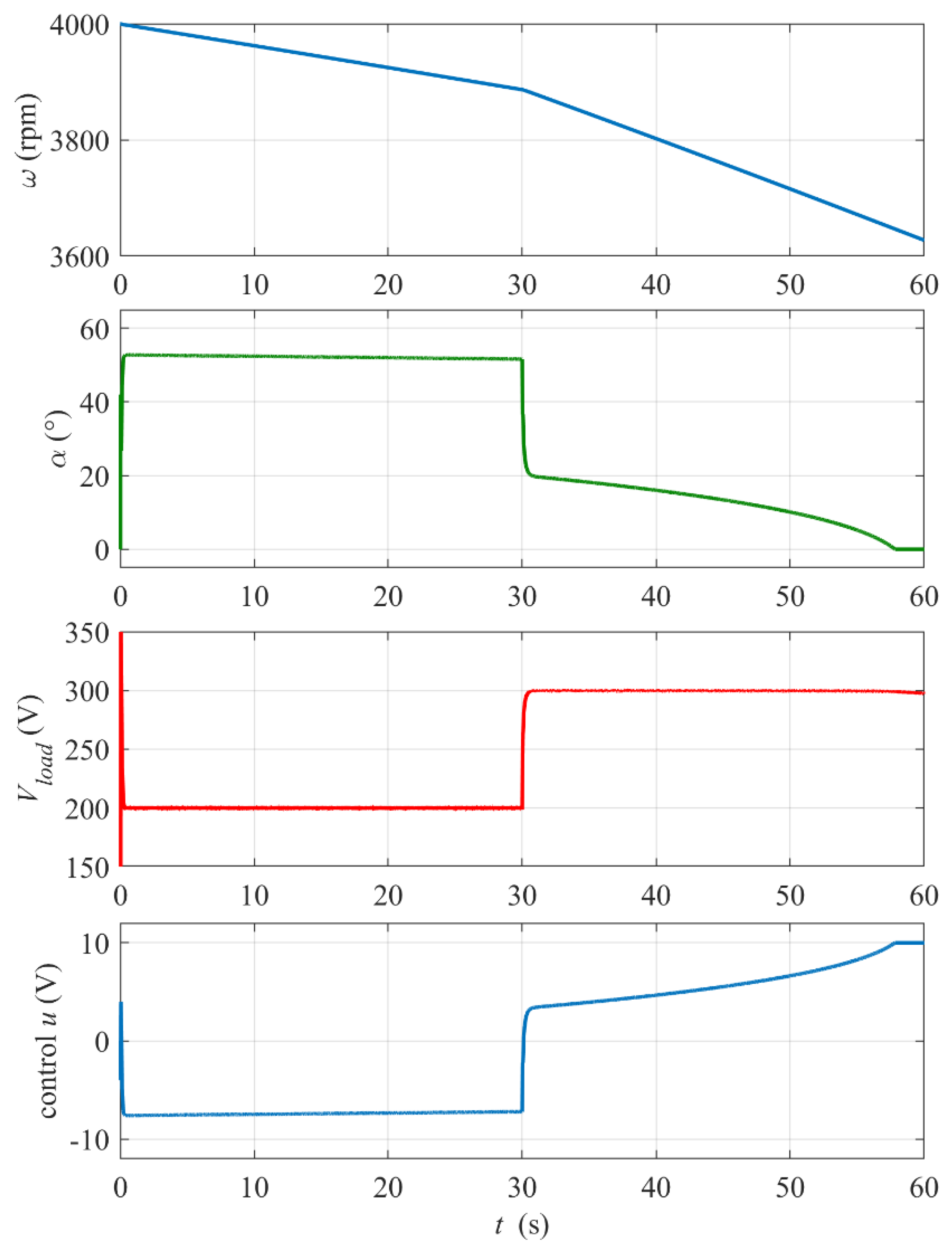
- dynamic response of the proposed control system to the step change in the output voltage reference Vload_ref and to the step change in the load power.
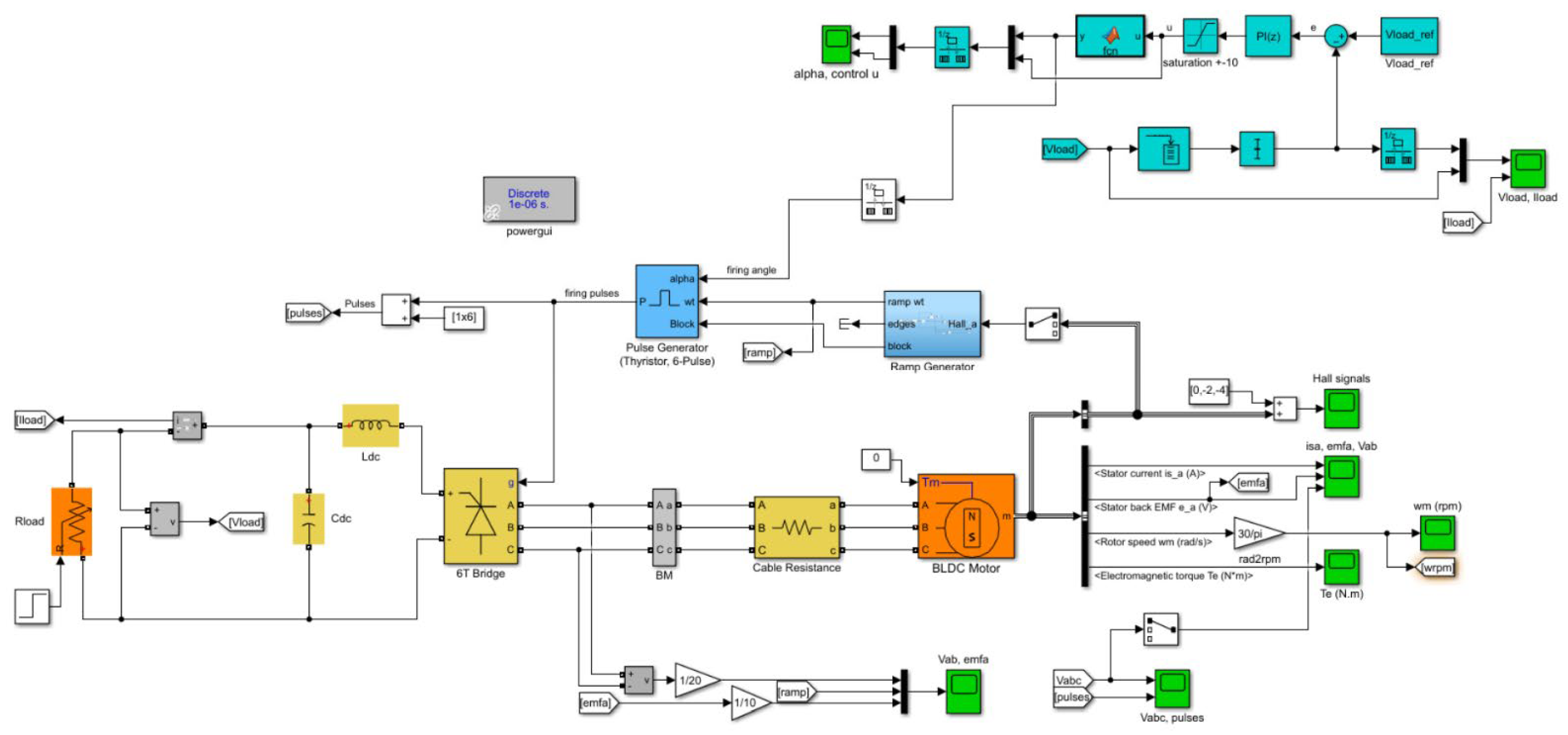
3.1. Simulation Model of the Energy Recovery Subsystem
- three-phase BLDC motor (operating in the energy generation mode) with the flywheel rotor
- three-phase rectifier: 6T thyristor bridge (the electrical diagram of the bridge is presented in Figure 4),
- passive components of the DC load circuit: inductance, capacitance and variable resistance.
- Rs—resistance of the stator windings,
- Ls—inductance of the stator windings,
- ia, ib, ic—phase currents,
- , , —phase electromotive forces (EMFs), in per-unit value to the amplitude of the flux λ,
- vab, vbc—phase-to-phase voltages,
- ωm—rotational velocity of the rotor,
- λ—amplitude of the flux induced by the permanent magnets of the rotor in the stator phases,
- p—number of pole pairs,
- Te—electromagnetic torque.
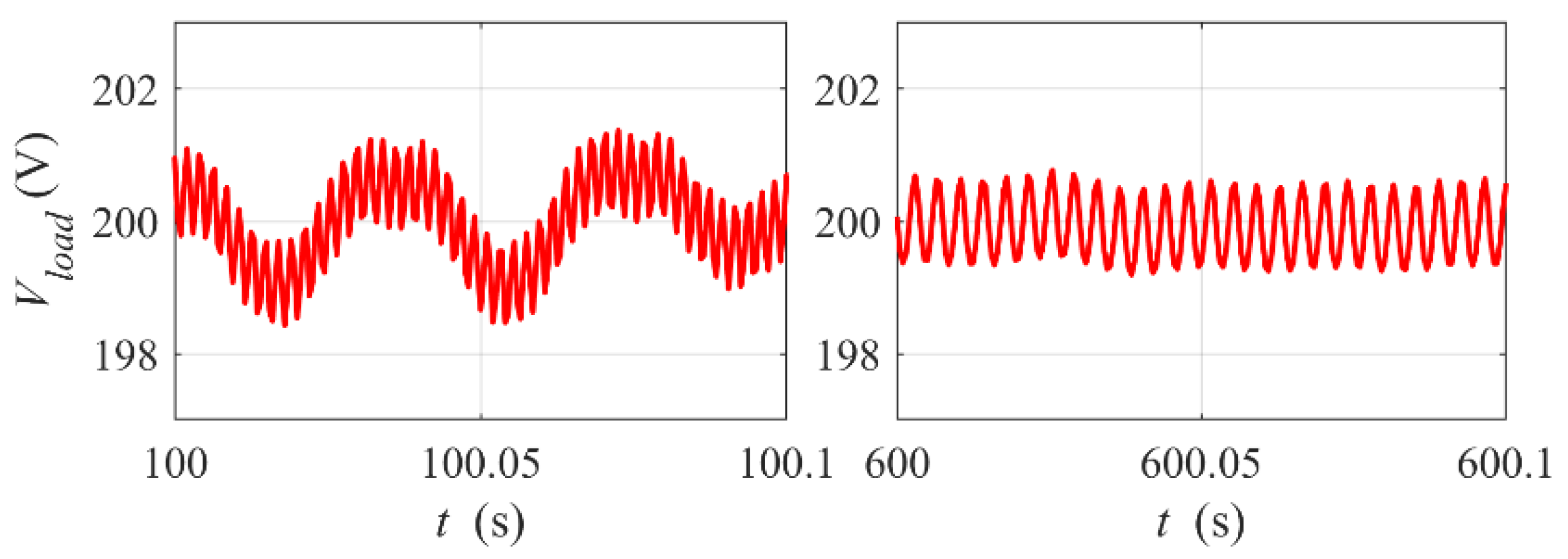
3.2. Simulation Results and Discussion
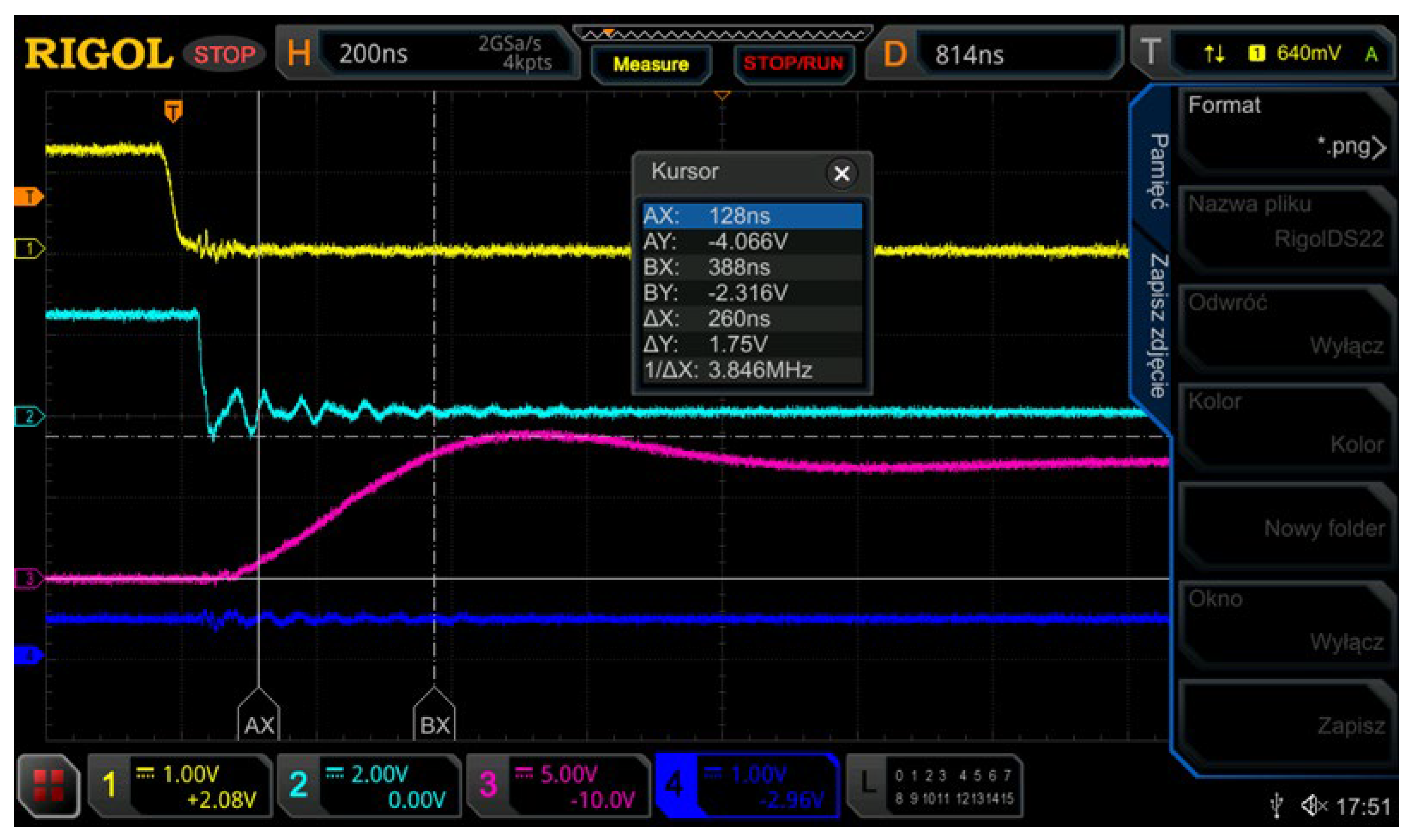
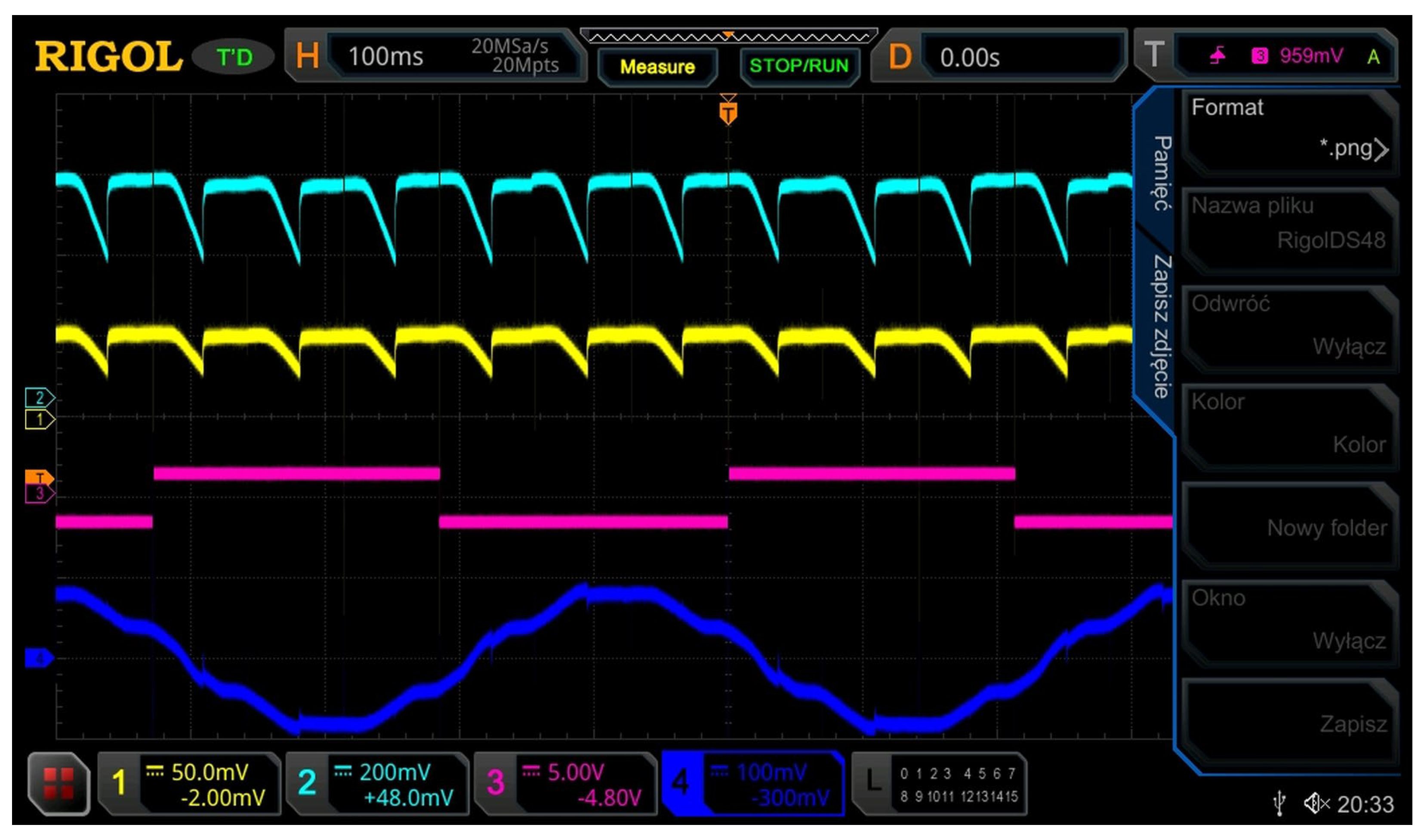
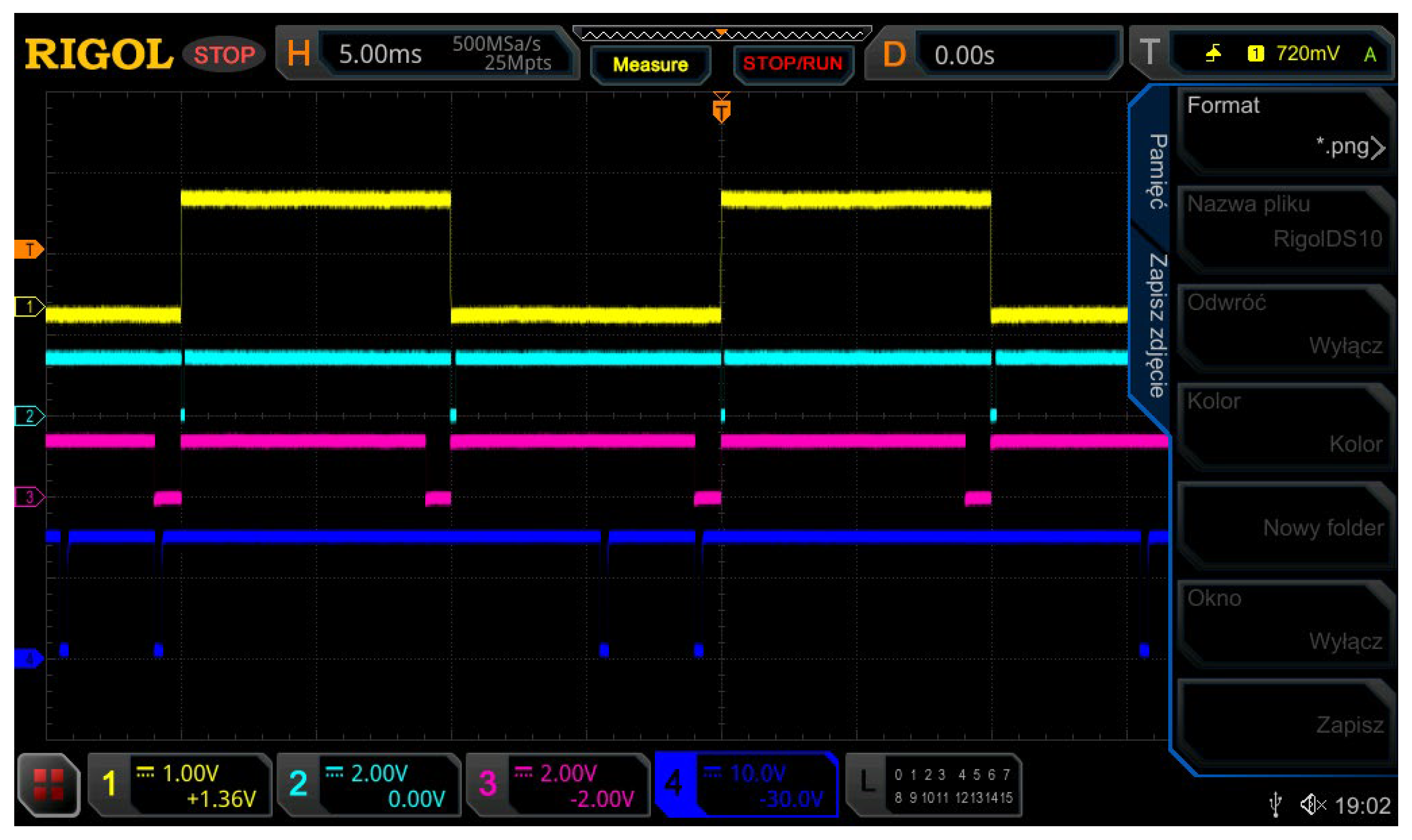
4. Experimental Results
5. Comparisons
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CAES | Compressed air energy storage |
| FES | Flywheel energy storage |
| H2 | Hydrogen energy storage |
| IGBT | Insulated gate bipolar transistor |
| LI-ION08 | Li-on battery discharged at 80% of its capacity |
| LI-ION02 | Li-on battery discharged at 20% of its capacity |
| Mogen | Permanent magnet brushless motor/generator |
| NaS | Sodium–sulfur batteries |
| PM BLDC | Pulse modulation brushless direct current |
| PMSM | Permanent magnet synchronous motor |
| PWM | Pulse width modulation |
| PSH | Pumped storage hydropower |
| RMF | Medium-frequency rectifier |
| UC | Ultracapacitors |
References
- Li, X.; Palazzolo, A. A review of flywheel energy storage systems: State of the art and opportunities. J. Energy Storage 2022, 46, 103576. [Google Scholar] [CrossRef]
- Olabi, A.G.; Wilberforce, T.; Abdelkareem, M.A.; Ramadan, M. Critical Review of Flywheel Energy Storage System. Energies 2021, 14, 2159. [Google Scholar] [CrossRef]
- Elbouchikhi, E.; Amirat, Y.; Feld, G.; Benbouzid, M.; Zhou, Z. A Lab-scale Flywheel Energy Storage System: Control Strategy and Domestic Applications. Energies 2020, 13, 653. [Google Scholar] [CrossRef] [Green Version]
- Galuszkiewicz, Z.; Sutkowski, M. System Przetwarzania, Magazynowania i Zwrotu Energii Elektrycznej KAPS. Polish Patent No. 225294, 20 September 2016. [Google Scholar]
- Han, Y.; Ren, Z.; Tong, Y. General Design Method of Flywheel Rotor for Energy Storage System. Energy Procedia 2021, 16, 359–364. [Google Scholar] [CrossRef] [Green Version]
- Mitali, J.; Dhinakaran, S.; Mohamad, A.A. Energy storage systems: A review. Energy Storage Sav. 2022, 1, 166–216. [Google Scholar] [CrossRef]
- Choudhury, S. Review of energy storage system technologies integration to microgrid: Types, control strategies, issues, and future prospects. J. Energy Storage 2022, 48, 103966. [Google Scholar] [CrossRef]
- Całus, D.; Gałuszkiewicz, Z.; Gałuszkiewicz, P. Porównanie Systemów Magazynowania Energii Elektrycznej—ProEnergo—Możliwości i Horyzonty Ekoinnowacyjności—Energetyka Odnawialna i Magazynowanie Energii; Instytut Naukowo-Wydawniczy “Spatium”: Radom, Poland, 2016; pp. 10–24. [Google Scholar]
- Rashid, M.H. Power Electronics Handbook, 3rd ed.; Butterworth-Heinemann is an Imprint of Elsevier: Burlington, MA, USA, 2011. [Google Scholar]
- Lai, C.S.; Locatelli, G.; Pimm, A.; Wu, X.; Lai, L.L. A review on long-term electrical power system modeling with energy storage. J. Clean. Prod. 2021, 280, 124298. [Google Scholar] [CrossRef]
- Taraft, S.; Rekioua, D.; Aouzellag, D. Wind Power Control System Associated to the Flywheel Energy Storage System Connected to the Grid. Energy Procedia 2013, 36, 1147–1157. [Google Scholar] [CrossRef] [Green Version]
- Martens, D. (Ed.) European Energy Storage Technology Development Roadmap towards 2030; European Association for Storage of Energy, European Energy Research Alliance. 2014. Available online: https://ease-storage.eu/wp-content/uploads/2015/10/EASE-EERA-recommendations-Roadmap-LR.pdf (accessed on 1 October 2022).
- IEA Analysis and EPRI (Electric Power Research Institute). Electrical Energy Storage Technology Options Report; EPRI: Palo Alto, CA, USA, 2010.
- Ruddell, A.J.; Schoennenbeck, G.S.; Jones, R.; Bleijs, J.A.M. Power Converters Flywheel Energy Storage Systems; Final Report of EU Project No JOR3-CT95-0070; European Commission: Brussels, Belgium, 1998. [Google Scholar]
- Šonský, J.; Tesař, V. Design of a stabilised flywheel unit for efficient energy storage. J. Energy Storage 2019, 24, 100765. [Google Scholar] [CrossRef]
- Hannan, M.A.; Wali, S.B.; Ker, P.J.; Rahman, M.S.A.; Mansor, M.; Ramachandaramurthy, V.K.; Muttaqi, K.M.; Mahlia, T.M.I.; Dong, Z.Y. Battery energy-storage system: A review of technologies, optimization objectives, constraints, approaches, and outstanding issues. J. Energy Storage 2021, 42, 103023. [Google Scholar] [CrossRef]
- Wicki, S.; Erik, G.; Hansen, B. Clean energy storage technology in the making: An innovation systems perspective on flywheel energy storage. J. Clean. Prod. 2017, 1562, 1118–1134. [Google Scholar] [CrossRef] [PubMed]
- Bazdar, E.; Sameti, M.; Nasiri, F.; Haghighat, F. Compressed air energy storage in integrated energy systems: A review. Renew. Sustain. Energy Rev. 2022, 167, 112701. [Google Scholar] [CrossRef]
- Barlik, R.; Nowak, M. Energoelektronika—Elementy, Podzespoły, Układy; Oficyna Wydawnicza Politechniki Warszawskiej: Warszawa, Poland, 2014. [Google Scholar]
- Koohi-Fayegh, S.; Rosen, M.A. A review of energy storage types, applications and recent developments. J. Energy Storage 2020, 27, 101047. [Google Scholar] [CrossRef]
- Wang, L. PID Control System Design and Automatic Tuning Using MATLAB/Simulink; Wiley-IEEE Press: Piscataway, NJ, USA, 2020. [Google Scholar]
- Zhang, X.; Yang, J. An improved discharge control strategy with load current and rotor speed compensation for high-speed flywheel energy storage system. In Proceedings of the 17th International Conference on Electrical Machines and Systems, Hangzhou, China, 22–25 October 2014; pp. 318–324. [Google Scholar]
- Chen, X.; Zhou, J.; Shi, M.; Yan, L.; Zuo, W.; Wen, J. A Novel Virtual Resistor and Capacitor Droop Control for HESS in Medium-Voltage DC System. IEEE Trans. Power Syst. 2019, 34, 2518–2527. [Google Scholar] [CrossRef]
- The Mathworks Inc. Simscape Electrical. Reference, R2022a; The Mathworks Inc.: Natick, MA, USA, 2022. [Google Scholar]
- Bose, B.K. Power Electronics and Motor Drives. Advances and Trends, 2nd ed.; Academic Press: London, UK, 2021. [Google Scholar]
- Khan, M.J.; Iqbal, M.T. Simplified modeling of rectifier-coupled brushless DC generators. In Proceedings of the 4th International Conference on Electrical and Computer Engineering, Dhaka, Bangladesh, 19–21 December 2006; pp. 349–352. [Google Scholar]
- Krause, P.C.; Wasynczuk, O.; Sudhoff, S.D. Analysis of Electric Machinery and Drive Systems; Wiley-IEEE Press: Piscataway, NJ, USA, 2013. [Google Scholar]
- Łastowiecki, J. Układy Pomiarowe Prądu w Energoelektronice; Centralny Ośrodek Szkolenia i Wydawnictw SEP: Warszawa, Poland, 2003. [Google Scholar]

| Parameter | Value | Unit |
|---|---|---|
| BLDC mogen | ||
| Nominal power Pn | 50 | kW |
| Nominal rotational speed ωmn | 8000 | rpm |
| Number of pole pairs, p | 1 | - |
| Stator resistance, Rs | 4.3 × 10−3 | Ω |
| Stator inductance, Ls | 69 × 10−6 | H |
| Flux linkage, λ | 0.42 | V·s |
| Cable resistance, Rcable | 2.9 × 10−3 | Ω |
| Flywheel (outrunner rotor) moment of inertia, J | 527.4 | kg·m2 |
| Flywheel viscous friction, B | 0.05 | N·m·s |
| 6T thyristor bridge | ||
| Snubber resistance, Rsnub | 47 | Ω |
| Snubber capacitance, Cs | 0.1 × 10−6 | F |
| Thyristor resistance in ON state, Ron | 0.001 | Ω |
| DC link (output circuit) | ||
| DC link coil, Ldc | 1 × 10−3 | H |
| DC link capacitance, Cdc | 20.8 × 10−3 | F |
| Load resistance, Rload | 0.5; 1.0 | Ω |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gałuszkiewicz, P.; Gałuszkiewicz, Z.; Baran, J. Simulation Studies of Energy Recovery in a BLDC Motor-Based Kinetic Energy Storage. Energies 2022, 15, 7494. https://doi.org/10.3390/en15207494
Gałuszkiewicz P, Gałuszkiewicz Z, Baran J. Simulation Studies of Energy Recovery in a BLDC Motor-Based Kinetic Energy Storage. Energies. 2022; 15(20):7494. https://doi.org/10.3390/en15207494
Chicago/Turabian StyleGałuszkiewicz, Patryk, Zbigniew Gałuszkiewicz, and Janusz Baran. 2022. "Simulation Studies of Energy Recovery in a BLDC Motor-Based Kinetic Energy Storage" Energies 15, no. 20: 7494. https://doi.org/10.3390/en15207494
APA StyleGałuszkiewicz, P., Gałuszkiewicz, Z., & Baran, J. (2022). Simulation Studies of Energy Recovery in a BLDC Motor-Based Kinetic Energy Storage. Energies, 15(20), 7494. https://doi.org/10.3390/en15207494






