Waveform Quality Evaluation Method of Variable-Frequency Current Based on Curve Fitting
Abstract
:1. Introduction
2. Calculation Method of WD Based on Curve Fitting
2.1. FFT Method for Calculating THD of Periodic Signals
2.2. Curve Fitting Method for WD of Periodic Signals
2.3. Calculation Method of WD of Variable-Frequency Signal Based on Curve Fitting
- (a)
- The goal is to find the optimal coefficient βj to minimize the sum of squared residuals; that is, the partial derivative of S over βj equals 0:
- (b)
- In nonlinear systems, Equation (10) is a function of variables and coefficients to be solved, and there is no analytical solution. Therefore, we give an initial value and use the iterative method to approximate the solution:where k is the number of iterations.
- (c)
- In order to make each iteration function linear, the nonlinear function is expanded to the Taylor series at βk:where .
- (d)
- At this time, the residual is expressed by:Equation (13) is substituted into Equation (10):The matrix form is:The final iteration formula of β is:where Jf is the Jacobian matrix of function y = f(x, β) versus β, .
3. Calculation Method for Waveform Distortion of Variable-Frequency Current of Inverter Output
3.1. Theoretical Model of Inverter Output Variable-Frequency Current
3.1.1. Theoretical Model of Linear Variable-Frequency Current
3.1.2. Theoretical Model of Nonlinear Variable-Frequency Current
3.2. Waveform Distortion of Variable-Frequency Current
3.2.1. Waveform Distortion of Linear Variable-Frequency Current
3.2.2. Waveform Distortion of Nonlinear Variable-Frequency Current
4. Simulation Verification
4.1. Waveform Quality Evaluation of Constant-Frequency Current
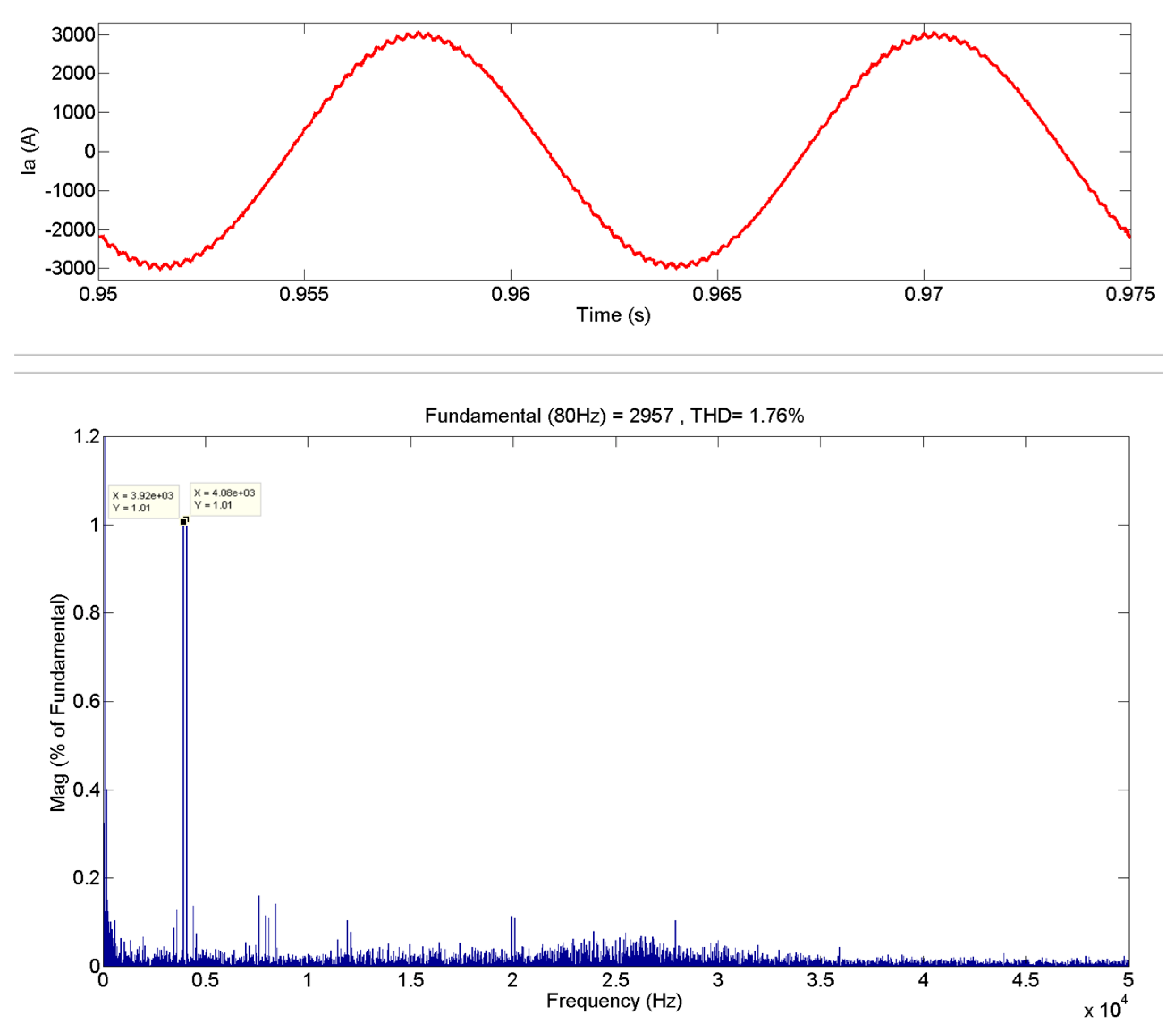
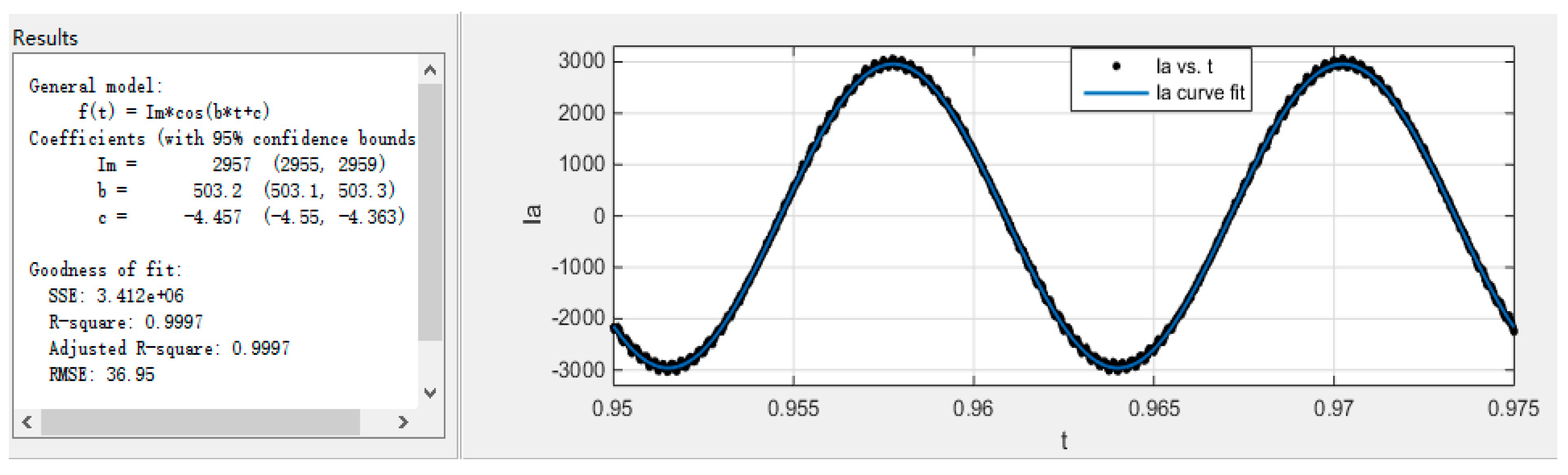
4.1.1. Waveform Quality Evaluation of Constant-Frequency Current for Higher Oversampling
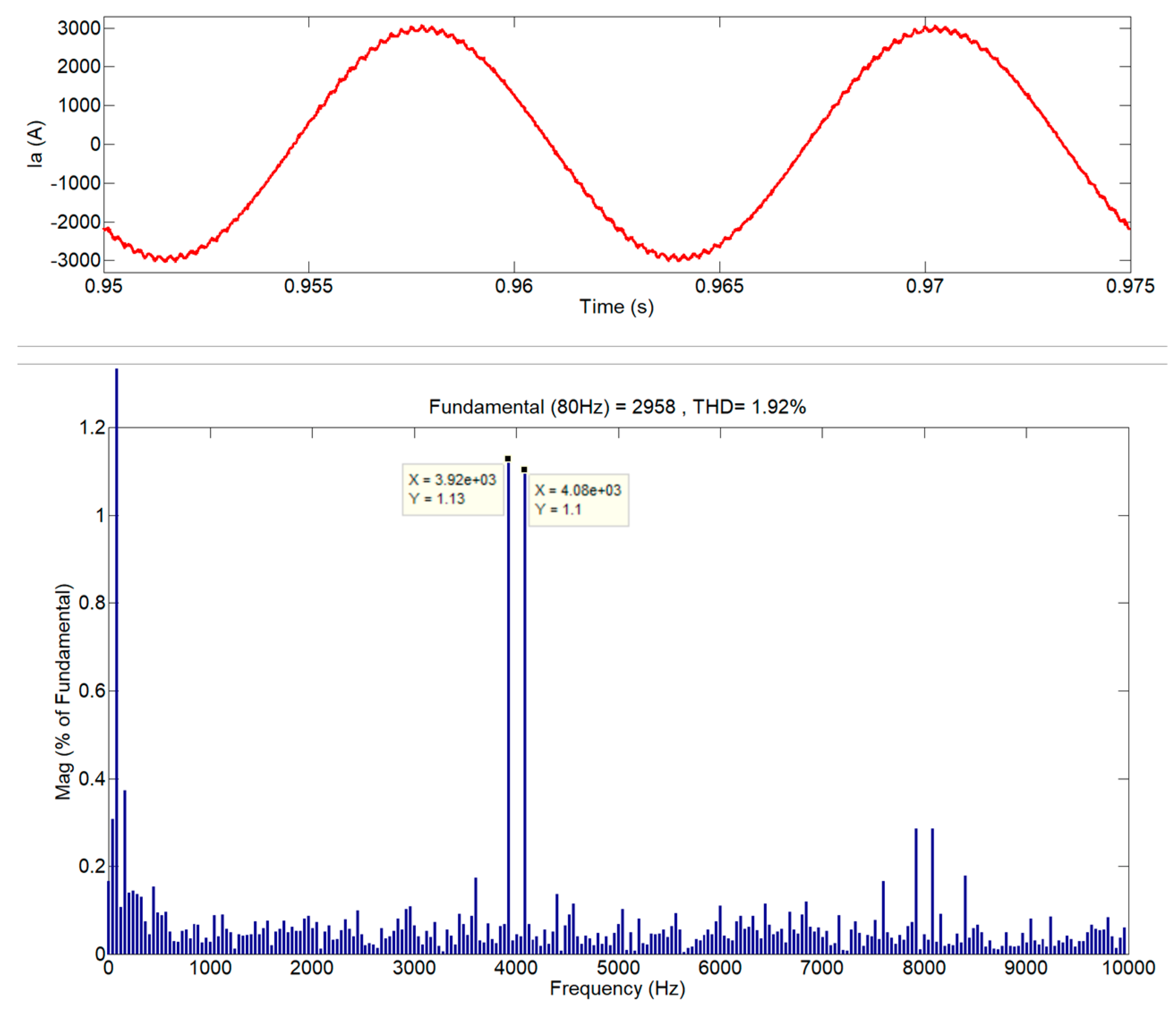
4.1.2. Waveform Quality Evaluation of Constant-Frequency Current for Lower Oversampling
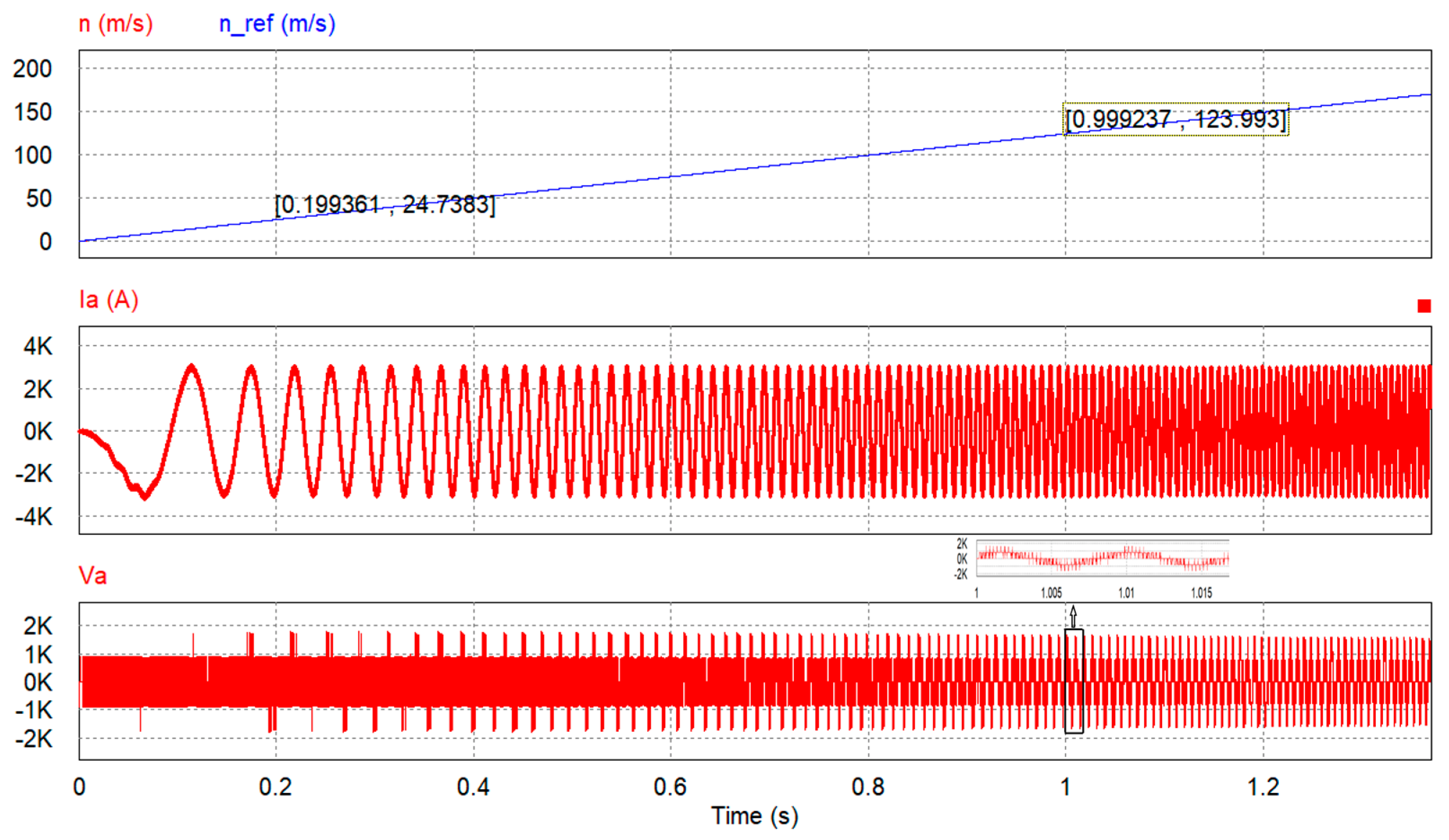
4.2. Waveform Quality Evaluation of Linear Variable-Frequency Current
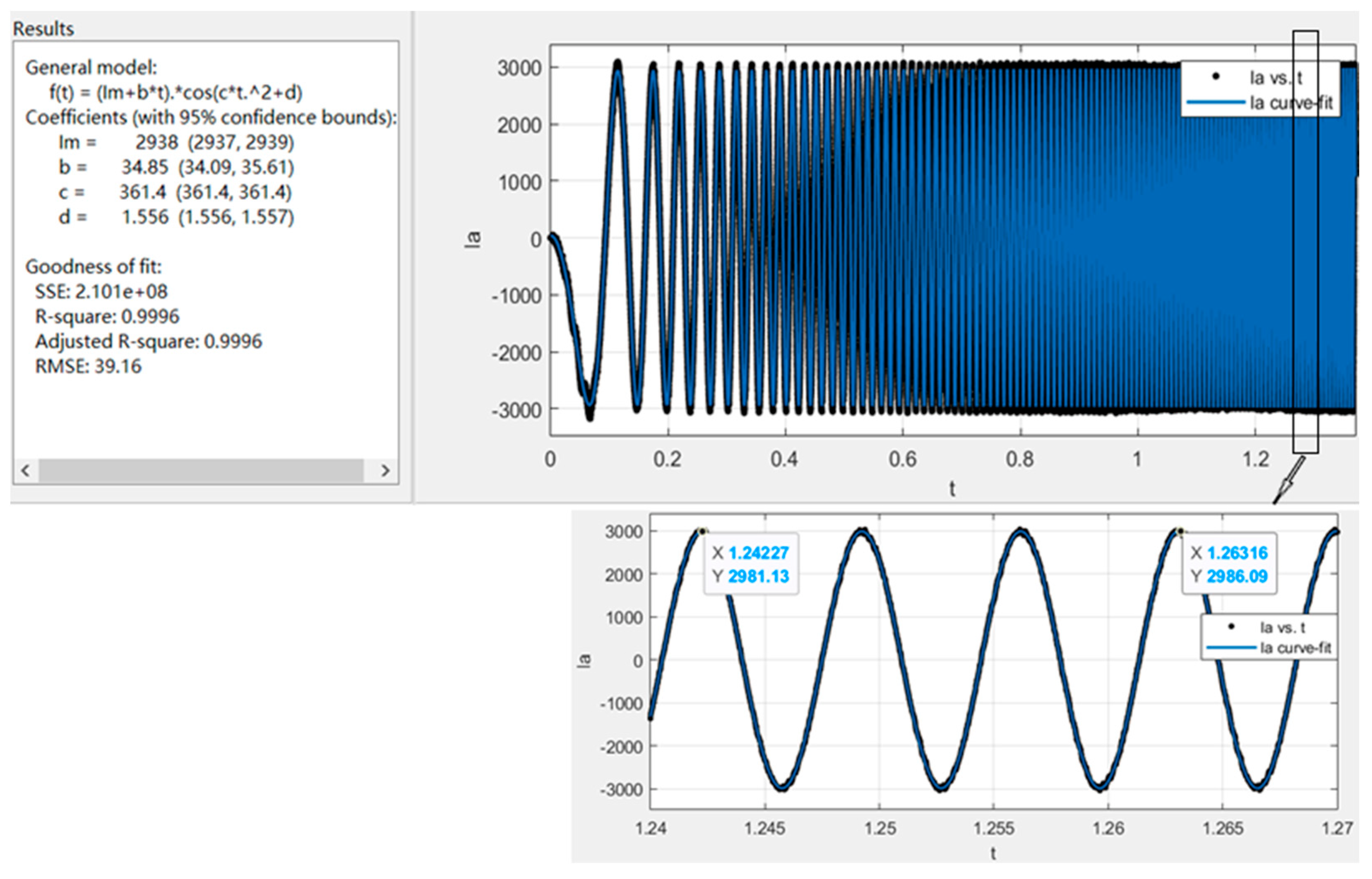
4.2.1. Simulation Calculation of IWDVF Based on Curve Fitting
4.2.2. Approximate Estimation of IWDVF with Average Value of Constant-Frequency ITHD
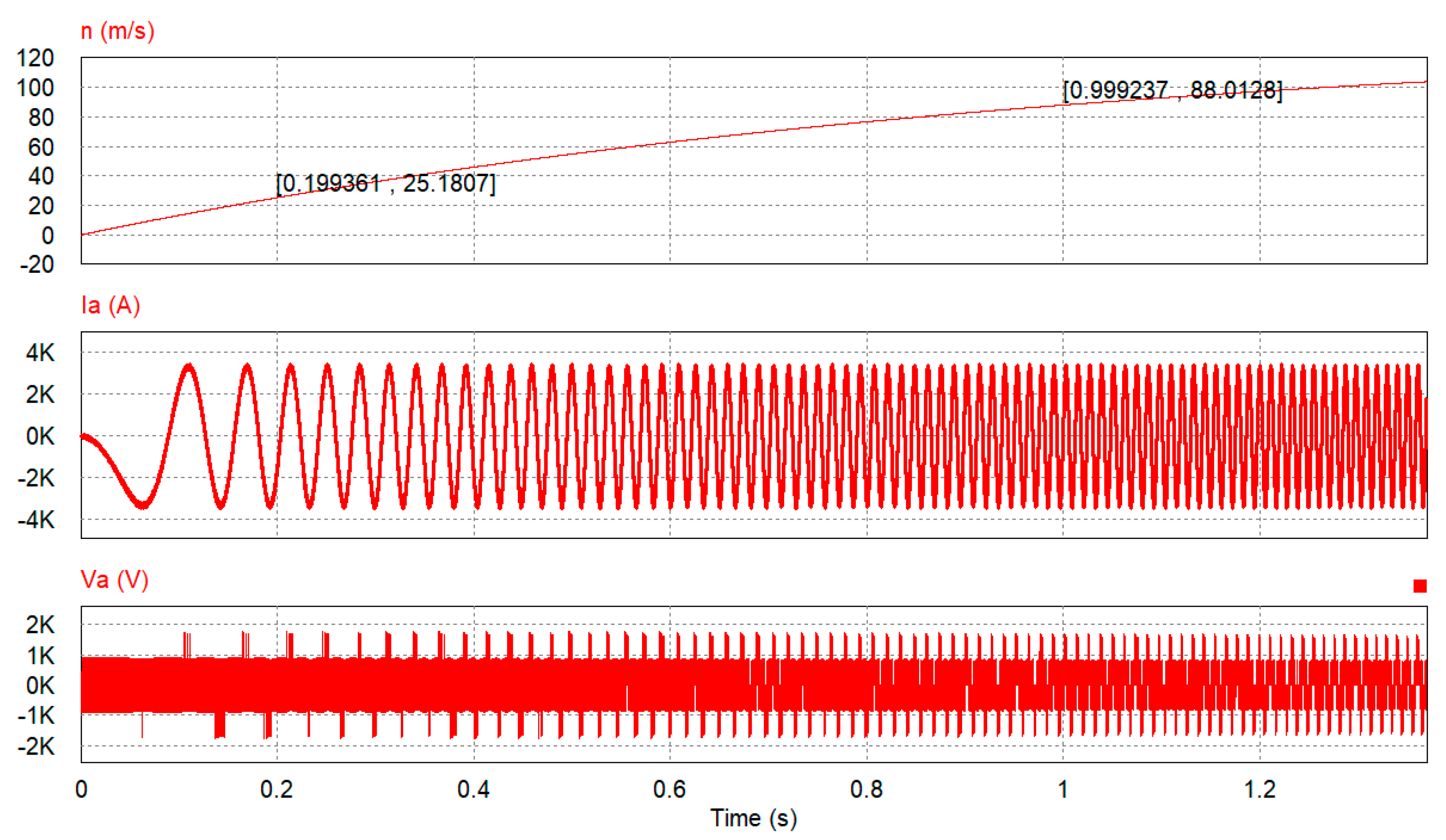
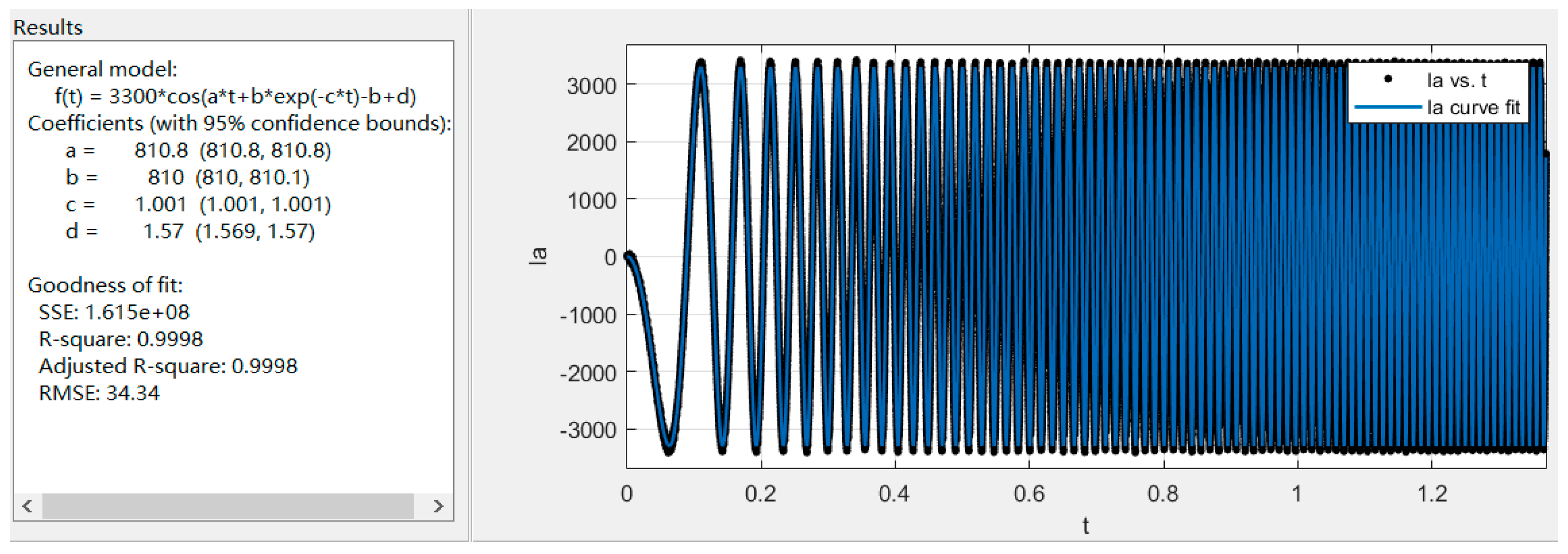
4.3. Waveform Quality Evaluation of Nonlinear Variable-Frequency Current
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, G.; Yan, Y.; Wang, Z.; Xia, C. An Analytical Evaluation Method for Output Waveform Quality of Three-level Inverters Based on the Amplitude of the Mean Current Ripple Vector. Proc. CSEE 2017, 37, 6410–6417. (In Chinese) [Google Scholar]
- Beig, A.R.; Kanukollu, S.; Al Hosani, K.; Dekka, A. Space-vector-based synchronized three-level discontinuous PWM for medium-voltage high-power VSI. IEEE Trans. Ind. Electron. 2014, 61, 3891–3901. [Google Scholar] [CrossRef]
- Kelly, J.; Aldaiturriaga, E.; Ruiz-Minguela, P. Applying international power quality standards for current harmonic distortion to wave energy converters and verified device emulators. Energies 2019, 12, 3654. [Google Scholar] [CrossRef] [Green Version]
- Xiao, X.; Collin, A.J.; Djokic, S.Z.; Yanchenko, S.; Möller, F.; Meyer, J.; Langella, R.; Testa, A. Analysis and Modelling of Power-Dependent Harmonic Characteristics of Modern PE Devices in LV Networks. IEEE Trans. Power Deliv. 2017, 32, 1014–1023. [Google Scholar] [CrossRef] [Green Version]
- IEEE Standard 519-2014; IEEE 519 Recommended Practice and Requirements for Harmonic Control in Electric Power Systems. IEEE: New York, NY, USA, 2014.
- IEEE Std. 1547-2018; Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces. IEEE: New York, NY, USA, 2018.
- Hu, Z.; Zhang, Y.; Yin, J.; Liu, F. Overview of Maglev electromagnetic boost launch technology for aerospace vehicles. Winged Missile 2016, 12, 54–59. [Google Scholar]
- Ma, W.; Xiao, F.; Nie, S. Applications and Development of Power Electronics in Electromagnetic Launch System. Trans. China Electrotech. Soc. 2016, 31, 1–10. [Google Scholar]
- Ma, W.; Lu, J. Electromagnetic Launch Technology. J. Natl. Univ. Def. Technol. 2016, 38, 1–5. [Google Scholar]
- Fair, H.D. Advances in Electromagnetic Launch Science and Technology and Its Applications. IEEE Trans. Magn. 2009, 45, 225–230. [Google Scholar] [CrossRef]
- Basir, M.S.S.M.; Ismail, R.C.; Yusof, K.H.; Katim, N.I.A.; Isa, M.N.M.; Naziri, S.Z.M. An implementation of Short Time Fourier Transform for Harmonic Signal Detection. J. Phys. Conf. Ser. 2020, 1755, 012013. [Google Scholar] [CrossRef]
- Arranz-Gimon, A.; Zorita-Lamadrid, A.; Morinigo-Sotelo, D.; Duque-Perez, O. A Review of Total Harmonic Distortion Factors for the Measurement of Harmonic and Interharmonic Pollution in Modern Power Systems. Energies 2021, 14, 6467. [Google Scholar] [CrossRef]
- Ma, L.; Zhou, L.; Wang, L.; Zhang, H. Adaptive harmonic detection algorithm based on fourier series. Electron. Meas. Technol. 2016, 39, 34–37. [Google Scholar]
- Zhao, Y.; Huo, K.; Chen, Z. Research and Implementation of AC Distortion Factor Measurement. Electr. Meas. Instrum. 2014, 51, 74–79. [Google Scholar]
- Liang, Z.; Zhu, J. The Correction of the Influence of Quantization Error to the Evaluation of the Distortion of Periodic Signal. Chin. J. Sci. Instrum. 2000, 21, 640–643. [Google Scholar]
- Martinek, R.; Rzidky, J.; Jaros, R.; Bilik, P.; Ladrova, M. Least mean squares and recursive least squares algorithms for total harmonic distortion reduction using shunt active power filter control. Energies 2019, 12, 1545. [Google Scholar] [CrossRef]
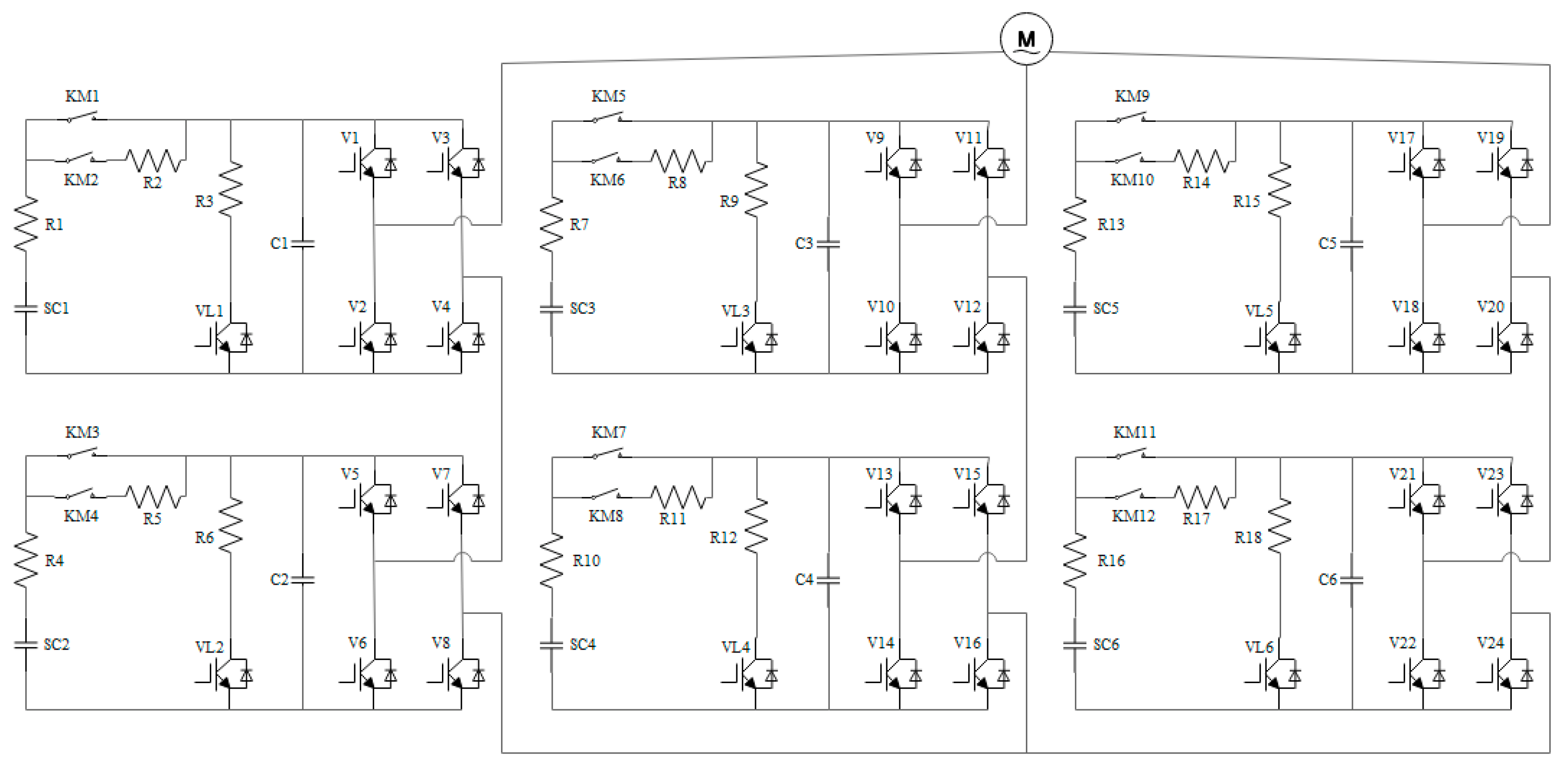

| H-Bridge Unit | Synchronous Motor | ||||
|---|---|---|---|---|---|
| SC1-6 | Supercapacitor capacitance | 17.37 F | Rs | Stator winding resistance | 0.0367 Ω |
| Supercapacitor voltage | 912 V | Ld, Lq | d-axis and q-axis inductance | 0.125 mH | |
| Supercapacitor internal resistance | 119.7 mΩ | J | Moment of inertia | 22.2 kg·m2 | |
| C1-6 | Support capacitance | 20 mF | B | Viscous friction coefficient | 0.25 N·s/m |
| R1,4,7,10,13,16 | Bus resistance | 0.4 mΩ | Ψf | Flux linkage | 0.91 Wb |
| V1-24 | IGBT rated voltage | 1700 V | P | Number of pole pairs | 2 |
| IGBT rated current | 3600 A | τ | Polar distance | 0.54 m | |
| Pn | Rated power | 4.5 MW | |||
| Curve Fitting | FFT | |||
|---|---|---|---|---|
| Sampling Frequency | Fitting Expression | RMSE | IWD | ITHD |
| fs = 100 kHz | 36.95 | 1.76% | 1.76% | |
| fs = 20 kHz | 40.29 | 1.92% | 1.92% | |
| f(Hz) | ITHD | f(Hz) | ITHD | f(Hz) | ITHD |
|---|---|---|---|---|---|
| 10 | 1.72% | 60 | 1.79% | 110 | 1.63% |
| 20 | 1.78% | 70 | 1.79% | 120 | 1.62% |
| 30 | 1.79% | 80 | 1.76% | 130 | 1.64% |
| 40 | 1.78% | 90 | 1.78% | 140 | 2.09% |
| 50 | 1.78% | 100 | 1.67% | 150 | 2.20% |
| Curve Fitting | FFT | |||
|---|---|---|---|---|
| Constant-frequency current | Fitting Expression | RMSE | IWD | ITHD |
| 36.95 | 1.76% | 1.76% | ||
| Fitting expression | RMSE | IWDVF | Average value of ITHD | |
| Linear variable-frequency current | 39.16 | 1.88% | 1.79% | |
| Nonlinear variable-frequency current | 34.34 | 1.47% | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, S.; Liu, Y. Waveform Quality Evaluation Method of Variable-Frequency Current Based on Curve Fitting. Energies 2022, 15, 7594. https://doi.org/10.3390/en15207594
Zhao S, Liu Y. Waveform Quality Evaluation Method of Variable-Frequency Current Based on Curve Fitting. Energies. 2022; 15(20):7594. https://doi.org/10.3390/en15207594
Chicago/Turabian StyleZhao, Shengquan, and Yaozong Liu. 2022. "Waveform Quality Evaluation Method of Variable-Frequency Current Based on Curve Fitting" Energies 15, no. 20: 7594. https://doi.org/10.3390/en15207594





