1. Introduction
Nowadays, the heat and electricity we use are mainly generated through power plants. During the combustion process of a station boiler, large amounts of polluting gases are produced, such as NOx, SO
2 and CO
2, that cause great harm to the human living environment. Simultaneously, a large amount of coal is consumed. Coal resources are becoming increasingly scarce; the goals of saving energy and emission reduction are imminent. The realization of dynamic multi-objective optimal control of boiler combustion process under variable loads is an effective method to reduce environmental pollution and save coal resources, and is called the boiler combustion optimization problem [
1,
2]. In order to solve the problem, the first priority is to establish the multi-dimensional feature model of the boiler combustion system. However, the boiler combustion system has complex characteristics with nonlinearity, strong coupling and large hysteresis, making it difficult to be modeled by traditional mathematical mechanistic methods. Zhou et al. have successively applied artificial neural networks or support vector machines (SVM) [
3,
4] combined with swarm intelligence optimization algorithms to model boiler combustion systems [
5,
6,
7,
8,
9,
10]. For example, ref. [
5] combined ANN with genetic algorithms (GA), ref. [
7] combined SVM and a meta-genetic algorithm (MGA), and ref. [
9] combined SVM and ant colony optimization (ACO) [
11]. These research results showed that good prediction results could be obtained via applying artificial neural networks and support vector machines. Li and Ma et al. applied various improved extreme learning machine (ELM) models [
12,
13,
14] to establish prediction models for boiler thermal efficiency, NOx emission concentration or SO
2 emission concentration [
15,
16,
17,
18,
19,
20,
21]. For example, Li et al. proposed the fast-learning networks (FNN) by connecting the input and output layers of ELM and implemented the fast modeling of boiler combustion systems; Ma et al. proposed an improved online sequential ELM and implemented the real-time modeling of boiler combustion systems. However, it was proven that in traditional ANN and ELM there exists an over-fitting problem when solving small sample data regression problems. In addition, the model computation speed of SVM is slow when solving the large sample data regression problem. This paper firstly uses a newly neural network, called broad learning system [
22], to solve the modeling problem of boiler combustion systems.
Broad learning system (BLS), as a new neural network algorithm proposed in 2018, has greater advantages in multi-dimensional feature learning and computing time compared to other deep learning algorithms, such as deep belief network (DBN) [
23], deep boltzmann machine (DBM) [
24] and convolutional neural network (CNN) [
25]. Chen et al. [
26] proposed several variants of BLS to solve regression problems, and experimental results showed that BLS variants had better performance than other state-of-the-art methods, such as conventional BLS, ELM and SVM. BLS has been researched and applied in many fields in recent years [
27,
28,
29,
30,
31,
32,
33,
34]. For example, Shuang and Chen [
33] combined fuzzy system with BLS, proposed a new neuro-fuzzy algorithm, and applied it to solve regression and classification problems. Zhao et al. [
34] extended BLS using a stream regularization framework and proposed a new algorithm for semi-supervised learning to solve complex data classification problems. However, the hyper-parameters of BLS could seriously affect its model performance. If the hyper-parameters are set too large, BLS encounters an over-fitting problem and spends more computation time. If the hyper-parameters are set too small, the generalization ability of BLS is weakened. BLS has more hyper-parameters, and every hyper-parameter needs to be set in a wide range, so the optimal combination of several hyper-parameters is difficult to determine by using traditional methods. It is of great research value to design a method to optimize the hyper-parameters of BLS to ensure its good model performance. Nacef et al. [
35] leverages deep learning and network optimization techniques to solve various network configuration and scheduling problems, enabling fast self-optimization and the lifecycle management of networks, and demonstrating the great role of optimization techniques in saving runtime and reducing computational costs. In addition, swarm intelligence optimization algorithms can provide substantial benefits in reducing computational effort and improving system performance without a priori knowledge of the system parameters [
36]. To address the above-mentioned problem, this paper proposes a kind of hyper-parameter self-optimized broad learning system, namely SSA-BLS. The proposed method mainly introduces the optimization mechanism of sparrow search algorithm [
37] to determine the optimal hyper-parameter combination of BLS through three different behaviors of the sparrow population during foraging, i.e., sparrows as explorers provide search directions and regions for the optimal hyper-parameter combinations, sparrows as followers search through the guidance of explorers, and sparrows as vigilantes rely on anti-predation strategy to avoid hyper-parameter combinations from falling into local optima. The sparrow search algorithm (SSA) is a new swarm intelligence optimization algorithm proposed in 2020. Compared with particle swarm optimization (PSO) [
38,
39], gravitational search algorithm (GSA) [
40] and grey wolf optimization (GWO) [
41], the SSA had better computation efficiency. This paper combines SSA with BLS to automatically adjust the hyper-parameters and obtain the optimal hyper-parameter combination. In SSA-BLS, a mechanism to achieve automatic optimization of hyperparameters with the objective of minimizing the average root-mean-square-error (RMSE) of the testing set after ten-fold cross-validation [
42] is proposed in order to obtain better model accuracy and model stability.
In order to verify the effectiveness of SSA-BLS, it was applied to ten benchmark regression datasets. Compared with BLS, RELM [
43] and KELM [
44,
45], SSA-BLS can achieve the best model accuracy and model stability whose hyper-parameters are determined by using the nested cross-validation method [
46].
Simultaneously, the proposed SSA-BLS was applied to establish the prediction comprehensive model of thermal efficiency, NOx emission concentration and SO2 emission concentration. Compared with conventional BLS, the proposed SSA-BLS has better model accuracy and stronger stability. The experimental results reveal that the model accuracy can reach 10−2-10−3 by SSA-BLS.
The contributions of this paper are summarized as follows:
- (1)
A novel optimized BLS is proposed. SSA is firstly used to optimize the hyper-parameters of BLS, which can determine the optimal hyper-parameter combination.
- (2)
The proposed SSA-BLS is used to solve the regression problem of ten benchmark datasets.
- (3)
The proposed SSA-BLS and traditional BLS are firstly applied to establish the prediction conventional model of one circulation fluidized bed boiler combustion system.
The structure of this paper is as follows: basic knowledge and related works are given in
Section 2; the proposed SSA-BLS is given in
Section 3;
Section 4 shows the performance evaluation of the SSA-BLS;
Section 5 addresses the real-world modelling problem; the conclusion of this paper is in
Section 6.
3. The Proposed SSA-BLS
In the BLS model, the randomly generated weights and biases as well as its five hyper-parameters (convergence coefficient , regularization coefficient , the number of feature nodes , the number of feature mapping groups and the number of enhancement nodes ) all have an impact on its performance. Among them, the most influential on its model accuracy and model stability are the hyper-parameters , and . However, these three hyper-parameters have a wide range of values, so it is difficult to determine the best combination of hyper-parameters by traditional methods. An optimized broad learning system by sparrow search algorithm with self-adjusting hyper-parameters, i.e., SSA-BLS, is proposed in this paper to enhance the model performance and generalization capability.
The pseudo-code of the proposed SSA-BLS algorithm is shown in Algorithm 1.
| Algorithm 1. The pseudo-code of SSA-BLS |
| | Input: |
| | MaxIter: the maximum iterations |
| | dim: the number of hyper-parameters to be optimized |
| | pop: the number of hyper-parameter combination populations |
| | lb&ub: hyper-parameter combination search range |
| | X: the initial population of hyper-parameter combinations |
| | Output: |
| | the optimal hyper-parameter combination |
| | best fitness value |
| | Iterative Curve |
| 1 | Establish an objective function , i.e., the AVG of RMSE |
| | obtained by 10-fold cross-validation; |
| 2 | Generate pop hyper-parameter combinations as initial population; |
| 3 | Calculate the fitness values by BLS; |
| 4 | whiledo |
| 5 | | | Randomly select hyper-parameter combinations as explorers, |
| | | | followers and vigilantes; |
| 6 | | | for eachdo |
| 7 | | | | | Using Equation (7) to update locations; |
| 8 | | | end |
| 9 | | | for eachdo |
| 10 | | | | | Using Equation (8) to update locations; |
| 11 | | | end |
| 12 | | | for eachdo |
| 13 | | | | | Using Equation (9) to update locations; |
| 14 | | | end |
| 15 | | | Calculate the fitness values by BLS; |
| 16 | | | Compare with previous ; |
| 17 | | | ifthe current values better than then |
| 18 | | | | | Update the and ; |
| 19 | | | end |
| 20 | | | Save current to ; |
| 21 | | | |
| 22 | end |
The determination steps of three hyper-parameters are summarized as follows:
- (1)
Generate a certain number of hyper-parameter combinations randomly as the initial population for optimization.
- (2)
Calculate the fitness value of the hyper-parameter combinations in the initial population, which is the average of the root mean square error (RMSE) obtained by 10-fold cross-validation of the testing set.
The expression for calculating the root mean square error (RMSE) is shown in Equation (10).
where
is the number of samples,
denotes the actual value and
denotes the predicted value.
The schematic diagram of the fitness value calculating process is shown in
Figure 2.
- (3)
A certain number of hyper-parameter combinations are randomly selected from the initial population as optimized explorers, and the positions are updated according to Equation (7).
- (4)
The other hyper-parameter combinations in the initial population act as optimized followers, and the positions are updated according to Equation (8).
- (5)
A certain number of hyper-parameter combinations are randomly selected from the optimized explorers and followers as the optimized vigilantes, and the positions are updated according to Equation (9).
- (6)
Repeat steps (3)–(5) until the maximum number of iterations is reached, and output the individual with the highest fitness value, i.e., the hyper-parameter combination that makes the smallest average of RMSE obtained from a 10-fold cross-validation of the testing set.
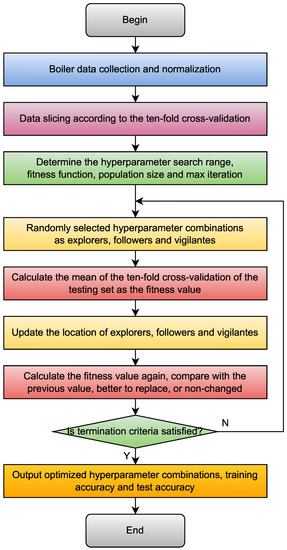
According to the above explanations, the flowchart of the SSA-BLS is shown in
Figure 3.
4. Simulation
In order to evaluate the performance of the proposed SSA-BLS, it was applied to the ten benchmark regression datasets listed in
Table 1, where the dataset Gasoline octane is from the web:
https://www.heywhale.com/home (accessed on 5 January 2022), Fuel consumption is from the web:
https://www.datafountain.cn (accessed on 10 January 2022) and the other datasets are from the web:
http://www.liaad.up.pt/~ltorgo/Regression/DtaSets.html (accessed on 9 December 2021). All evaluations for RELM, KELM, BLS and SA-ELM were carried out in MacOS Mojave 10.14.6 and Python 3.9.9, running on a laptop with AMD Intel Iris Plus Graphics 645 1536MB, Processor 1.4GHz Intel Core i5 and RAM 8GB 2133MHz.
The parameters in SSA-BLS were set as follows: the initial population size and the maximum number of iterations for hyper-parameter optimization were set to 20 and 100. The compression factor in the mapping layer was set to 0.8 and the regularization factor in the enhancement layer was set to 2. The optimization range of hyper-parameter combination is shown in
Table 2.
Model accuracy and model stability were assessed by the average (AVG) and standard deviation (Sd) of the RMSE obtained from the ten-fold cross-validation. The averages (AVG) of the MAPE obtained from the ten-fold cross-validation were also used to evaluate the model accuracy. A smaller average value indicates higher model accuracy, and a smaller standard deviation indicates better model stability, and vice versa.
SSA-BLS was applied to the ten benchmark regression datasets in
Table 1 and compared with BLS, RELM and KELM; the simulation results are shown in
Table 3,
Table 4 and
Table 5. The hyper-parameters of the compared algorithm are determined by using the nested cross-validation method [
42]. And the bolds in the table indicate the best experimental results of the four algorithms on each dataset.
As shown in
Table 4, for the testing samples of the datasets, compared with RELM, KELM and BLS, the proposed SSA-BLS obtains better model accuracy on nine benchmark regression problems (gasoline octane, fuel consumption, abalone, bank domains, Boston housing, delta elevators, forest fires, machine CPU, servo) and better model stability on seven benchmark regression problems (bank domains, Boston housing, forest fires, machine CPU, servo).
As shown in
Table 5, for the training samples of the datasets, compared with RELM, KELM and BLS, the proposed SSA-BLS obtains better model performance on all ten benchmark regression problems and for the testing samples of the datasets, the proposed SSA-BLS obtains better model performance on nine benchmark regression problems (except auto MPG).
The effectiveness of SSA-BLS is proved by the above simulation experiments. However, SSA-BLS requires more computing time to establish the model compared with other related algorithms, so it is not suitable for online learning. In this paper, model training and testing belong to offline learning, so this algorithm mainly pursues the accuracy and stability of the model.
5. Real-World Design Problem
As a new neural network algorithm, BLS can effectively solve the modeling problems of complex systems. In this paper, the proposed SSA-BLS was applied to establish the prediction models for thermal efficiency (TE), NOx emission concentration and SO2 emission concentration of a 330 MW circulating fluidized bed boiler (CFBB).
There are 27 variables affecting the thermal efficiency and harmful gas emission concentration of a CFBB, mainly including load, coal feeder feeding rate, the primary air velocity, the secondary air velocity, oxygen concentration in the flue gas and the carbon content of fly ash. The symbols and descriptions of each variable are shown in
Table 6. A total of 10,000 data samples are collected from a 330MW CFBB under different operating loads, some of which are shown in
Table 7.
The boiler data is normalized and divided into training sets and testing sets in the ratio of 7:3.
The proposed SSA-BLS and BLS are applied to this boiler data and the experimental results are shown in
Table 8,
Table 9,
Table 10 and
Table 11. The hyper-parameters of BLS are determined by using the nested cross-validation method [
42]. And the bolds in the table indicate the best experimental results of the four algorithms on each objective.
As shown in
Table 9,
Table 10 and
Table 11, compared with RELM, KELM and BLS, the proposed SSA-BLS obtained better model accuracy and model stability in the prediction models established for the NOx emissions concentration and thermal efficiency of CFBB both on the training set and testing set. However, its model prediction accuracy for the SO
2 emission concentration of CFBB was not as good as that of KELM.
The fitting diagrams and error diagrams of SSA-BLS for modeling the three objectives of CFBB on the testing set are shown in
Figure 4,
Figure 5,
Figure 6,
Figure 7,
Figure 8 and
Figure 9, where the red line and the blue line in the fitting diagram indicate the true values and predicted values of the partial testing set, and the curve in the error diagram represent the error of the predicted values compared to the true values for the testing set.
As shown in
Figure 4,
Figure 5,
Figure 6,
Figure 7,
Figure 8 and
Figure 9, the proposed SSA-BLS effectively establishes the prediction models for the three objectives of CFBB. The three prediction models all have great fitting effect and small fitting error on the testing set.
6. Conclusions
This paper proposed a novel optimized broad learning system by combining with a sparrow search algorithm. That is to say, the sparrow search algorithm was used to optimize the hyper-parameters of broad learning systems. Compared with other state-of-the-art methods, the proposed SSA-BLS reveals better regression accuracy and model stability on testing ten benchmark datasets. Additionally, the SSA-BLS was used to build the collective model of thermal efficiency, NOx and SO2 emissions concentration of one 330MW circulation fluidized bed boiler. Experiment results show that the model accuracy can be achieved 10−2–10−3. The proposed SSA-BLS is an effective modelling method.
However, the proposed SSA-BLS takes more time to determine the optimal hyperparameters. This method improves the accuracy of the model but reduces the speed of model computation. Moreover, this method is also not applicable to online modeling due to the long modeling time. In addition, SSA-BLS only tunes and optimizes the hyperparameters in terms of model accuracy, while ignoring the model stability aspects. In the future, the performance of SSA-BLS will be further improved, including computation speed, model complexity and generalization ability. Additionally, based on the established comprehensive model, we will use one heuristic optimization algorithm to adjust the boiler’s operational parameters for enhancing thermal efficiency and reducing NOx/SO2 emissions concentration.