Model NOx, SO₂ Emissions Concentration and Thermal Efficiency of CFBB Based on a Hyper-Parameter Self-Optimized Broad Learning System

Abstract

At present, establishing a multidimensional characteristic model of a boiler combustion system plays an important role in realizing its dynamic optimization and real-time control, so as to achieve the purpose of reducing environmental pollution and saving coal resources. However, the complexity of the boiler combustion process makes it difficult to model it using traditional mathematical methods. In this paper, a kind of hyper-parameter self-optimized broad learning system by a sparrow search algorithm is proposed to model the NOx, SO₂ emissions concentration and thermal efficiency of a circulation fluidized bed boiler (CFBB). A broad learning system (BLS) is a novel neural network algorithm, which shows good performance in multidimensional feature learning. However, the BLS has several hyper-parameters to be set in a wide range, so that the optimal combination between hyper-parameters is difficult to determine. This paper uses a sparrow search algorithm (SSA) to select the optimal hyper-parameters combination of the broad learning system, namely as SSA-BLS. To verify the effectiveness of SSA-BLS, ten benchmark regression datasets are applied. Experimental results show that SSA-BLS obtains good regression accuracy and model stability. Additionally, the proposed SSA-BLS is applied to model the combustion process parameters of a 330 MW circulating fluidized bed boiler. Experimental results reveal that SSA-BLS can establish the accurate prediction models for thermal efficiency, NOx emission concentration and SO₂ emission concentration, separately. Altogether, SSA-BLS is an effective modelling method.

1. Introduction

Nowadays, the heat and electricity we use are mainly generated through power plants. During the combustion process of a station boiler, large amounts of polluting gases are produced, such as NOx, SO₂ and CO₂, that cause great harm to the human living environment. Simultaneously, a large amount of coal is consumed. Coal resources are becoming increasingly scarce; the goals of saving energy and emission reduction are imminent. The realization of dynamic multi-objective optimal control of boiler combustion process under variable loads is an effective method to reduce environmental pollution and save coal resources, and is called the boiler combustion optimization problem [1,2]. In order to solve the problem, the first priority is to establish the multi-dimensional feature model of the boiler combustion system. However, the boiler combustion system has complex characteristics with nonlinearity, strong coupling and large hysteresis, making it difficult to be modeled by traditional mathematical mechanistic methods. Zhou et al. have successively applied artificial neural networks or support vector machines (SVM) [3,4] combined with swarm intelligence optimization algorithms to model boiler combustion systems [5,6,7,8,9,10]. For example, ref. [5] combined ANN with genetic algorithms (GA), ref. [7] combined SVM and a meta-genetic algorithm (MGA), and ref. [9] combined SVM and ant colony optimization (ACO) [11]. These research results showed that good prediction results could be obtained via applying artificial neural networks and support vector machines. Li and Ma et al. applied various improved extreme learning machine (ELM) models [12,13,14] to establish prediction models for boiler thermal efficiency, NOx emission concentration or SO₂ emission concentration [15,16,17,18,19,20,21]. For example, Li et al. proposed the fast-learning networks (FNN) by connecting the input and output layers of ELM and implemented the fast modeling of boiler combustion systems; Ma et al. proposed an improved online sequential ELM and implemented the real-time modeling of boiler combustion systems. However, it was proven that in traditional ANN and ELM there exists an over-fitting problem when solving small sample data regression problems. In addition, the model computation speed of SVM is slow when solving the large sample data regression problem. This paper firstly uses a newly neural network, called broad learning system [22], to solve the modeling problem of boiler combustion systems.

Broad learning system (BLS), as a new neural network algorithm proposed in 2018, has greater advantages in multi-dimensional feature learning and computing time compared to other deep learning algorithms, such as deep belief network (DBN) [23], deep boltzmann machine (DBM) [24] and convolutional neural network (CNN) [25]. Chen et al. [26] proposed several variants of BLS to solve regression problems, and experimental results showed that BLS variants had better performance than other state-of-the-art methods, such as conventional BLS, ELM and SVM. BLS has been researched and applied in many fields in recent years [27,28,29,30,31,32,33,34]. For example, Shuang and Chen [33] combined fuzzy system with BLS, proposed a new neuro-fuzzy algorithm, and applied it to solve regression and classification problems. Zhao et al. [34] extended BLS using a stream regularization framework and proposed a new algorithm for semi-supervised learning to solve complex data classification problems. However, the hyper-parameters of BLS could seriously affect its model performance. If the hyper-parameters are set too large, BLS encounters an over-fitting problem and spends more computation time. If the hyper-parameters are set too small, the generalization ability of BLS is weakened. BLS has more hyper-parameters, and every hyper-parameter needs to be set in a wide range, so the optimal combination of several hyper-parameters is difficult to determine by using traditional methods. It is of great research value to design a method to optimize the hyper-parameters of BLS to ensure its good model performance. Nacef et al. [35] leverages deep learning and network optimization techniques to solve various network configuration and scheduling problems, enabling fast self-optimization and the lifecycle management of networks, and demonstrating the great role of optimization techniques in saving runtime and reducing computational costs. In addition, swarm intelligence optimization algorithms can provide substantial benefits in reducing computational effort and improving system performance without a priori knowledge of the system parameters [36]. To address the above-mentioned problem, this paper proposes a kind of hyper-parameter self-optimized broad learning system, namely SSA-BLS. The proposed method mainly introduces the optimization mechanism of sparrow search algorithm [37] to determine the optimal hyper-parameter combination of BLS through three different behaviors of the sparrow population during foraging, i.e., sparrows as explorers provide search directions and regions for the optimal hyper-parameter combinations, sparrows as followers search through the guidance of explorers, and sparrows as vigilantes rely on anti-predation strategy to avoid hyper-parameter combinations from falling into local optima. The sparrow search algorithm (SSA) is a new swarm intelligence optimization algorithm proposed in 2020. Compared with particle swarm optimization (PSO) [38,39], gravitational search algorithm (GSA) [40] and grey wolf optimization (GWO) [41], the SSA had better computation efficiency. This paper combines SSA with BLS to automatically adjust the hyper-parameters and obtain the optimal hyper-parameter combination. In SSA-BLS, a mechanism to achieve automatic optimization of hyperparameters with the objective of minimizing the average root-mean-square-error (RMSE) of the testing set after ten-fold cross-validation [42] is proposed in order to obtain better model accuracy and model stability.

In order to verify the effectiveness of SSA-BLS, it was applied to ten benchmark regression datasets. Compared with BLS, RELM [43] and KELM [44,45], SSA-BLS can achieve the best model accuracy and model stability whose hyper-parameters are determined by using the nested cross-validation method [46].

Simultaneously, the proposed SSA-BLS was applied to establish the prediction comprehensive model of thermal efficiency, NOx emission concentration and SO₂ emission concentration. Compared with conventional BLS, the proposed SSA-BLS has better model accuracy and stronger stability. The experimental results reveal that the model accuracy can reach 10−2-10−3 by SSA-BLS.

The contributions of this paper are summarized as follows:

(1)

A novel optimized BLS is proposed. SSA is firstly used to optimize the hyper-parameters of BLS, which can determine the optimal hyper-parameter combination.

(2)

The proposed SSA-BLS is used to solve the regression problem of ten benchmark datasets.

(3)

The proposed SSA-BLS and traditional BLS are firstly applied to establish the prediction conventional model of one circulation fluidized bed boiler combustion system.

The structure of this paper is as follows: basic knowledge and related works are given in Section 2; the proposed SSA-BLS is given in Section 3; Section 4 shows the performance evaluation of the SSA-BLS; Section 5 addresses the real-world modelling problem; the conclusion of this paper is in Section 6.

2. Basic Knowledge and Related Works

2.1. Broad Learning System

Broad learning system (BLS), as a novel artificial neural network algorithm, is capable of replacing deep architecture. It adds a dynamic stepwise update mechanism and a sparse self-coding algorithm to the random vector functional-link neural network (RVFLNN) [47,48,49], which greatly improves the model computing efficiency.

As opposed to RVFLN, BLS replaces the input layer with the mapping layer. The mapping layer of BLS is obtained by sparse representation and linear transformation of the input layer data. The augmentation layer is obtained by applying a nonlinear transformation to the activation function mapping layer. BLS connects the mapping layer and the enhancement layer together with the output layer to solve the connection weight of the neural networks. The structure diagram of BLS is shown in Figure 1.

Where $X\in R^{N\times M}$ is the input data with sample size $N$ and dimension $M$, and $Y\in R^{N\times 1}$ is the output data with sample size $N$ and dimension 1.

Assuming that the network structure has $n$ feature mappings and each feature mapping has $k$ feature nodes, the expression of the $i$th feature mapping $Z_i$ is shown in Equation (1).

$$Z_i=\left[\begin{array}{ccc}{\varphi }_i\left(x_1{W}_{i1}+{\beta }_{i1}\right)& \cdots & {\varphi }_i\left(x_N{W}_{i1}+{\beta }_{i1}\right)\\ ⋮& \ddots & ⋮\\ {\varphi }_i\left(x_1{W}_{ik}+{\beta }_{ik}\right)& \cdots & {\varphi }_i\left(x_N{W}_{ik}+{\beta }_{ik}\right)\end{array}\right]={\varphi }_i\left(X{W}_{ei}+{\beta }_{ci}\right),i=1,2,\cdots ,n$$

(1)

where ${\varphi }_i$ denotes the feature mapping function, $W_{ik}\in R^{M\times K}$ is the connection weight of the $i$th group of feature mappings to all input data and ${\beta }_{c_i}\in R^{1\times K}$ is the bias of the $i$th group of feature mappings, then the expression of all feature mappings $Z^n$ in the feature node layer is shown in Equation (2).

$$Z^n={\left[\begin{array}{c}{\varphi }_1\left(X{W}_{e1}+{\beta }_{e1}\right)\\ {\varphi }_2\left(X{W}_{e2}+{\beta }_{e2}\right)\\ ⋮\\ {\varphi }_n\left(X{W}_{en}+{\beta }_{en}\right)\end{array}\right]}^T=\left[\begin{array}{c}\left.Z_1{Z}_2\cdots Z_n\right]\end{array}\right.,j=1,2,\dots ,m$$

(2)

Similarly, the expression for the $j$th group of enhanced nodes $H_j$ is shown in Equation (3).

$$H_j=\left[\begin{array}{ccc}{\zeta }_j\left(Z_1{W}_{j1}+{\beta }_{j1}\right)& \cdots & {\zeta }_j\left(Z_n{W}_{j1}+{\beta }_{j1}\right)\\ ⋮& \ddots & ⋮\\ {\zeta }_j\left(Z_1{W}_{jl}+{\beta }_{jl}\right)& \cdots & {\zeta }_j\left(Z_n{W}_{jl}+{\beta }_{jl}\right)\end{array}\right]={\zeta }_j\left(Z^n{W}_{hj}+{\beta }_{hj}\right),j=1,2,\cdots ,m$$

(3)

where ${\zeta }_j$ denotes the activation function, $l$ is the number of the $j$th group of augmented nodes and $W_{hj}\in R^{kn\times l}$ and ${\beta }_{hj}\in R^{1\times l}$ are the connection weights and biases randomly generated by the system, then the expression of all the feature augmentation $H^m$ in the augmented node layer is shown in Equation (4).

$$H^m={\left[\begin{array}{c}{\zeta }_1\left(Z^n{W}_{h1}+{\beta }_{h1}\right)\\ {\zeta }_2\left(Z^n{W}_{h2}+{\beta }_{h2}\right)\\ ⋮\\ {\zeta }_m\left(Z^n{W}_{hm}+{\beta }_{hm}\right)\end{array}\right]}^T=\left[H_1{H}_2\cdots H_m\right]$$

(4)

Then the expression of the final network output $\widehat{Y}$ is shown in Equation (5).

$$\begin{array}{l}\widehat{Y}=\left[Z_1,\dots ,Z_n\mid \zeta \left(Z^n{W}_{h1}+{\beta }_{h1}\right),\dots \dots ,\zeta \left(Z^n{W}_{hm}+{\beta }_{hm}\right)\right]W^m\\ \left. =\left[Z_1,\dots ,Z_n\mid H_1,\dots \dots ,H_m\right)\right]W^m\\ =\left[Z^n\mid H^m\right]W^m\end{array}$$

(5)

Then the expression for the final connection weight $W^m$ is shown in Equation (6).

$$W^m={\left[Z^n\mid H^m\right]}^{+}Y$$

(6)

2.2. Sparrow Search Algorithm

Sparrow search algorithm (SSA) [34] is a novel swarm intelligence optimization algorithm based on the foraging and anti-predatory behaviors of sparrows. Its bionic principle is as follows: sparrows as explorers provide the search direction and region for the population, sparrows as followers search through the guidance of explorers, and sparrows as vigilantes rely on anti-predation strategies to avoid the population from falling into a local optimal solution.

The location update rules for the three types of sparrows are as follows:

(1)

For sparrows as explorers, when the warning value is less than the safety value, it indicates that the sparrow has not found a predator and can perform a wide range of jumping searches, and when its warning value is greater than or equal to the safety value, it indicates that the sparrow has found a predator and immediately moves to other places for searching.

(2)

For the sparrow as a follower, when its fitness value is less than or equal to half of the sparrows, it indicates that the sparrow did not obtain food and needs to move to other places to search, and when its fitness value is greater than half of the sparrows, it indicates that the sparrow can obtain food and will conduct a random search at the current location.

(3)

For the sparrow as vigilant, when its fitness value is not equal to the current best fitness value, it indicates that the sparrow is at the edge of the population and is highly vulnerable to predators, and when its fitness value is equal to the current best fitness value, it indicates that the sparrow is in the middle of the population and needs to move closer to other sparrows to reduce the risk of being predated.

Suppose there are $S$ sparrows in a $D$-dimensional search space, then the position of the $i$th sparrow in the $D$-dimensional search space is $X_i=\left[x_{ia},\cdots ,x_{id},\cdots ,x_{iD}\right],i=1,2,\cdots ,S$, where $x_{id}$ is the position of the $i$th sparrow in the $d$-dimension.

Sparrows as explorers generally account for 10–20% of the population, and their position is updated by the expression shown in Equation (7).

$$x_{id}^{i+1}=\left\{\begin{array}{l}{x}_{id}^t\cdot exp\left(\frac{-i}{\alpha T}\right) R_2<S_T\\ x_{id}^t+QL R_2⩾S_T\end{array}\right.$$

(7)

where $t$ is the current number of iterations; $T$ is the maximum number of iterations; $\alpha$ is a uniform random number between $\left(0, 1\right]$; $Q$ is a random number obeying the standard normal distribution; $L$ is a matrix of size $1\times d$ and all elements are 1; $R_2\in \left[0, 1\right]$ is the warning value; $S_T\in \left[0.5, 1\right]$ is the safety value.

The other sparrows in the population act as followers, and the expression for their position update is shown in Equation (8).

$$x_{id}^{t+1}=\left\{\begin{array}{l}Q\cdot exp\left(\frac{x{w}_d^t-x_{id}^t}{i^2}\right) i>\frac{n}{2}\\ x{b}_d^{t+1}+\left|x_{id}^t-x{b}_d^{t+1}\right|A^{+}\cdot L i⩽\frac{n}{2}\end{array}\right.$$

(8)

where $A$ is a $1\times D$-dimensional matrix; $x{w}_d^t$ is the worst position of the sparrow in the $d$th dimension when the population undergoes the $t$th iteration; $x{b}_d^{t+1}$ is the optimal position of the sparrow in the $d$th dimension when the population undergoes the $t+1$th iteration.

The sparrows as vigilantes are some sparrows randomly selected from explorers and followers, generally accounting for 10–20% of the population size, and their position update expressions are shown in Equation (9).

$$x_{id}^{t+1}=\left\{\begin{array}{l}x{b}_d^t+\beta \left(x_{id}^t-x{b}_d^t\right) f_i\ne f_g\\ x_{id}^t+K\left(\frac{x_{id}^t-x{w}_d^t}{\left|f_i-f_w\right|+e}\right) f_i=f_g\end{array}\right.$$

(9)

where $\beta$ and $K$ are step control parameters, $\beta$ is a random number obeying standard normal distribution, and $K$ is a random number between [$-1, 1]$; $e$ is a very small constant to avoid the case that the denominator is 0; $f_i$ is the fitness value of the ith sparrow; $f_g$ and $f_w$ are the best fitness value and the worst fitness value in the current sparrow population.

3. The Proposed SSA-BLS

In the BLS model, the randomly generated weights and biases as well as its five hyper-parameters (convergence coefficient $s$, regularization coefficient $c$, the number of feature nodes $N_f$, the number of feature mapping groups $N_m$ and the number of enhancement nodes $N_e$) all have an impact on its performance. Among them, the most influential on its model accuracy and model stability are the hyper-parameters $N_f$, $N_m$ and $N_e$. However, these three hyper-parameters have a wide range of values, so it is difficult to determine the best combination of hyper-parameters by traditional methods. An optimized broad learning system by sparrow search algorithm with self-adjusting hyper-parameters, i.e., SSA-BLS, is proposed in this paper to enhance the model performance and generalization capability.

The pseudo-code of the proposed SSA-BLS algorithm is shown in Algorithm 1.

Algorithm 1. The pseudo-code of SSA-BLS
	Input:
	MaxIter: the maximum iterations
	dim: the number of hyper-parameters to be optimized
	pop: the number of hyper-parameter combination populations
	lb&ub: hyper-parameter combination search range
	X: the initial population of hyper-parameter combinations
	Output:
	the optimal hyper-parameter combination $X_{best}$
	best fitness value $f_{best}$
	Iterative Curve $IC$
1	Establish an objective function $f\left(x\right)$, i.e., the AVG of RMSE
	obtained by 10-fold cross-validation;
2	Generate pop hyper-parameter combinations as initial population;
3	Calculate the fitness values by BLS;
4	while$t<MaxIter$do
5			Randomly select hyper-parameter combinations as explorers,
			followers and vigilantes;
6			for each$i=explorer$do
7					Using Equation (7) to update locations;
8			end
9			for each$i=follower$do
10					Using Equation (8) to update locations;
11			end
12			for each$i=vigilante$do
13					Using Equation (9) to update locations;
14			end
15			Calculate the fitness values by BLS;
16			Compare with previous $f_{best}$;
17			ifthe current values better than $f_{best}$then
18					Update the $f_{best}$ and $X_{best}$;
19			end
20			Save current $f_{best}$ to $IC$;
21			$t=t+1$
22	end

The determination steps of three hyper-parameters are summarized as follows:

(1)

Generate a certain number of hyper-parameter combinations randomly as the initial population for optimization.

(2)

Calculate the fitness value of the hyper-parameter combinations in the initial population, which is the average of the root mean square error (RMSE) obtained by 10-fold cross-validation of the testing set.

The expression for calculating the root mean square error (RMSE) is shown in Equation (10).

$$RMSE=\sqrt{\frac{1}{N}{\displaystyle \sum }_{i=1}^T{\left(\widehat{y_i}-y_i\right)}^2}$$

(10)

where $T$ is the number of samples, $y_i$ denotes the actual value and $\widehat{y_i}$ denotes the predicted value.

The schematic diagram of the fitness value calculating process is shown in Figure 2.

(3)

A certain number of hyper-parameter combinations are randomly selected from the initial population as optimized explorers, and the positions are updated according to Equation (7).

(4)

The other hyper-parameter combinations in the initial population act as optimized followers, and the positions are updated according to Equation (8).

(5)

A certain number of hyper-parameter combinations are randomly selected from the optimized explorers and followers as the optimized vigilantes, and the positions are updated according to Equation (9).

(6)

Repeat steps (3)–(5) until the maximum number of iterations is reached, and output the individual with the highest fitness value, i.e., the hyper-parameter combination that makes the smallest average of RMSE obtained from a 10-fold cross-validation of the testing set.

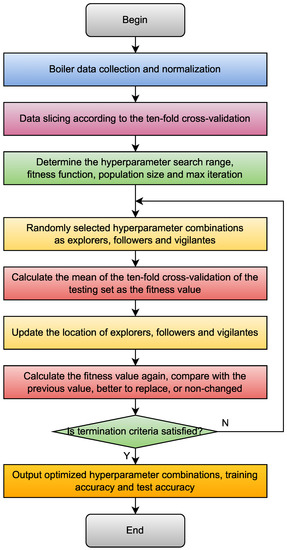
According to the above explanations, the flowchart of the SSA-BLS is shown in Figure 3.

4. Simulation

In order to evaluate the performance of the proposed SSA-BLS, it was applied to the ten benchmark regression datasets listed in

Table 1. Description of regression data sets.

Datasets	Attributes	Instances	Training Samples	Testing Samples
Gasoline octane	14	324	227	97
Fuel consumption	13	1067	747	320
Auto MPG	7	392	274	118
Abalone	8	4177	2923	1254
Bank domains	8	8192	3149	1350
Boston housing	13	506	354	152
Delta elevators	6	9517	6661	2856
Forest fires	12	517	361	156
Machine CPU	6	209	146	63
Servo	4	167	116	51

, where the dataset Gasoline octane is from the web: https://www.heywhale.com/home (accessed on 5 January 2022), Fuel consumption is from the web: https://www.datafountain.cn (accessed on 10 January 2022) and the other datasets are from the web: http://www.liaad.up.pt/~ltorgo/Regression/DtaSets.html (accessed on 9 December 2021). All evaluations for RELM, KELM, BLS and SA-ELM were carried out in MacOS Mojave 10.14.6 and Python 3.9.9, running on a laptop with AMD Intel Iris Plus Graphics 645 1536MB, Processor 1.4GHz Intel Core i5 and RAM 8GB 2133MHz.

The parameters in SSA-BLS were set as follows: the initial population size and the maximum number of iterations for hyper-parameter optimization were set to 20 and 100. The compression factor in the mapping layer was set to 0.8 and the regularization factor in the enhancement layer was set to 2. The optimization range of hyper-parameter combination is shown in

Table 2. The optimization range of hyper-parameter combination.

Hyper-Parameters	Meaning	Optimal Scope
$N_f$	Number of feature nodes	[1, 20]
$N_m$	Number of feature mapping groups	[1, 40]
$N_e$	Number of enhanced nodes	[1, 500]

.

Model accuracy and model stability were assessed by the average (AVG) and standard deviation (Sd) of the RMSE obtained from the ten-fold cross-validation. The averages (AVG) of the MAPE obtained from the ten-fold cross-validation were also used to evaluate the model accuracy. A smaller average value indicates higher model accuracy, and a smaller standard deviation indicates better model stability, and vice versa.

SSA-BLS was applied to the ten benchmark regression datasets in Table 1 and compared with BLS, RELM and KELM; the simulation results are shown in

Table 3. The RMSE of the four algorithms on the training set.

Datasets	RELM		KELM		BLS		SSA-BLS
	RMSE		RMSE		RMSE		RMSE
	AVG	SD	AVG	SD	AVG	SD	AVG	SD
Gasoline octane	4.47 × 10−2	9.02 × 10−3	3.83 × 10−2	7.99 × 10−3	3.86 × 10−2	8.16 × 10−3	3.78 × 10−2	8.16 × 10−3
Fuel consumption	2.47 × 10−2	8.38 × 10−4	1.79 × 10−2	1.49 × 10−4	4.09 × 10−2	1.76 × 10−3	9.93 × 10−3	2.37 × 10−3
Auto MPG	1.42 × 10−4	5.04 × 10−5	1.00 × 10−5	1.34 × 10−7	5.75 × 10−5	3.49 × 10−5	1.04 × 10−5	3.50 × 10−5
Abalone	1.38 × 10−5	8.43 × 10−6	2.70 × 10−6	4.41 × 10−8	4.06 × 10−3	5.37 × 10−3	4.82 × 10−8	7.11 × 10−8
Bank domains	3.01 × 10−4	3.47 × 10−5	4.13 × 10−6	2.57 × 10−8	5.57 × 10−5	3.32 × 10−5	7.59 × 10−9	7.82 × 10−9
Boston housing	7.23 × 10−4	1.72 × 10−4	6.83 × 10−6	6.83 × 10−8	1.86 × 10−5	1.07 × 10−5	9.89 × 10−8	6.25 × 10−8
Delta elevators	5.28 × 10−7	1.02 × 10−7	2.32 × 10−8	3.41 × 10−10	2.08 × 10−7	1.61 × 10−7	3.85 × 10−9	3.42 × 10−9
Forest fires	3.32 × 10−4	6.63 × 10−5	5.97 × 10−5	6.15 × 10−7	2.24 × 10−4	1.61 × 10−4	2.93 × 10−7	1.44 × 10−7
Machine CPU	1.33 × 10−4	1.52 × 10−4	3.42 × 10−5	3.56 × 10−6	8.86 × 10−7	5.15 × 10−7	2.57 × 10−8	1.28 × 10−8
Servo	1.44 × 10−4	5.06 × 10−5	3.70 × 10−5	3.96 × 10−7	6.42 × 10−4	5.02 × 10−4	3.83 × 10−7	2.87 × 10−7

,

Table 4. The RMSE of the four algorithms on the testing set.

Datasets	RELM		KELM		BLS		SSA-BLS
	RMSE		RMSE		RMSE		RMSE
	AVG	SD	AVG	SD	AVG	SD	AVG	SD
Gasoline octane	7.16 × 10−2	9.68 × 10−3	2.70 × 10−2	3.09 × 10−2	3.04 × 10−2	3.20 × 10−2	2.65 × 10−2	3.07 × 10−2
Fuel consumption	2.64 × 10−2	1.26 × 10−3	2.09 × 10−2	3.43 × 10−3	4.85 × 10−2	2.79 × 10−3	1.39 × 10−2	2.84 × 10−3
Auto MPG	2.06 × 10−4	5.65 × 10−5	1.09 × 10−5	2.18 × 10−6	5.82 × 10−5	3.58 × 10−5	1.19 × 10−5	3.06 × 10−5
Abalone	1.71 × 10−5	7.95 × 10−6	2.86 × 10−6	5.16 × 10−6	4.18 × 10−3	5.76 × 10−3	8.34 × 10−8	1.80 × 10−7
Bank domains	3.34 × 10−4	3.02 × 10−5	4.27 × 10−6	2.69 × 10−7	1.94 × 10−4	4.13 × 10−4	7.79 × 10−9	8.32 × 10−9
Boston housing	2.11 × 10−3	7.65 × 10−4	7.40 × 10−6	1.83 × 10−6	1.85 × 10−5	1.08 × 10−5	9.69 × 10−8	6.07 × 10−8
Delta elevators	6.18 × 10−7	1.26 × 10−7	3.04 × 10−8	6.40 × 10−9	2.08 × 10−7	1.61 × 10−7	3.85 × 10−9	3.41 × 10−9
Forest fires	1.99 × 10−3	1.21 × 10−3	7.24 × 10−5	1.45 × 10−5	2.2 × 10−4	1.58 × 10−4	2.94 × 10−7	1.43 × 10−7
Machine CPU	5.43 × 10−4	2.41 × 10−4	7.36 × 10−5	9.17 × 10−5	8.13 × 10−7	5.16 × 10−7	2.28 × 10−8	1.61 × 10−8
Servo	1.89 × 10−4	6.42 × 10−5	3.22 × 10−5	1.25 × 10−5	8.13 × 10−4	8.62 × 10−4	3.81 × 10−7	2.39 × 10−7

and

Table 5. The MAPE of the four algorithms on the training set and testing set.

Datasets	RELM		KELM		BLS		SSA-BLS
	Train	Test	Train	Test	Train	Test	Train	Test
Gasoline octane	8.16 × 10−1	1.33	2.57	3.68	9.29 × 10−1	1.00	9.24 × 10−1	9.76 × 10−1
Fuel consumption	2.56	2.59	2.41 × 10−1	4.16 × 10−1	2.63	2.71	1.09	2.59
Auto MPG	3.30 × 10−2	3.51 × 10−2	1.11 × 10−1	1.17 × 10−1	6.60 × 10−4	6.23 × 10−4	6.26 × 10−4	8.14 × 10−4
Abalone	2.56 × 10−2	2.01 × 10−2	2.00 × 10−2	2.13 × 10−2	2.51 × 10−1	2.56 × 10−1	2.18 × 10−6	2.30 × 10−6
Bank domains	3.62 × 10−1	3.67 × 10−1	3.68 × 10−2	3.71 × 10−2	7.99 × 10−2	8.04 × 10−2	9.60 × 10−7	9.68 × 10−7
Boston housing	9.81 × 10−1	1.23	3.86 × 10−2	4.31 × 10−2	4.51 × 10−4	4.57 × 10−4	8.54 × 10−6	8.32 × 10−6
Delta elevators	2.51 × 10−2	2.56 × 10−2	1.31 × 10−2	1.31 × 10−2	3.21 × 10−2	3.21 × 10−2	5.04 × 10−4	5.05 × 10−4
Forest fires	4.78 × 10−1	6.21 × 10−1	5.31 × 10−2	5.61 × 10−2	1.57 × 10−2	1.59 × 10−2	2.13 × 10−5	2.14 × 10−5
Machine CPU	2.05 × 10−2	1.27 × 10−1	1.41 × 10−1	1.76 × 10−1	5.73 × 10−5	5.69 × 10−5	1.46 × 10−6	1.47 × 10−6
Servo	2.62 × 10−3	3.29 × 10−3	5.95 × 10−2	6.44 × 10−2	6.06 × 10−3	7.91 × 10−3	1.12 × 10−5	1.39 × 10−5

. The hyper-parameters of the compared algorithm are determined by using the nested cross-validation method [42]. And the bolds in the table indicate the best experimental results of the four algorithms on each dataset.

As shown in Table 4, for the testing samples of the datasets, compared with RELM, KELM and BLS, the proposed SSA-BLS obtains better model accuracy on nine benchmark regression problems (gasoline octane, fuel consumption, abalone, bank domains, Boston housing, delta elevators, forest fires, machine CPU, servo) and better model stability on seven benchmark regression problems (bank domains, Boston housing, forest fires, machine CPU, servo).

As shown in Table 5, for the training samples of the datasets, compared with RELM, KELM and BLS, the proposed SSA-BLS obtains better model performance on all ten benchmark regression problems and for the testing samples of the datasets, the proposed SSA-BLS obtains better model performance on nine benchmark regression problems (except auto MPG).

The effectiveness of SSA-BLS is proved by the above simulation experiments. However, SSA-BLS requires more computing time to establish the model compared with other related algorithms, so it is not suitable for online learning. In this paper, model training and testing belong to offline learning, so this algorithm mainly pursues the accuracy and stability of the model.

5. Real-World Design Problem

As a new neural network algorithm, BLS can effectively solve the modeling problems of complex systems. In this paper, the proposed SSA-BLS was applied to establish the prediction models for thermal efficiency (TE), NOx emission concentration and SO₂ emission concentration of a 330 MW circulating fluidized bed boiler (CFBB).

There are 27 variables affecting the thermal efficiency and harmful gas emission concentration of a CFBB, mainly including load, coal feeder feeding rate, the primary air velocity, the secondary air velocity, oxygen concentration in the flue gas and the carbon content of fly ash. The symbols and descriptions of each variable are shown in

Table 6. Description of variable symbols.

Symbol Name	Description
17ANO037	Boiler load
AFCOALQ	The first coal feeder coal volume
BFCOALQ	The second coal feeder coal volume
CFCOALQ	The third coal feeder coal volume
DFCOALQ	The fourth coal feeder coal volume
18ANO074	Average bed temperature in the upper part of the dense phase zone of the furnace
05F051	Primary air flow at the left duct burner inlet
05F061	Right duct burner inlet primary air flow
05T457	Primary air temperature at the left duct burner inlet
05T467	Right duct burner inlet primary air temperature
06F061	Total right side secondary air flow
06F052	Left side internal secondary air distribution flow
06F062	Right side internal secondary air distribution flow
06T453	The second secondary fan motor drive end bearing temperature
06T463	The first secondary fan motor drive end bearing temperature
17I021	The first limestone powder conveying motor current
17I011	The second limestone powder conveying motor current
CEMSO2	CEMS flue gas O2 concentration
CEMSTEMP	CEMS flue gas temperature
08A051	Carbon content of fly ash at the inlet of the left EDC
08A061	Carbon content of fly ash at the inlet of the right EDC
05T402	The first Primary fan inlet temperature
05T403	The second Primary fan inlet temperature
12T612	The first old slagger outlet temperature
12T622	The second cold slagger outlet temperature
12T632	The third cold slagger outlet temperature
12T642	The fourth cold slagger outlet temperature
CEMSNOX	CEMS flue gas NOx concentration
CEMSSO2	CEMS flue gas SO2 concentration
TE	Boiler thermal efficiency

. A total of 10,000 data samples are collected from a 330MW CFBB under different operating loads, some of which are shown in

Table 7. The partial data of a 330MW CFBB operational conditions.

NO.	17ANO037	AFCOALQ	BFCOALQ	CFCOALQ	DFCOALQ	18ANO074	05F051	05F061	05T457	05T467	06F061	06F052	06F062	06T453	06T463
1	73.401	38.065	39.174	39.122	38	864.328	202.548	220.4	269.342	267.375	385.664	182.617	163.927	278.823	267.433
2	73.401	38.065	39.174	39.122	38	864.328	266.631	232.072	269.342	267.375	385.31	195.301	152.674	278.823	267.433
3	73.52	38.065	39.174	39.122	38	864.207	249.237	263.656	269.342	267.375	435.575	178.803	171.079	278.823	267.433
4	73.52	38.065	39.174	39.122	38	864.03	263.656	242.371	269.342	267.375	405.929	209.128	186.146	278.823	267.433
5	73.52	37.962	39.174	39.122	37.862	863.881	298.673	248.093	269.342	267.375	402.92	183.762	177.659	278.823	267.433
…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…
9996	96.318	56.966	52.712	52.953	56.528	866.957	419.973	368.935	273.729	270.847	976.991	569.881	669.725	284.775	268.966
9997	96.427	56.966	52.556	52.953	56.528	867.103	338.267	273.955	273.729	270.847	973.451	626.621	598.299	284.775	268.966
9998	96.427	56.966	52.403	52.953	56.528	867.278	386.329	349.71	273.729	270.847	1017.08	631.294	601.922	284.775	268.966
9999	96.427	56.966	52.273	52.801	56.528	867.39	405.325	343.073	273.729	270.847	1020.796	569.118	612.603	284.775	268.966
10000	96.427	56.966	52.273	52.689	56.528	867.557	313.549	324.306	273.729	270.847	1036.903	543.752	645.026	284.775	268.966
NO.	17I021	17I011	6CEMSO2	6CEMSTEMP	08A051	08A061	05T402	05T403	12T612	12T622	12T632	12T642	CEMSNOX	CEMSNOX	TE
1	102.876	116.074	5.554	152.655	0.847	0.316	25.65	24.901	42.858	45.355	51.829	36.858	128.395	225.285	90.55405
2	103.944	114.815	5.554	152.655	0.847	0.316	25.65	24.901	42.858	45.355	51.829	36.858	128.395	224.141	90.55405
3	103.296	113.175	5.554	152.655	0.847	0.316	25.65	24.901	42.858	45.355	51.829	36.858	128.929	223.378	90.55405
4	103.334	114.701	5.554	152.655	0.847	0.316	25.65	24.901	42.858	45.355	51.829	36.858	129.463	220.517	90.55405
5	104.059	113.328	5.554	152.655	0.847	0.316	25.65	24.901	42.858	45.355	51.829	36.858	129.463	218.61	90.55405
…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…
9996	102.914	116.684	4.921	156.637	1.405	0.167	30.235	28.193	39.127	37.046	36.846	47.32	160.436	144.991	90.30709
9997	102.914	116.99	4.921	156.637	1.405	0.167	30.235	28.193	39.127	37.046	36.846	47.32	160.436	147.089	90.30709
9998	103.792	117.714	4.921	156.637	1.405	0.167	30.235	28.193	39.127	37.046	36.846	47.32	160.436	148.615	90.30709
9999	102.418	115.998	4.921	156.637	1.405	0.167	30.235	28.193	39.127	37.046	36.192	47.32	160.436	150.14	90.30709
10000	101.541	115.731	4.921	156.637	1.405	0.167	30.235	28.193	39.127	37.046	36.192	47.32	159.826	151.666	90.30709

.

The boiler data is normalized and divided into training sets and testing sets in the ratio of 7:3.

The proposed SSA-BLS and BLS are applied to this boiler data and the experimental results are shown in

Table 8. The hyper-parameters of SSA-BLS and BLS for boiler data modeling.

Objectives	SSA-BLS
	N1	N2	N3
NOx	2	37	478
SO2	1	13	459
TE	2	27	296

,

Table 9. The RMSE of the four algorithms on the training set of boiler data.

Objectives	RELM		KELM		BLS		SSA-BLS
	RMSE		RMSE		RMSE		RMSE
	AVG	SD	AVG	SD	AVG	SD	AVG	SD
NOX	9.05 × 10−2	6.51 × 10−3	3.48 × 10−2	4.26 × 10−5	4.22 × 10−2	9.50 × 10−4	2.17 × 10−2	4.23 × 10−4
SO2	8.31 × 10−2	2.37 × 10−3	1.99 × 10−2	1.49 × 10−4	5.56 × 10−2	7.12 × 10−4	3.37 × 10−2	1.13 × 10−3
TE	4.52 × 10−2	1.01 × 10−2	2.04 × 10−2	3.36 × 10−5	5.96 × 10−2	1.20 × 10−3	4.41 × 10−3	1.72 × 10−4

,

Table 10. The RMSE of the four algorithms on the testing set of boiler data.

Objectives	RELM		KELM		BLS		SSA-BLS
	RMSE		RMSE		RMSE		RMSE
	AVG	SD	AVG	SD	AVG	SD	AVG	SD
NOX	8.91 × 10−2	5.94 × 10−3	7.49 × 10−2	2.36 × 10−3	6.53 × 10−2	6.55 × 10−2	2.75 × 10−2	1.83 × 10−3
SO2	7.91 × 10−2	2.09 × 10−2	4.12 × 10−2	5.53 × 10−3	5.82 × 10−2	4.98 × 10−3	3.59 × 10−2	1.94 × 10−3
TE	4.48 × 10−2	9.68 × 10−3	5.37 × 10−2	2.85 × 10−3	6.26 × 10−3	1.18 × 10−3	4.58 × 10−3	1.60 × 10−4

and

Table 11. The MAPE of the four algorithms on the training set and testing set of boiler data.

Objectives	RELM		KELM		BLS		SSA-BLS
	Training	Testing	Training	Testing	Training	Testing	Training	Testing
NOX	4.22	4.13	1.74	2.46	2.20	2.22	1.57	1.83
SO2	4.14	4.10	1.07	1.20	3.14	3.32	1.92	2.06
TE	2.28	2.26	9.26 × 10−2	1.98	3.03 × 10−1	3.09 × 10−1	2.10 × 10−1	2.18 × 10−1

. The hyper-parameters of BLS are determined by using the nested cross-validation method [42]. And the bolds in the table indicate the best experimental results of the four algorithms on each objective.

As shown in Table 9, Table 10 and Table 11, compared with RELM, KELM and BLS, the proposed SSA-BLS obtained better model accuracy and model stability in the prediction models established for the NOx emissions concentration and thermal efficiency of CFBB both on the training set and testing set. However, its model prediction accuracy for the SO₂ emission concentration of CFBB was not as good as that of KELM.

The fitting diagrams and error diagrams of SSA-BLS for modeling the three objectives of CFBB on the testing set are shown in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9, where the red line and the blue line in the fitting diagram indicate the true values and predicted values of the partial testing set, and the curve in the error diagram represent the error of the predicted values compared to the true values for the testing set.

As shown in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9, the proposed SSA-BLS effectively establishes the prediction models for the three objectives of CFBB. The three prediction models all have great fitting effect and small fitting error on the testing set.

6. Conclusions

This paper proposed a novel optimized broad learning system by combining with a sparrow search algorithm. That is to say, the sparrow search algorithm was used to optimize the hyper-parameters of broad learning systems. Compared with other state-of-the-art methods, the proposed SSA-BLS reveals better regression accuracy and model stability on testing ten benchmark datasets. Additionally, the SSA-BLS was used to build the collective model of thermal efficiency, NOx and SO₂ emissions concentration of one 330MW circulation fluidized bed boiler. Experiment results show that the model accuracy can be achieved 10⁻²–10⁻³. The proposed SSA-BLS is an effective modelling method.

However, the proposed SSA-BLS takes more time to determine the optimal hyperparameters. This method improves the accuracy of the model but reduces the speed of model computation. Moreover, this method is also not applicable to online modeling due to the long modeling time. In addition, SSA-BLS only tunes and optimizes the hyperparameters in terms of model accuracy, while ignoring the model stability aspects. In the future, the performance of SSA-BLS will be further improved, including computation speed, model complexity and generalization ability. Additionally, based on the established comprehensive model, we will use one heuristic optimization algorithm to adjust the boiler’s operational parameters for enhancing thermal efficiency and reducing NOx/SO₂ emissions concentration.