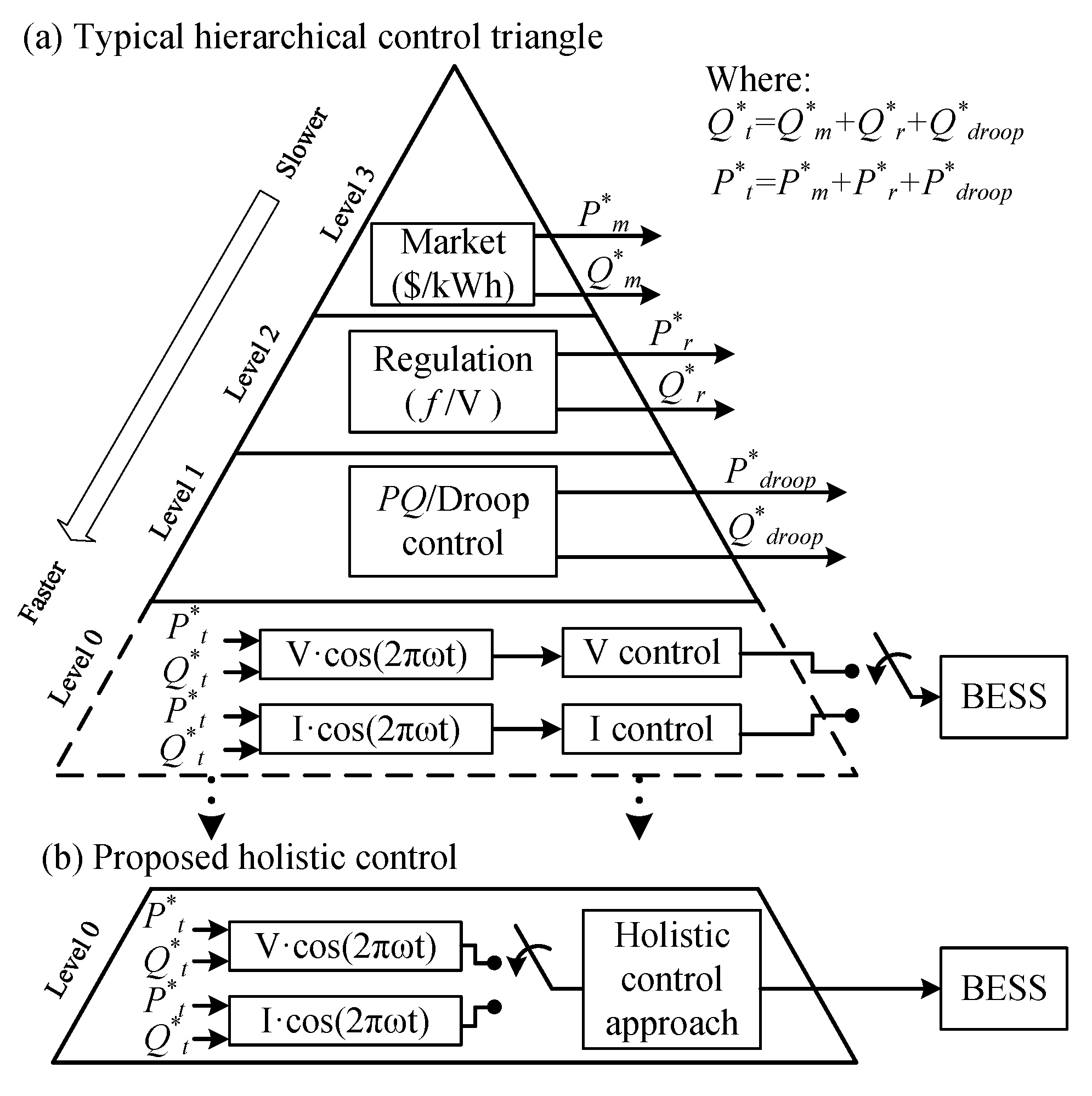
An Improvement of Holistic Control Tuning for Reducing Energy Consumption in Seamless Transitions for a BESS Grid-Connected Converter
Abstract
:1. Introduction
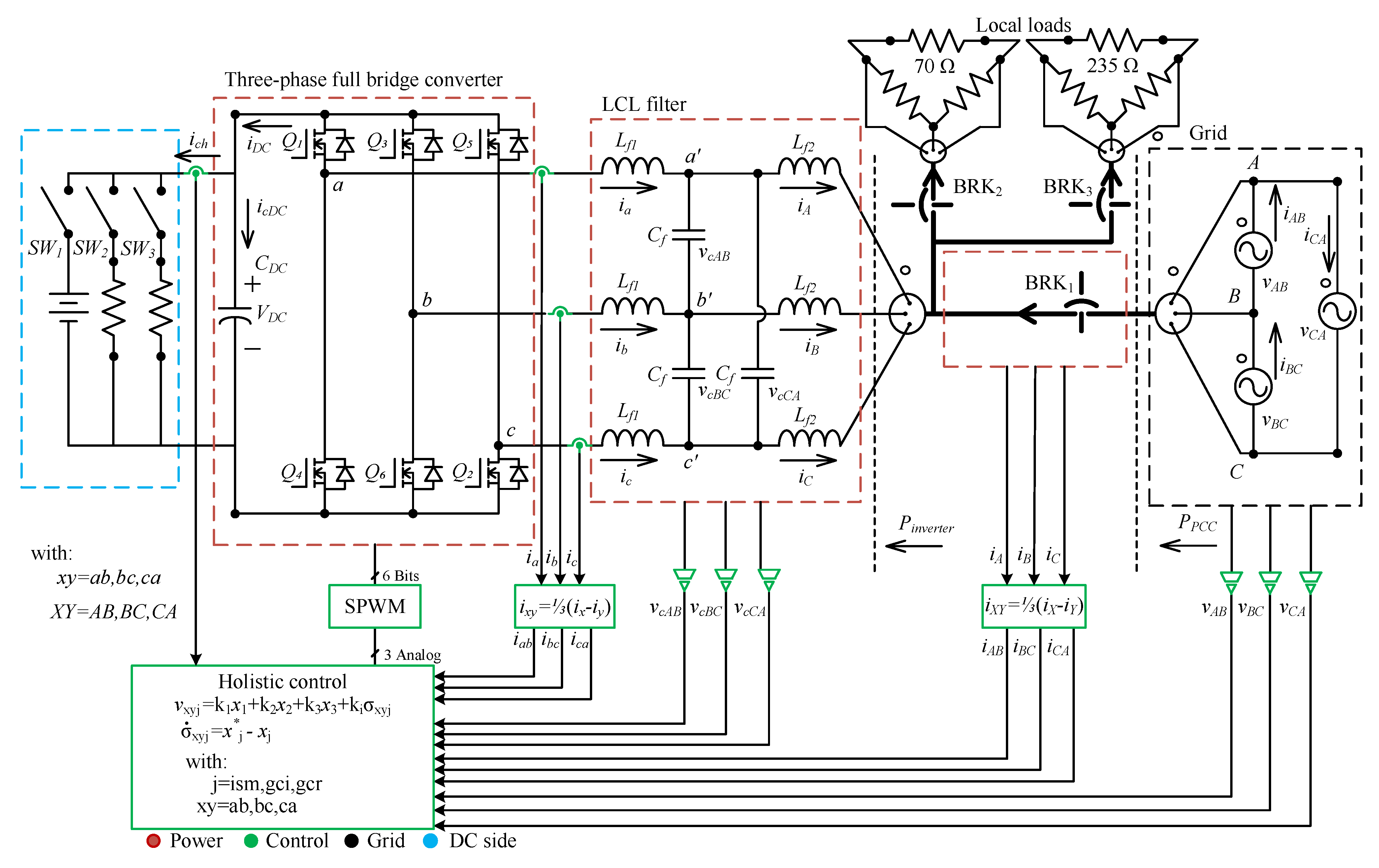
2. Modeling of the DC/AC Converter and LCL Filter
- , , are the delta-connected output voltages of the power converter.
- , , are the delta-connected capacitor voltages.
- , , are the currents through inductors .
- , , are the delta-connected capacitor currents.
- , , are the currents through inductors .
- , , are the delta-connected grid voltages.
- 1.
- The three-phase system is balanced.
- 2.
- A line-to-line modeling is considered.
- 3.
- The complete analysis is based on the average mathematical model.
- 4.
- The link capacitor voltage is not considered as a state variable. Additionally, the voltage is always bigger than the peak of line-to-line voltage.
- 5.
- The grid-connected converter works as an inverter if the currents , , and are in phase with the input voltages , , and , respectively. In this case, the active power flows from to the grid and the capacitor is not discharged because of the action of the DC/DC converter and the battery bank.
- 6.
- The grid-connected converter works as a rectifier if the input currents , , and are shifted 180° with respect to the input voltage , , and , respectively. In this case, the active power flows from the grid to the , and the capacitor is not overcharged because the DC/DC converter is charging the battery bank.
- 7.
- The analysis is performed considering the phase AB. Taking advantage of assumption (1), the rest of the control signals are obtained by shifting their phases by 120° and 240°, respectively.
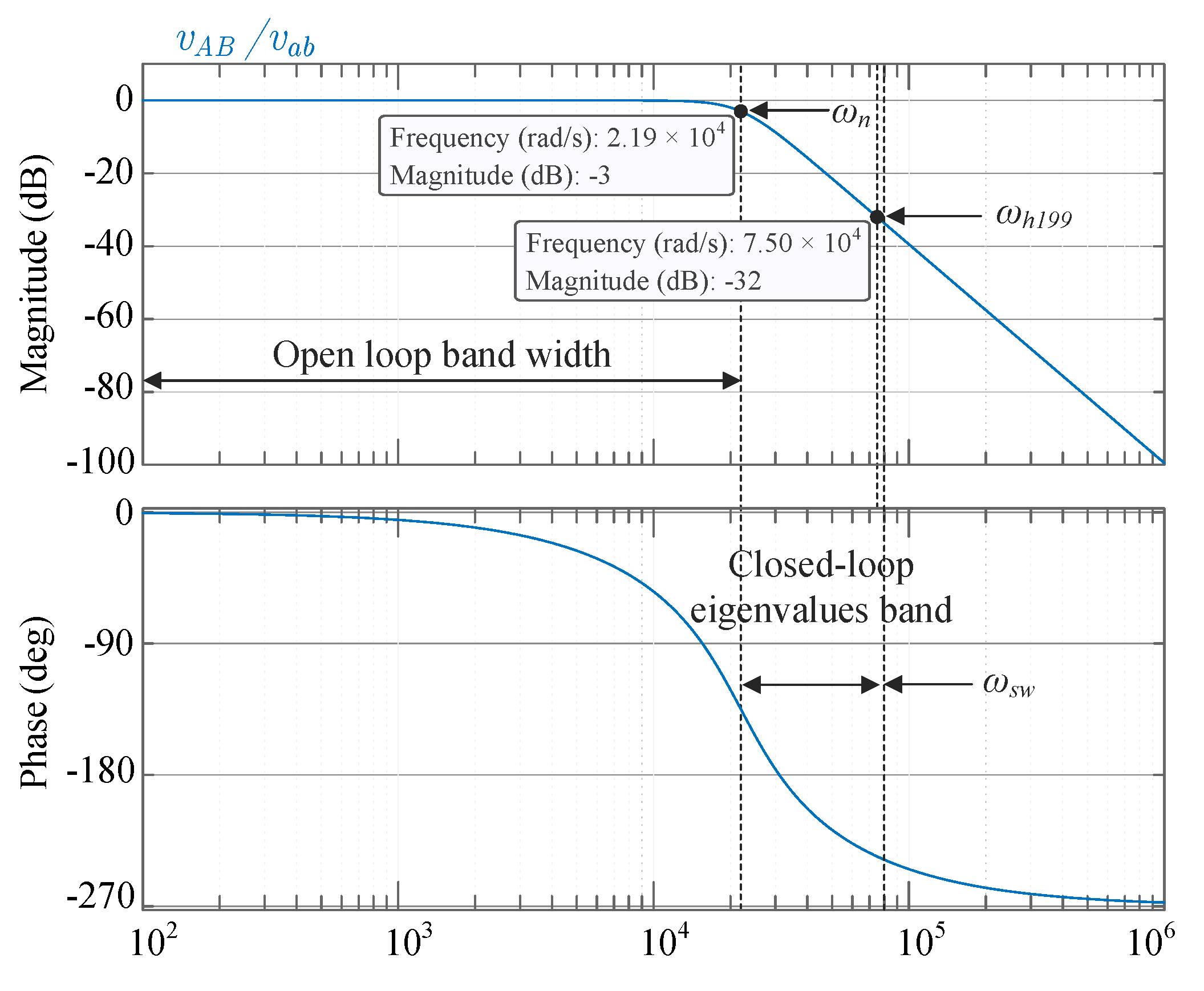
3. Butterworth LCL Filter Design
- 1.
- Switching frequency = 12,060 Hz; .
- 2.
- Amplitude and frequency modulation indexes and , respectively.
- 3.
- First relevant harmonic amplitude .
- 4.
- For the three-phase full-bridge converter, the double-edge naturally sampled PWM is taken for this work, and given this, the first carrier harmonic group has the more significant harmonic at being [34].
- 5.
- According to IEEE-1159, THD voltage at the connection point should be lower than 3%; to extensively fulfill this requirement, an attenuation for the first relevant harmonic was proposed of .
- 6.
- Rated load value for rated power. It is important to notice that the approach considers a resistive load; it means active power transference. Of course, the BESS operates under different modes and operating conditions, and the filter should be able to allow the transfer of the required power in both directions.
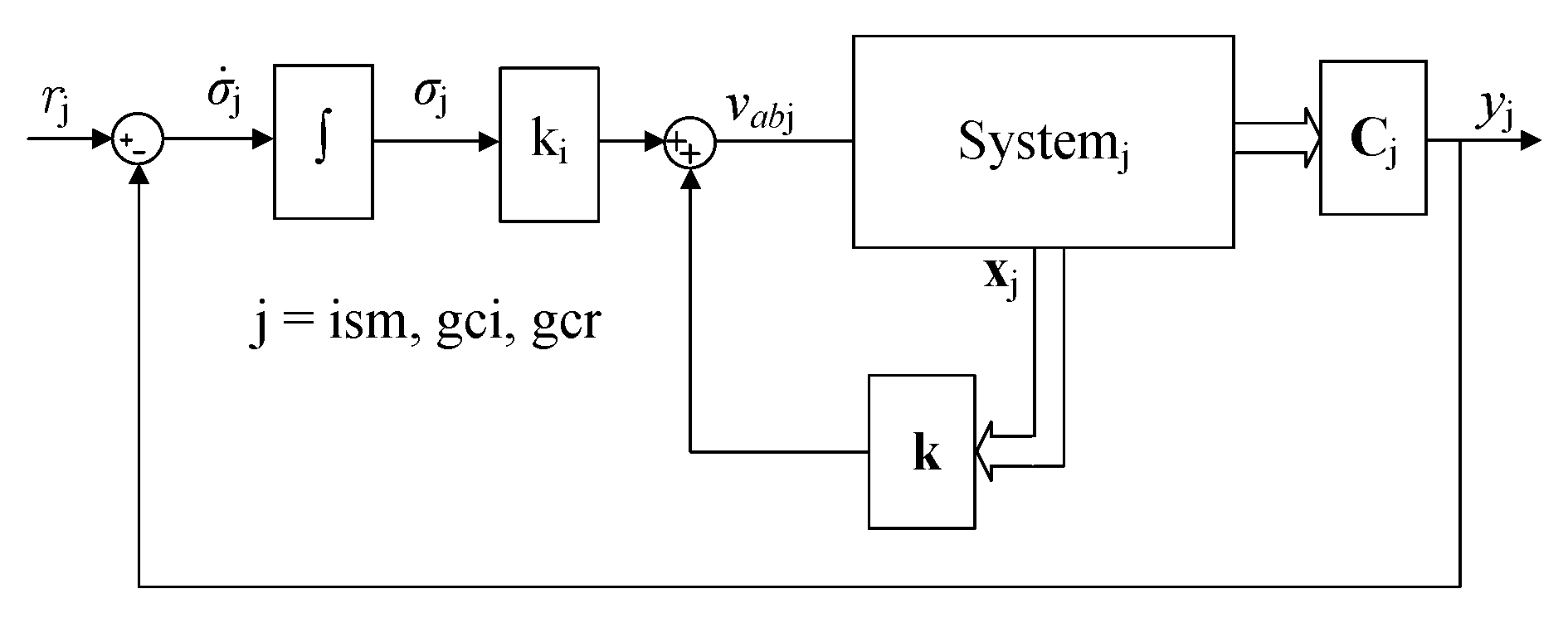
4. Improvement of the Holistic Control Tuning
- is the state vector.
- r is the reference of the controlled output.
- , , and are the state, input, and output matrices, respectively.
- is the error between the voltage reference and measured voltage.
- is the control law which modifies the inverter output.
- is the gain vector.
- is the gain of the integral action.
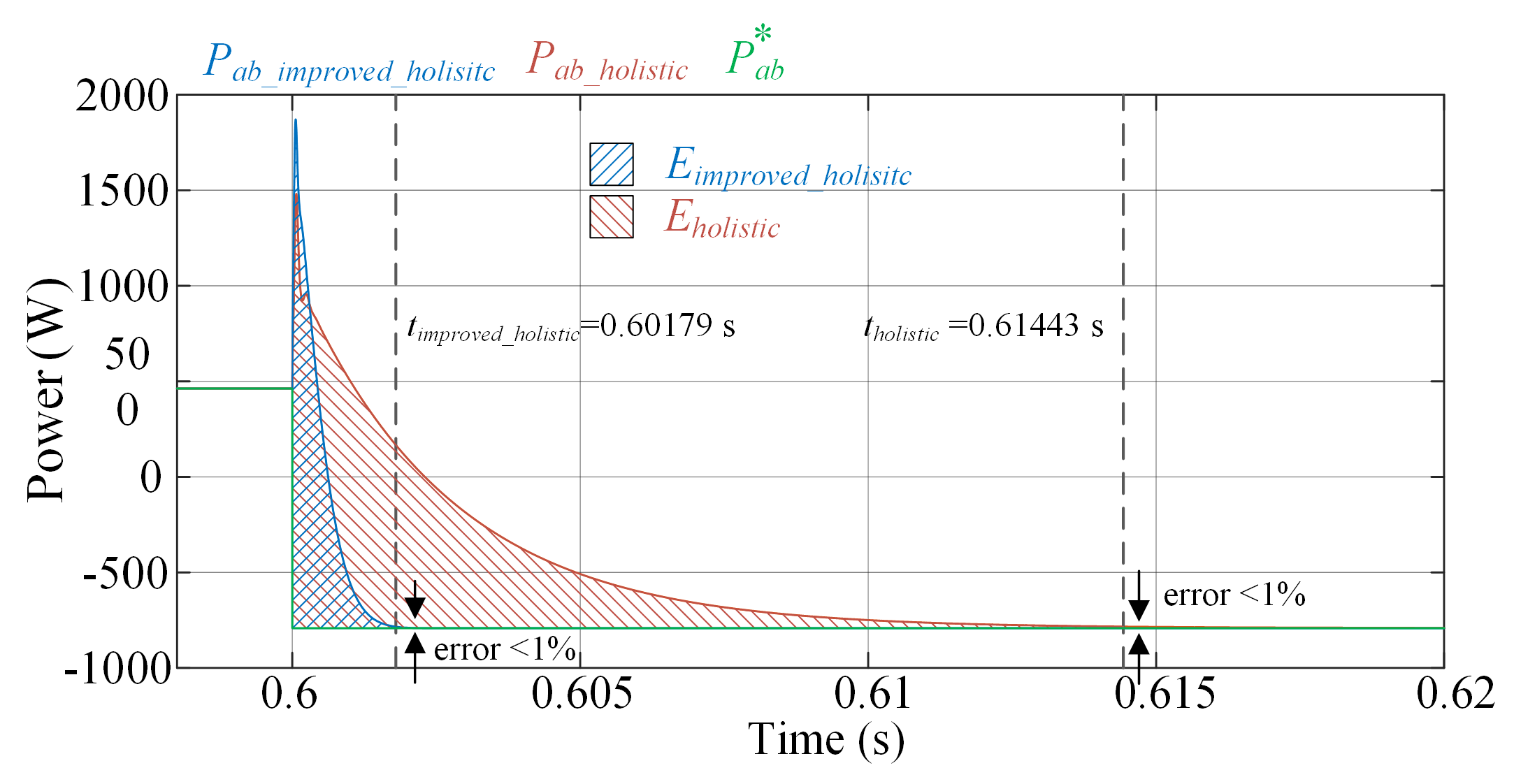
5. Energy Consumption When Changes Occur
- is the energy required by the improved holistic controller presented in this paper.
- is the energy required for the holistic controller given in [27].
- is the power at steady state due to the voltage and current reference, respectively.
- is the power delivered by the holistic control.
- is the power delivered by the improved holistic control.
- is the time at the event occurrence (Column 1, Table 5).
- is the settling time where the error is .
- is the settling time where the error is .
6. Simulation and Experimental Results of the Improved Holistic Control
6.1. Simulation Results
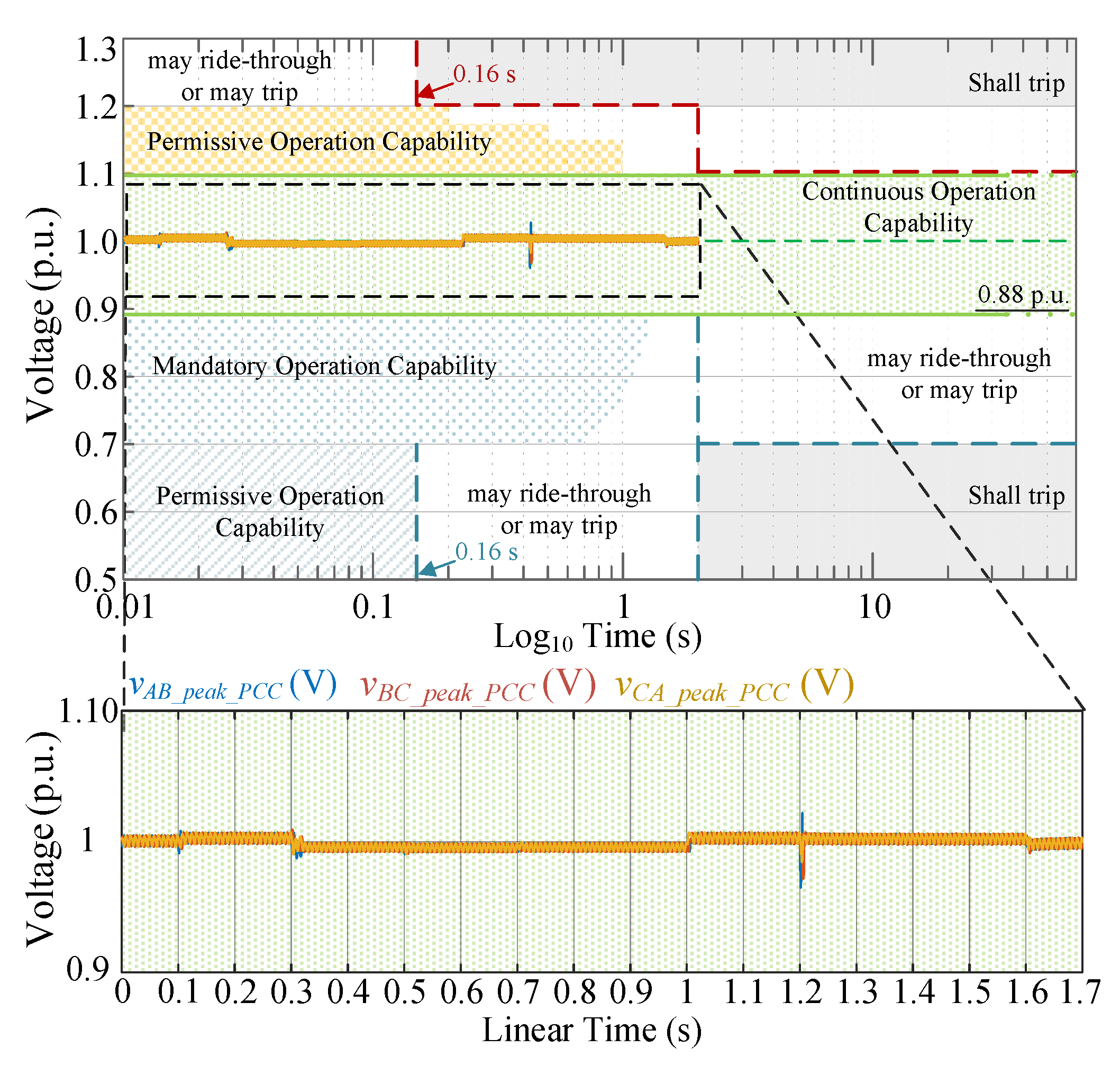
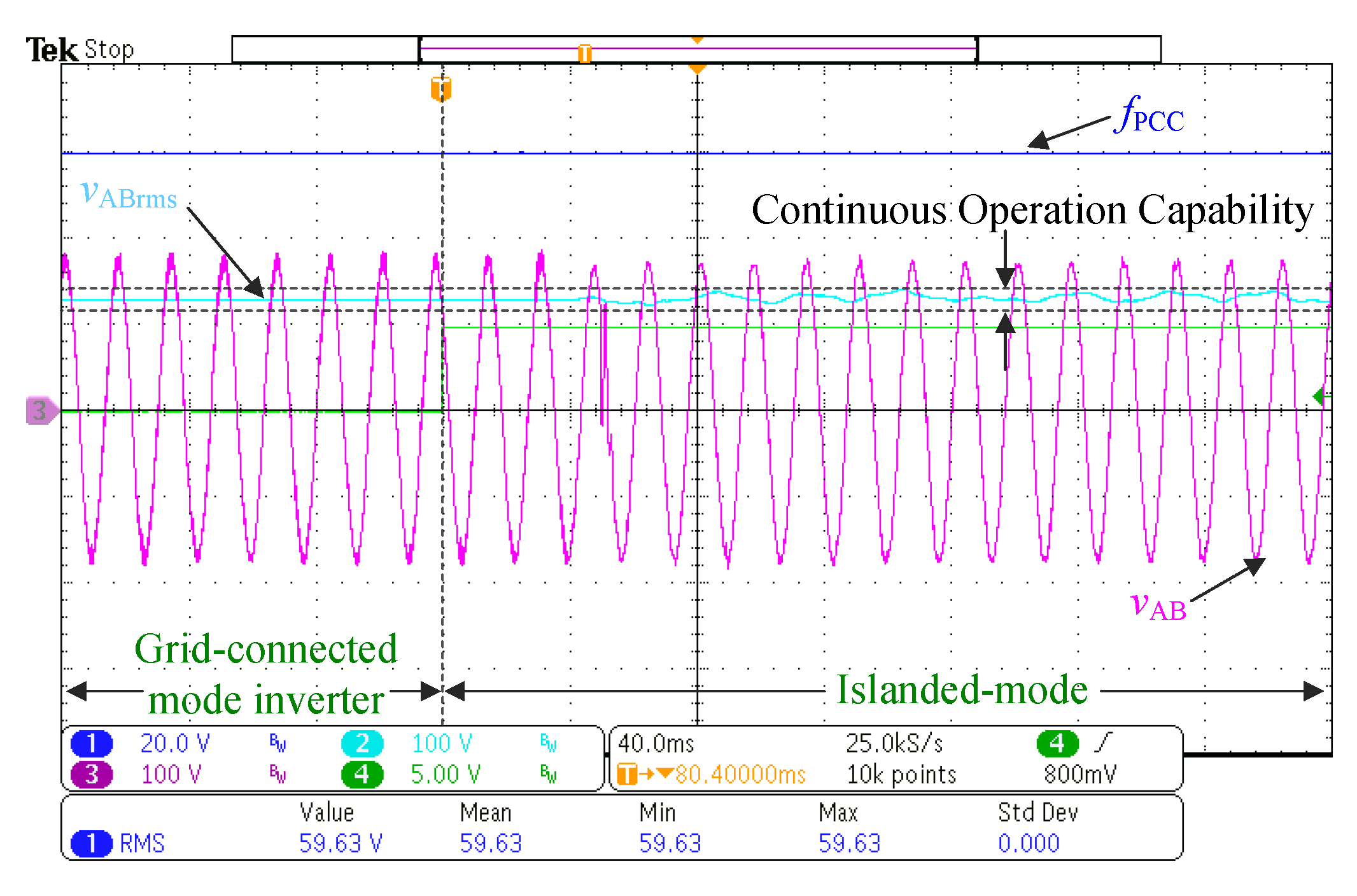
6.2. Experimental Results
- Three power inverters KIT8020CRD8FF1217P-1, SiC mosfet assembly.
- The inductors were built using air core.
- A 400 V, polypropylene capacitor.
- The controller is executed in the dSPACE platform CP1103.
7. Discussion
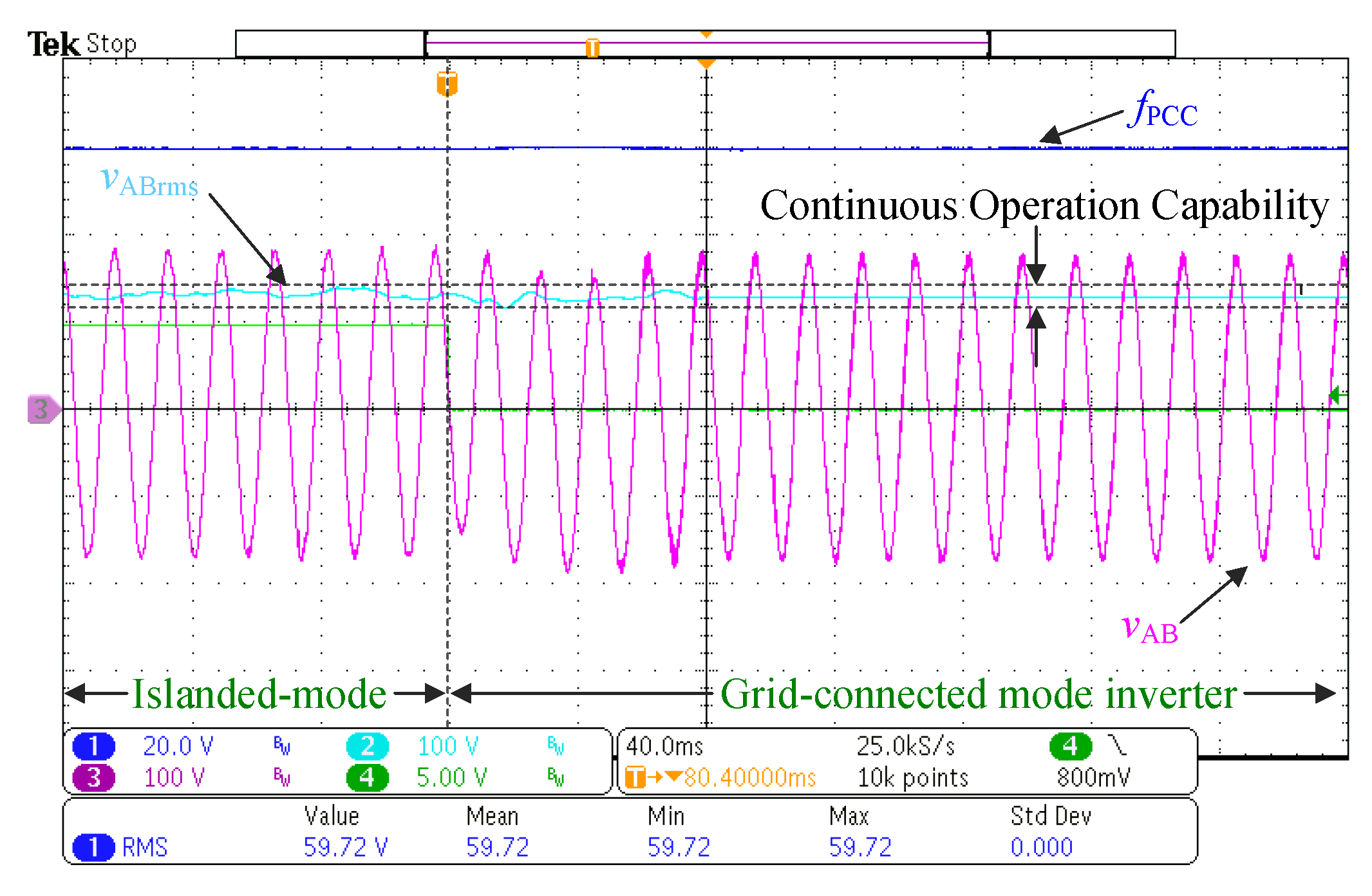
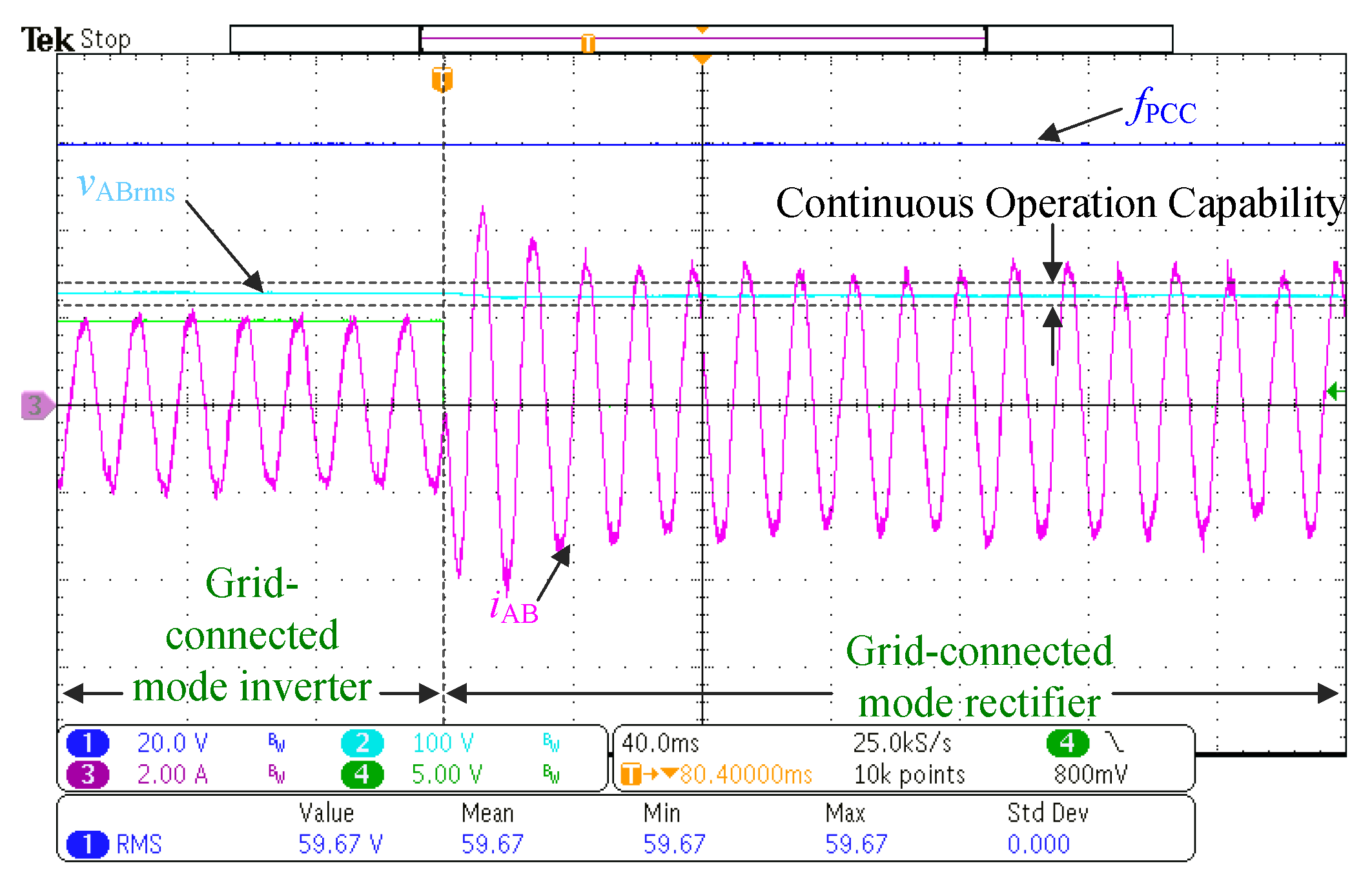
- Energy efficiency improvement during mode transitions and load transients.
- A test protocol that involves all the mode transitions and load transients on the fly for the experimental validation of the control scheme.
- A seamless transition capability is validated according to IEEE 1547-2018, which guarantees operation in the continuous region limited by the standard.
- One relevant result is the fact that the same polynomial tuning and filter design operates correctly when the converter is used as a rectifier without tuning changes.
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- IRENA. Electricity Storage Valuation Framework: Assessing System Value and Ensuring Project Viability. 2020. Available online: www.irena.org (accessed on 20 August 2022).
- Venkatesan, K.; Govindarajan, U.; Kasinathan, P.; Padmanaban, S.; Holm-Nielsen, J.B.; Leonowicz, Z. Economic analysis of HRES systems with energy storage during grid interruptions and curtailment in Tamil Nadu, India: A hybrid RBFNoeHo technique. Energies 2019, 12, 3047. [Google Scholar] [CrossRef] [Green Version]
- Lasseter, R. MicroGrids: A Conceptual Solution. In Proceedings of the 2002 IEEE Power Engineering Society Winter Meeting. Conference Proceedings (Cat. No.02CH37309), New York, NY, USA, 27–31 January 2002; Volume 1, pp. 305–308. [Google Scholar] [CrossRef]
- Rocabert, J.; Luna, A.; Blaabjerg, F.; Rodríguez, P. Control of Power Electronic Converters in AC Microgrids. Power Syst. 2012, 27, 329–355. [Google Scholar] [CrossRef]
- Karimi-Ghartemani, M.; Khajehoddin, S.A.; Piya, P.; Ebrahimi, M. Universal Controller for Three-Phase Inverters in a Microgrid. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 1342–1353. [Google Scholar] [CrossRef]
- Palizban, O.; Kauhaniemi, K.; Guerrero, J.M. Microgrids in active network management—Part I: Hierarchical control, energy storage, virtual power plants, and market participation. Renew. Sustain. Energy Rev. 2014, 36, 428–439. [Google Scholar] [CrossRef] [Green Version]
- Salehi, N.; Martinez-Garcia, H.; Velasco-Quesada, G.; Guerrero, J.M. A Comprehensive Review of Control Strategies and Optimization Methods for Individual and Community Microgrids. IEEE Access 2022. [Google Scholar] [CrossRef]
- D’Silva, S.; Shadmand, M.; Bayhan, S.; Abu-Rub, H. Towards grid of microgrids: Seamless transition between grid-connected and islanded modes of operation. IEEE Open J. Ind. Electron. Soc. 2020, 1, 66–81. [Google Scholar] [CrossRef]
- Bastidas-Rodríguez, J.D.; Ramos-Paja, C. Types of inverters and topologies for microgrid applications. Rev. Uis Ing. 2017, 16, 7–14. [Google Scholar] [CrossRef] [Green Version]
- Somakumar, R.; Kasinathan, P.; Monicka, G.; Rajagopalan, A.; Ramachandaramurthy, V.K.; Subramaniam, U. Optimization of emission cost and economic analysis for microgrid by considering a metaheuristic algorithm-assisted dispatch model. Int. J. Numer. Model. Electron. Netw. Devices Fields 2022, 35, e2993. [Google Scholar] [CrossRef]
- dos Santos Neto, P.J.; Barros, T.A.; Silveira, J.P.; Filho, E.R.; Vasquez, J.C.; Guerrero, J.M. Power management techniques for grid-connected DC microgrids: A comparative evaluation. Appl. Energy 2020, 269, 115057. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, P.; Xu, Z.; Chen, J. Smooth mode transition strategies of PV-BESS microgrids. In Proceedings of the 2017 2nd International Conference on Power and Renewable Energy, ICPRE 2017, Chengdu, China, 20–23 September 2017; pp. 709–716. [Google Scholar] [CrossRef]
- Cucuzzella, M.; Incremona, G.P.; Ferrara, A. Design of Robust Higher Order Sliding Mode Control for Microgrids. IEEE J. Emerg. Sel. Top. Circuits Syst. 2015, 5, 393–401. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Dong, Y.; Chen, Z.; Xie, X.; Sun, H.; Liu, Z. An integrated control strategy of battery energy storage system in microgrid. IET Conf. Publ. 2013, 2013, 2–40. [Google Scholar] [CrossRef]
- Fusero, M.; Tuckey, A.; Rosini, A.; Serra, P.; Procopio, R.; Bonfiglio, A. A comprehensive inverter-bess primary control for AC microgrids. Energies 2019, 12, 3810. [Google Scholar] [CrossRef] [Green Version]
- Zafar, S.; Sadiq, H.; Javaid, B.; Khalid, H.A. On PQ control of BESS in grid-connected mode and frequency control in Islanded-mode for micro-grid application. In Proceedings of the 2018 International Conference on Computing, Electronic and Electrical Engineering, ICE Cube 2018, Quetta, Pakistan, 8–9 October 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Shan, S.; Umanand, L. A Unified Controller for Utility-Interactive Uninterruptible Power Converters for Grid Connected and Autonomous Operations. IEEE Trans. Power Electron. 2019, 34, 3871–3887. [Google Scholar] [CrossRef]
- Bayhan, S.; Abu-Rub, H. A Simple Control Technique for Distributed Generations in Grid-Connected and Islanded Modes. IEEE Int. Symp. Ind. Electron. 2018, 2018, 1237–1242. [Google Scholar] [CrossRef]
- Onar, B.; evki Demirbas, S. A Survey on the Provision of Smooth Transition between Operation Modes in PV-BESS Microgrid. In Proceedings of the 2022 10th International Conference on Smart Grid (icSmartGrid), Singapore, 25–28 October 2022; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2022; pp. 203–207. [Google Scholar] [CrossRef]
- Kannan, S.; Gnanasekar, R.K.; Vasudevan, K. Novel Unified Control Strategies for Seamless Transfer of Operation of Three-Phase Pv-Inverter From Grid-Tied To Islanded Mode. In Proceedings of the CIRED, Ljubljana, Slovenia, 7–8 June 2018; pp. 7–8. [Google Scholar]
- Jaga, O.P.; Choudhuri, S.G. Seamless Transition between Grid-Connected and Islanded Operation Modes for Hybrid PV-BESS Combination Used in Single-Phase, Critical Load Applications. In Proceedings of the 2021 International Conference on Sustainable Energy and Future Electric Transportation (SEFET), Hyderabad, India, 21–23 January 2021. [Google Scholar] [CrossRef]
- IEEE 1547-2018; IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces Sponsored by the IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associate. IEEE: New York, NY, USA, 2018.
- Sindhuja, I.; Latha, Y.K.; Aparna, V. A unified seamless transfer control scheme for grid-connected and islanding modes of operation of grid- connected PV system. Indian J. Sci. Technol. 2016, 9, 1–8. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, J. Indirect current control based seamless transfer of three-phase inverter in distributed generation. IEEE Trans. Power Electron. 2014, 29, 3368–3383. [Google Scholar] [CrossRef]
- Mao, M.; Dong, Z.; Ding, Y.; Chang, L. A unified controller for A microgrid based on adaptive virtual impedance and conductance. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition, ECCE 2014, Pittsburgh, PA, USA, 14–18 September 2014; pp. 695–701. [Google Scholar] [CrossRef]
- Ganjian-Aboukheili, M.; Shahabi, M.; Shafiee, Q.; Guerrero, J.M. Seamless Transition of Microgrids Operation from Grid-Connected to Islanded Mode. IEEE Trans. Smart Grid 2020, 11, 2106–2114. [Google Scholar] [CrossRef]
- Nunez, C.; Visairo-Cruz, N.; Arellanes, A.; Mora, D.; Segundo, J. Holistic Control Approach for the Grid-Connected Converter of a Battery Energy Storage System. IEEE Access 2020, 8, 216844–216855. [Google Scholar] [CrossRef]
- Li, Z. Design and analysis of improved Butterworth low pass filter. In Proceedings of the 2007 8th International Conference on Electronic Measurement and Instruments, ICEMI, Xi’an, China, 16–19 August 2007; pp. 1729–1732. [Google Scholar] [CrossRef]
- Laghari, W.M.; Baloch, M.U.; Mengal, M.A.; Shah, S.J. Performance Analysis of Analog Butterworth Low Pass Filter as Compared to Chebyshev Type-I Filter, Chebyshev Type-II Filter and Elliptical Filter. Circuits Syst. 2014, 5, 209–216. [Google Scholar] [CrossRef] [Green Version]
- Sandhu, M.; Kaur, S.; Kaur, J. A Study on Design and Implementation of Butterworth, Chebyshev and Elliptic Filter with MatLab. Int. J. Emerg. Technol. Eng. Res. 2016, 4, 111–114. [Google Scholar]
- Jaga, O.P.; Gupta, R.; Jena, B.; GhatakChoudhuri, S. Bi-directional DC/DC Converters Used in Interfacing ESSs for RESs and EVs: A Review. IETE Tech. Rev. 2022, 10, 1–37. [Google Scholar] [CrossRef]
- Butterworth, S. On the Theory of Filter Amplifiers. Exp. Wirel. Wirel. Eng. 1930, 7, 536–541. [Google Scholar]
- Zverev, A.I. Handbook of Filter Synthesis; Westinghouse Electric Corporation: New York, NY, USA, 1967. [Google Scholar]
- Holmes, D.G.; Lipo, T.A. Pulse Width Modulation for Power Converters; Wiley-Interscience: New York, NY, USA, 2010. [Google Scholar] [CrossRef]
- Graham, D.; Lathrop, R.C. The synthesis of “optimum” transient response: Criteria and standard forms. Trans. Am. Inst. Electr. Eng. Part II Appl. Ind. 2013, 72, 273–288. [Google Scholar] [CrossRef]

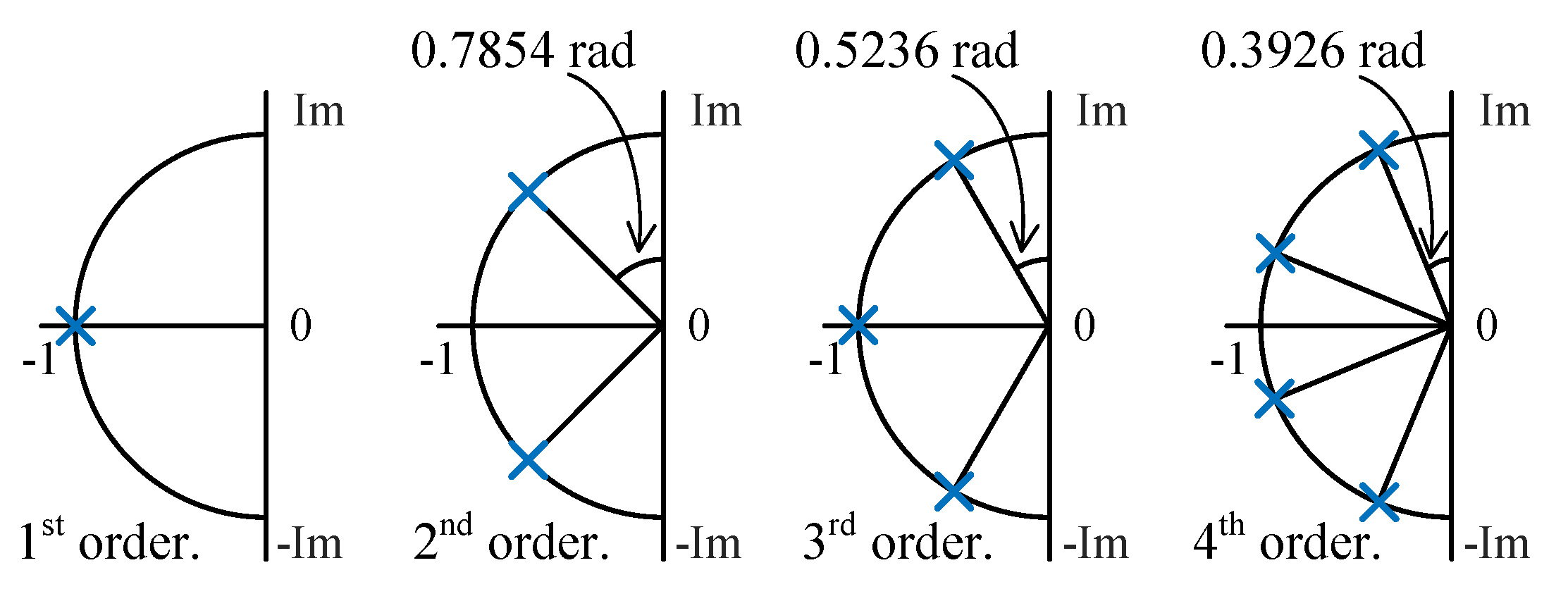




| Filter Order | Polynomial |
|---|---|
| 1. | |
| 2. | |
| 3. | |
| 4. |
| Operation | State | Input | Output | Eigenvalues |
|---|---|---|---|---|
| Mode | Matrix | Matrix | Matrix | (rad/s) |
| Islanded mode (ism) | ||||
| Grid-connected mode | ||||
| inverter (gci) | ||||
| Grid-connected mode | ||||
| rectifier (gcr) |
| Operation | Closed-Loop | Eigenvalues |
|---|---|---|
| Mode | Matrix | (rad/s) |
| Islanded mode | ||
| Grid-connected | ||
| mode (inverter) | ||
| Grid-connected | ||
| mode (rectifier) |
| Holistic Approach [27] | Improved Holistic Approach |
|---|---|
| and | and |
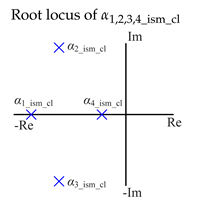 | 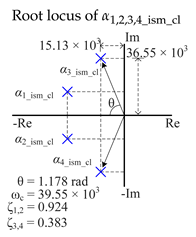 |
| As it can be seen, the dominant pole is overdamped; therefore, its step response is slow and energy wasting as Figure 7 shows. | As it can be seen, the dominant poles are underdamped; therefore, its step response is faster, and the energy transferred is improved than in [27]. |
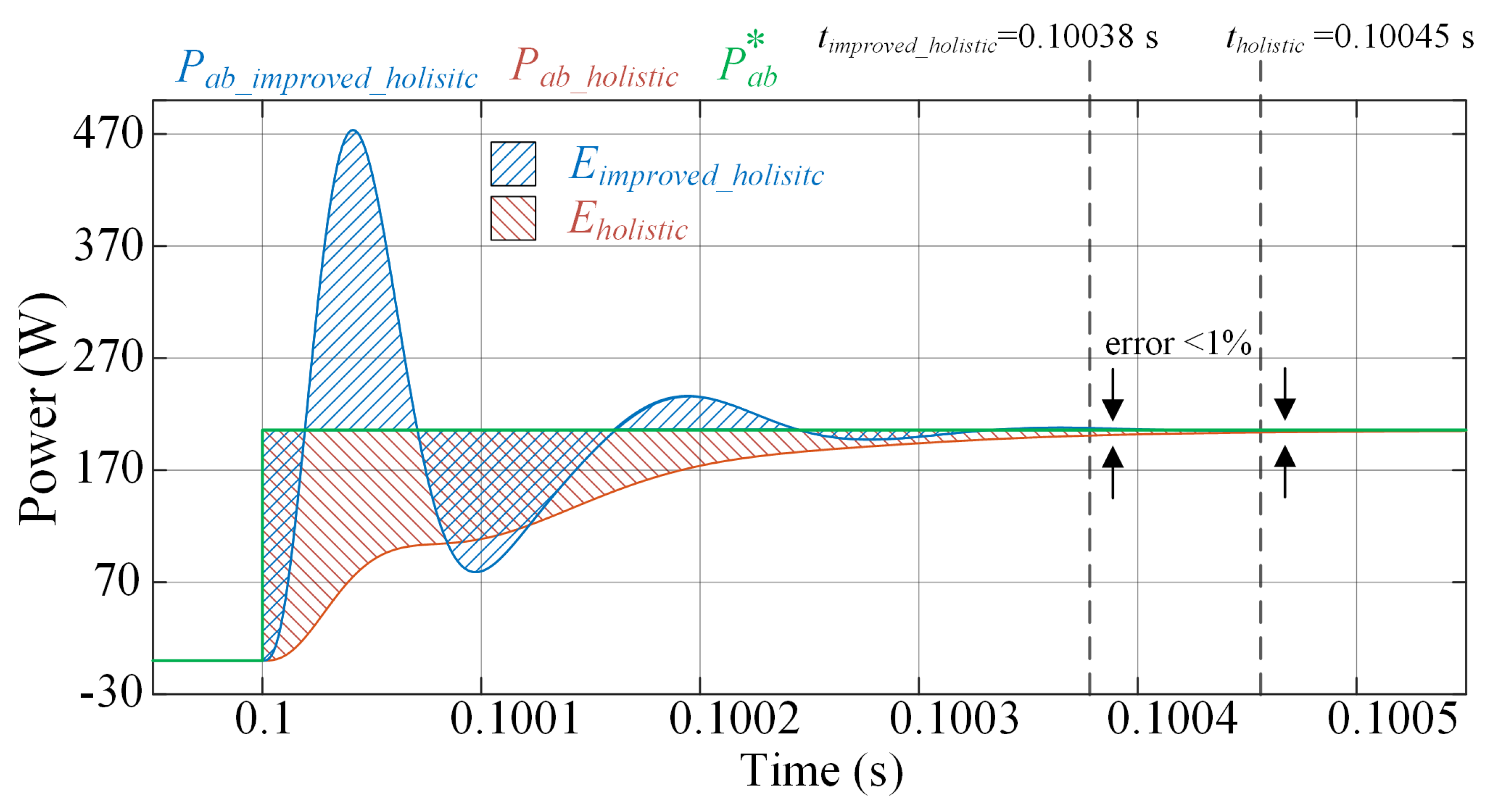
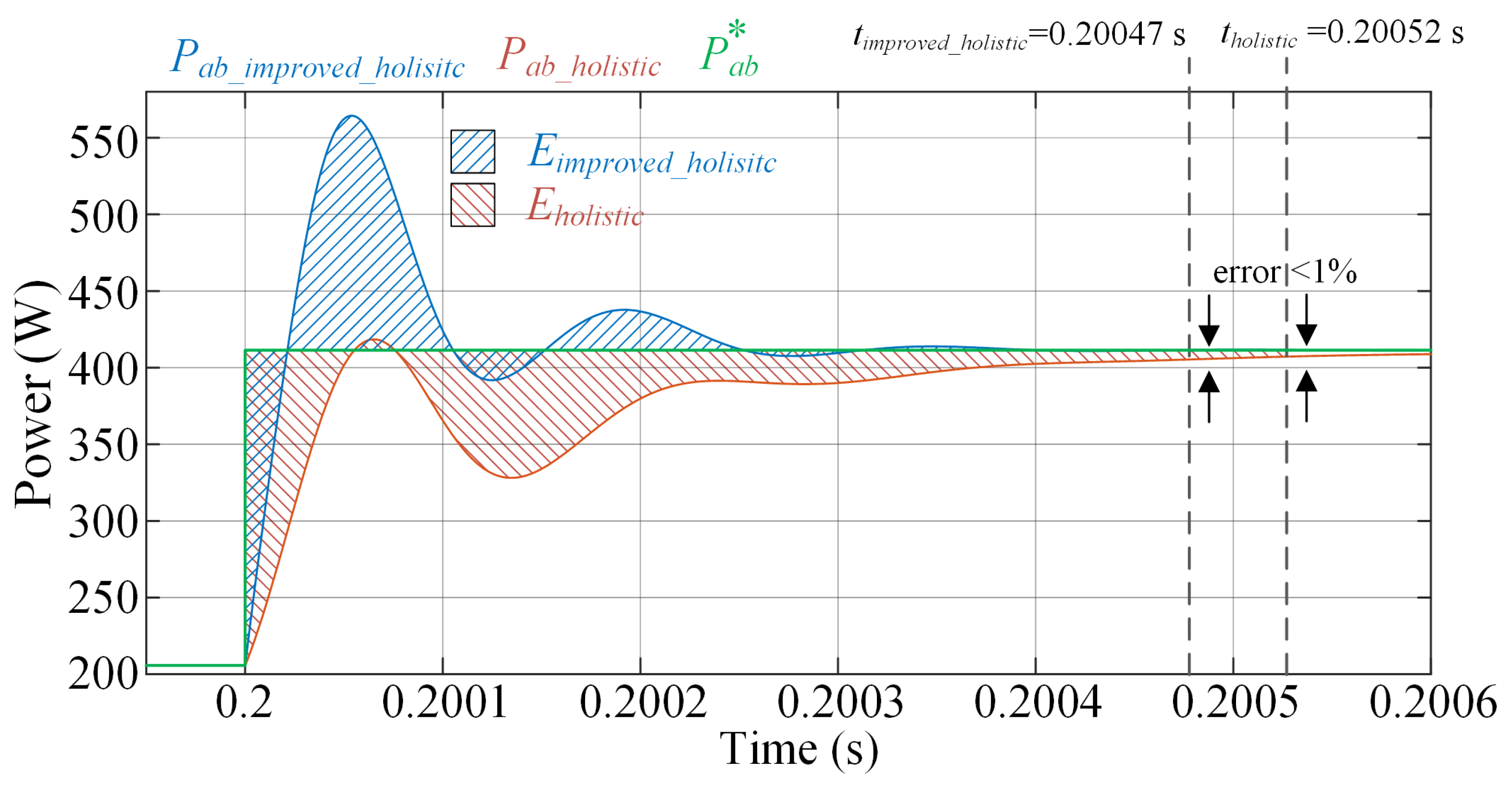
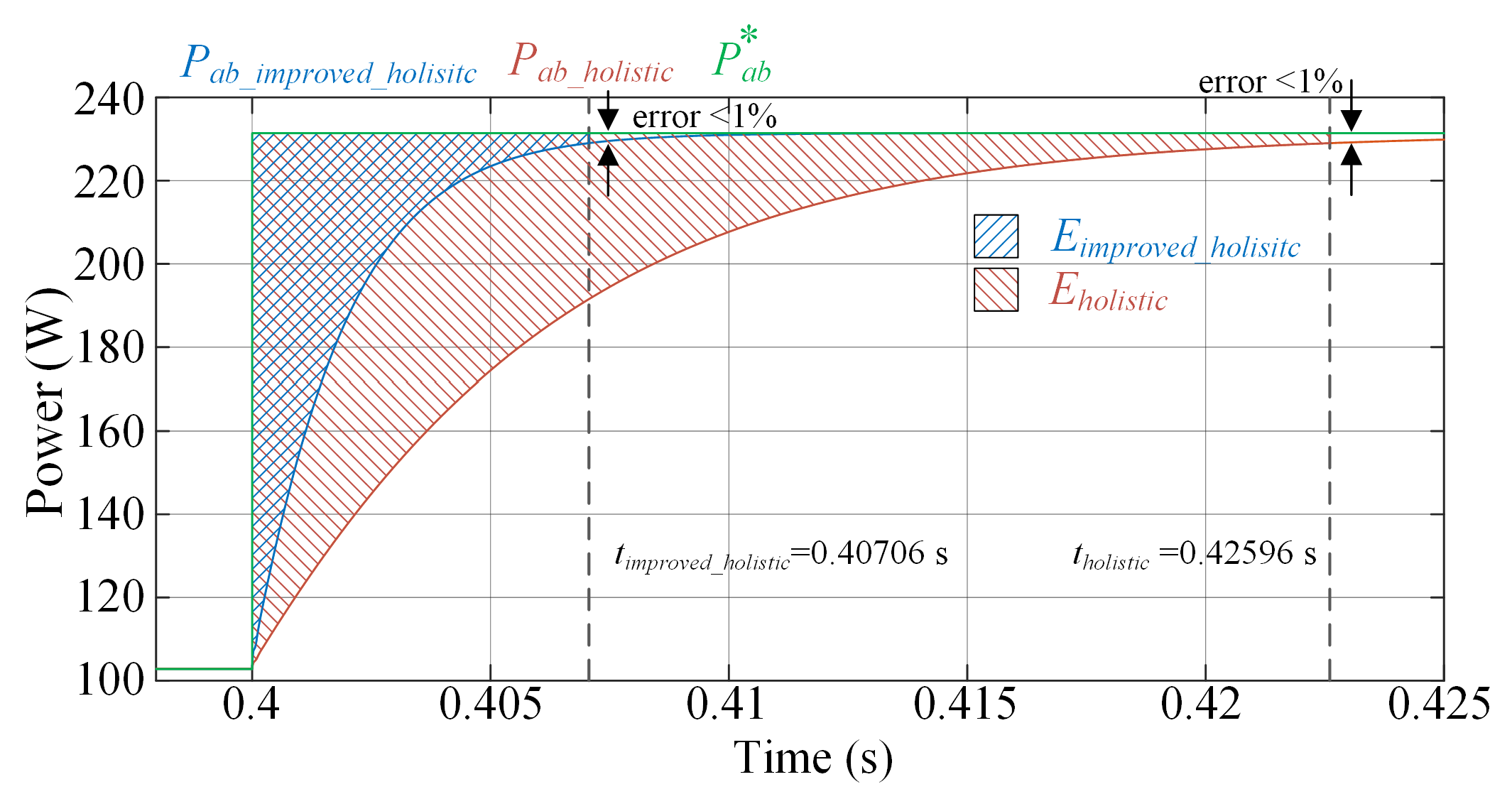
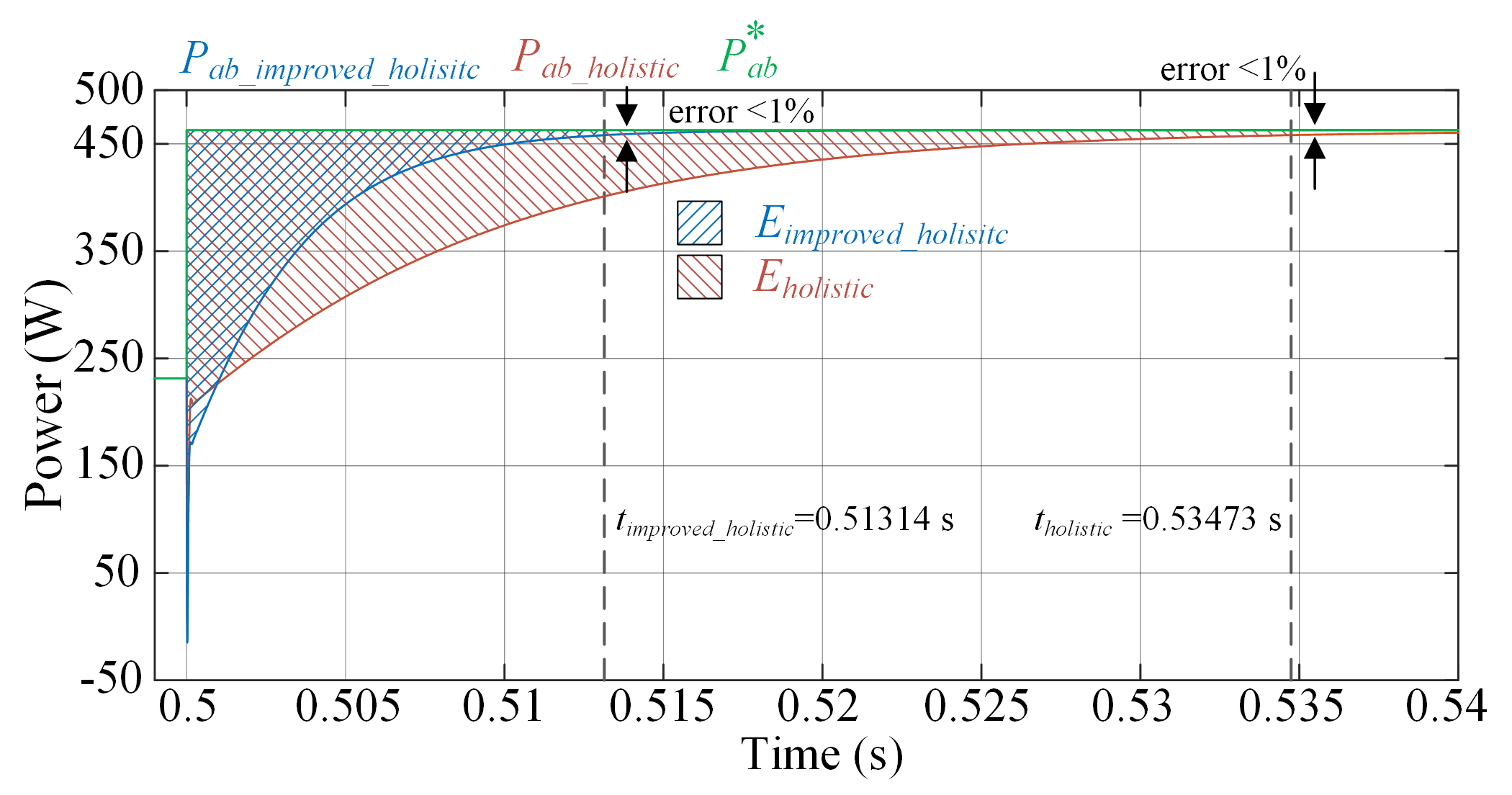
| Time (s) | Type of Event | Change Value According to the Event | Holistic Energy (J) | Improved Holistic Energy (J) | Energy Efficiency (%) |
|---|---|---|---|---|---|
| 0.1 | Voltage step ISM | to | 22.58 m | 19.87 m | 12.00 |
| 0.2 | Load transient ISM | to | 16.71 m | 12.14 m | 27.34 |
| 0.3 | Mode change ISM-GCI | to | 1.38 | 0.42 | 69.21 |
| 0.4 | Current step GCI | to | 4.80 | 1.48 | 69.16 |
| 0.5 | Load transient GCI | to | 29.08 | 11.13 | 61.72 |
| 0.6 | Mode change GCI-GCR | to | 24.22 | 2.40 | 90.09 |
| Parameter | Value |
|---|---|
| Grid voltage (AC: L-L, RMS) | 120V |
| Rated power | |
| Power factor | Near to unity |
| 300V | |
| THD of current | < |
| THD of voltage | < |
| Switching frequency | 12,060 Hz |
| Delta-LCL filter: | |
| Tuning gains | |
| Time (s) | Mode | = 617 W | BRK | BRK | BRK |
|---|---|---|---|---|---|
| 0–0.1 | Grid-connected mode inverter | Closed | Closed | Open | |
| 0.1–0.3 | Grid-connected mode inverter | Closed | Closed | Open | |
| 0.3–0.5 | Islanded mode | Open | Closed | Open | |
| 0.5–0.7 | Islanded mode | Open | Closed | Closed | |
| 0.7–1.0 | Islanded mode | Open | Closed | Open | |
| 1.0–1.2 | Grid-connected mode inverter | Closed | Closed | Open | |
| 1.2–1.6 | Grid-connected mode rectifier | Closed | Closed | Open | |
| 1.6–1.7 | Grid-connected mode rectifier | Closed | Open | Open |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arellanes, A.; Nuñez, C.; Visairo, N.; Valdez-Fernandez, A.A. An Improvement of Holistic Control Tuning for Reducing Energy Consumption in Seamless Transitions for a BESS Grid-Connected Converter. Energies 2022, 15, 7964. https://doi.org/10.3390/en15217964
Arellanes A, Nuñez C, Visairo N, Valdez-Fernandez AA. An Improvement of Holistic Control Tuning for Reducing Energy Consumption in Seamless Transitions for a BESS Grid-Connected Converter. Energies. 2022; 15(21):7964. https://doi.org/10.3390/en15217964
Chicago/Turabian StyleArellanes, Alberto, Ciro Nuñez, Nancy Visairo, and Andres A. Valdez-Fernandez. 2022. "An Improvement of Holistic Control Tuning for Reducing Energy Consumption in Seamless Transitions for a BESS Grid-Connected Converter" Energies 15, no. 21: 7964. https://doi.org/10.3390/en15217964
APA StyleArellanes, A., Nuñez, C., Visairo, N., & Valdez-Fernandez, A. A. (2022). An Improvement of Holistic Control Tuning for Reducing Energy Consumption in Seamless Transitions for a BESS Grid-Connected Converter. Energies, 15(21), 7964. https://doi.org/10.3390/en15217964