Experimental Thermodynamic Characterization of the Chalcopyrite-Based Compounds in the Ag–In–Te System for a Potential Thermoelectric Application

Abstract

The equilibrium concentration space of the Ag–In–Te system in the part AgInTe₂–Te–In₂Te₃ was studied through the modified solid-state electromotive force (EMF) method by dividing In₂Te₃–In₂Te₅–Ag₃In₉₇Te₁₄₇ (I), In₂Te₅–Te–Ag₃In₉₇Te₁₄₇ (II), Ag₃In₉₇Te₁₄₇–Te–AgIn₅Te₈ (III), AgIn₅Te₈–Te–AgIn₃Te₅ (IV), and AgIn₃Te₅–Te–AgInTe₂ (V), into separate phase regions at T ≤ 500 K. The formation of a thermodynamically stable combination of the binary and ternary phases in the (I)–(V) phase regions from a metastable phase mixture of substances was carried out at T ≤ 500 K in the R(Ag⁺) part of the positive electrode (PE) of the galvanic cells (GCs) of the structure: (−) C |∙| Ag |∙| SE |∙| R(Ag⁺) |∙| PE |∙| C (+), where C is the graphite (inert electrode), SE is the solid-state electrolyte (Ag₃GeS₃Br glass), and Ag is the left (negative) electrode. The Ag⁺ ions in the R(Ag⁺) region functioned as small nucleation centers for the formation of the stable phases. The spatial position of the (I)–(V) phase regions in the concentration space of the Ag–In–Te system relative to the position of silver was used to express the overall potential-forming reactions with the participation of the substances Ag, Te, In₂Te₅, Ag₃In₉₇Te₁₄₇, AgIn₅Te₈, AgIn₃Te₅, and AgInTe₂. The subsequent EMF measurements were carried out by applying the same GCs. The temperature dependences of the EMF of GCs with PE of the (I)–(V) phase regions were here used to determine, for the first time, the values of standard thermodynamic functions of the binary and ternary compounds. The determined values of the Gibbs energies of the formation of compounds are equal: $G_{{\mathrm{In}}_2{\mathrm{Te}}_5}^{○}=\left(182.7\pm 1.9\right) {\mathrm{kJ}·\mathrm{mol}}^{-1}$, $G_{{\mathrm{AgInTe}}_2}^{○}=\left(115.0\pm 3.1\right) {\mathrm{kJ}·\mathrm{mol}}^{-1}$, $G_{{\mathrm{AgIn}}_3{\mathrm{Te}}_5}^{○}=\left(301.5\pm 6.5\right) {\mathrm{kJ}·\mathrm{mol}}^{-1}$, $G_{{\mathrm{AgIn}}_5{\mathrm{Te}}_8}^{○}=\left(487.6\pm 11.3\right) {\mathrm{kJ}·\mathrm{mol}}^{-1}$, and $G_{{\mathrm{Ag}}_3{\mathrm{In}}_{97}{\mathrm{Te}}_{147}}^{○}=\left(8594\pm 189\right) {\mathrm{kJ}·\mathrm{mol}}^{-1}$ The correctness of the division of the equilibrium phase space of the Ag–In–Te system in the part AgInTe₂–Te–In₂Te₃ involving the AgInTe₂, AgIn₃Te₅, AgIn₅Te₈, and Ag₃In₉₇Te₁₄₇ compounds was confirmed by the agreement of the calculated and literature-based thermodynamic data for In₂Te₅ compound. Compositions of pairs of the ternary compounds for their subsequent practical application were proposed.

1. Introduction

The move towards a decarbonized energy future demands the discovery of new energy materials with unique properties, such as wider chemical and thermal stability ranges. Recent attempts in the search for advanced energy materials have shown progress in identifying promising materials for high-performance energy applications [1,2]. The search for new energy materials involves the determination of phase transformations, melting, phase equilibria with coexisting phases, and other application-based thermodynamic properties [3]. Recently, a novel approach for discovering new energy materials, called phase boundary mapping, has also been applied [4]. The latest thermal performance investigation of nanofluids for thermal management applications has also shown promising results for medium-temperature waste-heat recovery applications [5]. The availability of these data helps to optimize materials processing and the selection of high-performance and cost-effective materials [6]. The roles of materials design, experimental techniques, and computational tools in the discovery of new inorganic materials with unique properties are illustrated in Figure 1 [7].

The semiconductor compounds of the systems A ^I–B ^III–C ^VI (A ^I–Ag, Cu; B ^III–In, Al, Ga; C ^VI–Te, Se, S) with the chalcopyrite A ^IB ^IIIC ^VI₂ and defect-containing chalcopyrite A ^IB ^III_2n+1C ^VI_3n+2 (n = 1, 2) crystal structures are considered to be promising materials for various practical applications in non-linear optical devices, power generation, and converters of light and waste heat energy into electricity at moderate temperatures [8,9,10,11]. For example, the thermoelectric (TE) process, the conversion of waste heat energy into electricity by exploiting the temperature gradient, produces clean energy and reduces fossil fuel consumption [12,13,14]. Some, TE materials, such as these Ag–Se–Te-based materials, have the best TE performance, even at low temperatures [3].

A TE system is considered to be one of the preferred clean energy techniques because of its qualities, such as being small in size, having no moving parts, and having temperature control capacities [15]. TE technology provides the possibility to overcome the ever-growing energy demand and environmental crisis [16].

One of the most effective ways of using a temperature gradient for TE generation is to assemble numerous pairs of p/n elements made in the form of contact of two compounds from the same family. For this purpose, Fujii et al. [17] investigated and compared the electrical properties and electronic structure of the AgInTe₂ and AgIn₅Te₈ compounds separated in the T–x space of the Ag₂Te–In₂Te₃ cross-section at T < 680 K by a two-phase region [18,19,20,21]. Calculations of the electronic structure by applying Korringa–Kohn–Rostoker–Green’s method showed that these compounds have valence bands of the same shape and conduction bands of different shapes. It has been noted that the defect-containing chalcopyrite AgIn₅Te₈ can be a functioning n-type TE material due to its band structure [17].

The choice of the p-AgInTe₂ and n-AgIn₅Te₈ compounds for the creation of numerous pairs of the p/n components to obtain the high voltage may not be realized in practice due to thermodynamic reasons. The reason for this may be the intermediate compound AgIn₃Te₅, which is predicted for the equilibrium T–x space of the Ag₂Te–In₂Te₃ cross-section at moderate temperatures [22,23]. The lack of information about the AgIn₃Te₅ compound in [18,19,20,21] is probably related to the metastable state (for kinetic reasons) of the mixture of the AgInTe₂ and AgIn₅Te₈ compounds below 680 K. The possibility of overcoming kinetic obstacles to the formation of a thermodynamically stable set of chalcogenide and chalcohalide phases from a metastable phase mixture of compounds in the galvanic cells (GCs) with the participation of the Ag⁺ ions was reported in [24,25,26,27]. Nevertheless, there is a lack of information on the thermal stabilities and thermodynamic properties of the ternary compounds in the Ag–In–Te system.

The purpose of this work was to establish the phase composition of the equilibrium T–x space of the Ag–In–Te system in the AgInTe₂–Te–In₂Te₃ phase region below 500 K and to determine the standard thermodynamic quantities of the compounds. The established thermodynamic properties of the equilibrium phases in the Ag–In–Te system have a great fundamental and practical interest in materials science. For example, the obtained results can be applied for the scientifically based strategy of selected pairs of the p/n elements of the Ag–In–Te system for the TE applications.

2. Materials and Methods

The high-purity substances Ag, In, and Te (>99.99 wt.%, Alfa Aesar, Karlsruhe, Germany) were used for the synthesis of the binary and ternary compounds. The appropriately weighed and mixed pure substances were melted in an inert atmosphere. Melts of the mixtures were homogenized for 20 min, followed by cooling to room temperature at a rate of 5 K·min⁻¹. Polycrystalline powder samples from the crystallized melt were crushed to a particle size of ~5 μm and analyzed with the XRD technique before the preparation of the positive electrodes of the GCs. A diffractometer STOE STADI P, equipped with a linear position-sensitive detector PSD in a geometry of Guinier (transmission mode, CuKα₁ radiation, a bent Ge(111) monochromator, and a scan mode of 2θ/ω), was applied for the phase composition characterization of the samples. The following program modules, STOE WinXPOW [28], PowderCell [29], and FullProf [30], as well as databases [31,32], were used for the X-ray powder diffraction (XRPD) analysis.

Synthesis of the thermodynamically stable set of phases below 500 K from the metastable mixtures of silver, tellurium, and multicomponent compounds, and the subsequent electromotive force (EMF, E) measurements were performed with GCs of type (A): (−) C |∙| Ag |∙| SE |∙| R(Ag⁺) |∙| PE |∙| C (+), where C is the graphite (inert electrode), SE is the solid-state electrolyte (Ag₃GeS₃Br glass [33]), Ag is the left (negative) electrode, R(Ag⁺) is the buffer region of PE that contacts with the SE, and PE is the right (positive) electrode. The ratios of the initial components of the PE of GCs were determined from the potential-forming reactions in the phase region of the respective reactions. The components of the GCs were pressed through a 2 mm diameter hole, at 10⁸ Pa, which was arranged in a fluoroplastic matrix, up to a density of ρ = (0.93 ± 0.02)∙ρ₀, where ρ₀ is the density of the cast samples determined experimentally [34,35]. The process of forming the thermodynamically stable set of phases from the metastable phase mixture of finely dispersed substances was conducted in the R(Ag⁺) region. The Ag⁺ ions served as the small nucleation centers of formation of the stable phases [25,26,27]. After completion of the synthesis process, the GCs (A) were used for E vs. T measurements.

The experiments were conducted in a resistance furnace oriented horizontally, which is similar to those described in our previous work [36]. A flow of (10^–5 m³⋅min^–1) highly purified (99.99 vol.%) Ar (g) at P = 1.2⋅10⁵ Pa was utilized as a protective atmosphere, flowing from the left to the right electrodes of GCs. The uncertainty for the temperature was ± 0.5 K. The EMF values of the cells were measured using the high-resistance (input impedance of more than 10¹² Ω) Picotest M3500A universal digital multimeter. The equilibrium in GCs at each temperature was attained in <2 h. At equilibrium, the EMF records were stable, with negligible variations not exceeding ±0.2 mV [37]. The EMF vs. T dependences of GCs were analyzed by the methodology described in [38,39,40].

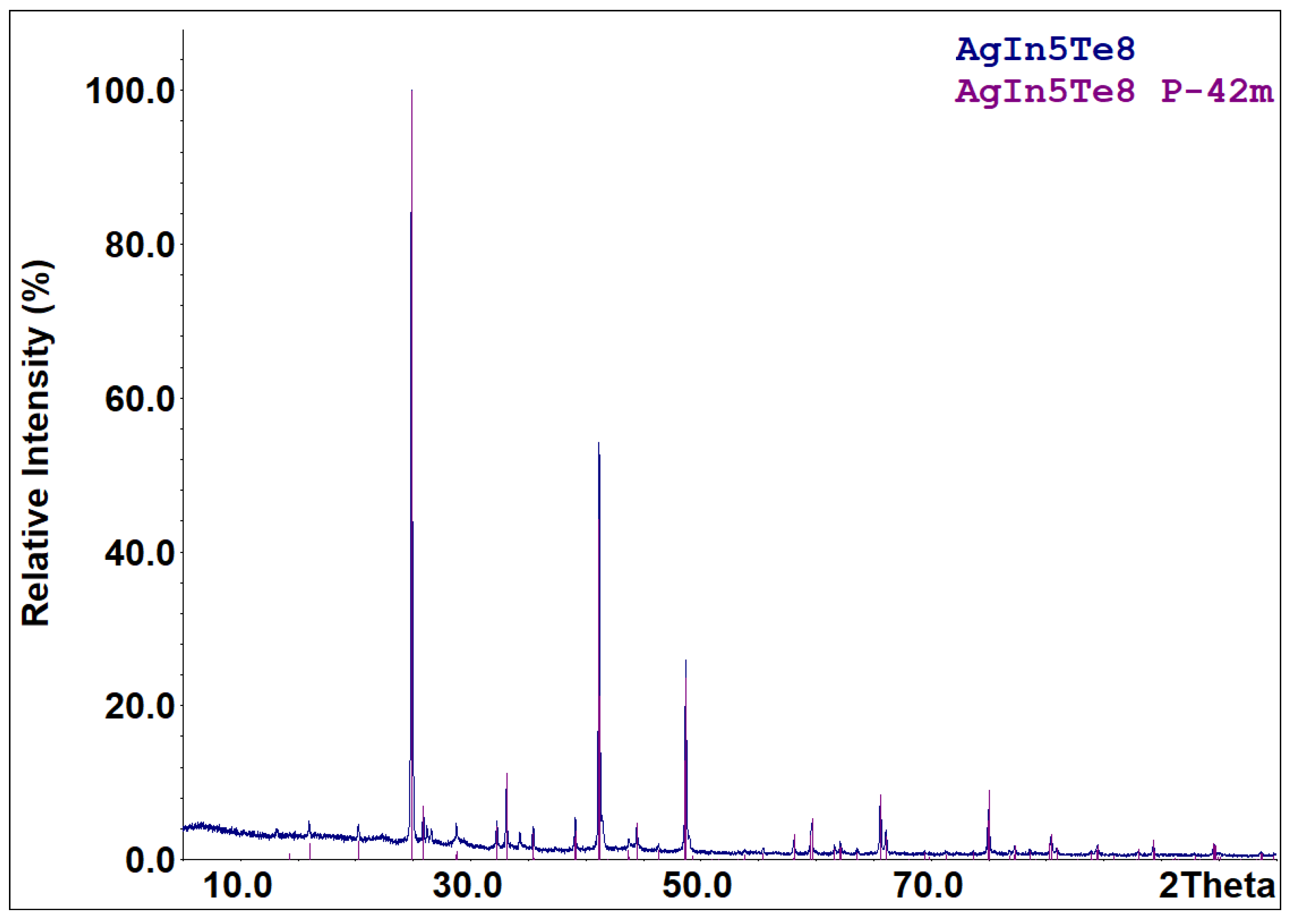
3. Results and Discussion

The phase equilibria of the Ag–In–Te system in the part AgInTe₂–Te–In₂Te₃ are shown in Figure 2.

The presence of five phase regions in this area was established using the EMF method. These five phase regions are: In₂Te₃–In₂Te₅–Ag₃In₉₇Te₁₄₇ (I), In₂Te₅–Te–Ag₃In₉₇Te₁₄₇ (II), Ag₃In₉₇Te₁₄₇–Te–AgIn₅Te₈ (III), AgIn₅Te₈–Te–AgIn₃Te₅ (IV), and AgIn₃Te₅–Te–AgInTe₂ (V). The following principles confirmed the validity of the presented division of the concentration space:

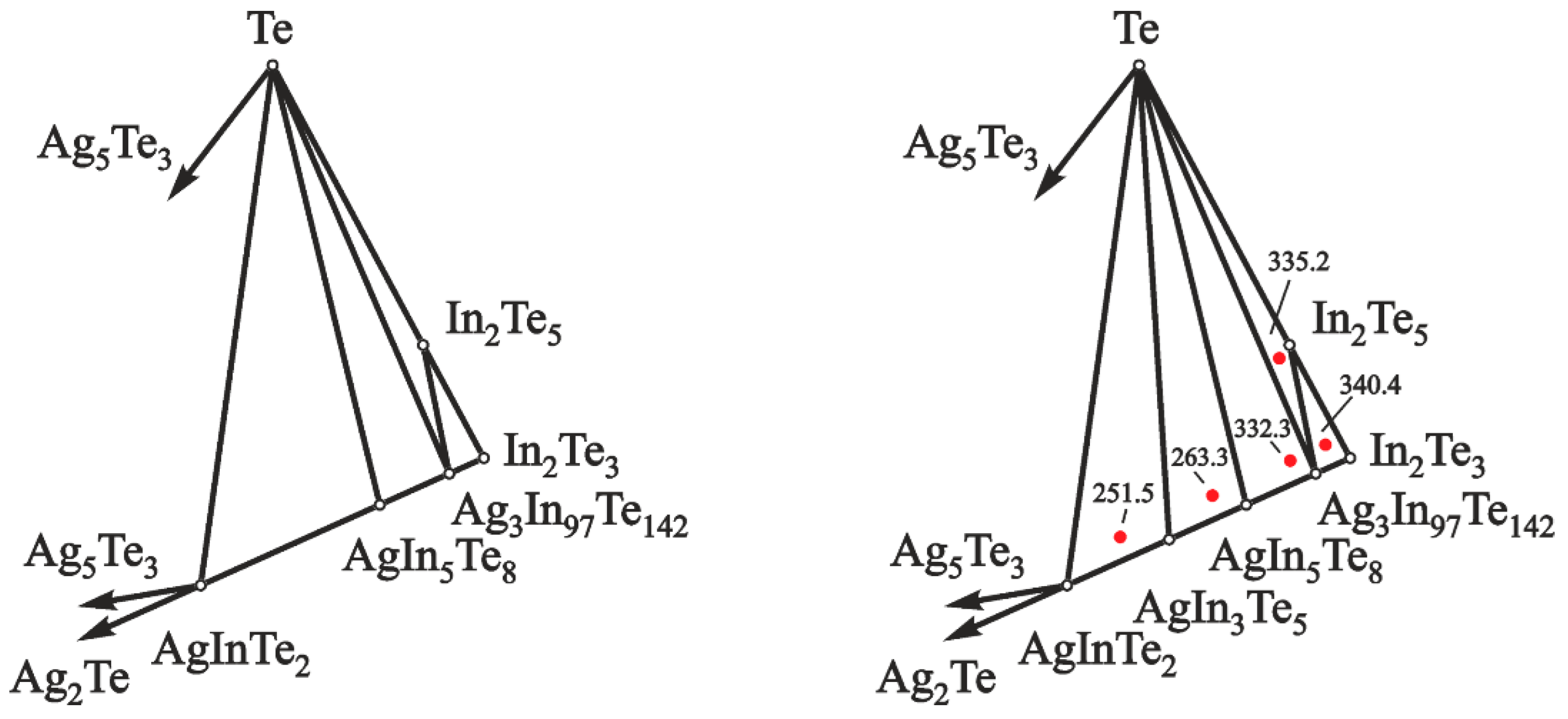
• the GCs with PE of the mentioned phase regions are characterized by different EMF values at the same temperature, Figure 2 (right);
• as the phase region approaches the position of silver composition, the EMF values of cells decrease [41]; and
• subsequent determination of thermodynamic data of the In₂Te₅ compound.

Following Figure 2, the phase regions (I)–(V) position relative to silver can be applied to determine the thermodynamic properties of the constituent compounds by the EMF method [42,43,44]. The formation reaction of the compound Ag₃In₉₇Te₁₄₇ from pure element Ag and binary compounds In₂Te₃ and In₂Te₅ in the phase region (I) can be expressed as:

12Ag = 12Ag ⁺ + 12e ⁻ – left electrode,

12Ag ⁺ + 12e ^– + 191In₂Te₃ + 3In₂Te₅ = 4Ag₃In₉₇Te₁₄₇ − right electrode,

12Ag + 191In₂Te₃ + 3In₂Te₅ = 4Ag₃In₉₇Te₁₄₇ − overall cell reaction.

(R1)

The overall potential-forming cell reactions in the PE of GCs for the phase regions (II)–(V) can be written as:

12Ag + 194In₂Te₅ = 4Ag₃In₉₇Te₁₄₇ + 382Te,

(R2)

82Ag + 5Ag₃In₉₇Te₁₄₇ + 41Te = 97AgIn₅Te₈,

(R3)

2Ag + 3AgIn₅Te₈ + Te = 5AgIn₃Te₅,

(R4)

2Ag + AgIn₃Te₅ + Te = 3AgInTe₂.

(R5)

Based on the reactions (R1)–(R5), compositions of powder mixtures of silver, tellurium along with binary and ternary compounds in the PE of GCs of the phase regions (I)–(V) were determined.

Part of the cooled melts of the compounds specified in reactions (R1)–(R5) is metastable. According to the X-ray diffraction results (Figure 3), the cooled melt of the formula composition Ag₃In₉₇Te₁₄₇ consists of characteristic peaks for the Ag_xIn_0.67Te (space group F-43m) and InTe (space group I4/mcm) phases. The diffraction pattern (Figure 4) of an aliquot of the as-synthesized compound AgIn₅Te₈ mainly identifies AgIn₅Te₈ as the primary phase and In₂Te₅ as a minor impurity. Solid-state vacuum annealing at 600 K for homogenization did not modify the phase composition of the specified cooled melts. Samples of the formula compositions In₂Te₃, In₂Te₅, and AgInTe₂ were crystallized as single-phase compounds. The process of forming the thermodynamically stable set of phases from the metastable mixture of components in the PE of GCs for the participation of Ag⁺ ions ended within 48 h at 500 K. The criterion for phase equilibria attainment in the PE’s R(Ag⁺) region is the reproducibility of the E vs. T dependencies of GCs during the thermal cycles.

The measured E vs. T values are compiled in

Table 1. A summary of the measured EMF values and temperatures of the GCs in different phase regions of the Ag–In–Te system.

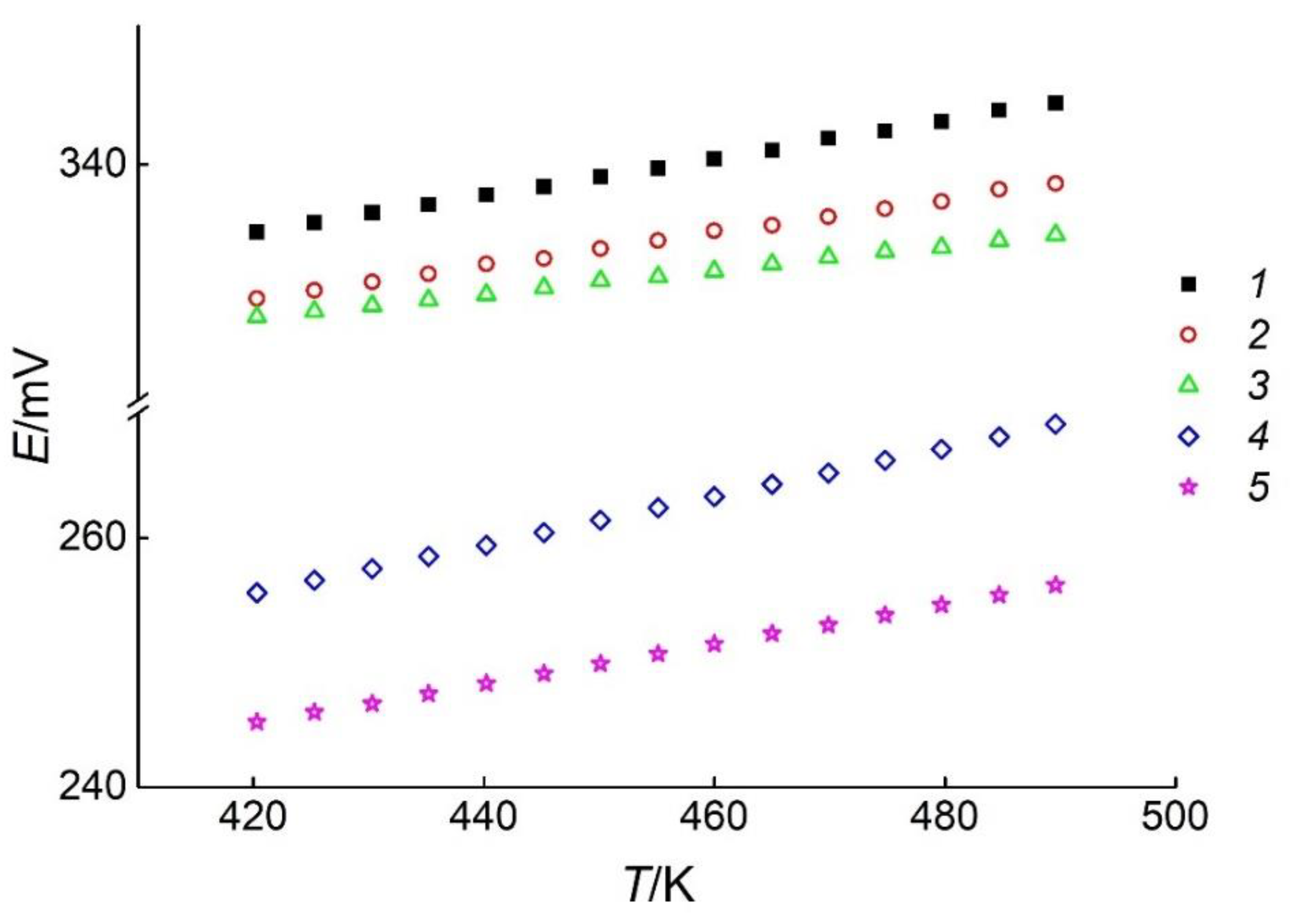
T/K	Phase Region
	(I)	(II)	(III)	(IV)	(V)
	E/mV	E/mV	E/mV	E/mV	E/mV
420.3	335.1	330.3	329.0	255.6	245.2
425.3	335.8	330.9	329.4	256.6	246.0
430.3	336.5	331.5	329.8	257.5	246.7
435.2	337.1	332.1	330.2	258.5	247.5
440.2	337.8	332.8	330.6	259.4	248.3
445.2	338.4	333.2	331.1	260.4	249.1
450.1	339.1	333.9	331.6	261.4	249.9
455.1	339.7	334.5	331.9	262.4	250.7
460.0	340.4	335.2	332.3	263.3	251.5
465.2	341.0	335.6	332.8	264.3	252.3
469.9	341.9	336.2	333.3	265.2	253.0
474.8	342.4	336.8	333.7	266.2	253.8
479.7	343.1	337.3	334.0	267.1	254.6
484.7	343.9	338.2	334.5	268.1	255.4
489.6	344.4	338.6	334.9	269.1	256.2

and plotted in Figure 5.

The analysis of the E vs. T dependences for the reactions (R1)–(R5) between 420 and 489 K was performed by the least-squares method [41,45] using Equation (1):

$$E=a+bT\equiv \overline{E}+b\left(T-\overline{T}\right),$$

(1)

where $\overline{E}=\frac{{\displaystyle \sum }{E}_i}{n}$, $\overline{T}=\frac{{\displaystyle \sum }{T}_i}{n}$ ($E_i$ is the EMF of the GC at temperature $T_i$, and $n$ is the number of experimental pairs $T_i$ and $E_i$).

The $a$ and $b$ coefficients were calculated by applying Equations (2) and (3):

$$a=\overline{E}-b\overline{T},$$

(2)

$$b=\frac{{\displaystyle \sum }\left[\left(E_i-\overline{E}\right)\left(T_i-\overline{T}\right)\right]}{{\displaystyle \sum }{\left(T_i-\overline{T}\right)}^2}.$$

(3)

The statistical dispersions of the uncertainties in the measurement consisted of the calculation variances in values of the EMF $E$ ($u_E^2$), coefficients $b$ ($u_b^2$) and $a$ ($u_a^2$), and the dispersions of the EMF values $\tilde{E}$ ($u_{\tilde{E}}^2$) calculated with Equation (1) are equal:

$$u_E^2=\frac{{\displaystyle \sum }{\left(E_i-{\tilde{E}}_i\right)}^2}{n-2},$$

(4)

$$u_b^2\left(T\right)=\frac{u_E^2}{{\displaystyle \sum }{\left(T_i-\overline{T}\right)}^2},$$

(5)

$$u_a^2\left(T\right)=\frac{u_E^2}{n}+\frac{u_E^2{\overline{T}}^2}{{\displaystyle \sum }{\left(T_i-\overline{T}\right)}^2},$$

(6)

$$u_{\tilde{E}}^2\left(T\right)=\frac{u_E^2}{n}+u_b^2{\left(T-\overline{T}\right)}^2.$$

(7)

Uncertainties (${\Delta }_i$) of the relative quantities can be calculated by the Equation (8):

$${\Delta }_i=k_{St}{u}_i$$

(8)

where $k_{St}$ is the Student’s coefficient, and $u_i$ is the standard deviation. At a confidence level of 95% and $n=15$, the Student’s coefficient is $k_{St}=2.131$ [45].

The final equation of the E vs. T dependences together with the statistical dispersions can be express as [43,44]:

$$E=a+bT\pm k_{St}\sqrt{\left(\frac{u_E^2}{n}+u_b^2{\left(T-\overline{T}\right)}^2\right)}.$$

(9)

As listed in Table 1, the values of the temperature and EMF were used to calculate the dispersions and coefficients of Equation (9) for the phase regions (I)–(V). The results of the calculations are presented in

Table 2. The E vs. T dependences for the type (A) GCs in the (I)–(V) phase regions of the Ag–In–Te system in the range between 420 and 489 K.

Phase region	$E=a+bT\pm k_{St}\sqrt{\left(\frac{u_E^2}{n}+u_b^2{\left(T-\overline{T}\right)}^2\right)}$
(I)	$E=278.46+134.75·{10}^{-3}T\pm 2.131\sqrt{\left(\frac{4.93·{10}^{-3}}{15}+7.19·{10}^{-7}{\left(T-455.03\right)}^2\right)}$
(II)	$E=279.96+119.81·{10}^{-3}T\pm 2.131\sqrt{\left(\frac{7.24·{10}^{-3}}{15}+1.05·{10}^{-6}{\left(T-455.03\right)}^2\right)}$
(III)	$E=292.83+85.96·{10}^{-3}T\pm 2.131\sqrt{\left(\frac{2.79·{10}^{-3}}{15}+4.06·{10}^{-7}{\left(T-455.03\right)}^2\right)}$
(IV)	$E=173.86+194.44·{10}^{-3}T\pm 2.131\sqrt{\left(\frac{1.12·{10}^{-3}}{15}+1.63·{10}^{-7}{\left(T-455.03\right)}^2\right)}$
(V)	$E=178.36+158.93·{10}^{-3}T\pm 2.131\sqrt{\left(\frac{1.01·{10}^{-3}}{15}+1.47·{10}^{-7}{\left(T-455.03\right)}^2\right)}$

.

The Gibbs energies (${\mathsf{\Delta }}_{\mathrm{r}}G$), enthalpies (${\mathsf{\Delta }}_{\mathrm{r}}H$), and entropies (${\mathsf{\Delta }}_{\mathrm{r}}S$) of the reactions (R1)–(R5) can be calculated by the thermodynamic Equations (10)–(12):

$${\mathsf{\Delta }}_{\mathrm{r}}G=-z·\mathrm{F}·E,$$

(10)

$${\mathsf{\Delta }}_{\mathrm{r}}H=-z·\mathrm{F}·\left[E-\left(dE/dT\right)T\right],$$

(11)

$${\mathsf{\Delta }}_{\mathrm{r}}S=z·\mathrm{F}·\left(dE/dT\right),$$

(12)

where $z$ is the number of electrons involved in the reactions (R1)–(R5), F is the Faraday constant, and E is the EMF of the GC.

The thermodynamic equations of the reactions (R1)–(R5) at 298 K were calculated using Equations (10)–(12) in the approximation ${\left(\frac{\partial {\mathsf{\Delta }}_{\mathrm{r}}H}{\partial T}\right)}_p=0$ and ${\left(\frac{\partial {\mathsf{\Delta }}_{\mathrm{r}}S}{\partial T}\right)}_p=0$ [46,47]. The results of the calculations are presented in

Table 3. The values of standard thermodynamic functions of the reactions (R1)–(R5).

Reaction	$-{\mathbf{\Delta }}_{\mathbf{r}}{\mathit{G}}^{○}$	$-{\mathbf{\Delta }}_{\mathbf{r}}{\mathit{H}}^{○}$	${\mathbf{\Delta }}_{\mathbf{r}}{\mathit{S}}^{○}$
	kJ·mol –1		J·(mol·K) −1
(R1)	368.9 ± 0.3	322.4 ± 1.0	156.0 ± 2.1
(R2)	365.5 ± 0.4	324.1 ± 1.2	138.7 ± 2.5
(R3)	2519.5 ± 1.7	2316.8 ± 4.9	680.1 ± 10.7
(R4)	44.73 ± 0.03	33.55 ± 0.08	37.52 ± 0.17
(R5)	43.56 ± 0.02	34.42 ± 0.07	30.67 ± 0.16

.

The standard Gibbs energies of the reactions (R1) and (R2) are related to the Gibbs energies of the compounds by Equations (13) and (14):

$${\Delta }_{\mathrm{r}\left(\mathrm{R}1\right)}{G}^{○}=4{\Delta }_{\mathrm{f}}{G}_{{\mathrm{Ag}}_3{\mathrm{In}}_{97}{\mathrm{Se}}_{147}}^{○}-191{\Delta }_{\mathrm{f}}{G}_{{\mathrm{In}}_2{\mathrm{Te}}_3}^{○}-3{\Delta }_{\mathrm{f}}{G}_{{\mathrm{In}}_2{\mathrm{Te}}_5}^{○},$$

(13)

$${\Delta }_{\mathrm{r}\left(\mathrm{R}2\right)}{G}^{○}=4{\Delta }_{\mathrm{f}}{G}_{{\mathrm{Ag}}_3{\mathrm{In}}_{97}{\mathrm{Se}}_{147}}^{○}-194{\Delta }_{\mathrm{f}}{G}_{{\mathrm{In}}_2{\mathrm{Te}}_5}^{○}.$$

(14)

Subtracting term-by-term, the left and right parts of Equations (13) and (14) can be written as follows:

$${\Delta }_{\mathrm{f}}{G}_{{\mathrm{In}}_2{\mathrm{Te}}_5}^{○}=\frac{1}{191}\left({\Delta }_{\mathrm{r}\left(\mathrm{R}1\right)}{G}^{○}-{\Delta }_{\mathrm{r}\left(\mathrm{R}2\right)}{G}^{○}\right)+{\Delta }_{\mathrm{f}}{G}_{{\mathrm{In}}_2{\mathrm{Te}}_3}^{○}.$$

(15)

In an analogous way, the equations to calculate the formation enthalpy and entropy of the In₂Te₅ compound can be expressed:

$${\Delta }_{\mathrm{f}}{H}_{{\mathrm{In}}_2{\mathrm{Te}}_5}^{○}=\frac{1}{191}\left({\Delta }_{\mathrm{r}\left(\mathrm{R}1\right)}{H}^{○}-{\Delta }_{\mathrm{r}\left(\mathrm{R}2\right)}{H}^{○}\right)+{\Delta }_{\mathrm{f}}{H}_{{\mathrm{In}}_2{\mathrm{Te}}_3}^{○},$$

(16)

$$S_{{\mathrm{In}}_2{\mathrm{Te}}_5}^{○}=\frac{1}{191}\left({\Delta }_{\mathrm{r}\left(\mathrm{R}1\right)}{S}^{○}-{\Delta }_{\mathrm{r}\left(\mathrm{R}2\right)}{S}^{○}\right)+2S_{\mathrm{Te}}^{○}+S_{{\mathrm{In}}_2{\mathrm{Te}}_3}^{○}.$$

(17)

The corresponding reactions to determine standard thermodynamic properties ${\Delta }_{\mathrm{f}}{G}^{○}$, ${\Delta }_{\mathrm{f}}{H}^{○}$, and $S^{○}$ of the Ag₃In₉₇Te₁₄₇, AgIn₅Te₈, AgIn₃Te₅, and AgInTe₂ compounds can be written in a similar way using reactions (R2)–(R5) with their appropriate stoichiometric numbers.

For the first time, the standard thermodynamic quantities for selected compounds of the Ag–In–Te system were calculated using Equations (15)–(17) and the thermodynamic data of the pure substances Ag, In, Te, and In₂Te₃ [48]. A comparative list of the determined quantities and the literature data is included in

Table 4. The standard thermodynamic quantities of elements and compounds in the Ag–In–Te system.

Phases	$-{\mathbf{\Delta }}_{\mathbf{f}}{\mathit{G}}^{○}$	$-{\mathbf{\Delta }}_{\mathbf{f}}{\mathit{H}}^{○}$	${\mathit{S}}^{○}$	Reference
	kJ⋅mol −1		J⋅(mol⋅K) −1
Ag	0	0	42.677	[48]
In	0	0	57.823	[48]
Te	0	0	49.497	[48]
In2Te3	182.733	191.627	234.304	[48]
In2Te5	–	191.6 ± 2.1	–	[49]
In2Te5	–	188.0 ± 1.3	–	[50]
In2Te5	182.7 ± 1.9	191.6 ± 3.4	333.4 ± 4.7	Present study
Ag3In97Te147	8954 ± 189	9374 ± 327	11,605 ± 425	Present study
AgIn5Te8	487.6 ± 11.3	507.1 ± 19.3	662.2 ± 20.5	Present study
AgIn3Te5	301.5 ± 6.5	311.0 ± 10.2	431.8 ± 18.2	Present study
AgInTe2	115.0 ± 3.1	115.1 ± 4.3	199.1 ± 6.6	Present study

.

The temperature-reliant formations of the Gibbs energies of the selected compounds of the Ag–In–Te system are described by Equations (18)–(22):

$${\Delta }_{\mathrm{f}}{G}_{{\mathrm{In}}_2{\mathrm{Te}}_5}/\left({\mathrm{kJ}·\mathrm{mol}}^{-1}\right)=-\left(191.6\pm 3.4\right)+\left(29.8\pm 0.4\right)\cdot {10}^{-3}T/\mathrm{K},$$

(18)

$${\Delta }_{\mathrm{f}}{G}_{{\mathrm{Ag}}_3{\mathrm{In}}_{97}{\mathrm{Te}}_{147}}/\left({\mathrm{kJ}·\mathrm{mol}}^{-1}\right)=-\left(9374\pm 327\right)+\left(1408\pm 52\right)\cdot {10}^{-3}T/\mathrm{K},$$

(19)

$${\Delta }_{\mathrm{f}}{G}_{{\mathrm{AgIn}}_5{\mathrm{Te}}_8}/\left({\mathrm{kJ}·\mathrm{mol}}^{-1}\right)=-\left(507.1\pm 19.3\right)+\left(65.6\pm 2.0\right)\cdot {10}^{-3}T/\mathrm{K},$$

(20)

$${\Delta }_{\mathrm{f}}{G}_{{\mathrm{AgIn}}_3{\mathrm{Te}}_5}/\left({\mathrm{kJ}·\mathrm{mol}}^{-1}\right)=-\left(311.0\pm 10.2\right)+\left(31.8\pm 1.4\right)\cdot {10}^{-3}T/\mathrm{K},$$

(21)

$${\Delta }_{\mathrm{f}}{G}_{{\mathrm{AgInTe}}_2}/\left({\mathrm{kJ}·\mathrm{mol}}^{-1}\right)=-\left(115.1\pm 4.3\right)+\left(0.4\pm 0.01\right)\cdot {10}^{-3}T/\mathrm{K}.$$

(22)

The agreement between the enthalpy of the formation of In₂Te₅ determined in the present study and those reported in [49,50] confirms the correctness of the division of the concentration space of the Ag–In–Te system in the part AgInTe₂–Te–In₂Te₃ and validates the accuracy of the determined thermodynamic values of the ternary compounds.

4. Conclusions

The following thermodynamically stable compounds of the AgInTe₂–Te–In₂Te₃ phase region were proven to exist below 500 K by means of the modified EMF method: In₂Te₅, Ag₃In₉₇Te₁₄₇, AgIn₅Te₈, AgIn₃Te₅, and AgInTe₂. It has been shown that the literature data on the phase equilibrium of AgInTe₂ and AgIn₅Te₈ compounds of the Ag₂Te–In₂Te₃ system below 500 K are unreliable for kinetic reasons. The equilibrium state of the phases in the AgInTe₂–AgIn₅Te₈ section was achieved by the reaction AgInTe₂ + AgIn₅Te₈ = 2AgIn₃Te₅, carried out with the participation of the Ag⁺ catalyst, as a small center for the nucleation of the AgIn₃Te₅ equilibrium phase. The Gibbs energy equations as a function of temperature, as well as the standard thermodynamic quantities of the binary and ternary compounds, were determined for the first time. From the thermodynamic perspective, the effective use of the temperature gradient for thermoelectric generation can be realized by using numerous pairs of the p/n components made in the form of contact of the following compounds: AgInTe₂/AgIn₃Te₅, AgIn₃Te₅/AgIn₅Te₈, and AgIn₅Te₈/Ag₃In₉₇Te₁₄₇.