Novel Off-Design Operation Maps Showing Functionality Limitations of Organic Rankine Cycle Validated by Experiments

Abstract

In this study, we developed a new methodology to analyze the off-design performance of the organic Rankine cycle. The methodology enabled us to predict the performance based on four-dimensional decision variables and a set of constraints. A corresponding formulation and algorithm with general applicability were constructed. The reliability and feasibility of this methodology were validated by a test rig of the cycle with R245fa as the working fluid and three experimental schemes. Under specific working conditions, the theoretical results illustrated the operation maps, functionality limitations, and their variation laws, considering the interactive characteristics among the variables. The functionality limitations predicted a maximum thermal efficiency of 9.42%, corresponding to a net power output of 697.1 W, whereas the maximum net power output was 2251.5 W, corresponding to a thermal efficiency of 8.04%. The experimental results indicated that when the R245fa mass flow rate was 0.120 kg/s, the experimental efficiency and power output were 6.94% and 1873.4 W, respectively; when the R245fa mass flow rate was 0.049 kg/s, they were 3.54% and 274.1 W, respectively. These findings were in good agreement with the theoretical results, with relative errors below 7.64%. This work is expected to be applied in future dynamic control systems to update the setting points and manipulated variables in real time.

1. Introduction

The rapid transition to renewable energy and energy efficiency was responsible for a quarter of global electricity production during 2018 and 2019. However, worldwide emissions still escalated, particularly due to the 30% increase in fossil fuel subsidies from 2017 to 2018 [1]. Thus, the flexible transformation of the heating, cooling, and transport sectors beyond the use of electricity from renewable energy sources is urgently needed to achieve a highly decarbonized future [1,2]. The organic Rankine cycle (ORC), with its compact configuration and economic feasibility, is attractive for all of the above sectors [3,4], specifically in the applications of solar energy [5], industrial waste heat [6], internal combustion engines, and heavy-duty diesel engines [7]. It employs low-boiling-point working fluids to generate power or to function as the primary drivers of polygeneration systems, which are typically powered by low-grade thermal energy. Recent developments in the ORC have leveraged the system scale, cost, and performance to approach the optimum theoretical design. This research has essentially focused on new cycle couplings, the selection of working fluids [8,9], and the identification of rated parameters [10,11] for specific (fixed) heat-source conditions [12]. In particular, the conditions of cooling source has often been optimized to match the variable heat released from the working fluid.

Aside from its conceptual and theoretical design, the ORC’s complicated operation and limited condition scope in dynamic surroundings have restricted its popularization thus far, especially in the field of solar energy [13,14,15]. The possible disturbances to the ORC in different sectors represents various off-design working conditions, and were summarized in our previous research [7]. Essentially, fluctuations in the heat source temperature or cooling source temperature are the most common and inevitable disturbances. Additionally, in the ORC application of industrial waste heat, the mass flow rate of the heat source, namely the exhaust gas, also fluctuates randomly [6]. Conversely, other liquid-state heat sources, such as diathermic oil in solar ORCs [16,17] and brine in geothermal ORCs [18], usually retain stable flow rates. Therefore, in response to such temperature disturbances, three degrees of freedom are typically manipulated in general ORC systems, namely the mass flow rates of the working fluid, heat source, and cooling source. However, determining the appropriate manipulation necessitates interdisciplinary research between the control science and thermophysical engineering fields. Specifically, the dynamic behavior of ORC systems under changeable working conditions must be considered to formulate reasonable control strategies. Prior dynamic research has mainly focused on model development [19] and validation [20], performance prediction [21], experiments on variable sensitivity [7,22,23,24,25], thermal inertia validation [26], and even control strategy tests [6]. However, owing to concerns regarding costs and time requirements, the coarse and aggregated data collected from such dynamic experiments have failed to evaluate the performance and provide the basis for operation maps under off-design working conditions. Thus, the operation boundaries within the scope of practical conditions remain elusive. This is mainly attributed to the interactions between operation variables, which results in excessive volumes of data for processing.

Nevertheless, the above explorations of the dynamic behavior of the ORC laid the foundations for the two common control strategies summarized in Figure 1. Figure 1a depicts the conventional control strategy, in which the manipulated variables are the pump speed (${\omega }_{\mathrm{p}}$) and the expander speed (${\omega }_{\exp }$), etc. The two manipulated variables mainly correspond to the controlled variables of the superheating degree (ΔT_sh) and the evaporation temperature (T_eva) [6,15]. Such conventional strategies feature fixed setting points for all off-design working conditions [27], with the controller acting according to the errors between the controlled variables and their setting values. For example, both Quoilin et al. [6]. and Seitz et al. [28] took the constant superheating degree of 15 K as the setting point to prevent droplets. Rathod et al. [29] experimentally implemented a superheat-tracking controller with a superheating degree of 60 °C.

However, under new off-design working conditions, the operation variables, especially the setting values, should be updated to achieve the optimal off-design performance. This led to the state-of-the-art control strategy shown in Figure 1b, where in the setting points are flexible instead of fixed and advanced control strategies are applied. It relies on an estimation of the off-design performance explicitly accounting for the interactions between the operation variables. Rathod et al. [29] designed and validated a nonlinear model predictive controller (MPC) for a heavy-duty-diesel-engine ORC, of which the superheating degree was tuned online ranging from 10 °C to 60 °C due to system aging. The tuned superheating degree of 60 °C remained constant even though the heat source conditions were variable. Taking into account a fluctuating waste heat source, Hernandez et al. [14] developed an adaptive control law for an MPC to maximize the power output of a small-scale ORC, implementing an optimizer for the evaporation temperature via a polynomial regression method. It was pointed out that the MPC outperformed the conventional PID strategy by up to 17% power output. In this manner, the controller enabled the adaptation to the new heat source working conditions in order to maximize the off-design power generation. However, the optimal evaporation temperature was correlated with the mass flow rate and the temperature of the heat source, which were derived from the experimental results involving a specific ORC test rig, as shown in Figure 1b. Thus, this finding was not universally applicable for achieving optimum off-design performance in general ORC applications. Furthermore, advanced control strategies such as model predictive control mainly aim to improve control system performance. Such strategies replace the estimation of a specific state by using transfer functions to characterize the ORC system as a multivariable and nonlinear model [29,30,31]. Zhang et al. [32] optimized the setting points of the evaporating pressure and the temperature at the evaporator outlet for a controlled ORC system by simulation. Considering that optimal setting points are difficult to analytically determine, the optimization was achieved by combining a genetic algorithm with a least-squares support vector machine rather than by establishing a precise model. The improvements in off-design performance achieved by advanced strategies are usually evaluated through comparisons with conventional strategies, due to the lack of explicit solutions. Consequently, the off-design functionality limitations of the ORC have not been identified as part of the assessment of control system performance or potential ORC enhancement.

In this regard, research on off-design ORC performance has garnered much attention. Such research has mainly aimed to optimize the design or performance of a single component. Narasimhan et al. [33] and Ma et al. [34] focused on the off-design performance of the expander in the ORC. Manente et al. [18] used MATLAB/Simulink to build an off-design model of the ORC that analyzed the effects of the ambient temperature and geofluid inlet temperature on the power output. Wang et al. [35] carried out a parametric analysis of a solar ORC, examining the effect of both the off-design ambient temperature and heat source mass flow rate on the net power output and exergy efficiency. However, such a parametric analysis based on a single variable was insufficient to achieve off-design optimization, as it did not reflect the influence of each variable on the performance. Liu et al. [36] comprehensively reviewed the simulation methods and tools for optimizing ORC performance under off-design working conditions. They concluded that such off-design studies usually neglect the influence of the heat source, heat sink, and ambient conditions. Chatzopoulou et al. [12,37] attempted the off-design optimization of an ORC-based system under variable heat-source conditions, considering the interactions among components and within the whole system. A detailed optimization plan for the whole system was designed, involving working fluid selection, heat transfer coefficients, and expander-type comparison. The theoretical off-design optimization plan was expected to inform design decisions.

In general, the abovementioned research on off-design optimization included: (1) studies evaluating the off-design performance of a single component, especially the expander, in order to optimize component design [33,34]; (2) studies using parametric analysis rather than off-design optimization to investigate the effect of the working conditions and the parameters on the performance [18,35]; (3) studies focusing on the achievement of an optimal ORC configuration by determining the appropriate component types and sizes [12,37]; and (4) studies adopting theoretical analysis or modeling for off-design optimization, without experimental validation.

Lecompte et al. [38] introduced a comprehensive off-design model of an individual ORC that required the pump and expander speeds as inputs alongside the heat source and sink conditions. Several values for the power output or the mass flow rate of the working fluid were predicted by the model and were validated by a small-scale ORC experiment with an algorithm for steady-state detection. Unfortunately, the authors neither developed off-design operation maps (as mentioned above) nor identified the off-design functionality limitations for the further assessment or dynamic optimization of the advanced control system.

Therefore, in an attempt to bridge the knowledge gap between fixed optimization and off-design optimization, this paper makes the following contributions:

• A methodology for determining the operation maps and functionality limitations of an ORC under specific working conditions was developed. This method surpasses those detailed in other off-design studies in the literature by accounting for the interactions among the multidimensional operation variables and a set of constraints.
• A corresponding formulation and algorithm with general applicability are presented, instead of an empirical formula from experimental results. These are expected to be expanded for the off-design optimization of universal ORC operation.
• The accuracy and reliability of the methodology were validated by three ORC experimental schemes, wherein the mass flow rate of the working fluid, heat source, and cooling source were regulated, respectively.

The paper is organized as follows. The theoretical analysis and algorithm for the novel off-design operation maps and functionality limitations are introduced in Section 2. The change law of the operation boundaries and the corresponding solution domain for off-design operation are presented and discussed in Section 3. The ORC platform established to validate the accuracy and reliability of the developed algorithm is described in Section 4.

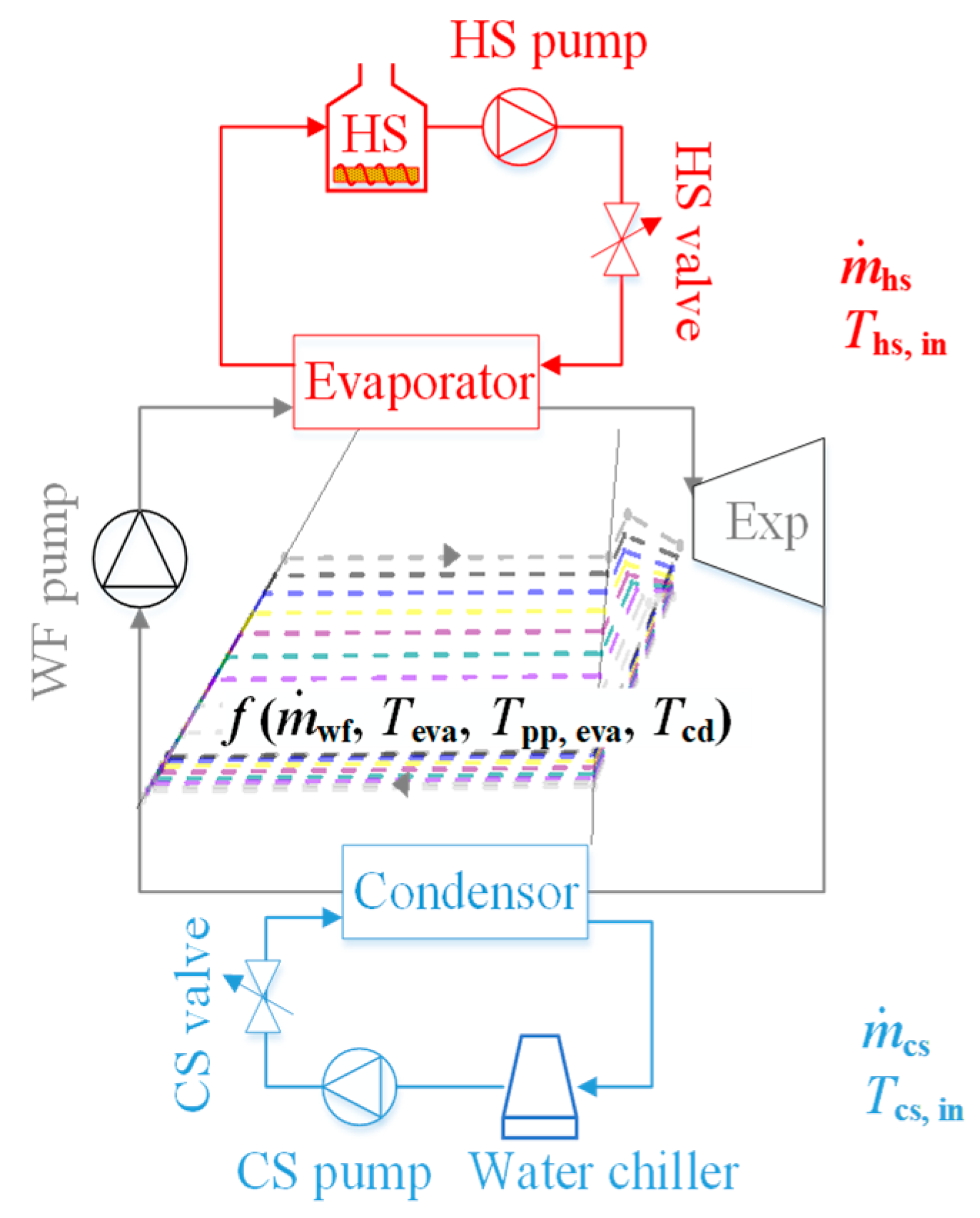
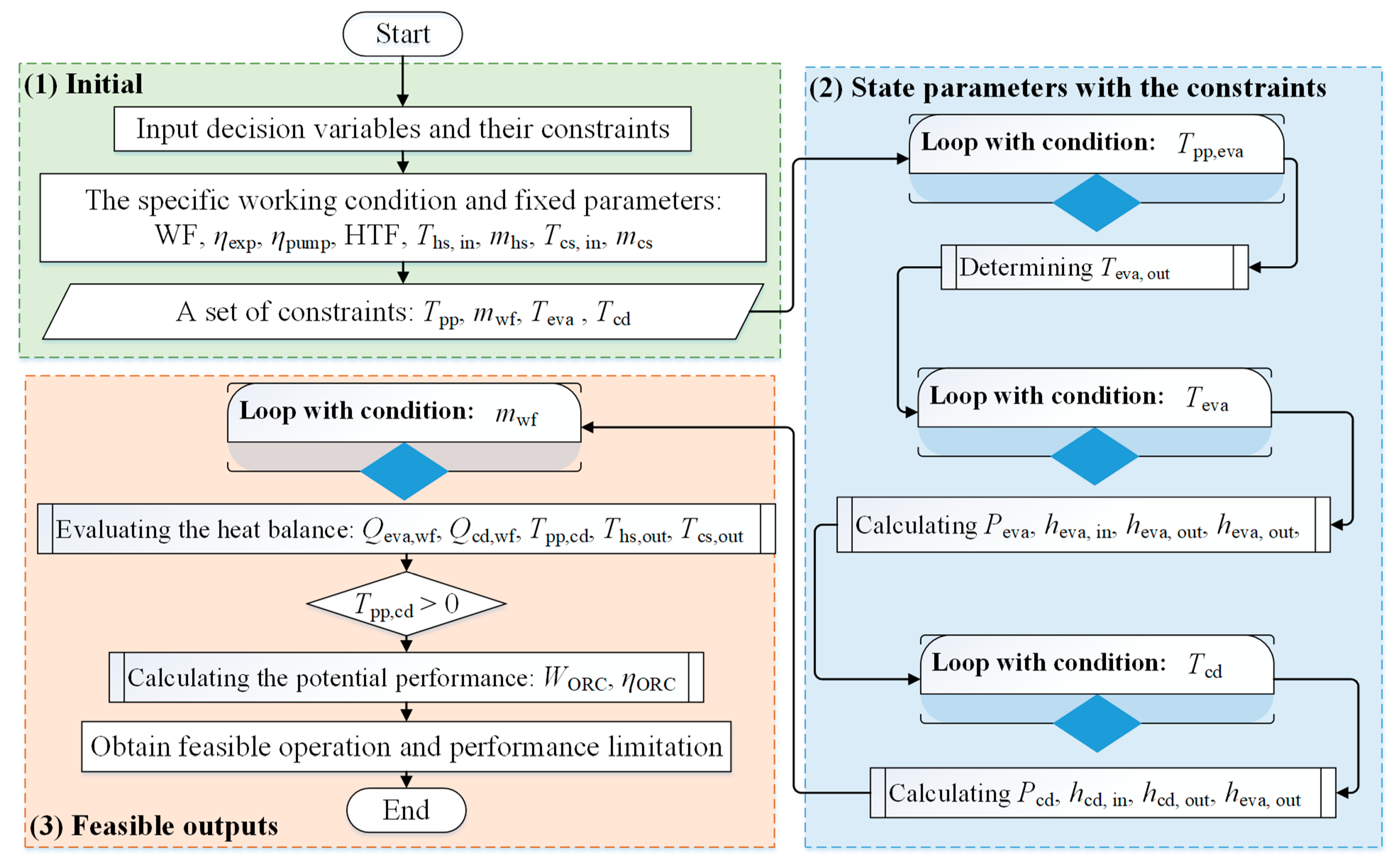
2. Theoretical Analysis and Methodology

As summarized in the introduction, the evaluation of the off-design performance is the prime requirement for updating the setting-point values for dynamic control. Figure 2 provides a schematic of an ORC system with a closed-type heat source and water-cooling source, which was built and tested in our previous research with R245fa as the working fluid [7]. In practical operation, the ORC has many variables due to the different thermophysical processes and complex coupling relationships between the three fluids. As a consequence, the system performance under new off-design working conditions may vary, depending on the combinations of variables. In order to determine the operation maps and functionality limitations of such a complex system, a general off-design performance formulation was developed on the basis of the ORC thermodynamic model, as presented in Equations (1)–(8).

The heat absorbed by the working fluid in the evaporator:

$${\dot{Q}}_{\mathrm{eva},\mathrm{wf}}={\dot{m}}_{\mathrm{wf}}·\left(h_{\mathrm{eva},\mathrm{out}}-h_{\mathrm{eva},\mathrm{in}}\right)$$

(1)

The heat released from the heat source:

$${\dot{Q}}_{\mathrm{eva},\mathrm{hs}}={\dot{m}}_{\mathrm{hs}}·\left(h_{\mathrm{hs},\mathrm{in}}-h_{\mathrm{hs},\mathrm{out}}\right)$$

(2)

The heat released from the working fluid in the condenser:

$${\dot{Q}}_{\mathrm{cd},\mathrm{wf}}={\dot{m}}_{\mathrm{wf}}·\left(h_{\mathrm{cd},\mathrm{in}}-h_{\mathrm{cd},\mathrm{out}}\right)$$

(3)

The heat absorbed by the cooling source:

$${\dot{Q}}_{\mathrm{cd},\mathrm{cs}}={\dot{m}}_{\mathrm{cs}}·\left(h_{\mathrm{cs},\mathrm{out}}-h_{\mathrm{cs},\mathrm{in}}\right)$$

(4)

The gross power of the expander:

$${\dot{W}}_{\exp }={\eta }_{\exp }·{\dot{m}}_{\mathrm{wf}}·\left(h_{\mathrm{eva},\mathrm{out}}-h_{\mathrm{cd},\mathrm{in},\mathrm{is}}\right)$$

(5)

The power consumed by the pump:

$${\dot{W}}_{\mathrm{pump}}={\dot{m}}_{\mathrm{wf}}·\left(h_{\mathrm{eva},\mathrm{in}}-h_{\mathrm{cd},\mathrm{out}}\right)$$

(6)

The net power of the ORC:

$${\dot{W}}_{\mathrm{ORC}}={\dot{W}}_{\exp }-{\dot{W}}_{\mathrm{p}}$$

(7)

The thermal efficiency of the ORC:

$${\eta }_{\mathrm{ORC}}=\frac{{\dot{W}}_{\mathrm{ORC}}}{{\dot{Q}}_{\mathrm{eva},\mathrm{wf}}}$$

(8)

Since the cycle is able to be formed only when the thermodynamic processes conform to a predefined pattern, the constraints on the variables should be considered to determine the operation map under off-design heat-source and cooling-source working conditions. In detail, the evaporation temperature (T_eva) and condensation temperature (T_cd) are bound by the inlet temperature of the heat source (T_hs,in) and the cooling source (T_cs,in), respectively. In the evaporator and condenser, the pinch-point temperature (T_pp,eva and T_pp,cd) should be positive for a normal heat-exchange process. Furthermore, at the evaporator outlet, the vapor quality ($x_{\mathrm{eva},\mathrm{out}}$) should reach one to avoid droplets forming in the following expander, which results in the superheating degree ($\Delta T_{\mathrm{sh}}$). Similarly, at the condenser outlet, the vapor quality ($x_{\mathrm{cd},\mathrm{out}}$) should reach zero to avoid cavitation in the following pump. Thus, the abovementioned constraints are defined as the associated set of constraints ($\overrightarrow{C}$), which are presented in Equations (10)–(15).

Considering the ORC performance indicators of net power (${\dot{W}}_{\mathrm{ORC}}$) (Equation (7)) and thermal efficiency (${\eta }_{\mathrm{ORC}}$) (Equation (8)) as the objective function ($\overrightarrow{F}$), the off-design performance function ($\overrightarrow{F}$) with the associated set of constraints ($\overrightarrow{C}$) was constructed. To solve the function, a vector with decision variables ($\overrightarrow{X}$) was considered, which consisted of the mass flow rate of the working fluid (${\dot{m}}_{\mathrm{wf}}$); the evaporation temperature (T_eva); the condensation temperature (T_cd); the pinch-point temperature in the evaporator (T_pp,eva) and in the condenser (T_pp,eva); the superheating degree in the evaporator (ΔT_sh); and the vapor quality at the outlet of the evaporator ($x_{\mathrm{eva},\mathrm{out}}$) and the condenser ($x_{\mathrm{cd},\mathrm{out}}$). Accordingly, the general off-design performance formulation is as follows, based on the typical single-objective optimization formulation described in [37].

Objective function: solve

$$\frac{\overrightarrow{F}=\left[{\dot{W}}_{\mathrm{ORC}}, {\eta }_{\mathrm{ORC}}\right]}{\overrightarrow{X}=\left[{\dot{m}}_{\mathrm{wf}}, T_{\mathrm{eva}}, T_{\mathrm{cd}}, T_{\mathrm{pp},\mathrm{eva}},T_{\mathrm{pp},\mathrm{cd}},\Delta T_{\mathrm{sh}},x_{\mathrm{eva},\mathrm{out}},x_{\mathrm{cd},\mathrm{out}} \right]}$$

(9)

Subject to:

$$T_{\mathrm{cs},\mathrm{in}}<T_{\mathrm{cd}}<T_{\mathrm{eva}}<T_{\mathrm{hs},\mathrm{in}}$$

(10)

$$T_{\mathrm{pp},\mathrm{eva}}>0$$

(11)

$$\Delta T_{\mathrm{sh}}\ge 0$$

(12)

$$x_{\mathrm{eva},\mathrm{out}}=1$$

(13)

$$T_{\mathrm{pp},\mathrm{cd}}>0$$

(14)

$$x_{\mathrm{cd},\mathrm{out}}=0$$

(15)

where the isentropic efficiency of the pump and the expander are assumed to be 0.75 and 0.7, respectively, in order to simplify the analysis.

The corresponding algorithm to determine the off-design performance is depicted in Figure 3. Typical cooling-source and heat-source conditions from the experiments are employed to illustrate the process of quantifying the operation maps and functionality limitations of the ORC under specific working conditions. However, we expect that the algorithm will be able to determine the off-design performance under any specific heat-source and cooling-source working conditions. The models included in Figure 3 were calculated using MATLAB and the thermodynamic properties of the R245fa fluid were acquired by linking MATLAB with the commercial software REFPROP 9.1 [39].

Specifically, the inlet temperature of the heat source (T_hs,in) was 82.0 °C; the mass flow rate of the heat source (${\dot{m}}_{\mathrm{hs}}$) was 0.635 kg/s; the inlet temperature of the cooling source (T_cs,in) was 20.0 °C; and the mass flow rate of the cooling source (${\dot{m}}_{\mathrm{cs}}$) was 0.650 kg/s. Ranges of the four decision variables were imposed as constraints within the algorithm: $T_{\mathrm{pp},\mathrm{eva}}\in \left(0 ℃,15.0 ℃\right]$,${\dot{m}}_{\mathrm{wf}}\in \left[0.029\mathrm{kg}/\mathrm{s},0.120\mathrm{kg}/\mathrm{s}\right]$, $T_{\mathrm{eva}}\in \left[33.4 ℃,93.0 ℃\right]$, and $T_{\mathrm{cd}}\in \left[22.0 ℃,32.0 ℃\right]$. The other decision variables, namely the superheating degree ($\Delta T_{\mathrm{sh}}$) and the pinch-point temperature in the condenser ($T_{\mathrm{pp},\mathrm{cd}}$), could thus be solved. Therefore, the off-design performance was essentially decided by the four-dimensional (4D) variables. The criterion for identifying the operation maps and functionality limitations using the 4D variables is that the pinch-point temperature in the condenser ($T_{\mathrm{pp},\mathrm{cd}}$) is above 0 K. During each iterative calculation, the specific values of the ${\dot{m}}_{\mathrm{wf}}$ were 0.029 kg/s, 0.041 kg/s, 0.052 kg/s, 0.063 kg/s, 0.075 kg/s, 0.085 kg/s, 0.098 kg/s, 0.107 kg/s, and 0.120 kg/s, respectively. Furthermore, for each iteration step, the value of T_pp,eva, T_eva, and T_cd was 1 °C.

3. Results and Discussion

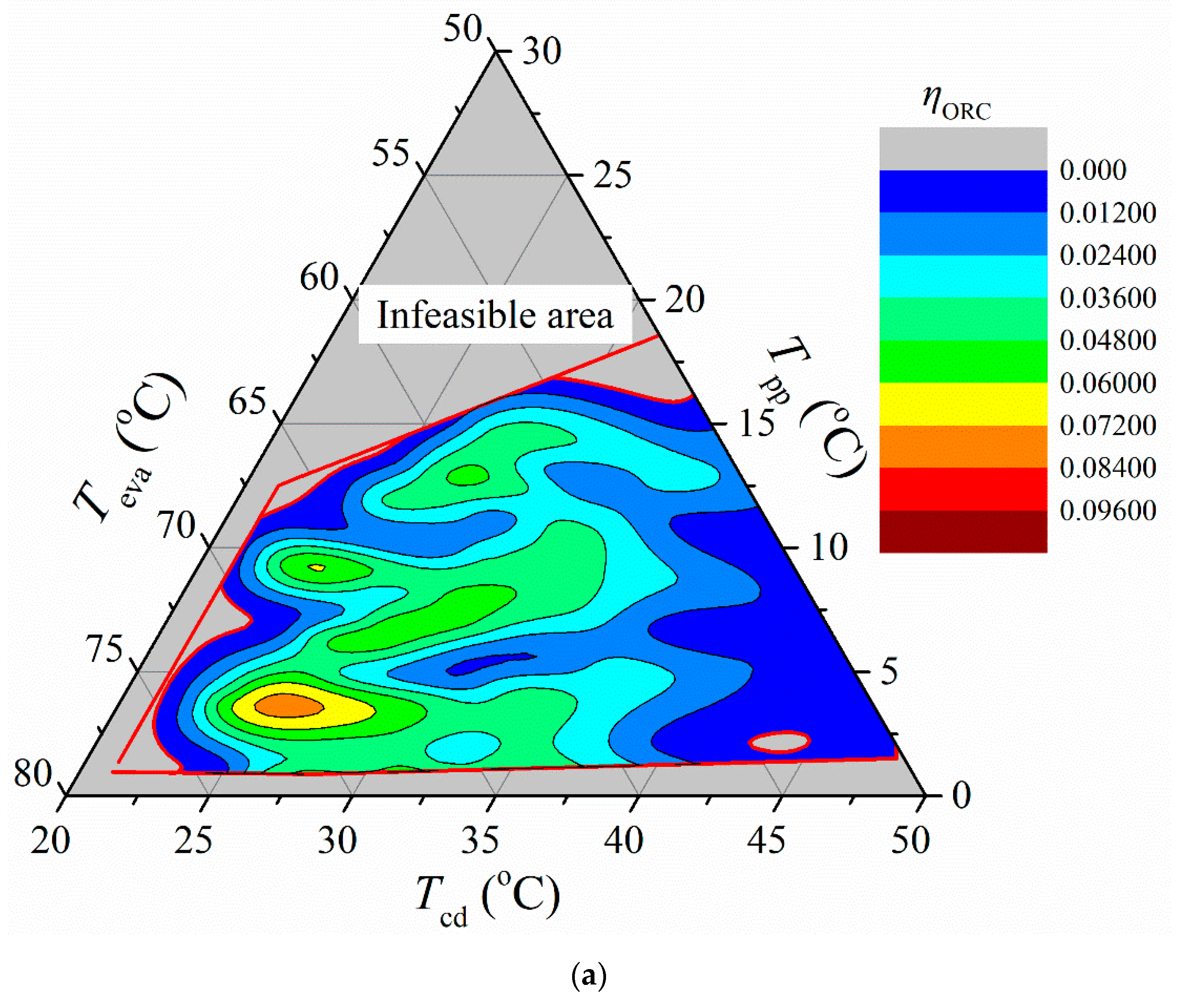
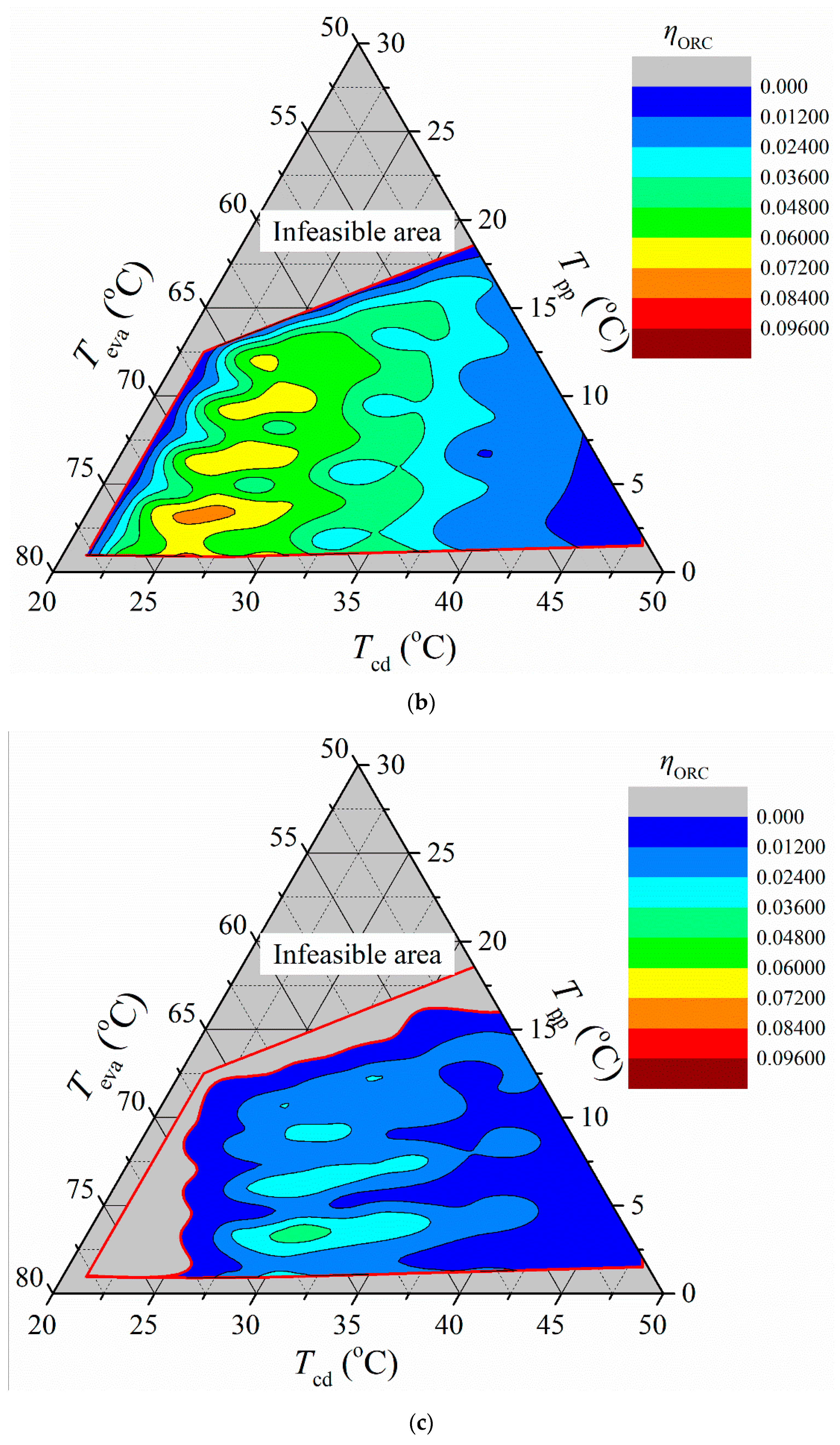
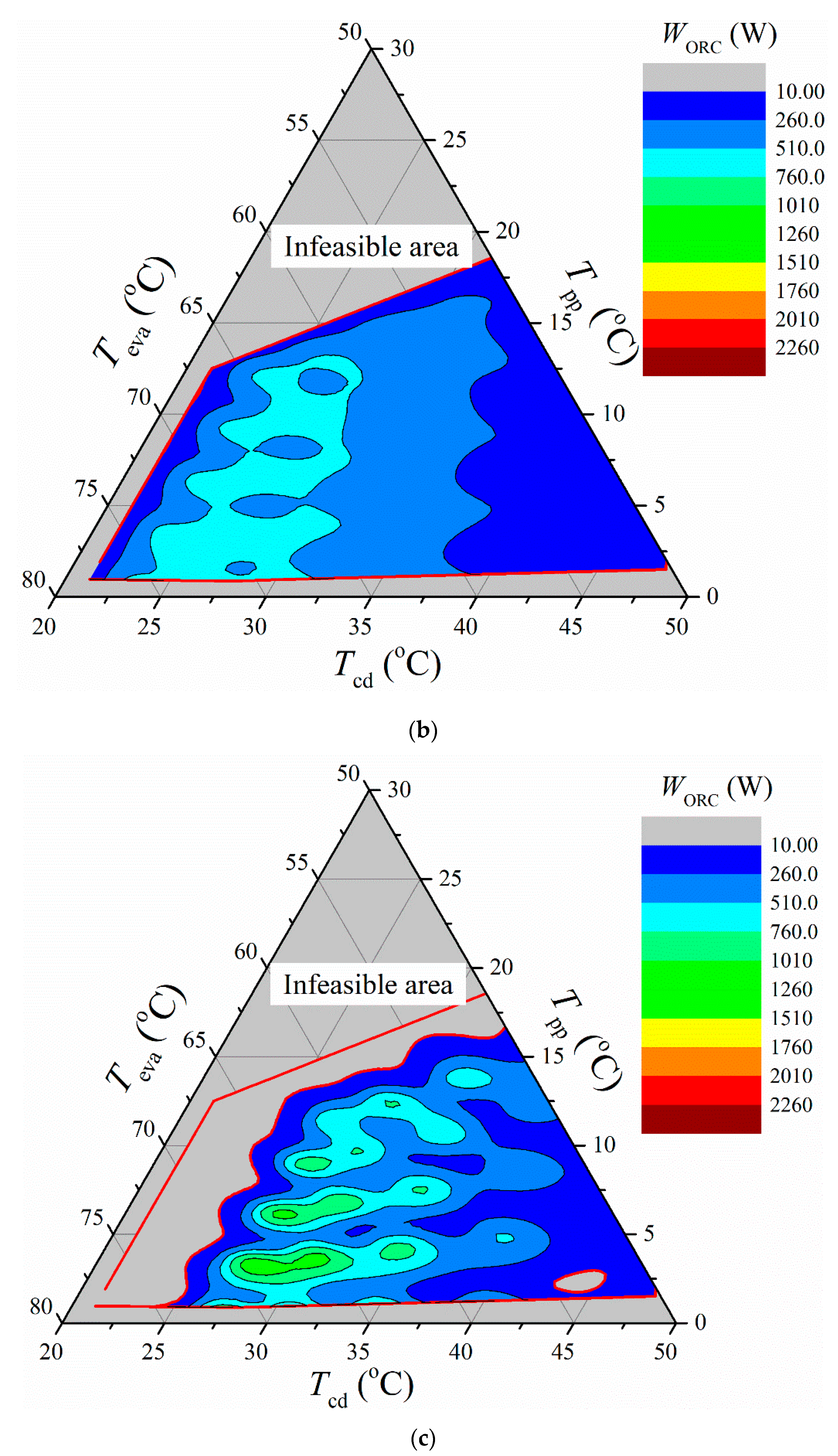
3.1. Operation Maps

Figure 4 depicts the thermal efficiency boundaries of the ORC with different combinations of 4D variables. The results showed that similar or identical ORC thermal efficiency (η_ORC) values could be obtained for different combinations of variables, as indicated by the areas of the same color in Figure 4. Meanwhile, a higher η_ORC was observed in the area with a higher evaporation temperature (T_eva), lower condensation temperature (T_cd), and lower pinch-point temperature in the evaporator (T_pp,eva). The corresponding η_ORC ranged between 7.2 and 8.4%. It should be mentioned that the highest η_ORC did not occur at the extreme point, defined as the working conditions with the maximum T_eva and minimum T_pp,eva and T_cd.

However, within the experimentally feasible range of R245fa mass flow rate (${\dot{m}}_{\mathrm{wf}}\in \left[0.029\mathrm{kg}/\mathrm{s},0.120\mathrm{kg}/\mathrm{s}\right]$), the η_ORC at the extreme point was a non-solution, as shown in Figure 4a. The range of the operation boundaries, namely the feasible area, was affected by the combination of the 4D variables. It should be pointed out that the 4D variables were mutual coupled and inter-restricted. This is explained by Figure 4b,c, with a specific ${\dot{m}}_{\mathrm{wf}}$ of 0.041 kg/s and 0.120 kg/s, respectively. When the ${\dot{m}}_{\mathrm{wf}}$ was 0.041 kg/s (Figure 4b), the range of the feasible η_ORC was wider, with a maximum value of 9.22%. Furthermore, the non-zero solution could only be achieved when the T_cd was higher than 23.0 °C. However, when the ${\dot{m}}_{\mathrm{wf}}$ was 0.120 kg/s, the range of the feasible η_ORC narrowed, with a maximum value of 8.15%. The η_ORC was below 0 in the area with a lower condensation temperature. To conclude, concerning the 4D variables, the maximum η_ORC and the feasible operation area with an η_ORC above 0 decreased as the ${\dot{m}}_{\mathrm{wf}}$ increased.

Figure 5 depicts the net power output (${\dot{W}}_{\mathrm{ORC}}$) boundaries of the ORC according to different 4D variable values. Similarly to the thermal efficiency (η_ORC) results, the system could achieve similar or identical ${\dot{W}}_{\mathrm{ORC}}$ values with different combinations of the variables. The higher ${\dot{W}}_{\mathrm{ORC}}$ values were located in the areas with higher T_eva, lower T_cd, and lower T_pp,eva values. The ${\dot{W}}_{\mathrm{ORC}}$ ranged between 1260.0 W and 1510.0 W, corresponding to the green area in Figure 5. Once again, the highest power output did not occur at the extreme point where the T_eva was at its maximum and the T_cd and T_pp,eva were at their minimum. Figure 5b indicates that when the ${\dot{m}}_{\mathrm{wf}}$ was 0.041 kg/s, the range of the feasible ${\dot{W}}_{\mathrm{ORC}}$ was wider, but with a lower maximum ${\dot{W}}_{\mathrm{ORC}}$ value of 894.5 W. Furthermore, the non-zero solution could only be achieved when the T_cd was higher than 23.0 °C. However, when the ${\dot{m}}_{\mathrm{wf}}$ was 0.120 kg/s, the range of the feasible ${\dot{W}}_{\mathrm{ORC}}$ narrowed, with a higher maximum ${\dot{W}}_{\mathrm{ORC}}$ value of 2288.6 W. Additionally, the ${\dot{W}}_{\mathrm{ORC}}$ was below 0 in the area with a lower T_cd. To conclude, concerning the 4D variables, the feasible operation area with a ${\dot{W}}_{\mathrm{ORC}}$ above 0 decreased in size as the ${\dot{m}}_{\mathrm{wf}}$ increased, which was consistent with the changes in the η_ORC. However, the maximum ${\dot{W}}_{\mathrm{ORC}}$ increased as the ${\dot{m}}_{\mathrm{wf}}$ increased.

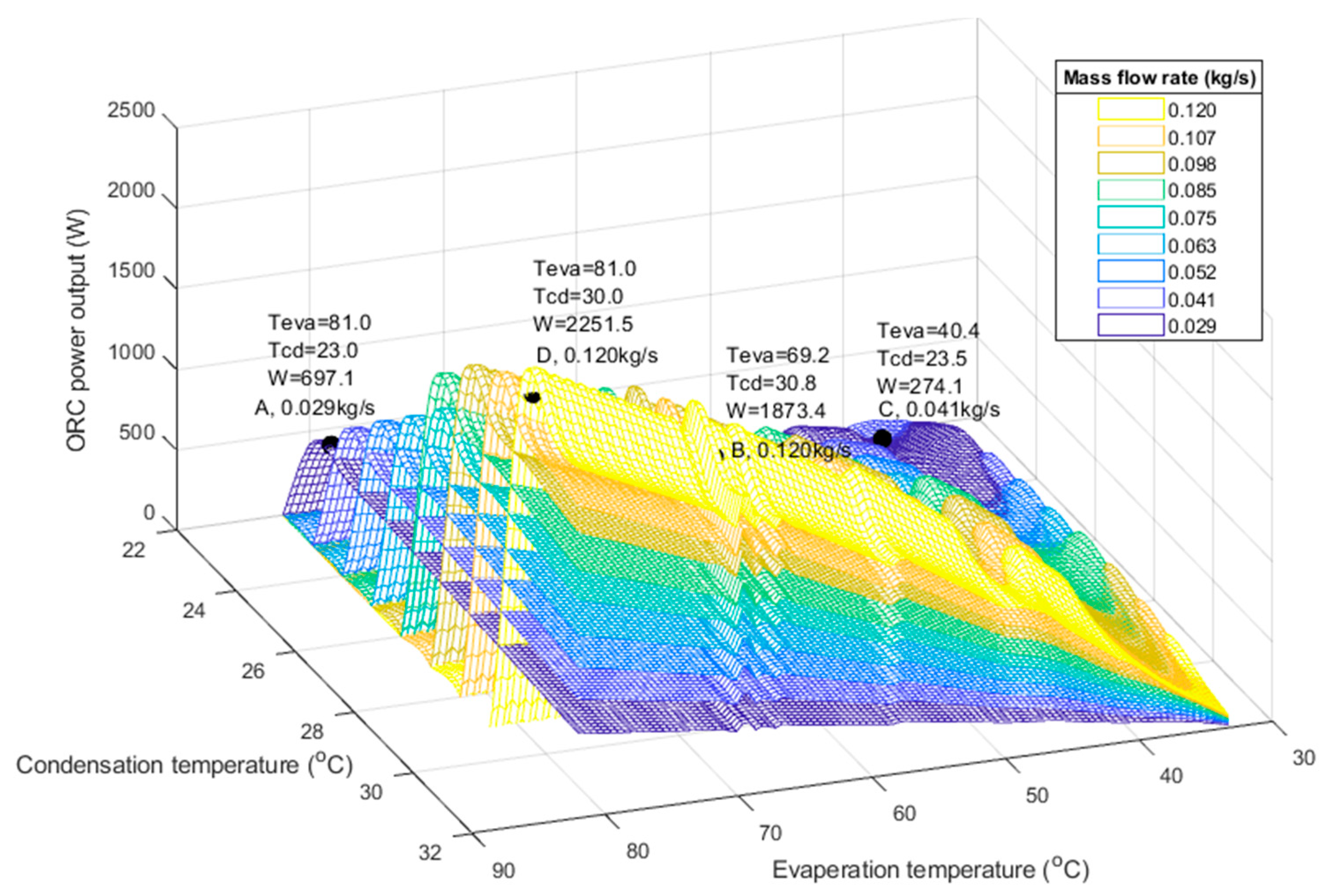
3.2. Solution Domain and Functionality Limitations

Based on the operation map, the solution domain within the 4D boundary conditions was further explored. Through the surface interpolation fitting of the calculated results, the solution domain of the η_ORC was obtained, as shown in Figure 6. The figure indicates that when the T_cd was 22.0 °C, the system was impossible to operate, regardless of the combination of the other three variables. As a result, the η_ORC is 0 in Figure 6, due to the low T_cd. Specifically, under known cooling-source conditions, namely an inlet temperature of 20.0 °C and an ${\dot{m}}_{\mathrm{cs}}$ of 0.650 kg/s, the absorbed heat power of the cooling source is equal to the released heat power of the working fluid. Thus, as the ${\dot{m}}_{\mathrm{wf}}$ value increased, the heat released by the working fluid in the condenser increased. This led to a higher outlet temperature in the cooling source, causing a temperature difference (namely, the pinch-point temperature in the condenser (T_pp,cd)) of less than zero. As a result, the heat transfer greatly deteriorated, and its performance may have been restricted. This led to the phenomenon that the feasible operation area of the ${\dot{W}}_{\mathrm{ORC}}$ decreased as the ${\dot{m}}_{\mathrm{wf}}$ increased.

As the ${\dot{m}}_{\mathrm{wf}}$ increased from 0.029 kg/s to 0.120 kg/s, the T_cd, which guarantees a normal heat transfer process, increased from 22.0 °C to 29.0 °C. This meant that the non-zero solution area of the η_ORC moved in the direction of an increasing T_cd. This explained the phenomena illustrated in Figure 4, where the operation boundary decreased as the ${\dot{m}}_{\mathrm{wf}}$ increased. In addition, the solution for the highest η_ORC was 9.42%, located at point A in Figure 6. Correspondingly, the ${\dot{m}}_{\mathrm{wf}}$ was 0.029 kg/s, the evaporation temperature was 81.0 °C, and the T_cd was 23.0 °C. With the increase in the ${\dot{m}}_{\mathrm{wf}}$, the maximum η_ORC of each ${\dot{m}}_{\mathrm{wf}}$ presented a declining trend, reaching 8.15% when the ${\dot{m}}_{\mathrm{wf}}$ increased to 0.120 kg/s. It should be pointed out that, within the solution domain, the ${\dot{m}}_{\mathrm{wf}}$ had no influence on the η_ORC when the combination of the T_eva, T_cd, and T_pp,eva was identical for different R245fa mass flow rates. On the other hand, with a constant ${\dot{m}}_{\mathrm{wf}}$ value, the η_ORC increased as the T_eva increased but decreased as the T_cd increased.

It is important to emphasize that the 4D variables are interactive and mutually coupled. In addition to the constraint that the T_eva is higher than the T_cd, the T_pp,eva and the range of the T_eva are inter-restricted, as shown in Figure 7. Due to the limitations of the heat-source conditions, with an inlet temperature of 82.0 °C and an ${\dot{m}}_{\mathrm{hs}}$ of 0.635 kg/s, each T_pp,eva corresponded to a different range of T_eva values. With the increase in the T_pp,eva, the maximum viable T_eva decreased. To guarantee the superheating temperature at the outlet of the evaporator, the maximum T_eva was 67.0 °C under the selected 4D boundary conditions when the T_pp,eva was 15.0 °C. However, when the T_pp,eva was 1.0 °C, the maximum T_eva was 81.0 °C. Figure 7 shows that as the T_pp,eva decreased, the range of the T_eva increased.

Figure 8 depicts the solution domain of the ${\dot{W}}_{\mathrm{ORC}}$. In terms of the variation laws of the operation boundaries, the results were the same as those for the η_ORC. When the T_cd was 22 °C, the system was impossible to operate, regardless of the combination of the other three variables. Specifically, the ${\dot{W}}_{\mathrm{ORC}}$ was zero, corresponding to the infeasible η_ORC in Figure 4. As the ${\dot{m}}_{\mathrm{wf}}$ increased from 0.029 kg/s to 0.120 kg/s, the T_cd, which guarantees a normal heat transfer process, increased from 22.0 °C to 29.0 °C. This meant that the non-zero solution area of the ${\dot{W}}_{\mathrm{ORC}}$ moved in the direction of an increasing T_cd. Similarly, the 4D variables were mutually coupled and inter-restricted.

In contrast to the change laws of the η_ORC, the ${\dot{W}}_{\mathrm{ORC}}$ was determined by the ${\dot{m}}_{\mathrm{wf}}$. Thus, the ${\dot{W}}_{\mathrm{ORC}}$ at the maximum η_ORC, namely point A, was only 697.2 W, which was attributed to the lower ${\dot{m}}_{\mathrm{wf}}$ of 0.029 kg/s. The maximum ${\dot{W}}_{\mathrm{ORC}}$ was located at point D in Figure 8, with a value of 2251.5 W. The corresponding ${\dot{m}}_{\mathrm{wf}}$ was 0.120 kg/s, the T_eva was 81.0 °C, the T_cd was 30.0 °C, and the η_ORC was 8.04%.

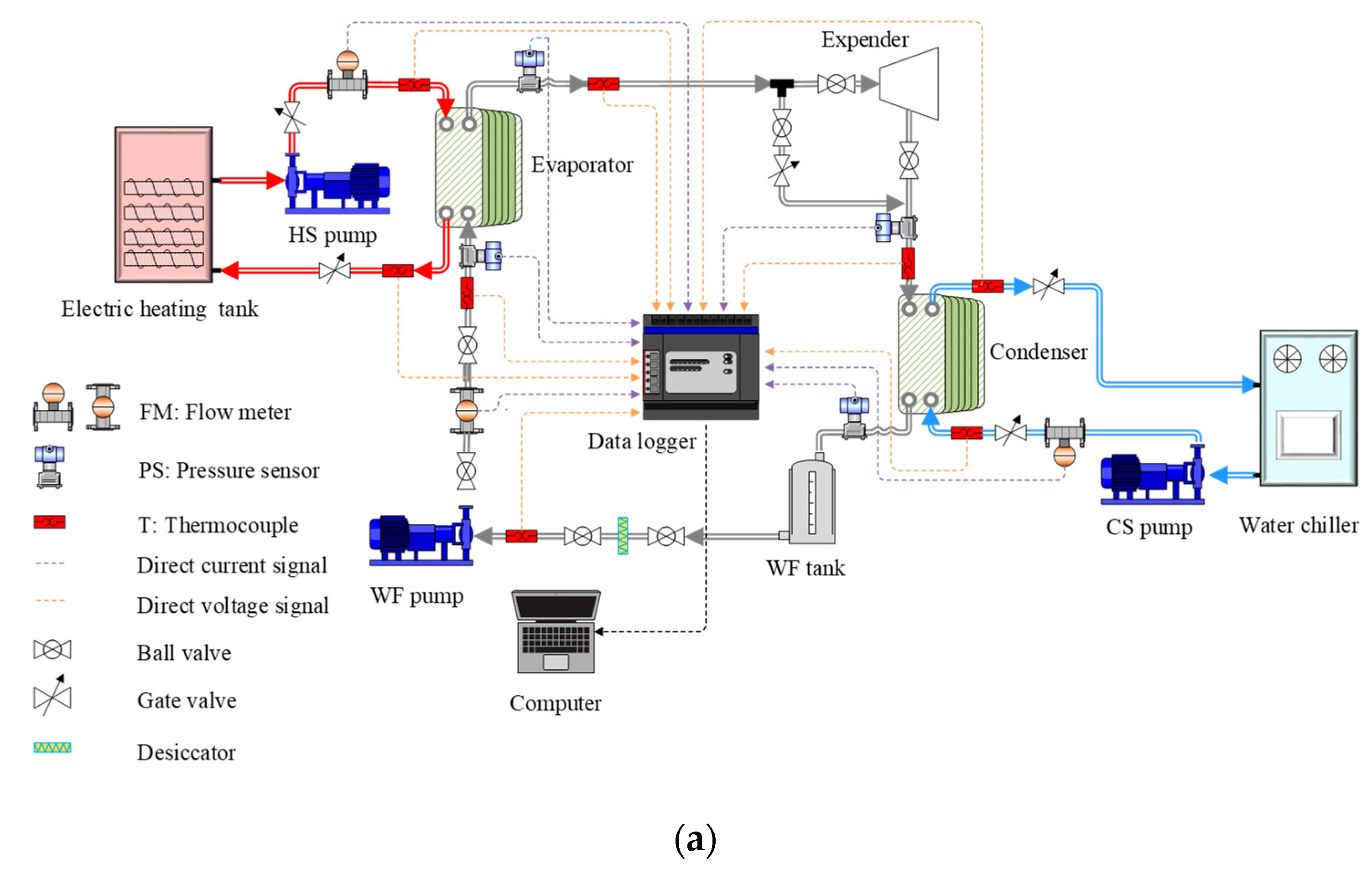
4. Experimental Validation

4.1. Description of the Test Rig

Figure 9 shows the test rig and a schematic of the experimental ORC system, using R245fa as the working fluid. It should be noted that the test rig lacked an expander due to the problem of expander leakage. Instead, a self-made expansion valve was employed to temporarily take the place of the expander, consisting of a ball valve and a gate valve, as shown in Figure 9a. The heat source adopted was hot water with a maximum thermal power of 4 $\times$ 2.5 kW achieved by electrical heaters. The cooling source was a 7.5 kW water chiller. The specific parameters and a description of the system can be found in [7]. The variables in the test rig included the mass flow rate of the working fluid (${\dot{m}}_{\mathrm{wf}}$), the heat source (${\dot{m}}_{\mathrm{hs}}$), and the cooling source (${\dot{m}}_{\mathrm{cs}}$). Specifically, the ${\dot{m}}_{\mathrm{wf}}$ was manipulated by regulating the motor speed of the working fluid pump, and the ${\dot{m}}_{\mathrm{hs}}$ and ${\dot{m}}_{\mathrm{cs}}$ were manipulated by opening valves on the heating and cooling water loops, respectively. Except for the bypass valves of the expander, which had specific and constant opening positions, the rest of the valves in Figure 9a were kept fully open during the test.

Three experimental schemes were tested, within which the ${\dot{m}}_{\mathrm{wf}}$, ${\dot{m}}_{\mathrm{hs}}$, and ${\dot{m}}_{\mathrm{cs}}$ values were regulated, respectively. It should be mentioned that the electric power for the heat source was kept constant at 10.0 kW for all the schemes. In the scheme with the regulation of the ${\dot{m}}_{\mathrm{wf}}$, the values of the ${\dot{m}}_{\mathrm{wf}}$ were the same to those mentioned in Section 2. The other initial working conditions also corresponded with the conditions described in Section 2. Specifically, the inlet temperature of the heat source was 82.0 °C, with an ${\dot{m}}_{\mathrm{hs}}$ of 0.630 kg/s, and the inlet temperature of the cooling source was 20.9 °C, with an ${\dot{m}}_{\mathrm{cs}}$ of 0.641 kg/s. The other two experimental schemes were implemented to help draw up the operation maps of the ORC depicted in Figure 4 and Figure 5. When the ${\dot{m}}_{\mathrm{hs}}$ was regulated, the inlet temperature of the heat source was 85.8 °C and the inlet temperature of the cooling source was 20.4 °C, with an ${\dot{m}}_{\mathrm{cs}}$ of 0.644 kg/s and an ${\dot{m}}_{\mathrm{wf}}$ of 0.040 kg/s. The mass flow rate of the heat source was decreased from 0.633 kg/s to 0.156 kg/s. When the ${\dot{m}}_{\mathrm{cs}}$ was regulated, the inlet temperature of the heat source was 87.3 °C, with an ${\dot{m}}_{\mathrm{hs}}$ of 0.139 kg/s; the inlet temperature of the cooling source was 20.2 °C, and the ${\dot{m}}_{\mathrm{wf}}$ was 0.039 kg/s. The mass flow rate of the cooling source was decreased from 0.642 kg/s to 0.081 kg/s.

The reliability and feasibility of the above test were validated by uncertainty and heat-balance analysis. The uncertainty of the indirect measurements, such as the heat transfer of the fluids, was less than 20% under most working conditions. The discrepancy in the evaporator and condenser ranged between 2.51% and 21.45% under the above working conditions [7].

4.2. Algorithm Validation

Figure 10 depicts the variation ranges in the T-s diagram of the system, corresponding to the above three schemes. The initial stable operation parameters are represented by the solid line, while the final stable operation parameters are represented by the dashed line and the shaded area. Figure 10a indicates that as the ${\dot{m}}_{\mathrm{wf}}$ decreased from 0.120 kg/s to 0.029 kg/s, the evaporation and condensation pressure declined, while the superheating degree and the irreversibility increased obviously. The pinch-point temperature in the evaporator increased as the ${\dot{m}}_{\mathrm{wf}}$ decreased, with a range of 4.0~6.0 °C. Furthermore, the opposite variation trend was observed in the condenser, with a range of 1.0~2.0 °C. Thus, the variable operation parameters confirmed the interactions between the operation variables, in agreement with the comparisons of ORC performance under different 4D variable combinations. Meanwhile, Figure 11 shows that the higher the ${\dot{m}}_{\mathrm{wf}}$. the greater the ${\dot{W}}_{\mathrm{ORC}}$ and η_ORC. It should be mentioned that both the inlet and outlet temperatures of the heat source declined (Figure 10a). This was due to the high ${\dot{m}}_{\mathrm{wf}}$ during operation, which caused a more heat to be absorbed by the working fluid than the available electric heating power of 10 kW. Thus, for the system driven by the closed-type heat source of the electric heater, the premise of the operation optimization was to sustain the heat balance in the evaporator. On this basis, under the requirement that the superheating degree in the evaporator was above 0 K, the higher the ${\dot{m}}_{\mathrm{wf}}$, the higher the evaporation pressure, resulting in a higher ${\dot{W}}_{\mathrm{ORC}}$ and η_ORC.

Figure 10b indicates that as the ${\dot{m}}_{\mathrm{hs}}$ decreased from 0.633 kg/s to 0.156 kg/s, the outlet temperature of the heat source and the irreversibility in the evaporator decreased. The pinch-point temperature in the evaporator presented a declining trend and ranged from 14.4 to 10.1 °C. The pinch-point temperature in the condenser approached but remained higher than 0 °C. The ${\dot{m}}_{\mathrm{wf}}$ was fixed at 0.040 kg/s. In this manner, even though the ${\dot{m}}_{\mathrm{hs}}$ changed, the heat transfer of the working fluid remained at 9306.2 W and matched the electric heating power of 10 kW. Thus, the closed-type heat source was in an equilibrium state, resulting in a relatively constant outlet temperature of the heat source in the evaporator, ranging between 85.8 and 83.1 °C. In terms of the operation optimization, it can be concluded that the lower the ${\dot{m}}_{\mathrm{hs}}$, the lower the irreversibility in the evaporator. Figure 10c indicates that as the ${\dot{m}}_{\mathrm{cs}}$ decreased from 0.642 to 0.081 kg/s, the outlet temperature of the cooling source in the condenser increased. This led to an increase in the condensation temperature and the pressure of the working fluid. The pinch-point temperature in the evaporator presented a declining trend, with a range of 12.0~9.4 °C. The pinch-point temperature in the condenser approached but remained higher than 0 °C. Similarly, the closed-type heat source was in an equilibrium state due to the constant ${\dot{m}}_{\mathrm{wf}}$ of 0.040 kg/s, resulting in a relatively constant outlet temperature for the heat source in the evaporator, ranging between 85.1 and 87.3 °C. In terms of the operation optimization, the higher the ${\dot{m}}_{\mathrm{cs}}$, the lower the condensation pressure. As a result, the ${\dot{W}}_{\mathrm{ORC}}$ of the system could be promoted. However, it is important to avoid an excessive ${\dot{m}}_{\mathrm{cs}}$ value, which may cause heat transfer deterioration and decrease the thermal efficiency [40].

In general, the results from all three schemes depicted in Figure 10 showed that the operation variables were numerous, mutually coupled, and inter-restricted. Our findings indicated that the main operation variables were the T_pp,eva, ${\dot{m}}_{\mathrm{wf}}$, T_eva, and T_c, which was in agreement with the 4D variables proposed in Section 2.

Figure 11 shows the results predicted by Equations (8)–(15) for the experimental working conditions, with the expander replaced by the expansion valve. When the ${\dot{m}}_{\mathrm{wf}}$ decreased, the power consumed by the pump (${\dot{W}}_{\mathrm{pump},\mathrm{ER}}$) and the loss of the expander power output (${\dot{W}}_{\exp ,\mathrm{loss}}$) decreased. However, the net power output of the ORC (${\dot{W}}_{\mathrm{ORC},\mathrm{ER}}$) and its efficiency (η_ORC,ER) also decreased. Specifically, the ${\dot{W}}_{\mathrm{ORC},\mathrm{ER}}$ decreased from 1874.7 W to 148.5 W, and the η_ORC,ER decreased from 6.94% to 2.33%. When the ${\dot{m}}_{\mathrm{hs}}$ decreased, the ${\dot{W}}_{\mathrm{ORC},\mathrm{ER}}$ decreased from 274.1 W to 229.2 W, while the η_ORC,ER remained at about 3.55%. On the contrary, when the ${\dot{m}}_{\mathrm{cs}}$ decreased, the ${\dot{W}}_{\mathrm{ORC},\mathrm{ER}}$ increased slightly from 211.7 W to 244.5 W, while the η_ORC,ER decreased slightly from 3.56% to 3.08%. For all the experimental schemes illustrated in Figure 11, even though the combinations of operation variables differed, the system could achieve a similar performance. This phenomenon supported the operation maps presented in Section 3, corresponding to the areas of the same color in Figure 4 and Figure 5.

Furthermore, we used the experimental results to validate the reliability and accuracy of the solution domain for the η_ORC in Figure 6 and for the ${\dot{W}}_{\mathrm{ORC}}$ in Figure 8. Point B in Figure 6 and Figure 8 indicates the optimal performance achieved by the experiment, which corresponded to the conditions and results when the ${\dot{m}}_{\mathrm{wf}}$ was 0.120 kg/s. The experimental thermal efficiency (η_ORC,ER) was 6.94%, located in the solution domain with the ${\dot{m}}_{\mathrm{wf}}$ of 0.120 kg/s, while its theoretical value was 6.41%, with a relative error of 7.64%. The experimental power output (${\dot{W}}_{\mathrm{ORC},\mathrm{ER}}$) was 1873.4 W, also located in the solution domain with the ${\dot{m}}_{\mathrm{wf}}$ of 0.120 kg/s, while its theoretical value was 1770.3 W, with a relative error of 5.56%. Point C in Figure 6 and Figure 8 corresponds to the experimental results for the initial steady-state conditions, with an ${\dot{m}}_{\mathrm{wf}}$ of 0.041 kg/s. The η_ORC,ER was about 3.54%, while the theoretical value was 3.61%, with a relative error of 1.98%. The ${\dot{W}}_{\mathrm{ORC},\mathrm{ER}}$ was 274.1 W, while the theoretical value was 289.75 W, with a relative error of 5.71%.

Table 1. Comparison between the experimental and theoretical results.

Parameter	Point B			Point C
	Experimental Result	Theoretical Result	Relative Error (%)	Experimental Result	Theoretical Result	Relative Error (%)
4D variables
${\dot{m}}_{\mathrm{wf}}$ (kg/s)	0.120	0.120	0	0.041	0.041	0
Teva (°C)	69.2	67.0	3.18	40.8	41.8	2.45
Tc (°C)	30.8	30.1	2.27	23.5	24	2.13
Predicted performance
${\dot{W}}_{\mathrm{ORC}}$ (W)	1874.7	1770.3	5.56	274.1	289.75	5.71
ηORC (%)	6.94	6.41	7.64	3.54	3.61	1.98

presents a comparison of the ORC parameters between the experimental and theoretical results. The relative errors for the system performance were acceptable, which was attributed to the appropriateness of the hypothesis in the theoretical analysis, the limited experimental conditions, and the interpolation technique. It should be mentioned that since the T_pp,eva could not be identified in the solution domain, it could not be predicted as were the other parameters in Table 1.

5. Conclusions

ORC systems usually operate under variable heat-source and cooling-source conditions. In this work, a methodology was developed and applied to generate off-design ORC operation maps and a solution domain to determine the functionality limitations. A corresponding formulation and algorithm with general applicability were developed and characterized by 4D decision variables, including ${\dot{m}}_{\mathrm{wf}}$, T_pp,eva, T_eva, and T_cd. The interactions among the variables and a set of constraints were also identified. The algorithm could be used in ORC dynamic controllers to update the setting points and adjust the operation in real time. Based on our prior knowledge of the variable constraints from the ORC test rig, we provided both quantitative and qualitative results. Furthermore, three experimental schemes were implemented in the ORC test rig to verify the reliability and accuracy of the proposed methodology. The conclusions were as follows.

(1)

The off-design performance was indicated by operation maps, which were decided by different combinations of the 4D variables. Under the designated working conditions and constraints, a higher η_ORC was generally located in the area with a higher T_eva and lower ${\dot{m}}_{\mathrm{wf}}$, T_cd, and T_pp,eva. On the other hand, a higher ${\dot{W}}_{\mathrm{ORC}}$ was generally located in the area with the higher T_eva and ${\dot{m}}_{\mathrm{wf}}$, but lower T_cd and T_pp,eva.

(2)

The operation boundaries changed according to the combinations of 4D variables. Under the same T_eva, T_cd, and T_pp,eva combination, the feasible areas of both the η_ORC and ${\dot{W}}_{\mathrm{ORC}}$ decreased as the ${\dot{m}}_{\mathrm{wf}}$ increased due to the limitation of the T_pp,cd for successful heat transfer.

(3)

The functionality limitations were further predicted by the solution domains corresponding to the operation maps. The maximum η_ORC was 9.42%, with a ${\dot{W}}_{\mathrm{ORC}}$ of 697.1 W. The maximum ${\dot{W}}_{\mathrm{ORC}}$ was 2251.5 W, with an η_ORC of 8.04%. Similar or even identical performances were achieved by numerous combinations of the 4D variables.

(4)

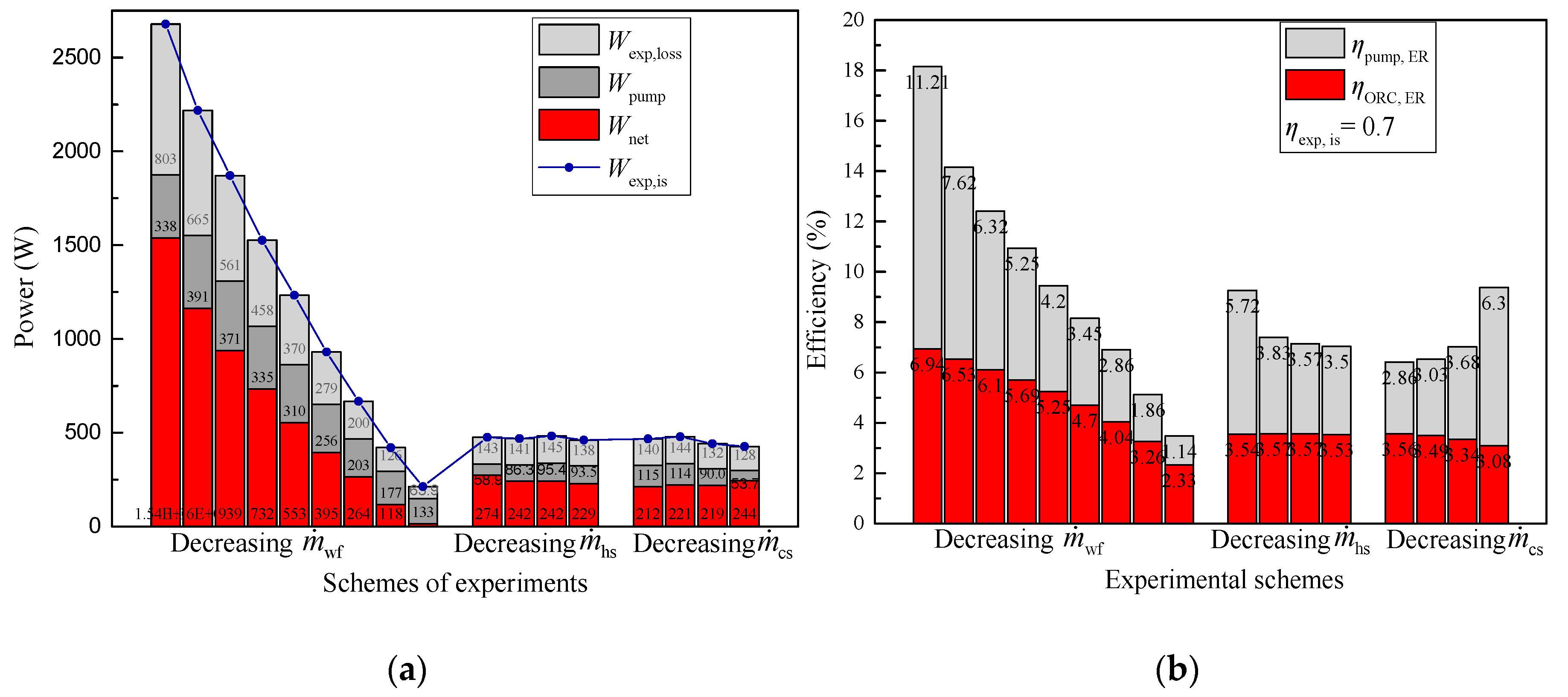
The accuracy and reliability of the algorithm were validated by experimental results with an ${\dot{m}}_{\mathrm{wf}}$ value of 0.049 kg and 0.12 kg/s, respectively. Agreement between the theoretical and experimental results was obtained, with a relative error for system performance below 7.64%.

(5)

The novel finding that a similar or even identical performance could be achieved under different variable combinations was proven by the experimental results with the regulation of the ${\dot{m}}_{\mathrm{wf}}$, ${\dot{m}}_{\mathrm{hs}}$, and ${\dot{m}}_{\mathrm{cs}}$ values, respectively. When the ${\dot{m}}_{\mathrm{wf}}$ was 0.049 kg/s, the corresponding η_ORC,ER fluctuated around 3.08~3.56%, and the ${\dot{W}}_{\mathrm{ORC},\mathrm{ER}}$ fluctuated from 211.7 to 274.1 W, even though the ${\dot{m}}_{\mathrm{wf}}$ and ${\dot{m}}_{\mathrm{cs}}$ were changed substantially.

The identification of identical and similar performance values in the solution domain indicated that alternative combinations of operation variables could be used to expand the control schemes in response to off-design working conditions. However, any concrete proposals should be further investigated to design dynamic control strategies for ORC operation. ORC functionality limitations as guides for control design should be evaluated in future work.