A Critical Review of Optimization Strategies for Simultaneous Integration of Distributed Generation and Capacitor Banks in Power Distribution Networks
Abstract
1. Introduction
1.1. Overview of Electrical Power System
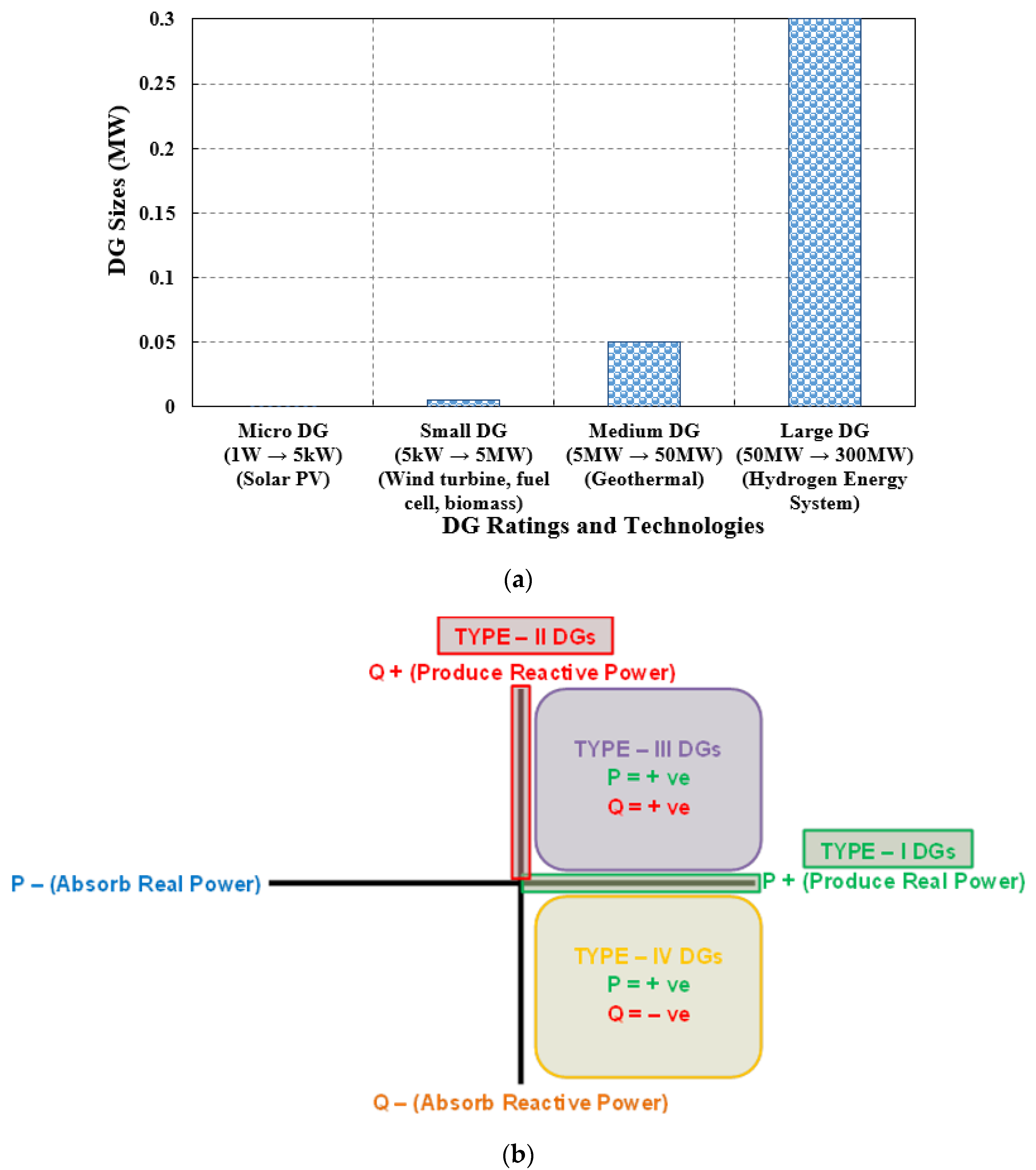
1.2. Distributed Generation (DG)
1.3. Shunt Capacitor Banks (SCB)
1.4. Need to Optimize the DG and SCB Allocation
- Reducing the total power loss;
- Improving the voltage profile;
- Increasing the overall efficiency and reliability of the power supply;
- Deferring the development of new centrally operated generation and transmission systems;
- Providing fast development and construction of new power supply units to cope with the growing load demand;
- Reducing the power transmission and distribution costs;
- Reducing the peak load shaving at the transmission side.
1.5. Benefits of Simultaneous DG and SCB Integration
1.6. Related Work
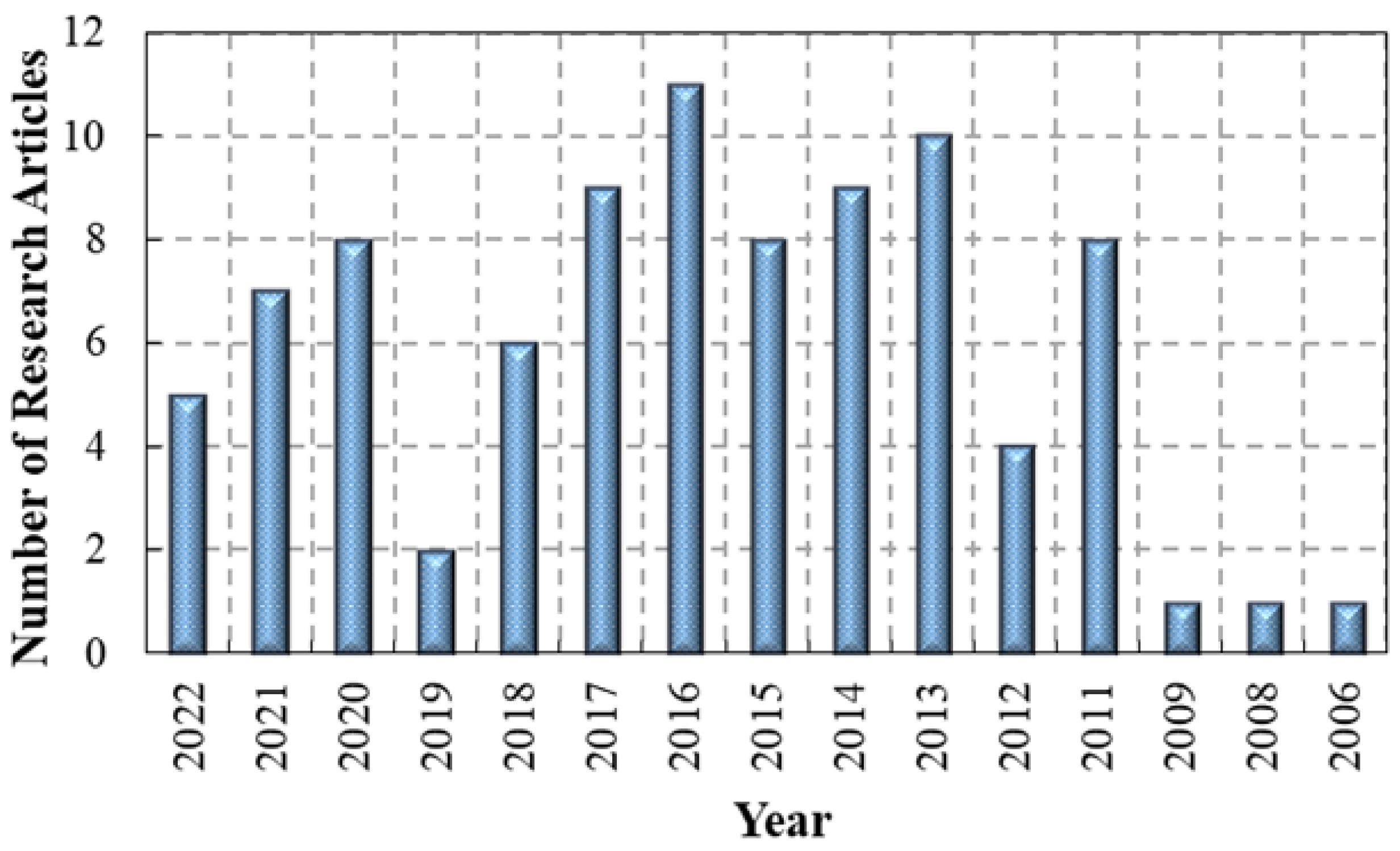
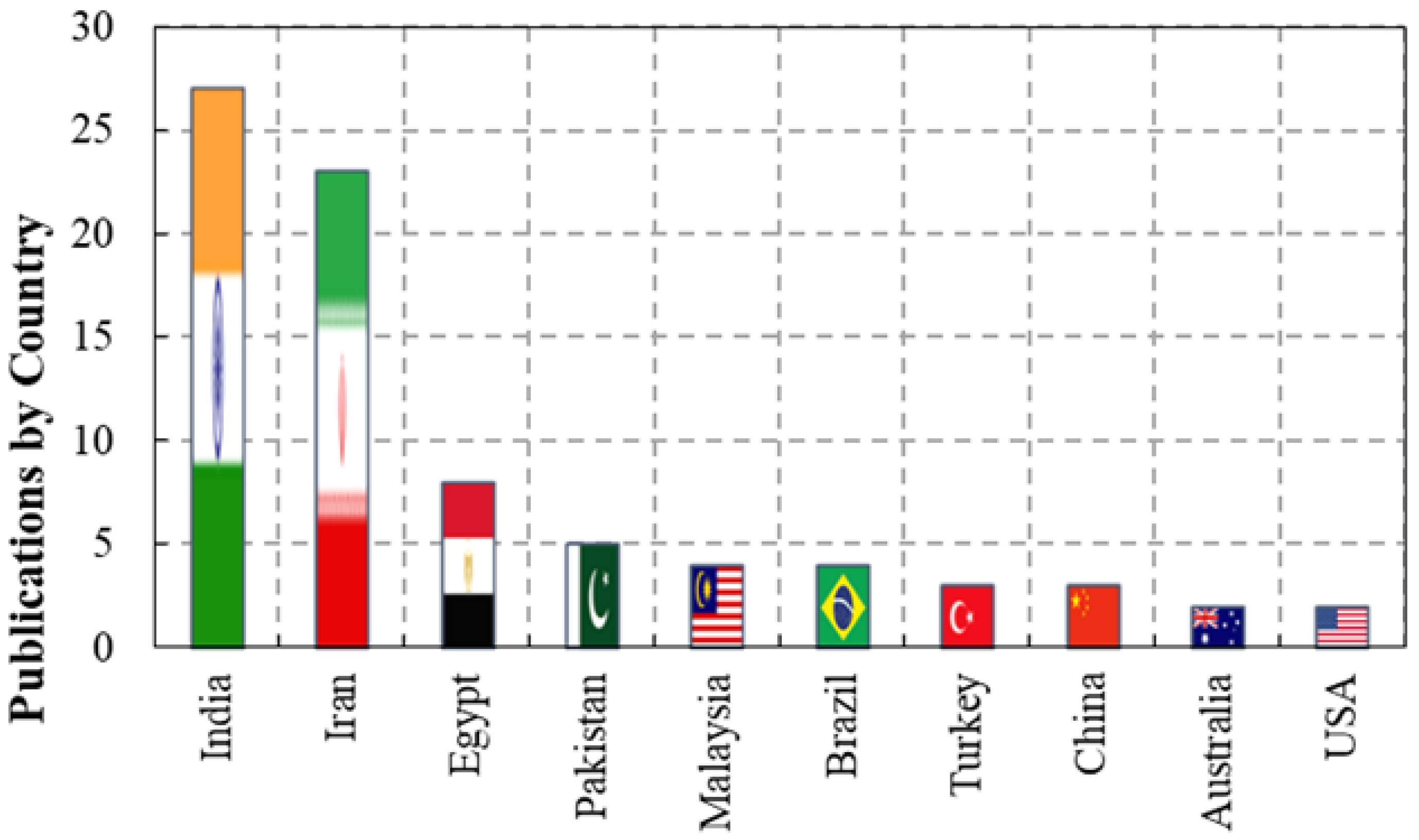
1.7. Review Methodology
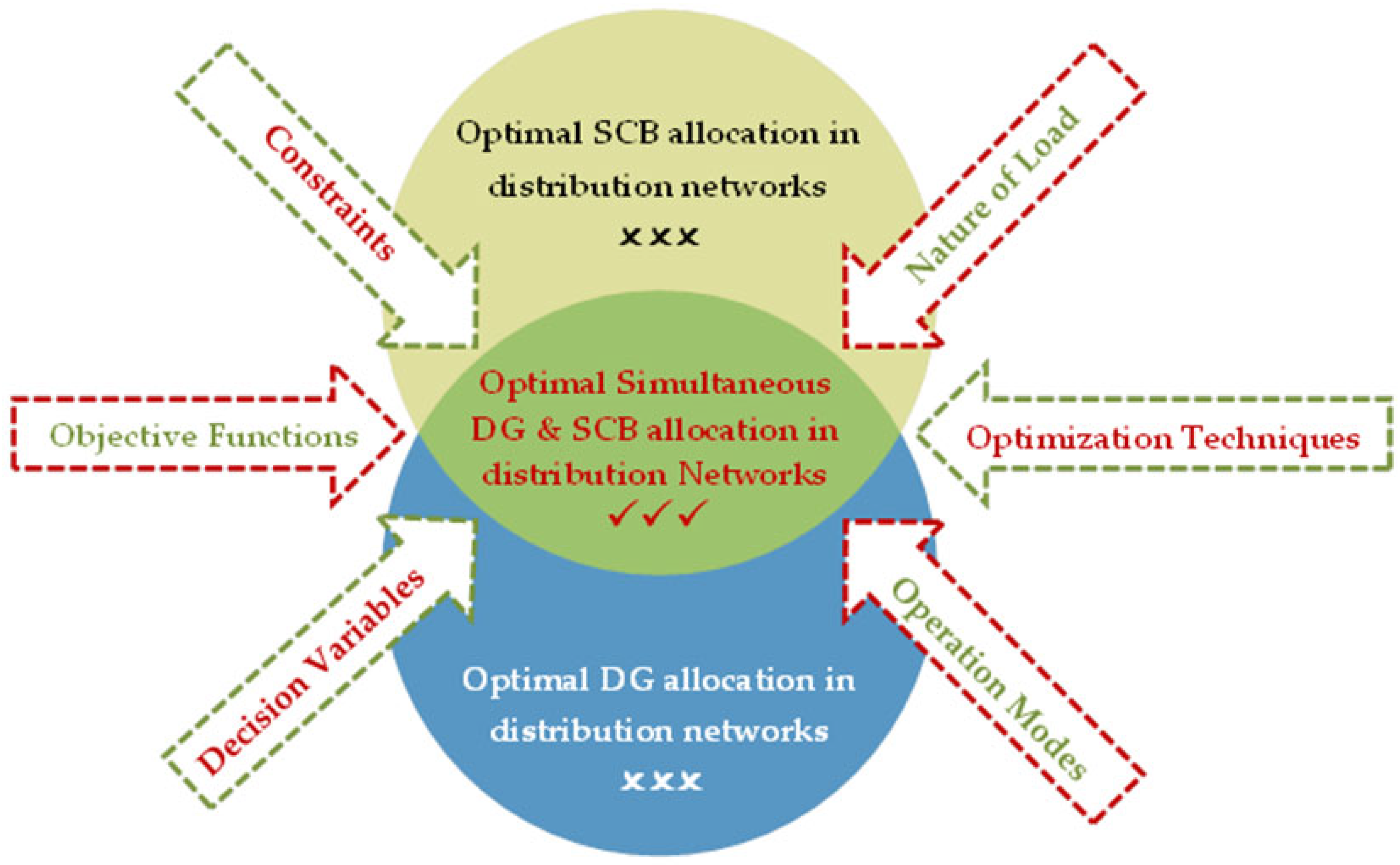
2. Planning Framework for DG and SCB Optimal Allocation
2.1. Objective Functions
2.2. Optimization Techniques
2.2.1. Conventional Techniques
2.2.2. Metaheuristic Optimization Techniques
Nature-Inspired Metaheuristic Optimization Techniques
Society or Physics-Inspired Metaheuristic Optimization Techniques
Hybrid Metaheuristic Optimization Techniques
| Ref #/Year | Optimization Technique(s) | Research Objectives | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Real Power/Energy Loss or Real Power Injection | Reactive Power/Energy Loss or Reactive Power Injection | Voltage Profile/Deviation/Sag | Voltage Stability | Power Quality (THD, Resonance, etc.) | Reliability (SAIDI, SAIFI, CAIDI, ENS, etc.) | Line Loading–Network Security/Capacity Installed P-Q Capacity/Switching Operations | Load Balancing/Transfer Capability/Power Factor | Cost of Power/Energy Loss | Capital/Running Costs of DGs/SCBs | Other Economic Objectives (Costs of: Power Purchase, Transmission, Reliability, Risk, etc.) | Gas Emissions & Other Environmental Objectives | ||
| [115] 2006 | TS | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✗ | ✗ |
| [102] 2008 | PSO | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✗ |
| [103] 2009 | PSO | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ |
| [76] 2011 | GA | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [65] 2011 | GA | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [93] 2011 | GA | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [94] 2011 | GA | ✓ | ✗ | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✗ |
| [53] 2011 | DE | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [68] 2011 | OPF | ✗ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [123] 2011 | BF-PSO | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✗ | ✗ |
| [126] 2011 | Fuzzy | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✗ | ✗ |
| [127] 2012 | GA | ✓ | ✗ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ |
| [117] 2012 | MSA | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✗ | ✗ |
| [75] 2012 | GA | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ |
| [96] 2012 | GA | ✓ | ✗ | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ | ✗ | ✓ | ✓ | ✗ |
| [55] 2013 | Analytical | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [100] 2013 | FGA | ✗ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✗ | ✗ | ✗ |
| [60] 2013 | PSO | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [56] 2013 | PSO | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [81] 2013 | DPSO | ✓ | ✓ | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [105] 2013 | BPSO | ✓ | ✗ | ✓ | ✗ | ✗ | ✓ | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ |
| [128] 2013 | BPSO | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✗ |
| [69] 2013 | BGSA | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [108] 2013 | MA | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✗ |
| [106] 2013 | WIPSO | ✗ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✗ |
| [129] 2014 | MPSO | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ |
| [64] 2014 | ABC-AIS | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [35] 2014 | DICA | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [52] 2014 | GA | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [97] 2014 | GA | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✗ |
| [83] 2014 | ICA-GA | ✓ | ✗ | ✓ | ✓ | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ |
| [31] 2014 | BSA | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [51] 2014 | BFOA | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [30] 2014 | TLBO | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✗ |
| [70] 2015 | BCAB | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [71] 2015 | IGA, IPSO, ICSO | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [72] 2015 | ITLBO | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [88] 2015 | NSGA-II | ✓ | ✗ | ✗ | ✓ | ✗ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [87] 2015 | MOPSO | ✓ | ✗ | ✗ | ✓ | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ |
| [98] 2015 | GA | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✗ | ✗ |
| [34] 2015 | GA | ✓ | ✗ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ |
| [95] 2015 | GA | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✗ | ✗ |
| [84] 2015 | WNN | ✓ | ✗ | ✓ | ✓ | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ |
| [89] 2016 | NSGA-II | ✗ | ✗ | ✓ | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [111] 2016 | BBO | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✗ |
| [112] 2016 | IMDE | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ | ✗ |
| [73] 2016 | SOS | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [54] 2016 | HAS-PABC | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [122] 2016 | MTLBO | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✗ |
| [104] 2016 | MOPSO | ✓ | ✗ | ✗ | ✓ | ✗ | ✗ | ✓ | ✗ | ✗ | ✓ | ✓ | ✓ |
| [125] 2016 | TS-CBGA | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✗ |
| [29] 2016 | GA | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✗ |
| [86] 2016 | Analytical | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ |
| [82] 2017 | HAS-PABC | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [32] 2017 | GABC | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [85] 2017 | PSO | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [50] 2017 | AGPSO | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [61] 2017 | BSA | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [33] 2017 | CSA | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [79] 2017 | MOPSO | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [63] 2017 | MOEA/D | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [91] 2017 | Analytical | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [59] 2018 | GMSA | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [57] 2018 | GA, PSO | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [113] 2018 | CSA | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✗ | ✗ |
| [130] 2018 | WCA | ✓ | ✗ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✗ | ✓ |
| [62] 2018 | WIPSO-GSA | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [101] 2018 | ESGA | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ |
| [77] 2019 | ALO | ✓ | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [131] 2019 | SSA | ✓ | ✗ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ |
| [132] 2020 | SSA | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ |
| [133] 2020 | TPA | ✓ | ✗ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✗ |
| [134] 2020 | OCSO | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✗ | ✗ |
| [58] 2020 | EGA | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [78] 2020 | MOPSO | ✓ | ✗ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [74] 2020 | CSA | ✓ | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [80] 2020 | ABC | ✓ | ✗ | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [135] 2020 | Analytical | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✗ | ✗ |
| [66] 2021 | DE | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [110] 2021 | IMPA | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [114] 2021 | MSFLA | ✓ | ✗ | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ |
| [99] 2021 | SHO | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✗ | ✗ |
| [67] 2021 | PSO-OS | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [124] 2021 | EGWO-PSO | ✓ | ✗ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ |
| [136] 2021 | IJaya | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [137] 2022 | BWOs | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [138] 2022 | CBA | ✓ | ✗ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [139] 2022 | GA | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ |
| [140] 2022 | GA | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [141] 2022 | JSA | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
2.2.3. Constraints
Power System Constraints
DG Constraints
SCB Constraints
2.2.4. Decision Variables
2.2.5. Nature of Load
2.2.6. Operation Modes
3. Limitations of the Existing Studies
- Most of the approaches consider only the active power injection of the DG, i.e., DGs’ operation at the unity power factor;
- DGs’ operations at optimal power factor and network constraint of were unnoticed in the majority of the studies;
- The location or sizes of DGs and/or SCBs were considered fixed in some studies;
- Variations in loading conditions are avoided;
- SCBs are assumed as a continuous source of reactive power, whereas they are commonly available in discrete sizes (constant type) in the market;
- Islanded operation of the distribution networks as MG and efficient utilization of the installed DG and SCB units during the islanded operation has not been addressed;
- The proposed optimization techniques’ function usually involves more steps or depends on the proper selection of algorithm-specific parameters. Therefore, their implementation is problematic, raising the need to implement new established and improved optimization algorithms.
4. Conclusions and Future Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Lim, J.S.; Manan, Z.A.; Alwi, S.R.W.; Hashim, H. A review on utilisation of biomass from rice industry as a source of renewable energy. Renew. Sustain. Energy Rev. 2012, 16, 3084–3094. [Google Scholar] [CrossRef]
- Anaya, K.L.; Pollitt, M.G. Integrating distributed generation: Regulation and trends in three leading countries. Energy Policy 2015, 85, 475–486. [Google Scholar] [CrossRef]
- Ruggiero, S.; Varho, V.; Rikkonen, P. Transition to distributed energy generation in Finland: Prospects and barriers. Energy Policy 2015, 86, 433–443. [Google Scholar]
- Theo, W.L.; Lim, J.S.; Ho, W.S.; Hashim, H.; Lee, C.T. Review of distributed generation (DG) system planning and optimisation techniques: Comparison of numerical and mathematical modelling methods. Renew. Sustain. Energy Rev. 2017, 67, 531–573. [Google Scholar]
- Zhou, W.; Lou, C.; Li, Z.; Lu, L.; Yang, H. Current status of research on optimum sizing of stand-alone hybrid solar–wind power generation systems. Appl. Energy 2010, 87, 380–389. [Google Scholar]
- Jia, L.; Tong, L. Renewables and Storage in Distribution Systems: Centralized vs. Decentralized Integration. IEEE J. Sel. Areas Commun. 2016, 34, 665–674. [Google Scholar] [CrossRef]
- Bamigbola, O.; Ali, M.; Oke, M. Mathematical modeling of electric power flow and the minimization of power losses on transmission lines. Appl. Math. Comput. 2014, 241, 214–221. [Google Scholar] [CrossRef]
- Fathabadi, H. Novel filter based ANN approach for short-circuit faults detection, classification and location in power transmission lines. Int. J. Electr. Power Energy Syst. 2016, 74, 374–383. [Google Scholar] [CrossRef]
- Willis, H.L.; Scott, W.G. Distributed Power Generation: Planning and Evaluation; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Machowski, J.; Bialek, J.W.; Bumby, J.R. Power System Dynamics: Stability and Control; John Wiley & Sons, Inc.: Warsaw, Poland, 2008. [Google Scholar]
- Alanne, K.; Saari, A. Distributed energy generation and sustainable development. Renew. Sustain. Energy Rev. 2006, 10, 539–558. [Google Scholar] [CrossRef]
- Ackermann, T.; Andersson, G.; Söder, L. Distributed generation: A definition. Electr. Power Syst. Res. 2001, 57, 195–204. [Google Scholar] [CrossRef]
- Viral, R.; Khatod, D.K. Optimal planning of distributed generation systems in distribution system: A review. Renew. Sustain. Energy Rev. 2012, 16, 5146–5165. [Google Scholar]
- Zubo, R.H.A.; Mokryani, G.; Rajamani, H.-S.; Aghaei, J.; Niknam, T.; Pillai, P. Operation and Planning of Distribution Networks With Integration of Renewable Distributed Generators Considering Uncertainties: A Review. Renew. Sustain. Energy Rev. 2017, 72, 1177–1198. [Google Scholar]
- El-Fergany, A. Optimal allocation of multi-type distributed generators using backtracking search optimization algorithm. Int. J. Electr. Power Energy Syst. 2015, 64, 1197–1205. [Google Scholar] [CrossRef]
- International Energy Agency. Distributed Generation in Liberalised Electricity Markets; International Energy Agency: Paris, France, 2002; pp. 1–125. [Google Scholar]
- Ho, W.S.; Macchietto, S.; Lim, J.S.; Hashim, H.; Muis, Z.A.; Liu, W.H. Optimal scheduling of energy storage for renewable energy distributed energy generation system. Renew. Sustain. Energy Rev. 2016, 58, 1100–1107. [Google Scholar] [CrossRef]
- Strupeit, L.; Palm, A. Overcoming barriers to renewable energy diffusion: Business models for customer-sited solar photovoltaics in Japan, Germany and the United States. J. Clean. Prod. 2016, 123, 124–136. [Google Scholar] [CrossRef]
- Parida, A.; Choudhury, S.; Chatterjee, S.; Chatterjee, D. A rule based electrical energy distribution model for energy efficiency in technical institutions: A case study. Energy Build. 2016, 126, 508–516. [Google Scholar] [CrossRef]
- Prakash, P.; Khatod, D.K. Optimal sizing and siting techniques for distributed generation in distribution systems: A review. Renew. Sustain. Energy Rev. 2016, 57, 111–130. [Google Scholar] [CrossRef]
- Subramani, R.; Vijayalakshmi, C. Design of lagrangian decomposition model for energy management using SCADA system. Smart Innov. Syst. Technol. 2016, 49, 353–361. [Google Scholar]
- Jain, M.; Gupta, S.; Masand, D.; Agnihotri, G. Real-Time Implementation of Islanded Microgrid for Remote Areas. J. Control Sci. Eng. 2016, 2016, 5710950. [Google Scholar] [CrossRef]
- Lee, S.-J.; Kim, J.-H.; Kim, C.-H.; Kim, S.-K.; Kim, E.-S.; Kim, D.-U.; Mehmood, K.K.; Khan, S.U. Coordinated Control Algorithm for Distributed Battery Energy Storage Systems for Mitigating Voltage and Frequency Deviations. IEEE Trans. Smart Grid 2015, 7, 1713–1722. [Google Scholar] [CrossRef]
- Neagle, N.M.; Samson, D.R. Loss Reduction from Capacitors Installed on Primary Feeders. Trans. Am. Inst. Electr. Eng. Part III Power Appar. Syst. 1956, 75, 950–959. [Google Scholar]
- Sultana, S.; Roy, P. Optimal capacitor placement in radial distribution systems using teaching learning based optimization. Int. J. Electr. Power Energy Syst. 2014, 54, 387–398. [Google Scholar] [CrossRef]
- Nojavan, S.; Jalali, M.; Zare, K. Optimal allocation of capacitors in radial/mesh distribution systems using mixed integer nonlinear programming approach. Electr. Power Syst. Res. 2014, 107, 119–124. [Google Scholar] [CrossRef]
- Singh, H.; Hao, S.; Papalexopoulos, A. Transmission congestion management in competitive electricity markets. IEEE Trans. Power Syst. 1998, 13, 672–680. [Google Scholar] [CrossRef]
- Aman, M.; Jasmon, G.; Bakar, A.; Mokhlis, H.; Karimi, M. Optimum shunt capacitor placement in distribution system—A review and comparative study. Renew. Sustain. Energy Rev. 2014, 30, 429–439. [Google Scholar] [CrossRef]
- Rahmani-Andebili, M. Simultaneous placement of DG and capacitor in distribution network. Electr. Power Syst. Res. 2016, 131, 1–10. [Google Scholar] [CrossRef]
- Rahiminejad, A.; Aranizadeh, A.; Vahidi, B. Simultaneous distributed generation and capacitor placement and sizing in radial distribution system considering reactive power market. J. Renew. Sustain. Energy 2014, 6, 043124. [Google Scholar] [CrossRef]
- Syed, M.S.; Injeti, S.K. Simultaneous optimal placement of DGs and fixed capacitor banks in radial distribution systems using BSA optimization. Int. J. Comput. Appl. 2014, 108, 28–35. [Google Scholar]
- Dixit, M.; Kundu, P.; Jariwala, H.R. Incorporation of distributed generation and shunt capacitor in radial distribution system for techno-economic benefits. Eng. Sci. Technol. Int. J. 2017, 20, 482–493. [Google Scholar] [CrossRef]
- Samal, P.; Mohanty, S.; Ganguly, S. Planning of distributed generation and capacitor in an unbalanced radial distribution system using cuckoo search algorithm. In Proceedings of the 2016 19th International Conference on Electrical Machines and Systems (ICEMS), Chiba, Japan, 13–16 November 2016. [Google Scholar]
- Pradeepa, H.; Ananthapadmanabha, T.; Rani, D.N.S.; Bandhavya, C. Optimal allocation of combined DG and capacitor units for voltage stability enhancement. Procedia Technol. 2015, 21, 216–223. [Google Scholar] [CrossRef]
- Mahari, A.; Mahari, A. Optimal DG and capacitor allocation in distribution systems using DICA. J. Eng. Sci. Technol. 2014, 9, 641–656. [Google Scholar]
- Tan, W.S.; Hassan, M.Y.; Majid, S.; Rahman, H.A. Optimal distributed renewable generation planning: A review of different approaches. Renew. Sustain. Energy Rev. 2013, 18, 626–645. [Google Scholar] [CrossRef]
- Paliwal, P.; Patidar, N.; Nema, R. Planning of grid integrated distributed generators: A review of technology, objectives and techniques. Renew. Sustain. Energy Rev. 2014, 40, 557–570. [Google Scholar] [CrossRef]
- Sultana, U.; Khairuddin, A.B.; Aman, M.; Mokhtar, A.; Zareen, N. A review of optimum DG placement based on minimization of power losses and voltage stability enhancement of distribution system. Renew. Sustain. Energy Rev. 2016, 63, 363–378. [Google Scholar] [CrossRef]
- Jordehi, A.R. Allocation of distributed generation units in electric power systems: A review. Renew. Sustain. Energy Rev. 2016, 56, 893–905. [Google Scholar] [CrossRef]
- Pesaran, M.H.A.; Huy, P.D.; Ramachandaramurthy, V.K. A review of the optimal allocation of distributed generation: Objectives, constraints, methods, and algorithms. Renew. Sustain. Energy Rev. 2017, 75, 293–312. [Google Scholar] [CrossRef]
- Singh, A.; Parida, S. A review on distributed generation allocation and planning in deregulated electricity market. Renew. Sustain. Energy Rev. 2018, 82, 4132–4141. [Google Scholar] [CrossRef]
- Singh, B.; Sharma, J. A review on distributed generation planning. Renew. Sustain. Energy Rev. 2017, 76, 529–544. [Google Scholar] [CrossRef]
- Khatib, T.; Ibrahim, I.A.; Mohamed, A. A review on sizing methodologies of photovoltaic array and storage battery in a standalone photovoltaic system. Energy Convers. Manag. 2016, 120, 430–448. [Google Scholar] [CrossRef]
- Al-Falahi, M.; Jayasinghe, S.G.; Enshaei, H. A review on recent size optimization methodologies for standalone solar and wind hybrid renewable energy system. Energy Convers. Manag. 2017, 143, 252–274. [Google Scholar] [CrossRef]
- Abdmouleh, Z.; Gastli, A.; Ben-Brahim, L.; Haouari, M.; Al-Emadi, N.A. Review of optimization techniques applied for the integration of distributed generation from renewable energy sources. Renew. Energy 2017, 113, 266–280. [Google Scholar] [CrossRef]
- Ehsan, A.; Yang, Q. Optimal integration and planning of renewable distributed generation in the power distribution networks: A review of analytical techniques. Appl. Energy 2018, 210, 44–59. [Google Scholar] [CrossRef]
- Kishore, C.; Ghosh, S.; Engineering, I. Literature Survey on Optimal Capacitor Placement and Size in Radial Distribution Networks. Int. J. Sci. Res. Educ. 2016, 4, 5567–5570. [Google Scholar]
- Sonwane, P.M. DBEK. Optimal capacitor placement and sizing in unbalanced distribution. Int. J. Innov. Res. Adv. Eng. 2008, 2, 103–113. [Google Scholar]
- Gupta, T. A Review of Various Techniques for Optimal Placement of Capacitors for Reactive. Power Control 2015, 3, 2–5. [Google Scholar]
- Srinivasan, G.; Visalakshi, S. Application of AGPSO for Power loss minimization in Radial Distribution Network via DG units, Capacitors and NR. Energy Procedia 2017, 117, 190–200. [Google Scholar]
- Imran, M.A.; Kowsalya, M. Optimal Distributed Generation and capacitor placement in power distribution networks for power loss minimization. Int. Conf. Adv. Electr. Eng. 2014, 12, 1–6. [Google Scholar]
- Saonerkar, A.K.; Bagde, B.Y. Optimized DG placement in radial distribution system with reconfiguration and capacitor placement using genetic algorithm. In Proceedings of the 2014 IEEE International Conference on Advanced Communications, Control and Computing Technologies, Ramanathapuram, India, 8–10 May 2014; pp. 1077–1083. [Google Scholar]
- Gunda, J.; Khan, N.A. Optimal Location and Sizing of DG and Shunt Capacitors Using Differential Evolution. Int. J. Soft Comput. 2011, 6, 128–135. [Google Scholar] [CrossRef]
- Muthukumar, K.; Jayalalitha, S. Optimal placement and sizing of distributed generators and shunt capacitors for power loss minimization in radial distribution networks using hybrid heuristic search optimization technique. Int. J. Electr. Power Energy Syst. 2016, 78, 299–319. [Google Scholar] [CrossRef]
- Gopiya Naik, S.; Khatod, D.K.; Sharma, M.P. Optimal allocation of combined DG and capacitor for real power loss minimization in distribution networks. Int. J. Electr. Power Energy Syst. 2013, 53, 967–973. [Google Scholar] [CrossRef]
- Aman, M.M.; Jasmon, G.B.; Solangi, K.H.; Bakar, A.H.A.; Mokhlis, H. Optimum Simultaneous DG and Capacitor Placement on the Basis of Minimization of Power Losses. Int. J. Comput. Electr. Eng. 2013, 5, 516–522. [Google Scholar] [CrossRef]
- Lotfi, H.; Elmi, M.B.; Saghravanian, S. Simultaneous placement of capacitor and DG in distribution networks using particle swarm optimization algorithm. Int. J. Smart Electr. Eng. 2018, 7, 35–41. [Google Scholar]
- Almabsout, E.A.; El-Sehiemy, R.A.; An, O.N.U.; Bayat, O. A Hybrid Local Search-Genetic Algorithm for Simultaneous Placement of DG Units and Shunt Capacitors in Radial Distribution Systems. IEEE Access 2020, 8, 54465–54481. [Google Scholar] [CrossRef]
- Mohamed, E.; Mohamed, A.-A.A.; Mitani, Y. Hybrid GMSA for Optimal Placement and Sizing of Distributed Generation and Shunt Capacitors. J. Eng. Sci. Technol. Rev. 2018, 11, 55–65. [Google Scholar] [CrossRef]
- Musa, I.; Zahawi, B.; Gadoue, S.M. Integration of induction generator based distributed generation and shunt compensation capacitors in power distribution networks. In Proceedings of the 4th International Conference on Power Engineering, Energy and Electrical Drives, Istanbul, Turkey, 13–17 May 2013; pp. 1105–1109. [Google Scholar]
- Fadel, W.; Kilic, U.; Taskin, S. Placement of Dg, Cb, and Tcsc in radial distribution system for power loss minimization using back-tracking search algorithm. Electr. Eng 2017, 99, 791–802. [Google Scholar] [CrossRef]
- Rajendran, A.; Narayanan, K. Optimal multiple installation of DG and capacitor for energy loss reduction and loadability enhancement in the radial distribution network using the hybrid WIPSO–GSA algorithm. Int. J. Ambient. Energy 2018, 41, 129–141. [Google Scholar] [CrossRef]
- Biswas, P.P.; Mallipeddi, R.; Suganthan, P.; Amaratunga, G.A. A multiobjective approach for optimal placement and sizing of distributed generators and capacitors in distribution network. Appl. Soft Comput. 2017, 60, 268–280. [Google Scholar] [CrossRef]
- Muhtazaruddin, M.N.; Tuyen, N.D.; Fujita, G.; Bin, J.J.J. Optimal distributed generation and capacitor coordination for power loss minimization. In Proceedings of the 2014 IEEE PES T&D Conference and Exposition, Chicago, IL, USA, 14–17 April 2014; pp. 1–4. [Google Scholar]
- Rugthaicharoencheep, N.; Nedphograw, S.; Wanaratwijit, W. Distribution system operation for power loss minimization and improved voltage profile with distributed generation and capacitor placements. In Proceedings of the 2011 4th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), Weihai, China, 6–9 July 2011; pp. 1185–1189. [Google Scholar]
- Salkuti, S.R. Optimal location and sizing of shunt capacitors and distributed generation in power distribution systems. ECTI Trans. Electr. Eng. Electron. Commun. 2021, 19, 34–42. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, A.; Zhao, C.; Zhang, Z. Optimal Placement and Capacity of Combined DGs and SCs in Radial Distribution Networks Based on PSO-OS Algorithm. IAENG Int. J. Comput. Sci. 2021, 48, 236–249. [Google Scholar]
- Wang, M.; Zhong, J. A novel method for distributed generation and capacitor optimal placement considering voltage profiles. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–6. [Google Scholar]
- Khan, N.A.; Ghosh, S.; Ghoshal, S.P. Binary Gravitational Search based Algorithm for Optimum Siting and Sizing of DG and Shunt Capacitors in Radial Distribution Systems. Energy Power Eng. 2013, 5, 1005–1010. [Google Scholar] [CrossRef]
- Khan, N.A.; Ghoshal, S.P.; Ghosh, S. Optimal Allocation of Distributed Generation and Shunt Capacitors for the Reduction of Total Voltage Deviation and Total Line Loss in Radial Distribution Systems Using Binary Collective Animal Behavior Optimization Algorithm. Electr. Power Components Syst. 2014, 43, 119–133. [Google Scholar] [CrossRef]
- Kanwar, N.; Gupta, N.; Niazi, K.R.; Swarnkar, A. Improved meta-heuristic techniques for simultaneous capacitor and DG allocation in radial distribution networks. Int. J. Electr. Power Energy Syst. 2015, 73, 653–664. [Google Scholar] [CrossRef]
- Kanwar, N.; Gupta, N.; Niazi, K.; Swarnkar, A. Simultaneous allocation of distributed resources using improved teaching learning based optimization. Energy Convers. Manag. 2015, 103, 387–400. [Google Scholar] [CrossRef]
- Lalitha, M.P.; Babu, P.S.; Adivesh, B. Optimal distributed generation and capacitor placement for loss minimization and voltage profile improvement using symbiotic organisms search algorithm. Int. J. Electr. Eng. 2016, 9, 249–261. [Google Scholar]
- Uchendu, M.; Alberah, J.; Olarinoye, G.A. A Cuckoo Search Algorithm-based Placement of Distributed Generation and Shunt Capacitor Bank on Radial Distribution Networks. Int. Conf. Electr. Eng. Appl. 2020, 5, 176–181. [Google Scholar]
- Sadighmanesh, A.; Zare, K.; Sabahi, M. Distributed Generation unit and Capacitor Placement for Multi-objective Optimization. Int. J. Electr. Comput. Eng. (IJECE) 2012, 2, 615–620. [Google Scholar] [CrossRef]
- Kalantari, M.; Kazemi, A. Placement of distributed generation unit and capacitor allocation in distribution systems using genetic algorithm. In Proceedings of the 2011 10th International Conference on Environment and Electrical Engineering, Rome, Italy, 8–11 May 2011. [Google Scholar]
- Abul’Wafa, A.R. Ant-lion optimizer-based multi-objective optimal simultaneous allocation of distributed generations and synchronous condensers in distribution networks. Int. Trans. Electr. Energy Syst. 2019, 29, 1–14. [Google Scholar] [CrossRef]
- Malik, M.Z.; Kumar, M.; Soomro, A.M.; Baloch, M.H.; Farhan, M.; Gul, M.; Kaloi, G.S. Strategic planning of renewable distributed generation in radial distribution system using advanced MOPSO method. Energy Rep. 2020, 6, 2872–2886. [Google Scholar] [CrossRef]
- Kumar, M.; Nallagownden, P.; Elamvazuthi, I. Optimal Placement and Sizing of Renewable Distributed Generations and Capacitor Banks into Radial Distribution Systems. Energies 2017, 10, 811. [Google Scholar] [CrossRef]
- Yousefzadeh, M.; Najafi, H.R.; Monfared, E. Simultaneous Optimal Placement and Sizing of Distributed Generation Resources and Capacitor Banks in Neyriz Distribution Systems for Reliability Improvement and Losses Reduction Using Artificial Bee Colony Algorithm. In Proceedings of the First National Conference on Applied Research in Electrical Engineering, Tehran, Iran, 31 May 2020; pp. 1–8. [Google Scholar]
- Heydari, M.; Hosseini, S.; Gholamian, S. Optimal Placement and Sizing of Capacitor and Distributed Generation with Harmonic and Resonance Considerations Using Discrete Particle Swarm Optimization. Int. J. Intell. Syst. Appl. 2013, 5, 42–49. [Google Scholar] [CrossRef]
- Muthukumar, K.; Jayalalitha, S. Integrated approach of network reconfiguration with distributed generation and shunt capacitors placement for power loss minimization in radial distribution networks. Appl. Soft Comput. J. 2017, 52, 1262–1284. [Google Scholar]
- Moradi, M.H.; Zeinalzadeh, A.; Mohammadi, Y.; Abedini, M. An efficient hybrid method for solving the optimal sitting and sizing problem of DG and shunt capacitor banks simultaneously based on imperialist competitive algorithm and genetic algorithm. Int. J. Electr. Power Energy Syst. 2014, 54, 101–111. [Google Scholar] [CrossRef]
- Ozgonenel, O.; Karagol, S.; Terzi, U.K. A novel approach for distributed renewable generation and shunt capacitor placing in smart-grid. In Proceedings of the IEEE PES Innovative Smart Grid Technologies, Istanbul, Turkey, 2 February 2015; pp. 1–6. [Google Scholar]
- Ghanegaonkar, S.P.; Pande, V. Optimal hourly scheduling of distributed generation and capacitors for minimisation of energy loss and reduction in capacitors switching operations. IET Gener. Transm. Distrib. 2017, 11, 2244–2250. [Google Scholar] [CrossRef]
- Doostan, M.; Navaratnan, S.; Mohajeryami, S.; Cecchi, V. Concurrent placement of distributed generation resources and capacitor banks in distribution systems. In Proceedings of the 2016 North American Power Symposium (NAPS), Denver, CO, USA, 18–20 September 2016. [Google Scholar]
- Zeinalzadeh, A.; Mohammadi, Y.; Moradi, M.H. Optimal multi objective placement and sizing of multiple DGs and shunt capacitor banks simultaneously considering load uncertainty via MOPSO approach. Int. J. Electr. Power Energy Syst. 2015, 67, 336–349. [Google Scholar] [CrossRef]
- Gallano, R.J.C.; Nerves, A.C. Multi-objective optimization of distribution network reconfiguration with capacitor and distributed generator placement. In Proceedings of the IEEE Reg 10 Annual Internationl Conferences Proceedings/TENCON, Bangkok, Thailand, 22–25 October 2015. [Google Scholar]
- Jannat, M.B.; Savić, A.S. Optimal capacitor placement in distribution networks regarding uncertainty in active power load and distributed generation units production. IET Gener. Transm. Distrib. 2016, 10, 3060–3067. [Google Scholar] [CrossRef]
- Mady, I. Optimal sizing of capacitor banks and distributed generation in distorted distribution networks by genetic algorithms. In Proceedings of the CIRED 2009—20th International Conference and Exhibition on Electricity Distribution, Prague, Czech Republic, 8–11 June 2009. [Google Scholar]
- Mahmoud, K. Optimal integration of DG and capacitors in distribution systems. In Proceedings of the 18th Internationl Middle-East Power System Conferences MEPCON 2016, Cairo, Egypt, 27–29 December 2016; pp. 651–655. [Google Scholar]
- Gavrilas, M. Heuristic and metaheuristic optimization techniques with application to power systems. In Proceedings of the International Conference on Mathematical Methods and Computational Techniques in Electrical Engineering, Bucharest, Romania, 16–18 October 2010; pp. 95–103. [Google Scholar]
- Ardakani, M.H.M.; Abadi, M.Z.M.; Abadi, M.H.Z.M.; Khodadadi, A. Distributed generation and capacitor banks placement in order to achieve the optimal real power losses using GA. Int. J. Comput. Sci. Technol. 2011, 2, 400–404. [Google Scholar]
- Taher, S.A.; Hasani, M.; Karimian, A. A novel method for optimal capacitor placement and sizing in distribution systems with nonlinear loads and DG using GA. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 851–862. [Google Scholar] [CrossRef]
- Farag, H.E.Z.; El-Saadany, E.F. Optimum shunt capacitor placement in distribution networks with high penetration of renewable energy resources using genetic algorithms. In Proceedings of the IEEE PES Innovative Smart Grid Technologies, Istanbul, Turkey, 12–15 October 2015; pp. 1–6. [Google Scholar]
- Mahaei, S.M.; Sami, T.; Shilebaf, A.; Jafarzadeh, J. Simultaneous placement of distributed generations and capacitors with multi-objective function. In Proceedings of the 2012 Proceedings of 17th Conference on Electrical Power Distribution, Tehran, Iran, 2–3 May 2012; pp. 1–9. [Google Scholar]
- Biswas, S.; Goswami, S.K.; Chatterjee, A. Optimal distributed generation placement in shunt capacitor compensated distribution systems considering voltage sag and harmonics distortions. IET Gener. Transm. Distrib. 2014, 8, 783–797. [Google Scholar] [CrossRef]
- Gholami, R.; Shahabi, M.; Haghifam, M.-R. An efficient optimal capacitor allocation in DG embedded distribution networks with islanding operation capability of micro-grid using a new genetic based algorithm. Int. J. Electr. Power Energy Syst. 2015, 71, 335–343. [Google Scholar] [CrossRef]
- Naderipour, A.; Abdul-Malek, Z.; Hajivand, M.; Seifabad, Z.M.; Farsi, M.A.; Nowdeh, S.A.; Davoudkhani, I.F. Spotted hyena optimizer algorithm for capacitor allocation in radial distribution system with distributed generation and microgrid operation considering different load types. Sci. Rep. 2021, 11, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Reddy, S.C.; Prasad, P.V.; Laxmi, A.J. Placement of distributed generator, capacitor and DG and capacitor in distribution system for loss reduction and reliability improvement. J. Electr. Eng. 2013, 13, 329–337. [Google Scholar]
- Mehmood, K.K.; Kim, C.-H.; Khan, S.U.; Haider, Z.M. Unified Planning of Wind Generators and Switched Capacitor Banks: A Multiagent Clustering-Based Distributed Approach. IEEE Trans. Power Syst. 2018, 33, 6978–6988. [Google Scholar] [CrossRef]
- Zou, K.; Agalgaonkar, A.P.; Muttaqi, K.M.; Perera, S. Optimisation of Distributed Generation Units and shunt capacitors for economic operation of distribution systems. In Proceedings of the Australasian Universities Power Engineering Conference, Sydney, Australia, 14–17 December 2008; pp. 1–7. [Google Scholar]
- Zou, K.; Agalgaonkar, A.P.; Muttaqi, K.M.; Perera, S. Voltage support by distributed generation units and shunt capacitors in distribution systems. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting, PES, Calgary, AB, Canada, 26–30 July 2009; pp. 1–8. [Google Scholar]
- Kayal, P.; Chanda, C. Strategic approach for reinforcement of intermittent renewable energy sources and capacitor bank for sustainable electric power distribution system. Int. J. Electr. Power Energy Syst. 2016, 83, 335–351. [Google Scholar] [CrossRef]
- Baghipour, R.; Hosseini, S.M. Placement of DG and Capacitor for Loss Reduction, Reliability and Voltage Improvement in Distribution Networks Using BPSO. Int. J. Intell. Syst. Appl. 2012, 4, 57–64. [Google Scholar] [CrossRef]
- Arulraj, R.; Kumarappan, N.; Vigneysh, T. Optimal location and sizing of DG and capacitor in distribution network using weight-improved particle swarm optimization algorithm (WIPSO). In Proceedings of the 2013 International Mutli-Conference on Automation, Computing, Communication, Control and Compressed Sensing (iMac4s), Kottayam, India, 22–23 March 2013; pp. 759–764. [Google Scholar]
- Moscato, P. On Evolution, Search, Optimization, Genetic Algorithms and Martial Arts towards Memetic Algorithms; Technical Report C3P 826, Caltech Con-Current Computation Program 158-79; California Institute of Technology: Pasadena, CA, USA, 1989. [Google Scholar]
- Sajjadi, S.M.; Haghifam, M.-R.; Salehi, J. Simultaneous placement of distributed generation and capacitors in distribution networks considering voltage stability index. Int. J. Electr. Power Energy Syst. 2013, 46, 366–375. [Google Scholar] [CrossRef]
- Chu, S.; Tsai, P.; Pan, J. Cat Swarm Optimization. Trends Artif. Intell. 2006, 5, 854–858. [Google Scholar]
- Eid, A.; Kamel, S.; Abualigah, L. Marine predators algorithm for optimal allocation of active and reactive power resources in distribution networks. Neural Comput. Appl. 2021, 33, 14327–14355. [Google Scholar] [CrossRef]
- Ghaffarzadeh, N.; Sadeghi, H. A new efficient BBO based method for simultaneous placement of inverter-based DG units and capacitors considering harmonic limits. Int. J. Electr. Power Energy Syst. 2016, 80, 37–45. [Google Scholar] [CrossRef]
- Khodabakhshian, A.; Andishgar, M.H. Simultaneous placement and sizing of DGs and shunt capacitors in distribution systems by using IMDE algorithm. Int. J. Electr. Power Energy Syst. 2016, 82, 599–607. [Google Scholar] [CrossRef]
- Biswal, S.; Ghosh, A.; Kumar, S.; Chakraborty, N.; Goswami, S.K. Cuckoo Search Algorithm Based Cost Minimization by Optimal DG and Capacitor Integration in Radial Distribution Systems. In Proceedings of the 20th National Power Systems Conference (NPSC), Tiruchirappalli, India, 14–16 December 2018; pp. 3–8. [Google Scholar]
- Lotfi, H. Optimal sizing of distributed generation units and shunt capacitors in the distribution system considering uncertainty resources by the modified evolutionary algorithm. J. Ambient Intell. Humaniz. Comput. 2021, 13, 4739–4758. [Google Scholar] [CrossRef]
- Golshan, M.H.; Arefifar, S. Distributed generation, reactive sources and network-configuration planning for power and energy-loss reduction. IEE Proc.-Gener. Transm. Distrib. 2006, 153, 127–136. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Elmitwally, A.; Eldesouky, A. An approach for placement and sizing of capacitor banks in distribution networks with distributed wind generation. Int. Trans. Electr. Energy Syst. 2012, 23, 539–552. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. BGSA: Binary gravitational search algorithm. Nat. Comput. 2009, 9, 727–745. [Google Scholar] [CrossRef]
- Atashpaz-Gargari, E.; Lucas, C. Imperialist competitive algorithm: An algorithm for optimization inspired by imperialistic competition. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 4661–4667. [Google Scholar]
- Rao, R.V.; Savsani, V.J.; Balic, J. Teaching-learning-based optimization algorithm for unconstrained and constrained real-parameter optimization problems. Eng. Optim. 2012, 44, 1447–1462. [Google Scholar] [CrossRef]
- Rahiminejad, A.; Hosseinian, S.H.; Vahidi, B.; Shahrooyan, S. Simultaneous Distributed Generation Placement, Capacitor Placement, and Reconfiguration using a Modified Teaching-Learning-based Optimization Algorithm. Electr. Power Compon. Syst. 2016, 44, 1631–1644. [Google Scholar] [CrossRef]
- Hooshmand, R.A.; Mohkami, H. New optimal placement of capacitors and dispersed generators using bacterial foraging oriented by particle swarm optimization algorithm in distribution systems. Electr. Eng. 2011, 93, 43–53. [Google Scholar] [CrossRef]
- Venkatesan, C.; Kannadasan, R.; Alsharif, M.; Kim, M.-K.; Nebhen, J. A Novel Multiobjective Hybrid Technique for Siting and Sizing of Distributed Generation and Capacitor Banks in Radial Distribution Systems. Sustainability 2021, 13, 3308. [Google Scholar] [CrossRef]
- Pereira, B.R.; Martins Da Costa, G.R.M.; Contreras, J.; Mantovani, J.R.S. Optimal distributed generation and reactive power allocation in electrical distribution systems. IEEE Trans. Sustain. Energy 2016, 7, 975–984. [Google Scholar] [CrossRef]
- Dukpa, A.; Venkatesh, B.; Chang, L. Fuzzy Stochastic Programming Method: Capacitor Planning in Distribution Systems With Wind Generators. IEEE Trans. Power Syst. 2011, 26, 1971–1979. [Google Scholar] [CrossRef]
- Esmaeilian, H.R.; Darijany, O.; Mohammadian, M. Optimal placement and sizing of DGs and capacitors simultaneously in radial distribution networks based on voltage stability security margin. Turk. J. Electr. Eng. Comput. Sci. 2012, 212, 1–14. [Google Scholar]
- Baghipour, R.; Hosseini, S.M. Optimal Placement and Sizing of DG in Capacitor Compensated Distribution Networks Using Binary Particle Swarm Optimization. J. Soft Comput. Inf. Technol. 2015, 3, 29–37. [Google Scholar]
- Jain, N.; Singh, S.; Srivastava, S. PSO based placement of multiple wind DGs and capacitors utilizing probabilistic load flow model. Swarm Evol. Comput. 2014, 19, 15–24. [Google Scholar] [CrossRef]
- El-Ela, A.A.A.; El-Sehiemy, R.A.; Abbas, A.S. Optimal Placement and Sizing of Distributed Generation and Capacitor Banks in Distribution Systems Using Water Cycle Algorithm. IEEE Syst. J. 2018, 12, 3629–3636. [Google Scholar] [CrossRef]
- Sambaiah, K.S.; Jayabarathi, T. Optimal allocation of renewable distributed generation and capacitor banks in distribution systems using salp swarm algorithm. Int. J. Renew. Energy Res. 2019, 9, 96–107. [Google Scholar]
- Dehghani, M.; Montazeri, Z.; Malik, O.P. Optimal Sizing and Placement of Capacitor Banks and Distributed Generation in Distribution Systems Using Spring Search Algorithm. Int. J. Emerg. Electr. Power Syst. 2020, 21, 1–9. [Google Scholar] [CrossRef]
- Tolabi, H.; Ara, A.L.; Hosseini, R. A new thief and police algorithm and its application in simultaneous reconfiguration with optimal allocation of capacitor and distributed generation units. Energy 2020, 203, 117911. [Google Scholar] [CrossRef]
- Das, S.; Malakar, T. Estimating the impact of uncertainty on optimum capacitor placement in wind-integrated radial distribution system. Int. Trans. Electr. Energy Syst. 2020, 30, 1–23. [Google Scholar] [CrossRef]
- Salas, R.W.; Melgar-Dominguez, O.D.; Mantovani, J.R.S. Optimal allocation of distributed generation and reactive power in simplified distribution systems. In Proceedings of the IEEE PES Transmission & Distribution Conference and Exhibition—Latin America (T&D LA), Montevideo, Uruguay, 28 September–2 October 2020; pp. 1–6. [Google Scholar]
- Leghari, Z.H.; Hassan, M.Y.; Said, D.M.; Memon, Z.A.; Hussain, S. An efficient framework for integrating distributed generation and capacitor units for simultaneous grid- connected and islanded network operations. Int. J. Energy Res. 2021, 45, 1–39. [Google Scholar] [CrossRef]
- Leghari, Z.H.; Hussain, S.; Memon, A.; Memon, A.H.; Baloch, A.A. Parameter-Free Improved Best-Worst Optimizers and Their Application for Simultaneous Distributed Generation and Shunt Capacitors Allocation in Distribution Networks. Int. Trans. Electr. Energy Syst. 2022, 2022, 6833488. [Google Scholar] [CrossRef]
- Mouwafi, M.T.; El-Sehiemy, R.A.; El-Ela, A.A.A. A two-stage method for optimal placement of distributed generation units and capacitors in distribution systems. Appl. Energy 2022, 307, 118188. [Google Scholar] [CrossRef]
- Pereira, L.D.; Yahyaoui, I.; Fiorotti, R.; de Menezes, L.S.; Fardin, J.F.; Rocha, H.R.; Tadeo, F. Optimal allocation of distributed generation and capacitor banks using probabilistic generation models with correlations. Appl. Energy 2022, 307, 118097. [Google Scholar] [CrossRef]
- Martins, A.S.C.; de Araujo, L.R.; Penido, D.R.R. Sensibility Analysis with Genetic Algorithm to Allocate Distributed Generation and Capacitor Banks in Unbalanced Distribution Systems. Electr. Power Syst. Res. 2022, 209, 107962. [Google Scholar] [CrossRef]
- Eid, A. Cost-based analysis and optimization of distributed generations and shunt capacitors incorporated into distribution systems with nonlinear demand modeling. Expert Syst. Appl. 2022, 198, 116844. [Google Scholar] [CrossRef]
- Ugranlı, F.; Karatepe, E. Multiple-distributed generation planning under load uncertainty and different penetration levels. Int. J. Electr. Power Energy Syst. 2013, 46, 132–144. [Google Scholar] [CrossRef]
- Shahabi, M.; Haghifam, M.R.; Mohamadian, M.; Nabavi-Niaki, S.A. Microgrid Dynamic Performance Improvement Using a Doubly Fed Induction Wind Generator. IEEE Trans. Energy Convers. 2009, 24, 137–145. [Google Scholar] [CrossRef]


| Feature | Centralized Power Generation | Distributed Generation |
|---|---|---|
| Generation capacity | Large in order to achieve economies of scale; the reported range is 100–1000 MW | Below and up to 300 MW |
| Location | Located distant from the load centers, generally close to the resource extraction locations | Integrated with customer facilities and situated closer to the power consumption centers |
| Location of penetration to the electrical system | Connected to a high-voltage transmission system, which step-up electricity before transmission to substations (for further distribution) to reduce line losses | On-grid: Connected to a lower-voltage distribution system or customer facilities. Off-grid: DG that is not connected to the utility grid operates independently with customer facilities or in a microgrid system. |
| Ref. # | Power System Constraints | DG Constraints | SCB Constraints | VR | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Power Balance | Bus Voltage | Current Flow Limits | Power Flow Limits | THD | Radial Topology | No-Load Point Interruption | Size | Site | Number of Units | Penetration | Power Factor | Size | Site | Number of Units | Penetration | Tap Positions | |
| [115] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||
| [102] | ✓ | ✓ | |||||||||||||||
| [103] | ✓ | ✓ | |||||||||||||||
| [76] | ✓ | ✓ | ✓ | ||||||||||||||
| [65] | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||
| [93] | ✓ | ✓ | ✓ | ✓ | |||||||||||||
| [94] | ✓ | ✓ | ✓ | ||||||||||||||
| [53] | ✓ | ✓ | ✓ | ||||||||||||||
| [68] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||
| [123] | ✓ | ✓ | ✓ | ✓ | |||||||||||||
| [126] | ✓ | ✓ | ✓ | ✓ | |||||||||||||
| [127] | ✓ | ✓ | ✓ | ||||||||||||||
| [117] | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||
| [75] | ✓ | ✓ | ✓ | ✓ | |||||||||||||
| [96] | |||||||||||||||||
| [55] | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||
| [100] | ✓ | ✓ | ✓ | ||||||||||||||
| [60] | ✓ | ✓ | ✓ | ||||||||||||||
| [56] | ✓ | ✓ | ✓ | ||||||||||||||
| [81] | ✓ | ✓ | |||||||||||||||
| [105] | ✓ | ✓ | |||||||||||||||
| [128] | ✓ | ✓ | |||||||||||||||
| [69] | ✓ | ||||||||||||||||
| [108] | ✓ | ✓ | ✓ | ||||||||||||||
| [106] | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||
| [129] | ✓ | ✓ | ✓ | ✓ | |||||||||||||
| [64] | ✓ | ✓ | ✓ | ✓ | |||||||||||||
| [35] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||
| [52] | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||
| [97] | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||
| [83] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||
| [31] | ✓ | ✓ | ✓ | ||||||||||||||
| [51] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||
| [30] | ✓ | ✓ | ✓ | ||||||||||||||
| [70] | ✓ | ✓ | ✓ | ||||||||||||||
| [71] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||
| [72] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||
| [88] | ✓ | ✓ | ✓ | ✓ | |||||||||||||
| [87] | ✓ | ✓ | ✓ | ✓ | |||||||||||||
| [98] | ✓ | ✓ | ✓ | ✓ | |||||||||||||
| [34] | ✓ | ✓ | ✓ | ✓ | |||||||||||||
| [95] | ✓ | ✓ | |||||||||||||||
| [89] | ✓ | ✓ | |||||||||||||||
| [84] | |||||||||||||||||
| [111] | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||
| [112] | ✓ | ✓ | ✓ | ||||||||||||||
| [73] | ✓ | ✓ | ✓ | ||||||||||||||
| [54] | ✓ | ✓ | ✓ | ||||||||||||||
| [122] | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||
| [104] | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||
| [125] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||
| [29] | ✓ | ✓ | |||||||||||||||
| [86] | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||
| [82] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||
| [32] | ✓ | ✓ | ✓ | ✓ | |||||||||||||
| [85] | ✓ | ✓ | ✓ | ✓ | |||||||||||||
| [50] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||
| [61] | ✓ | ✓ | ✓ | ✓ | |||||||||||||
| [33] | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||
| [79] | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||
| [63] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||
| [91] | ✓ | ✓ | |||||||||||||||
| [59] | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||
| [57] | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||
| [113] | ✓ | ✓ | ✓ | ✓ | |||||||||||||
| [130] | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||
| [62] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||
| [101] | ✓ | ||||||||||||||||
| [77] | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||
| [131] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||
| [132] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||
| [133] | ✓ | ✓ | ✓ | ✓ | |||||||||||||
| [134] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||
| [58] | ✓ | ✓ | ✓ | ✓ | |||||||||||||
| [78] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||
| [74] | ✓ | ✓ | ✓ | ||||||||||||||
| [80] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||
| [135] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||
| [66] | ✓ | ✓ | |||||||||||||||
| [110] | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||
| [114] | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||
| [99] | ✓ | ✓ | ✓ | ||||||||||||||
| [67] | ✓ | ✓ | ✓ | ✓ | |||||||||||||
| [124] | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||
| [136] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||
| [137] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||
| [138] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||
| [139] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||
| [140] | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||
| [141] | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||||
| Ref. # | DG Variables | SCB Variables | Position of Network Switches | Voltage Regulator | TCSC Firing Angle & Location | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Size | Location | Quantity | Type | pfDG | Size | Location | Quantity | Tap Position | Location | |||
| [115] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [102] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [103] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [76] | ✓ | ✓ | ||||||||||
| [65] | ✓ | |||||||||||
| [93] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [94] | ✓ | ✓ | ||||||||||
| [53] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [68] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [123] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [126] | ✓ | ✓ | ||||||||||
| [127] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [117] | ✓ | ✓ | ||||||||||
| [75] | ||||||||||||
| [96] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [55] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [100] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [60] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [56] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [81] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [105] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [128] | ||||||||||||
| [69] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [108] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [106] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [129] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [64] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [35] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [52] | ✓ | |||||||||||
| [97] | ✓ | ✓ | ||||||||||
| [83] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [31] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [51] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [30] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [70] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [71] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [72] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [88] | ✓ | ✓ | ✓ | |||||||||
| [87] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [98] | ✓ | ✓ | ||||||||||
| [34] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [95] | ✓ | ✓ | ||||||||||
| [89] | ✓ | ✓ | ||||||||||
| [84] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [111] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [112] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [73] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [54] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||
| [122] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [104] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [125] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [29] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [86] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [82] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [32] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [85] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [50] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [61] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||
| [33] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [79] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [63] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [91] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [59] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [57] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [113] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [130] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [62] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [101] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [77] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [131] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [132] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [133] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [134] | ✓ | ✓ | ||||||||||
| [58] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [78] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [74] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [80] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [135] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [66] | ✓ | ✓ | ||||||||||
| [110] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [114] | ✓ | ✓ | ||||||||||
| [99] | ✓ | ✓ | ||||||||||
| [67] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [124] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [136] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [137] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [138] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [139] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [140] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [141] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| Ref. # | Ignored Active Power Loss Minimization | Ignored Reactive Power Loss Minimization | Ignored Voltage Profile Improvement | Assumed Fixed Size and/or Location for Dg Units | Assumed Fixed Size and/or Location for Scb Units | Ignored Reactive Power Injection from Dgs | Constraint | Assumed Scb as a Continuous Power Source | Proposed Technique Involve More Steps or Tunable Parameters | Worked Only on the Grid-Connected Operation | Evaluated the Network Performance at Fixed Load | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [115] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [102] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [103] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [76] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [65] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||
| [93] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||
| [94] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [53] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||
| [68] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [123] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [126] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [127] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [117] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [75] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||
| [96] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [55] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [100] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [60] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [56] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [81] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [105] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [128] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [69] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [108] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [106] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [129] | ✓ | ✓ | ✓ | |||||||||
| [64] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [35] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [52] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [97] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [83] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [31] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [51] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [30] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [70] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [71] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [72] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [88] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||
| [87] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [98] | ✓ | ✓ | ✓ | |||||||||
| [34] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [95] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [89] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [84] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [111] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [112] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [73] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [54] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [122] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [104] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [125] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [29] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [86] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [82] | ✓ | ✓ | ✓ | |||||||||
| [32] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [85] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [50] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [61] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [33] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [79] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [63] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [91] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [59] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [57] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [113] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [130] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [62] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [101] | ✓ | ✓ | ✓ | |||||||||
| [77] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [131] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [132] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [133] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||
| [134] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [58] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [78] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [74] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [80] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [135] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [66] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [110] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [114] | ✓ | ✓ | ✓ | |||||||||
| [99] | ✓ | ✓ | ✓ | |||||||||
| [67] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [124] | ✓ | ✓ | ✓ | ✓ | ||||||||
| [136] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [137] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [138] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [139] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [140] | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [141] | ✓ | ✓ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leghari, Z.H.; Kumar, M.; Shaikh, P.H.; Kumar, L.; Tran, Q.T. A Critical Review of Optimization Strategies for Simultaneous Integration of Distributed Generation and Capacitor Banks in Power Distribution Networks. Energies 2022, 15, 8258. https://doi.org/10.3390/en15218258
Leghari ZH, Kumar M, Shaikh PH, Kumar L, Tran QT. A Critical Review of Optimization Strategies for Simultaneous Integration of Distributed Generation and Capacitor Banks in Power Distribution Networks. Energies. 2022; 15(21):8258. https://doi.org/10.3390/en15218258
Chicago/Turabian StyleLeghari, Zohaib Hussain, Mahesh Kumar, Pervez Hameed Shaikh, Laveet Kumar, and Quynh T. Tran. 2022. "A Critical Review of Optimization Strategies for Simultaneous Integration of Distributed Generation and Capacitor Banks in Power Distribution Networks" Energies 15, no. 21: 8258. https://doi.org/10.3390/en15218258
APA StyleLeghari, Z. H., Kumar, M., Shaikh, P. H., Kumar, L., & Tran, Q. T. (2022). A Critical Review of Optimization Strategies for Simultaneous Integration of Distributed Generation and Capacitor Banks in Power Distribution Networks. Energies, 15(21), 8258. https://doi.org/10.3390/en15218258