Creep Phenomenon in a Multiple-Input Single-Output Control System of a Piezoelectric Bimorph Actuator
Abstract
:1. Introduction
2. Research Methods
2.1. Research Object
2.2. Measurement System
3. Results
3.1. Program of Laboratory Experiments
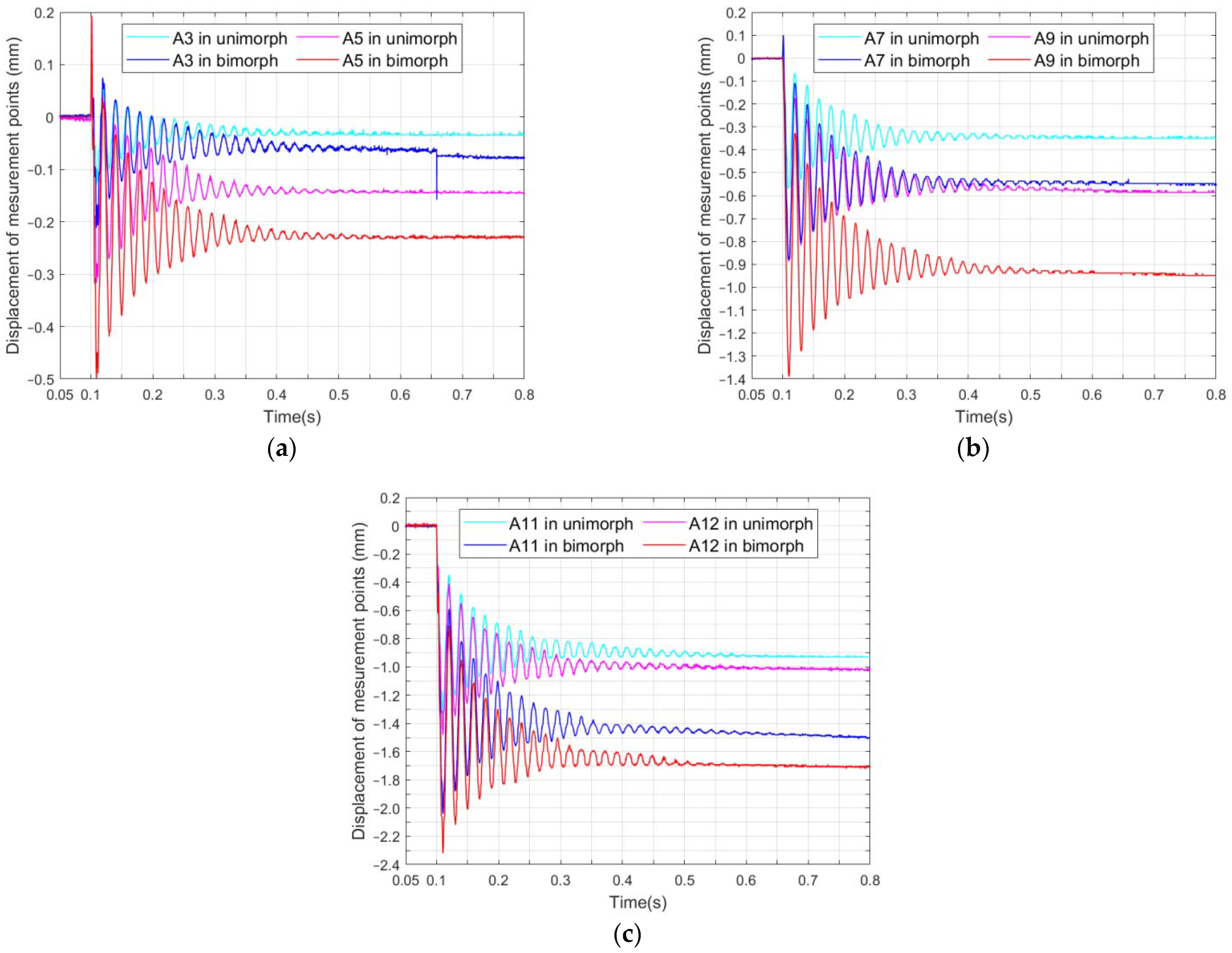
3.2. Transient Part of Actuator Step Response
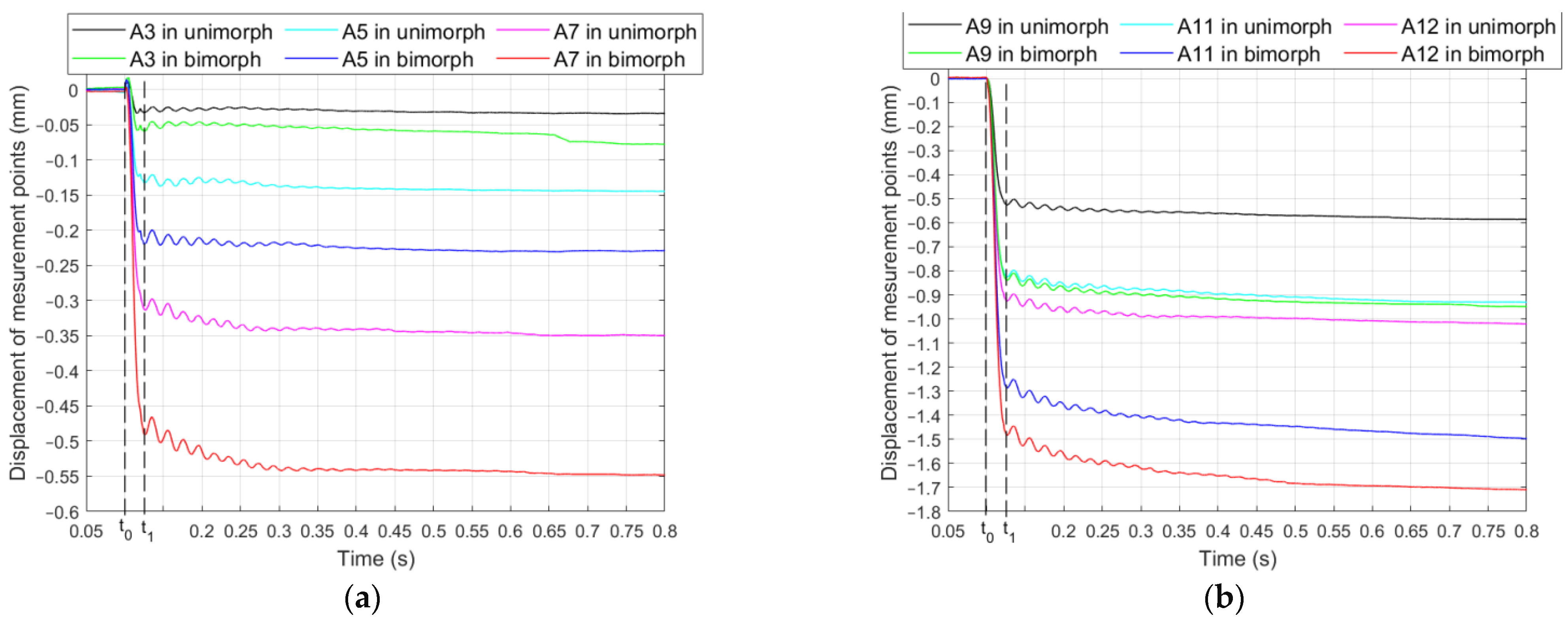
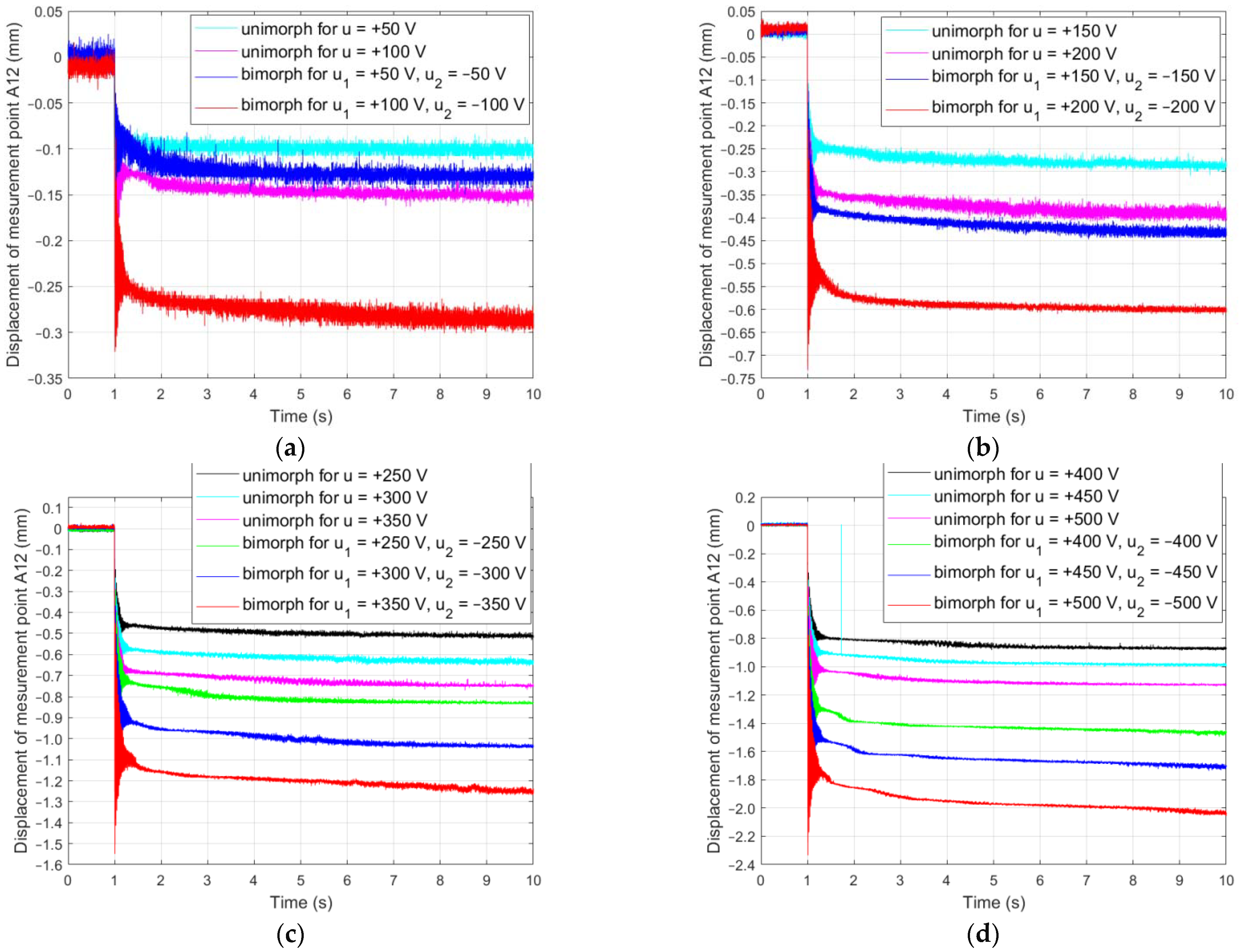
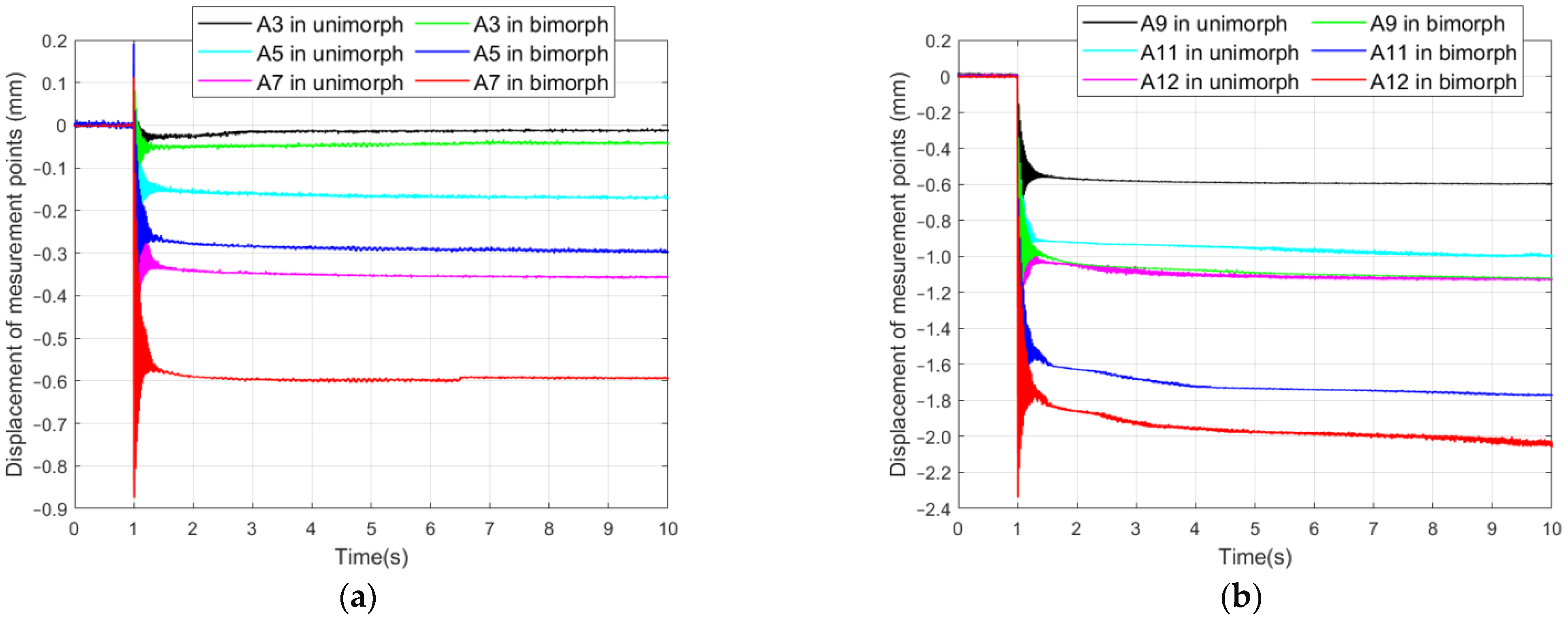
3.3. A Course of Creep Phenomenon
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mohith, S.; Upadhya, A.R.; Karanth, N.; Kulkarni, S.M.; Rao, M. Recent trends in piezoelectric actuators for precision motion and their applications: A review. Smart Mater. Struct. 2020, 30, 013002. [Google Scholar] [CrossRef]
- Yang, C.; Youcef-Toumi, K. Principle, implementation, and applications of charge control for piezo-actuated nanopositioners: A comprehensive review. Mech. Syst. Signal Process. 2022, 171, 108885. [Google Scholar] [CrossRef]
- Giri, A.M.; Ali, S.F.; Arockiarajan, A. Piezoelectric unimorph and bimorph cantilever configurations: Design guidelines and strain assessment. Smart Mater. Struct. 2022, 31, 035003. [Google Scholar] [CrossRef]
- Ramegowda, P.C.; Ishihara, D.; Takata, R.; Niho, T.; Horie, T. Finite element analysis of a thin piezoelectric bimorph with a metal shim using solid direct-piezoelectric and shell inverse-piezoelectric coupling with pseudo direct-piezoelectric evaluation. Compos. Struct. 2020, 245, 112284. [Google Scholar] [CrossRef]
- El-Sayed, A.M.; Abo-Ismail, A.; El-Melegy, M.T.; Hamzaid, N.A.; Abu Osman, N.A. Development of a micro-gripper using piezoelectric bimorphs. Sensors 2013, 13, 5826–5840. [Google Scholar] [CrossRef] [Green Version]
- Tan, D.; Yavarow, P.; Erturk, A. Nonlinear elastodynamics of piezoelectric macro-fiber composites with interdigitated electrodes for resonant actuation. Compos. Struct. 2018, 187, 137–143. [Google Scholar] [CrossRef]
- Chilibon, I.; Dias, C.; Inacio, P.; Marat-Mendes, J. PZT and PVDF bimorph actuators. J. Optoelectron. Adv. Mater. 2007, 9, 1939–1943. [Google Scholar]
- Donoso, A.; Sigmund, O. Optimization of piezoelectric bimorph actuators with active damping for static and dynamic loads. Struct. Multidiscip. Optim. 2009, 38, 171–183. [Google Scholar] [CrossRef] [Green Version]
- Hu, K.M.; Li, H.; Wen, L.H. Experimental study of axial-compressed macro-fiber composite bimorph with multi-layer parallel actuators for large deformation actuation. J. Intell. Mater. Syst. Struct. 2020, 31, 1101–1110. [Google Scholar] [CrossRef]
- Chattaraj, N.; Ganguli, R. Performance improvement of a piezoelectric bimorph actuator by tailoring geometry. Mech. Adv. Mater. Struct. 2018, 25, 829–835. [Google Scholar] [CrossRef]
- Low, T.S.; Guo, W. Modeling of a three-layer piezoelectric bimorph beam with hysteresis. J. Microelectromech. Syst. 1995, 4, 230–237. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, Y.; Lou, J.; Wei, Y.; Fu, L. Development and hybrid position/force control of a dual-drive macro-fiber-composite microgripper. Sensors 2018, 18, 1301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karpelson, M.; Wei, G.Y.; Wood, R.J. Driving high voltage piezoelectric actuators in microrobotic applications. Sens. Actuators A Phys. 2012, 176, 78–89. [Google Scholar] [CrossRef]
- Jain, R.K.; Majumder, S.; Ghosh, B.; Saha, S. Deflection control for piezoelectric actuator through voltage signal and it’s application in micromanipulation. Mech. Syst. Signal Process. 2015, 62, 305–323. [Google Scholar] [CrossRef]
- Rios, S.A.; Fleming, A.J. A new electrical configuration for improving the range of piezoelectric bimorph benders. Sens. Actuators A Phys. 2015, 224, 106–110. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, Y.; Chen, C. Micro converter with a high step-up ratio to drive a piezoelectric bimorph actuator applied in mobile robots. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418763458. [Google Scholar] [CrossRef] [Green Version]
- Cen, L.; Erturk, A. Bio-inspired aquatic robotics by untethered piezohydroelastic actuation. Bioinspiration Biomim. 2013, 8, 016006. [Google Scholar] [CrossRef] [Green Version]
- Grzybek, D. Control System for Multi-Input and Simple-Output Piezoelectric Beam Actuator Based on Macro Fiber Composite. Energies 2022, 15, 2042. [Google Scholar] [CrossRef]
- Grzybek, D. LQG Control of the Smart Truss with the Piezoelectric Active Members. In Solid State Phenomena; Kot, A., Ed.; Trans Tech Publications Ltd.: Zurich, Switzerland, 2014; Volume 208, pp. 125–133. [Google Scholar]
- Rakotondrabe, M.; Haddab, Y.; Lutz, P. Nonlinear modeling and estimation of force in a piezoelectric cantilever. In Proceedings of the 2007 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Zurich, Switzerland, 4–7 September 2007; pp. 1–6. [Google Scholar]
- Jung, H.; Gweon, D.G. Creep characteristics of piezoelectric actuators. Rev. Sci. Instrum. 2000, 71, 1896–1900. [Google Scholar] [CrossRef] [Green Version]
- Changhai, R.; Lining, S. Hysteresis and creep compensation for piezoelectric actuator in open-loop operation. Sens. Actuators A Phys. 2005, 122, 124–130. [Google Scholar] [CrossRef]
- Qiu, J.; Tani, J.; Ueno, T.; Morita, T.; Takahashi, H.; Du, H. Fabrication and high durability of functionally graded piezoelectric bending actuators. Smart Mater. Struct. 2003, 12, 115. [Google Scholar] [CrossRef]
- Gu, G.Y.; Zhu, L.M.; Su, C.Y.; Ding, H.; Fatikow, S. Modeling and control of piezo-actuated nanopositioning stages: A survey. IEEE Trans. Autom. Sci. Eng. 2014, 13, 313–332. [Google Scholar] [CrossRef]
- Yong, Y.K.; Moheimani, S.R.; Kenton, B.J.; Leang, K.K. Invited review article: High-speed flexure-guided nanopositioning: Mechanical design and control issues. Rev. Sci. Instrum. 2012, 83, 121101. [Google Scholar] [CrossRef] [PubMed]
- Sabarianand, D.V.; Karthikeyan, P.; Muthuramalingam, T. A review on control strategies for compensation of hysteresis and creep on piezoelectric actuators based micro systems. Mech. Syst. Signal Process. 2020, 140, 106634. [Google Scholar] [CrossRef]
- Liu, Y.; Shan, J.; Qi, N. Creep modeling and identification for piezoelectric actuators based on fractional-order system. Mechatronics 2013, 23, 840–847. [Google Scholar] [CrossRef]
- Schröck, J.; Meurer, T.; Kugi, A. Control of a flexible beam actuated by macro-fiber composite patches: II. Hysteresis and creep compensation, experimental results. Smart Mater. Struct. 2010, 20, 015016. [Google Scholar] [CrossRef]
- Escareno, J.; Abadie, J.; Piat, E.; Rakotondrabe, M. Robust micro-positionnig control of a 2DOF piezocantilever based on an extended-state LKF. Mechatronics 2019, 58, 82–92. [Google Scholar] [CrossRef] [Green Version]
- Smart Material—Home of the MFC. Available online: https://www.smart-material.com/MFC-product-mainV2.html (accessed on 25 September 2022).
- Zhang, S.Q.; Li, Y.X.; Schmidt, R. Modeling and simulation of macro-fiber composite layered smart structures. Compos. Struct. 2015, 126, 89–100. [Google Scholar] [CrossRef]
- TD250 V9 Six Channel +/−250 V Amplifier. Manual and Specifications. Available online: https://www.piezodrive.com/wp-content/uploads/2022/04/TD250-V9-R1.pdf (accessed on 26 September 2022).
- RT-DAC/Zynq User’s Manual. Available online: http://www.inteco.com.pl/Docs/Rtdac_Zynq.pdf (accessed on 26 September 2022).
- Sioma, A. Geometry and resolution in triangulation vision systems. In Proceedings of the Photonics Applications in Astronomy, Communications, Industry, and High Energy Physics Experiments 2020, Wilga, Poland, 31 August–2 September 2020; Romaniuk, R.S., Linczuk, M., Eds.; SPIE: Bellingham, WA, USA; Volume 11581, pp. 264–271. [Google Scholar]
- Romaszko, M.; Sapiński, B.; Sioma, A. Forced vibrations analysis of a cantilever beam using the vision method. J. Theor. Appl. Mech. 2015, 53, 243–254. [Google Scholar] [CrossRef]
- Wang, X.; Pommier-Budinger, V.; Reysset, A.; Gourinat, Y. Simultaneous compensation of hysteresis and creep in a single piezoelectric actuator by open-loop control for quasi-static space active optics applications. Control Eng. Pract. 2014, 33, 48–62. [Google Scholar] [CrossRef]

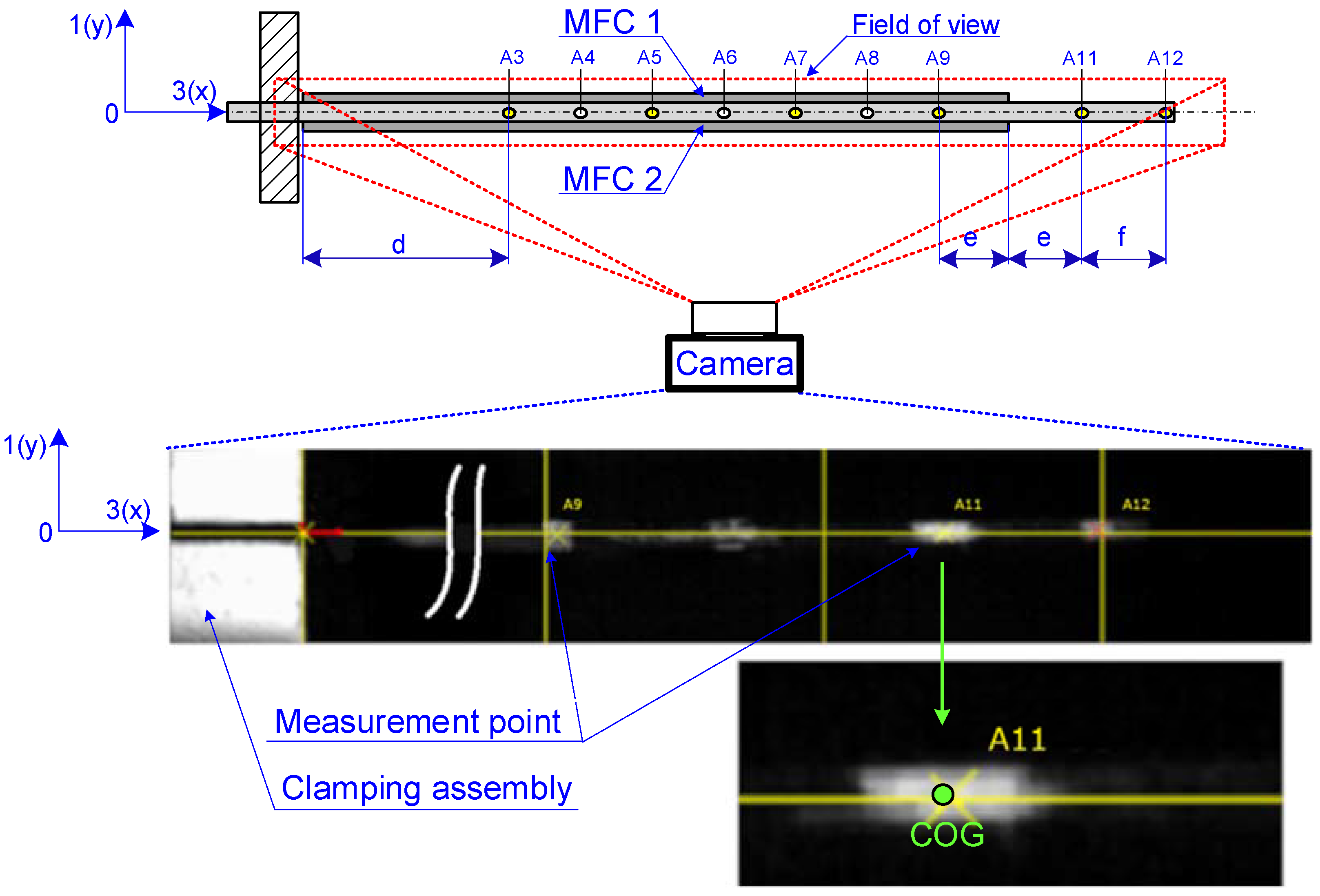
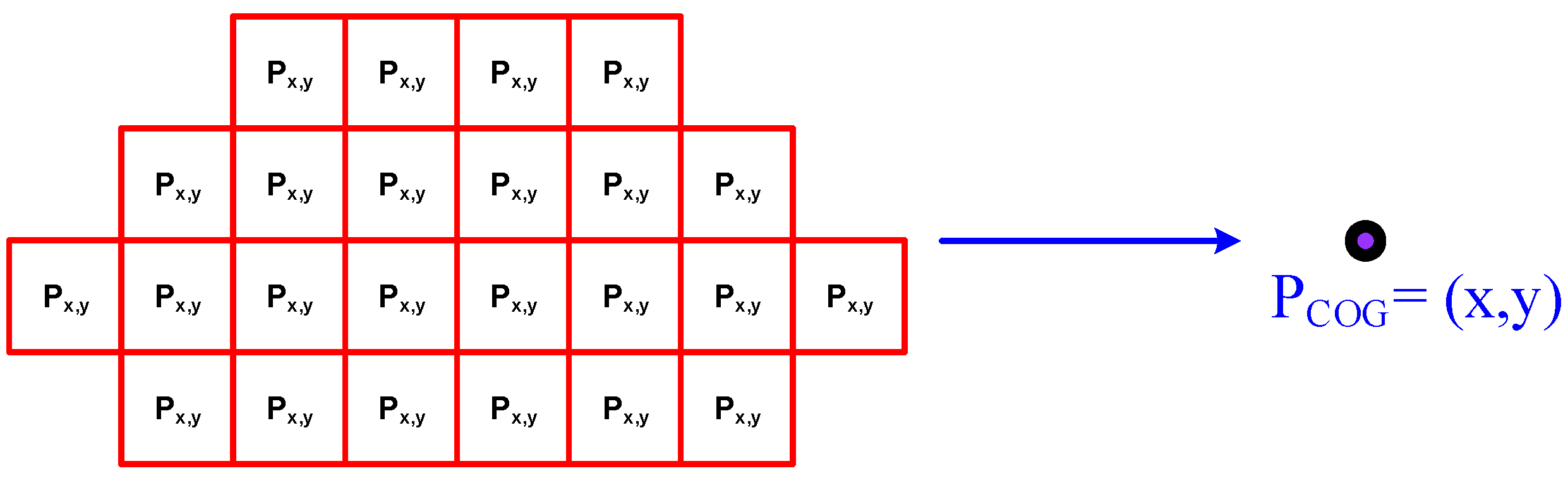
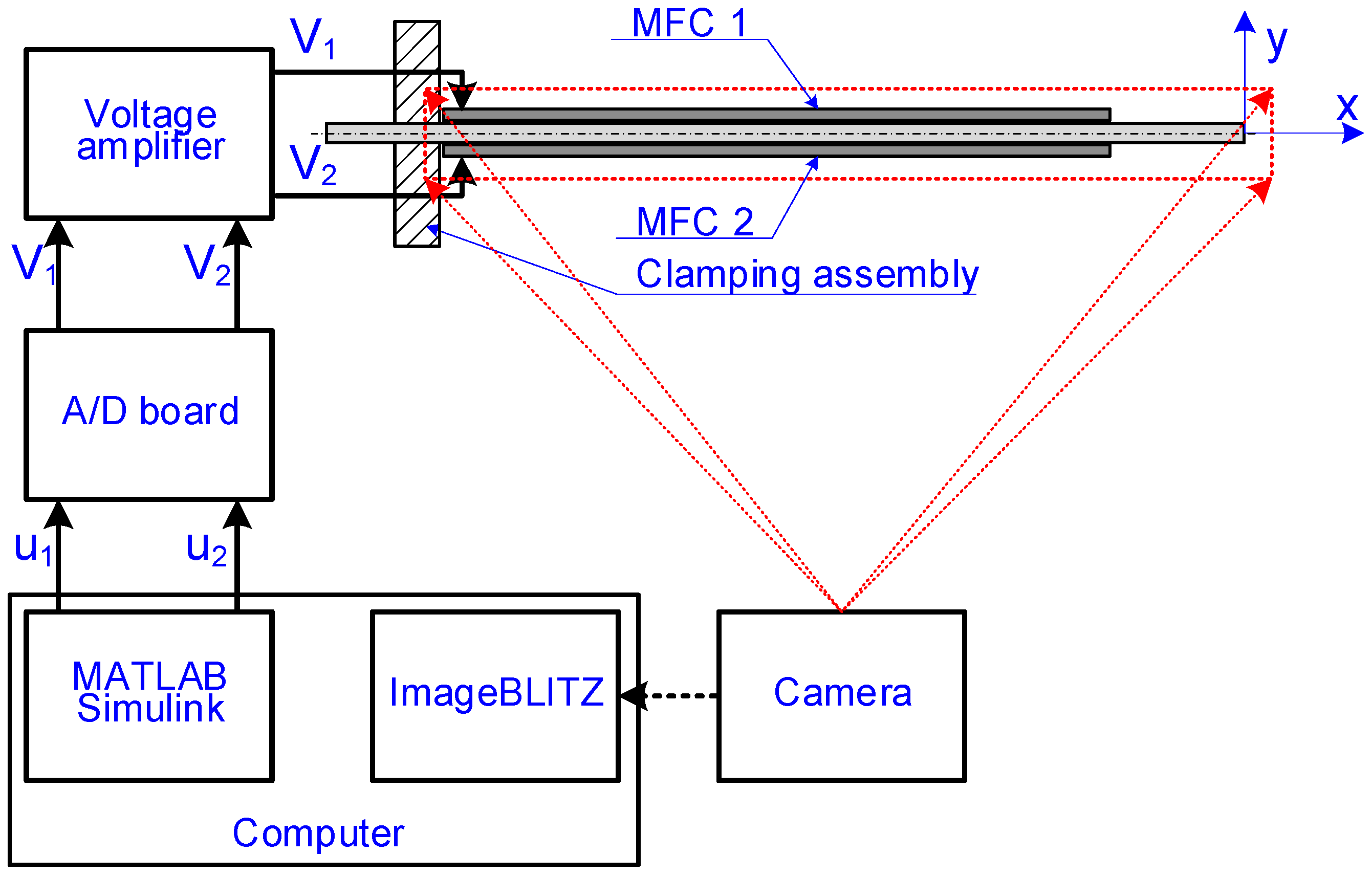


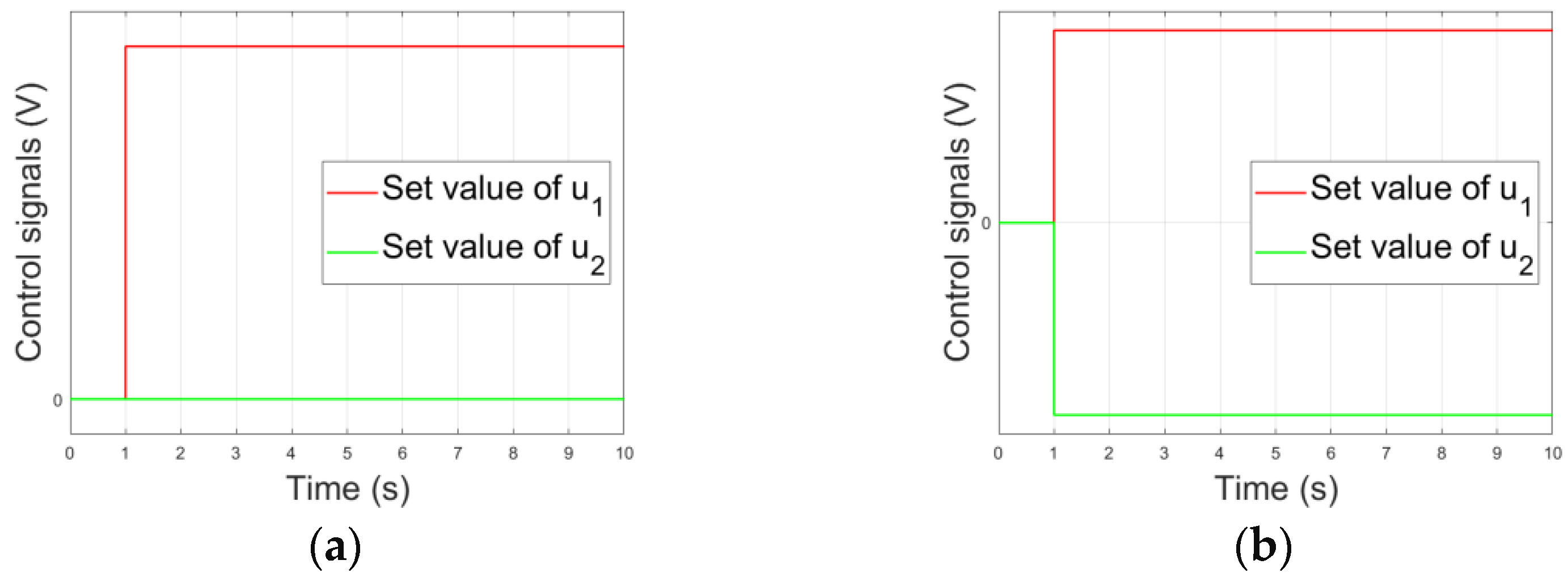
| Dimension | Value | Value | |
|---|---|---|---|
| Length of MFC patch | 100 | Width of FR-4 layer | 20 |
| Length of active area in MFC patch | 85 | Thickness of FR-4 layer | 1 |
| Width of MFC patch | 20 | Distance “a” | 2 |
| Width of active area in MFC patch | 14 | Distance “b” | 20 |
| Thickness of MFC patch | 0.3 | Distance “c” | 122 |
| Number of Experiment | ||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| Signal name | Symbol | Unit | Set values in experiment | |||||||||
| Control voltage of MFC 1 | V1 | V | +500 | +450 | +400 | +350 | +300 | +250 | +200 | +150 | +100 | +50 |
| Control voltage of MFC 2 | V2 | V | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Number of experiment | ||||||||||||
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |||
| Signal name | Symbol | Unit | Set values in experiment | |||||||||
| Control voltage of MFC 1 | V1 | V | +500 | +450 | +400 | +350 | +300 | +250 | +200 | +150 | +100 | +50 |
| Control voltage of MFC 2 | V2 | V | –500 | –450 | –400 | –350 | –300 | –250 | –200 | –150 | –100 | –50 |
| Number of Experiment | ||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Measurement point | Position change caused by a creep phenomenon (µm) | |||||||||
| A3 | 18 | – 17 | 23 | – 1 | 5 | 3 | – 23 | 2 | 1 | – 6 |
| A5 | – 22 | 1 | – 9 | – 15 | – 10 | – 6 | – 12 | – 10 | 2 | 1 |
| A7 | – 37 | 1 | – 24 | – 18 | 30 | 28 | – 6 | 41 | 6 | 2 |
| A9 | – 52 | – 30 | – 52 | – 14 | – 33 | – 33 | – 7 | 13 | 20 | 22 |
| A11 | – 97 | – 100 | – 89 | – 80 | – 64 | – 33 | – 11 | – 11 | – 16 | – 7 |
| A12 | – 111 | – 95 | – 87 | – 75 | – 66 | – 52 | – 41 | – 40 | – 23 | – 5 |
| Number of experiment | ||||||||||
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| Measurement point | Position change caused by a creep phenomenon (µm) | |||||||||
| A3 | 10 | 10 | – 1 | – 13 | 2 | – 2 | – 7 | 1 | 3 | – 1 |
| A5 | – 41 | – 34 | – 39 | – 12 | 15 | – 16 | – 2 | – 5 | – 1 | – 6 |
| A7 | – 41 | – 6 | – 82 | – 53 | – 49 | – 17 | 12 | – 5 | – 14 | 6 |
| A9 | – 156 | – 120 | – 96 | – 82 | – 59 | – 47 | – 36 | – 25 | 13 | 21 |
| A11 | – 251 | – 204 | – 166 | – 131 | – 89 | – 105 | – 46 | – 55 | – 63 | – 24 |
| A12 | – 304 | – 219 | – 183 | – 167 | – 139 | – 109 | – 77 | – 57 | – 42 | – 35 |
| Value of Control Voltage u in an Unimorph (V) | ||||||||||
| +500 | +450 | +400 | +350 | +300 | +250 | +200 | +150 | +100 | +50 | |
| Value of Control Voltage u1 in Bimorph (V) | ||||||||||
| +500 | +450 | +400 | +350 | +300 | +250 | +200 | +150 | +100 | +50 | |
| Value of Control Voltage u2 in Bimorph (V) | ||||||||||
| –500 | –450 | –400 | –350 | –300 | –250 | –200 | –150 | –100 | –50 | |
| Measurement Point | Point Displacement in a Bimorph/Point Displacement in an Unimorph (%) | |||||||||
| A3 | 144 | – 258 | 204 | 1300 | 160 | 266 | – 169 | 150 | – 300 | – 183 |
| A5 | 186 | 3600 | 433 | – 125 | – 350 | 267 | – 600 | -200 | 250 | 800 |
| A7 | 111 | 800 | 342 | 294 | 363 | 261 | – 400 | 212 | 433 | – 300 |
| A9 | 300 | 400 | 185 | 586 | 179 | 142 | 514 | 392 | 135 | 105 |
| A11 | 259 | 204 | 187 | 164 | 139 | 318 | 418 | 500 | 394 | 343 |
| A12 | 274 | 231 | 210 | 223 | 211 | 210 | 188 | 143 | 183 | 700 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grzybek, D.; Sioma, A. Creep Phenomenon in a Multiple-Input Single-Output Control System of a Piezoelectric Bimorph Actuator. Energies 2022, 15, 8267. https://doi.org/10.3390/en15218267
Grzybek D, Sioma A. Creep Phenomenon in a Multiple-Input Single-Output Control System of a Piezoelectric Bimorph Actuator. Energies. 2022; 15(21):8267. https://doi.org/10.3390/en15218267
Chicago/Turabian StyleGrzybek, Dariusz, and Andrzej Sioma. 2022. "Creep Phenomenon in a Multiple-Input Single-Output Control System of a Piezoelectric Bimorph Actuator" Energies 15, no. 21: 8267. https://doi.org/10.3390/en15218267
APA StyleGrzybek, D., & Sioma, A. (2022). Creep Phenomenon in a Multiple-Input Single-Output Control System of a Piezoelectric Bimorph Actuator. Energies, 15(21), 8267. https://doi.org/10.3390/en15218267







