Uses of Superconducting Magnetic Energy Storage Systems in Microgrids under Unbalanced Inductive Loads and Partial Shading Conditions
Abstract
1. Introduction
2. State of the Art
2.1. SMES
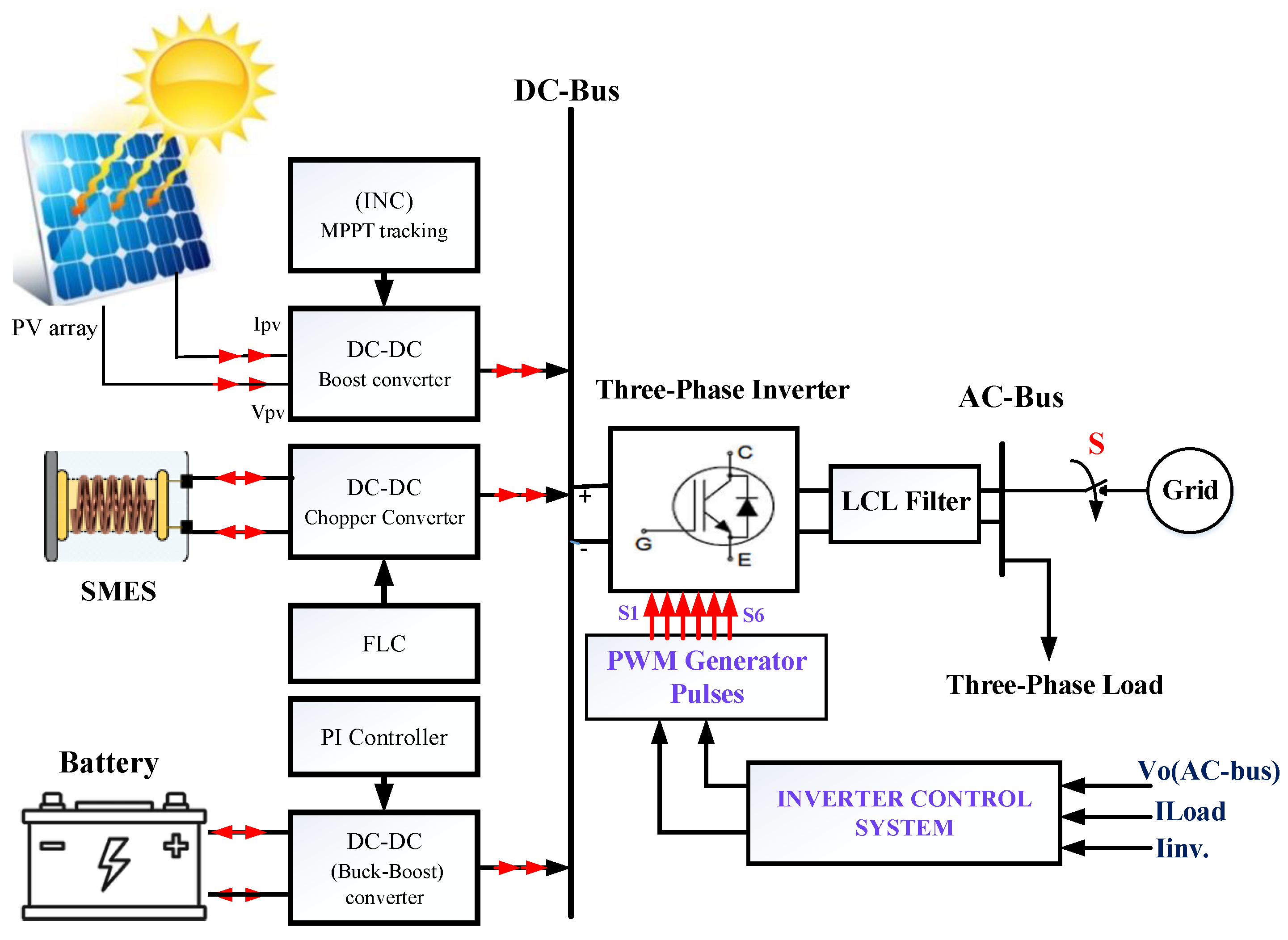
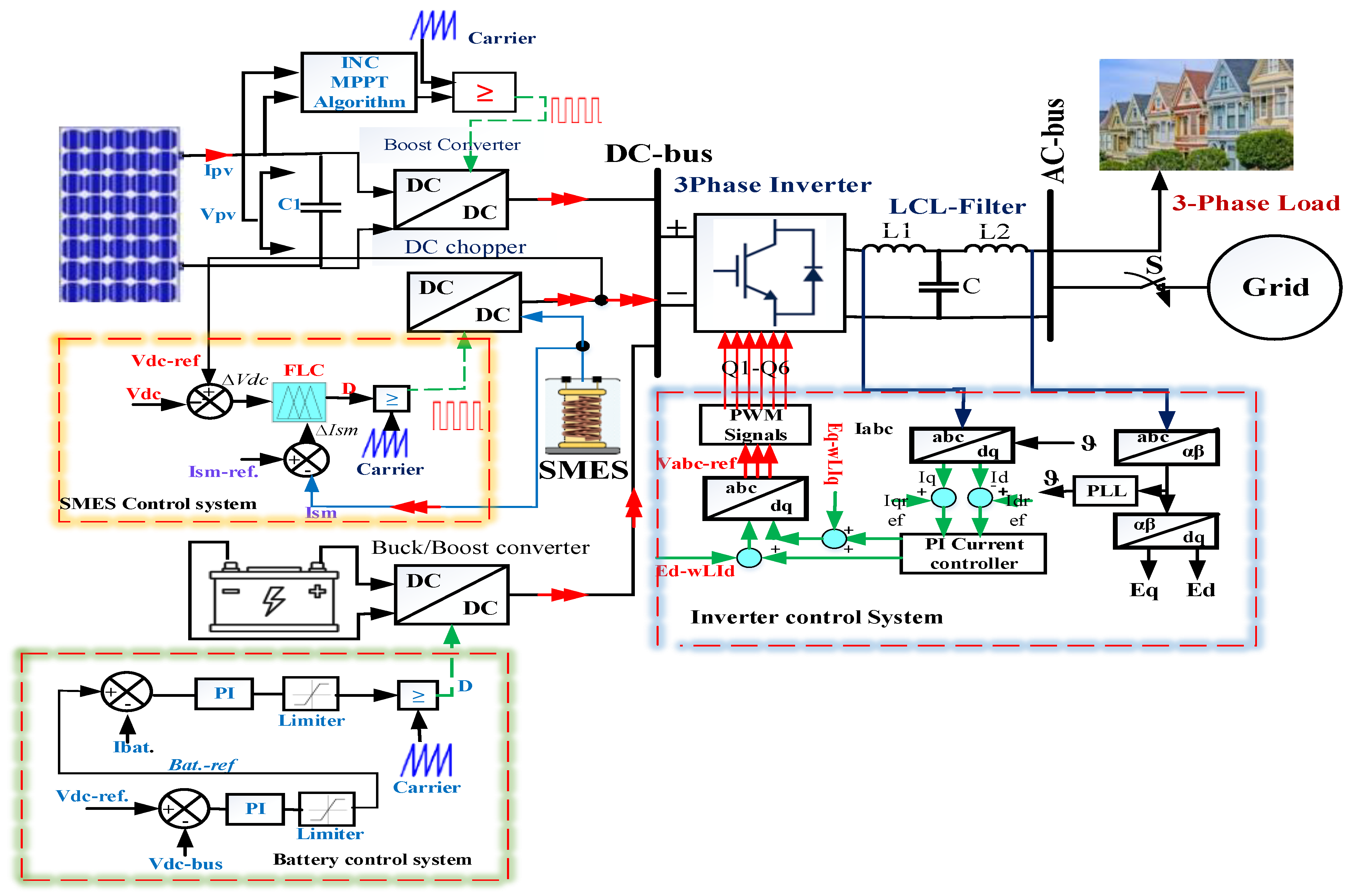
2.2. System Description and HESS Control Design
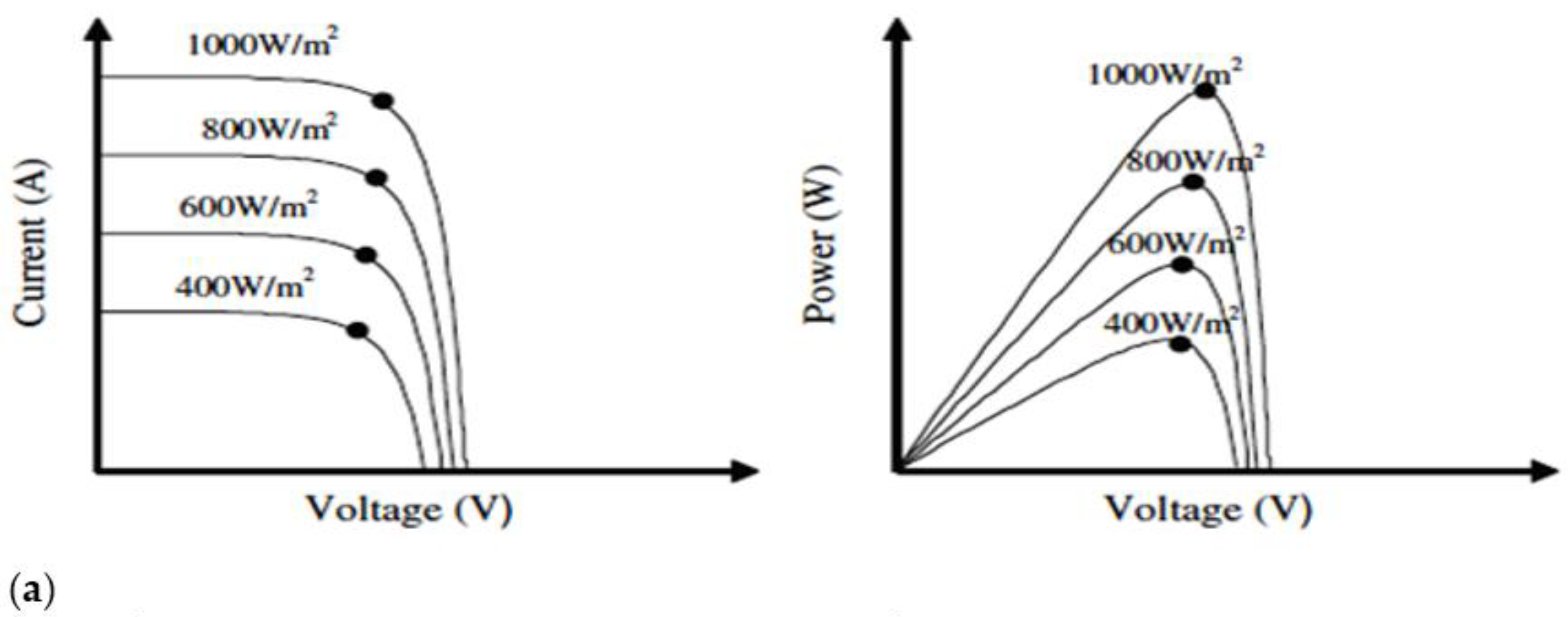
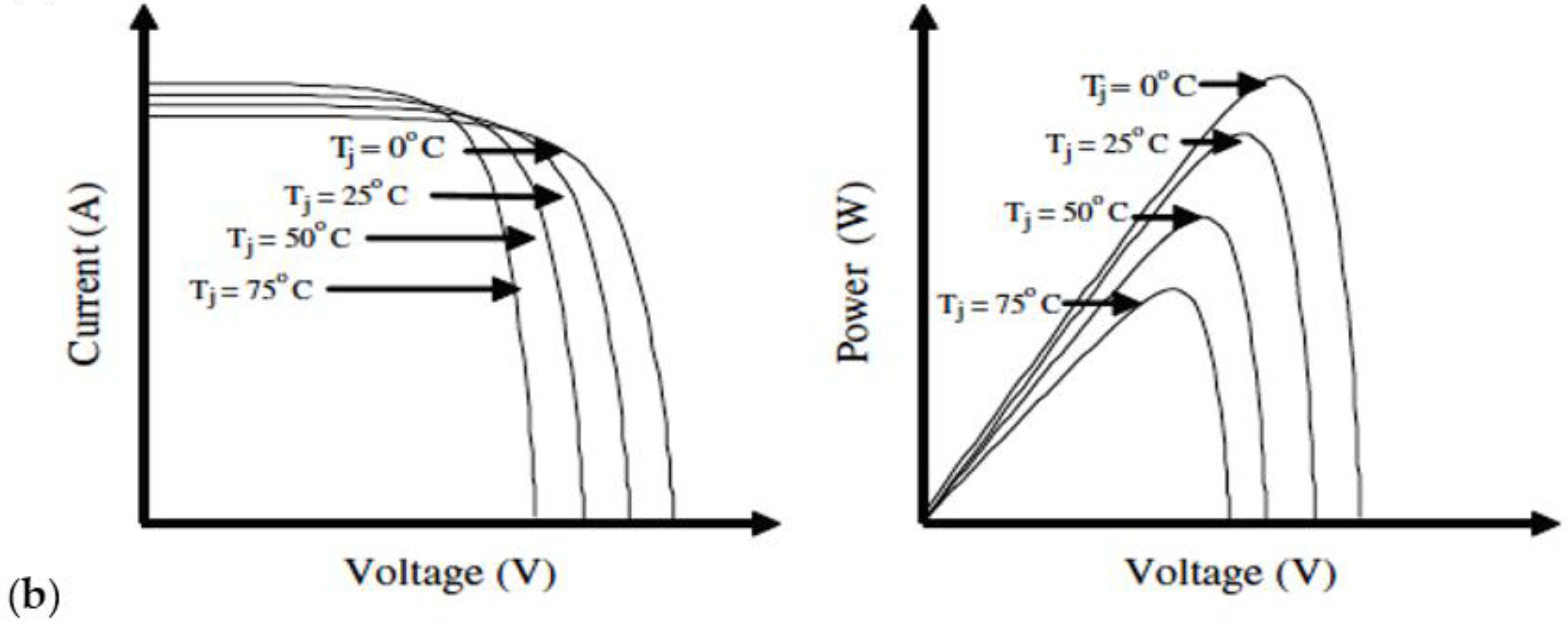
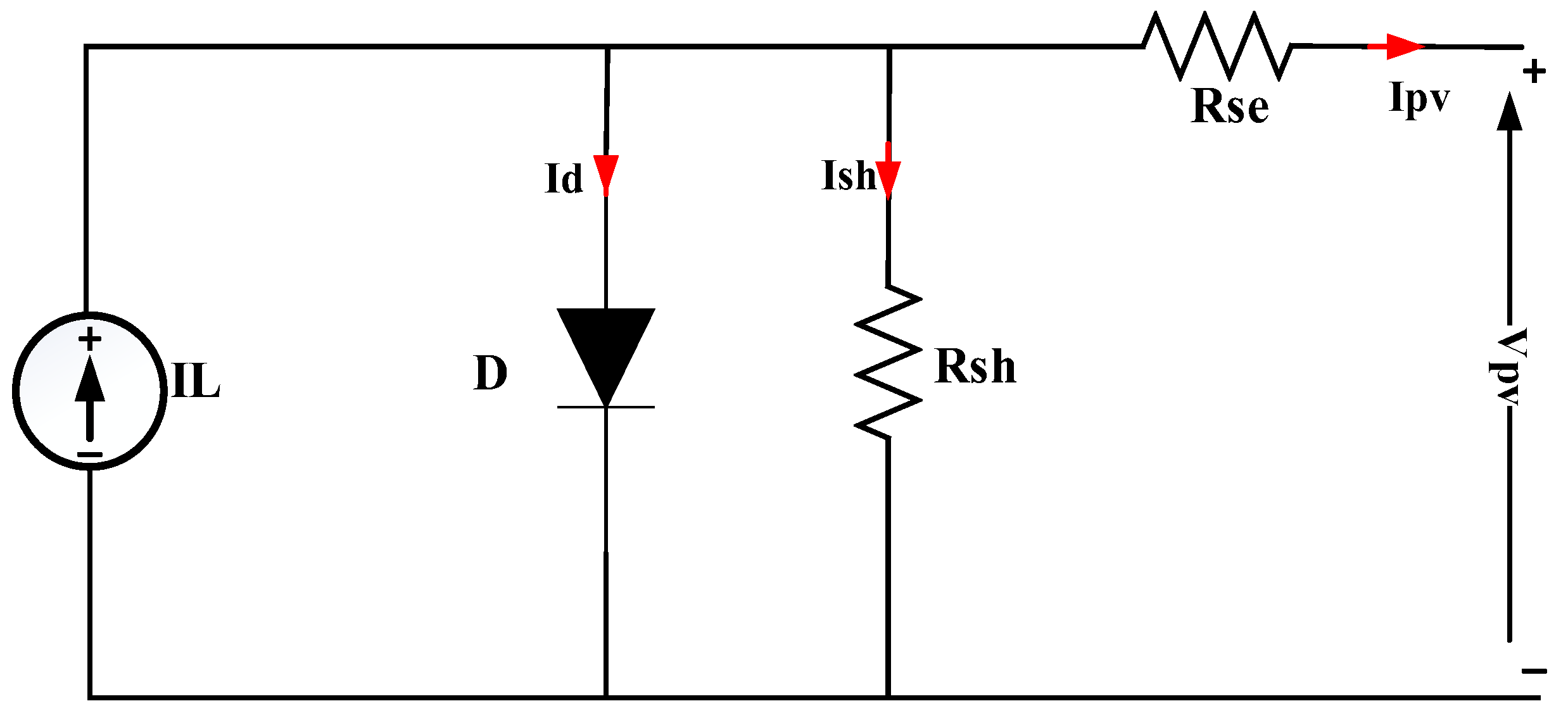
2.2.1. PV System
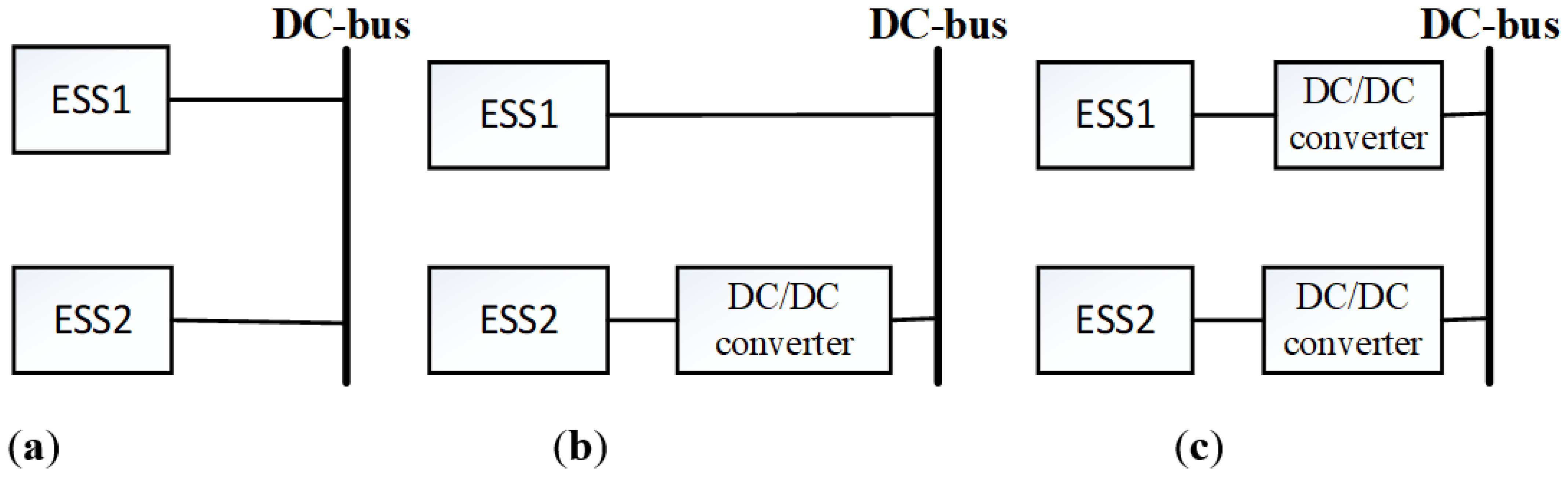
2.2.2. Hybrid Energy Storage Systems (HESS)
3. Proposed Control Techniques
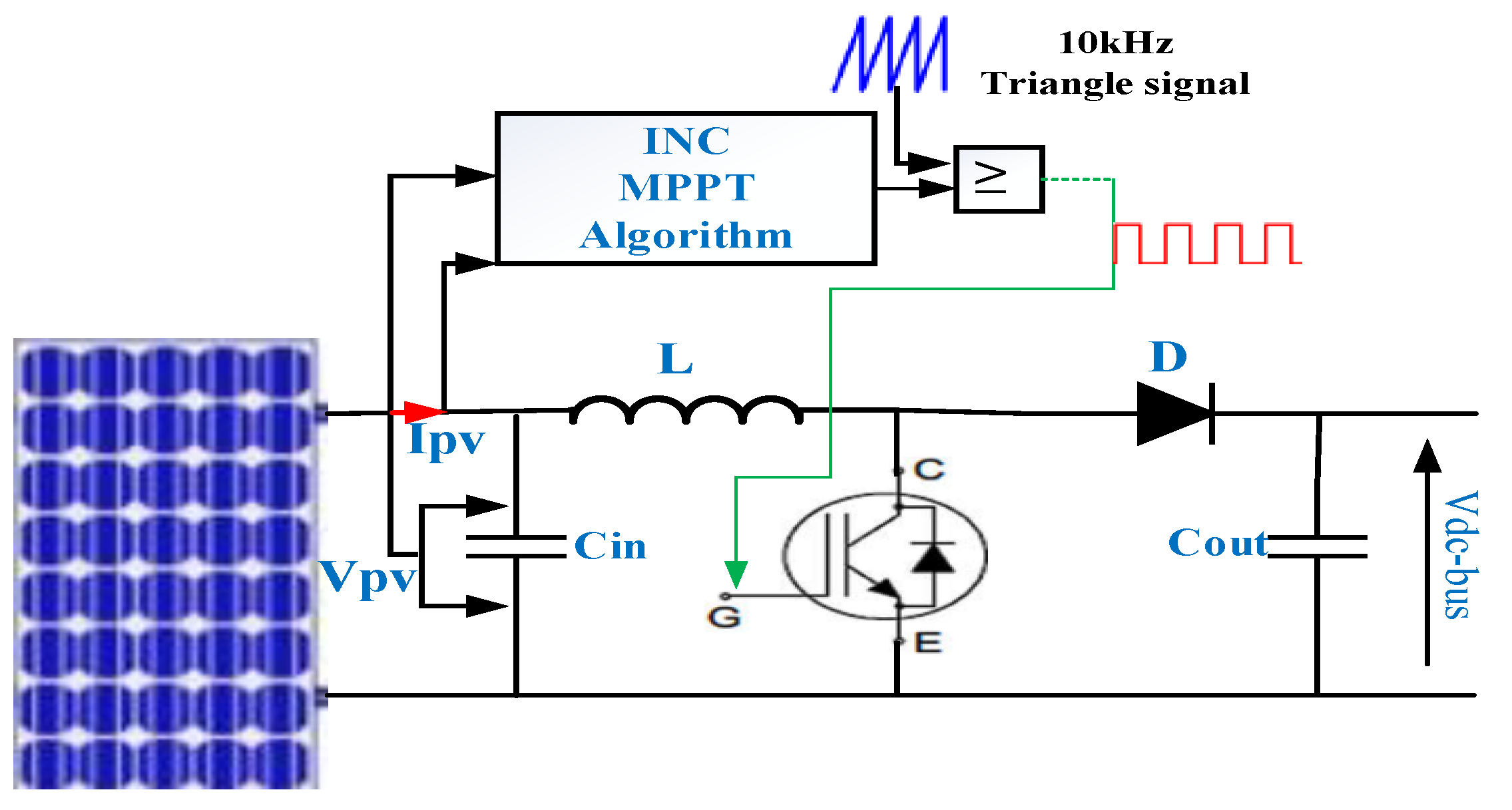
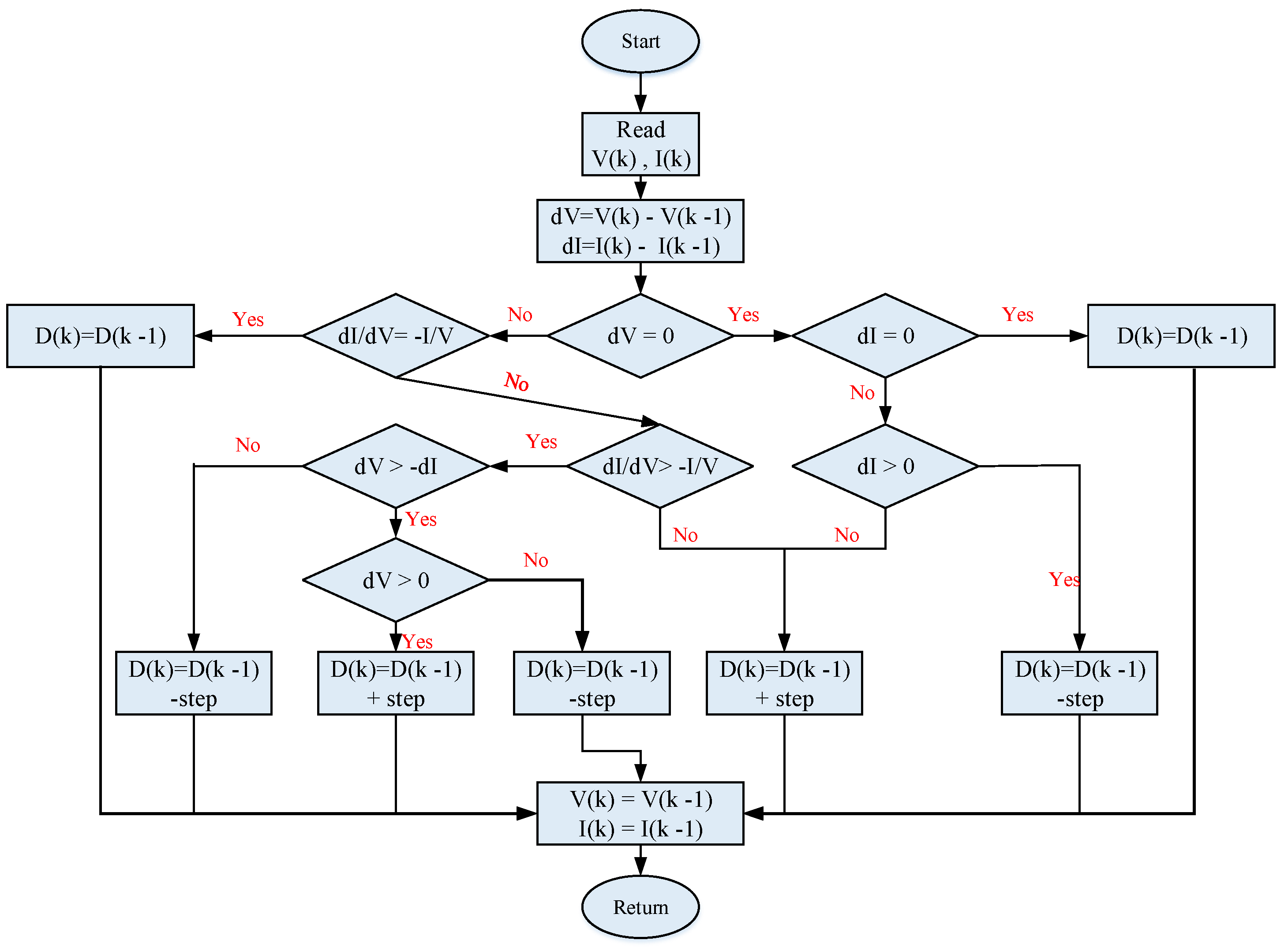
3.1. PV Boost/MPPT Control and Design
3.2. BESS Design and Control
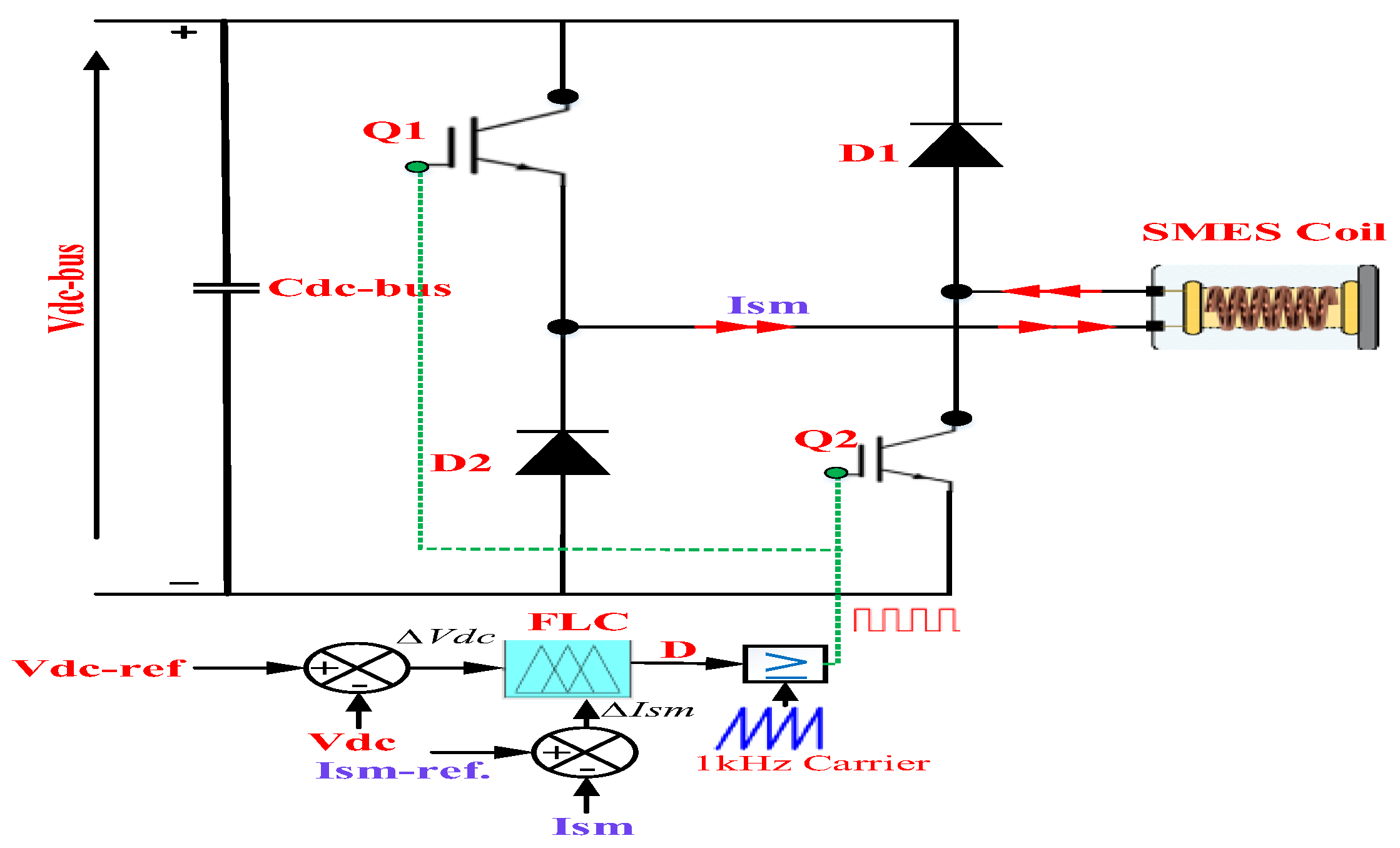
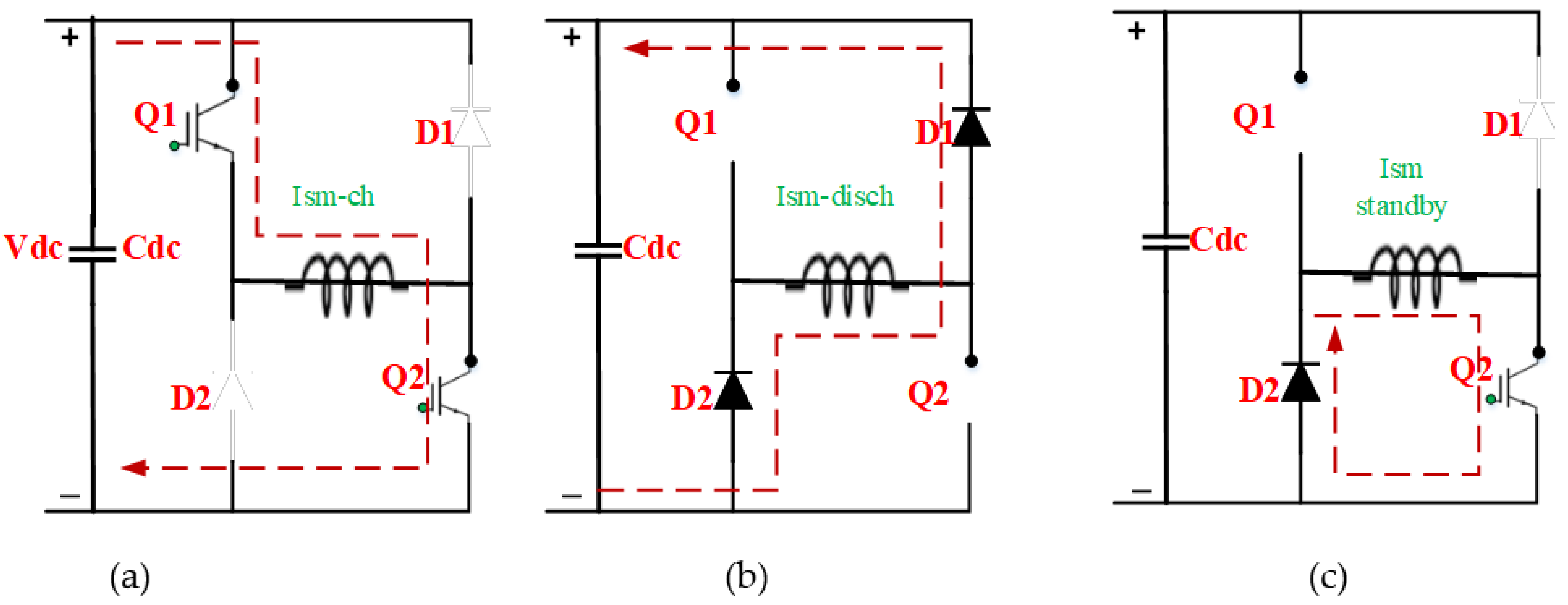
3.3. SMES System Design and Control
- (i)
- When the power characteristic Ppv = Pload, the desired VDC−bus in this case is equal to the Vdc reference, and the storage system is in standby mode, with no exchange of power; ∆Vdc in the control system equals zero and bus regulation is by only the PV system.
- (ii)
- When the error voltage becomes positive (high), this indicates that the VDC−bus is swelling, so the surplus power is absorbed from the SMES coil, the power characteristic is Ppv − Psm = Pload, and bus regulation is based on the SMES.
- (iii)
- When the error voltage becomes more positive (higher), the surplus power is absorbed from BESS in this case, and the power characteristic is Ppv − Pbat. = Pload, and bus regulation is based on the battery.
- (iv)
- When the error voltage becomes negative (low), this indicates that the VDC−bus is sagging (dropping), and the power characteristic is Ppv + Psm = Pload. In this case, the SMES coil injects power into the DC bus.
- (v)
- When the error voltage becomes more negative (lower), this indicates that the VDC−bus is dropping, and the power characteristic is Ppv + Pbat. = Pload. In this case, the battery injects power into the DC bus.
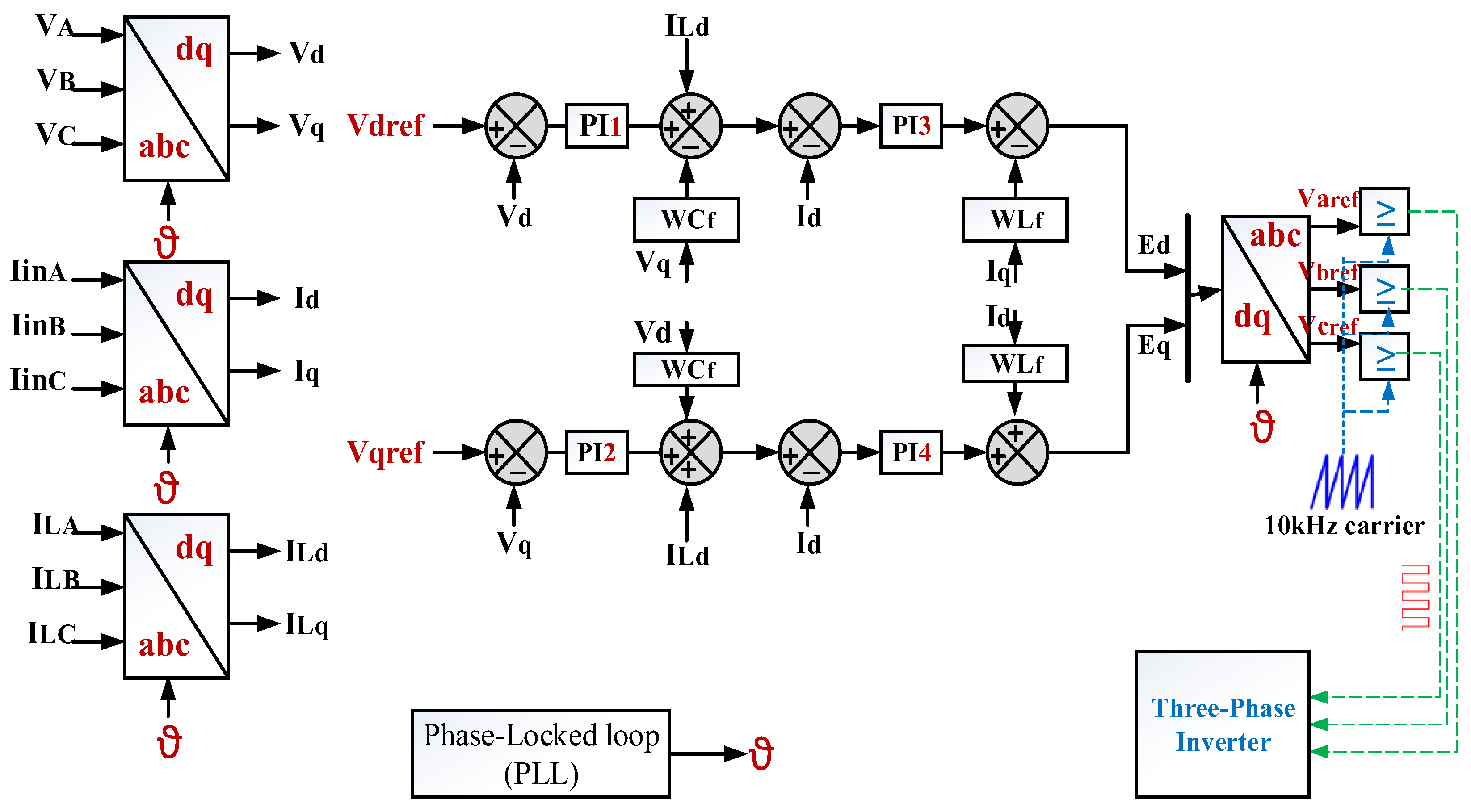
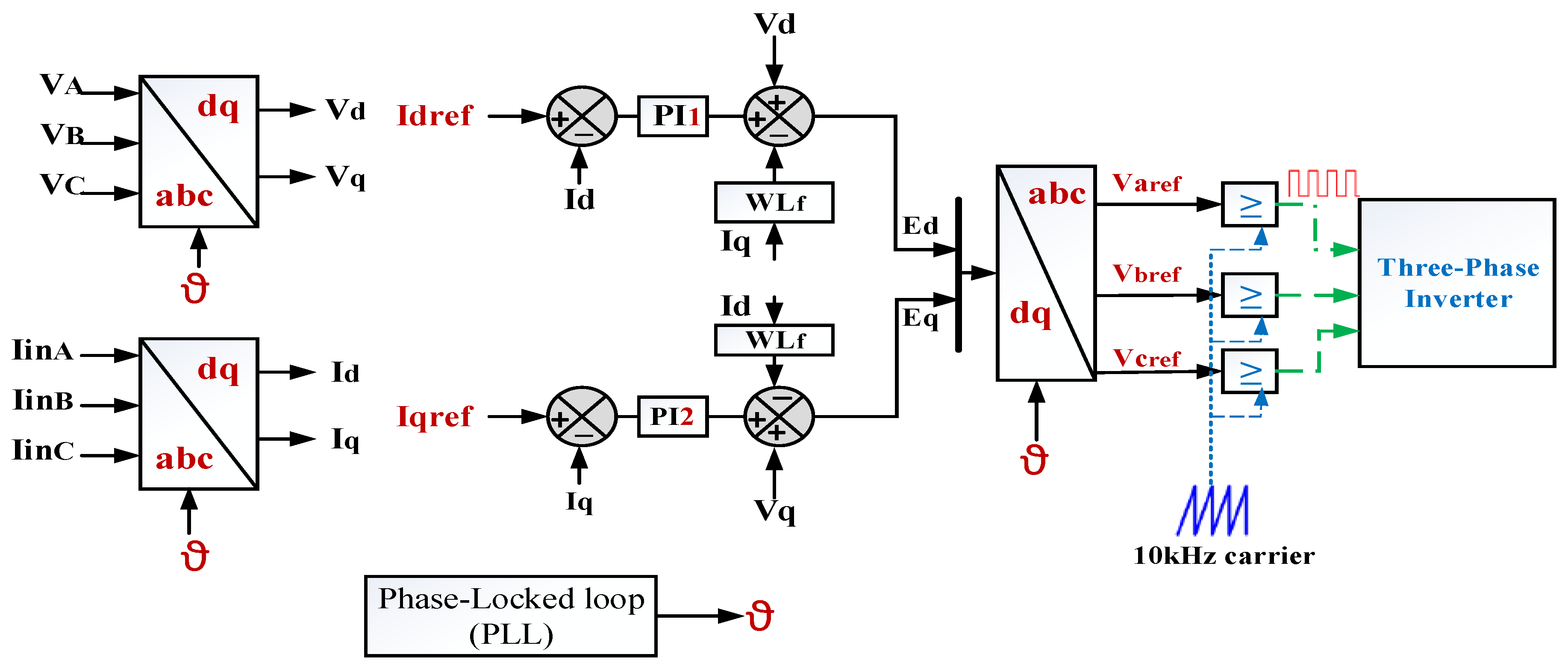
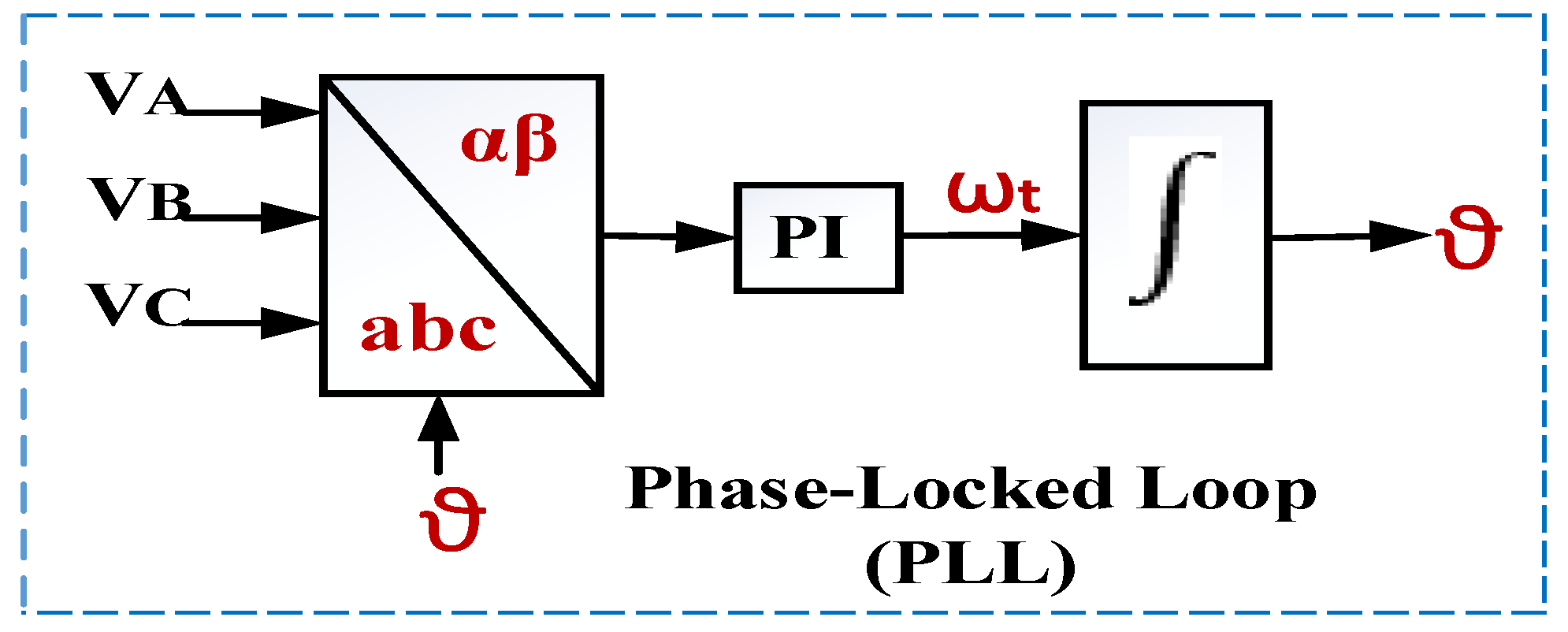
3.4. Inverter Control and LCL Filter Design
3.4.1. Inverter Control
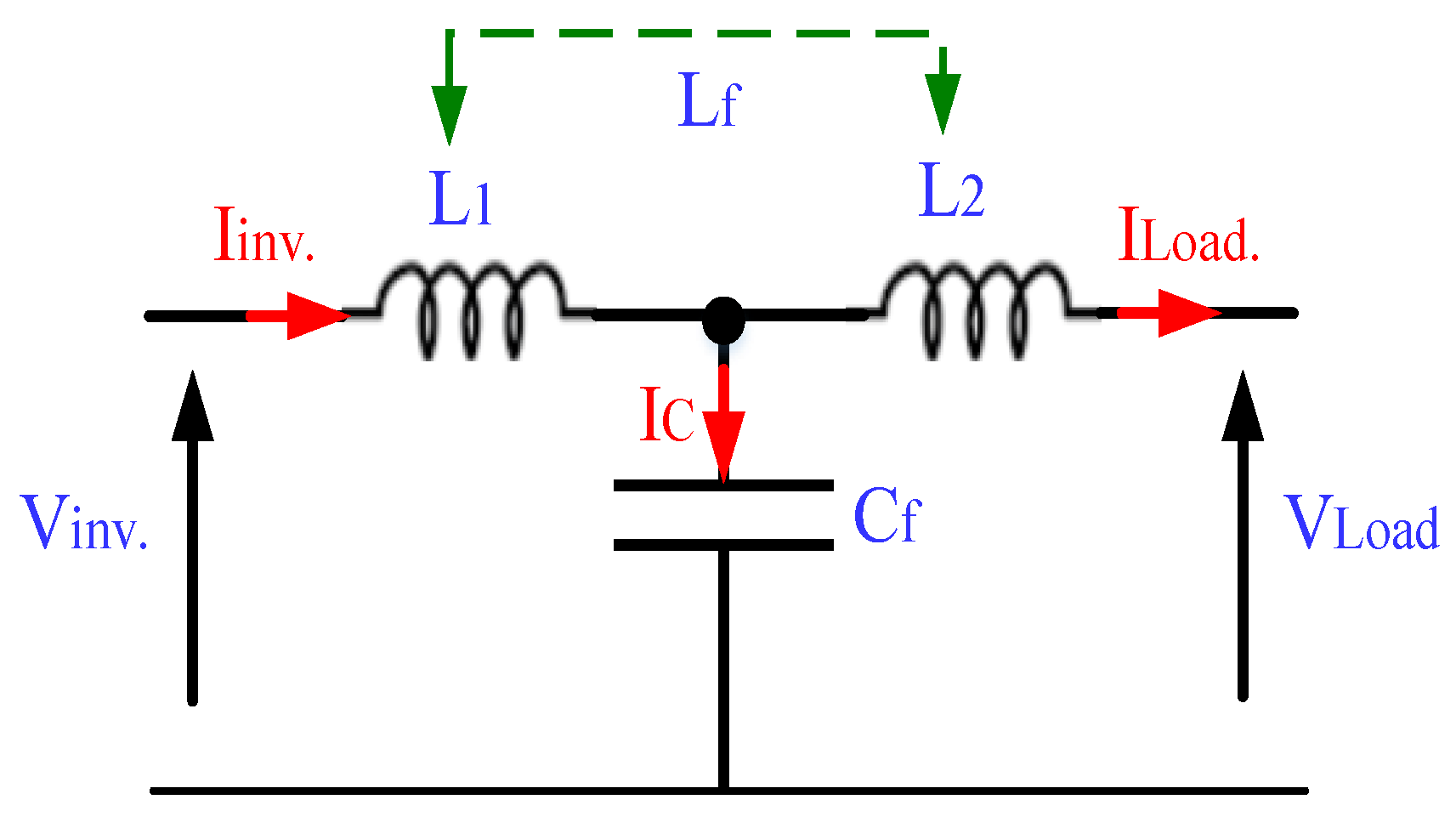
3.4.2. LCL Filter Design
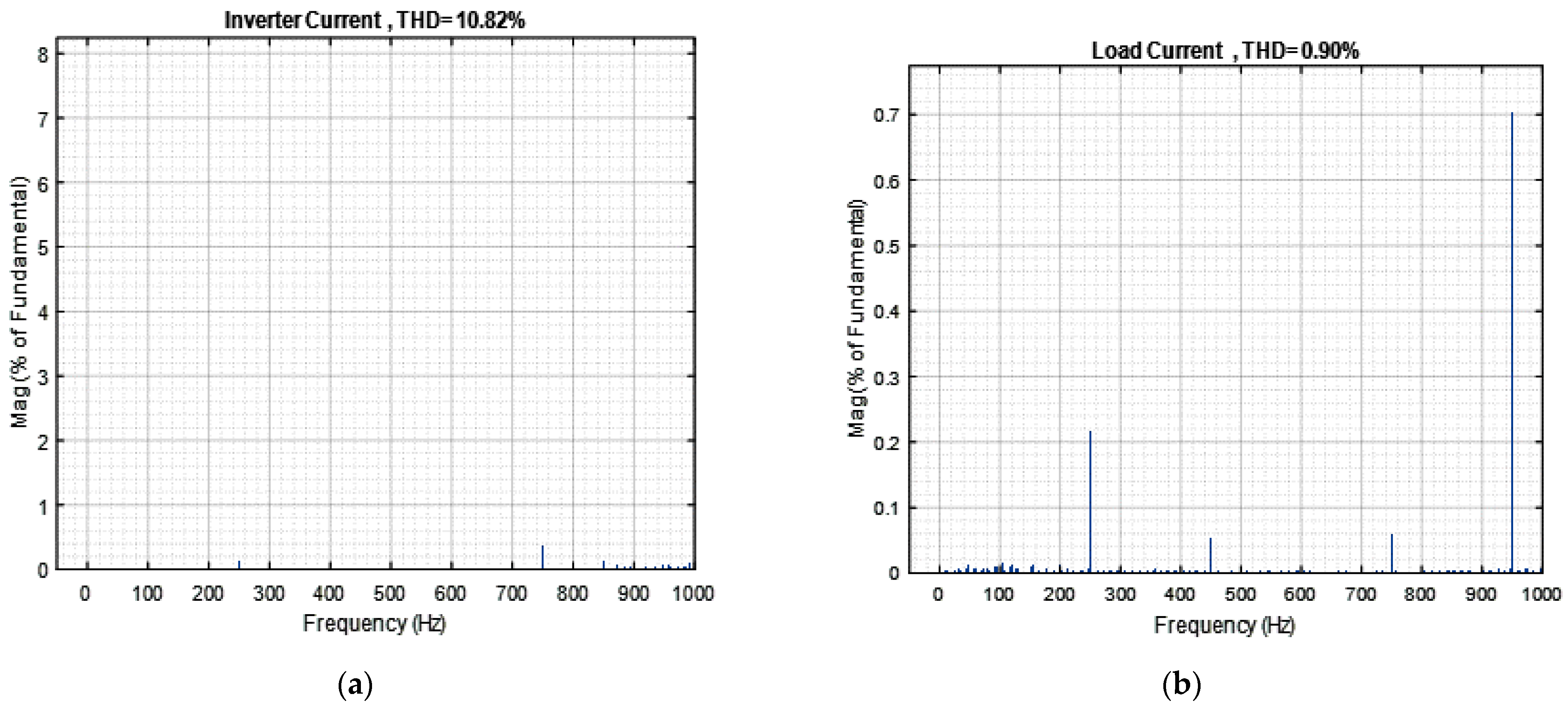
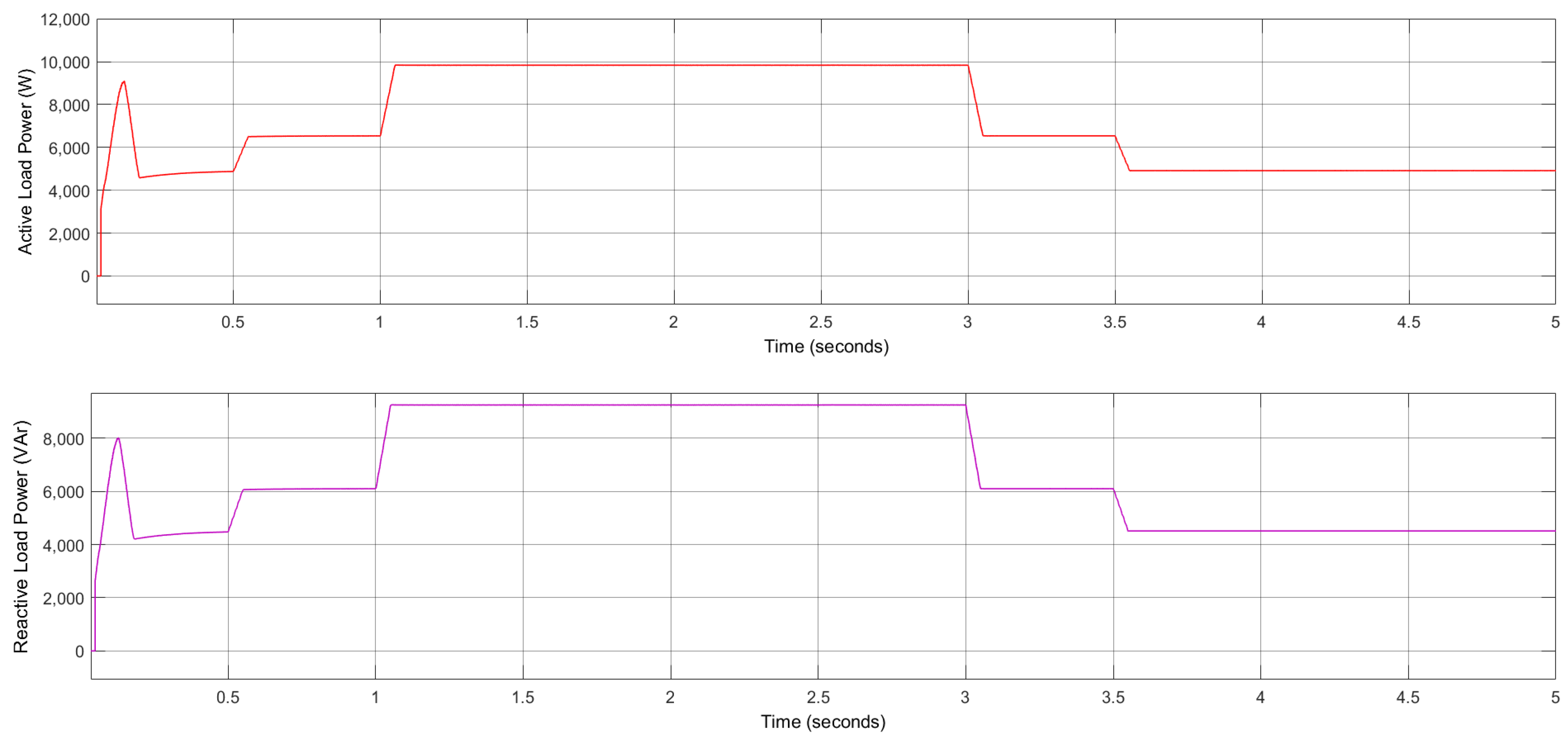
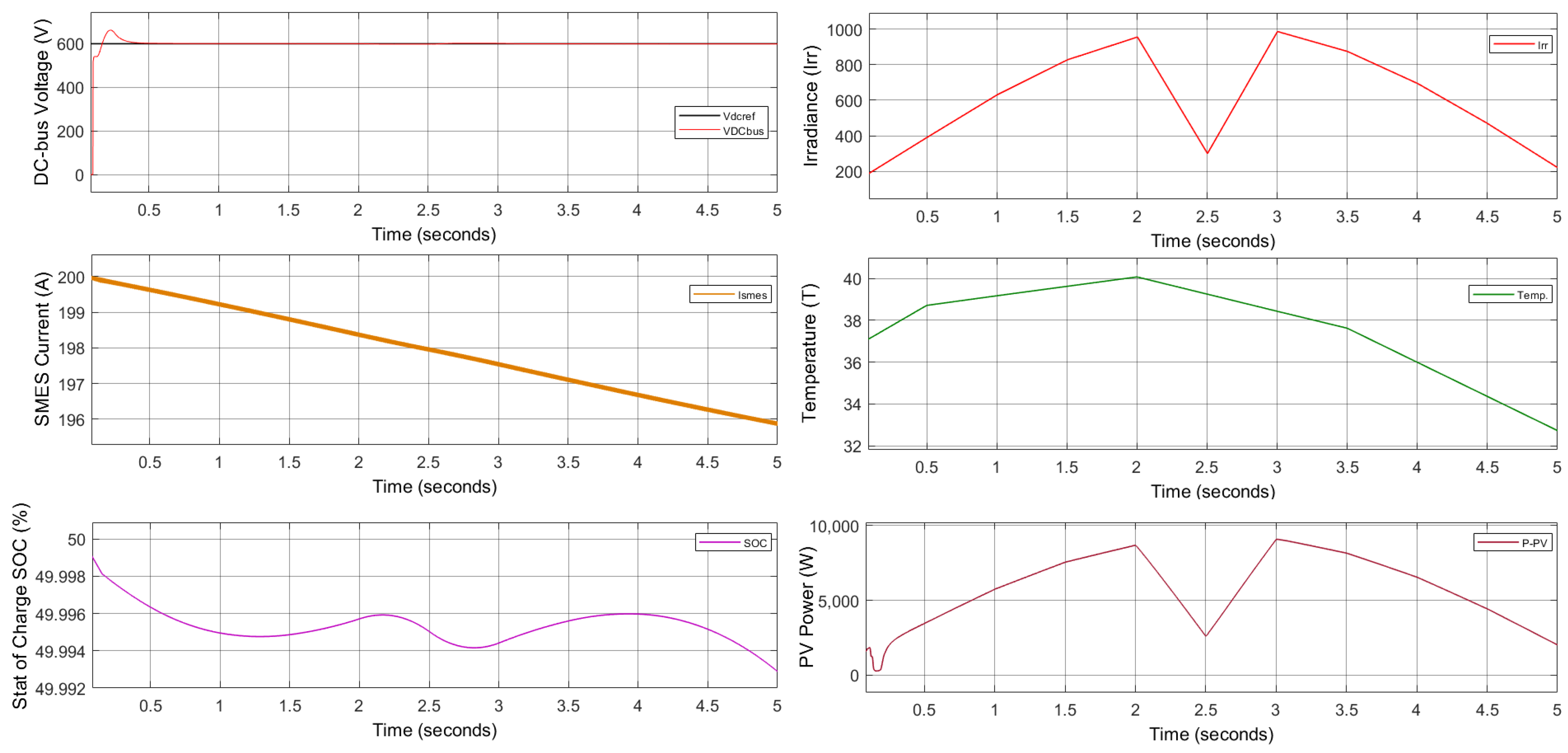
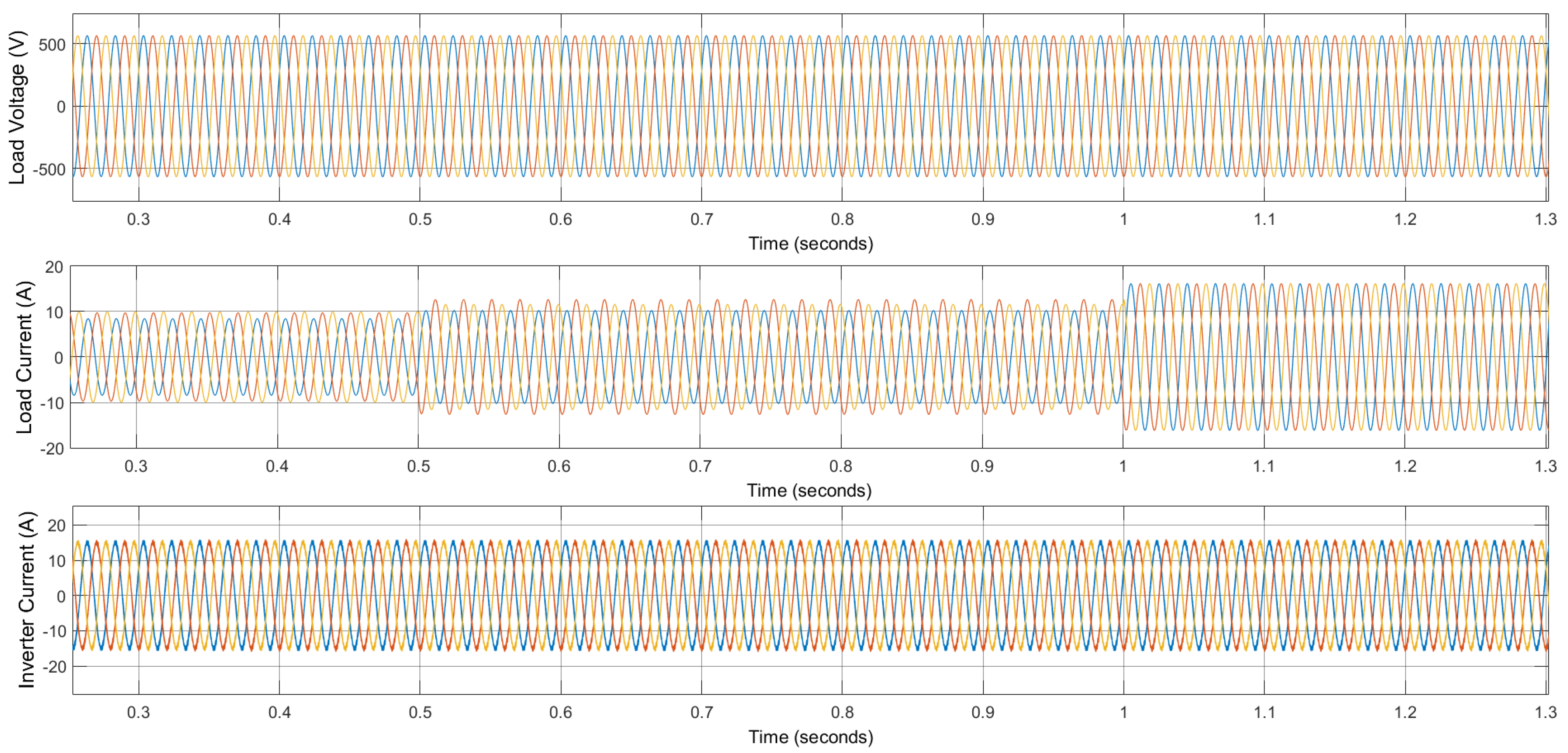
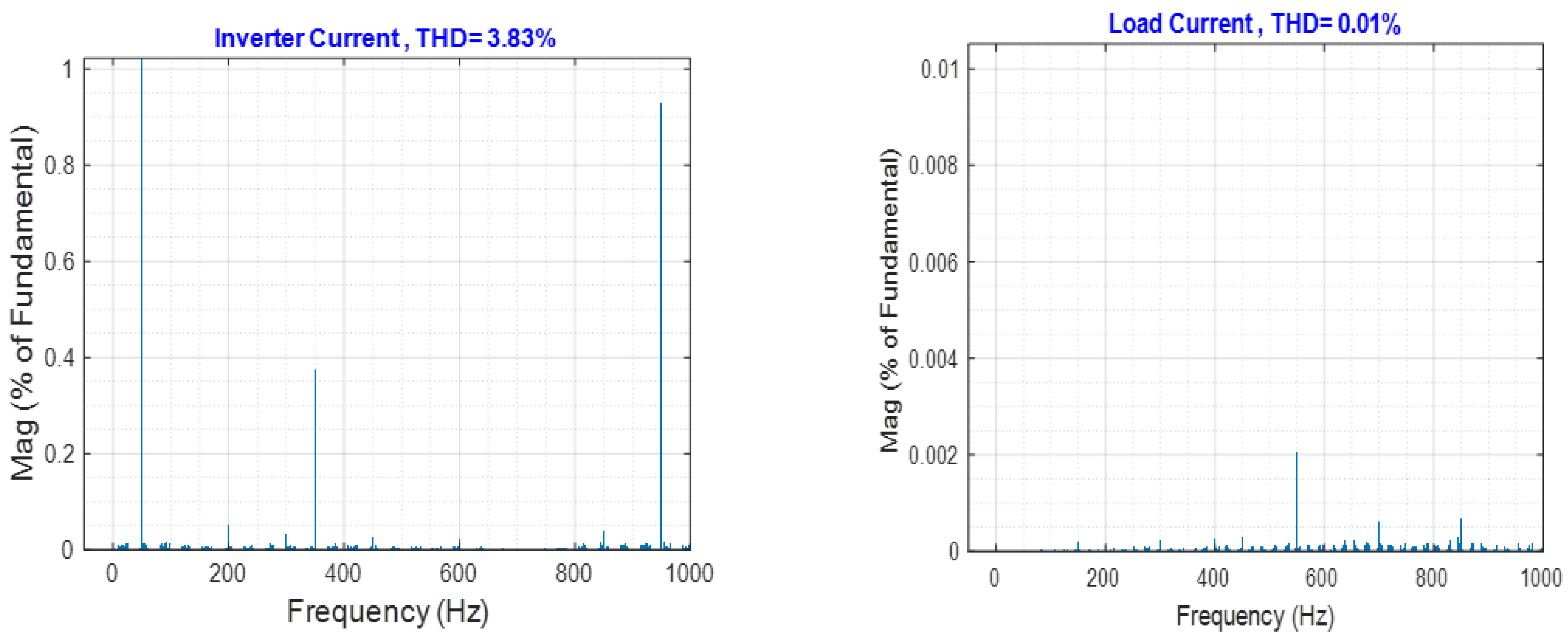
4. Simulation Results and Discussion
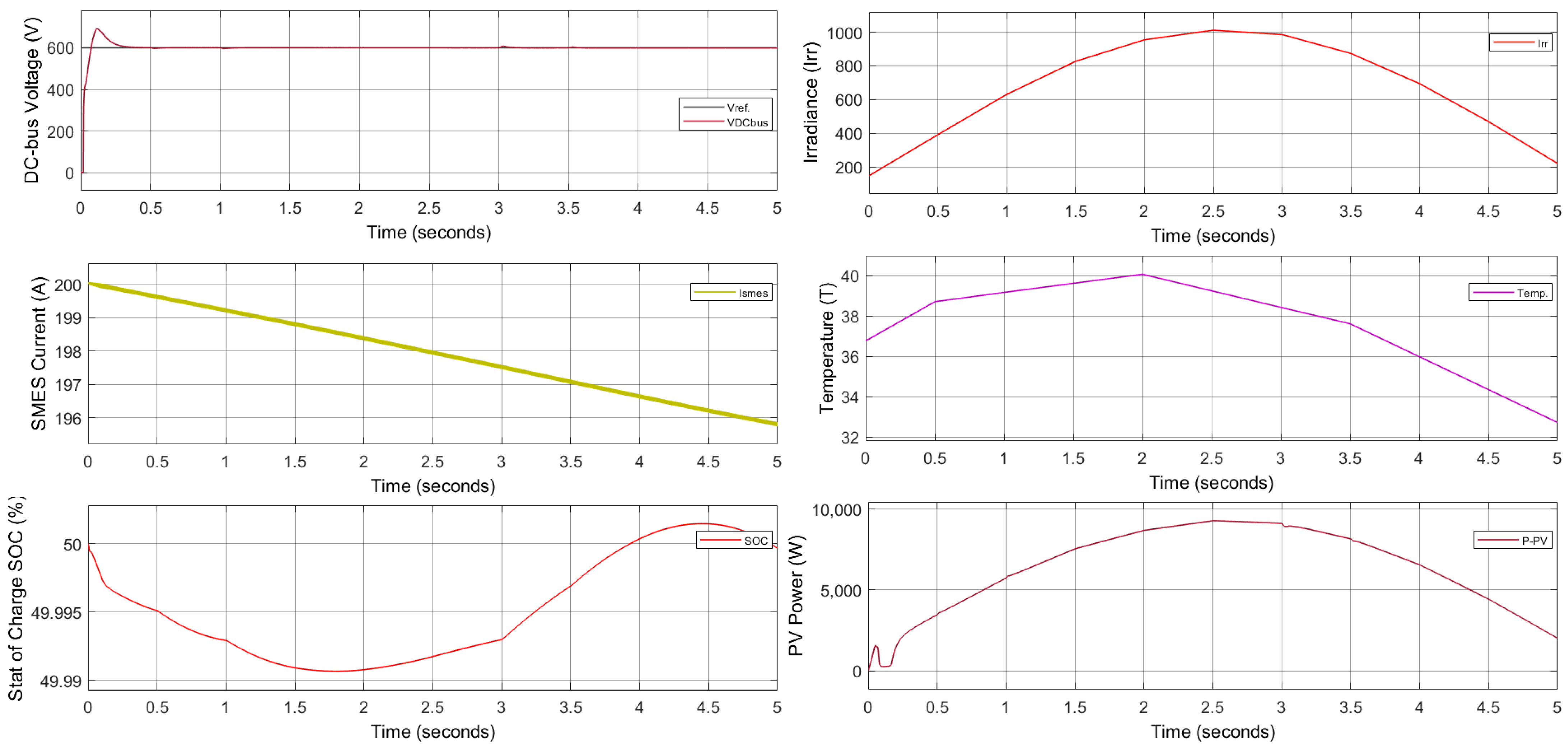
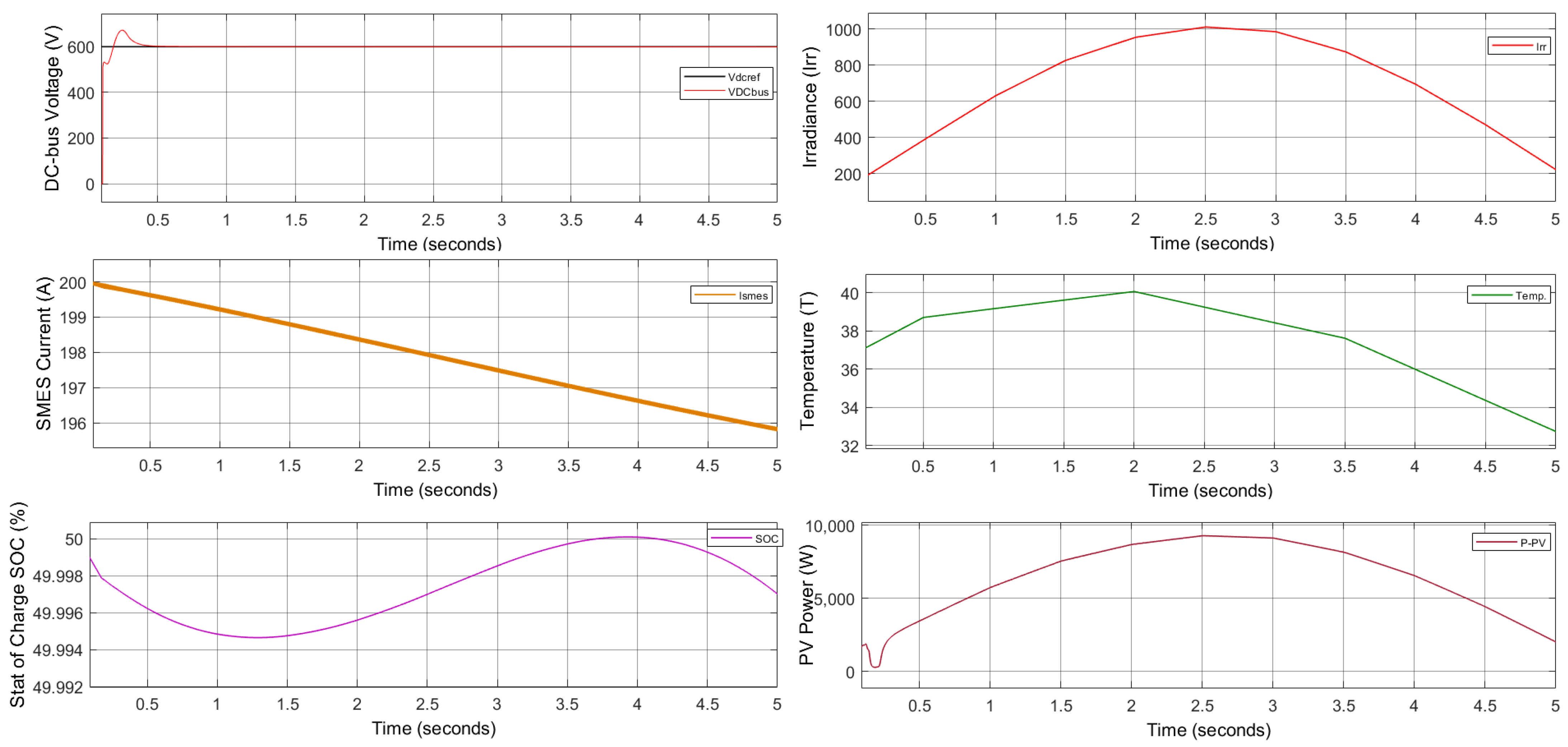
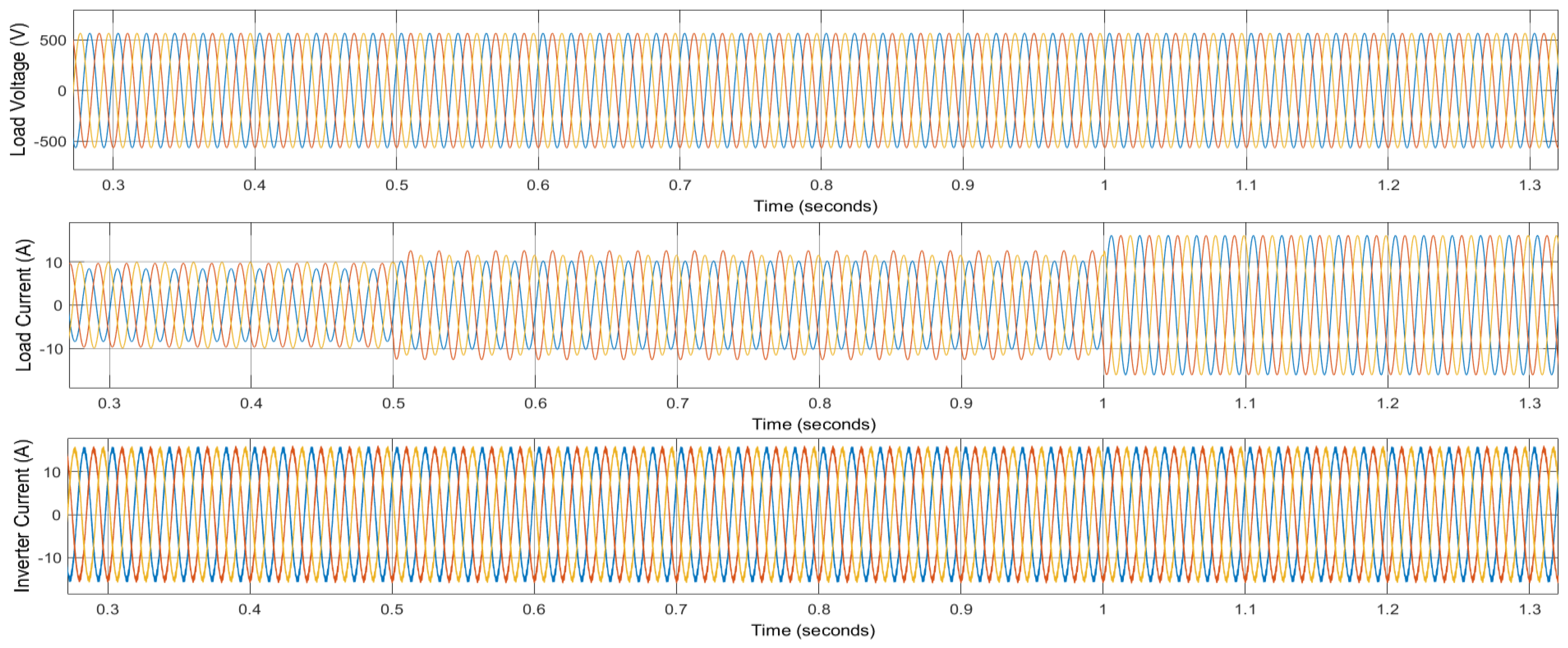
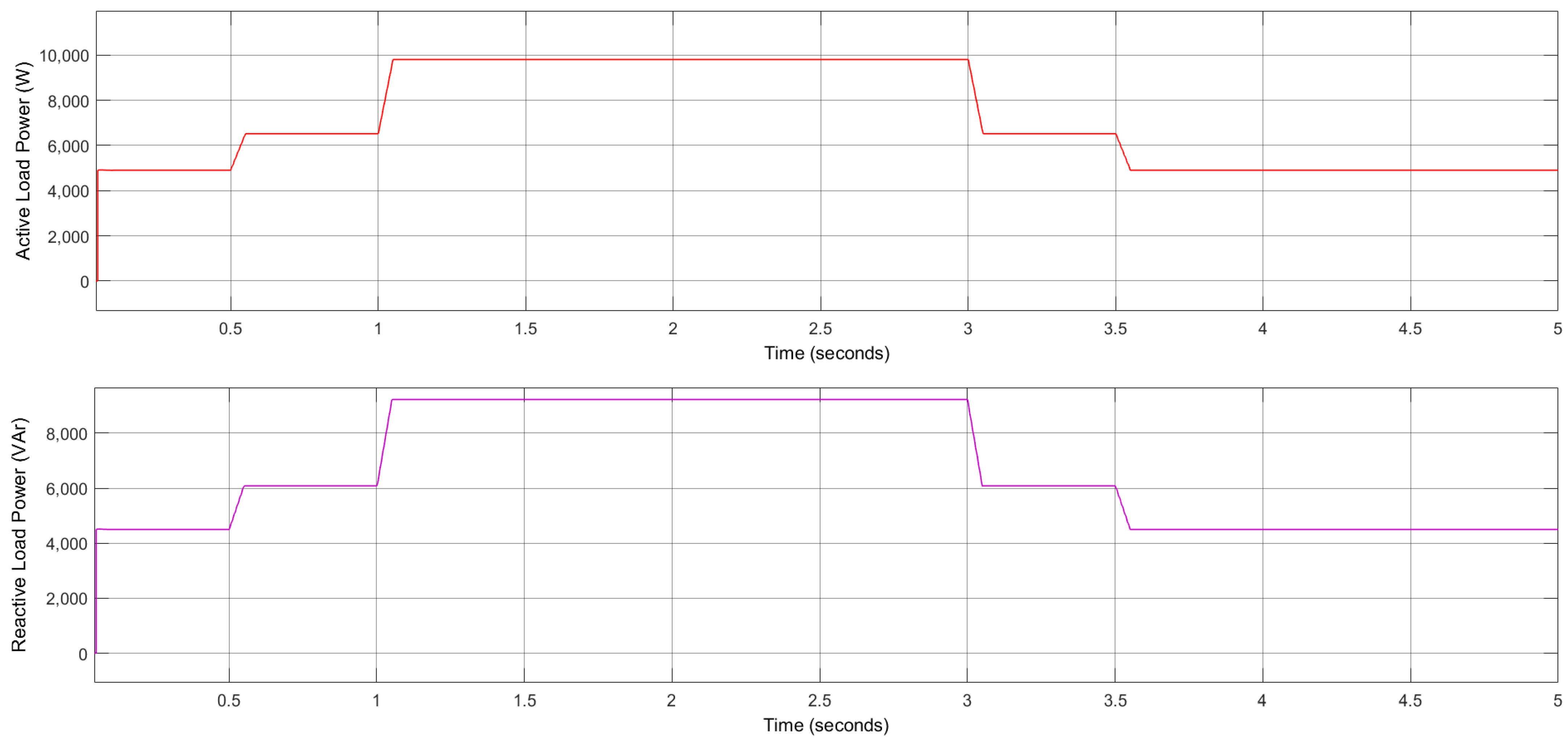
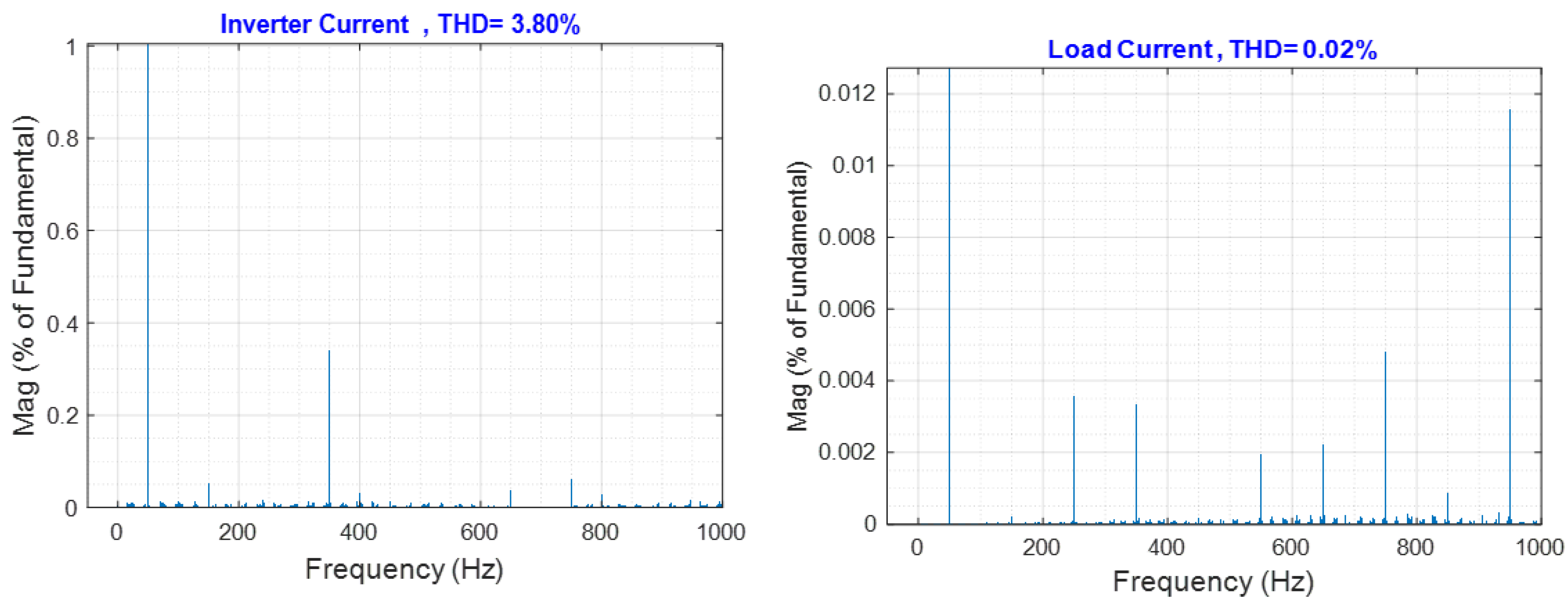
4.1. Result 1: Standalone Mode
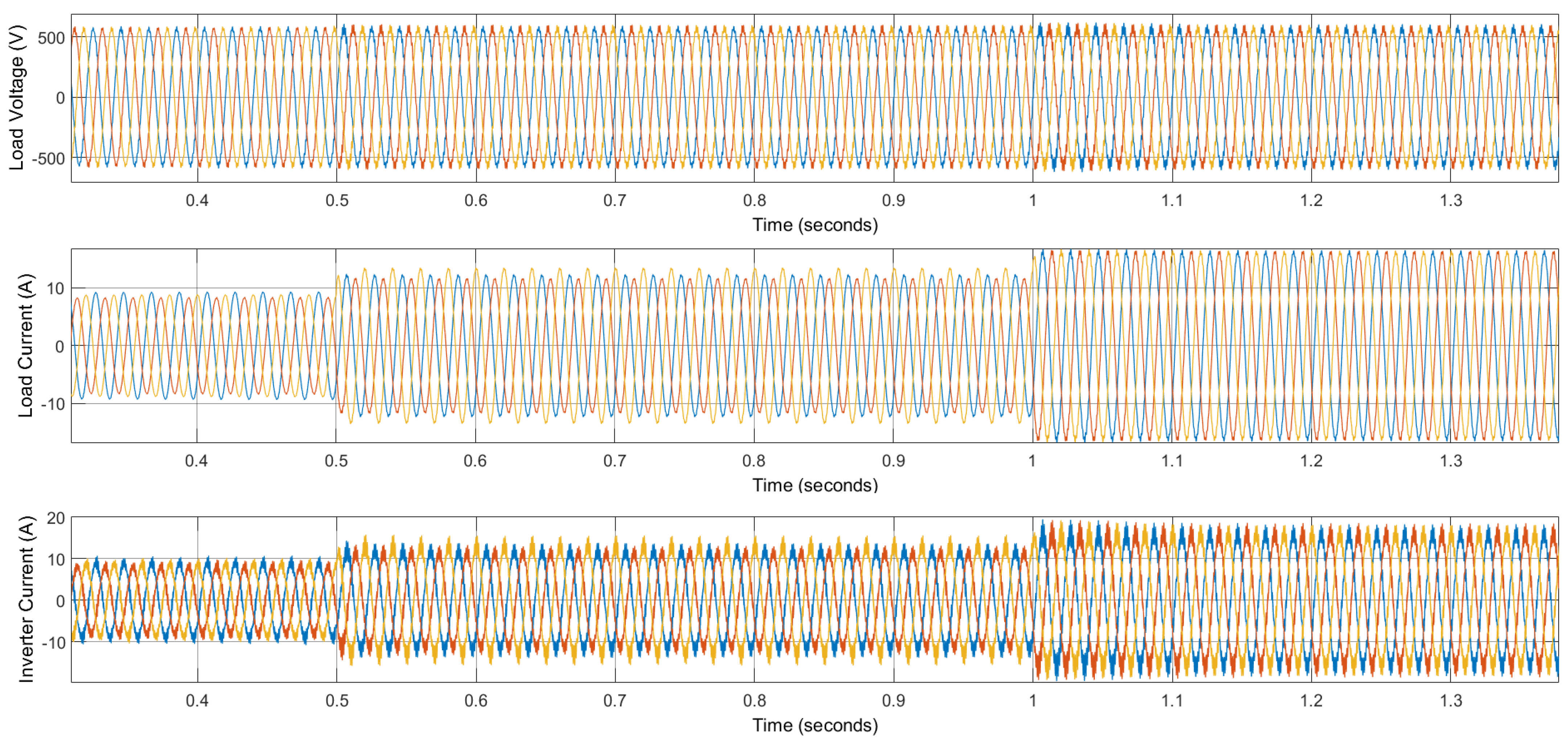
4.2. Result 2: Grid-Connected Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, S.; Liu, P.; Li, Z. Low Carbon Transition Pathway of Power Sector with High Penetration of Renewable Energy. Renew. Sustain. Energy Rev. 2020, 130, 109985. [Google Scholar] [CrossRef]
- Global, E. Outlook 2019: Scaling up the Transition to Electric Mobility, May 2019; International Energy Agency: Paris, France, 2019. [Google Scholar]
- Chaouachi, A.; Kamel, R.M.; Andoulsi, R.; Nagasaka, K. Multiobjective Intelligent Energy Management for a Microgrid. IEEE Trans. Ind. Electron. 2012, 60, 1688–1699. [Google Scholar] [CrossRef]
- Mansour-Saatloo, A.; Agabalaye-Rahvar, M.; Mirzaei, M.A.; Mohammadi-Ivatloo, B.; Abapour, M.; Zare, K. Robust Scheduling of Hydrogen Based Smart Micro Energy Hub with Integrated Demand Response. J. Clean. Prod. 2020, 267, 122041. [Google Scholar] [CrossRef]
- Juma, M.I.; Mwinyiwiwa, B.M.M.; Msigwa, C.J.; Mushi, A.T. Design of a Hybrid Energy System with Energy Storage for Standalone DC Microgrid Application. Energies 2021, 14, 5994. [Google Scholar] [CrossRef]
- Lonkar, M.; Ponnaluri, S. An Overview of DC Microgrid Operation and Control. In Proceedings of the IREC2015 The Sixth International Renewable Energy Congress, Sousse, Tunisia, 24–26 March 2015; pp. 1–6. [Google Scholar]
- Farhadi, M.; Mohammed, O. Energy Storage Technologies for High-Power Applications. IEEE Trans. Ind. Appl. 2015, 52, 1953–1961. [Google Scholar] [CrossRef]
- Jing, W.; Lai, C.H.; Wong, W.S.H.; Wong, M.L.D. A Comprehensive Study of Battery-Supercapacitor Hybrid Energy Storage System for Standalone PV Power System in Rural Electrification. Appl. Energy 2018, 224, 340–356. [Google Scholar] [CrossRef]
- Castaings, A.; Lhomme, W.; Trigui, R.; Bouscayrol, A. Comparison of Energy Management Strategies of a Battery/Supercapacitors System for Electric Vehicle under Real-Time Constraints. Appl. Energy 2016, 163, 190–200. [Google Scholar] [CrossRef]
- Yuan, Y.; Sun, C.; Li, M.; Li, Q. Determination of Optimal Supercapacitor-Lead-Acid Battery Energy Storage Capacity for Smoothing Wind Power Using Empirical Mode Decomposition and Neural Network. Electr. Power Syst. Res. 2015, 127, 323–331. [Google Scholar] [CrossRef]
- Li, J.; Xiong, R.; Yang, Q.; Liang, F.; Zhang, M.; Yuan, W. Design/Test of a Hybrid Energy Storage System for Primary Frequency Control Using a Dynamic Droop Method in an Isolated Microgrid Power System. Appl. Energy 2017, 201, 257–269. [Google Scholar] [CrossRef]
- Bizon, N. Effective Mitigation of the Load Pulses by Controlling the Battery/SMES Hybrid Energy Storage System. Appl. Energy 2018, 229, 459–473. [Google Scholar] [CrossRef]
- Coelho, V.N.; Coelho, I.M.; Coelho, B.N.; de Oliveira, G.C.; Barbosa, A.C.; Pereira, L.; de Freitas, A.; Santos, H.G.; Ochi, L.S.; Guimarães, F.G. A Communitarian Microgrid Storage Planning System inside the Scope of a Smart City. Appl. Energy 2017, 201, 371–381. [Google Scholar] [CrossRef]
- Guo, Q.; Zhang, P.; Bo, L.; Zeng, G.; Li, D.; Fan, J.D.; Liu, H. An Application of High-Temperature Superconductors YBCO to Magnetic Separation. Int. J. Mod. Phys. B 2017, 31, 1745001. [Google Scholar] [CrossRef]
- Ichinose, A.; Horii, S.; Doi, T. Possibility of Material Cost Reduction toward Development of Low-Cost Second-Generation Superconducting Wires. Jpn. J. Appl. Phys. 2017, 56, 103101. [Google Scholar] [CrossRef]
- Shawyer, R. Second Generation EmDrive Propulsion Applied to SSTO Launcher and Interstellar Probe. Acta Astronaut. 2015, 116, 166–174. [Google Scholar] [CrossRef]
- Gubser, D.U. Superconductivity Research and Development: Department of Defense Perspective. Appl. Supercond. 1995, 3, 157–161. [Google Scholar] [CrossRef]
- Shimizu, T.; Underwood, C. Super-Capacitor Energy Storage for Micro-Satellites: Feasibility and Potential Mission Applications. Acta Astronaut. 2013, 85, 138–154. [Google Scholar] [CrossRef]
- Patel, M.R. Spacecraft Power Systems; CRC Press: Boca Raton, FL, USA, 2004; ISBN 0429124112. [Google Scholar]
- Jin, J.X. HTS Energy Storage Techniques for Use in Distributed Generation Systems. Phys. C Supercond. 2007, 460, 1449–1450. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, L.; Wang, X.; Chen, L.; Chen, Y. The Impact of SFCL and SMES Integration on the Distance Relay. Phys. C Supercond. Appl. 2016, 530, 151–159. [Google Scholar] [CrossRef]
- Ali, M.H.; Wu, B.; Dougal, R.A. An Overview of SMES Applications in Power and Energy Systems. IEEE Trans. Sustain. Energy 2010, 1, 38–47. [Google Scholar] [CrossRef]
- Ren, L.; Tang, Y.; Shi, J.; Dou, J.; Zhou, S.; Jin, T. Techno-Economic Evaluation of Hybrid Energy Storage Technologies for a Solar–Wind Generation System. Phys. C Supercond. 2013, 484, 272–275. [Google Scholar] [CrossRef]
- Dufo-López, R.; Lujano-Rojas, J.M.; Bernal-Agustín, J.L. Comparison of Different Lead–Acid Battery Lifetime Prediction Models for Use in Simulation of Stand-Alone Photovoltaic Systems. Appl. Energy 2014, 115, 242–253. [Google Scholar] [CrossRef]
- Li, N.; Chen, Z.; Ren, W.; Li, F.; Cheng, H.-M. Flexible Graphene-Based Lithium Ion Batteries with Ultrafast Charge and Discharge Rates. Proc. Natl. Acad. Sci. USA 2012, 109, 17360–17365. [Google Scholar] [CrossRef]
- Sun, Q.; Xing, D.; Yang, Q.; Zhang, H.; Patel, J. A New Design of Fuzzy Logic Control for SMES and Battery Hybrid Storage System. Energy Procedia 2017, 105, 4575–4580. [Google Scholar] [CrossRef]
- Akshay, R.S.R.; Abraham, R.J. Load Following Performance in a Deregulated Power System with Static Synchronous Compensator and Super Magnetic Energy Storage. Energy Syst. 2022, 1–20. [Google Scholar] [CrossRef]
- Annapoorani, K.I.; Rajaguru, V.; Padmanabhan, S.A.; Kumar, K.M.; Venkatachalam, S. Fuzzy Logic-Based Integral Controller for Load Frequency Control in an Isolated Micro-Grid with Superconducting Magnetic Energy Storage Unit. Mater. Today Proc. 2022, 58, 244–250. [Google Scholar] [CrossRef]
- Alkhafaji, A.S.; Trabelsi, H. Survey a Superconducting Magnetic Energy Storage SMES with PV System to Enhance the Microgrid. In Proceedings of the 2022 19th International Multi-Conference on Systems, Signals & Devices (SSD), Setif, Algeria, 6–10 May 2022. [Google Scholar]
- Abdelbadie, H.T.K.; Taha, A.T.M.; Hasanien, H.M.; Turky, R.A.; Muyeen, S.M. Stability Enhancement of Wind Energy Conversion Systems Based on Optimal Superconducting Magnetic Energy Storage Systems Using the Archimedes Optimization Algorithm. Processes 2022, 10, 366. [Google Scholar] [CrossRef]
- Kotb, K.M.; Elmorshedy, M.F.; Salama, H.S.; Dán, A. Enriching the Stability of Solar/Wind DC Microgrids Using Battery and Superconducting Magnetic Energy Storage Based Fuzzy Logic Control. J. Energy Storage 2022, 45, 103751. [Google Scholar] [CrossRef]
- Jin, J.X.; Wang, J.; Yang, R.H.; Zhang, T.L.; Mu, S.; Fan, Y.J.; Xing, Y.Q. A Superconducting Magnetic Energy Storage with Dual Functions of Active Filtering and Power Fluctuation Suppression for Photovoltaic Microgrid. J. Energy Storage 2021, 38, 102508. [Google Scholar] [CrossRef]
- Salama, H.S.; Vokony, I. Voltage and Frequency Control of Balanced/Unbalanced Distribution System Using the SMES System in the Presence of Wind Energy. Electricity 2021, 2, 205–224. [Google Scholar] [CrossRef]
- Said, S.M.; Ali, A.; Hartmann, B. Tie-Line Power Flow Control Method for Grid-Connected Microgrids with SMES Based on Optimization and Fuzzy Logic. J. Mod. Power Syst. Clean Energy 2020, 8, 941–950. [Google Scholar] [CrossRef]
- Hashem, M.; Abdel-Salam, M.; El-Mohandes, M.T.; Nayel, M.; Ebeed, M. Optimal Placement and Sizing of Wind Turbine Generators and Superconducting Magnetic Energy Storages in a Distribution System. J. Energy Storage 2021, 38, 102497. [Google Scholar] [CrossRef]
- Molina-Ibáñez, E.-L.; Rosales-Asensio, E.; Pérez-Molina, C.; Pérez, F.M.; Colmenar-Santos, A. Analysis on the Electric Vehicle with a Hybrid Storage System and the Use of Superconducting Magnetic Energy Storage (SMES). Energy Rep. 2021, 7, 854–873. [Google Scholar] [CrossRef]
- Alkafaji, A.S.; Al-Samawi, A.A.; Trabelsi, H. Hybrid Energy Storage Review for Renewable Energy System Technologies and Applications. In Proceedings of the 2021 18th International Multi-Conference on Systems, Signals & Devices (SSD), Monastir, Tunisia, 22–25 March 2021; pp. 1059–1067. [Google Scholar]
- Luongo, C.A. Superconducting Storage Systems: An Overview. IEEE Trans. Magn. 1996, 32, 2214–2223. [Google Scholar] [CrossRef]
- Boffmann, E.; Alcorn, J.; Chen, W.; Hsu, Y.; Purcell, J.; Schermer, R. Design of the BPA Superconducting 30-MJ Energy Storage Coil. IEEE Trans. Magn. 1981, 17, 521–524. [Google Scholar] [CrossRef]
- Sharma, A. Properties & Applications of Superconductors. Available online: https://www.yourelectricalguide.com/2019/07 (accessed on 26 September 2022).
- Ilieva, K.; Dinolov, O. State-of-the-Art of Superconducting Materials and Their Energy-Efficiency Applications. In Proceedings of the 2020 7th International Conference on Energy Efficiency and Agricultural Engineering, EE and AE 2020, Ruse, Bulgaria, 11–13 June 2020; pp. 10–14. [Google Scholar] [CrossRef]
- Peake, S. Renewable Energy: Power for a Sustainable Future, 4th ed.; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Rekioua, D.; Matagne, E. Optimization of Photovoltaic Power Systems Modelization, Simulation and Control; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Lalouni, S.; Rekioua, D.; Rekioua, T.; Matagne, E. Fuzzy logic control of standalone photovoltaic system with battery storage. J. Power Sources 2009, 193, 899–907. [Google Scholar] [CrossRef]
- Eltamaly, A.M. Performance of MPPT Techniques of Photovoltaic Systems Under Normal and Partial Shading Conditions; Elsevier Inc.: Amsterdam, The Netherlands, 2018; Volume 1, ISBN 9780128132173. [Google Scholar]
- Fathima, A.H.; Palanisamy, K. Energy storage systems for energy management of renewables in distributed generation systems. In Energy Management of Distributed Generation Systems; Mihet-Popa, L., Ed.; Books on Demand: Norderstedt, Germany, 2016. [Google Scholar]
- Yekini Suberu, M.; Wazir Mustafa, M.; Bashir, N. Energy Storage Systems for Renewable Energy Power Sector Integration and Mitigation of Intermittency. Renew. Sustain. Energy Rev. 2014, 35, 499–514. [Google Scholar] [CrossRef]
- Alternative Energy. Common Types of Solar Cells. 18 August 2015. Available online: http://www.altenergy.org/renewables/solar/common-types-of-solar-cells.html (accessed on 26 September 2022).
- Kobayashi, K.; Takano, I.; Sawada, Y. A study on a two stage maximum power point tracking control of a photovoltaic system under partially shaded insolation conditions. In Proceedings of the 2003 IEEE Power Engineering Society General Meeting, Toronto, ON, Canada, 13–17 July 2003. [Google Scholar]
- Kotb, K.M.; Elmorshedy, M.F.; Dán, A. Performance Assessment of Integrating SMES and Battery Storage Systems with Renewable DC-Bus Microgrids: A Comparison. Period. Polytech. Electr. Eng. Comput. Sci. 2021, 65, 382–393. [Google Scholar] [CrossRef]
- Shengqing, L.; Fujun, L.; Jian, Z.; Wen, C.; Donghui, Z. An Improved MPPT Control Strategy Based on Incremental Conductance Method. Soft Comput. 2020, 24, 6039–6046. [Google Scholar] [CrossRef]
- Rashid, M.H. Power Electronics Devices, Circuits, and Applications, 4th ed.; Pearson Education Limited: London, UK, 2014. [Google Scholar]
- Sun, Q.; Xing, D.; Alafnan, H.; Pei, X.; Zhang, M.; Yuan, W. Design and Test of a New Two-Stage Control Scheme for SMES-Battery Hybrid Energy Storage Systems for Microgrid Applications. Appl. Energy 2019, 253, 113529. [Google Scholar] [CrossRef]
- Hava, A.M.; Ayhan, U.; Aban, V.V. A DC Bus Capacitor Design Method for Various Inverter Applications. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition, ECCE 2012, Raleigh, NC, USA, 15–20 September 2012; pp. 4592–4599. [Google Scholar] [CrossRef]
- European Commsions’s Photovolitaic Geographical Information System (PVGIS). [Online]. Available online: https://re.jrc.ec.europa.eu/pvg_tools/en/tools.html#TMY (accessed on 26 September 2022).
- Farh, H.M.H.; Othman, M.F.; Eltamaly, A.M.; Al-Saud, M.S. Maximum Power Extraction from a Partially Shaded PV System Using an Interleaved Boost Converter. Energies 2018, 11, 2543. [Google Scholar] [CrossRef]
- Eltamaly, A.M. An Improved Cuckoo Search Algorithm for Maximum Power Point Tracking of Photovoltaic Systems under Partial Shading Conditions. Energies 2021, 14, 953. [Google Scholar] [CrossRef]






| Material | Critical Temperature (K) | Material | Critical Temperature (K) |
|---|---|---|---|
| Niobium (Nb) | 9.26 | Bismuth strontium calcium copper oxide (Bi+Sr–Cu–O) | 22 |
| Niobium–Titanium All oy (NbTi) | 9.2 | HgBa2Ca2Cu3O8+δ | 133 |
| Niobium–Tin (Nb3Sn) | 18 | Yttrium barium copper oxide (YBCO) | 93 |
| Magnesium Diboride (MgB2) | 39 | Thorium hydride (ThH10) | 231 |
| lanthanum Barium Copper Oxide (La2–xBaxCuO4) | 30 | Lanthanum decahydride (LaH10) | 250 |
| Parallel String | 4 | Current at the MPP Imp (A) | 8.15 |
|---|---|---|---|
| Series-connected modules/string | 10 | Max. power Pmax. (W) | 10 KW |
| Open-circuit voltage Voc (V) | 37.3 | Temperature coefficient of Voc (%/deg.) | −0.369 |
| Short-circuit current Isc (A) | 8.66 | Temperature coefficient of Isc (%/deg.) | 0.089 |
| Voltage at the MPP Vmp (V) | 30.7 | Peak Efficiency | 15.29% |
| Parameters | Power KW | Fsw. (kHz) | VPV (V) | IPV (A) | VDC−bus (V) | Iboost (A) | ΔV 1% | ΔI 3% | L (mH) | Cout (μF) |
|---|---|---|---|---|---|---|---|---|---|---|
| Value | 10 | 10 | 300 | 33.33 | 600 | 16.667 | 6 | 1 | 15 | 140 |
| Parameters | NO of Battery | Vbattery (V) | Ah | Total Power kW/h | Total Voltage (V) | Lbattery (mH) | Cbattery (µF) | Switching Freq. (Hz) |
|---|---|---|---|---|---|---|---|---|
| Value | 17 | 12 | 50 | 10 | 200 | 13.33 | 62.5 | 10 kHz |
| PI Controller No. | PI1 | PI2 |
|---|---|---|
| Proportional gain Kp | 1.5 | 1 |
| Integral gain Ki | 25 | 100 |
| PI Controller No. | PI1 | PI2 | PI3 | PI4 |
|---|---|---|---|---|
| Proportional gain (Kp) | 0.1 | 0.1 | 30 | 30 |
| Integral gain (Ki) | 100 | 100 | 200 | 200 |
| Unbalance Load | Unbalance Load | Balance Load | |||
|---|---|---|---|---|---|
| PL1 (kW) | PL2 (kW) | QL1 (kVAr) | QL2 (kVAr) | PL3 (kW) | QL3 (kVAr) |
| 4.938 | 6.538 | 4.512 | 6.1 | 9.830 | 9.235 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alkhafaji, A.S.; Trabelsi, H. Uses of Superconducting Magnetic Energy Storage Systems in Microgrids under Unbalanced Inductive Loads and Partial Shading Conditions. Energies 2022, 15, 8597. https://doi.org/10.3390/en15228597
Alkhafaji AS, Trabelsi H. Uses of Superconducting Magnetic Energy Storage Systems in Microgrids under Unbalanced Inductive Loads and Partial Shading Conditions. Energies. 2022; 15(22):8597. https://doi.org/10.3390/en15228597
Chicago/Turabian StyleAlkhafaji, Ahmed Samawi, and Hafedh Trabelsi. 2022. "Uses of Superconducting Magnetic Energy Storage Systems in Microgrids under Unbalanced Inductive Loads and Partial Shading Conditions" Energies 15, no. 22: 8597. https://doi.org/10.3390/en15228597
APA StyleAlkhafaji, A. S., & Trabelsi, H. (2022). Uses of Superconducting Magnetic Energy Storage Systems in Microgrids under Unbalanced Inductive Loads and Partial Shading Conditions. Energies, 15(22), 8597. https://doi.org/10.3390/en15228597








