1. Introduction
Ejectors/eductors are mechanical devices that operate on the principle of converting primary flow energy into secondary fluid entrainment. They are among the standard industrial devices used for moving liquid, particles, and gas or to create a vacuum. The principal fluid might be either liquid or gas, depending on the application [
1,
2]. They can also perform multiple fluid dynamic features like multiphase mixing, heat and mass transfer, pumping, fluid flow expansion, and compression [
3,
4,
5]. The absence of moving parts and simple construction make them some of the more widely preferred multifunctional components [
6].
The existing literature outlines the role of the eductor and how it might be modified for different uses. Most of the existing literature focuses on air jet or steam jet systems, with only a few studies conducted on water-jet eductors. Zhang et al. [
7] performed an experimental and empirical study of flow inside a water jet eductor. The secondary source used in this study was superheated steam from a steam generator. Axial pressure measurements were performed to explain the phenomenon. The pressure along the axial direction decreased up to the exit of the throat for the selected geometry. Shah et al. [
8] conducted a numerical and experimental study of a steam jet ejector with the primary fluid being superheated steam and the secondary fluid being cooling water. Their numerical study considered an infinite source of liquid, which is not difficult to approximate, since water is in liquid form under standard conditions. This is among the limited studies considering the mass transfer rate during the computational analysis of ejectors. Banu et al. [
9] performed a numerical and experimental study for a refrigeration application with a primary fluid of superheated steam. The primary focus of the study is to evaluate the influence of primary fluid swirl on the performance of ejectors. An increase in primary fluid swirl was found to have enhanced entrainment. Yan et al. [
10] performed an experimental study with swirling primary fluid (water) to entrain steam from the secondary source. These swirling vanes introduced vortices resulting in more significant interaction time between the fluids for better mixing [
11,
12]. Narabayashi et al. [
13] experimentally studied an ejector for a passive core injection system to be used in next-generation reactors, with primary water, and secondary steam fitted with throat drains. The use of steam from a high-pressure turbine to run the steam injector reduced the plant efficiency by 1%. Yan et al. [
14] performed experiments with primary steam and secondary water for heating purposes. A shock wave was reported to occur during phase change within the flow channel. One of the key factors in the existing literature is the use of an infinite and common secondary source (e.g., superheated steam, compressed air, or water). Some of the practical aspects that have been identified as significant knowledge gaps are the behavior of eductor-aided sub-atmospheric saturation conditions, low-grade heat input for phase transformation, and synchronous multifunctional activity in eductors (e.g., combined degassing, pumping, and heat exchange). In addition, for applications that include 2 phase single species flows, eductors can be developed to function as a direct contact heat transfer device/condenser.
This work focuses on two objectives: First, determining the influence of eductor operating conditions on the sub-atmospheric vapor generation at the secondary flow source and condensation within the eductor. Second, establishing a foundation for the verification of computational studies on the thermo-fluid analysis of similar phenomena. The plan is to develop an eductor for use as an active vapor transfer and condensation unit for desalination systems. During this study, the pressure at different axial positions and the influence of phase change during direct contact condensation were examined, along with the eductor-aided saturation process in a control volume. The thermodynamic mechanism of heat transfer (explored using a T-S diagram), calculation of the overall heat transfer coefficient, and overall exergy analysis are three major theoretical knowledge contributions that can provide a new direction to the existing work. The outcome of this work can also be referenced for verification of computational activities related to the following four thermal-fluid processes: flow dynamics in eductors, heat and mass transfer, multiphase fluid mixing, and sub-atmospheric saturation.
2. Eductors for Active Vapor Transport and Condensation
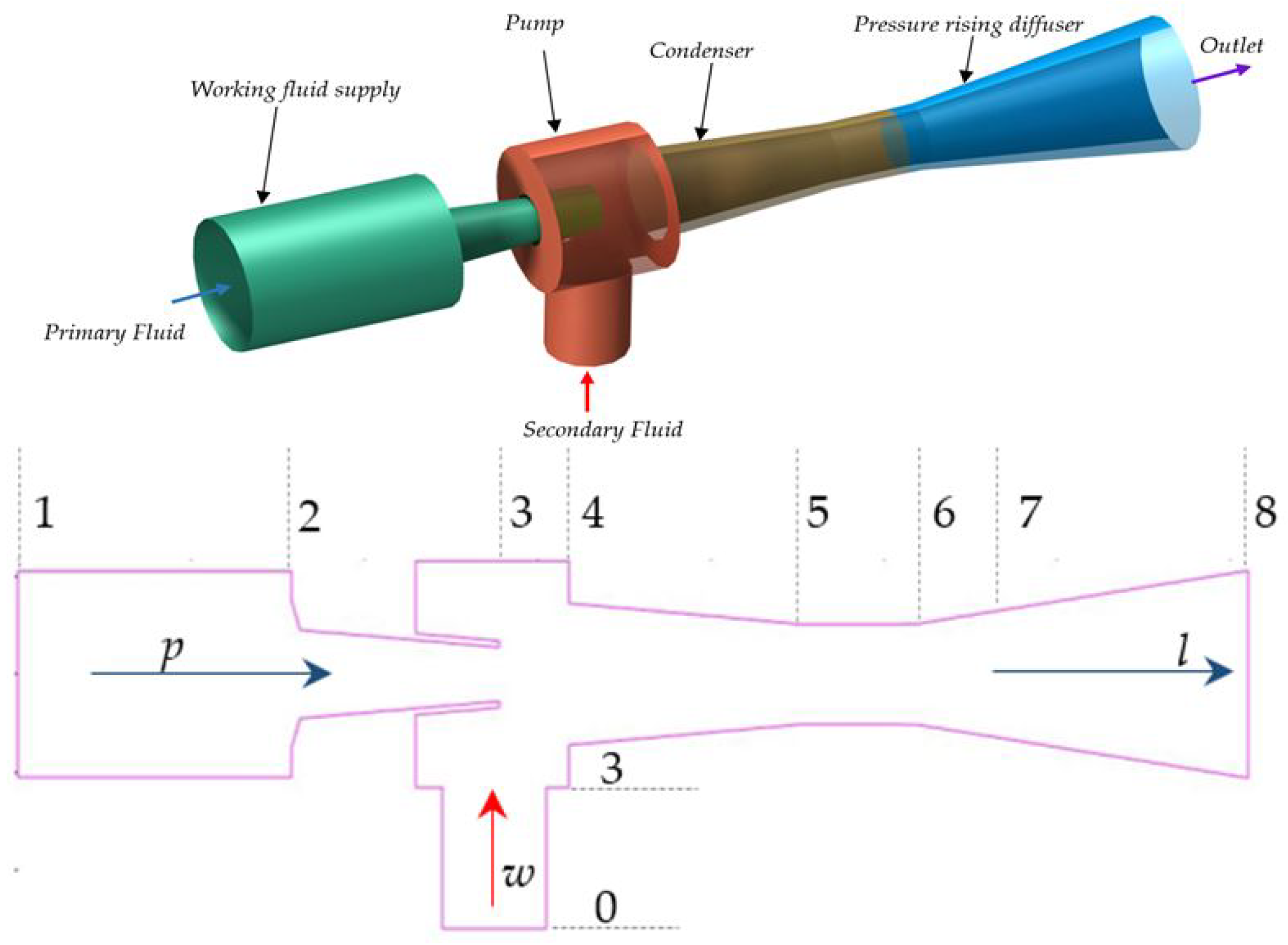
The primary and secondary inlet, as well as the suction chamber, mixing chamber, throat, and diffuser, make up an eductor. Eductors work by converting pressure energy into velocity energy, with secondary entrainment occurring in the low-pressure zone. When a high-velocity primary fluid leaves the primary nozzle, it generates a continuous eddy current in the surrounding fluid, keeping the suction chamber at low pressure. When connected to a secondary fluid source, the secondary port degasses the area between the secondary fluid surface and the mixing chamber before pulling it to the mainstream. The physical model of an eductor for active vapor transfer and condensation is shown in
Figure 1. The input work supply pump, condenser, and pressure rising diffuser are the main functional components. The working fluid, in this case, is liquid water, which serves numerous roles during the energy conversion. Liquid works as a working fluid in the pumping portion, pulling secondary fluid (water vapor) into the mainstream. This flow is caused by a positive pressure difference between the secondary fluid source and the suction chamber. In addition, it works as a condensing/cooling fluid in the condenser by direct contact condensation and cooling. A single-phase fluid made up of the primary and secondary flows exits the eductor system through the diffuser at a pressure higher than the secondary flow inlet but lower than the primary flow inlet. The greater the rate of condensation, the greater the entrainment because the collapsing vapor bubbles resulting from condensation form large empty volumes, allowing for additional incoming flow to fill the space. Outlet pressure is a limiting component; raising the outlet pressure improves the condensation rate but obstructs the fluid flow; thus, entrainment rises for a brief period before progressively decreasing.
The performance of the eductor is defined in terms of its entrainment ratio and pressure ratio. The entrainment ratio is defined as the ratio of the mass flow rate of secondary fluid that is pumped into the system to the mass flow rate of the primary fluid that is driving the pumping action, given by Equation (
1).
The pressure ratio is defined as the mechanical compression capacity of the entrained vapor, given by Equation (
2).
Figure 2 is the estimated T-s diagram for a two-phase single species flow, with condensing secondary flow. The high velocity subcooled liquid (primary fluid) reaches the suction chamber at a constant temperature and slightly higher entropy due to its low pressure. As a result of the pressure difference between the secondary source and the suction chamber, saturated vapor (secondary fluid) enters the system from 3w. Inside the chamber, the two phases interact with each other and the energy exchange is initiated. At the secondary fluid inlet, the energy balance between the vapor source and the suction chamber can explain the vapor rising phenomenon in the eductor. Applying this energy balance, the secondary mass flow rate can be described through Equation (
3):
In addition, the primary fluid mass flow rate can be estimated by continuity and the Bernoulli equation applied to the primary nozzle:
The velocity of the subcooled liquid is initially much higher than the saturated vapor, hence the effect of the friction between the phases at their interface propels the movement of the secondary fluid. This shear stress between the phases due to leading and lagging velocity is given by:
With the thermal interaction between the two phases, the vapor fraction starts decreasing in the annular flow surrounding the primary fluid flow. The sub-cooled liquid continues to receive thermal energy (the latent heat of vaporization) released during the phase change. The pressure energy in the fluid also varies due to the variation in the axial cross section of the eductor. By the time, the primary and secondary fluids reach the throat, complete condensation takes place, and the two streams finally form a homogeneous mixture in the diffuser (between points 7 and 8). Although the local heat transfer coefficient at a given axial location, in this case, is a function of the local pressure and the inter-phase area between
Section 4,
Section 5 and
Section 6, the overall coefficient of heat transfer can be defined by:
where
is the overall convective heat transfer coefficient,
is vapor mass flow rate,
is the latent heat of condensation,
is vapor temperature (secondary fluid),
is the liquid temperature (primary fluid), and
is the total surface area of interphase interface.
3. Experimental Description
Figure 3 is the schematic view of the components for the experimental setup, together with the position of the sensors and the instrumentation. The major components of the setup include a centrifugal pump, pressure tank, eductor, viewing piece, sump, piping, and instrumentation for data acquisition and recording. A piezo-resistive sensor for suction pressure measurement and pressure transducers for the pressures at other locations are connected to a Datataker DT80, along with thermocouples for temperature measurements. In open loop operation, the primary flow sub-cooled liquid water is pumped using a centrifugal pump to the inlet of the eductor and the outlet is discharged to the sump. The setup can also function in closed-loop operation for particle tracking and flow visualization. The low-pressure secondary vapor is generated by supplying heat to a vacuum-sealed conical flask via a plate heater. The power rating of the plate heater is described in
Table 1. The reliability of the experimental setup has been ensured through sensor calibration, repeatability testing, and uncertainty analysis. The relative uncertainty of the sensors used in the system is in the range of ±0.4% to 1.2%.
Figure 4 is the experimental setup built at the Thermo-Fluid lab, RMIT University, Australia for performance estimation of eductors. For this experiment, the primary flow creates a low pressure in the space between the water surface in the conical flask (
Figure 4d) and the eductor suction chamber, hence allowing the secondary fluid in the flask to reach saturation at lower temperatures. The generated vapor is entrained into the mainstream of the eductor where the exchange of heat and mass occurs between the primary and secondary fluid streams. To maintain consistency, all the experiments were conducted at a constant heat supply rate from the plate heater and a constant inlet pressure. The valve VV308-02 was fully opened and VV308-06 was fully closed. Eductors operate on the pressure difference between their inlet and outlet; therefore, given the constant inlet pressure condition, the experiment was performed by controlling the outlet pressure, which in turn varied the suction pressure of the eductor. Six different opening levels of VV308-03 were selected to measure the influence of backpressure on performance. The operational conditions have been described in
Table 1. The axial pressure was measured using pressure taps in three different axial positions (suction chamber, mixing chamber, and throat) (
Figure 4a). The eductor used for this study is a 3D printed part reverse-engineered from a commercial eductor design and modified to accommodate three pressure ports for experiments (see
Figure 4a).
4. Results and Discussion
This section describes the experimental results with regard to three different criteria: thermal saturation phenomenon, axial flow in non-condensing and condensing cases, and functional performance of the eductor (i.e., working range for outlet pressure and entrainment ratio).
4.1. Sub-Atmospheric Vapor Generation
In the experimental setup (
Figure 4 and
Figure 5), the secondary flow of water vapor was produced by heating liquid water inside a sealed conical flask using a plate heater, while the pressure inside the flask was controlled by the eductors suction action to maintain sub-atmospheric conditions. This section describes the thermal saturation phenomenon and the influence of the eductors parameters on the process. This is one of the contrasting features of this study, i.e., where the response of an eductor to a finite secondary source has been evaluated. In practice, an unlimited vapor source will be of no practical interest during hybrid desalination.
Figure 5 is a schematic of the conversion of mechanical and thermal energy within an eductor. The mechanical energy in the primary fluid is used to maintain low pressure and pumping of the secondary fluid. Similarly, the thermal energy contributes to saturated vapor generation and direct contact condensation (DCC) of the secondary fluid.
There are two thermocouples fitted in the vapor generation apparatus of the experimental setup to monitor the conditions during evaporation of the secondary fluid: the first one submerged in the liquid water towards the base of the flask and the second one suspended near the mouth of the flask. The measurement of suction pressure was performed at about 29 cm above the mouth of the flask. In the following section, the key observations made during the experiments regarding the secondary fluid evaporation under sub-atmospheric conditions with respect to the operational characteristic of the eductor have been discussed.
Figure 5 and
Figure 6 show secondary flow (suction) pressure, secondary fluid liquid temperature, and secondary fluid vapor temperature measurements successively as the secondary fluid changes from subcooled to saturated condition, while the primary flow is maintained at back pressure 1 (BP
1). In
Figure 5 and
Figure 6, before the start of active vapor transfer (i.e., during secondary fluid heating), the pressure fluctuations were monitored in the suction chamber, with an average pressure of 83 kPa being recorded. Although the secondary fluid temperature was well below the saturation temperature corresponding to the measured suction pressure, there was no vapor generation and, therefore, no vapor transfer. The vapor generation only started when the secondary fluid temperature reached the saturation condition, allowing active vapor transfer to occur between the vapor generation source and the eductor. It can be seen in
Figure 5 and
Figure 6 that there was a period of abrupt pressure drop, known as coughing flow, which represents the period in which a small amount of vapor is generated, pushing the small amount of air present in the flask to the suction chamber, which in turn is extracted by the eductor. This removal of air, while the secondary fluid has not reached saturation temperature, causes the suction pressure to drop for a short period, as can be seen in the figure. This coughing effect is observed for almost all operating conditions and is one of the important start-up considerations that large-scale applications need to consider to prevent collapsing of the secondary fluid pipe due to the sudden vacuum created.
After the secondary fluid reaches thermal saturation, the vapor flow starts, and the average suction pressure stabilizes at 85 kPa. Compared to when the secondary fluid is sub-cooled, large fluctuations in suction pressure are observed when the secondary fluid reaches thermal saturation. The accompanying small fluctuations in temperature could be due to these changes in pressure causing a change in the saturation point. This fluctuation in the suction pressure is due to the direct condensation of water vapor in the sub-cooled primary flow (liquid water). The vapor bubbles from the secondary fluid flow enter the sub-cooled primary flow and abruptly collapse due to rapid heat and mass transfer. This gives rise to pressure waves (shock waves) which are recorded as large fluctuations in the suction pressure measurement.
With increasing back pressure in the system, the fluctuations in the suction pressure become even greater. This is due to the shifting of the condensation region towards the mixing chamber, which is closer to the suction port. Similarly, a similar behavior was reported during the computational study by Koirala et al. [
15]. The mechanical performance of the system is negatively affected by the back pressure; however, an improvement in thermal performance has been observed. The study shows that for two phase single-species condensing flow, thermal activity has a greater contribution to entrainment compared to mechanical work. The increase in condensation rate with larger interaction time allows more vapor to enter the system, but this is limited to the critical point as a certain amount of mechanical work is essential to accelerate the process. The effect on pressure and entrainment has been elaborated on in the following sections.
4.2. Axial Pressure Distribution
4.2.1. Non-Condensing Flow
Figure 7 is the pressure distribution measurement over the axial points P
1, P
2, and P
3 (as shown in
Figure 4a at different back pressures for secondary non-condensing flow (air)). The lowest pressures for P
1, P
2, and P
3 were measured at BP
2 conditions with values of approximately 70 kPa, 75 kPa, and 90 kPa (absolute) respectively. Similarly, the highest pressures for P
1, P
2, and P
3 were measured at BP
6 condition with values of 92 kPa, 98 kPa, and 110 kPa (absolute), respectively. In an eductor, the two-phase region with the lowest pressure is at point P
1, which is measured via a tapping fitted in the wall of the suction chamber. This is the region immediately after the primary nozzle where the two phases (primary and secondary fluids) first come in contact and start to mix. The design and arrangement of this component play an important role in the entrainment capacity of an eductor. The most suitable positioning will maintain the largest possible pressure difference between the secondary source and the eductor flow path, resulting in the highest level of entrainment. With increasing backpressure, the pressure at each of these points was measured and found to increase.
4.2.2. Condensing Flow
Figure 8 is the graph for the time-averaged pressure distribution measurements at the axial points P
1, P
2, and P
3 for different back pressures, with secondary condensing flow (water vapor), at the same conditions defined in the previous section. For each of the points, the lowest pressure was measured at the back pressure BP
1, and highest pressure was measured for the back pressure BP
6. The lowest pressures of 69 kPa, 72 kPa, and 87 kPa (absolute) were measured under conditions P
1, P
2, and P
3 respectively at BP
1 condition. Similarly, the highest-pressure values of 92 kPa, 98 kPa, and 108 kPa (absolute) were measured at P
1, P
2, and P
3, respectively, at BP
6 condition. The impact of back pressure was found to be greater at P
2 compared to P
1 and P
3.
4.3. Influence of Condensation
4.3.1. Quantitative Study
Figure 9 shows the comparative study of pressure fluctuation between condensing and non-condensing cases for different back pressure conditions at points P
1, P
2, and P
3. In most of the experiments related to phase change, condensation was reported to result in large bubbles collapsing. They are either visually monitored or measured through pressure fluctuations. Here, a statistical method based on the standard deviation was selected to summarize the variation in the crest and trough from mean pressure values. The cases with the non-condensing flow can be considered as controls or references, where, except for some minor condensation of atmospheric moisture, the air is largely dry. The condensing flow contains a finite volume of water vapor. In the case of BP
1, i.e., the lowest back pressure, the largest fluctuation was measured at P
3 (in the throat); hence, most of the mass transfer occurred there. For the cases of BP
2, BP
3, and BP
4, the fluctuation tends to stabilize due to the damping action of the increased back pressure. In addition, the largest fluctuation was also found to shift toward P
2, indicating that most of the condensation starts to occur in this region. For the cases of BP
5 and BP
6, with further increased damping, most of the condensation was measured to occur in the suction chamber and the mixing chamber. The influence of this is also reported in
Figure 6.
4.3.2. Qualitative Study of Eductor Mechanism
Figure 10 shows the adjustments made to the experimental setup to visually observe if complete condensation occurs within the system. On the basis of the prior literature, it would be expected that there would be bubbles in the water stream in case of unfinished condensation. During the entire series of experiments; however, no bubbles were observed beyond this point. Therefore, it can be assumed that under the operational conditions applied, complete condensation occurs within the eductor system. It is necessary, however, to find the mechanism of mass transfer over the axial region of the inter-phase interaction within the eductor.
The answer to this question regarding the mechanism of mass transfer helps to strengthen the understanding related to internal flow. There is evidence of visualization practices for internal flows in the existing literature. Yang et al. [
16] studied the condensation of steam in a sub-cooled water pool using a nozzle and barrel adjustment. Innings et al. [
17] visually studied steam condensation in an ultra-high temperature treatment system.
The current study developed a cascade geometry,
Figure 11, to make visual records of the condensing flow of low-pressure vapor into a sub-cooled water jet. The
Figure 12 is the pressure distribution plotted based on the computational analysis. The setup was designed such that the pressure distribution within the cascade channel becomes like the eductor. It is analogous to the axisymmetric geometry of an eductor, extruded to have a similar wall pressure. The flow video was taken at a frame rate of 480 FPS. There are records of theoretical descriptions of flow within an eductor, but visual evidence of actual flow is missing. This is the first experimental evidence showing the mechanism of mass transfer between low-pressure secondary fluid vapor and primary fluid water jet.
Figure 13 is a summary of the images showing two-phase mixing and mass transfer within the cascade. It includes two phase regions between the suction chamber and the diffuser. At the primary fluid volume flow rate of 6.2 LPM and vapor temperature of 98.24 °C, the low-pressure vapor slowly entrains into the main flow stream. The thick mixing region can be clearly seen, where the saturated vapor is in transition to reach the compressed liquid. The vapor axially oscillates between the mixing chamber and throat. The axial pressure is a function of back pressure, in this case, it gradually increases from the suction chamber to the diffuser [
18]. Hence the saturated vapor initially entrained in the passage starts condensing through this non-constant cross-sectional mixing chamber. At the same time, the vapor temperature is also gradually decreasing, and hence the point of complete condensation shifts to the start of the mixing chamber. The varying area of the vapor–liquid interface and the resulting variation in the heat and mass transfer coefficient results in the oscillations observed. This is also visible in the pressure fluctuations seen in
Figure 6.
4.4. Performance of Eductor
4.4.1. Entrainment Ratio
Figure 14 shows the plot for the entrainment ratio with respect to the pressure ratio of the eductor. Here, the pressure ratio is defined as the ratio of the difference between the outlet and suction pressure to the difference between inlet and suction pressure (see Equation (
5)-1). With increasing pressure ratio, the entrainment ratio was measured to decrease. The highest entrainment ratio of 0.0001452 was recorded for a pressure ratio of 0.17. The measurements were taken until the condition in
Figure 14 was achieved. During the experiments, the pressure ratio was controlled by controlling the back pressure (outlet pressure of the Po system). The momentum transfer from the high-velocity jet to the surrounding fluid in the suction chamber performs degassing and creates a low-pressure zone. The secondary fluid at higher pressure flows inward to maintain equilibrium. In the case of a control volume with a finite secondary fluid source, the available secondary fluid is pumped in, and the remaining energy is used to maintain the sub-atmospheric pressure. The total energy is divided into entraining the secondary flow and maintaining the system’s sub-atmospheric condition. The entrainment ratio and pressure ratio are the dimensionless numbers defining these two functional characteristics of an eductor. From the Equations (
1) and (
2), this can further aid in visualizing the characteristics of an eductor as both a compressor and a pump during simultaneous operation.
4.4.2. Maximum Operational Range
Figure 15 shows the optimal operating conditions (points) of the eductor at different inlet pressures. It is at the value of back pressure (outlet pressure Po) where there will be no secondary entrainment. Any further increase in the outlet (back) pressure value will result in reverse flow through the secondary nozzle. The respective flow rate has also been plotted to visualize the total energy of the system. With increasing inlet pressure, the difference between inlet pressure and the ultimate back pressure point is larger. The conversion of energy as the primary fluid moves axially forward is the prime operational characteristic. The conversion of pressure energy to kinetic energy, and then to pressure energy with positive action of friction on the interface for the work done is the specific modality of conversion. The value of inlet pressure and corresponding flow rate describe the total inlet energy. The measured value of optimum compressibility (outlet pressure) for the corresponding inlet conditions creates an idea of the operational extent of eductor.
4.4.3. Efficiency and Exergy Analysis
- i
Efficiency
As the eductor can perform multiple functions based on its application, e.g., compression, pumping, mixing, condensing, degassing, etc., its efficiencies are also defined accordingly. In this application, defining the eductor as a compressor tends to cover most of its functionality. Therefore, the compression efficiency of the eductor has been defined as the ratio of the rate of work carried out on the secondary fluid to the rate of work supplied by the primary fluid (see Equation (
5)-7). The maximum efficiency of 12% was calculated for the eductor operating at BP
5 (
Figure 16). This efficiency term incorporates the effect of multiple functions that occur in the background. The work involves degassing the suction chamber, pumping secondary fluid into the chamber and then in the direction of the outlet, exchange of thermal energy and mass between the two fluid streams, and finally releasing at a pressure higher than the suction pressure. The system is analogous to the piston-cylinder system, where the cylinder is the eductor, the piston is the primary fluid, and the volume X is the suction chamber. When the piston moves in the direction A, X becomes a low-pressure zone, as the volume increases but the mass content of the system remains constant. As soon as the valve is opened, the surrounding fluid rushes into volume X. With an eductor, the primary fluid sweeps away the gas content in the suction chamber, converting it to a low-pressure volume analogous to X, as soon as the secondary inlet valve is opened, as the fluid rushes in to fill the space. The pressure difference is the prime driving force within the eductor, which can be further aided by mass transfer due to condensation. The efficiency for other functions (e.g., pumping efficiency, heat, and mass transfer performance, etc.) can be higher or lower, as the definitions of input and output for these functions can vary. The compression efficiency is a good indicator of overall performance, as it is the result of all the mechanisms that occur within an eductor (Equation (
7)).
- ii
Exergy (xE) analysis
Exergy analysis has been performed to analyze the energy destruction within an eductor system for different back pressures. Equations (
8)–(
10) define the inlet, suction, and outlet-specific exergy, respectively. The exergy and exergy destruction in the eductor were calculated using Equation (
11) and Equation (
12), respectively. The dead state pressure and temperatures were taken to be 100 kPa and 295.4 K, respectively. For the exergy analysis, velocities of the primary and secondary fluid have been calculated based on the flow measurements. The velocity of the primary fluid at point 1 was estimated using the volume flow rate, specific volume, and cross-sectional area at point 1 (
Figure 17). A vortex flow meter (Grundfos VFS 2-40) was used to measure the volume flow rate of the primary fluid. The velocity of the secondary fluid at point 3 was estimated based on the average mass flow rate, specific volume, and cross-sectional area at point 3. The average mass flow rate of the secondary fluid was estimated based on the change in the mass of the secondary fluid in the boiling flask over the period of the experiment. The specific volume of the secondary fluid was assumed to be equal to a specific volume of saturated water vapor at the suction pressure measured at point 3. The diameter of inlet, outlet, suction, and nozzle are 22 mm, 20 mm, 22 mm, and 5 mm, respectively. Standard water property tables were used to estimate the values of specific enthalpy and specific entropy at different points in the eductors at measured pressures and temperatures [
19].
The calculation of exergy for different locations within the eductor was calculated using the following equations;
The general exergy equation can be written as:
Overall exergy destruction is given by:
It is shown that greater exergy is destroyed with a larger secondary flow inside the system.
Figure 18 shows the exergy destruction within the eductor. Future optimization of eductors will include increasing secondary flow into the system as a primary focus; hence, it will also be essential to work toward minimizing exergy destruction to offset this trend and ensure high performance.
The efficiency and exergy destruction at BP
6 is estimated to be minimal. At point BP
6, the back pressure is the highest and the driving pressure difference is the lowest. This results in a minimum secondary flow, and from Equation (
7), it can be seen that the efficiency will decrease with a drop in the secondary flow rate; hence the lowest efficiency among the six back pressure conditions tested. Another observation is that at BP
6, the exergy destruction is also minimum, and this also can be attributed to the minimum secondary flow rate. Consider Equation (
12), which has three exergy terms, the first and third term in that equation is related to the liquid phase of the fluid and this phase does not have a significant temperature change. The second term is related to the vapor phase, which undergoes a phase change and hence the largest contribution to the exergy. Therefore, in BP
6, the rate of exergy destruction is minimal, corresponding to the lowest mass flow rate of the secondary fluid.
5. Eductor for Membrane Distillation
The thermal desalination technologies are energy-intensive processes, but utilization of waste heat (especially low-grade heat) would make it feasible on synergetic (combined recovery of energy and water production) grounds. All thermal systems require large condensers/heat exchangers either for vapor condensation or cooling of the condensing fluid. Although they have large recovery ratios, effective recovery using low-grade heat requires sub-atmospheric vapor generation and large condensers for sensible cooling. The application of eductors for combined vacuum generation, vapor transfer, and condensation would significantly reduce the footprint of existing technology. Eductors are simple static mechanical devices capable of performing multiple fluid functions: pumping, degassing, mixing, direct contact condensing, and compressing. Focusing on MD, replacing the vacuum pump and condenser with an eductor would simplify the existing system and could enhance performance.
Membrane Distillation (MD) is a hybrid technology that is driven thermally and separated through hydrophobic membranes. Based on the permeate flux management method, they are classified into Direct Contact MD (DCMD), Vacuum MD (VMD), Air Gap MD (AGMD), and Sweep Gas MD (SGMD), as shown in
Figure 19 [
20,
21]. All of these processes have a feed and a permeate chamber. At the feed side, continuous feed circulation/recirculation occurs, allowing evaporation at the membrane surface. The hydrophobic nature of the membrane material allows the vapor to cross the membrane boundary while preventing the flow of liquid feed water from crossing. The mechanism of transmembrane vapor transfer mechanism and the management of this vapor differentiate these processes.
For a general Vacuum Membrane Distillation process, feed pressure and temperature, permeate side pressure, permeate vapor suction, condensation, and freshwater transfer are the primary operations and variables. The eductor is capable of vacuum generation, pumping, mixing, heat and mass transfer, and higher-pressure discharge. These capabilities align perfectly with the permeate side operational requirements of a VMD.
Figure 20 is the schematic layout of an ejector-based VMD process. The vapor separates from the feed through a hydrophobic membrane (details on VMD can be accessed through), since the permeate chamber pressure is maintained lower than the vapor pressure, condensation does not occur, and the vapor is entrained by the eductor (where there is already primary fluid flow). The primary fluid and secondary fluid (the vapor) mix, transferring mass followed and heat before finally discharging as a single phase fluid at a pressure higher than the secondary (vapor) pressure. Particularly, in an off-grid small-scale desalination unit, this technology could ensure simplicity and reliability. There is great potential for an eductor to improve the sustainable production of freshwater using the abundance of low-grade thermal energy available (solar, industrial waste heat, etc.).
6. Conclusions
In contrast to the previous literature, this study developed the eductor as an active vapor transfer and condensation device. A single species fluid (water) with two phases (liquid water as the primary, and water vapor as the secondary) has been used for this study. The prime objective of this application of the eductor is to use the eductor in MD. The study also discusses the operational characteristics of two-phase single species flow within an eductor, to identify the operational range in the developed system.
The series of experiments studied eductor behavior at six different back pressure conditions, and the results have been discussed. With increasing back pressure, the pressure around the suction chamber and the mixing chamber increased. This negatively affected the entrainment of the secondary fluid in the system. One way to identify the zone of condensation was to measure the static pressure. During the phase change from saturated vapor to mixture, a large quantity of vapor bubbles collapse, and the surrounding water molecules rush into the voids. This forms large pressure fluctuations within the flow region, which could be measured. The visualization experiments performed suggest that this filling of voids by liquid is an oscillating phenomenon that is a result of the eductor geometry and plays a vital role during sub-atmospheric thermal saturation.
In applications where the mixing of primary and secondary fluid does not have any influence on the desired product, eductors can be used to maintain sub-atmospheric pressure, secondary pumping, control of vapor generation, and direct contact condensation. The control of all these parameters can be conducted precisely and non-invasively by controlling the back pressure or pressure difference. This strengthens the usability of the eductor in MD for fresh water production.
It was shown that the larger the secondary mass flow rate, the larger the exergy destruction calculated. Hence, design optimization focusing on the entrainment ratio should also target the pressure ratio to have minimum exergy destruction.
This study contributes to flow phenomena studies, along with providing experimental data for verification of computational models related to thermal saturation, mixing of condensing flow, mixing of non-condensing flow, and phase transformation. More studies are required to focus on the factors that influence the frequency of oscillation during direct contact condensation between two-phase flows. In addition to the study of fundamental flow physics, the performance study of eductor-based MD is an additional important topic for the future study.
Author Contributions
Conceptualization, methodology, experiments, writing, R.K., K.I. and A.D.; experiments, visualization, editing, R.K., X.Z., E.R. and A.D.; editing, supervision, K.I. and A.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| Er | Entrainment ratio |
| Pr | Pressure Ratio |
| ṁ | Mass Flow rate |
| Density |
| P | Pressure |
| V | Velocity |
| T | Temperature |
| hc | Heat Transfer Coefficient |
| BP | Back Pressure |
| DCC | Direct Contact Condensation |
| eductor | Efficiency of eductor |
| xe | Specific Exergy |
| xE | Exergy |
| Subscript |
| S | Suction |
| i | Inlet |
| O | Outlet |
| V | Water Vapor |
| l | Water Liquid |
| r | Region |
| p | Phase |
| d | Destruction |
References
- Koirala, R.; Ve, Q.L.; Date, A.; Inthavong, I.; Akbarzadeh, A. Influence of inlet pressure and geometric variations on the applicability of Eductor in low temperature thermal desalinations. J. King Saud Univ. Eng. Sci. 2021. [Google Scholar] [CrossRef]
- Kumar, R.A.; Rajesh, G. Physics of vacuum generation in zero-secondary flow ejectors. Phys. Fluids 2018, 30, 066102. [Google Scholar] [CrossRef]
- Yang, X.; Long, X.; Yao, X. Numerical investigation on the mixing process in a steam ejector with different nozzle structures. Int. J. Therm. Sci. 2012, 56, 95–106. [Google Scholar] [CrossRef]
- Ksenofontov, B.; Vasilieva, Y.; Kaptinova, S. An ejector for mixing a reagent with discharge water. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2019; Volume 492. [Google Scholar]
- Mueller, N.H. Water Jet Pump. J. Hydraul. Div. 1964, 90, 83–113. [Google Scholar] [CrossRef]
- Elbel, S.; Hrnjak, P. Ejector Refrigeration: An overview of Historical and present developments with an Emphasis on Air-Conditioning Applications. In Proceedings of the International Refrigeration Air-conditioning Conference, West Lafayette, IN, USA, 14–17 July 2008. [Google Scholar]
- Zhang, Z.; Chong, D.; Yan, J. Modeling and experimental investigation on water-driven steam injector for waste heat recovery. Appl. Therm. Eng. 2012, 40, 189–197. [Google Scholar] [CrossRef]
- Shah, A.; Chughtai, I.R.; Inayat, H. Experimental and numerical analysis of steam jet pump. Int. J. Mutiphase Flow 2012, 37, 1305–1314. [Google Scholar] [CrossRef]
- Banu, J.P.; Mallikarjuna, J.M.; Mani, A. Experimental and numerical investigation of Ejector jet refrigeration system with primary steam swirl. In Proceedings of the International Refrigeration and Air Conditioning Conference, West Lafayette, IN, USA, 11–14 July 2016. [Google Scholar]
- Yan, J.; Chong, D.; Wu, X. Effect of swirling vanes on performance of steam–water jet injector. Appl. Therm. Eng. 2010, 30, 623–630. [Google Scholar] [CrossRef]
- Cramers, P.H.; Beenackers, A.A. Influence of the ejector configuration, scale and the gas density on the mass transfer characteristics of gas-liquid ejectors. Chem. Eng. J. 2001, 82, 131–141. [Google Scholar] [CrossRef]
- Cramers, P.H.; Smit, L.; Leuteritz, G.M.; Dierendonck, L.L.V.; Beenackers, A.A. Hydrodynamics and local mass transfer characteristics of gas-liquid ejectors. Chem. Eng. J. Biochem. Eng. J. 1993, 53, 67–73. [Google Scholar] [CrossRef]
- Narabayashi, T.; Mizumachib, W.; Mori, M. Study on two-phase flow dynamics in steam injectors. Nucl. Eng. Des. 1997, 175, 147–156. [Google Scholar] [CrossRef]
- Yan, J.J.; Shao, S.-P.; Liu, J.-P.; Zhang, Z. Experiment and analysis on performance of steam-driven jet injector for district-heating system. Appl. Therm. Eng. 2005, 25, 1153–1167. [Google Scholar] [CrossRef]
- Koirala, R.; Date, A.; Inthavong, K. Numerical study of flow inside water jet eductor. Exp. Comput. Multiph. Flow 2021. [Google Scholar]
- Yang, X.; Chong, D.; Liu, J.; Zong, X. Pressure oscillation induced by steam jet condensation in subcooled water flow in a channel. Int. J. Heat Mass Transf. 2016, 98, 426–437. [Google Scholar] [CrossRef]
- Innings, F.; Hamberg, L. Steam condensation dynamics in annular gap and multi-hole steam injectors. Procedia Food Sci. 2011, 1, 1278–1284. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.J.; Lee, S.C.; Bankoff, S.G. Heat transfer and interfacial drag in countercurrent steam-water stratified flow. Int. J. Multiphase Flow 1985, 11, 593–606. [Google Scholar] [CrossRef]
- Cengel, Y.A.; Boles, M.A. Thermodynamics: An Engineering Approach; McGraw-Hill Education: New York, NY, USA, 2014; Volume 8. [Google Scholar]
- Belessiotis, V.; Kalogirou, S.; Delyannis, E. Membrane Distillation. In Thermal Solar Desalination: Methods Systems; Elsevier: Amsterdam, The Netherlands, 2016; pp. 191–251. [Google Scholar]
- Lawson, K.W.; Lloyd, D.R. Membrane Distillation. J. Membr. Sci. 1997, 124, 1–25. [Google Scholar] [CrossRef]
Figure 1.
Physical model of eductor.
Figure 1.
Physical model of eductor.
Figure 2.
T-S diagram estimated for the eductor.
Figure 2.
T-S diagram estimated for the eductor.
Figure 3.
Schematic diagram of experimental setup.
Figure 3.
Schematic diagram of experimental setup.
Figure 4.
Experimental setup at Thermo-fluid Lab-RMIT.
Figure 4.
Experimental setup at Thermo-fluid Lab-RMIT.
Figure 5.
Fluid energy scenario in the eductor.
Figure 5.
Fluid energy scenario in the eductor.
Figure 6.
Pressure and temperature measured at secondary source for different back pressures.
Figure 6.
Pressure and temperature measured at secondary source for different back pressures.
Figure 7.
Axial pressure distribution in non-condensing flow.
Figure 7.
Axial pressure distribution in non-condensing flow.
Figure 8.
Axial pressure distribution in condensing flow.
Figure 8.
Axial pressure distribution in condensing flow.
Figure 9.
Deviation from the mean pressure.
Figure 9.
Deviation from the mean pressure.
Figure 10.
Visual inspection of bubbles.
Figure 10.
Visual inspection of bubbles.
Figure 11.
3D printed transparent cascade.
Figure 11.
3D printed transparent cascade.
Figure 12.
The pressure distribution between eductor and cascade for the analogy of the study.
Figure 12.
The pressure distribution between eductor and cascade for the analogy of the study.
Figure 13.
Framewise observation of phase change within Eductor cascade.
Figure 13.
Framewise observation of phase change within Eductor cascade.
Figure 14.
Entrainment ratio vs. Pressure ratio for eductor.
Figure 14.
Entrainment ratio vs. Pressure ratio for eductor.
Figure 15.
Optimum operational point of eductor.
Figure 15.
Optimum operational point of eductor.
Figure 16.
Efficiency of Eductor at different back pressure.
Figure 16.
Efficiency of Eductor at different back pressure.
Figure 17.
Locations in eductor for exergy (xE) analysis.
Figure 17.
Locations in eductor for exergy (xE) analysis.
Figure 18.
Exergy destruction in Eductor.
Figure 18.
Exergy destruction in Eductor.
Figure 19.
Membrane Distillation Desalination Processes.
Figure 19.
Membrane Distillation Desalination Processes.
Figure 20.
Eductor-based MD process.
Figure 20.
Eductor-based MD process.
Table 1.
Operational parameters of Eductor.
Table 1.
Operational parameters of Eductor.
| Parameter | Description | Units |
|---|
| Inlet Pressure | 168.3 | kPa |
| Inlet Temperature | 22.4 | °C |
| Inlet Flow rate | 16.54 | LPM |
| Outlet Pressure | BP1 | BP2 | BP3 | BP4 | BP5 | BP6 | kPa |
| | 98.67 | 100.12 | 101.99 | 106.31 | 111.70 | 118.83 | |
| Suction Temperature | BP1 | BP2 | BP3 | BP4 | BP5 | BP6 | °C |
| | 93.61 | 94.54 | 95.26 | 96.48 | 98.37 | 105.1 | |
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).