Utilization of Electric Vehicle Grid Integration System for Power Grid Ancillary Services
Abstract
:1. Introduction
2. Power Grid Ancillary Services and EV Grid Integration Model
2.1. Grid Ancillary Service Using EVGI
2.1.1. Real and Reactive Power Supply
2.1.2. Voltage Regulation
2.1.3. Frequency Regulation
2.1.4. Power Quality Improvement and Harmonics Reduction
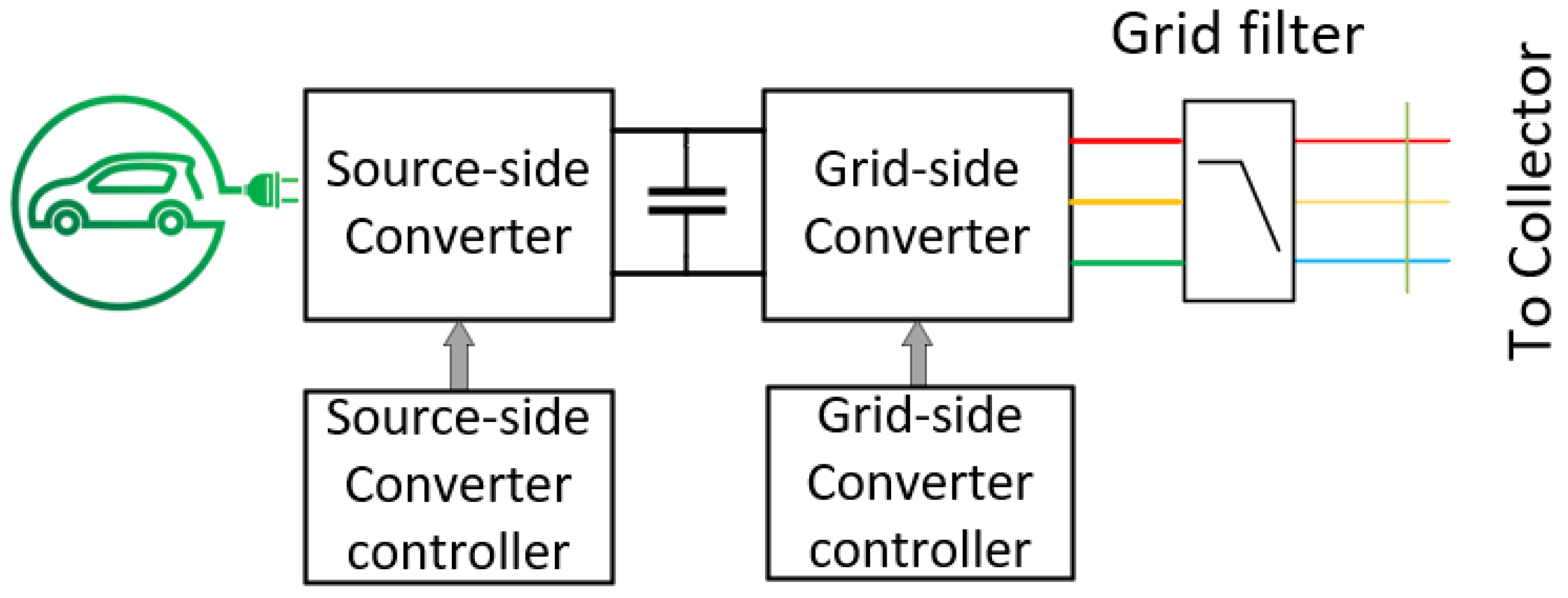
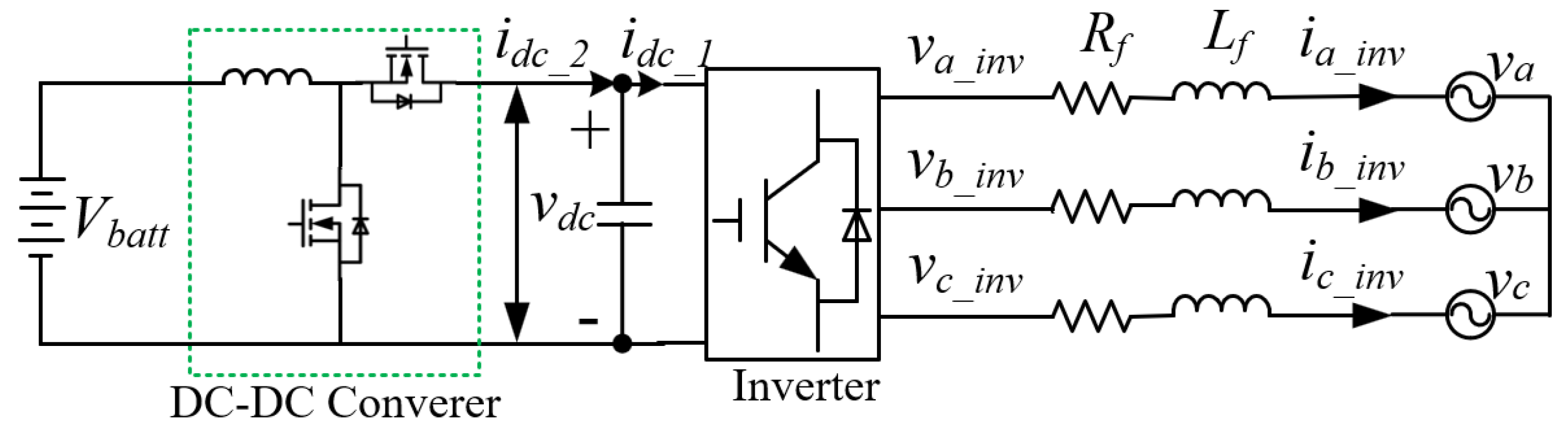
2.2. Inverter Interfaced EVGI System Model
3. Grid Connected Inverter Modelling and Control
3.1. Grid Connected Inverter Model in the d-q Reference Frame
3.2. Vector Control Design of a Three-Phase GCI in the d-q Reference Frame
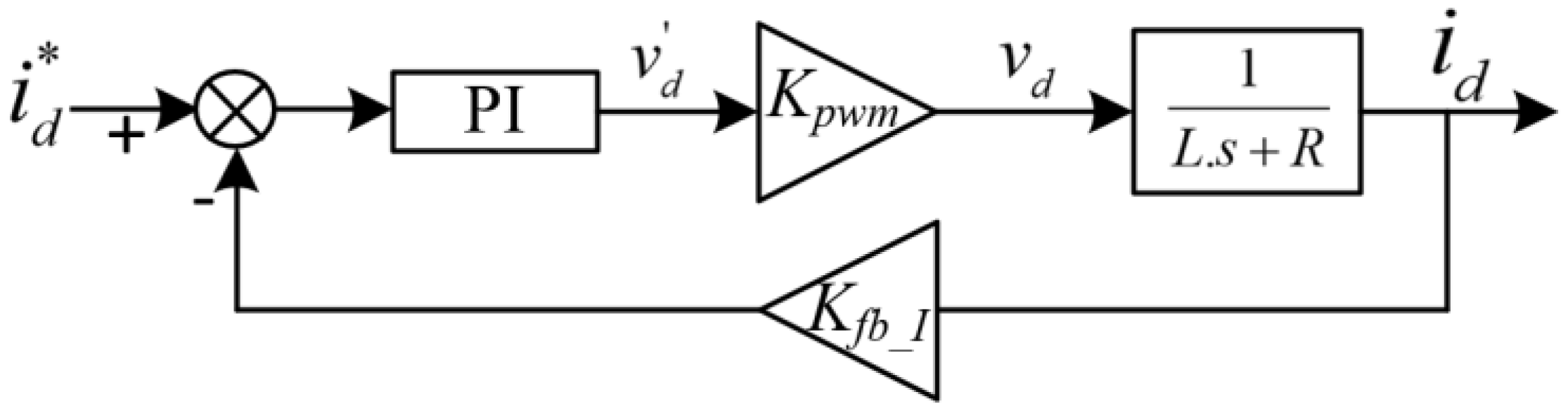
3.2.1. Inner Control Loop Design
3.2.2. Outer Control Loops Design
- (a)
- DC bus voltage control
- (b)
- Reactive power control
- (c)
- PCC bus voltage control
- (d)
- Real power and primary frequency control
4. EMT Simulation of Inverter-Interfaced EVGI System for Ancillary Services
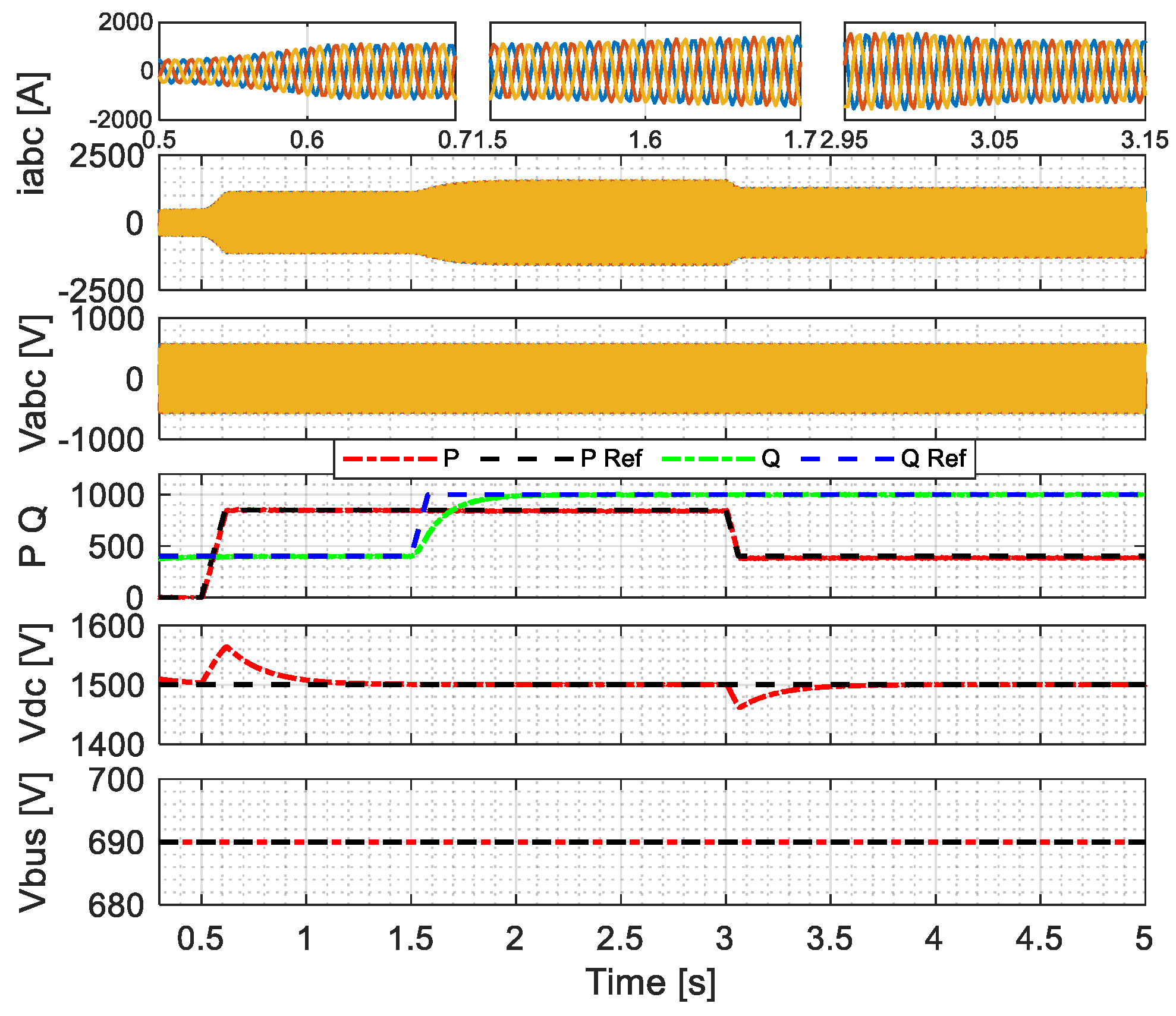
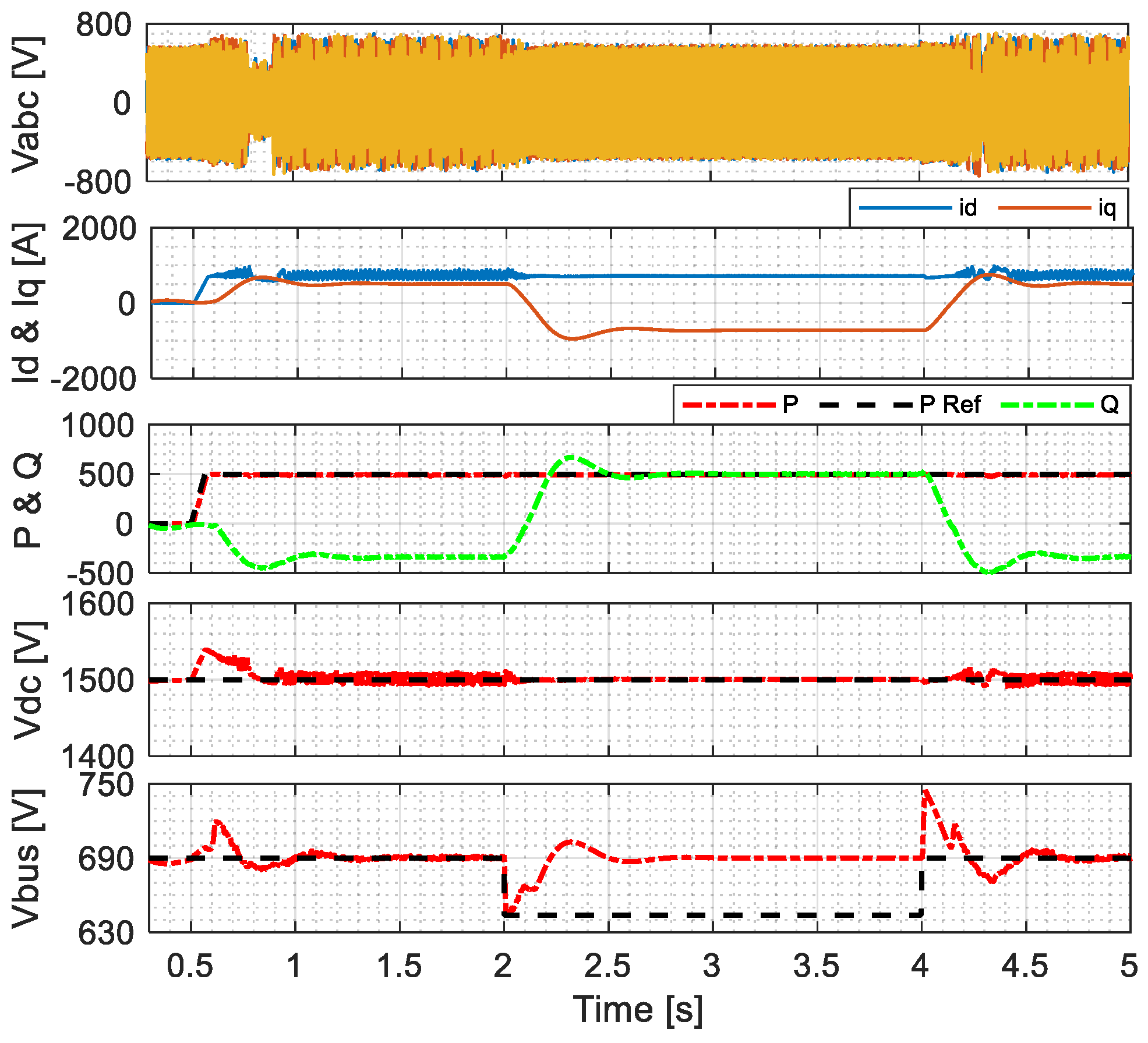
4.1. Real and Reactive Power Supply
4.2. Voltage Support Using Reactive Power
4.3. Frequency Regulation
4.4. Harmonics Reduction
5. Performance Comparison
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| AC | Alternating Current |
| DC | Direct Current |
| DER | Distributed Energy Resource |
| DG | Distributed Generation |
| EMT | Electromagnetic Transient |
| ESS | Energy Storage System |
| EV | Electric Vehicle |
| EVGI | Electric Vehicle Grid Integration |
| GCI | Grid-connected inverter |
| G2V | Grid to Vehicle |
| PCC | Point of Common Coupling |
| PV | Photovoltaic |
| RES | Renewable Energy Source |
| RMS | Root Mean Square |
| SOC | State of Charge |
| SOH | State of Health |
| WT | Wind Turbine |
| V2G | Vehicle-to-Grid |
References
- Shareef, H.; Islam, M.M.; Mohamed, A. A review of the stage-of-the-art charging technologies, placement methodologies, and impacts of electric vehicles. Renew. Sustain. Energy Rev. 2016, 64, 403–420. [Google Scholar] [CrossRef]
- Das, H.S.; Rahman, M.M.; Li, S.; Tan, C.W. Electric vehicles standards, charging infrastructure, and impact on grid integration: A technological review. Renew. Sustain. Energy Rev. 2020, 120, 109618. [Google Scholar] [CrossRef]
- Rahman, S.; Khan, I.A.; Amini, M.H. A Review on Impact Analysis of Electric Vehicle Charging on Power Distribution Systems. In Proceedings of the 2020 2nd International Conference on Smart Power & Internet Energy Systems (SPIES), Bangkok, Thailand, 15–18 September 2020; pp. 420–425. [Google Scholar] [CrossRef]
- Roy, R.; Alahakoon, S.; Arachchillage, S. Grid Impacts of Uncoordinated Fast Charging of Electric Ferry. Batteries 2021, 7, 13. [Google Scholar] [CrossRef]
- Leemput, N.; Geth, F.; Van Roy, J.; Delnooz, A.; Buscher, J.; Driesen, J. Impact of Electric Vehicle On-Board Single-Phase Charging Strategies on a Flemish Residential Grid. IEEE Trans. Smart Grid 2014, 5, 1815–1822. [Google Scholar] [CrossRef]
- Veldman, E.; Verzijlbergh, R.A. Distribution Grid Impacts of Smart Electric Vehicle Charging From Different Perspectives. IEEE Trans. Smart Grid 2014, 6, 333–342. [Google Scholar] [CrossRef]
- Calearo, L.; Thingvad, A.; Suzuki, K.; Marinelli, M. Grid Loading Due to EV Charging Profiles Based on Pseudo-Real Driving Pattern and User Behavior. IEEE Trans. Transp. Electrif. 2019, 5, 683–694. [Google Scholar] [CrossRef] [Green Version]
- Solanke, T.U.; Ramachandaramurthy, V.K.; Yong, J.Y.; Pasupuleti, J.; Kasinathan, P.; Rajagopalan, A. A review of strategic charging–discharging control of grid-connected electric vehicles. J. Energy Storage 2020, 28, 101193. [Google Scholar] [CrossRef]
- Mukherjee, J.C.; Gupta, A. A Review of Charge Scheduling of Electric Vehicles in Smart Grid. IEEE Syst. J. 2014, 9, 1541–1553. [Google Scholar] [CrossRef]
- Tan, K.M.; Ramachandaramurthy, V.K.; Yong, J.Y. Integration of electric vehicles in smart grid: A review on vehicle to grid technologies and optimization techniques. Renew. Sustain. Energy Rev. 2016, 53, 720–732. [Google Scholar] [CrossRef]
- Yilmaz, M.; Krein, P.T. Review of the impact of vehicle-to-grid technologies on distribution systems and utility interfaces. IEEE Trans. Power Electron. 2012, 28, 5673–5689. [Google Scholar] [CrossRef]
- Campbell, J. Ancillary Services Provided from DER; Oak Ridge National Lab.(ORNL): Oak Ridge, TN, USA, 2005. [Google Scholar] [CrossRef] [Green Version]
- Aziz, M. Electric vehicle utilization for ancillary grid services. AIP Conf. Proc. 2018, 1931, 030069. [Google Scholar] [CrossRef]
- Wu, C.; Mohsenian-Rad, A.-H.; Huang, J. Vehicle-to-grid systems: Ancillary services and communications. In Smart Grid Communications and Networking; Cambridge University Press: Cambridge, UK, 2012; pp. 91–108. [Google Scholar] [CrossRef]
- Hernández, J.; Sutil, F.J.S.; Vidal, P.; Rus-Casas, C. Primary frequency control and dynamic grid support for vehicle-to-grid in transmission systems. Int. J. Electr. Power Energy Syst. 2018, 100, 152–166. [Google Scholar] [CrossRef]
- Ravi, S.S.; Aziz, M. Utilization of Electric Vehicles for Vehicle-to-Grid Services: Progress and Perspectives. Energies 2022, 15, 589. [Google Scholar] [CrossRef]
- Yilmaz, M.; Krein, P.T. Review of benefits and challenges of vehicle-to-grid technology. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 3082–3089. [Google Scholar] [CrossRef]
- Zhou, K.; Cheng, L.; Wen, L.; Lu, X.; Ding, T. A coordinated charging scheduling method for electric vehicles considering different charging demands. Energy 2020, 213, 118882. [Google Scholar] [CrossRef]
- Iqbal, S.; Xin, A.; Jan, M.U.; Rehman, H.U.; Masood, A.; Rizvi, S.A.A.; Salman, S. Aggregated Electric Vehicle-to-Grid for Primary Frequency Control in a Microgrid- A Review. In Proceedings of the IEEE 2nd International Electrical and Energy Conference (CIEEC), Beijing, China, 4–7 November 2018; pp. 563–568. [Google Scholar] [CrossRef]
- Saldaña, G.; San Martín, J.I.; Zamora, I.; Asensio, F.J.; Oñederra, O. Electric Vehicle into the Grid: Charging Methodologies Aimed at Providing Ancillary Services Considering Battery Degradation. Energies 2019, 12, 2443. [Google Scholar] [CrossRef]
- Wang, J.; Bharati, G.R.; Paudyal, S.; Ceylan, O.; Bhattarai, B.P.; Myers, K.S. Coordinated Electric Vehicle Charging With Reactive Power Support to Distribution Grids. IEEE Trans. Ind. Inform. 2018, 15, 54–63. [Google Scholar] [CrossRef]
- Pirouzi, S.; Aghaei, J.; Niknam, T.; Khooban, M.H.; Dragicevic, T.; Farahmand, H.; Korpas, M.; Blaabjerg, F. Power Conditioning of Distribution Networks via Single-Phase Electric Vehicles Equipped. IEEE Syst. J. 2019, 13, 3433–3442. [Google Scholar] [CrossRef] [Green Version]
- Aziz, M.; Oda, T.; Kashiwagi, T. Extended utilization of electric vehicles and their re-used batteries to support the building energy management system. Energy Procedia 2015, 75, 1938–1943. [Google Scholar] [CrossRef] [Green Version]
- Behravesh, V.; Keypour, R.; Foroud, A.A. Control strategy for improving voltage quality in residential power distribution network consisting of roof-top photovoltaic-wind hybrid systems, battery storage and electric vehicles. Sol. Energy 2019, 182, 80–95. [Google Scholar] [CrossRef]
- Kaur, K.; Kumar, N.; Singh, M. Coordinated Power Control of Electric Vehicles for Grid Frequency Support: MILP-Based Hierarchical Control Design. IEEE Trans. Smart Grid 2018, 10, 3364–3373. [Google Scholar] [CrossRef]
- Arias, N.B.; Hashemi, S.; Andersen, P.B.; Traholt, C.; Romero, R. V2G enabled EVs providing frequency containment reserves: Field results. In Proceedings of the 2018 IEEE International Conference on Industrial Technology (ICIT), Lyon, France, 20–22 February 2018; pp. 1814–1819. [Google Scholar] [CrossRef] [Green Version]
- Rahmani-Andebili, M. Spinning Reserve Capacity Provision by the Optimal Fleet Management of Plug-In Electric Vehicles Considering the Technical and Social Aspects. In Planning and Operation of Plug-In Electric Vehicles; Springer: Berlin/Heidelberg, Germany, 2019; pp. 49–74. [Google Scholar] [CrossRef]
- Izadkhast, S.; Garcia-Gonzalez, P.; Frìas, P.; Ramìrez-Elizondo, L.; Bauer, P. An aggregate model of plug-in electric vehicles including distribution network characteristics for primary frequency control. IEEE Trans. Power Syst. 2015, 31, 2987–2998. [Google Scholar] [CrossRef]
- Buja, G.; Bertoluzzo, M.; Fontana, C. Reactive Power Compensation Capabilities of V2G-Enabled Electric Vehicles. IEEE Trans. Power Electron. 2017, 32, 9447–9459. [Google Scholar] [CrossRef]
- Tan, K.M.; Padmanaban, S.; Yong, J.Y.; Ramachandaramurthy, V.K. A multi-control vehicle-to-grid charger with bi-directional active and reactive power capabilities for power grid support. Energy 2019, 171, 1150–1163. [Google Scholar] [CrossRef]
- Khalid, M.S.; Lin, X.; Zhuo, Y.; Kumar, R.; Rafique, M.K. Impact of Energy Management of Electric Vehicles on Transient Voltage Stability of Microgrid. World Electr. Veh. J. 2015, 7, 577–588. [Google Scholar] [CrossRef] [Green Version]
- Ebrahimzadeh, E.; Blaabjerg, F. Reactive Power Role and Its Controllability in AC Power Transmission Systems. In Reactive Power Control in AC Power Systems; Springer: Berlin/Heidelberg, Germany, 2017; pp. 117–136. [Google Scholar] [CrossRef]
- Sortomme, E.; El-Sharkawi, M.A. Optimal Scheduling of Vehicle-to-Grid Energy and Ancillary Services. IEEE Trans. Smart Grid 2011, 3, 351–359. [Google Scholar] [CrossRef]
- Tang, C.; Qu, H. Development of Ancillary Services in the Electricity Market of China and its Joint Market Optimization Model. IOP Conf. Series: Earth Environ. Sci. 2020, 571, 012029. [Google Scholar] [CrossRef]
- Almeida, P.R.; Soares, F.; Lopes, J.P. Electric vehicles contribution for frequency control with inertial emulation. Electr. Power Syst. Res. 2015, 127, 141–150. [Google Scholar] [CrossRef] [Green Version]
- Datta, M.; Senjyu, T. Fuzzy Control of Distributed PV Inverters/Energy Storage Systems/Electric Vehicles for Frequency Regulation in a Large Power System. IEEE Trans. Smart Grid 2013, 4, 479–488. [Google Scholar] [CrossRef]
- Teke, A.; Saribulut, L.; Tumay, M. A novel reference signal generation method for power-quality improvement of unified power-quality conditioner. IEEE Trans. Power Deliv. 2011, 26, 2205–2214. [Google Scholar] [CrossRef]
- Hong, Y.-Y.; Chen, Y. Placement of power quality monitors using enhanced genetic algorithm and wavelet transform. IET Gener. Transm. Distrib. 2011, 5, 461–466. [Google Scholar] [CrossRef]
- Wasiak, I.; Pawelek, R.; Mienski, R.; Gburczyk, P. Using energy storage for energy management and load compensation in LV microgrids. In Proceedings of the 2012 IEEE 15th International Conference on Harmonics and Quality of Power, Hong Kong, China, 17–20 June 2012; pp. 904–908. [Google Scholar] [CrossRef]
- Mikkili, S.; Panda, A. Real-time implementation of PI and fuzzy logic controllers based shunt active filter control strategies for power quality improvement. Int. J. Electr. Power Energy Syst. 2012, 43, 1114–1126. [Google Scholar] [CrossRef]
- Mahela, O.P.; Shaik, A.G. Topological aspects of power quality improvement techniques: A comprehensive overview. Renew. Sustain. Energy Rev. 2016, 58, 1129–1142. [Google Scholar] [CrossRef]
- Adib, A.; Mirafzal, B.; Wang, X.; Blaabjerg, F. On Stability of Voltage Source Inverters in Weak Grids. IEEE Access 2018, 6, 4427–4439. [Google Scholar] [CrossRef]
- Li, S.; Haskew, T.A.; Hong, Y.-K.; Xu, L. Direct-current vector control of three-phase grid-connected rectifier–inverter. Electr. Power Syst. Res. 2010, 81, 357–366. [Google Scholar] [CrossRef]
- Zhou, K.; Wang, D. Relationship between space-vector modulation and three-phase carrier-based PWM: A comprehen-sive analysis [three-phase inverters]. IEEE Trans. Ind. Electron. 2002, 49, 186–196. [Google Scholar] [CrossRef] [Green Version]
- Pilehvar, M.S.; Mirafzal, B. A Frequency Control Method for Islanded Microgrids Using Energy Storage Systems. In Proceedings of the 2020 IEEE Applied Power Electronics Conference and Exposition (APEC), New Orleans, LA, USA, 15–19 March 2020; pp. 2327–2332. [Google Scholar] [CrossRef]
- Irfan, M.; Rangarajan, S.S.; Collins, E.; Senjyu, T. Enhancing the Power Quality of the Grid Interactive Solar Photovoltaic-Electric Vehicle System. World Electr. Veh. J. 2021, 12, 98. [Google Scholar] [CrossRef]
- Javadi, A.; Al-Haddad, K. A Single-Phase Active Device for Power Quality Improvement of Electrified Transportation. IEEE Trans. Ind. Electron. 2015, 62, 3033–3041. [Google Scholar] [CrossRef]
- Zargar, B.; Wang, T.; Pitz, M.; Bachmann, R.; Maschmann, M.; Bintoudi, A.; Zyglakis, L.; Ponci, F.; Monti, A.; Ioannidis, D. Power Quality Improvement in Distribution Grids via Real-Time Smart Exploitation of Electric Vehicles. Energies 2021, 14, 3533. [Google Scholar] [CrossRef]
- Knezovic, K.; Martinenas, S.; Andersen, P.B.; Zecchino, A.; Marinelli, M. Enhancing the Role of Electric Vehicles in the Power Grid: Field Validation of Multiple Ancillary Services. IEEE Trans. Transp. Electrif. 2016, 3, 201–209. [Google Scholar] [CrossRef]






| Parameters | Values | Unit |
|---|---|---|
| Rated power | 1.5 | MW |
| Rated PCC Voltage | 690 | Vrms |
| DC bus voltage | 1500 | V |
| LCL filter inductance (Lf, Lg) | 0.02 | mH |
| LCL filter resistance | 0.003 | Ω |
| LCL filter Capacitance | 25 | µF |
| DC–DC converter inductor | 5 | mH |
| DC–DC converter inductor resistance | 0.003 | Ω |
| DC–DC converter capacitor | 100 | µF |
| References | Real and Reactive Power | Voltage Regulation | Frequency Regulation | PQ Improvement/Harmonic Reduction |
|---|---|---|---|---|
| Buja, G., et. al. [29] | √ | - | - | - |
| Tan, K.M., et al. [30] | √ | - | - | - |
| Khalid, M.S., et. al. [31] | - | √ | - | - |
| Hernández, J.C., et al. [15] | - | - | √ | - |
| Irfan, M., et al. [46] | - | - | - | √ |
| Javadi, A., and K. Al-Haddad [47] | - | - | - | √ |
| Zargar, B., et al. [48] | √ | - | - | √ |
| Knezović, K., et al. [49] | - | √ | √ | - |
| This paper | √ | √ | √ | √ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Das, H.S.; Nurunnabi, M.; Salem, M.; Li, S.; Rahman, M.M. Utilization of Electric Vehicle Grid Integration System for Power Grid Ancillary Services. Energies 2022, 15, 8623. https://doi.org/10.3390/en15228623
Das HS, Nurunnabi M, Salem M, Li S, Rahman MM. Utilization of Electric Vehicle Grid Integration System for Power Grid Ancillary Services. Energies. 2022; 15(22):8623. https://doi.org/10.3390/en15228623
Chicago/Turabian StyleDas, Himadry Shekhar, Md Nurunnabi, Mohamed Salem, Shuhui Li, and Mohammad Mominur Rahman. 2022. "Utilization of Electric Vehicle Grid Integration System for Power Grid Ancillary Services" Energies 15, no. 22: 8623. https://doi.org/10.3390/en15228623






