PV-CrackNet Architecture for Filter Induced Augmentation and Micro-Cracks Detection within a Photovoltaic Manufacturing Facility

Abstract

Photovoltaic cell manufacturing is a rigorous process involving many stages where the cell surface is exposed to external pressure and temperature differentials. This provides fertile ground for micro-cracks to develop on the cell surface. At present, domain experts carry out a manual inspection of the cell surface to judge if any micro-cracks are present. This research looks to overcome the issue of cell data scarcity through the proposed filter-induced augmentations, thus providing developers with an effective, cost-free mechanism for generating representative data samples. Due to the abstract nature of the cell surfaces, the proposed augmentation strategy is effective in generating representative samples for better generalization. Furthermore, a custom architecture is developed that is computationally lightweight compared to state-of-the-art architectures, containing only 7.01 million learnable parameters while achieving an F1-score of 97%.

1. Introduction

Global emissions and their mitigation are a shared concern across the globe, giving rise to the field of renewable energy, from which solar power is accepted as one of the practically feasible options, deployable at all levels of society. Manifesting its signification and mitigation of C02 emissions, an example is presented of a solar deployment project based in California, where 113,533 domestic solar deployments have resulted in the reduction of 696,544 metric tons of CO₂ emissions [1].

Similar to other manufacturing procedures, photovoltaic (PV) cell production is a rigorous and delicate process, vulnerable to the emergence of defects such as micro-cracks. Micro-cracks are a common defect produced by unwarranted mechanical or thermal stress during fabrication [2]. Micro-cracks can also be difficult to detect with the human eye. Hence, electroluminescence (EL) imaging is utilized for the detection of micro-cracks [3] in multi-crystalline PV cells [4].

Presently, quality inspection within PV manufacturing facilities is a manual process involving domain experts, analyzing EL images of PV cell surfaces at various manufacturing stages. This not only leads to increased costs for recruiting experts or third-party inspection organizations but also increases inspection time and can increase the error rate due to human bias. This provides a segue into the case for implementing computer vision as a non-invasive mechanism integrated into the existing quality inspection process for assisting with the detection of defective PV cells in a timely and cost-effective manner [5]. This research addresses the issue of data scarcity for EL-based PV samples representative of manufacturing facilities and presents a highly generalized CNN for micro-crack detection with EL-based PV samples.

1.1. Literature Review

Studying the present literature concerning the quality inspection of PV cells via automation, it can be stated that active research is taking place, with researchers exploring the use of deep learning, in particular computer vision, for PV fault detection.

Starting with machine learning, Hussain et al. [6] present a framework for deciding if the use of machine/deep learning is required for detecting PV faults compared to conventional statistical methods. The authors utilize ‘kMeans’ for obtaining labels for the unclassified dataset before training on a wide range of machine learning algorithms as well as a multilayer perceptron neural network. The authors report respectable performance for most algorithms, ranging from 94 to 100%. Although the performance is impressive, the research lacks in differentiating on surface faults rather than focusing on post-deployment disconnection faults.

Akram et al. [7] present a deep learning architecture based on convolutional neural networks (CNN) for the detection of defects on the PV cell surface. After developing and training an ‘isolated model’ based on EL PV cell samples, the authors implement transfer learning with the aim of tuning the trained architecture for infrared PV cell surface samples, reporting an impressive accuracy of 99.23%. With regards to the size of the dataset, it can be classified as small, i.e., less than 800 images. However, further inspection into the PV cell surface faults shows the faults had to be artificially generated onto the PV cell surface, which could raise questions on the representativeness and true generalization of the trained architecture.

Ahmad et al. [8] develop a CNN-inspired architecture for fault detection with EL extract samples of the PV cell surface. The authors report a respectable accuracy of 91.58%. The authors lay emphasis on the importance of data inspection and representative augmentations before delving deeper into their proposed architecture. The presented architecture consists of eight convolutional blocks followed by a single fully connected layer. Looking deeper into the development logic for the internal convolutional layers, many filters were implemented within each convolutional block, i.e., 32 filters each for the first 4 layers, followed by 64 for the next two layers, with 128 in the final two layers. The increased number of convolutional filters would have a significant impact on the computational load of the architecture if explored as part of the research.

Dunderdale et al. [9] propose a feature-oriented, deep-learning strategy for the detection of defective PV cell surfaces. For the purpose of benchmarking, the dataset is trained on the VGG-16 [10] and MobileNet [11] architectures. Furthermore, the authors provide a comparison between the de facto ADAM optimizer against the stochastic gradient descent (SGD). The latter provided an accuracy of 85.8% for the VGG-16 architecture, while a poor result was recorded when utilizing the ADAM as the optimizer (27.4%). Conversely, MobileNet achieved the highest accuracy of 89.5% based on the application of generic augmentations, namely, sample rotations, when utilizing ADAM as the optimizer. Although an explanation for these results was not provided, MobileNet is understood to be a more computationally lightweight architecture used in object detection applications [12] due to the utilization of depth-wise convolutions, which lessen computations by as much as ninefold [13].

Pierdicca et al. [14] select the VGG-16 network for the detection of defective PV cell surfaces. The rationale for selecting VGG-16 as opposed to computationally more friendly architectures is given as simplicity of implementation and development. Though ongoing development in the field of deep learning by various companies has led to frameworks such as PyTorch (Facebook) and TensorFlow (Google). These frameworks make the development and testing of various state-of-the-art architectures simpler, enabling users to develop architectures that are both higher performant and computationally lightweight at the same time. Computational data with regards to the trained architecture would have provided a broader spectrum for evaluating the VGG-16 architecture, unearthing factors such as high convergence time compared to other architectures implementing various strategies for speeding the convergence process, such as batch normalization [15].

Deitsch et al. [16] demonstrate PV fault detection of multiple defects on PV cell surfaces via machine learning (SVM) and deep learning (CNN). Focusing on the CNN, the proposed architecture achieved an accuracy of 88.42% based on the implementation of transfer learning. The tuning of the architecture is performed in two stages. Firstly, the weights of the fully connected layer are randomly initialized with ADAM selected as the optimizer. This is followed by the random initiating of weights for the previous convolutional layers with respect to the fully connected layer, this time selecting SGD-M as the optimizer.

Hussain et al. [17] propose the detection of micro-cracks with PV cell surfaces through the development of a custom CNN architecture, achieving an overall F1-score of 98.8%. The authors provide an in-depth comparison of the proposed architecture across a wide range of metrics consisting of architectural, computational, and post-deployment performance. Furthermore, the comparison is extended to SOTA architectures, with the developed architecture achieving the highest performance in 4 out of 5 metrics.

Tang et al. [18] present a CNN-inspired architecture for the detection of faults within EL-based PV cell surfaces. Interestingly, the authors implement a generative adversarial network (GAN) as their data augmentation strategy for introducing representative variance. The fact that a GAN is essentially an architecture itself, which is computationally demanding, makes its rationale is not clear especially when generic augmentations can be applied at a fraction of the computational load compared to the GAN. The authors report an accuracy of 83% post-implementation of GAN for generating new data samples, again questioning the selection of GAN for augmentation purposes.

Summing up the literature, it can be observed that although research in the automation of PV fault detection is actively being pursued, there is a lack of practical considerations. In particular, there is a dearth of literature addressing faults originating within PV manufacturing facilities focusing on not only the lack of representative data scaling but also the development of computationally lightweight architectures that can be integrated into existing quality inspection protocols to assist and enhance EL-based PV fault detection at an early stage before PV Modules are shipped to client sites.

1.2. Paper Contribution

This research is focused on two primary objectives and hence makes two contributions. Procuring EL-based PV cell surface images from within a PV manufacturing site is significantly more difficult than post-deployment data due to logistical and access restrictions within manufacturing facilities. However, as PV cells are more at risk of developing defects as a result of manual handling and development processes, it is paramount for researchers to access quality data that can be utilized to train architectures for deployment within manufacturing facilities. To address the issue of data scarcity, our first contribution comes in the form of filter-induced augmentations (FIA). FIA makes use of convoluted filter outputs without optimized backpropagation for generating representative PV cell surface samples. The FIA is based on the development of a custom CNN architecture consisting of two convolutional blocks and two fully connected layers.

Secondly, the custom CNN architecture is utilized for training by enabling the backpropagation of weights via the SGD-M optimizer. The developed architecture contains a lightweight footprint with only 7.01 million learnable parameters. In order to manifest the efficiency of the developed architecture and FIA mechanism, the results are presented in an iterative manner, comparing the original dataset, generic applied augmentations, and the proposed FIA-generated dataset.

2. Methodology

2.1. Dataset

The dataset utilized for undertaking this research comprised of PV-cell images procured at the PV manufacturing facility, manually inspected and labeled by domain experts.

Table 1. Original dataset.

Class	Samples
Normal	140
Defective	200

presents the status of the dataset consisting of the following two classes: normal and defective. Based on the number of samples within each class, it can be concluded that the dataset is significantly small in sample quantity for developing a robust, highly generalized architecture, that can differentiate between the two classes.

Figure 1 presents a sample set of (A) normal and (B) defective PV cell surfaces. Before applying any augmentations with the objective to scale the original dataset, it was essential to study and comprehend the visual differentiation features of the two classes as well as the degree of variance at an internal class level. Simply by inspecting Figure 1, we can deduce various considerations regarding the level of variance, global and internal differential features as well as external factors impacting resultant surface images. Starting with global-level variance, it can be observed that there is an element of surface heterogeneity with regard to the texture. For example, the far left and right images for the normal class Figure 1A present a clearer PV cell surface image as opposed to the center image. This is a significant observation, as the textural differential within the normal class, may lead to the developed architecture falsely generalizing on the assumption that only clear surface images belong to the normal class.

When comparing the normal and defective classes, the significance of internal and external factors on the resultant cell image can be appreciated. Taking Figure 1A far right as an example compared to Figure 1B far right, it can be observed that an element of shading or poor filter quality has induced pixel shading on a certain locality of the normal cell. When comparing this to the defective cell, the similarity between the micro-crack and the shading is obvious and hence an increased chance of misclassification.

As evident from all sample images within Figure 1, the fundamental component for a PV cell surface is the busbar, facilitating energy flow from the cell surface. However, even this mandatory component is manifested in various configurations. For example, Figure 1A,B far left images present intermittent busbar configuration whilst Figure 1B center presents the complete ‘cross-surface’ configuration, and Figure 1A center presents a ‘cut-off’ busbar configuration. Furthermore, the starkness of the busbar also varies, leading to the potential misclassification of busbar configurations that consist of lighter pixel intensities as micro-cracks and hence a defective cell.

2.2. Generic Domain Augmentations

Post data inspection, a hypothesis was formed stating that; While there is variance within the present dataset at both global and internal class levels, it could be addressed via representative data modeling as opposed to random application of augmentations for simply increasing the size of the dataset. Hence, the size of the dataset post augmentations was capped at 777 samples from the initial size of 340 images. The capping of the dataset was also representative of the practical limitations of PV data procurement from within PV manufacturing facilities due to restricted access and lack of open-source data.

The augmentations for data transformation belonged to one of the following two categories: translational invariance and translational equivariance. Translational invariance was represented as follows:

$$f(t\left(a\right))=f\left(a\right)$$

(1)

where $f$ equates to the function for the image (a) and $t$ equates to the applied transformation.

Translational invariance was reserved for utilization during the designing of the architectures internal layers as it would not have any physical implications on the dataset i.e., increase dataset size as evident via the equation. Explaining further, translational invariance attempts to preserve regional transformations through aggregation. Thus, it was decided that this type of transformation resulting in aggregation of local features would be more useful during the design stage of the architecture as information propagates deeper through the architectural layers. For instance, the application of max-pooling between the convolution layers would create regional invariance by accepting only the max value from each feature map. Therefore, translational equivariance was selected as the framework for data scaling.

$$f(t\left(a\right))=t\left(f\left(a\right)\right)$$

(2)

where $f$ equates to the function for the image (a) and $t$ equates to the applied transformation.

Comparing the above equation with that for translational invariance it can be seen that translational equivariance would transform the input image with respect to the kind of transformation $t$, applied. Each augmentation presented in the subsequent sections was selected based on its probability of occurrence within a PV manufacturing complex due to internal and external factors such as varying production line configurations, EL camera specifications, etc.

Orientation-Based Scaling (Generic)

PV cells go through various stages from silicon ingots to wafer slicing and hence are processed on various production line configurations. Additionally, the EL quality inspection can happen at various stages of PV manufacturing. The aforementioned production-based processes can lead to varying orientations of the resultant PV cell surface images procured such as varying orientation, hence the vertical flipping was selected amongst other techniques to generate representative samples, accordingly, as shown in Figure 2.

Figure 3 presents the application of the horizontal orientation. The rationale was similar to that of vertical orientation i.e., a practical case due to production line or EL camera configuration. It is important to note that the augmentations were not applied indiscriminately as this would result in cases of duplication. For example, implementing ‘horizontal’ technique to a normal cell image with an approximately uniform surface would result in a replication of the input image due to the symmetrical configuration of the busbars.

The tertiary augmentation technique selected was pixel-shifting with respect to the image width. The inspiration could again be traced back to the device-induced variance and production lines configuration variations from factory to factory. The procedure of EL image acquisition requires PV cell to be shielded from external light. Hence EL shields are utilized but may not always be in perfect alignment with respect to the PV cell, resulting in border cut-off discrepancies in the acquired image.

Additionally, based on considerations such as location, inspection procedures, and EL camera specifications, a certain level of shift may be noted in the obtained images. The same underlying principle provides justification for implementing ‘pixel-shifting’ with respect to the height. Figure 4 presents the (A) input image, (B) width-shifting, and (C) height-shifting implementations. It can be observed that the use of both techniques was not excessive, but rather representative of ground realities i.e., input images were not pixel-shifted by a significant percentage such as 50%.

The status of the transformed dataset with respect to the number of samples within each class is presented in

Table 2. Transformed dataset.

Class	Samples
Normal	282
Defective	787

. The fact that post augmentations the dataset contained a total of 787 samples, shows that indiscriminate use of augmentations for significantly increasing the dataset was not the motive.

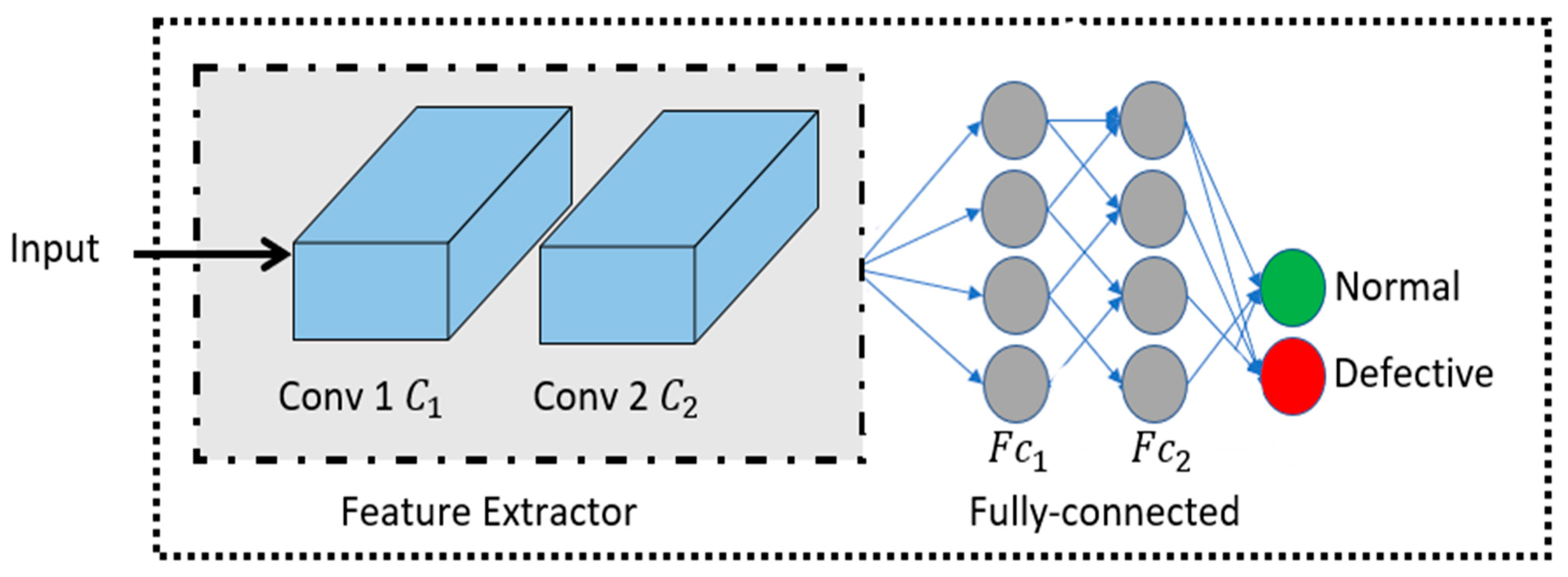
2.3. Proposed PV-CrackNet Architecture

The research was based on two distinct research objectives. Firstly, the development of a lightweight CNN architecture that is compatible for deployment onto computationally constrained edge devices and secondly to address the issue of EL-based PV data procurement from within PV manufacturing facilities. Both objectives directed our research towards the development of a custom CNN architecture rather than implementing transfer learning, as evidenced in the results section. The development of a custom architecture would enable the suppression of the architectural and computational complexities associated with CNNs by reducing the internal convolutional blocks and the number of filters implemented within each block.

Figure 5 presents the internal architectural block diagram of the proposed architecture. It can be observed that only two convolutional blocks were implemented. This was due to the fact that during the data inspection section, discussed earlier, it was concluded that, though variance existed at global and internal class levels, the level of diversity in the variance was not high, mostly limited to surface textural differentials, light intensities, hardware induced and busbar configurations. Hence, by implementing a smaller number of convolutional blocks with carefully tuned filters, there was a high probability of capturing the underlying differentiating features between the two classes.

The first convolutional block consisted of 12 filters with each filter’s dimensions defined as 3 × 3 pixels. It may be argued as to why an odd number was selected for the filter dimensions. The justifications for this were that as opposed to an even-dimensional filter (e.g., 2 × 2 pixels) an odd filter provides a center pixel for filter output encoding. In the case of an even filter due to the lack of a center pixel, aliasing errors would occur. The dimensions of the resultant feature maps from the initial convolutional block were ascertained via.

$$n_{out}=[\frac{n_{in}-2_p-k}{s}]+1$$

(3)

where $n_{out}$ = resultant features, $n_{in}$= Nu. of input features, p = padding dimensions, k = kernel dimensions, s = stride

Equation (3) provided the number of output feature maps that were utilized as input to the second convolutional block consisting of 24 filters. Moreover, from the block diagram in Figure 5, it can be noticed that the number of filters was doubled during the transition from convolutional block one to convolutional block two. The rationale behind this was that the initial layer would carry out a highly abstract feature extraction process looking for features such as lines and edges. Whilst the second convolutional block would go deeper into the extraction of useful features to provide an input to the two fully connected layers and hence require more filters.

Max-pooling was also utilized as a translational invariant component, enabling the aggregation of local features, and reducing positional dependencies. ReLu was selected as the activation due to it having an edge over its predecessors (Sigmoid and TanH) in addressing the issue of vanishing gradients. From the resultant dimensions post the application of Max-pooling, it can be observed that there was a 50% reduction in output dimensions. This was due to the max-pooling being defined with a stride of 2, per the equation above. The number of learnable parameters was calculated via,

$$\left(n\times m\times I+1\right)\times k$$

(4)

where n, m = filter sizes, I = input features, k = resultant feature maps.

The second i.e., last convolutional block was flattened before being utilized as input to the first fully connected layer, hence the filter dimensions presented in the above equations were no longer required for calculating the resultant number of learnable parameters, resulting in,

$$\left(In+1\right)\times On$$

(5)

where In = input neurons, On = output neurons.

As per the internal architectural block diagram, the proposed architecture with respect to the convolutional blocks and fully connected layers consisted of 7.01 million parameters. Figure 6 presents a more abstract view of the proposed PV-CrackNet architecture consisting of two convolutional blocks followed by two fully connected layers.

2.4. Filter-Induced Augmentations (FIA)

As mentioned earlier, the second part of the research objective was to address the issue of data scarcity. Quality data procurement especially in the form of EL-based PV cell images at present can be seen as a difficult task as evident from the lack of open-source datasets, hence hindering the development of automated quality inspection solutions within PV quality inspection. Although generic augmentations have been proposed in an earlier section, as evident from the results section, these augmentations although were justified in terms of their representativeness to production-based variance, were not sufficient in providing the architecture with a truly representative dataset for efficient generalization.

Based on the above premise, FIA was proposed to address the issue of generating representative data samples. The inspiration was derived from the fact that earlier convolutional layers learn more abstract representations. These may not be suitable for highly complex feature-intensive image domains such as facial recognition, however as the EL process essentially provides an abstract resultant image with limited variance (discussed earlier), coupled with the fact that the PV-CrackNet contained only two convolutional blocks, there was a possibility that the resultant feature maps could be utilized as representative samples. In order to achieve the extraction of gradients with respect to the input image, the gradients at the prediction layer were back propagated with being passed onto the loss function, essentially disabling the backpropagation post-optimization. The raw gradient via backpropagation containing the same number of pixels as the input image provided a resultant image that could be visually inspected and added to the generated dataset if it was deemed to be representative of production floor conditions. The process flow for FIA is presented in Figure 7.

As shown in Figure 7, the conventional backpropagation route was disabled and instead the raw gradients were projected back onto the input image for comparison.

Figure 8 presents a comparison of an input image with that of the generated output via FIA (A) input image, (B) generated image. The generated image can be labeled as representative of real variance caused by varying EL filter specifications. Furthermore, notice that the key underlying feature distribution of the input image is intact.

2.5. Reactivating Optimizer

After completing the process of data generation via FIA, the optimizer was reactivated, whilst the FIA procedure was disabled, as shown in Figure 9. Stochastic gradient descent with momentum (SGD-M) was selected as the optimizer for updating the weights with respect to the prediction loss via backpropagation. The SGD-M can be termed as an extension of the plain gradient descent as it replaces the gradient with the moving average of the gradient. Gradient descent-based updating is expressed as,

$$w_t=w_{t-1}-a{g}_{t-1}$$

(6)

Replacing the gradient with moving average of gradient over time,

$$w_t=w_{t-1}-a{v}_{t-1}$$

(7)

Moving average is calculated,

$$v_t=\beta v_{t-1}+\left(1-\beta \right)g_{t-1}$$

(8)

Moving average of the gradient was computed via the equation above, ‘$g_t$’ contained the gradient from the previous step. Furthermore, the equation manifests the fact that the entire gradient was not utilized, rather gradient ‘mixing’ with the moving average was implemented until reaching $\beta v_{t-1}$. The moving average $v_{0 }$ begins as a vector of zeros, gradually accumulating the moving average of the gradients whilst combining $v_t=\beta v_{t-1}+\left(1-\beta \right)g_{t-1}$ at each step. Consequently, the present gradient was not actioned upon, rather historical gradients were registered and deposited within $v_{t }$. Momentum ($\beta )$ was a hyper-parameter set by default to 0.9,

$$v_{0 }=0$$

(9)

$$v_1=\beta v_0+\left(1-\beta \right)g_0=\left(1-\beta \right)g_0$$

(10)

$$v_2=\beta v_1+\left(1-\beta \right)g_1=\left(1-\beta \right)g_0+\left(1-\beta \right)g_1$$

(11)

The activation of the optimizer enabled the training of the architecture, whilst the data generation process was disabled, shown in Figure 9.

3. Results

3.1. Hyper-Parameters

This section of the research presents a comparison of the proposed PV-CrackNet architecture’s performance on the original, generic, and FIA-augmented datasets. Google Colaboratory was selected as the virtual training environment due to its free GPU access for speeding up the training process. The access to GPU was however time constrained due to the subscription to the free tier.

The hyperparameters defined at a global level for providing a fair performance comparison are presented in

Table 3. Hyperparameters.

Batch Size	32
Epochs	40
Optimizer	SGD-M
Learning Rate	0.02

. As mentioned earlier, due to the limited GPU access, the number of epochs was capped at 40. Additionally, to assist with faster training, the learning rate was set to 0.02.

3.2. Original Dataset Performance

Although the data in its original form was significantly small in size and, more importantly, representative variance, to provide a fair comparison, the architecture was trained on the raw dataset, and the results are presented in Figure 10. Figure 10A presents the loss, and through its interpretation, it can be said that the architecture had stopped any useful learning after a couple of epochs.

Furthermore, the significant increase between the training and validation loss is evident from the fact that the dataset in its present form was not sufficient. When observing the training and validation accuracy, the increasing differential again hints at insufficient data supply.

It may be argued that the architecture had not been given adequate training time, hence increasing the training time (epochs) could have yielded better results. The argument is countered by pointing out from Figure 10B that the validation accuracy stagnates after around 30 epochs, this stagnation remains until the training is complete, demonstrating that training time was not an issue but rather a lack of representative data.

3.3. Generic-Augmented Dataset Performance

The next iteration was the application of generic yet representative augmentations. Figure 11 presents the performance of the trained architecture with respect to the translational equivariance-based augmentations presented in the methodology section. These consisted of readily available augmentation techniques within Pytorch, namely, horizontal and vertical rotations, and image shifting.

A clear improvement in performance can be observed, with the validation loss (Figure 11A) reducing to 0.1314 as compared to 0.4797 for the original data. Similarly, the validation accuracy (Figure 11B) improved to 96.1% as compared to 84.4% for the original data. Furthermore, the differential between the two respective accuracies, known as overfitting, also decreased from 15.1% (original data) to 6.8%.

A critical analysis shows that although the degree of overfitting had decreased by 8.4%, the difference between the training and validation accuracies stood at 6.8%, indicating that further improvements to the model could be made via a more representative dataset.

3.4. Filter-Induced Augmentations Dataset Performance

The final iteration, aimed at improving the performance whilst further suppressing the degree of overfitting, was based on the proposed FIA mechanism. As evident from the generic augmentation testing, the validation accuracies had surpassed 90%, hence the evaluation was broadened to include not only the accuracy but also the precision, recall, and F1-score. The performance of the architecture via FIA is presented in

Table 4. FIA performance.

Training Acc	99.11%
Validation Acc	97.42%
Precision	98%
Recall	96%
F1-score	97%

.

It is evident from Table 4 that the FIA produced the highest performance. Starting with the performance with respect to the degree of overfitting, the difference between the training and validation stood at its lowest point (1.69%), compared to 15.1% (original data) and 6.8% (generic augmented data), as shown in Figure 12. The fact that the validation accuracy was the highest at 97.42% and the degree of overfitting was at its lowest (1.69%) demonstrates that the proposed FIA mechanism was effective in providing a representative dataset, which was well-generalized upon by the proposed PV-CrackNet architecture.

To provide a more robust analysis, the precision, recall, and F1-score were also inspected. Precision was the highest at 98%, whilst the recall stood at a respective 96%. Overall, the proposed PV-CrackNet performance could be gauged via the F1-score at an impressive 97%.

4. Discussion

The results section demonstrated the effectiveness of the proposed FIA mechanism for generating representative samples and resulting in a highly generalized architecture. However, the generalization of the architecture was not the only objective of this research. The second objective was based on the development of a lightweight architecture in order to be computationally efficient.

To evaluate the effectiveness of the developed PV-CrackNet architecture, the computational complexities of various state-of-the-art architectures were evaluated. The evaluation was based on the number of learnable parameters as shown in

Table 5. Computational comparison.

Architecture	Parameters (M)
PV-CrackNet	7.01
VGG-19 [19]	143.67
ResNet-18 [20]	11.69
AlexNet [21]	61.0
GoogleNet [22]	13.0

.

It can be clearly observed via Table 5, that the proposed architecture contained the least number of parameters at 7.01 million, whilst the VGG-19 was the most computationally demanding with 143.67 million learnable parameters. The number of learnable parameters would have a direct implication on the training process, as a higher number of learnable parameters would require more training time/resources for the architecture to converge.

AlexNet was the second-most computationally demanding with 61 million parameters. This was interesting, as its internal block composition with respect to the convolutional layers was the most similar to the proposed PV-CrackNet. Although AlexNet contained only five convolutional blocks followed by three fully connected layers, its internal filter configurations had an adverse impact on the computational complexity of the network. For example, the initial convolutional block contained 11 × 11-pixel filters as opposed to the PV-CrackNet initiating with 3 × 3-pixel filters. As a result, the convolutional process resulted in an increased number of computations.

5. Conclusions

In conclusion, it can be stated with confidence that the presented research was highly successful in achieving the two research objectives. The first objective i.e., addressing the issue of EL-based data scarcity, was addressed via the FIA mechanism. The effectiveness of the FIA in generating highly representative samples was demonstrated by the fact that it reached the highest validation accuracy of 97.42% with the lowest degree of overfitting at 1.69%.

The second objective was achieved by demonstrating, via a comparison of various state-of-the-art architectures with the proposed PV-CrackNet with respect to the number of learnable parameters. The developed architecture again provided the highest performance, consisting of only 7.01 million parameters, evidencing the claim of developing a computationally lightweight architecture.

Commenting on the marketing potential, the proposed PV-CrackNet can be integrated into existing quality inspection processes within PV manufacturing facilities for enhancing their production output in terms of efficiency. Additionally, third-party PV quality inspection firms can utilize PV-CrackNet for automating defect detection and providing their clients with a higher degree of confidence in the shipped PV panels.

Furthermore, due to the abstract nature of images within various other domains, the proposed FIA mechanism can be implemented for introducing representative variance whilst addressing the issue of data scarcity, i.e., retina-based exudate detection data enhancements and defect accentuation [23] or industrial infrastructure defect detection [24].