Multi-Parameter Optimization of Heat Dissipation Structure of Double Disk Magnetic Coupler Based on Orthogonal Experimental Design
Abstract
:1. Introduction
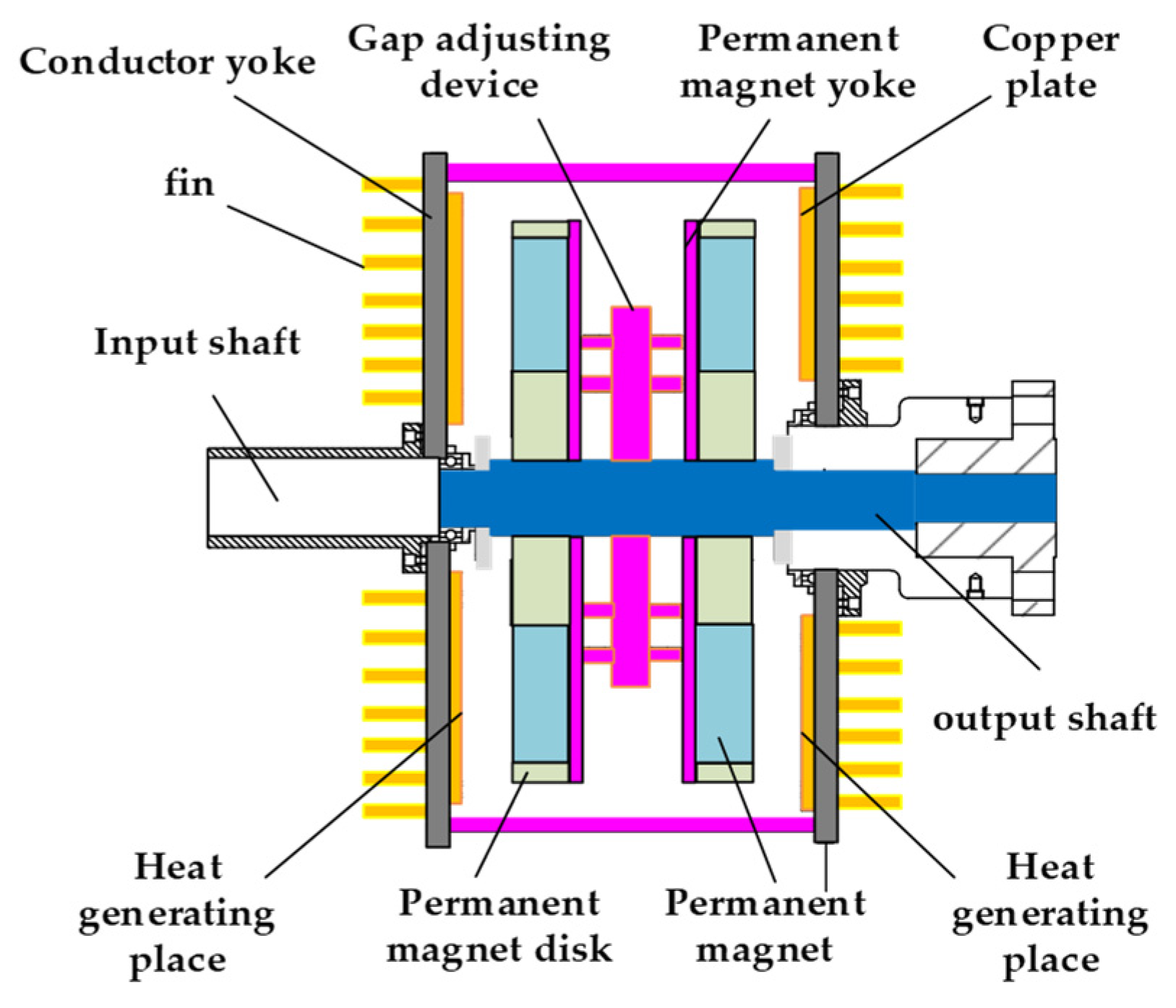
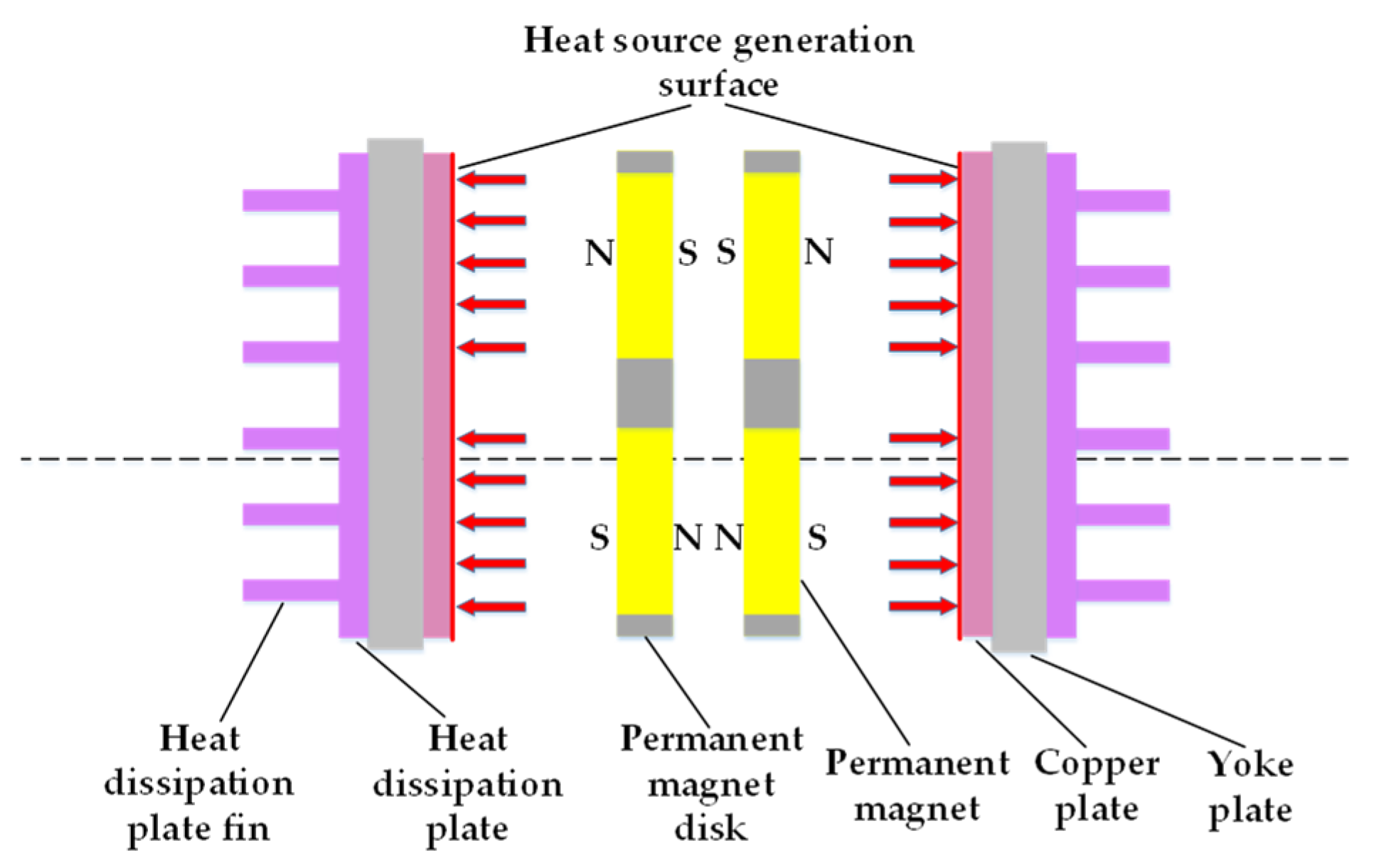
2. Structure and Working Principle of Double Disk Magnetic Coupler
2.1. Structure
2.2. Working Principle
3. Numerical Calculation Method
3.1. Gas Heat Transfer Control Equation
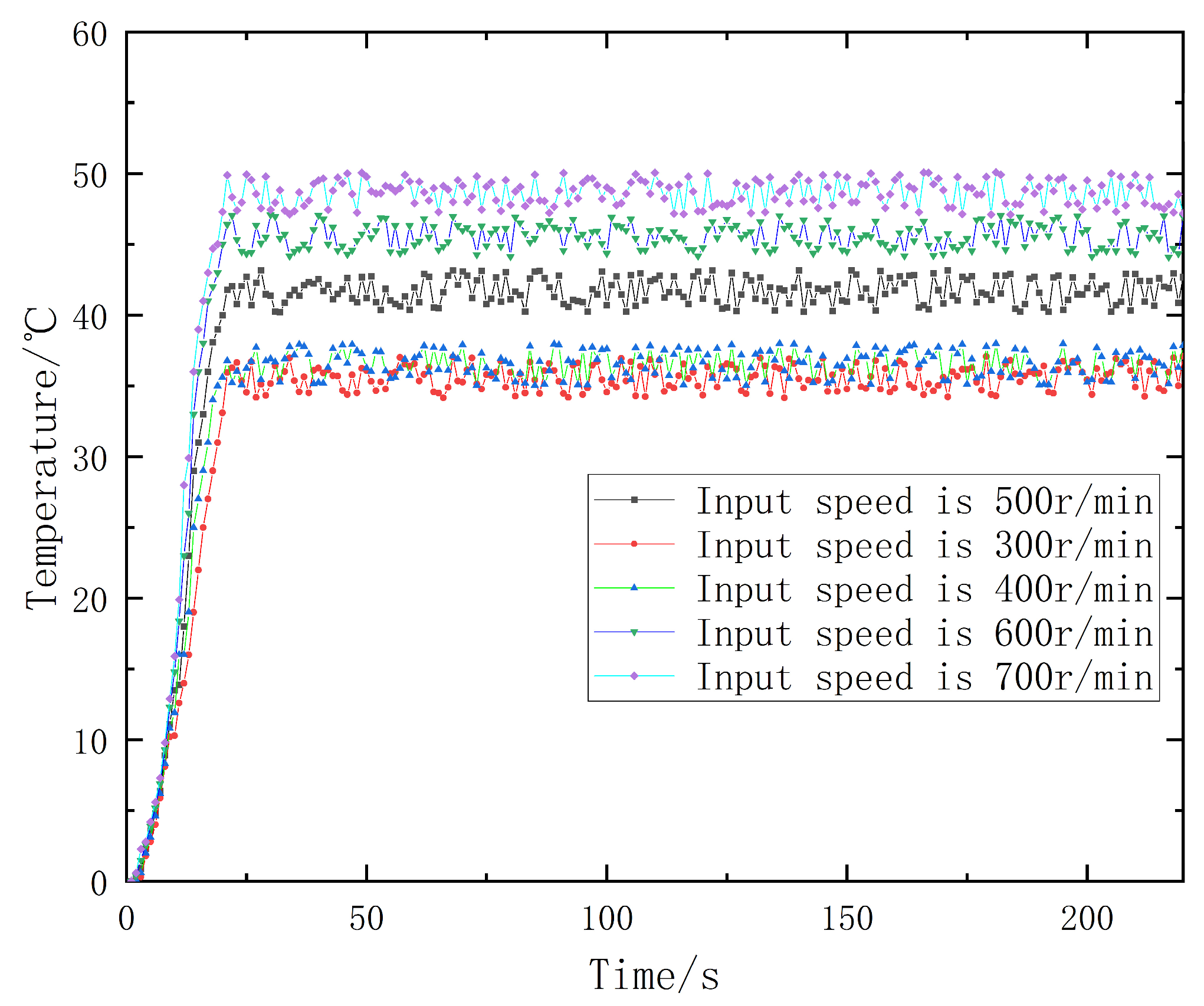
3.2. Boundary Parameter Setting
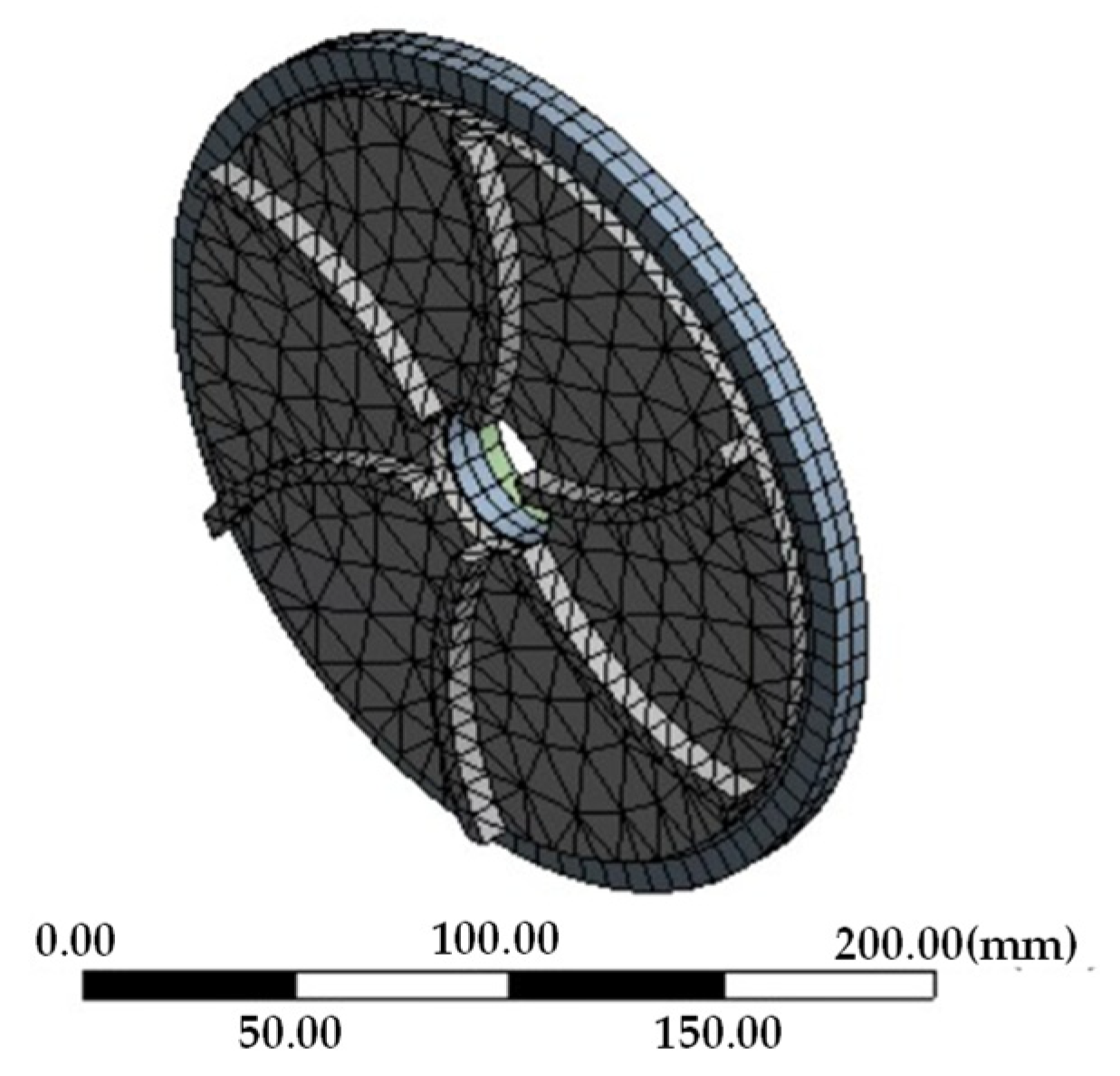
4. Fluid–Solid–Heat Coupling Finite Element Simulation
4.1. Three-Dimensional Model of Heat Dissipation Structure
4.2. Permanent Magnetic Field and Temperature Field Coupling Platform
5. Orthogonal Experimental Design
5.1. Structural Parameter Model
5.2. Improved Response Surface Design Principle
5.3. Orthogonal Experimental Design and Simulation
5.4. Analysis of Variance in Orthogonal Experiment
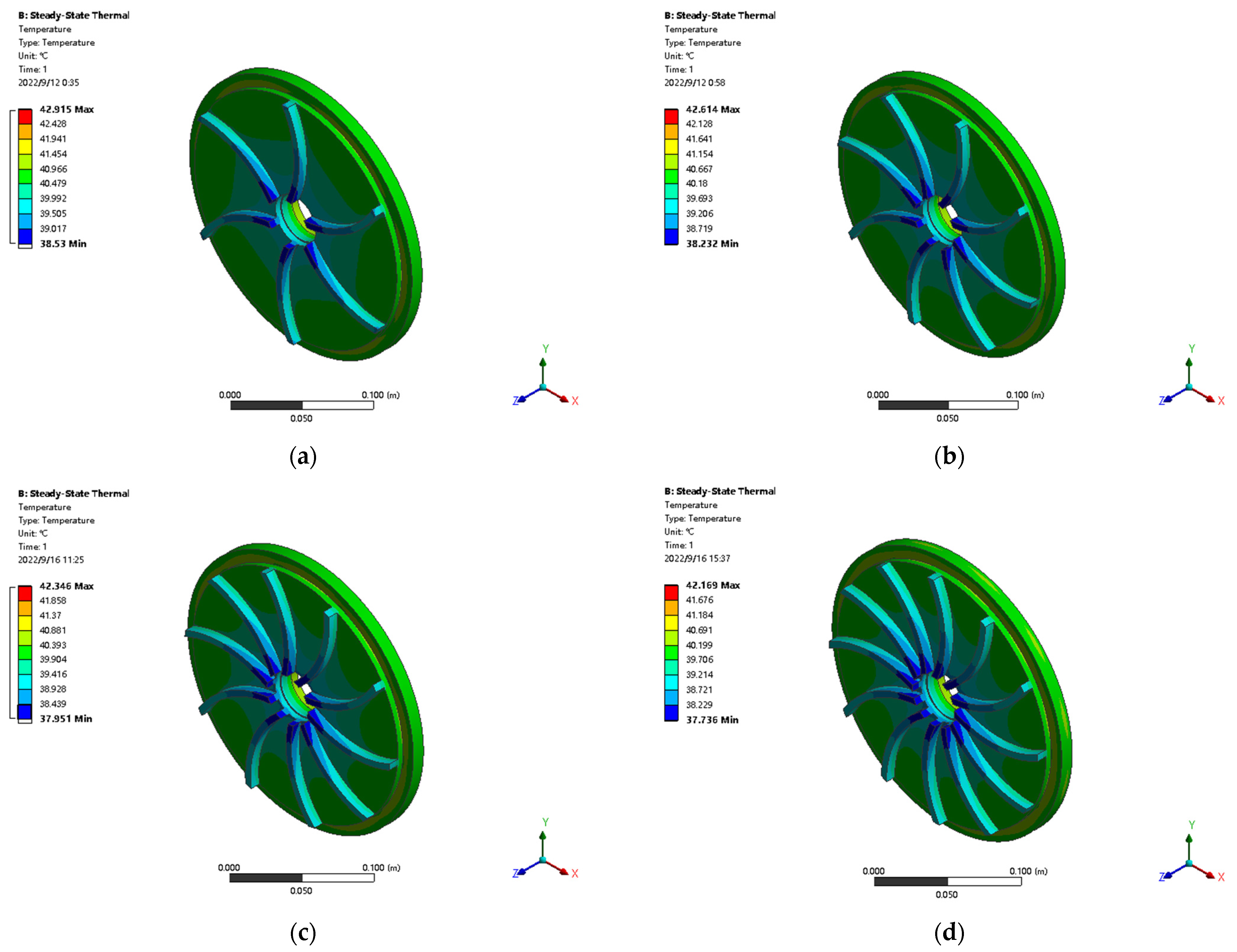
6. Heat Dissipation Performance Analysis
6.1. Significant Impact
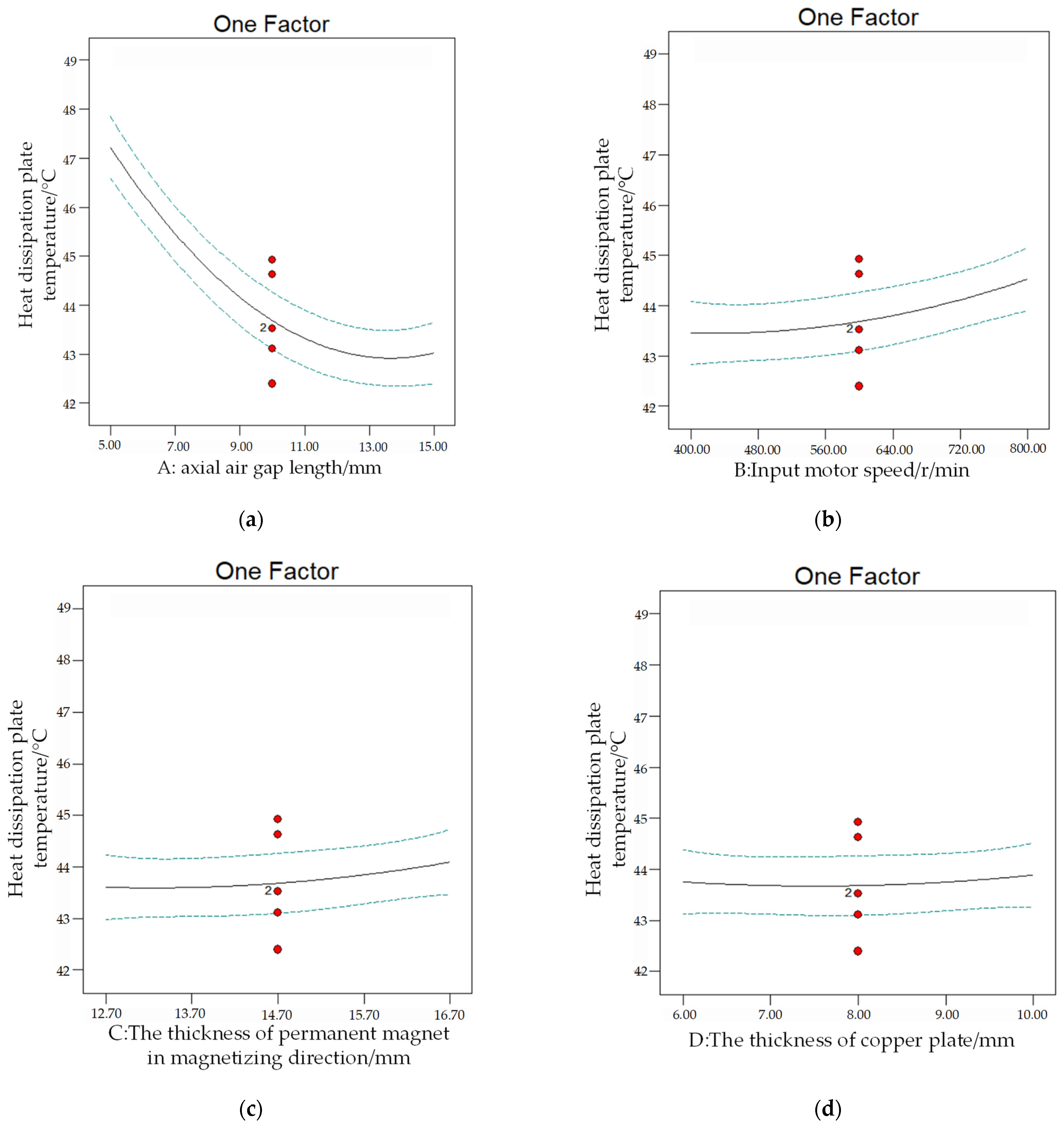
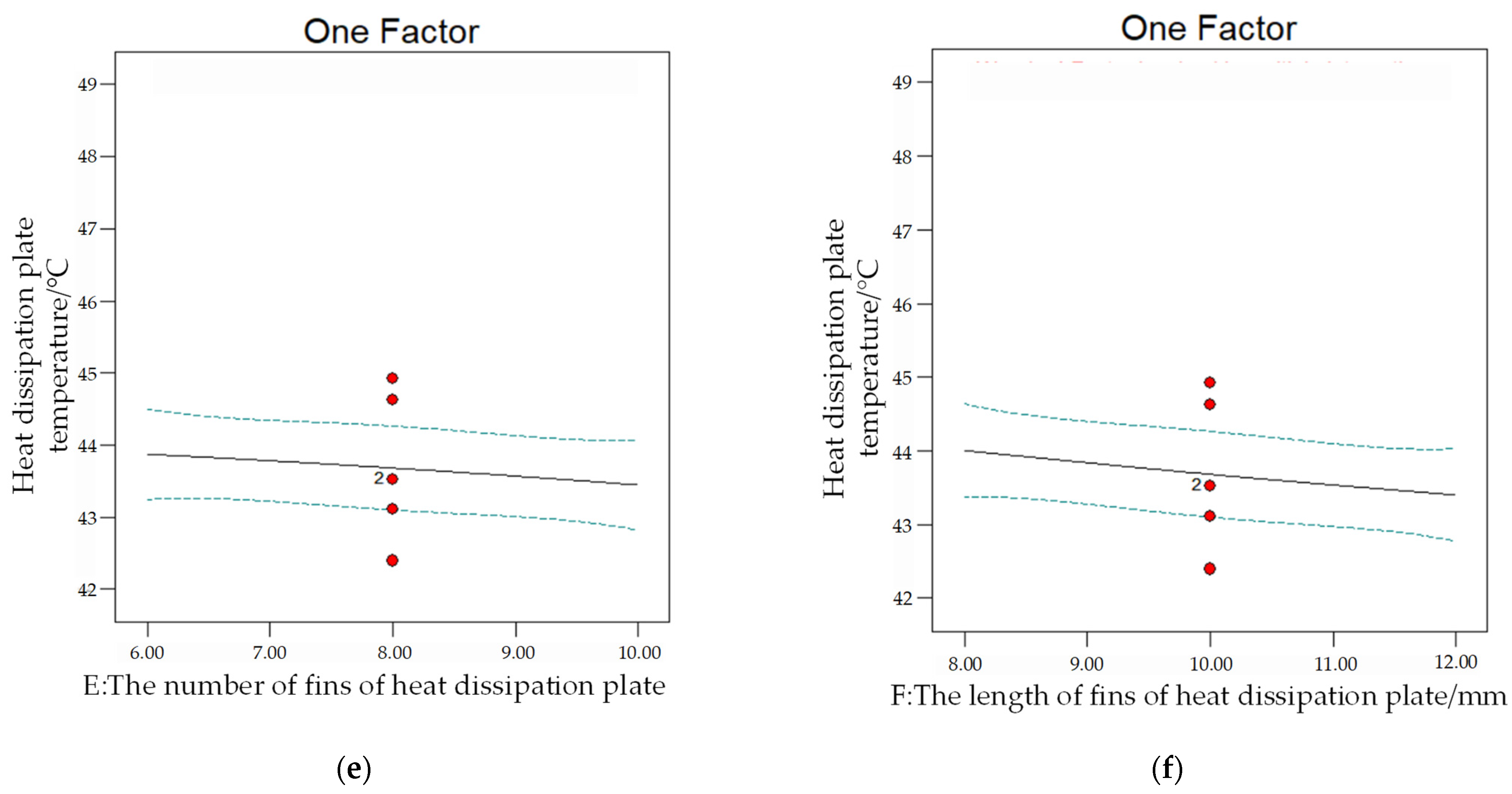
6.2. Single Factor Analysis
6.3. Two-Factor Analysis
7. Orthogonal Experiment Optimization
7.1. Simulation Optimal Conditions and Results
7.2. Physical Test
7.3. Comparison between Simulation and Physical Tests
8. Conclusions
- A six-factor and three-level experiment based on the improved response surface method is designed, and it is found that different variable factors have a certain influence on the heat dissipation effect of the heat dissipation structure model of the double disk magnetic coupler. After analyzing its heat dissipation performance, it can be observed that the order of significant influence from high to low is as follows: axial air gap length > input motor speed > the length of the fins of the heat dissipation plate > the thickness of the permanent magnet in the magnetizing direction > the number of fins of the heat dissipation plate > the thickness of the copper plate. The increase in the axial air gap length can effectively reduce the temperature rise, and the maximum decrease can reach 9.76%, which has an obvious effect. According to the single-factor and double-factor influence change diagram of the temperature of the heat dissipation plate, the response of different influence factors can be intuitively expressed, which is helpful to find the optimal direction of the heat dissipation structure.
- The parameters of the optimized heat dissipation structure obtained by orthogonal experimental design are as follows: the axial air gap length is 15.00 mm, the input motor speed is 500.00 r/min, the thickness of the permanent magnet in the magnetizing direction is 13.00 mm, the thickness of the copper plate is 7.00 mm, the number of fins of the heat dissipation plate is 10, and the length of the fins of the heat dissipation plate is 12.00 mm. The corresponding value of the objective function, namely the minimum temperature of the heat dissipation plate, is 41.8409 °C. Under this heat dissipation structure, the optimum heat dissipation performance of the double disk magnetic coupler can be achieved.
- According to the influence law and optimal parameters of the temperature characteristic index of the heat dissipation plate, the physical experiment was designed. The heat dissipation performance of the theoretical and practical heat dissipation structure before and after optimization under actual working conditions was verified. The simulation results are in good agreement with the physical test results, with a maximum error of 4.8%. The error between the simulation results of the optimal parameter combination and the physical test results after correction is only 1.9%, with high accuracy, which verifies the correctness of the numerical model. The research results have reference significance for guiding the optimization of the heat dissipation structure parameters of the double disk magnetic coupler.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Florio, F.; Sinha, G.; Sundararaman, R. Designing high-accuracy permanent magnets for low-power magnetic resonance imaging. IEEE Trans. Magn. 2018, 54, 5300209. [Google Scholar] [CrossRef]
- Lopez-Alcolea, F.J.; Real, J.V.D.; Roncero-Sanchez, P.; Torres, A.P. Modeling of a Magnetic Coupler Based on Single- and Double-Layered Rectangular Planar Coils With In-Plane Misalignment for Wireless Power Transfer. IEEE Trans. Power Electron. 2020, 35, 5102–5121. [Google Scholar] [CrossRef]
- Hogberg, S.; Jensen, B.B.; Bendixen, F.B. Design and Demonstration of a Test-Rig for Static Performance-Studies of Permanent Magnet Couplings. IEEE Trans. Magn. 2013, 49, 5664–5670. [Google Scholar] [CrossRef]
- Wolnik, T.; Glinka, T. Axial forces of magnetic pull in a disc type induction motor-experimental test. Prz. Elektrotechniczny 2019, 95, 127–132. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Wang, K.F.; Wang, B.L.; Zheng, L.; Zhang, C.W.A. Fracture analysis of superconducting composites with a sandwich structure based on electromagnetic-thermal coupled model. Acta Mech. 2019, 230, 4435–4451. [Google Scholar] [CrossRef]
- Bujakiewicz-korońska, R.; Koroński, J. The principle of minimum entropy production for diffusion and heat transfer in open systems. Czas. Techniczne. Nauk. Podstawowe 2011, 108, 23–35. [Google Scholar]
- Morrison, A.T. Optimization of heat sink fin geometries for heat sinks in natural convection. In Proceedings of the Conference on Thermal Phenomena in Electronic Systems IEEE, Austin, TX, USA, 5–8 February 1992. [Google Scholar]
- Marignetti, F.; Colli, V.D. Thermal Analysis of an Axial Flux Permanent-Magnet Synchronous Machine. IEEE Trans. Magn. 2009, 45, 2970–2975. [Google Scholar] [CrossRef]
- Bar-Cohen, A.; Iyengar, M.; Kraus, A.D. Design of Optimum Plate-Fin Natural Convective Heat Sinks. J. Electron. Packag. 2003, 125, 208–216. [Google Scholar] [CrossRef]
- Yang, C.J.; Yuan, A.R.; Chen, Z.Q.; Wu, Y.Z.; Zhang, X.F.; Liu, K. Mechanical characteristics and speed regulation characteristics of disk solid asynchronous magnetic coupling. J. Mot. Control. 2019, 23, 9. [Google Scholar]
- Wang, L.; Jia, Z.Y.; Zhu, Y.Q.; Liu, H.; Zhang, L. Temperature field of high-power auxiliary cooling magnetic coupling for mining. J. Mech. Eng. 2018, 54, 7. [Google Scholar]
- Ge, Y.J.; Zhang, J.; Jiang, H.; Wang, X.; Wan, Z.W. Operation characteristic analysis and heat dissipation structure design of copper sleeve type magnetic coupling. Mech. Transm. 2018, 42, 71–75. [Google Scholar]
- Maltseva, V.E.; Andreev, S.V.; Neznakhin, D.S.; Urzhumtsev, A.N.; Selezneva, N.V.; Volegov, A.S. The Magnetic Properties of a NdFeB Permanent Magnets Prepared by Selective Laser Sintering. Phys. Met. Metallogr. 2022, 123, 740–745. [Google Scholar] [CrossRef]
- Wang, H.; Monroe, J.G.; Kumari, S.; Leontsev, S.O.; Vasquez, E.S.; Thompson, S.M.; Berg, M.J.; Walters, D.K.; Walters, K.B. Analytical model for electromagnetic induction in pulsating ferrofluid pipe flows. Int. J. Heat Mass Transf. 2021, 175, 121325. [Google Scholar] [CrossRef]
- Zhalnin, R.V.; Ladonkina, M.E.; Masyagin, V.F.; Tishkin, V.F. Solution of 3D heat conduction equations using the discontinuous Galerkin method on unstructured grids. J. Samara State Tech. Univ. Ser. Phys. Math. Sci. 2015, 19, 523–533. [Google Scholar]
- Roth, G.A.; Aydogan, F. Derivation of new mass, momentum, and energy conservation equations for two-phase flows. Prog. Nucl. Energy 2015, 80, 90–101. [Google Scholar] [CrossRef]
- Patil, M.; Muddebihal, A. To Study the Steady State Thermal Analysis of Steam Turbine Casing. Int. J. Innov. Res. Sci. Eng. Technol. 2016, 5, 2347–6710. [Google Scholar]
- Han, X.X.; Lin, W.; Qiu, A.; Feng, Z.Q.; Wu, J.M.; Tang, Y.H.; Zhao, C.B. Understanding vortex-induced vibration characteristics of a long flexible marine riser by a bidirectional fluid-structure coupling method. J. Mar. Sci. Technol. 2020, 25, 620–639. [Google Scholar] [CrossRef]
- Wang, A.W.; Fan, D.W.; Pan, Y.S.; Zhao, B.Y.; Dai, L.P. Expansion-friction energy-absorbing anti-impact anchor cable and its mechanical characteristics. J. Coal Sci. 2022, 47, 695–710. [Google Scholar]
- Liu, B.F.; Li, J.; He, J. Study on hyperspectral remote sensing monitoring and diagnosis model of total phosphorus content in maize leaves. J. Agric. Mach. 2015, 46, 252–258+280. [Google Scholar]




| Name | Parameter Value/mm | ||
|---|---|---|---|
| Length/Outside Diameter | Width/Inner Diameter | Thickness | |
| Permanent magnet | 50.8 | 25.4 | 12.7 |
| Permanent magnet disk | 200 | 30 | 12.7 |
| Copper plate | 200 | 38 | 6 |
| Yoke plate | 220 | 38 | 10 |
| Heat dissipation plate | 200 | 40 | 5 |
| Name | Attribute |
|---|---|
| Permanent magnet | UH NdFeB, Curie temperature: 150 °C |
| Permanent magnet disk | Aluminum |
| Copper plate | Copper |
| Yoke plate | Q235 |
| Heat dissipation plate | Q235 |
| Factor | Level | ||
|---|---|---|---|
| −1 | 0 | 1 | |
| Axial air gap length | 5 | 10 | 15 |
| Input motor speed | 400 | 600 | 800 |
| The thickness of the permanent magnet in the magnetizing direction | 12.7 | 14.7 | 16.7 |
| The thickness of the copper plate | 6 | 8 | 10 |
| The number of fins of the heat dissipation plate | 6 | 8 | 10 |
| The length of the fins of the heat dissipation plate | 8 | 10 | 12 |
| Test Number | Axial Air Gap Length A/mm | Input Motor Speed B/r/min | The Thickness of Permanent Magnet in Magnetizing Direction C/mm | The Thickness of Copper Plate D/mm | The Number of Fins of Heat Dissipation Plate E | The Length of Fins of Heat Dissipation Plate F/mm | The Temperature of Heat Dissipation Plate T/°C |
|---|---|---|---|---|---|---|---|
| 1 | 5 | 400 | 14.7 | 6 | 8 | 10 | 47.121 |
| 2 | 5 | 400 | 14.7 | 8 | 8 | 8 | 47.231 |
| 3 | 5 | 400 | 14.7 | 8 | 8 | 12 | 47.529 |
| 4 | 5 | 400 | 14.7 | 10 | 8 | 10 | 47.011 |
| 5 | 5 | 600 | 12.7 | 8 | 6 | 10 | 47.301 |
| 6 | 5 | 600 | 12.7 | 8 | 10 | 10 | 47.202 |
| 7 | 5 | 600 | 16.7 | 8 | 6 | 10 | 47.362 |
| 8 | 5 | 600 | 16.7 | 8 | 10 | 10 | 47.688 |
| 9 | 5 | 800 | 14.7 | 6 | 8 | 10 | 48.064 |
| 10 | 5 | 800 | 14.7 | 8 | 8 | 8 | 48.698 |
| 11 | 5 | 800 | 14.7 | 8 | 8 | 12 | 46.825 |
| 12 | 5 | 800 | 14.7 | 10 | 8 | 10 | 48.273 |
| 13 | 10 | 400 | 12.7 | 8 | 6 | 10 | 41.861 |
| 14 | 10 | 400 | 12.7 | 8 | 10 | 10 | 43.537 |
| 15 | 10 | 400 | 16.7 | 8 | 6 | 10 | 44.251 |
| 16 | 10 | 400 | 16.7 | 8 | 10 | 10 | 43.861 |
| 17 | 10 | 600 | 12.7 | 6 | 8 | 8 | 44.203 |
| 18 | 10 | 600 | 12.7 | 6 | 8 | 12 | 43.638 |
| 19 | 10 | 600 | 12.7 | 10 | 8 | 8 | 45.014 |
| 20 | 10 | 600 | 12.7 | 10 | 8 | 12 | 43.239 |
| 21 | 10 | 600 | 14.7 | 6 | 6 | 8 | 44.058 |
| 22 | 10 | 600 | 14.7 | 6 | 6 | 12 | 43.833 |
| 23 | 10 | 600 | 14.7 | 6 | 10 | 8 | 43.754 |
| 24 | 10 | 600 | 14.7 | 6 | 10 | 12 | 42.661 |
| 25 | 10 | 600 | 14.7 | 8 | 8 | 10 | 44.628 |
| 26 | 10 | 600 | 14.7 | 8 | 8 | 10 | 43.524 |
| 27 | 10 | 600 | 14.7 | 8 | 8 | 10 | 43.517 |
| 28 | 10 | 600 | 14.7 | 8 | 8 | 10 | 42.392 |
| 29 | 10 | 600 | 14.7 | 8 | 8 | 10 | 43.107 |
| 30 | 10 | 600 | 14.7 | 8 | 8 | 10 | 44.918 |
| 31 | 10 | 600 | 14.7 | 10 | 6 | 8 | 44.394 |
| 32 | 10 | 600 | 14.7 | 10 | 6 | 12 | 44.172 |
| 33 | 10 | 600 | 14.7 | 10 | 10 | 8 | 43.926 |
| 34 | 10 | 600 | 14.7 | 10 | 10 | 12 | 43.752 |
| 35 | 10 | 600 | 16.7 | 10 | 8 | 12 | 43.964 |
| 36 | 10 | 600 | 16.7 | 10 | 8 | 8 | 43.057 |
| 37 | 10 | 600 | 16.7 | 6 | 8 | 12 | 43.911 |
| 38 | 10 | 600 | 16.7 | 6 | 8 | 8 | 45.033 |
| 39 | 10 | 800 | 12.7 | 8 | 6 | 10 | 45.664 |
| 40 | 10 | 800 | 12.7 | 8 | 10 | 10 | 43.229 |
| 41 | 10 | 800 | 16.7 | 8 | 6 | 10 | 45.836 |
| 42 | 10 | 800 | 16.7 | 8 | 10 | 10 | 44.837 |
| 43 | 15 | 400 | 14.7 | 6 | 8 | 10 | 42.722 |
| 44 | 15 | 400 | 14.7 | 8 | 8 | 8 | 43.619 |
| 45 | 15 | 400 | 14.7 | 8 | 8 | 12 | 42.633 |
| 46 | 15 | 400 | 14.7 | 10 | 8 | 10 | 42.814 |
| 47 | 15 | 600 | 12.7 | 8 | 6 | 10 | 43.137 |
| 48 | 15 | 600 | 12.7 | 8 | 10 | 10 | 42.683 |
| 49 | 15 | 600 | 16.7 | 8 | 6 | 10 | 43.562 |
| 50 | 15 | 600 | 16.7 | 8 | 10 | 10 | 43.184 |
| 51 | 15 | 800 | 14.7 | 6 | 8 | 10 | 43.765 |
| 52 | 15 | 800 | 14.7 | 8 | 8 | 8 | 43.745 |
| 53 | 15 | 800 | 14.7 | 8 | 8 | 12 | 43.326 |
| 54 | 15 | 800 | 14.7 | 10 | 8 | 10 | 44.773 |
| Error | Sum of Squares of Fluctuations | Freedom | Mean Square Deviation | F-Value | p-Value | Saliency Judgment |
|---|---|---|---|---|---|---|
| Fitting | 153.90 | 27 | 5.70 | 11.85 | <0.0001 | Significant |
| Residual | 12.51 | 26 | 0.48 | - | - | - |
| Missing term | 8.04 | 21 | 0.38 | 0.43 | 0.9221 | Not significant |
| Six Factors | Axial Air Gap Length | Input Motor Speed | The Thickness of Permanent Magnet in Magnetizing Direction | The Thickness of Copper Plate | The Number of Fins of Heat Dissipation Plate | The Length of Fins of Heat Dissipation Plate |
|---|---|---|---|---|---|---|
| The amplitude of the increase | 0.23% | 2.30% | 0.92% | 0.46% | - | - |
| The amplitude of the reduction | 9.76% | - | - | 0.23% | 0.92% | 1.15% |
| Serial Number | Axial Air Gap Length (mm) | Input Motor Speed (r/min) | The Thickness of Permanent Magnet in Magnetizing Direction (mm) | The Thickness of Copper Plate (mm) | The Number of Fins of Heat Dissipation Plate | The Length of Fins of Heat Dissipation Plate (mm) | Simulation Results | Physical Test Results | Error |
|---|---|---|---|---|---|---|---|---|---|
| Heat Dissipation Plate Temperature (°C) | Heat Dissipation Plate Temperature (°C) | ||||||||
| 1 | 15 | 300 | 13 | 8 | 10 | 12 | 35.1 | 36.8 | 4.8% |
| 2 | 15 | 400 | 13 | 8 | 10 | 12 | 36.7 | 38.0 | 3.5% |
| 3 | 15 | 500 | 13 | 8 | 10 | 12 | 41.8 | 42.6 | 1.9% |
| 4 | 15 | 600 | 13 | 8 | 10 | 12 | 45.4 | 47.3 | 4.2% |
| 5 | 15 | 700 | 13 | 8 | 10 | 12 | 48.6 | 49.5 | 1.8% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Ma, X.; Hu, Z.; Sun, S. Multi-Parameter Optimization of Heat Dissipation Structure of Double Disk Magnetic Coupler Based on Orthogonal Experimental Design. Energies 2022, 15, 8801. https://doi.org/10.3390/en15238801
Wang S, Ma X, Hu Z, Sun S. Multi-Parameter Optimization of Heat Dissipation Structure of Double Disk Magnetic Coupler Based on Orthogonal Experimental Design. Energies. 2022; 15(23):8801. https://doi.org/10.3390/en15238801
Chicago/Turabian StyleWang, Shuang, Xin Ma, Zeyong Hu, and Shousuo Sun. 2022. "Multi-Parameter Optimization of Heat Dissipation Structure of Double Disk Magnetic Coupler Based on Orthogonal Experimental Design" Energies 15, no. 23: 8801. https://doi.org/10.3390/en15238801
APA StyleWang, S., Ma, X., Hu, Z., & Sun, S. (2022). Multi-Parameter Optimization of Heat Dissipation Structure of Double Disk Magnetic Coupler Based on Orthogonal Experimental Design. Energies, 15(23), 8801. https://doi.org/10.3390/en15238801






