Fast Fault Detection and Active Isolation of Bidirectional Z-Source Circuit Breaker with Mechanical Switch
Abstract
:1. Introduction
- Active operation in case of fault;
- Immediate operation without fault detection sensor;
- SCR enables fast speed;
- Easy to control;
- Suppressing the rise of fault current due to the current limiting capability of the ZCB.
2. Bidirectional Z-Source Circuit Breaker Overview with Mechanical Switches
2.1. Bidirectional Z-Source Circuit Breaker
2.2. Z-Source Circuit Breaker with Mechanical Switch Zero-Crossing Time
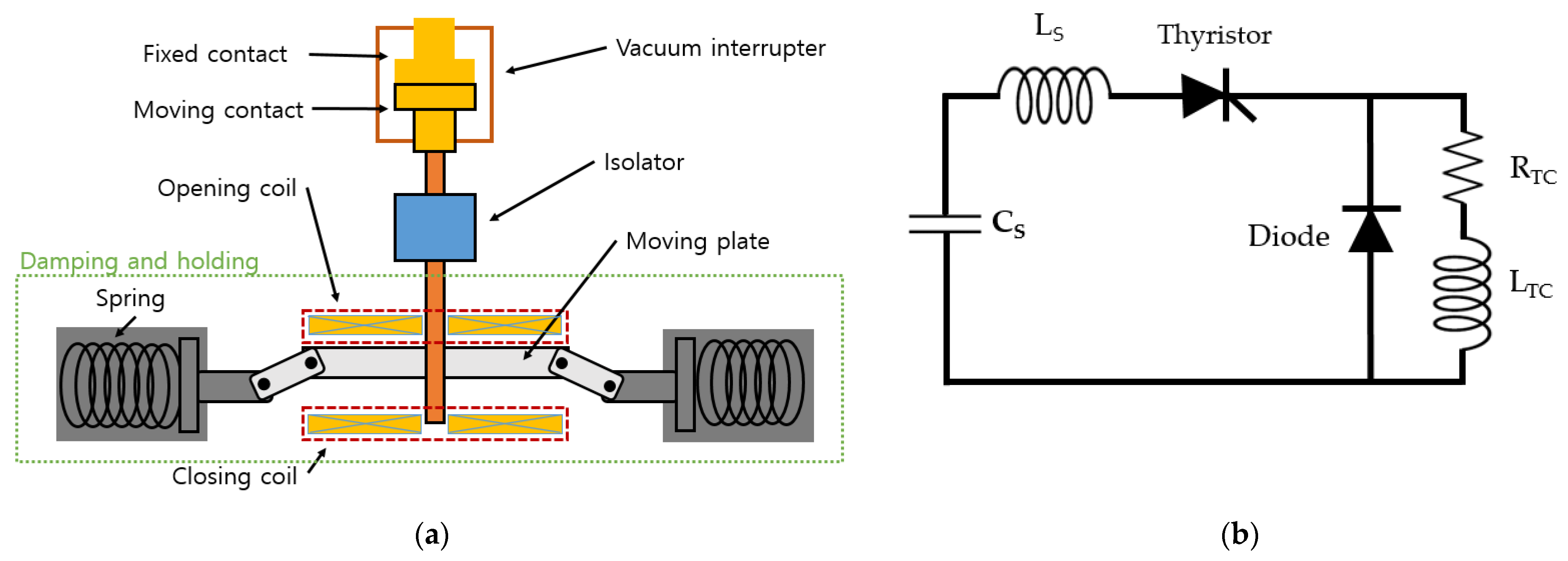
2.3. Thomson Coil Actuator Background
3. Circuit Breaker Modeling
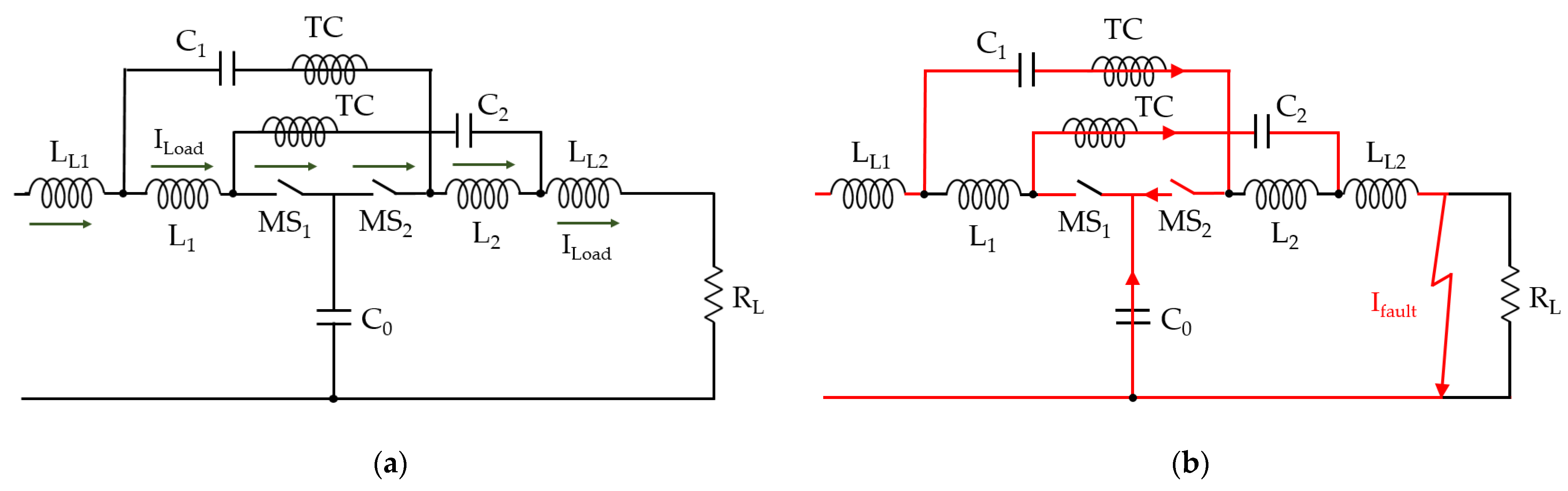
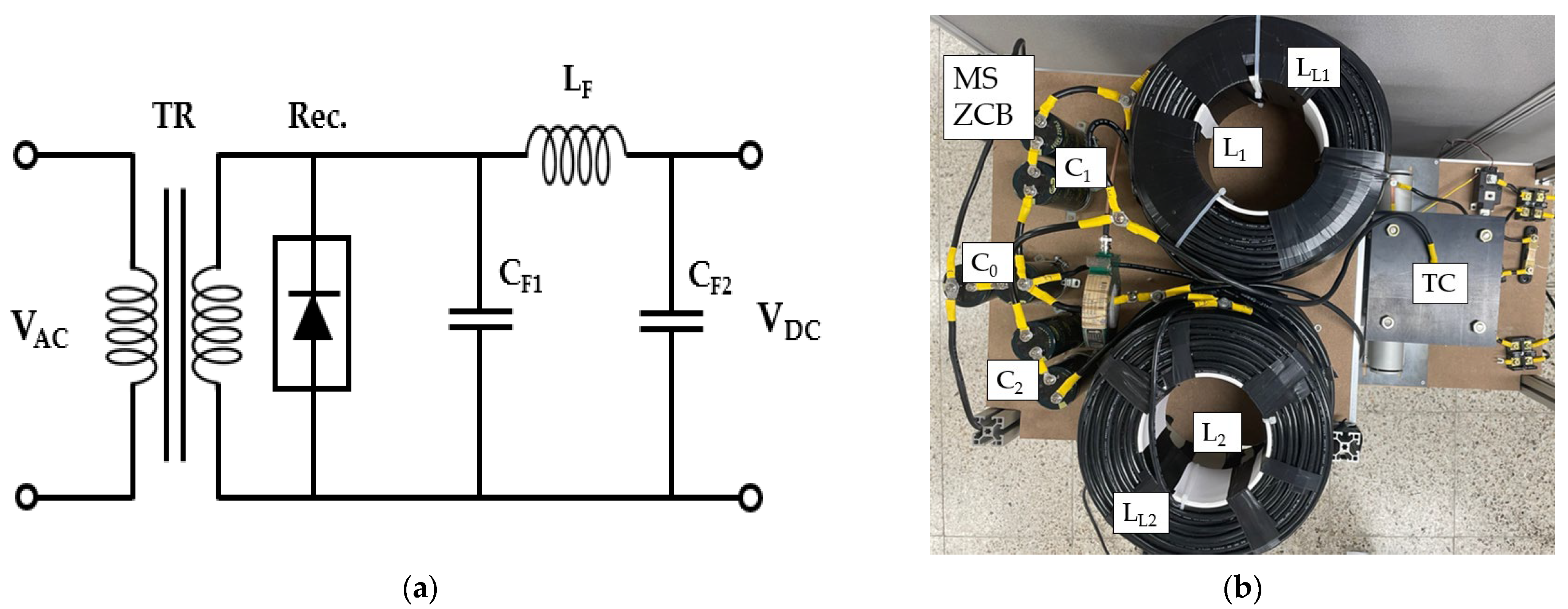
3.1. Proposed Z-Source Circuit Breaker with Mechanical Switch
3.2. Current Flowing to During a Fault
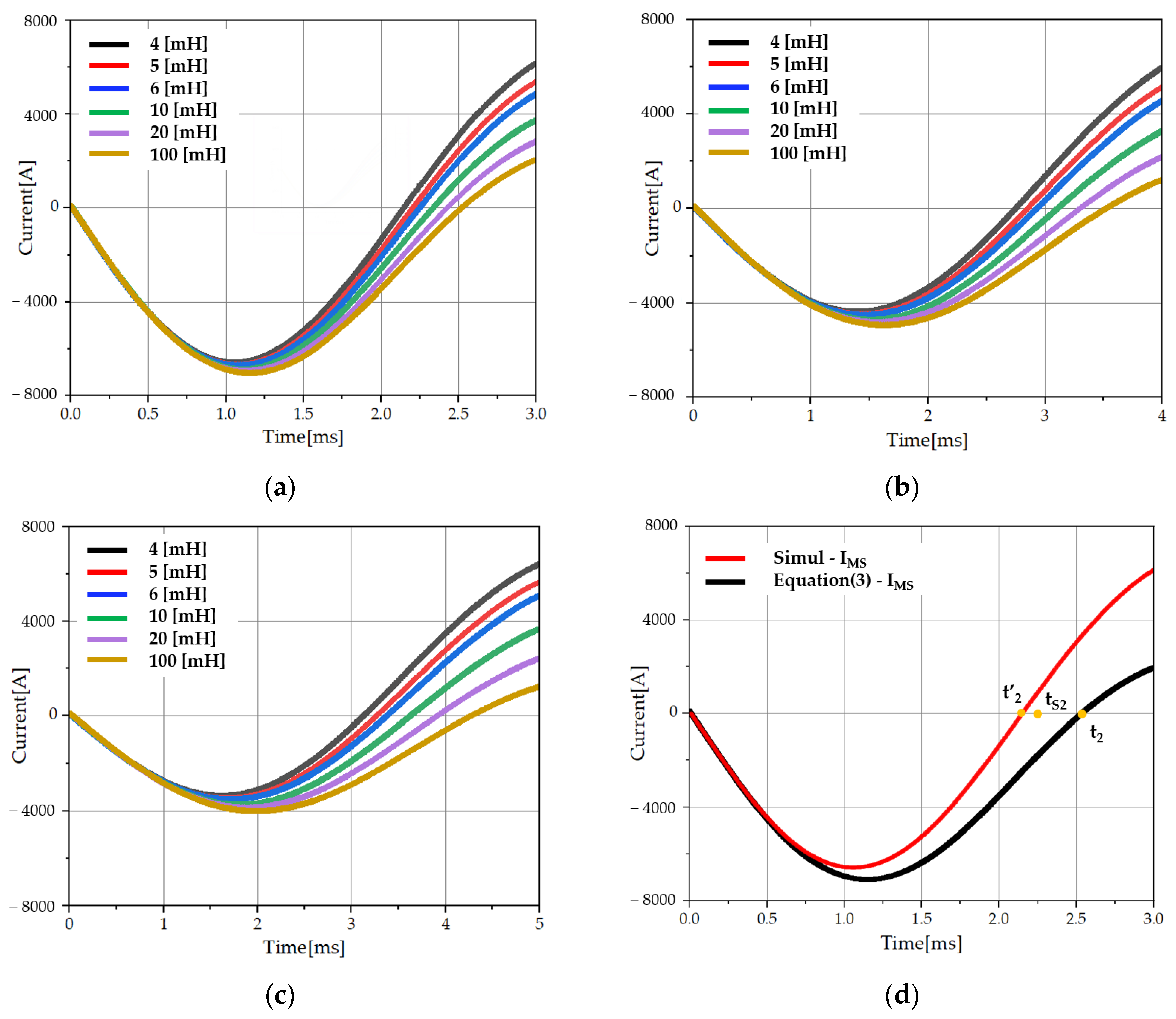
3.3. Current Zero-Crossing Time t1, t2
3.4. Peak Current of IC2
4. Experiment and Simulation
4.1. Mechanical Switch Z-Source Circuit Breaker Simulation
4.2. Thomson Coil Actuator Simulation
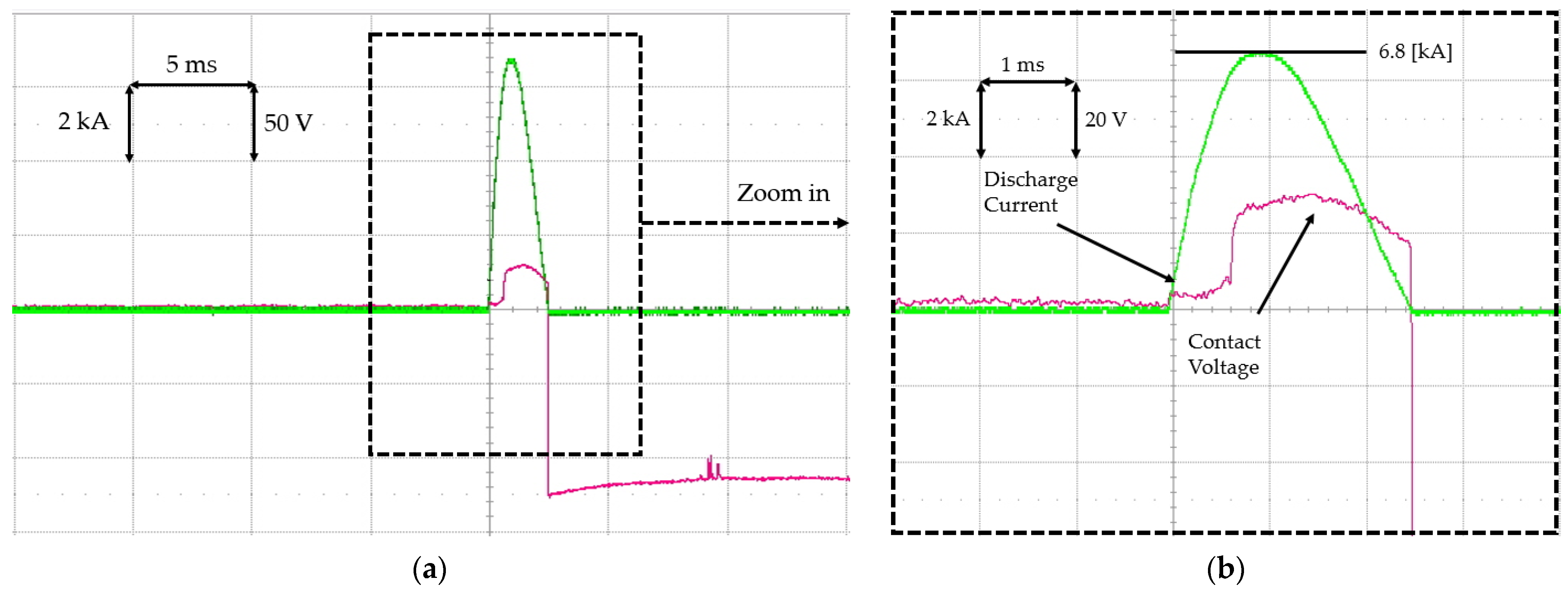
4.3. Experimental Verification and Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hou, L.; Chen, D.; Li, T.; Zhao, M.; Ren, H. Design and Research on DC Electric Leakage Protection Circuit Breaker. Energies 2022, 15, 5605. [Google Scholar] [CrossRef]
- Raghavendra, V.I.; Banavath, S.N.; Thamballa, S. Modified Z-Source DC Circuit Breaker with Enhanced Performance during Commissioning and Reclosing. IEEE Trans. Power Electron. 2022, 37, 910–919. [Google Scholar] [CrossRef]
- Cairoli, P.; Dougal, R.A. New horizons in dc shipboard power systems: New fault protection strategies are essential to the adoption of dc power systems. IEEE Electrif. Mag. 2013, 1, 38–45. [Google Scholar] [CrossRef]
- Teng, S.; Zhang, Z.; Xiao, L. Research on a novel DC circuit breaker based on artificial current zero-crossing. IEEE Access 2020, 8, 36070–36079. [Google Scholar] [CrossRef]
- Al-Khafaf, H.; Asumadu, J. Efficient protection scheme based on y-source circuit breaker in bi-directional zones for mvdc micro-grids. Inventions 2021, 6, 18. [Google Scholar] [CrossRef]
- Hategekimana, P.; Ferre, A.J.; Bernuz, J.M.R.; Ntagwirumugara, E. Fault Detecting and Isolating Schemes in a Low-Voltage DC Microgrid Network from a Remote Village. Energies 2022, 15, 4460. [Google Scholar] [CrossRef]
- Barnes, M.; Vilchis-Rodriguez, D.; Pei, X.; Shuttleworth, R.; Cwikowski, O.; Smith, A. HVDC Circuit Breakers-A Review. IEEE Access 2020, 8, 211829–211848. [Google Scholar] [CrossRef]
- Franck, C.M. HVDC circuit breakers: A review identifying future research needs. IEEE Trans. Power 2011, 26, 998–1007. [Google Scholar] [CrossRef] [Green Version]
- Pei, X.; Cwikowski, O.; Vilchis-Rodriguez, D.S.; Barnes, M.; Smith, A.C.; Shuttleworth, R. A review of technologies for MVDC circuit breakers. In Proceedings of the IECON Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2016. [Google Scholar] [CrossRef]
- Mokhberdoran, A.; Carvalho, A.; Leite, H.; Silva, N. A review on HVDC circuit breakers. In Proceedings of the Renewable Power Generation Conference, Naples, Italy, 24–25 September 2014. [Google Scholar] [CrossRef]
- Wu, Y.; Hu, Y.; Wu, Y.; Rong, M.; Yi, Q. Investigation of an active current injection DC circuit breaker based on a magnetic induction current commutation module. IEEE Trans. Power Deliv. 2018, 33, 1809–1817. [Google Scholar] [CrossRef]
- Shi, Z.Q.; Zhang, Y.K.; Jia, S.L.; Song, X.C.; Wang, L.J.; Chen, M. Design and numerical investigation of a HVDC vacuum switch based on artificial current zero. IEEE Trans. Dielectr. Elect. Insul. 2015, 22, 135–141. [Google Scholar] [CrossRef]
- Ludin, G.A.; Amin, M.A.; Matayoshi, H.; Rangarajan, S.S.; Hemeida, A.M.; Takahashi, H.; Senjyu, T. Solid-State DC Circuit Breakers and Their Comparison in Modular Multilevel Converter Based-HVDC Transmission System. Electronics 2021, 10, 1204. [Google Scholar] [CrossRef]
- Lumen, S.M.S.; Kannan, R.; Yahaya, N. DC circuit breaker: A comperhensive review of solid state topologies. In Proceedings of the IEEE International Conference on Power and Energy (PECon), Penang, Malaysia, 7–8 December 2020. [Google Scholar] [CrossRef]
- Sano, K.; Takasaki, M. A surgeless solid-state DC circuit breaker for voltage-source-converter-based HVDC systems. IEEE Trans. Ind. Appl. 2014, 50, 2690–2699. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, V.-V.; Son, H.-I.; Nguyen, T.-T.; Kim, H.-M.; Kim, C.-K. A novel topology of hybrid HVDC circuit breaker for VSC-HVDC application. Energies 2017, 10, 1675. [Google Scholar] [CrossRef] [Green Version]
- Khalid, S.; Raza, A.; Alqasemi, U.; Sobahi, N.; Yousaf, M.Z.; Abbas, G.; Jamil, M. Technical Assessment of Hybrid HVDC Circuit Breaker Components under M-HVDC Faults. Energies 2021, 14, 8148. [Google Scholar] [CrossRef]
- Bösche, D.; Wilkening, E.; Köpf, H.; Kurrat, M. Hybrid DC Circuit Breaker Feasibility Study. IEEE Trans. Compon. Packag. Manuf. Technol. 2017, 7, 354–362. [Google Scholar] [CrossRef]
- Cho, Y.M.; Lee, K.A. Experimental Study on Splitter Plate for Improving the Dielectric Recovery Strength of Low-Voltage Circuit Breaker. Electronics 2020, 9, 2148. [Google Scholar] [CrossRef]
- Corzine, K.A.; Ashton, R.W. A new Z-source DC circuit breaker. IEEE Trans. Power Electron. 2012, 27, 2796–2804. [Google Scholar] [CrossRef]
- Peng, F.Z. Z-source inverter. IEEE Trans. Ind. Appl. 2003, 39, 504–510. [Google Scholar] [CrossRef]
- Corzine, K.A.; Ashton, R.W. Structure and analysis of the Z-source MVDC breaker. In Proceedings of the IEEE Electric Ship Technologies Symposium, Arlington, VA, USA, 4–6 April 2011. [Google Scholar] [CrossRef]
- Chang, A.H.; Sennett, B.R.; Avestruz, A.T.; Leeb, S.B.; Kirtley, J.L. Analysis and design of DC system protection using Z-source circuit breaker. IEEE Trans. Power Electron. 2015, 31, 1036–1049. [Google Scholar] [CrossRef]
- Savaliya, S.G.; Fernandes, B.G. Analysis and Experimental Validation of Bidirectional Z-Source DC Circuit Breakers. IEEE Trans. Ind. Electron. 2019, 67, 4613–4622. [Google Scholar] [CrossRef]
- Bhatta, S.; Zhang, Y.; Fu, R. Comparative Analysis of Power Loss Associated with Topology of Bi-Directional Z-Source Circuit Breakers. In Proceedings of the IEEE 2018 SoutheastCon 2018, St. Petersburg, FL, USA, 19–22 April 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Ryan, D.J.; Torresan, H.D.; Bahrani, B. A bidirectional series Z-source circuit breaker. IEEE Trans. Power Electron. 2017, 33, 7609–7621. [Google Scholar] [CrossRef]
- Keshavarzi, D.; Ghanbari, T.; Farjah, E. A Z-source-based bidirectional DC circuit breaker with fault current limitation and interruption capabilities. IEEE Trans. Power Electron. 2016, 32, 6813–6822. [Google Scholar] [CrossRef]
- Bhatta, S.; Fu, R.; Zhang, Y. A New Method of Detecting and Interrupting High Impedance Faults by Specifying the Z-Source Breaker in DC Power Networks. Electronics 2020, 9, 1654. [Google Scholar] [CrossRef]
- Fu, R.; Bhatta, S.; Keller, J.M.; Zhang, Y. Assessment of Cable Length Limit for Effective Protection by Z-Source Circuit Breakers in DC Power Networks. Electronics 2021, 10, 183. [Google Scholar] [CrossRef]
- Mackey, L.; Rachi, M.R.K.; Peng, C.; Husain, I. Optimization and control of a z-source, ultrafast mechanically switched, high-efficiency dc circuit breaker. IEEE Trans. Ind. Appl. 2020, 56, 2871–2879. [Google Scholar] [CrossRef]
- Lim, D.K.; Woo, D.K.; Kim, I.W.; Shin, D.K.; Ro, J.S.; Chung, T.K.; Jung, H.K. Characteristic analysis and design of a Thomson coil actuator using an analytic method and a numerical method. IEEE Trans. Magn. 2013, 49, 5749–5755. [Google Scholar] [CrossRef]
- Wu, Y.; Wu, Y.; Rong, M.; Yang, F.; Zhong, J.; Li, M.; Hu, Y. A new Thomson coil actuator: Principle and analysis. IEEE Trans. Compon. Packag. Manuf. Technol. 2015, 5, 1644–1655. [Google Scholar] [CrossRef]
- Augustin, T.; Parekh, M.; Magnusson, J.; Becerra, M.; Nee, H.P. Thomson-coil actuator system for enhanced active resonant DC circuit breakers. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 10, 800–810. [Google Scholar] [CrossRef]
- Pham, M.T.; Ren, Z.; Li, W.; Koh, C.S. Optimal design of a Thomson-coil actuator utilizing a mixed-integer-discrete-continuous variables global optimization algorithm. IEEE Trans. Magn. 2011, 47, 4163–4166. [Google Scholar] [CrossRef]







| C (mF) | LL (mH) | L (mH) | t2 (ms) | t’2 (ms) |
|---|---|---|---|---|
| 1 | 1 | 4 | 2.55 | 2.04 |
| 5 | 2.125 | |||
| 6 | 2.186 | |||
| 10 | 2.318 | |||
| 20 | 2.429 | |||
| 100 | 2.525 | |||
| 2 | 4 | 3.61 | 2.407 | |
| 5 | 2.579 | |||
| 6 | 2.708 | |||
| 10 | 3.008 | |||
| 20 | 3.282 | |||
| 100 | 3.539 | |||
| 3 | 4 | 4.42 | 2.526 | |
| 5 | 2.763 | |||
| 6 | 2.947 | |||
| 10 | 3.4 | |||
| 20 | 3.843 | |||
| 100 | 4.291 |
| VCharge (V) | LS (µH) | LTC (µH) | CS (mF) | Discharge Current (kA) | |
|---|---|---|---|---|---|
| TC operating circuit | 400 | 26 | 4.4 | 17.25 | 7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.-S.; Cho, Y.-M.; Lee, K.-A.; Rhee, J.-H. Fast Fault Detection and Active Isolation of Bidirectional Z-Source Circuit Breaker with Mechanical Switch. Energies 2022, 15, 8899. https://doi.org/10.3390/en15238899
Lee H-S, Cho Y-M, Lee K-A, Rhee J-H. Fast Fault Detection and Active Isolation of Bidirectional Z-Source Circuit Breaker with Mechanical Switch. Energies. 2022; 15(23):8899. https://doi.org/10.3390/en15238899
Chicago/Turabian StyleLee, Hyeon-Seung, Young-Maan Cho, Kun-A Lee, and Jae-Ho Rhee. 2022. "Fast Fault Detection and Active Isolation of Bidirectional Z-Source Circuit Breaker with Mechanical Switch" Energies 15, no. 23: 8899. https://doi.org/10.3390/en15238899
APA StyleLee, H.-S., Cho, Y.-M., Lee, K.-A., & Rhee, J.-H. (2022). Fast Fault Detection and Active Isolation of Bidirectional Z-Source Circuit Breaker with Mechanical Switch. Energies, 15(23), 8899. https://doi.org/10.3390/en15238899






