Study on the Performance of Variable Density Multilayer Insulation in Liquid Hydrogen Temperature Region
Abstract
1. Introduction
2. Model and Calculation Procedure
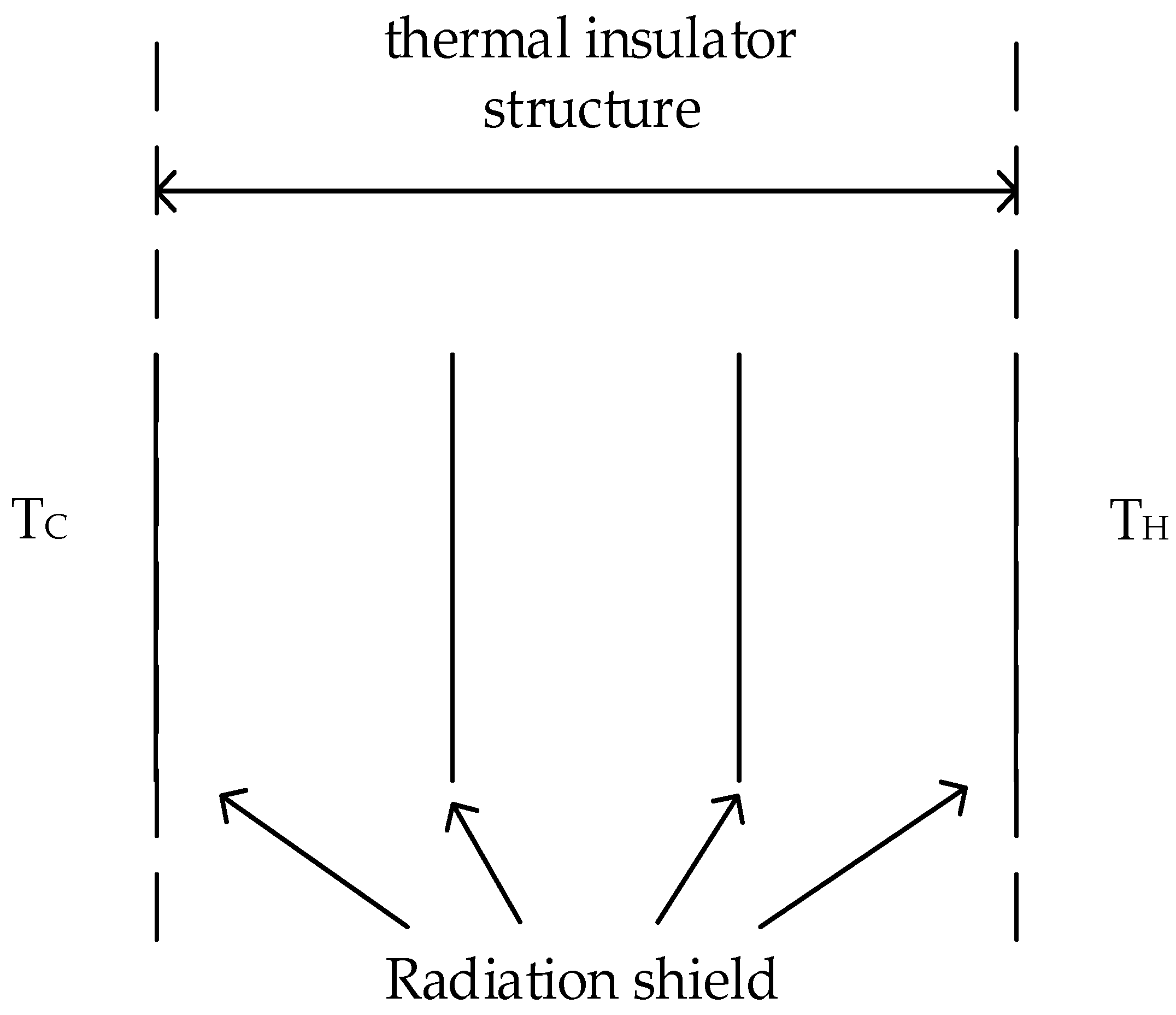
2.1. Heat Transfer Model
2.2. Calculation Procedure
2.3. Variable-Density Configuration Method
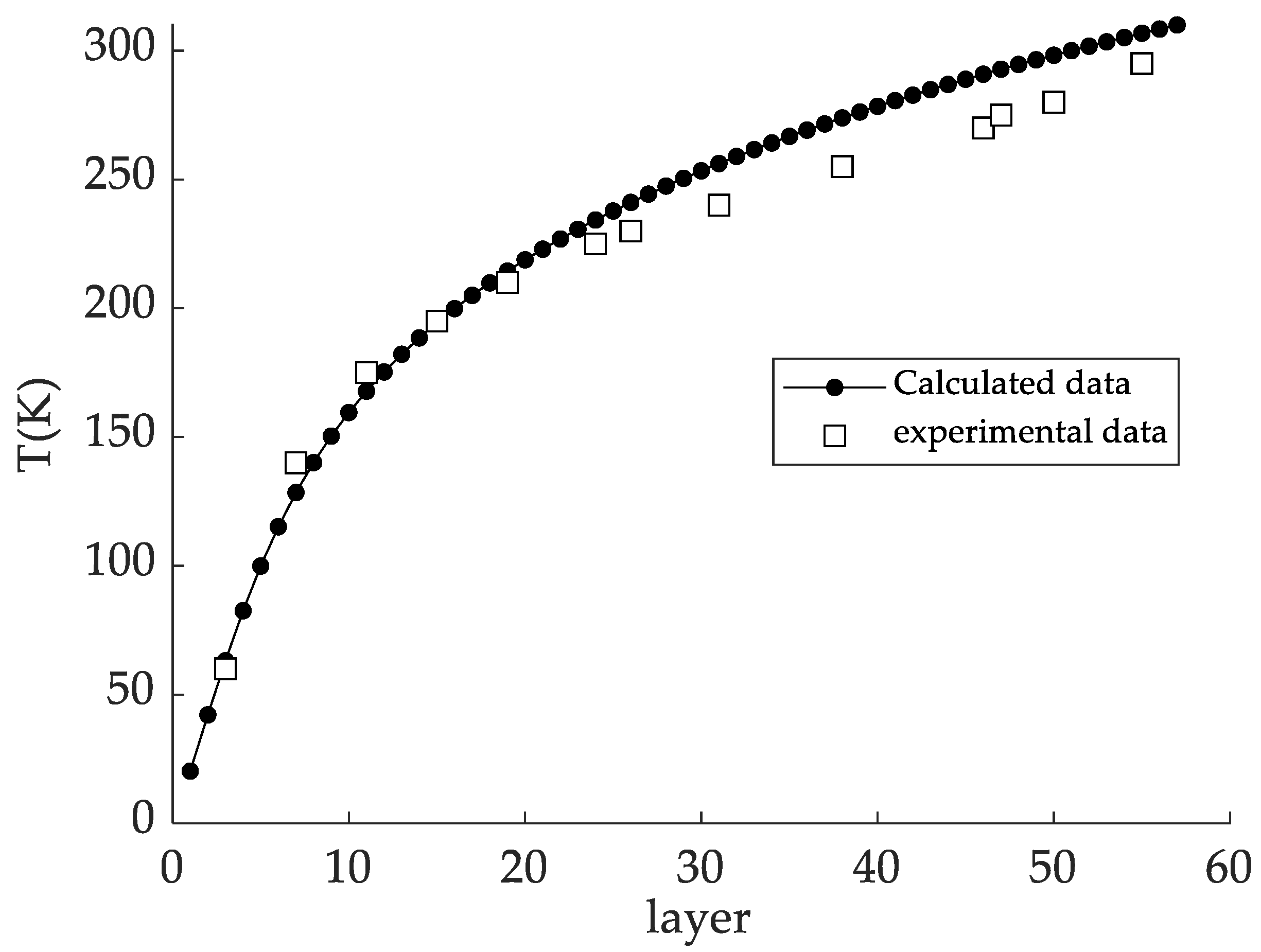
3. Validation of the Configuration Method
4. Results and Discussion
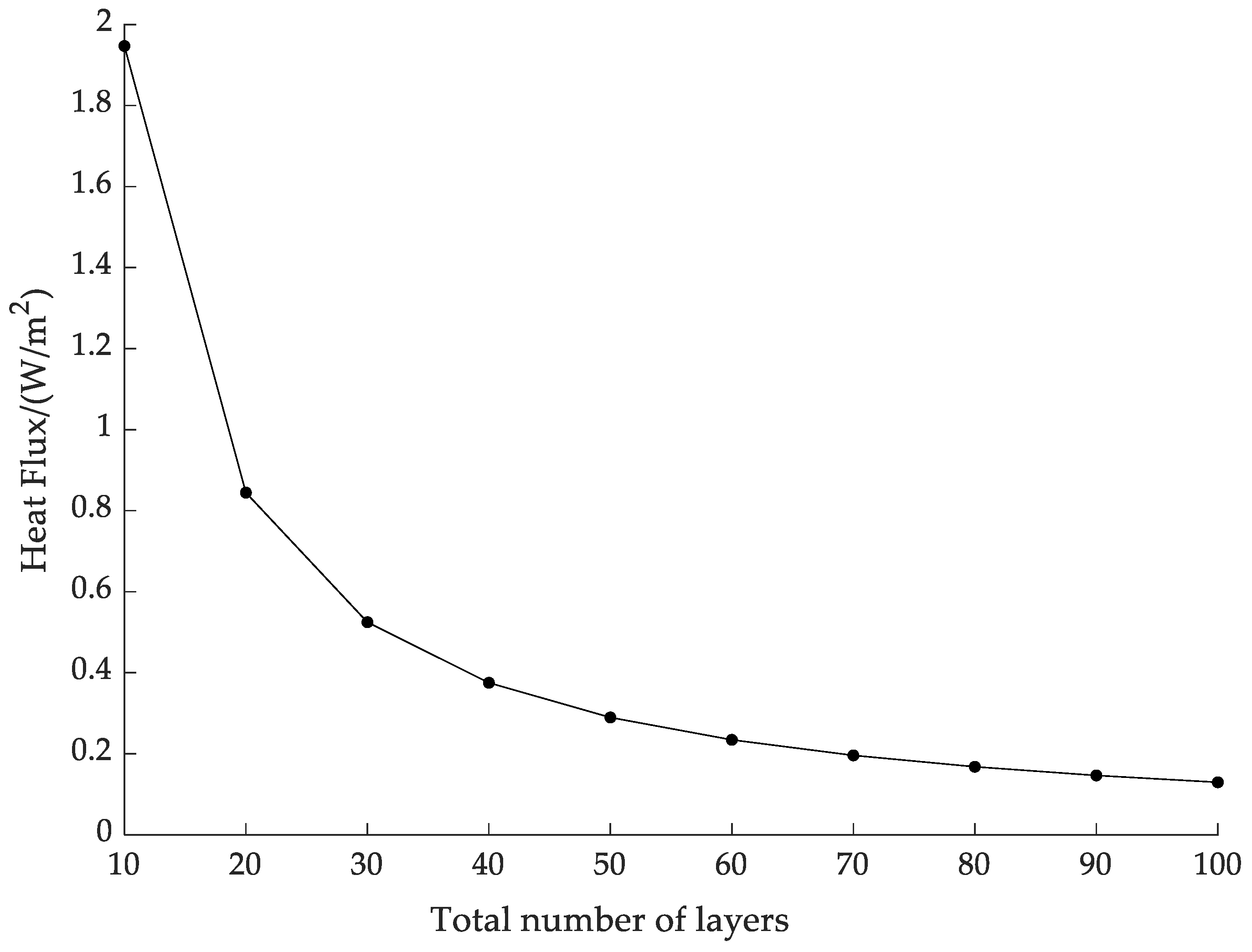
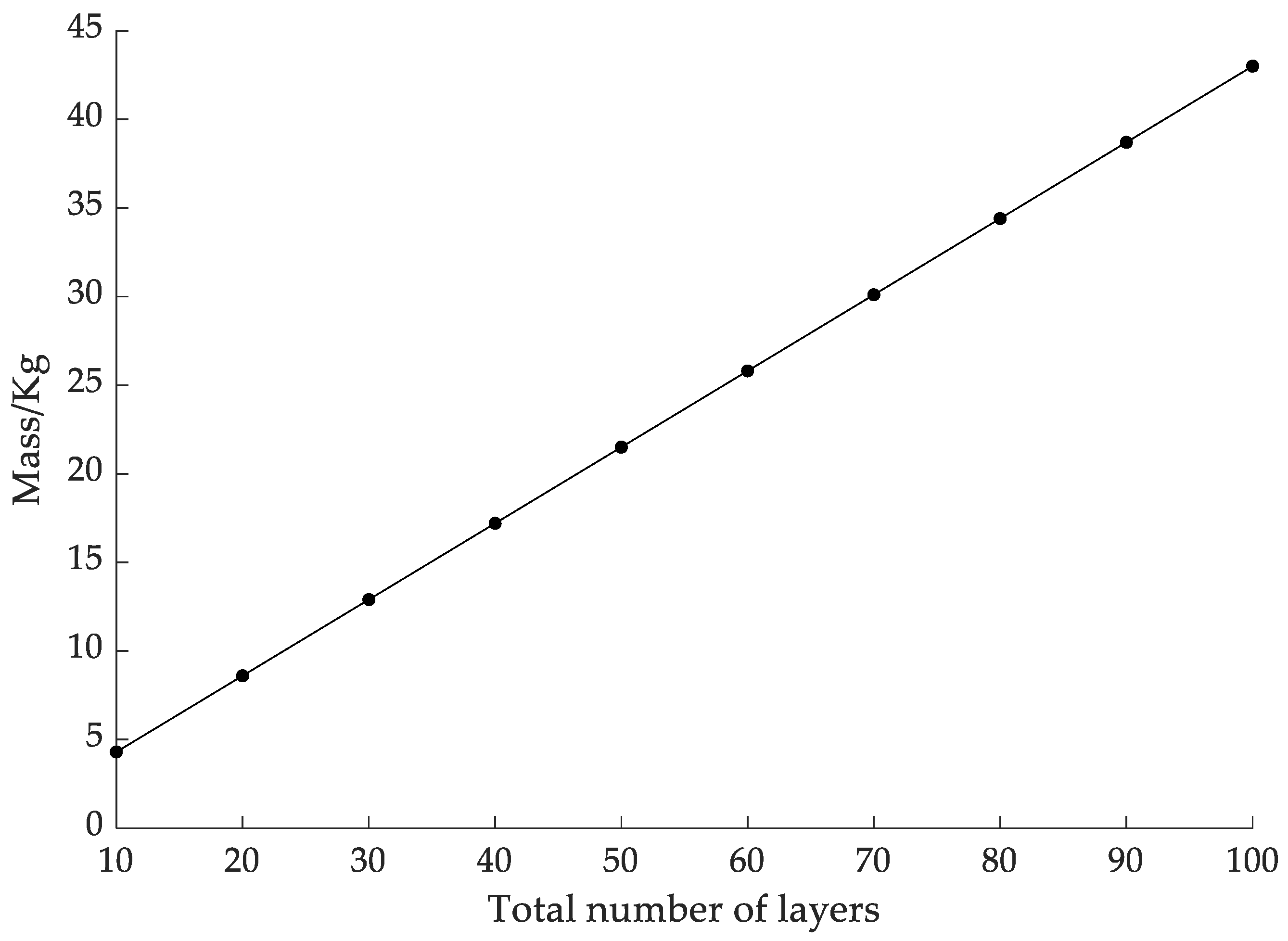
4.1. Effect of the Total Number of Layers on Heat Flux Density
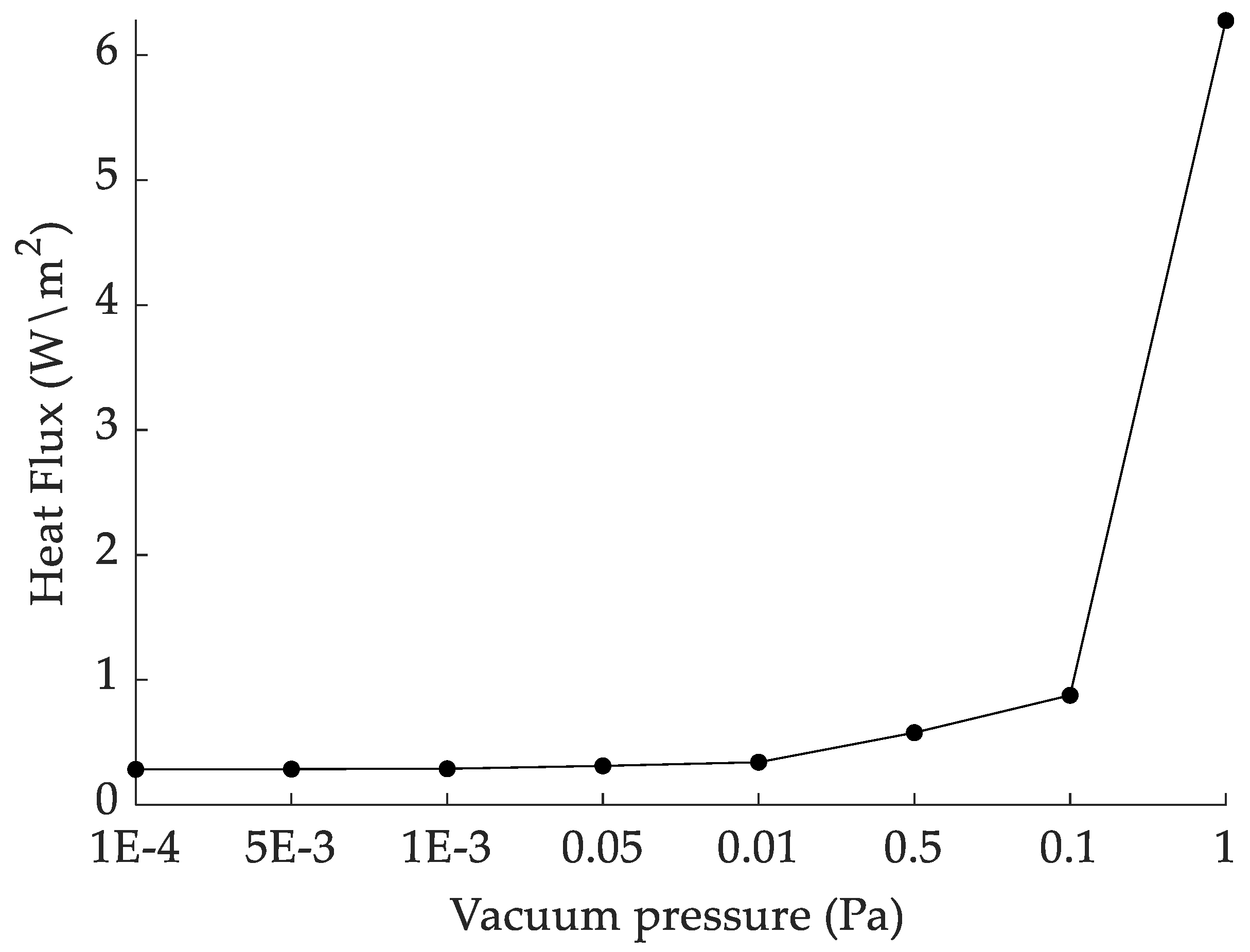
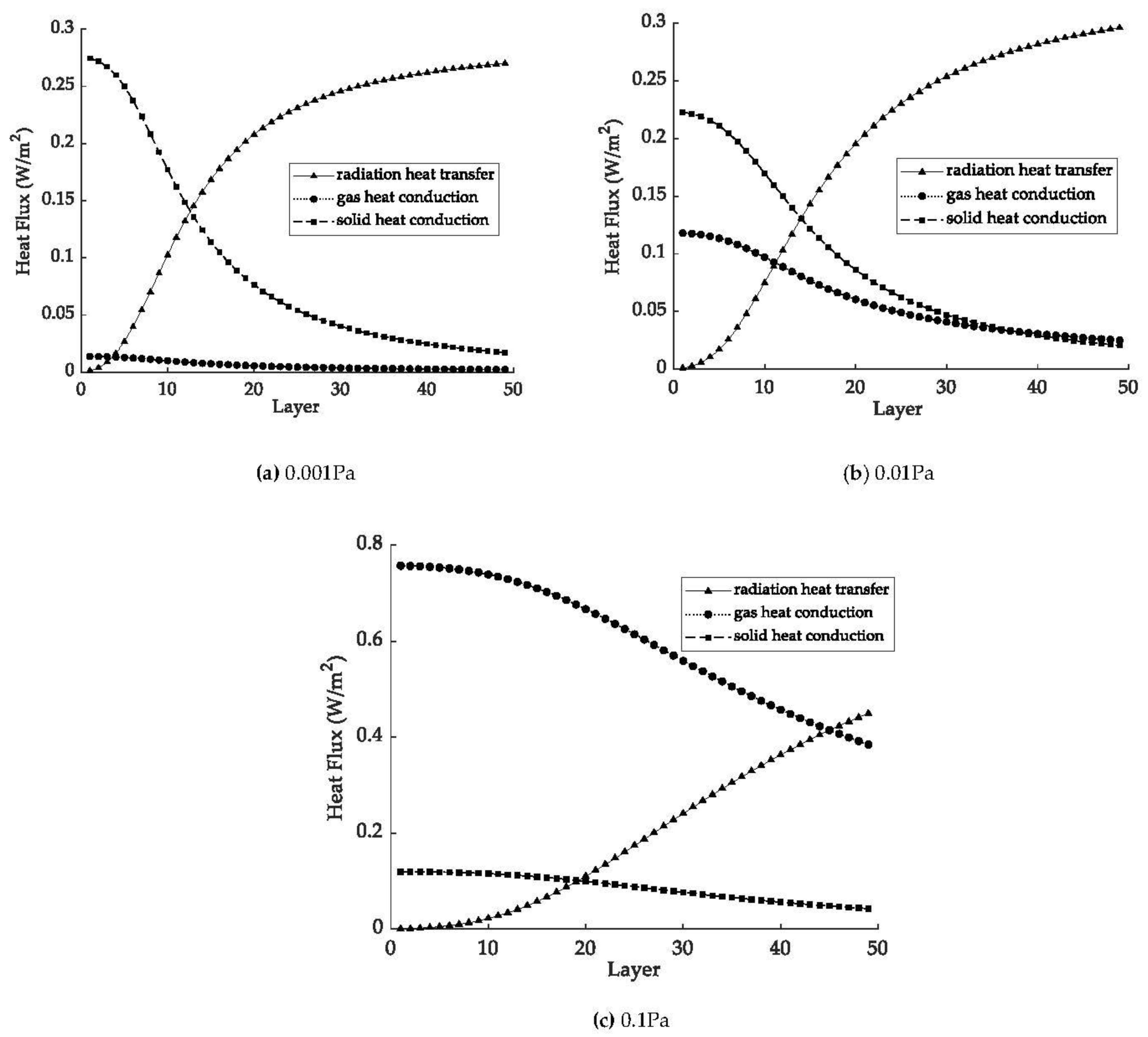
4.2. Effect of a Vacuum on Heat Flux
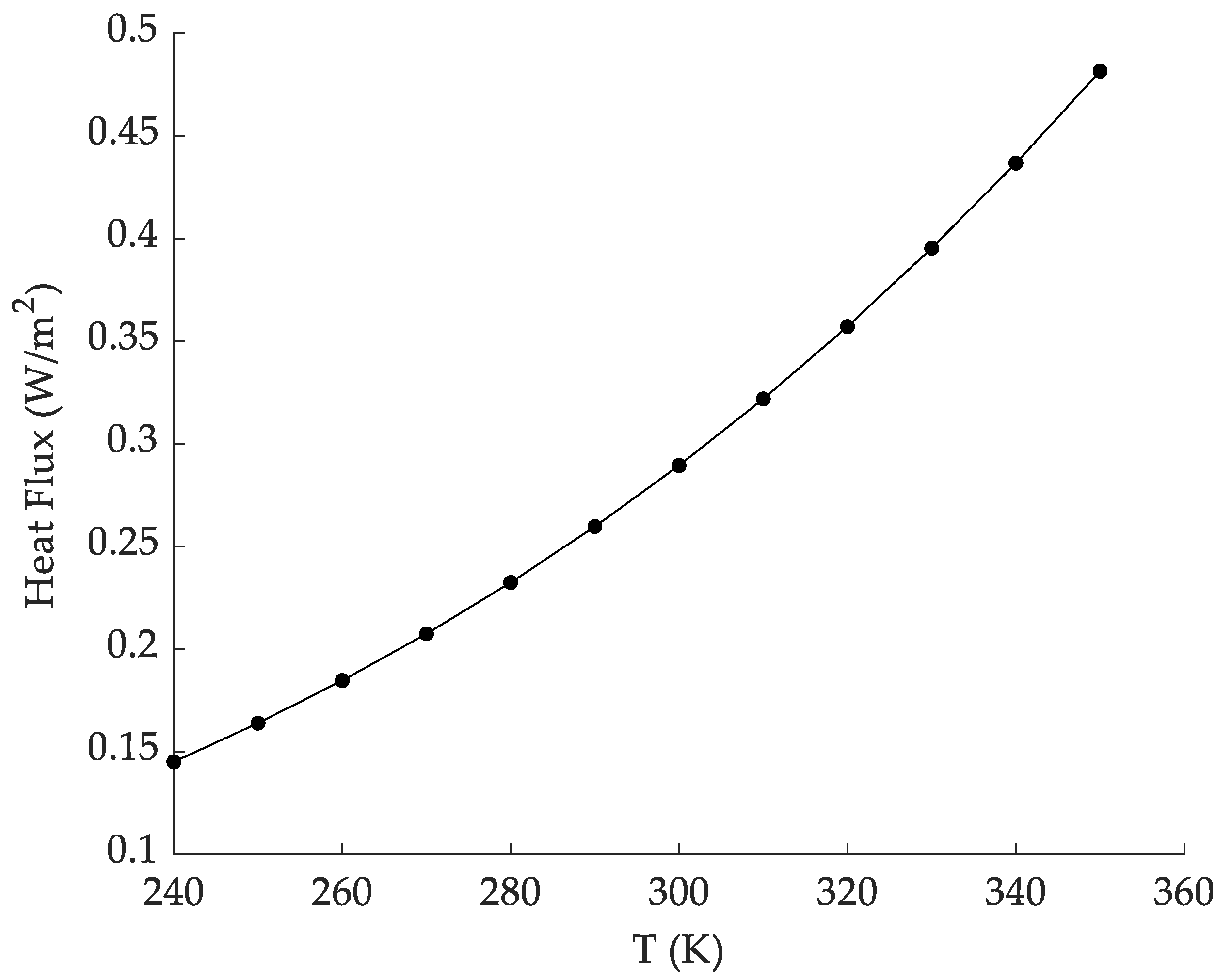
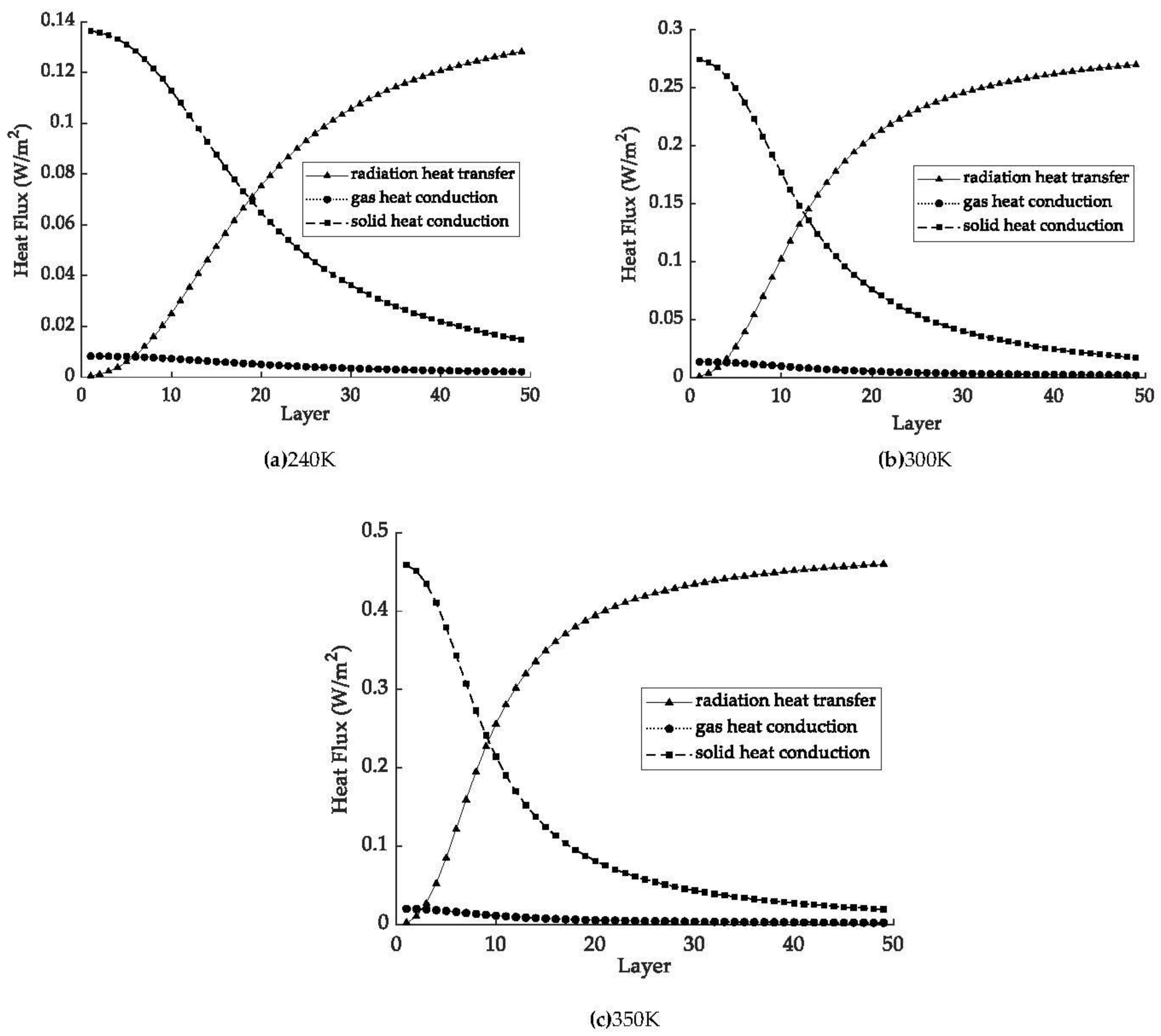
4.3. Effect of the Thermal Boundary Temperature on Heat Flux
4.4. Optimization of Variable-Density Configuration
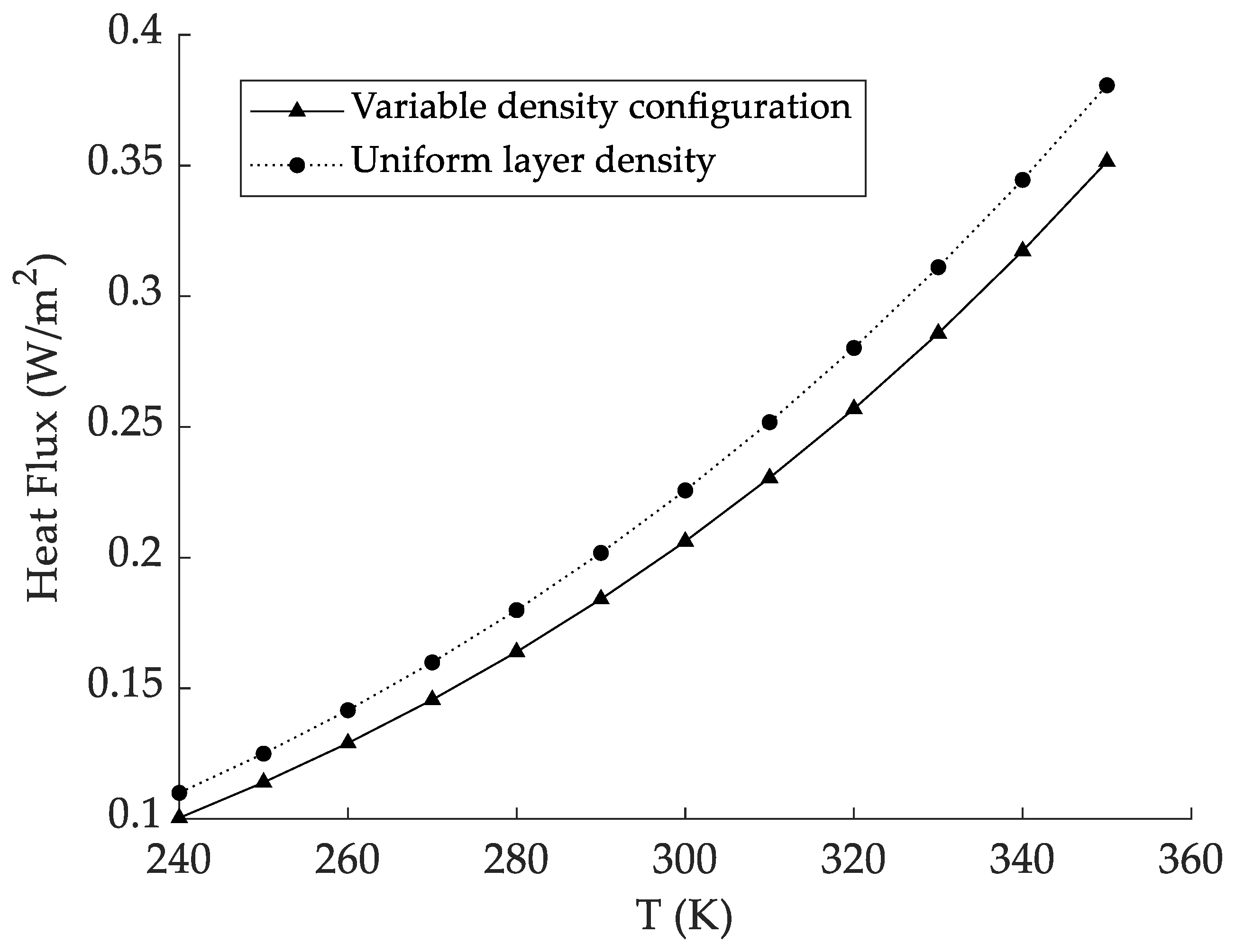
4.5. Comparison with Uniform-Layer Density at Different Thermal Boundary Temperatures
5. Conclusions
- As the total number of layers increases, the heat flux gradually decreases, but more layers do not mean that it is better. When the number of layers reaches 50, the heat flux tends to decrease gently, but the total mass and thickness of the insulation layer linearly increase. Therefore, the total number of layers needs to be selected according to the specific situation.
- When the pressure is lower than 0.01 Pa, the heat flux has no obvious change, and the residual gas conduction is negligible. When the pressure increases to more than 0.01 Pa, the heat flux changes significantly, and the residual gas thermal conductivity cannot be ignored. When this occurs, the multilayer insulation structure loses the vacuum environment, so the pressure should be kept below 0.01 Pa.
- With increases in the thermal boundary temperature, the heat flux increases and is strongly influenced by the temperature. Radiation heat transfer is the main heat transfer path in vacuum multilayer insulation. As the thermal boundary temperature increases, the proportion of radiation heat transfer heat flux in the total heat flux also increases. The proposed variable-density configuration method based on the control variable method and the insertion by region method can optimize the variable-density configuration and obtain an accurate configuration for layer density. At liquid hydrogen temperatures with a fixed thermal boundary of 300 K and 61 layers of radiation shields, the optimal variable-density configuration is 4 layers inserted in the low-density region, 15 layers inserted in the medium-density region and 38 layers inserted in the high-density region. The heat flux is 0.2062 W/m2, which is 8.6% lower than that of the uniform-layer density. In the range of 240 K to 350 K, the thermal insulation performance is better than that of a uniform-layer density.
Author Contributions
Funding
Conflicts of Interest
References
- Majumdar, A.; Deutch, J.M.; Prasher, R.S.; Griffin, T.P. A Framework for a Hydrogen Economy. Joule 2021, 5, 1905–1908. [Google Scholar] [CrossRef]
- Khan, I.; Hou, F.; Zakari, A.; Tawiah, V.K. The dynamic links among energy transitions, energy consumption, and sustainable economic growth: A novel framework for IEA countries. Energy 2021, 222, 119935. [Google Scholar] [CrossRef]
- Kovač, A.; Paranos, M.; Marciuš, D. Hydrogen in energy transition: A review. Int. J. Hydrogen Energy 2021, 46, 10016–10035. [Google Scholar] [CrossRef]
- Lin, R.H.; Zhao, Y.Y.; Wu, B.D. Toward a hydrogen society: Hydrogen and smart grid integration. Int. J. Hydrogen Energy 2020, 45, 20164–20175. [Google Scholar] [CrossRef]
- Elberry, A.M.; Thakur, J.; Santasalo-Aarnio, A.; Larmi, M. Large-scale compressed hydrogen storage as part of renewable electricity storage systems. Int. J. Hydrogen Energy 2021, 46, 15671–15690. [Google Scholar] [CrossRef]
- Staffell, I.; Scamman, D.; Velazquez Abad, A.; Balcombe, P.; Dodds, P.E.; Ekins, P.; Shah, N.; Ward, K.R. The role of hydrogen and fuel cells in the global energy system. Energy Environ. Sci. 2019, 12, 463–491. [Google Scholar] [CrossRef]
- Boretti, A. Hydrogen internal combustion engines to 2030. Int. J. Hydrogen Energy 2020, 45, 23692–23703. [Google Scholar] [CrossRef]
- Stepien, Z. A Comprehensive Overview of Hydrogen-Fueled Internal Combustion Engines: Achievements and Future Challenges. Energies 2021, 14, 6504. [Google Scholar] [CrossRef]
- Yukesh Kannah, R.; Merrylin, J.; Poornima Devi, T.; Kavitha, S.; Sivashanmugam, P.; Kumar, G.; Rajesh Banu, J. Food waste valorization: Biofuels and value added product recovery. Bioresour. Technol. Rep. 2020, 11, 100524. [Google Scholar] [CrossRef]
- Olabi, A.G.; Saleh Bahri, A.; Abdelghafar, A.A.; Baroutaji, A.; Sayed, E.T.; Alami, A.H.; Rezk, H.; Abdelkareem, M.A. Large-vscale hydrogen production and storage technologies: Current status and future directions. Int. J. Hydrogen Energy 2021, 46, 23498–23528. [Google Scholar] [CrossRef]
- Calise, F. Recent Advances in Green Hydrogen Technology. Energies 2022, 15, 5828. [Google Scholar] [CrossRef]
- Moradi, R.; Groth, K.M. Hydrogen storage and delivery: Review of the state of the art technologies and risk and reliability analysis. Int. J. Hydrogen Energy 2019, 44, 12254–12269. [Google Scholar] [CrossRef]
- Aziz, M. Liquid Hydrogen: A Review on Liquefaction, Storage, Transportation, and Safety. Energies 2021, 14, 5917. [Google Scholar] [CrossRef]
- Johnson, W.L. Optimization of layer densities for multilayered insulation systems. AIP Conf. Proc. 2010, 1218, 804–811. [Google Scholar]
- Johnson, W.; Fesmire, J.E. Thermal performance of low layer density multilayer insulation using liquid nitrogen. Adv. Cryog. Eng. 2012, 1434, 39–46. [Google Scholar]
- Johnson, W. Thermal analysis of low layer density multilayer insulation test results. Adv. Cryog. Eng. 2012, 1434, 1519–1526. [Google Scholar]
- Wang, J.; Zhan, Y.; Wang, W.; Wang, R. Optimization and performance of highly efficient hydrogen getter applied in high vacuum multilayer insulation cryogenic tank. Vacuum 2018, 149, 87–92. [Google Scholar] [CrossRef]
- Martin, J.J.; Hastings, L. Large-Scale Liquid Hydrogen Testing of Variable Density Multilayer Insulation with a Foam Substrate; NASA: Washington, DC, USA, 2001. [Google Scholar]
- Hastings, L.J.; Hedayat, A.; Brown, T.M. Analytical Modeling and Test Correlation of Variable Density Multilayer Insulation for Cryogenic Storage; NASA: Washington, DC, USA, 2004. [Google Scholar]
- Hedayat, A.; Hastings, L.J.; Brown, T. Analytical modeling of variable density multilayer insulation for cryogenic storage. AIP Conf. Proc. 2002, 613, 1557–1564. [Google Scholar]
- Huang, Y.; Wang, B.; Zhou, S.; Wu, J.; Lei, G.; Li, P.; Sun, P. Modeling and experimental study on combination of foam and variable density multilayer insulation for cryogen storage. Energy 2017, 123, 487–498. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Y.; Zhou, G. Insulation performance of foam during the terrestrial and ascent period. Appl. Therm. Eng 2018, 145, 364–374. [Google Scholar] [CrossRef]
- Zheng, J.; Chen, L.; Wang, J.; Xi, X.; Zhu, H.; Zhou, Y.; Wang, J. Thermodynamic analysis and comparison of four insulation schemes for liquid hydrogen storage tank. Energy Convers. Manag. 2019, 186, 526–534. [Google Scholar] [CrossRef]
- Zheng, J.; Chen, L.; Cui, C.; Guo, J.; Zhu, W.; Zhou, Y.; Wang, J. Experimental study on composite insulation system of spray on foam insulation and variable density multilayer insulation. Appl. Therm. Eng. 2018, 130, 161–168. [Google Scholar] [CrossRef]
- Zheng, J.; Chen, L.; Wang, J.; Zhou, Y.; Wang, J. Thermodynamic modeling and optimization of self-evaporation vapor cooled shield for liquid hydrogen storage tank. Energy Convers. Manag. 2019, 184, 74–82. [Google Scholar] [CrossRef]
- Xu, X.; Xu, H.; Yang, B.; Chen, L.; Wang, J. A Novel Composite Insulation System of Hollow Glass Microspheres and Multilayer Insulation with Self-Evaporating Vapor Cooled Shield for Liquid Hydrogen Storage. Energy Technol. 2020, 8, 2000591. [Google Scholar] [CrossRef]
- Wang, P.; Ji, L.; Yuan, J.; An, Z.; Yan, K.; Zhang, J. Modeling and optimization of composite thermal insulation system with HGMs and VDMLI for liquid hydrogen on orbit storage. Int. J. Hydrogen Energy 2020, 45, 7088–7097. [Google Scholar] [CrossRef]
- Wang, P.; Ji, L.; Yuan, J.; An, Z.; Yan, K.; Zhang, J. The influence of inner material with different average thermal conductivity on the performance of whole insulation system for liquid hydrogen on orbit storage. Int. J. Hydrogen Energy 2021, 46, 10913–10923. [Google Scholar] [CrossRef]
- Jiang, W.; Sun, P.; Li, P.; Zuo, Z.; Huang, Y. Transient thermal behavior of multi-layer insulation coupled with vapor cooled shield used for liquid hydrogen storage tank. Energy 2021, 231, 120859. [Google Scholar] [CrossRef]
- McIntosh, G.E. Layer by Layer MLI Calculation Using a Separated Mode Equation. Adv. Cryog. Eng. 1994, 39, 1683–1690. [Google Scholar]
- Stochl, R.J.; Dempsey, P.J.; Leonard, K.R.; McIntosh, G.E. Variable Density MLI Test Results; Springer: Boston, MA, USA, 1996. [Google Scholar]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, K.; Chen, J.; Tian, X.; He, Y. Study on the Performance of Variable Density Multilayer Insulation in Liquid Hydrogen Temperature Region. Energies 2022, 15, 9267. https://doi.org/10.3390/en15249267
Li K, Chen J, Tian X, He Y. Study on the Performance of Variable Density Multilayer Insulation in Liquid Hydrogen Temperature Region. Energies. 2022; 15(24):9267. https://doi.org/10.3390/en15249267
Chicago/Turabian StyleLi, Kecen, Jie Chen, Xueqin Tian, and Yujing He. 2022. "Study on the Performance of Variable Density Multilayer Insulation in Liquid Hydrogen Temperature Region" Energies 15, no. 24: 9267. https://doi.org/10.3390/en15249267
APA StyleLi, K., Chen, J., Tian, X., & He, Y. (2022). Study on the Performance of Variable Density Multilayer Insulation in Liquid Hydrogen Temperature Region. Energies, 15(24), 9267. https://doi.org/10.3390/en15249267




