Dynamic Strategy for Effective Current Reduction in Brushless DC Synchronous Motors Fault Tolerant Operation

Abstract

This work presents a flexible strategy for RMS current reduction of healthy phases for brushless DC synchronous motors (BLDC) operating in phase opening failure, avoiding motor degradation without reducing its performance and allowing safe shutdown when a phase failure is detected. After the diagnosis of an open-phase failure, a corrective action divided into three steps is proposed. First, the traditional Six-Step operating mode with 120° electric degrees is changed to a new operating mode that uses the two healthy phases at 180° electric degrees to reduce torque loss due to phase failure. Second, a trapezoidal shape (with adjustable angles according to the RMS current level) is imposed as a current reference for the controller to reduce the current level and, consequently, improve the efficiency of the motor. Third, the passband of the speed control loop is reduced to minimize the influence of speed oscillations in controller failure. The experimental results presented show that the mode of operation with the proposed dynamic current reduction strategy allows an approximate reduction of up to 27% in the effective current and up to 41% in the motor temperature variation, compared to the usual failure mode of operation of the BLDC motor without the proposed strategy. The dynamics of change in the trapezium angle allowed a weighting between the current level and the oscillation of the speed, preventing the motor in phase failure from having a high-speed variation.

1. Introduction

Brushless DC synchronous motors (BLDC) can be found in applications such as robotics, aerospace, electric vehicle, manufacturing processes, and servo drives, among other applications where high propulsion and performance are required thanks to the higher density of power and torque per amp that can be achieved with these type of motors [1,2]. The use of robust and reliable drive systems in BLDC motors in many of these applications is essential. For example, a fault-tolerant drive and control system on BLDC motors used in drones can prevent large material losses and reduce the risk of accidents during a phase-out emergency through a safe landing [3].

Also, control systems applied to drive DC motors for reliable operation must be taken into consideration. In [4], the authors considered the nonlinearities of DC motors to propose two controllers: one based on sliding mode control (SMC) and the other based on linear active disturbance rejection (LADRC) control to control the speed of the motor. According to the authors, the control system response to parameter variations and varying load torque is achieved using the SMC, while the LADRC is not robust against parameter variations. These nonlinearities were also presented in induction motors that can compromise the use of this type of motor, especially in electric vehicle drives [5].

Among the possible failures in BLDC motors, one can mention: opening the phase; short phase; irregularities in the airgap; problems in motor eccentricity; and bearings; among others [6]. Open-phase failures represent 30% to 35% of situations that impair the normal operation of the motor, and are usually caused by a defect in the motor connectors, failures in inverter transistors, or cable disruptions, among other reasons [7].

For the development of fault tolerant control for the BLDC motor, it is necessary to: (i) perform a detection and an identification (complete diagnosis) of the fault and (ii) drive strategies for complete or partial system repair [8]. Recently, one of the research approaches to fault tolerance in motors has been the implementation of redundancies (e.g., inverters with extra arms) [9]. However, such techniques bring disadvantages, such as project complexity, high maintenance and implementation cost, and high volume.

In such a situation, the motor starts operating only in two phases. Given the above, there is great motivation for the development of solutions to make the activation of the BLDC motor tolerant to open circuit failures, to keep the operation at safe levels long enough to shut down the load without damage.

According to [10], the choice of the motor along with its speed and torque control play an important role in realizing its operational characteristics. In [11], a method for minimizing torque loss is proposed. It is based on a nonlinear automatic control used to mitigate the cogging torque presented in BLDC motors, which tends to affect motor control. Another issue related to torque loss is addressed in [4], where a current optimization-based fault-tolerant control is proposed to minimize the proportion of torque loss for standard Permanent Magnet Synchronous Motor (PMSM) drives under open-phase fault and open-switch fault conditions. The article proposes a current control designed to minimize torque loss without changing the mathematical model of the faulty motor.

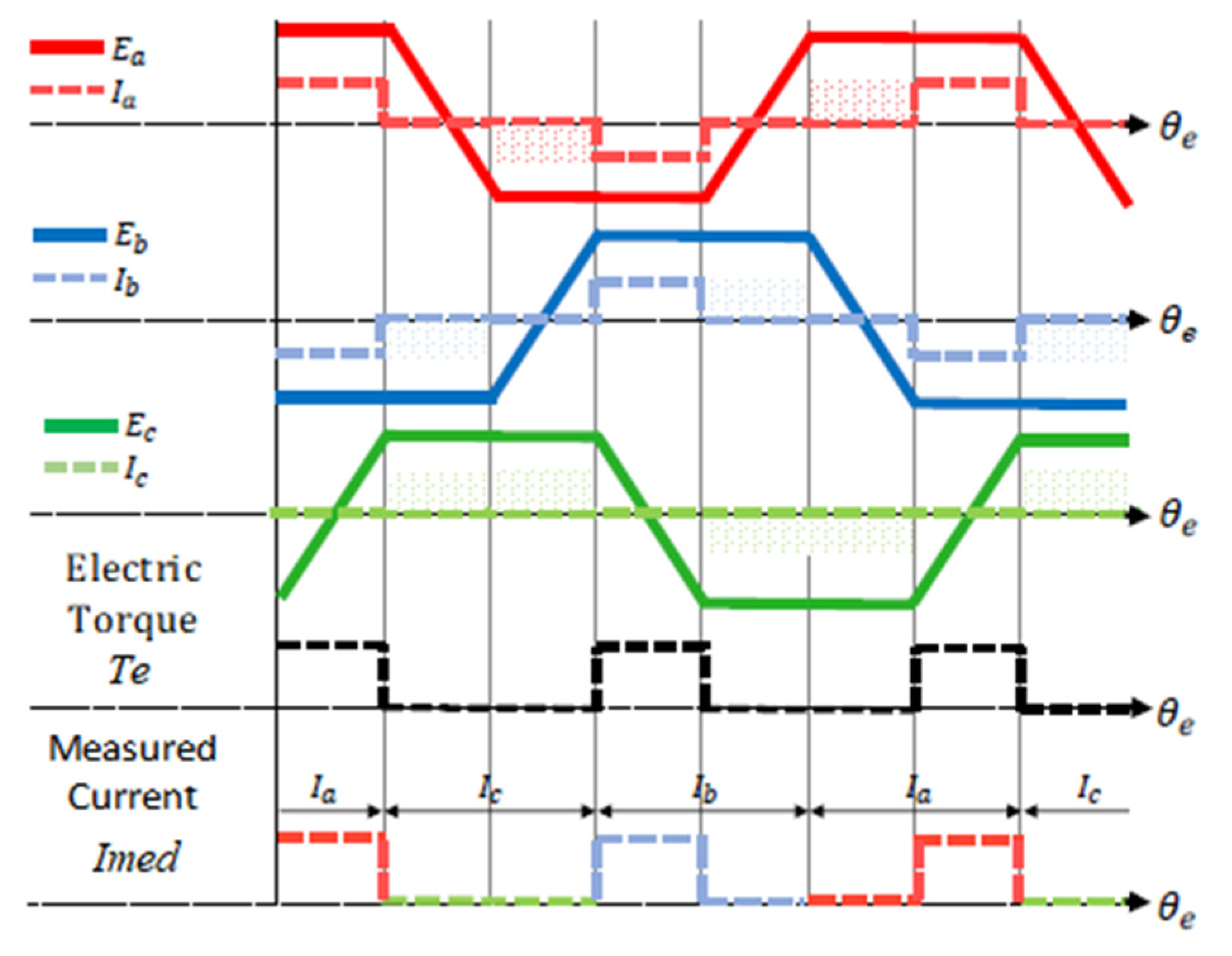
In [12], the authors discussed torque ripple minimization when direct torque control is applied, and in [13] the torque is analyzed when DC motors are running in the fault phase and an operating mode for the fault phase is discussed. The torque analysis shows that there is a reduction in output power of one-third when the motor operates in an open loop [13]. The operating mode presented in [13] uses the healthy phases of the motor in 180° electric degrees conduction to correct the lack of torque of the missing phase. A challenge that has been verified when implementing the operating mode on three-phase BLDC motors without redundancy is that when operating with only two phases, oscillatory torque and speed are available due to the absence of flux/torque when the rotor is in the electric position of the missing winding. To compensate for the loss of one-third of the torque during failure, a traditional cascading control tends to impose a very high reference on the current loop to compensate for the absence of flux in the electrical position of the open-phase, increasing the effective value of the motor current. This causes further deterioration of healthy coils or even exceeds the limits of the motor-rated current.

An improvement in postfault drivability when the motor is subject to an open-switch fault is presented in [14]. First, a tracking of the health reference vector based on the mathematical analysis of the post-fault voltage vectors was performed. Then, the post-fault currents were predicted based on the location of the post-fault voltage vectors. According to the authors, the method can improve the ability to maintain torque output.

Analysis of stator phase current signals with Fast Fourier Transform (FFT) is presented in [15]. The authors used the extended Park vector analysis of the stator current for the detection of stator winding faults. The fault was detected by observing the increase in the 2f_s component amplitude in the stator phase current. This increase in the f_s component was verified in [16]. The analysis shows that when the motor is subject to a stator winding fault, the fs component increases in amplitude in the negative sequence of the current, but the positive sequence is not affected due to stator winding failure.

In [17], the author proposed to slow down the current controller and impose on the current shape a trapezoidal curve when the BLDC motor was operating in the phase-out situation. By reducing the speed of the controller (decreasing its passing band) the speed control will not detect the oscillations caused by the phase fault, preventing the controller from correcting this oscillation, increasing the current reference and, consequently, increasing the level of the effective current. By imposing a trapezoidal shape on the current of the BLDC motor operating in phase-fault, the author ensured an increase in efficiency of the BLDC motor due to the current’s alignment with the phase-induced voltages and their similar shape, that is, the same harmonic content of induced voltages [18].

However, by imposing a trapezoidal shape on the current of a BLDC motor when it is operating in phase-fault to improve motor efficiency, the author was limiting the performance of the motor so that the effective current did not exceed a limit value. A consequence of this technique was a large oscillation in the speed of the motor, especially at low speeds, because the control minimized the current in the electrical position where there was no flow of the missing phase.

This paper presents an alternative for flexibilization of the strategy presented in [17]. The flexibility takes place by transforming the trapezoid into a dynamic trapezoid with adjustable angles according to the effective current level required to drive the motor load. This proposal allows the motor to work with higher levels of effective current when it is possible, avoiding higher levels of ripple in the motor when more electrical torque is released.

As the main contribution, the dynamic trapezoid strategy results in a reduction of effective currents in healthy phases and does not let the effective current value exceed the maximum limit of the coils. The strategy does not require structural redundancies, has easy implementation via software, and has a low computational cost. The decrease in the effective current values of the healthy phases of the BLDC motor directly reflects on the final values of motor temperature.

2. BLDC Motor

BLDC motors use permanent magnets in the rotor (and therefore synchronous) with an induced waveform (back-electromotive force—BEMF), preferably trapezoidal, for switching, because the switching on these motors is performed electronically and usually through a three-phase inverter bridge in a six-pulse operation mode (Six-Step).

2.1. BLDC Motor Modelling

The mathematical model of the BLDC motors consists of two dynamics: electrical and mechanical. For a balanced three-phase BLDC motor, the dynamics are given by [19].

$$\left[\begin{array}{c}{V}_a\\ V_b\\ V_c\end{array}\right]=R_s\left[\begin{array}{c}{I}_a\\ I_b\\ I_c\end{array}\right]+\left(L-M\right)\left[\begin{array}{c}\frac{d{I}_a}{d_t}\\ \frac{d{I}_b}{d_t}\\ \frac{d{I}_c}{d_t}\end{array}\right]+\left[\begin{array}{c}{E}_a\\ E_b\\ E_c\end{array}\right]$$

(1)

$$T_e=T_l+B\omega +J\frac{d\omega }{d_t}$$

(2)

In the equations above, $V_{a, }$, $V_b$ and $V_c$ are the stator voltages. The stator currents are $I_{a, }$, $I_b$ and $I_c$. The self-inductance and mutual inductance are $L$ and $M$, respectively. The BEMF are defined as $E_{a, }$, $E_b$ and $E_c$. In the mechanical equation, $T_e$ and $T_L$ are the electromagnetic torque and the load torque, respectively. The viscous friction is given by $B$, the motor inertia is $J$ and the angular speed is $\omega$. The BEMF of each phase is given by

$$E_a=k\omega f\left({\theta }_e\right),$$

(3)

$$E_b=k\omega f\left({\theta }_e+120°\right),$$

(4)

$$E_c=k\omega f\left({\theta }_e-120°\right)$$

(5)

${\theta }_e=\left(P/2\right){\theta }_r$ and $f\left({\theta }_e\right)$ is the unit trapezoidal wave present in the voltage induced in the BLDC. Moreover, it is assumed that the inductances do not vary depending on the position of the rotor and, therefore, the reluctance torque can be considered negligible, decoupling the electrical dynamics of each phase [20].

2.2. Six-Step Operation Mode on BLDC Motors

Among the various existing forms of BLDC motor drive, the Six-Step operating mode is predominant due to its easy implementation and the low computational cost required.

The Six-Step operating mode is based on the preset of the phase current format to take advantage of the knowledge of BEMF’s trapezoidal format in the BLDC motor [20]. The technique divides the electric angle of the motor into six regions, where each region has a combination of switching of the inverter keys previously defined. The Six-Step operation mode can still be set to 120° or 180°, according to the driving angle imposed on the currents flowing through the coils. Of the two possibilities, switching through Six-Step in 120° driving is the most used because it is easy to implement. Moreover, it is not necessary to implement a vector control, the sensorless control does not require sophisticated models, and switching losses are reduced because only two switches are triggered in each switching region. However, the operation mode of the inverter switch through the Six-Step in 120° conduction can result in a high torque pulse when switching between regions, and the harmonic content of the currents is usually impaired due to the current shape [20].

Figure 1 shows the Six-Step operation mode with 120° electric driving. Note that, taking phase a as an example in region 1, the switch is closed during the positive level of the E_a induced voltage (E_p—Peak induced voltage) and the negative level of E_b (−E_p). Therefore, the current I_a will be positive (reaching its peak I_p value after a short transient) and the current I_b will be negative (−I_p) during this switching period. As a result, the power supplied by each phase during the steady state for that switching period will be a constant value equal to

$$P_a=E_p{I}_p$$

(6)

$$P_b=-E_b\left(-I_p\right)=P_a$$

(7)

$$P_{total}=P_a+P_b=2E_p{I}_p.$$

(8)

Through some algebraic manipulations in the power equations in (8) and mechanical dynamics in (2), it is possible to define the torque provided by the motor during any switching period as

$$T_e=\frac{1}{\omega }\frac{P}{2}\left(E_a{I}_a+E_b{I}_b+E_c{I}_c \right).$$

(9)

2.3. Maximum Operating Efficiency

The maximum efficiency condition of BLDC motors can be obtained from the analysis of (9). From this equation, one can notice that the torque is proportional to the sum of the products of the phase-induced voltages E_a, E_b, and E_c and by the phase currents I_a, I_b, and I_c. Therefore, the maximum efficiency condition is obtained when this sum of products is maximum with the minimum possible current. From the concept of electrical power, it is known that this condition occurs when the following criteria are met [18]:

• phase currents are perfectly aligned with phase-induced voltages
• the currents have the same format, i.e., the same harmonic content as the BEMFs.

Therefore, by imposing currents with the same shape and aligned with the induced voltages, maximum operating efficiency is obtained.

2.4. Traditional Cascading Control of Speed and Torque

The velocity control loop considered in this article is cascaded with the torque/current control according to Figure 2. The measured or estimated speed ω_med is compared with its desired reference ω_ref to generate an error signal (e_ω) speed reference. To regulate ω_med, the output of the C1 speed controller is used as a reference for the current, because the current is proportional to the torque through the flux constant k. The I_ref current reference is then compared with the actual motor current Imed to generate a current reference error signal (e1) that will allow the closing of the internal loop through the C2 controller. In turn, the C2 controller acts directly on the cyclic inverter ratio d [5].

As in the Six-Step operation mode in driving 120° electric, only two phases of the motor conduct at the same time, and the current flowing through the motor (I_med) is the same measure on the DC link of the inverter. Figure 1 shows the six possible switching regions.

Table 1. Currents in 120° Six-Step Operation.

Shaft Position	Region	Ia	Ib	Ic
0° < $\theta$ ≤ 60°	1	Imed	−Imed
60° < $\theta$ ≤ 120°	2	Imed		−Imed
120° < $\theta$ ≤ 180°	3		Imed	−Imed
180° < $\theta$ ≤ 240°	4	−Imed	Imed
240° < $\theta$ ≤ 300°	5	−Imed		Imed

, adapted from [7], shows the value of the currents observed by the controller for each region (or sector) of switching.

3. BLDC Motor Drive under Phase-Fault

Consider the BLDC motor with the Six-Step operation mode conducting at 120° electric degree, as in the previous section, but now running with a phase fault. Figure 3 shows the main waveforms (assuming a fault in phase c) without any correction for the phase fault. One can notice that of the six switching regions, only two regions produce torque, that is, the motor has zero torque most of the time when running with a phase fault. Analyzing Figure 3, the motor loses approximately two-thirds of the average torque when compared to the motor running under normal conditions, as shown in Figure 1. Another issue is the wide range of the electric cycle without torque, which can cause the motor to stop permanently when driving loads with low inertia that has its motion halted in an electrical position without torque.

3.1. Phase Fault BLDC Motor Drive without Current Reduction Strategy

The situation presented previously can be mitigated by adapting the operation mode to run using the healthy phases of the BLDC motor, such as, for example, the activation of the BLDC motor through an inverter bridge to drive the motor at 180° electrical degrees [13], as shown in Figure 4.

To apply the strategy presented in Figure 4, it is necessary to ensure the synchronization of line current I_ab with the line voltage E_ab (BEMF—between the healthy phases of the motor). It is observed in Figure 4 that there is negative torque in phases a and b, but the sum of torques is always greater than or equal to zero when using the Six-Step operation mode in a 180° electrical degrees conduction. This results in reduced torque intervals, including an instant of null torque. Because of this variable torque, there is a speed oscillation in the motor. However, the mode of operation presented allowed us to reduce the loss of the average torque from two-thirds to one-third (value calculated through the geometry of the torque curves).

The reduced and zero torque intervals during the electrical cycle directly affect the control loop shown in Figure 2. To illustrate this situation, Figure 5 shows a numerical simulation of a motor operating with a fault in phase c using the operation mode presented in [13]. The motor data used to generate the simulations and the experimental results of this article are presented in

Table 2. Motor Parameters.

Parameters	Value
Rs	3.5 Ω
L	52 mH
k	0.43 V.s/rad
Imax	2.5 A
ωrated	4000 rpm
P	4
J	1.1 × 10−3 kg.m2
B	0.72 × 10−3 N.m.s

. The load torque applied in the simulation was 0.45 N.m, which represents 50% of the maximum engine torque.

For the C1 and C2 controllers shown in Figure 2, the simplified transfer functions were considered

$$\frac{e_{\omega }\left(s\right)}{I_{ref}\left(s\right)}=\frac{2k}{J}\frac{1}{s+B/J}$$

(10)

$$\frac{e_J\left(s\right)}{I_{ref}\left(s\right)}=\frac{V_{DC}}{2}\frac{1}{s+R_s/L}$$

(11)

which represent the transfer function of the speed error by the reference current and the transfer function of the current error by the cyclic ratio of the inverter, respectively. The C1 and C2 controllers designed and implemented in this work have a pole at the origin to cancel the reference error in steady-state; a zero to cancel the pole of the transfer function, allowing one to obtain a useful, larger band, to transform the open loop into a curve with the decay of 20 dB per decade throughout the frequency band, and a gain to adjust zero gain at a given cutoff frequency. The designed controllers are presented below:

$$C1=K_{C1}\frac{s+B/J}{s}$$

(12)

$$C2=K_{C2}\frac{s+R_s/J}{s}$$

(13)

where the values of K_C1 and K_C2 were set at 2.98 and 0.44, enabling a cutting frequency for the closed-loop system of 1 kHz to C1 and 5 kHz to C2.

Figure 5 shows the cascading control loop acting in the correction of the speed error caused by the lack of torque in coil c. When the rotor is in the electrical position of phase c magnetic axis (highlighted area in Figure 5), the motor does not produce torque to balance the load torque, and then the controller acts by elevating the currents of phases a and b to increase the electrical torque due to the lack of flux in phase c coil. However, the fluxes of phases a and b, according to Figure 5b, do not have a significant value in the region to generate the necessary torque, because they are in the reversal instant of the trapezoidal wave.

This situation causes an RMS current of 1.31 A to flow in phases a and b, as shown in Figure 5c. Since the RMS value of the current without a phase fault is 0.51 A for the same load condition, there is an increase of approximately 2.5% of the motor current due to the phase fault.

The increase in the RMS current value shown in Figure 5 causes heating in the temperature of the healthy motor coils, since the current is directly linked to joule losses in the motor. This represents a large part of the electrical losses in an electric motor, along with the hysteresis losses. The speed oscillates, as expected, due to the lack of flux in coil c. The speed variation is approximately 30 rpm.

3.2. Phase Fault BLDC Motor Drive with Current Reduction Strategy

The current reduction strategy proposed in [17] to complement the mode of operation presented in [13] has two main objectives: (i) to make the controller less sensitive to speed oscillations, thereby avoiding the increase in the current when the rotor is in an angular position that affects the torque when the fault occurs and (ii) to impose on current the same wave format of the induced voltage E_ab, when both are in sync, thus achieving the best efficiency of the motor in a fault condition. The strategy presented is commonly used in power factor correction strategies, in the sense that it seeks to align current and voltage, resulting in a power factor close to the unit [18]. Figure 6 presents the current reduction strategy [17].

To reduce the interference of the speed oscillations seen by the current control loop, Controller C1of Figure 2 was replaced by a new L₁ controller with a reduced passing band of a decade compared to C2. This results in a slower speed control action, reducing the influence of oscillations in I_ref. The block diagram of the proposed control loop is presented in Figure 7. In this diagram, it is possible to observe that I_ref is synchronized with E_ab when multiplied by a unit trapezoidal wave with the same shape and in phase with E_ab. The efficiency increase resulting from this synchronization is reflected in lower values in the healthy coils of the BLDC motor, reducing its degradation.

Figure 8 presents the simulation results for the current reduction strategy presented in [17]; the comparations presented here are made concerning Figure 5. Analyzing Figure 5 and Figure 8, it is observed that the waveform of the speed was modified in the case without the strategy, but the amplitude of the oscillation was similar. Using the proposed strategy, we obtained a change of Δ_speed from 30 rpm to 38 rpm, an increase of approximately 1.23. There is also a small change in the behavior of the induced voltage in the motor, as this is a function of the speed derivative.

Also in Figure 8, it is observed that the motor current presents a trapezoidal shape in sync with the induced voltage E_ab. The RMS value of the current obtained with the proposed strategy was 0.85 A, which is 35% lower when compared to the result without the strategy. This significant reduction in the RMS value allows the operation of the motor in a condition of phase fault for a long time during an emergency, if necessary, as the lower dissipation of energy will preserve the healthy coils of the BLDC motor.

4. Flexible Current Reduction Strategy

The technique proposed in [17] aims to maximize the efficiency of the BLDC motor when it is working with a phase fault. The results observed in the simulations are a lower RMS current level and a higher speed ripple. The ripple in speed is caused by the limitation of the current in the electrical positions where there is an open-phase fault, because the torque component is a product between the flux and the electric current of the motor, and, by limiting the current in the form of a trapezoid, the torque is limited in regions where there is little flux presented in the healthy phases of the motor, causing a ripple in the speed wave. It can also be concluded that it would be possible to achieve a higher electrical torque in the motor by increasing the electric current circulating in the healthy phases in these electrical positions, decreasing the ripple, and increasing the electric current of the motor, as seen in the simulation without the strategy of reducing current in Section 3.1.

To avoid speed ripples in systems that are more fragile and sensitive to this type of disturbance, such as drones or electric vehicles for example, and where the BLDC motor in phase fault is allowed to work with little load or that does not need to work at maximum load during the safe shutdown of a failed BLDC motor, flexibility in the proposed current reduction strategy in [17] is proposed in this work. This flexibility deals with the change of the internal base angle of the trapezoid, which changes according to the reference current level (I_ref—see Figure 7) requested by the controller. This changes the angle of the trapezoid base from 45°, for the most critical situations where it is necessary to maximize the efficiency of the motor and reduce the level of the RMS electric current, up to 90°, changing the imposed waveform into a rectangle for less critical situations where the RMS current level of the motor is not high and it is possible to penalize the current in exchange for a lower speed ripple. The waveform used to modulate the reference current presented in Figure 7 is replaced by the trapezoid dynamic waveform shown in Figure 9.

The rule for defining the angle used at the base of the trapezoid in Figure 9 is presented in Algorithm 1. The calculation of the equation used in the algorithm was defined so that the RMS level of electric current in the healthy phases of the motor does not exceed the value of 1.9 A during the motor drive, and the maximum peak value in the motor electric current made available by the inverter does not exceed 2.5 A.

Algorithm 1 Trapezoid Angle Definition

1: if (Ire f > 2.3 A) then 2:    θBase ← 607 − 225 ∗ Ire f 3:    if (θBase < 45°) then θBase ← 45° 4:    if (θBase > 90°) then θBase ← 90° 5: else 6:    θBase ← 90°

The values of the L1 and C2 controllers presented in Figure 7 remained with the same values as presented in Section 3, and the L1 controller has a reduced passing band that results in a slower speed control action, reducing the influence of oscillations in I_ref. Figure 10 presents the simulation results for the proposed flexibility through dynamic trapezoid. Analyzing the current format, it is possible to conclude that the motor operates below the maximum limit of the RMS electric current (1.90 A), because the trapezoid shape has an angle of 90° at the base, forming a rectangle. The value of the RMS electric current during operation at 500 rpm and with 50% of maximum torque is 0.94 A. The RMS value with dynamic flexibilization is between the values obtained with the reduction technique presented (0.81 A) and the operation without the technique (1.31 A). The speed variation (Δ_speed) with the flexibility technique has been reduced to 30 rpm, which is the same value as the current reduction technique that uses all energy available (without efficiency) to try to keep the electric torque of the motor close to the mechanical load torque in the electrical cycle region of the faulty coil.

Figure 11 demonstrates the behavior of the control as the load increase is performed and, consequently, the increase in the reference current (I_ref). It is observed that with the increase in the reference current, the dynamic technique is equal to the fixed trapezoid in a way that does not allow it to exceed the maximum effective value and not exceed the maximum peak value.

5. Experimental Results

A BLDC motor with the parameters presented in Table 2 was used to validate the proposed current reduction using the flexibilization strategy. The test results presented were obtained with the Analysis Equipment WT500 of the manufacturer Yokogawa.

5.1. Phase-Fault Drive

To validate the efficiency of the proposed strategy, four comparative tests were performed:

• The traditional three-phase motor drive uses the 120° Six-Step operation mode.
• Phase fault drive with the switching of two healthy phases at 180° without the current reduction strategy.
• Phase fault drive with the switching of two healthy phases at 180° with the current reduction strategy.
• Phase fault drive with the switching of two healthy phases at 180° with the proposed strategy.

The tests were performed with the speed reference equal to 250 rpm. The load torque (T_l) used in all tests was 0.48 N.m, which represents approximately 50% of the maximum engine torque. The parameters analyzed were efficiency; RMS current, and speed oscillation (Δ_speed).

(1) Motor under normal conditions: Figure 12 shows the motor driven under normal conditions (with all three phases in operation) with a six-step operating mode with 120° electric driving. The RMS current of the BLDC motor for the applied torque T_l is 0.61 A. In this situation, the motor presented a Δ_speed of approximately 6 rpm.

(2) Phase fault drive with the 180° switching of the two healthy phases without the current reduction strategy: Figure 13 presents the waveforms of the current when the BLDC motor operates in phase fault with the mode of operation presented in [9] without any strategy of reducing the RMS current of the healthy phases, only using the switching between the two healthy phases of the engine in 180° electric driving. In this operating condition, the RMS current in each phase of the motor for the applied torque T_l is 1.34 A. Therefore, the increase in RMS current in the phase is approximately 120% when compared to the operation under normal conditions. The motor presented a Δ_speed of approximately 25 rpm. It can be observed that even when raising the current at points where there is no significant flux due to the fault phase, there is no significant torque production to avoid speed oscillation.

(3) Phase fault drive by switching the two healthy phases with conduction in 180° electric with the current reduction strategy: Figure 14 presents the waveforms of the BLDC motor current when operating under phase with the mode of operation presented in [9] along with the current reduction strategy presented in [10]. In this operating condition, the RMS current in each phase of the motor for the applied torque T_l is 0.99 A. Therefore, the increase of RMS current in the phase is approximately 62% when compared to the motor operating under normal conditions. The motor presented a Δ_speed of approximately 40 rpm. The results show that the technique presented by the author in [17] is effective in reducing the motor current, but the technique penalizes the speed of the motor, as expected.

(4) Phase fault drive using two healthy phase commutation with 180° switching along with the proposed strategy: Figure 15 presents the waveforms of the current of the BLDC motor when operating under phase fault with the mode of operation presented in [9] along with the proposed strategy presented in this article. In this operating condition, the RMS current in each phase of the motor for the applied torque T_l is 1.10 A. Therefore, the increase in the RMS current in the phase is approximately 80% when compared to the motor operating under normal conditions. The motor presented a Δ_speed of approximately 25 rpm.

The results show that the strategy presented in [17] was able to reduce the level of electric current in the motor compared to the drive without the strategy and equalized the speed wave to the same delta presented in the drive without the current reduction strategy. It is also possible to determine by the waveform that the motor operates with a low current level because the wave is rectangular.

The results presented show that there is a compromise between a lower level of RMS current in the motor and a greater oscillation of the speed, resulting from the new torque format. However, one can conclude that it is not necessary to perform the drive without the strategy to obtain a lower speed oscillation, because the flexibility of the technique already guarantees an oscillation in the speed with the same magnitude as the drive without the technique, and with a reduction of 18% of the electric current level (from 1.34 A to 1.10 A) that may avoid a significant increase in the motor temperature, as will be seen in the next subsection of this article, because the joule losses of a system are related to the square of the current in the circuit.

The tests presented were performed in low rotation, because this is the situation in which the worst performances of the proposed strategy are expected. This is because low rotation is not enough to store inertial energy and, consequently, does not soften the speed oscillation.

The speed oscillation in the experimental tests was negligible when the motor operated at speeds above 1000 rpm, for example. In systems where there is a large amount of mass such as electric vehicles, for example, this speed oscillation would be negligible.

5.2. Temperature Test

Practical tests were performed to verify the influence of the RMS motor current on the temperature of the BLDC motor coils. The tests were performed at the speed of 250 rpm with torque T_l (50% of the maximum torque of the engine), the same condition that resulted in the current values presented in

Table 3. Comparation Between the Operating Modes Presented.

	Without Phase Fault	Phase Fault without Current Reduction Strategy	Phase Fault with Current Reduction Strategy	Phase Fault with Proposed Strategy
IRMSPhase	0.61 A	1.34 A	0.99 A	1.10 A
Δspeed	6 rpm	25 rpm	40 rpm	25 rpm
Δtemp	15 °C	44 °C	26 °C	33 °C
Consumed Power	15 W	24 W	19 W	21 W
Current increase *		+120%	+62%	+80%
Temperature increase *		+193%	+73%	+124%

* Compared to the motor operating under normal conditions.

. All tests were performed at room temperature (23 °C) and with a duration of 80 min.

Figure 16 shows the results of the temperature test for each operating condition. It is observed that the motor operating without fault phase reached a temperature variation (Δ_temp) of approximately 15 °C at the end of the test. The motor operating in fault phase conditions without any current reduction strategy obtained a Δ_temp of approximately 44 °C (an increase of 193% when the motor operates without a phase). The motor operating in fault phase conditions with the current reduction strategy obtained a Δ_temp of approximately 26 °C (an increase of 73% when the engine operates without a phase).

The motor operating in fault phase conditions with the flexibility of the current reduction strategy obtained a Δ_temp of approximately 33 °C (an increase of 124% when the engine operates without phase fault).

The results of the temperature test demonstrate the importance of observing the RMS current of the motor when operating in fault phase condition. In situations where the motor operates close to its power limit, a fault phase may damage the remaining phases of the motor if the fault is not handled properly.

A comparative analysis between the modes of operation, summing up the results found as well as the respective powers consumed by the motor, can be seen in Table 3.

6. Conclusions

This article presents the development of a flexible current reduction strategy for BLDC motors operating in fault phase condition. The proposed strategy has a low implementation cost through a change in the traditional 120° Six-Step operation mode to an operation mode that performs the switching of the two healthy phases of the engine in 180° electric driving with a dynamic trapezoidal current format programmed for the healthy stages of the stator, without the need for special inverters or redundancies.

By imposing the dynamic trapezoidal shape, it is possible to make the proposed current reduction strategy presented in [17] more flexible, allowing that when the motor is driven with a low load coupled to the shaft, it is possible to penalize the RMS electric current level in exchange for a lower ripple in the motor speed. However, when the motor is driven with a load close to the maximum level of the fault phase operating condition, the RMS current reduction strategy is triggered by turning the wave shape into a trapezoid to ensure that the current level is as low as possible in exchange for the speed ripple penalty. The proposed flexibilization strategy was experimentally tested, showing a considerable reduction in the values of the RMS current and the motor temperature achieved during the fault.

Thus, the objective of reducing the variables harmful to the motor was validated. Although the strategy proposed in this work considered a reduced band in speed control, it was not possible to perceive a significant impairment in the performance of the system. Due to the loss of one-third of the characteristic power in a BLDC motor when driven through only two phases, the strategy to operate the BLDC motor with phase fault is recommended for loads that do not require, when in fault, nominal torque and speed conditions simultaneously.