Abstract
Improving air quality, reducing greenhouse gas emissions, and achieving independence from fossil fuels have led most countries towards deploying solar photovoltaics (PV) in the power distribution grid and electrifying the transportation fleet. Internal combustion engine (ICE) vehicles are, in particular, one of the main culprits of injecting greenhouse gas emissions into the atmosphere, making electric vehicles (EVs) an important tool in combating climate change. Despite their considerable environmental and economic benefits, the integration of PVs and EVs can introduce unique operational challenges for the power distribution grid. If not coordinated, high penetration of PVs and EVs can result in variety of power quality issues, such as instances of overvoltage and undervoltage, frequency fluctuations, and/or increased losses. This paper proposes a mixed-integer multi-objective nonlinear optimization model for optimal energy dispatch in a power distribution grid with high penetration of PV and EV resources. The model proposed here is an extension of the traditional voltage and var optimization (VVO) into a comprehensive and coordinated control of voltage, active power, and reactive power. A modified version of the IEEE 123-bus test distribution system is used to demonstrate the effectiveness of the proposed solution.
1. Introduction
Renewable energy resources, especially solar PV, are viewed as an effective solution for reducing the injection of greenhouse gas emissions into the atmosphere [1]. This has resulted in an upward trend in deploying rooftop PV resources in power distribution systems worldwide. Although switching to renewable power generation can help us in our fight against climate change, it is by no means sufficient. About 23% of the carbon dioxide in the atmosphere is, in fact, caused by transportation, especially gasoline-fueled vehicles. This has led to the global push towards electrification of the transportation fleet by using electric vehicles [2], which offer significantly higher efficiencies compared to their ICE counterparts. EVs convert over 77% of their stored energy into moving energy, compared to about an average of 20% for ICE vehicles [3]. Despite their significant benefits, both PVs and EVs can introduce operational challenges associated with power and voltage quality in the distribution grid. Distributed PVs that operate based on maximum power point tracking (MPPT) can negatively impact power losses, increase operational stresses on assets, and/or cause instances of node overvoltage. EVs, on the other hand, introduce an additional source of demand, which, if not mitigated, may result in increased power losses, increased operational costs, localized congestion, instances of node undervoltage, higher stresses on assets, and in extreme cases, component failures and widespread outages. Hence, the operation, reliability, and security of the power grid must be carefully evaluated in the presence of high PV and EV penetration levels [4].
While at low penetration levels PV resources can operate in an uncoordinated way with no major negative impacts on the grid, this is not the case when the penetration level exceeds certain thresholds. Under such scenarios, the traditionally radial distribution network can turn into one with bidirectional flows of power, which could adversely impact line flows, power losses, node voltages, and the effectiveness of system protection [5]. A crude way to address these issues would be to curtail the power produced by the PVs, reducing their overall impact on grid operation. However, curtailment of PV power would be a waste of the valuable solar resource. This further underlines the need for coordinating the power injection from rooftop PVs with the power grid’s management of voltage and reactive power.
The same applies to the EV demand. The various zero-emission targets adopted by different countries, complemented by government-backed incentive programs [6], have led to a rise in adoption of these vehicles: a trend that is likely to continue globally. EVs charge their batteries either at the owner’s residence or at public charging stations located in parking lots, residential neighborhoods, and/or commercial buildings. Power consumed by an EV charger (Level 1 and Level 2) can range between 1.44 kW and 19.2 kW, which could significantly impact the peak load. To put this in better perspective, the average demand at a residential house can be around 1.24 kW [7]. Hence, if not mitigated, the additional demand due to EV charging can potentially lead to localized congestion and circuit overloads, increased systems losses, and instances of node undervoltage.
Of course, the operational challenges stated above can be alleviated by reinforcing the distribution grid through upgrades and design redundancies. However, this is a costly solution that can only be implemented over the long term. An alternative is to coordinate the operation of PVs and EVs with power grid dispatch in order to ensure that power and voltage quality expectations are met. This way, the penetration level of PVs and EVs can be increased without jeopardizing the reliability and security of the power system [8]. Devising such a solution is the focal point of the current paper. A voltage, var, and watt optimization (VVWO) model is proposed here for coordinated control of PV resources and EV charging stations (EVCS) in a three-phase unbalanced power distribution grid. The model is formulated as mixed-integer nonlinear multi-objective optimization, where the objectives are to minimize power losses, minimize PV power curtailment, minimize EVCS load curtailment, and minimize node voltage variations. A goal programming approach is adopted to ensure that the Pareto optimal solution is found. It is assumed in this paper that PVs can participate in reactive power control via their smart inverters (i.e., can either inject or absorb reactive power), while EVCSs can only consume reactive power. The effectiveness of the proposed model is validated using a modified version of the IEEE 123-bus test distribution system.
The rest of this paper is organized as follows: Section 2 presents a review of the literature related to control and management of EV resources. The proposed methodology is provided in Section 3, followed by a case study and discussion of results in Section 4. Finally, concluding remarks appear in Section 5 of the paper.
2. EV Management in Distribution Systems: A Review of the Literature
It has been shown in the literature that high EV penetration levels can cause operational challenges for the power grid. An agent-based model developed in [9] showed that distribution feeders with high R/X ratios are most susceptible to EV charging load and more likely to experience overloads. A study of various EV penetration levels in [10] concluded that a 60% penetration can lead to a 15% rise in grid investment expenses and a 40% increase in power losses. Similar studies are reported in the literature that analyze the impacts of EVs on the distribution grid [11,12,13,14,15], and have identified operational challenges such as voltage violations in remote nodes [13], general instances of undervoltage [15], and overloading of the main distribution substation [14].
Some researchers have studied various EV charging strategies to assess their effectiveness in alleviating some of the negative impacts mentioned above. For instance, authors in [16] compared coordinated and uncoordinated charging strategies in a residential network and verified that uncontrolled EV charging could cause voltage imbalance and overload problems, while those issues would not exist with the coordinated approach. Authors in [17] investigated the maximum permissible penetration level of EVs under dump and smart charging strategies and concluded that the latter would allow for a significantly higher penetration level without violating any of the power grid constraints. Other researchers have explored the optimal allocation of EVCSs with the goal of preventing power grid operational issues. Objective functions considered include minimizing voltage violations and power losses [18], minimizing load curtailment [19], minimizing driving distance and power losses while improving voltage stability [20], minimizing power losses and improving voltage stability [21], and minimizing the investment costs and power losses [22]. Some have considered not just the optimal locations but also the optimal sizes (ratings) of the EVCSs in order to minimize the total costs [23], minimize investment costs and driving distances and maximize the loading capacity [24], or minimize power losses [25]. As another example, the authors in [26] proposed a two-stage solution, where the optimal EVCS locations were first found using a distance coefficient, and were then used to determine the optimal sizing based on network demand. Other objectives considered in the literature for EVCS siting/sizing include the stability of the power grid [27] and the charging service availability in the transportation network [28].
In parallel to this, some researchers have proposed solutions for coordinated control of EV charging while considering distributed energy resources (DER). For instance, authors in [29] modeled both energy storage systems (ESS) and dispatchable DER units and developed a solution to reduce operating costs, while penalizing EVCS load curtailment. Authors in [30] introduced a framework to control EV charging/discharging and PV curtailment in order to minimize the operational costs. They developed a coordinated model consisting of home energy management systems and the energy management system of the distribution grid and considered the information exchange between the two. A solution was proposed in [31] for a microgrid equipped with EVs, battery energy storage, and PV, with the goal of minimizing the charging costs and the operational stresses on grid components caused by EV charging. A solution for coordination of PVs and EV charging was also presented in [32] to minimize the curtailment of PV active power and EV demand, while considering voltage issues in the distribution system. A similar approach was proposed in [33]. Authors in [34] developed a dual-stage coordination methodology to control PV generation and EV demand while considering voltage regulation and system losses. In [35], a PV-EV coordination strategy was introduced while considering both transmission and distribution networks. The main objective in this work was to enable higher penetration levels of EVs and PVs without violating system constraints. As another example, authors in [36] proposed a solution to enable EV charging under peak load conditions, while considering power losses, network reconfiguration, and line maintenance. Another network reconfiguration methodology considering EV integration was presented in [37], where the authors included the cost of carbon emissions as their objective function.
Table 1 provides an overview of the solution methods proposed in the literature related to management of EVs in the distribution grid. The most common limitation of the majority of existing solutions is the usage of a simplified version of the problem, either in terms of modeling (e.g., by ignoring asymmetries and unbalanced operation) or the solution methodology adopted (i.e., simplified linear optimization models, which can only provide an approximate solution, or meta-heuristic optimization approaches, which cannot guarantee global optimality). Further, multi-objective optimization models proposed in the literature often form an aggregate objective function as the sum of individual objectives. This approach fails to reach the Pareto optimal solution and runs the risk of having one or more objectives dominating others. This is especially true when weight coefficients are assigned to prioritize individual objective functions because those coefficient values are normally subjective. The methodology proposed in this paper intends to address all of the above issues: the power system is modeled in detail, with all equations representing the unbalanced power flow as well as system components incorporated into the problem formulation, and a goal programming approach is adopted to ensure the Pareto optimality of the final solution (see Section 3 for more details).

Table 1.
Review of the literature related to management and integration of EVs in the power distribution system.
3. Problem Formulation
The problem addressed in this paper is the coordinated optimal dispatch of all active and reactive resources in a power distribution grid, known as VVWO, for a system equipped with voltage regulating transformers, rooftop PV, and EV charging stations. It is formulated as a mixed-integer nonlinear multi-objective optimization model, which is solved subject to various operational constraints.
3.1. Objective Functions
Objective functions of the proposed multi-objective framework are defined as follows.
3.1.1. System Loss Minimization
This objective function ensures that active and reactive power losses across the system are minimized by optimally delivering power to the loads via the most appropriate routes and using local PV resources as much as needed. This objective function is modeled as in Equation (1).
3.1.2. Minimization of PV Active Power Curtailment
In an effort to operate the grid in a sustainable fashion, another operational goal here is to minimize the total amount of active power curtailed from rooftop PVs and maximize their local generation, as expressed in Equation (2).
3.1.3. Minimization of EVCS Load Curtailment
It is assumed that at any point in time, several EVs are present at each charging station, waiting or continuing to be charged. It is further assumed that each EV owner wishes to achieve his/her target charging level as closely as possible. However, the amount of charge provided to the EVs must be coordinated with the operational constraints of the grid. This objective function intends to achieve the target EV charge levels as much as technically possible, as expressed in Equation (3).
3.1.4. Improve Voltage Profile
High PV and EV penetration levels can cause voltage rises and drops across the system, respectively. This objective function intends to improve (flatten) the voltage profile by achieving node voltages as close to the rated 1 per unit as possible. It can easily be seen that in certain cases, this objective may become at odds with objective (1), e.g., when reducing node voltages through conservation voltage reduction can help with reducing losses (especially in networks dominated by constant impedance loads). There are several methods to reach this goal, such as curtailing active power from PVs, coordinating EV charging levels, and injecting/absorbing reactive power through smart inverters. The objective function is shown in Equation (4).
3.2. Constraints
The above objective functions are optimized subject to the following operational constraints.
Equations (5) and (6) represent the real and imaginary parts of the currents flowing through each line in the system. These equations provide means to represent the network model and include power flow equations in the problem formulation. The benefit of using this approach is that the usage of phasors (and hence, the nonlinear sine and cosine functions) can be avoided. This significantly reduces the complexity of the model and enhances convergence.
KVL constraints are expressed for all lines as shown in Equations (7) and (8):
Loads and EVCSs are expressed in Cartesian form as shown in Equations (9)–(12):
Equations (13)–(16) represent voltage regulators (VRs), which, without loss of generality, are assumed in this paper to be ideal transformers. In all these equations, bus j is assumed to be the secondary of the VR.
Other operational constraints include the bus voltage limits according to ANSI bounds as well as the limits on the power flow through lines:
Equations (19) and (20) represent the upper and lower limits for the active and reactive powers of rooftop PVs. It is assumed here that PVs, equipped with smart inverters, can either absorb or inject reactive power. Similar equations have been introduced for EVCSs (see Equations (21) and (22)). However, an EVCS is assumed to only be able to absorb reactive power from the grid, as shown in Equation (23).
The total energy delivered to the individual EVs is equal to the sum of the energies delivered in each hour during the dispatch period, as shown in Equation (24). Note that due to the time step of analysis, i.e., one hour, powers are equal to energies in value, which is why the time variable can be dropped. The amount of energy delivered to each EV is less than or equal to the desired level, as shown in Equation (25), but must be as close to it as possible, as ensured by Equation (3).
Finally, VR tap range is expressed as in Equation (26), which indicates that the tap position can change in 16 steps in each direction.
The problem formulation also includes all the relevant integrality constraints that are omitted here for brevity.
3.3. Solution Methodology
The optimization problem is solved by minimizing (1)–(4) subject to constraints (5)–(26). The multi-objective formulation is modeled using Chebyshev goal programming, because it allows different objective functions to strike a balance and does not artificially prioritize one objective over the others. To model the problem, every objective function is first assigned a target (goal) value. These values are the goals that we hope to achieve in the multi-objective setting. Naturally, not all objectives may achieve their global optima at the same time since they can at times be contradictory to one another. To reflect this, the goal for each objective is set to be the same as its corresponding global optimum with a 10% margin of error. This number is chosen heuristically and is intended to allow the objectives of the multi-objective framework to deteriorate compared to their single objective optima. The overall problem can then be formulated as follows:
Subject to:
Equation (27) denotes the linear objective function, i.e., minimizing the maximum deviation of the four objectives. Constrain (28) forces each objective function to be less than the target value defined by the user. However, since this may not be possible within a multi-objective framework, a deficiency variable has been added for each objective function to change the constraints from hard constraints to soft ones. Since the unit for each of the objectives is different, the deficiency variables are all normalized based on their corresponding target values, and a variable L has then been defined as the upper bound for the normalized deficiency variables, as shown in Equation (29).
4. Case Study
4.1. Test System
The proposed solution is applied to a modified version of the IEEE 123-bus test distribution system (Figure 1) [38]. The system base is considered to be 5MVA and 4.16 kV for power and voltage, respectively. The total peak demand of the system is 3490 kW (0.698 p.u.) of active power and 1920 kvar (0.384 p.u.) of reactive power (see Figure 2). A total of 42 PV panels have been added to the system, with a total rated power of 3490 kW (0.698 p.u.), representing a 100% penetration level. The locations and ratings of PV resources are provided in Table 2. In addition, five EVCSs have been added to the network, with a total of 96 level 2 chargers allocated to different stations as listed in Table 3. The maximum power of each charging point is considered to be 7.7 kW. Moreover, there are two fixed capacitors in the system that can inject up to 750 kvar (0.15 p.u.) of reactive power. The PCC is assumed to be a reference bus, and as such, its voltage is set to be 1 per unit. To better regulate the voltage, the system is equipped with four voltage regulators and an OLTC, each with 32 tap positions (16 positions in each direction, as indicated in Equation (26)).
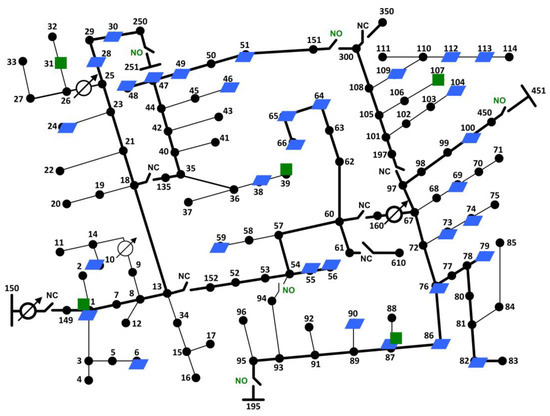
Figure 1.
Schematic diagram of the test distribution system, expanded with additional PV panels (denoted by blue squares) and EVCSs (denoted by green squares).
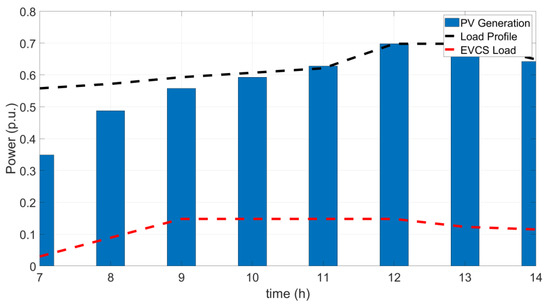
Figure 2.
Hourly variations of active powers for PV generation, EVCS load, and demand over the course of dispatch.

Table 2.
Locations and power ratings of PV resources.

Table 3.
Locations and rated capacities of EVCSs.
4.2. Simulation Results
The optimization problem in Section 3 is modeled in GAMS (General Algebraic Modeling System) software and solved using the BONMIN (Basic Open-source Nonlinear Mixed Integer programming) solver. The following case studies are considered here, with results tabulated in Table 4:
- • Case 0: Base case, with no PV or EVCS.
- • Case 1: System with the EVCSs.
- • Case 2: System with PVs.
- • Case 3: Considering PVs and EVCSs in the system.

Table 4.
Simulation results for the four cases. The numbers reported are the average values for the duration of dispatch (8 h). All values are provided in per unit, based on a base power of 5 MVA.
Table 4.
Simulation results for the four cases. The numbers reported are the average values for the duration of dispatch (8 h). All values are provided in per unit, based on a base power of 5 MVA.
| Case Number | Active Power Losses | Reactive Power Losses | PCC Active Power | PCC Reactive Power | EVCS Active Demand | EVCS Reactive Demand | PV Active Power * | PV Reactive Power * |
|---|---|---|---|---|---|---|---|---|
| Case 0 | 0.2835 | 0.159 | 0.908 | 0.3527 | N/A | N/A | N/A | N/A |
| Case 1 | 0.3271 | 0.148 | 1.0703 | 0.3421 | 0.1186 | 0.0004 | N/A | N/A |
| Case 2 | 0.0470 | 0.1653 | 0.0900 | 0.3604 | N/A | N/A | 0.5816 | −0.0018 |
| Case 3 | 0.0898 | 0.1509 | 0.2513 | 0.3456 | 0.1186 | 0.00055 | 0.5816 | −0.00044 |
* Reactive power from PVs can be positive when consuming reactive power and can be negative when generating reactive power.
4.2.1. Case 0: Base Case
In this case, no PVs or EVCSs exist in the system and, hence, the two objective functions to be minimized are the power losses in the system and deviations in node voltages, i.e., Equations (1) and (4). This case study is considered as the baseline for comparison against other use cases. Figure 3 illustrate the active power consumed from the point of common coupling (PCC), and the maximum power reached is 3490 kW at t = 12 h. As reported in Table 4, average active power losses over the dispatch period are 1417.5 kW (0.2835 p.u,) and node voltages lie between 0.992 and 1.012 as shown in Figure 4a. The only source of active power in this case is the main grid, and reactive power is supported by both the main grid and the fixed capacitor banks.
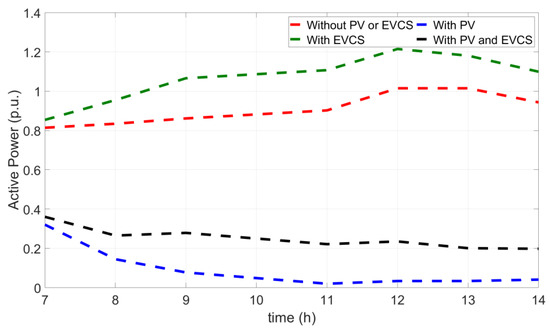
Figure 3.
Hourly variations of the active power delivered from the PCC under the different cases.
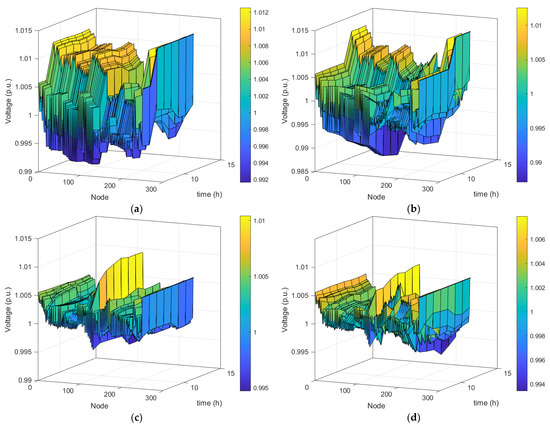
Figure 4.
Comparison of node voltages during the course of dispatch: (a) Case 0; (b) Case 1; (c) Case 2; (d) Case 3.
4.2.2. Case 1: System with EVCS
5 EVCSs are added to the distribution network with a peak demand of 0.148 p.u., as illustrated in Figure 1. As expected, the demand increases significantly, which also raises the power losses by 10.5% compared to the base case. In addition, since the PCC is the only source for active power and the main one for reactive support, its power injection increases proportionally. The addition of EVCSs causes some node voltages to drop compared to the base case (see Figure 4b). At the same time, the model ensures that the additional load from the EVCSs does not lead to violation of any operational constraints, i.e., no line overloads or node overvoltage/undervoltage instances.
4.2.3. Case 2: System with PV
In this case, 42 PV panels, with a total capacity of 0.698 p.u., are added to the system, with the irradiance curve shown in Figure 2. In comparison to the base case, the average PCC active power drops to 0.09 p.u, since most of the demand is supplied locally. This causes the system losses to also decrease by almost 47%. PVs participate in reactive power compensation and generate about 0.0018 p.u. of reactive power to maintain the voltages as close to 1 p.u as possible. This is illustrated in Figure 4c., where node voltages lie between 1.01 and 0.995 with a mean of 1.002 p.u. Similar to above, this is achieved while ensuring all operational constraints are met.
4.2.4. Case 3: System with PV and EVCS
When both PVs and EVCSs are added to the system, demand increases (due to EVs) but the local generation by the PVs helps with voltage regulation and losses. It can be seen that PVs manage to respond to a significant portion of the EVCS demand, which is why power losses are reduced compared to case 2, and significantly less active power is provided by the PCC. Node voltages lie between 1.006 p.u and 0.994 p.u, as illustrated in Figure 4d. With the proposed solution, a high level of PV penetration is reached while also accommodating the 96 L2 chargers. The optimal values of the objective functions in this case are provided in Table 5. The single objective values (column 2, Table 5) are associated with each objective function being solved in isolation. The goal values are assigned considering a small percentage of deterioration with respect to the single optima (column 3, Table 5). The solution to the multi-objective model (column 4, Table 5) indicates that two of the objective functions fail to achieve their single objective optima. This is normal within a multi-objective framework since many objective functions may be contradictory to one another, which makes it impossible to achieve all single objective optima simultaneously.

Table 5.
Optimal values for single objectives and the multi-objective for Case 3.
4.3. Discussion
If not coordinated, high penetration levels of PVs and EVCSs in the distribution grid can lead to operational issues such as node overvoltage or undervoltage instances, increased power losses, and possible curtailment of EV demand. The results of the current study indicate that optimal coordination between PV and EVCS resources can lead to improved performance in the power distribution system without violating any operational constraints. Such an approach can facilitate high penetration levels of renewable energy resources in the power distribution grid, even as high as 100%. Coordinated PV and EVCS control can also maintain a relatively flat voltage profile. As expected, local PV generation helps with the increased demand due to EVCS load, while also significantly reducing power losses, e.g., a reduction of 68% compared to the base case in this study.
In such multi-objective settings, it is important to find the Pareto optimal solution because some objective functions may be contradictory to one another. Heuristic approaches for prioritizing objectives over one another or sequential models in which objectives are solved in the order from the most important to the least important fail to provide Pareto optimality and their outcome will be subjective.
The problem of VVWO, as studied in this paper, can suffer from the curse of dimensionality. This is especially true when the three-phase unbalanced nature of the grid needs to be taken into account (as was the case in this paper). For larger scale distribution systems or to study longer time horizons, it may be necessary to use alternative methodologies to improve tractability and convergence. One option could be a decentralized approach in which the problem is solved as a multi-level optimization model, each layer focused on a specific part of the grid, with an upper layer, which would coordinate their actions. An alternative would be to reduce/remove nonlinearities by using a simplified load flow model (unlike the one used in this paper); however, such an approach will likely provide sub-optimal results and may not be able to guarantee that all constraints are met at all times.
The model proposed in this paper is deterministic in nature, i.e., it is assumed that the hourly levels of solar irradiance and EVCS demand are known. In general, this may not be the case. EV demand can demonstrate significant variability during the course of the day and solar irradiance, especially on windy and cloudy days, can be highly stochastic. In order to obtain a better picture of the impacts of PVs and EVs on the power distribution grid, these uncertainties need to be incorporated into the problem formulation. To do this, the proposed model can be extended by using two-stage or multi-stage stochastic programming approaches (when probability distributions of uncertain parameters are known) or developing robust optimization models (when only the ranges of uncertainties are known, but not the associated distributions).
5. Conclusions
Electrification of the transportation fleet and reverting to renewable energy resources such as solar PV are effective steps towards achieving sustainability and slowing down global warming. Despite their clear economic and environmental benefits, PVs and EVs, when deployed at high penetration levels, may introduce operational challenges in the power distribution system. If not coordinated with the distribution management system, they may lead to severe power and voltage quality issues and may in extreme cases jeopardize the stability and security of the power grid. A solution was proposed in this paper to integrate both PVs and EVs into the voltage and reactive power control of the grid. The proposed solution provides optimal dispatch strategies for rooftop PVs and EV charging stations such that operational constraints of the system, e.g., node voltages and line flows, are maintained. The model was formulated as mixed-integer nonlinear multi-objective optimization, where the objectives are to minimize power losses, minimize active power curtailment of PVs, minimize demand curtailment of EVCSs, and minimize node voltage deviations from rated values. This multi-objective model was solved using Chebyshev goal programming in order to find the Pareto optimal solution so that no single objective function dominates others. The effectiveness of the proposed model was validated on a modified version of the IEEE 123-bus test distribution system, considering a three-phase unbalanced system. The simulation results indicate that with optimal coordination between PVs, EVCSs, and other voltage control devices in the system, it is possible to support up to 100% PV penetration while accommodating variable EV demand without violating any system constraints. In this study, the hourly levels of solar irradiance and the demand levels of EVCSs were assumed to be known. Future research will focus on incorporating uncertainties into the problem formulation.
Author Contributions
Both authors have been involved in the various stages of this research. The following details the task assignment. Conceptualization, S.M.; methodology, S.M. and A.A.; software, A.A.; validation, A.A. and S.M.; formal analysis, A.A. and S.M.; investigation, A.A. and S.M.; resources, S.M.; data curation, A.A. and S.M.; writing—original draft preparation, A.A. and S.M.; writing—review and editing, S.M.; visualization, A.A.; supervision, S.M.; project administration, S.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are openly available in reference [38].
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Indices and Superscripts | |
| c | superscript to indicate fixed capacitor. |
| d | superscript to indicate demand. |
| EV | superscript to indicate electric vehicle. |
| i, j, k | index for buses (nodes). |
| imag | superscript to indicate the imaginary part of a complex number. |
| f | index for objective functions of the multi-objective framework. |
| p | index for phases. |
| pri | superscript to indicate the primary side of a transformer or a voltage regulator. |
| PV | superscript to indicate solar PV. |
| rated | superscript to indicate rated power. |
| real | superscript to indicate the real part of a complex number. |
| sec | superscript to indicate the secondary side of a transformer or a voltage regulator. |
| t | index for time. |
| v | index for electric vehicles. |
| VR | superscript to indicate a voltage regulator. |
| y | superscript to indicate shunt admittance. |
| Sets | |
| B | set of buses (nodes). |
| T | time period of study. |
| Parameters | |
| Bi,p | susceptance of the shunt admittance for bus i that is connected to phase p. |
| susceptance of fixed capacitor for bus i that is connected to phase p. | |
| Gi,p | conductance of shunt admittance for bus i that is connected to phase p. |
| conductance of fixed capacitor for bus i that is connected to phase p. | |
| maximum current that can flow through the line between i and j, associated with phase p. | |
| rated active power of EVCS at bus i connected to phase p. | |
| active power of load at bus i connected to phase p. | |
| rated active power of PV at bus i connected to phase p. | |
| reactive power of load at bus i connected to phase p. | |
| Ri,j,p | resistance of the line between buses i and j that is connected to phase p. |
| Tf | target value for the objective function f in the multi-objective framework. |
| ui,j,p | binary parameter indicating if there is a line between bus i and j, associated with phase p (=1, if a line exists, and 0 otherwise). |
| binary parameter indicating if there is a fixed capacitor connected to phase p of bus i (=1, if a fixed capacitor is connected, and 0 otherwise). | |
| binary parameter indicating if there is a load connected to phase p of bus i (=1, if a load is connected, and 0 otherwise). | |
| binary parameter indicating if there is a PV connected to phase p of bus i (=1, if PV is connected, and 0 otherwise). | |
| binary parameter indicating if there is a voltage regulator connected to phase p between buses i and j (=1, if a VR is connected, and 0 otherwise). | |
| binary parameter indicating if there is a shunt admittance connected to phase p of bus i (=1, if a shunt admittance is connected, and 0 otherwise). | |
| Xi,j,p | reactance of the line between buses i and j that is connected to phase p. |
| αt | irradiance level at time t. |
| Variables | |
| bf | Deficiency variable associated with the objective function f in the multi-objective framework. |
| real part of the current that flows in the line between buses i and j associated with phase p. | |
| imaginary part of the current that flows in the line between buses i and j associated with phase p. | |
| real part of the current consumed by EVCS at bus i connected to phase p. | |
| imaginary part of the current consumed by EVCS at bus i connected to phase p. | |
| real part of the current consumed by load at bus i connected to phase p. | |
| imaginary part of the current consumed by load at bus i connected to phase p. | |
| real part of the current injected by PV at bus i connected to phase p. | |
| imaginary part of the current injected by PV at bus i connected to phase p. | |
| real part of the current at the primary side of the VR that is located between buses i and j, associated with phase p. | |
| imaginary part of the current at the primary side of the VR that is located between buses i and j, associated with phase p. | |
| real part of the current at the secondary side of the VR that is located between buses i and j, associated with phase p. | |
| imaginary part of the current at the secondary side of the VR that is located between buses i and j, associated with phase p. | |
| L | maximum deviation of the objective functions from the target values. |
| Of | optimal value for the objective function f in the multi-objective optimization framework. |
| active power of EVCS at phase p of bus i. | |
| active power of PV at phase p of bus i. | |
| reactive power of EVCS at phase p of bus i. | |
| reactive power of PV at phase p of bus i, negative value indicating absorbing. | |
| integer variable representing the tap position of the VR located between buses i and j, associated with phase p. | |
| real part of the voltage of bus i at phase p. | |
| imaginary part of the voltage of bus i at phase p. | |
| voltage magnitude of bus i at phase p. |
References
- Shah, R.; Mithulananthan, N.; Bansal, R.C.; Ramachandaramurthy, V.K. A review of key power system stability challenges for large-scale PV integration. Renew. Sustain. Energy Rev. 2015, 41, 1423–1436. [Google Scholar] [CrossRef]
- Coignard, J.; MacDougall, P.; Stadtmueller, F.; Vrettos, E. Will Electric Vehicles Drive Distribution Grid Upgrades? The Case of California. IEEE Electrif. Mag. 2019, 7, 46–56. [Google Scholar] [CrossRef]
- Sanguesa, J.A.; Torres-Sanz, V.; Garrido, P.; Martinez, F.J.; Marquez-Barja, J.M. A Review on Electric Vehicles: Technologies and Challenges. Smart Cities 2021, 4, 372–404. [Google Scholar] [CrossRef]
- Dubey, A.; Santoso, S. On Estimation and Sensitivity Analysis of Distribution Circuit’s Photovoltaic Hosting Capacity. IEEE Trans. Power Syst. 2017, 32, 2779–2789. [Google Scholar] [CrossRef]
- Lazarou, S.; Vita, V.; Ekonomou, L. Protection Schemes of Meshed Distribution Networks for Smart Grids and Electric Vehicles. Energies 2018, 11, 3106. [Google Scholar] [CrossRef]
- Arias, N.B.; Hashemi, S.; Andersen, P.B.; Træholt, C.; Romero, R. Distribution System Services Provided by Electric Vehicles: Recent Status, Challenges, and Future Prospects. IEEE Trans. Intell. Transp. Syst. 2019, 20, 4277–4296. [Google Scholar] [CrossRef]
- Donadee, J.; Shaw, R.; Garnett, O.; Cutter, E.; Min, L. Potential Benefits of Vehicle-to-Grid Technology in California: High Value for Capabilities Beyond One-Way Managed Charging. IEEE Electrif. Mag. 2019, 7, 40–45. [Google Scholar] [CrossRef]
- Jafari, M.; Olowu, T.O.; Sarwat, A.I. Optimal Smart Inverters Volt-VAR Curve Selection with a Multi-Objective Volt-VAR Optimization using Evolutionary Algorithm Approach. In Proceedings of the 2018 North American Power Symposium (NAPS), Fargo, ND, USA, 9–11 September 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Falco, M.; Arrigo, F.; Mazza, A.; Bompard, E.; Chicco, G. Agent-based Modelling to Evaluate the Impact of Plug-in Electric Vehicles on Distribution Systems. In Proceedings of the 2019 International Conference on Smart Energy Systems and Technologies (SEST), Porto, Portugal, 9–11 September 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Fernandez, L.P.; Roman, T.G.S.; Cossent, R.; Domingo, C.M.; Frias, P. Assessment of the Impact of Plug-in Electric Vehicles on Distribution Networks. IEEE Trans. Power Syst. 2011, 26, 206–213. [Google Scholar] [CrossRef]
- Shafiee, S.; Fotuhi-Firuzabad, M.; Rastegar, M. Investigating the impacts of plug-in hybrid electric vehicles on distribution congestion. In Proceedings of the 22nd International Conference and Exhibition on Electricity Distribution (CIRED 2013), Stockholm, Sweden, 10–13 June 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Qian, K.; Zhou, C.; Allan, M.; Yuan, Y. Modeling of Load Demand Due to EV Battery Charging in Distribution Systems. IEEE Trans. Power Syst. 2011, 26, 802–810. [Google Scholar] [CrossRef]
- Raouf, A.A.; Best, R.J.; Morrow, D.J.; Cupples, A.; Bailie, I. Impact of the deployment of solar photovoltaic and electrical vehicle on the low voltage unbalanced networks and the role of battery energy storage systems. J. Energy Storage 2021, 42, 102975. [Google Scholar] [CrossRef]
- MMeđugorac; Capuder, T.; Skok, M.; Škrlec, D.; Bago, D. On the role and the value of flexibility options in planning of distribution networks with high penetration of electric vehicle charging stations: Case study of Mostar. In Proceedings of the CIRED Porto Workshop 2022: E-Mobility and Power Distribution Systems, Porto, Portugal, 2–3 June 2022; pp. 414–418. [Google Scholar] [CrossRef]
- Simarro-garcía, A.; Villena-Ruiz, R.; Honrubia-Escribano, A.; Gómez-lázaro, E. Impacts of electric vehicle charging stations on a greek distribution network. In Proceedings of the CIRED Porto Workshop 2022: E-Mobility and Power Distribution Systems, Porto, Portugal, 2–3 June 2022; pp. 452–456. [Google Scholar] [CrossRef]
- Verzijlbergh, R.A.; Lukszo, Z.; Slootweg, J.G.; Ilic, M.D. The impact of controlled electric vehicle charging on residential low voltage networks. In Proceedings of the 2011 International Conference on Networking, Sensing and Control, Delft, The Netherlands, 11–13 April 2011; pp. 14–19. [Google Scholar] [CrossRef]
- Lopes, J.A.P.; Soares, F.J.; Almeida, P.M.; da Silva, M.M. Smart charging strategies for electric vehicles: Enhancing grid performance and maximizing the use of variable renewable energy resources. In Proceedings of the 24th International Battery, Hybrid and Fuel Cell Electric Vehicle Symposium & Exhibition 2009: (EVS 24), Stavanger, Norway, 13–16 May 2009; pp. 2680–2690. [Google Scholar]
- Pal, A.; Bhattacharya, A.; Chakraborty, A.K. Allocation of EV Fast Charging Station with V2G Facility in Distribution Network. In Proceedings of the 2019 8th International Conference on Power Systems (ICPS), Jaipur, India, 20–22 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Sultan, I.A.; Swief, R.A.; Ezzat, M.; Abdel-Salam, T.S. Optimal Reliable Electrical Vehicles Charging Stations Applying Grey Wolf Technique. In Proceedings of the 2022 International Telecommunications Conference (ITC-Egypt), Alexandria, Egypt, 26–28 July 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Boonraksa, T.; Marungsri, B. Optimal Fast Charging Station Location for Public Electric Transportation in Smart Power Distribution Network. In Proceedings of the 2018 International Electrical Engineering Congress (iEECON), Krabi, Thailand, 7–9 March 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Cheng, S.; Gao, P.-F. Optimal allocation of charging stations for electric vehicles in the distribution system. In Proceedings of the 2018 3rd International Conference on Intelligent Green Building and Smart Grid (IGBSG), Yilan, Taiwan, 22–25 April 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Yan, X.; Duan, C.; Chen, X.; Duan, Z. Planning of Electric Vehicle charging station based on hierarchic genetic algorithm. In Proceedings of the 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 31 August–3 September 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Liu, Z.; Wen, F.; Ledwich, G. Optimal Planning of Electric-Vehicle Charging Stations in Distribution Systems. IEEE Trans. Power Deliv. 2013, 28, 102–110. [Google Scholar] [CrossRef]
- Wang, L.; Kwon, J.; Verbas, O.; Rousseau, A.; Zhou, Z. Charging Station Planning to Maximize Extra Load Hosting Capacity in Unbalanced Distribution System. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Ahmad, F.; Iqbal, A.; Ashraf, I.; Marzband, M.; Khan, I. Optimal Siting and Sizing Approach of Plug-in Electric Vehicle Fast Charging Station using a Novel Meta-heuristic Algorithm. In Proceedings of the 2022 2nd International Conference on Emerging Frontiers in Electrical and Electronic Technologies (ICEFEET), Patna, India, 24–25 June 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Li, M.; Hou, T.; Xie, H.; Hu, Z.; Li, Y.; Wang, Q. Two-stage allocation of electric vehicle charging stations considering coordinated charging scenario. In Proceedings of the 2022 IEEE 5th International Electrical and Energy Conference (CIEEC), Nangjing, China, 27–29 May 2022; pp. 4982–4987. [Google Scholar] [CrossRef]
- Kunj, T.; Pal, K. Optimal location Planning of EV Charging Station in Existing Distribution Network with stability condition. In Proceedings of the 2020 7th International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 27–28 February 2020; pp. 1060–1065. [Google Scholar] [CrossRef]
- Shi, X.; Xu, Y.; Guo, Q.; Sheng, Y.; Sun, H.; Chen, F.; Zhang, Y. A novel planning approach for the fast charging station in an integrated system. CSEE J. Power Energy Syst. 2022; to be published. [Google Scholar] [CrossRef]
- Sabillon-Antunez, C.; Melgar-Dominguez, O.D.; Franco, J.F.; Lavorato, M.; Rider, M.J. Volt-VAr Control and Energy Storage Device Operation to Improve the Electric Vehicle Charging Coordination in Unbalanced Distribution Networks. IEEE Trans. Sustain. Energy 2017, 8, 1560–1570. [Google Scholar] [CrossRef]
- Kikusato, H.; Mori, K.; Yoshizawa, S.; Fujimoto, Y.; Asano, H.; Hayashi, Y.; Kawashima, A.; Inagaki, S.; Suzuki, T. Electric Vehicle Charge–Discharge Management for Utilization of Photovoltaic by Coordination Between Home and Grid Energy Management Systems. IEEE Trans. Smart Grid 2019, 10, 3186–3197. [Google Scholar] [CrossRef]
- Kermia, M.H.; Boche, J.; Abbes, D. Predictive energy management in an electric vehicle charging station. In Proceedings of the CIRED Porto Workshop 2022: E-Mobility and Power Distribution Systems, Porto, Portugal, 2–3 June 2022; pp. 935–939. [Google Scholar] [CrossRef]
- Wang, L.; Dubey, A.; Gebremedhin, A.H.; Srivastava, A.K.; Schulz, N. MPC-Based Decentralized Voltage Control in Power Distribution Systems With EV and PV Coordination. IEEE Trans. Smart Grid 2022, 13, 2908–2919. [Google Scholar] [CrossRef]
- Chaouachi, A.; Bompard, E.; Fulli, G.; Masera, M.; de Gennaro, M.; Paffumi, E. Assessment framework for EV and PV synergies in emerging distribution systems. Renew. Sustain. Energy Rev. 2016, 55, 719–728. [Google Scholar] [CrossRef]
- Dutta, A.; Ganguly, S.; Kumar, C. Coordinated Volt/Var Control of PV and EV Interfaced Active Distribution Networks Based on Dual-Stage Model Predictive Control. IEEE Syst. J. 2022, 16, 4291–4300. [Google Scholar] [CrossRef]
- Rabiee, A.; Keane, A.; Soroudi, A. Enhanced Transmission and Distribution Network Coordination to Host More Electric Vehicles and PV. IEEE Syst. J. 2022, 16, 2705–2716. [Google Scholar] [CrossRef]
- Wang, J.; Di, F.; Meng, H.; Meng, M.; Luo, X.; Wang, Y. Coordinated Distribution Reconfiguration with Maintenance Scheduling Considering Electric Vehicles Charging Uncertainty. In Proceedings of the 2022 IEEE 5th International Electrical and Energy Conference (CIEEC), Nangjing, China, 27–29 May 2022; pp. 168–173. [Google Scholar] [CrossRef]
- Gao, F.; Du, K.; Chen, X.; Xu, Y.; Li, D. Reconfiguration of the electric vehicle integrated distribution system considering carbon-reduction benefit. In Proceedings of the 2022 IEEE 5th International Electrical and Energy Conference (CIEEC), Nangjing, China, 27–29 May 2022; pp. 4975–4981. [Google Scholar] [CrossRef]
- Schneider, K.P.; Mather, B.A.; Pal, B.C.; Ten, C.W.; Shirek, G.J.; Zhu, H.; Fuller, J.C.; Pereira, J.L.R.; Ochoa, L.F.; de Araujo, L.R.; et al. Analytic Considerations and Design Basis for the IEEE Distribution Test Feeders. IEEE Trans. Power Syst. 2017, 33, 3181–3188. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).