Series RLC Resonant Circuit Used as Frequency Multiplier
Abstract
:1. Introduction
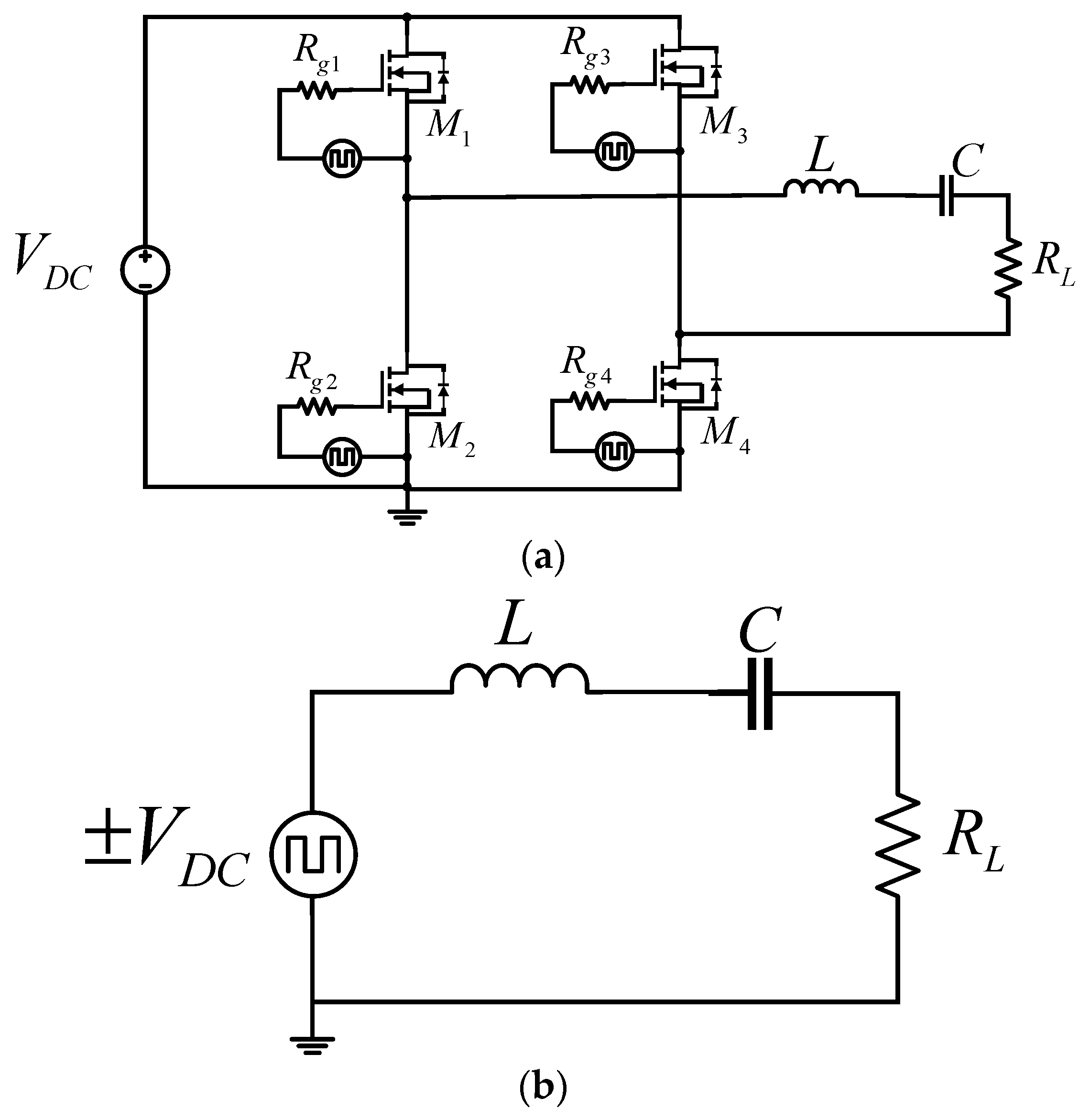
2. Analysis of the Circuit
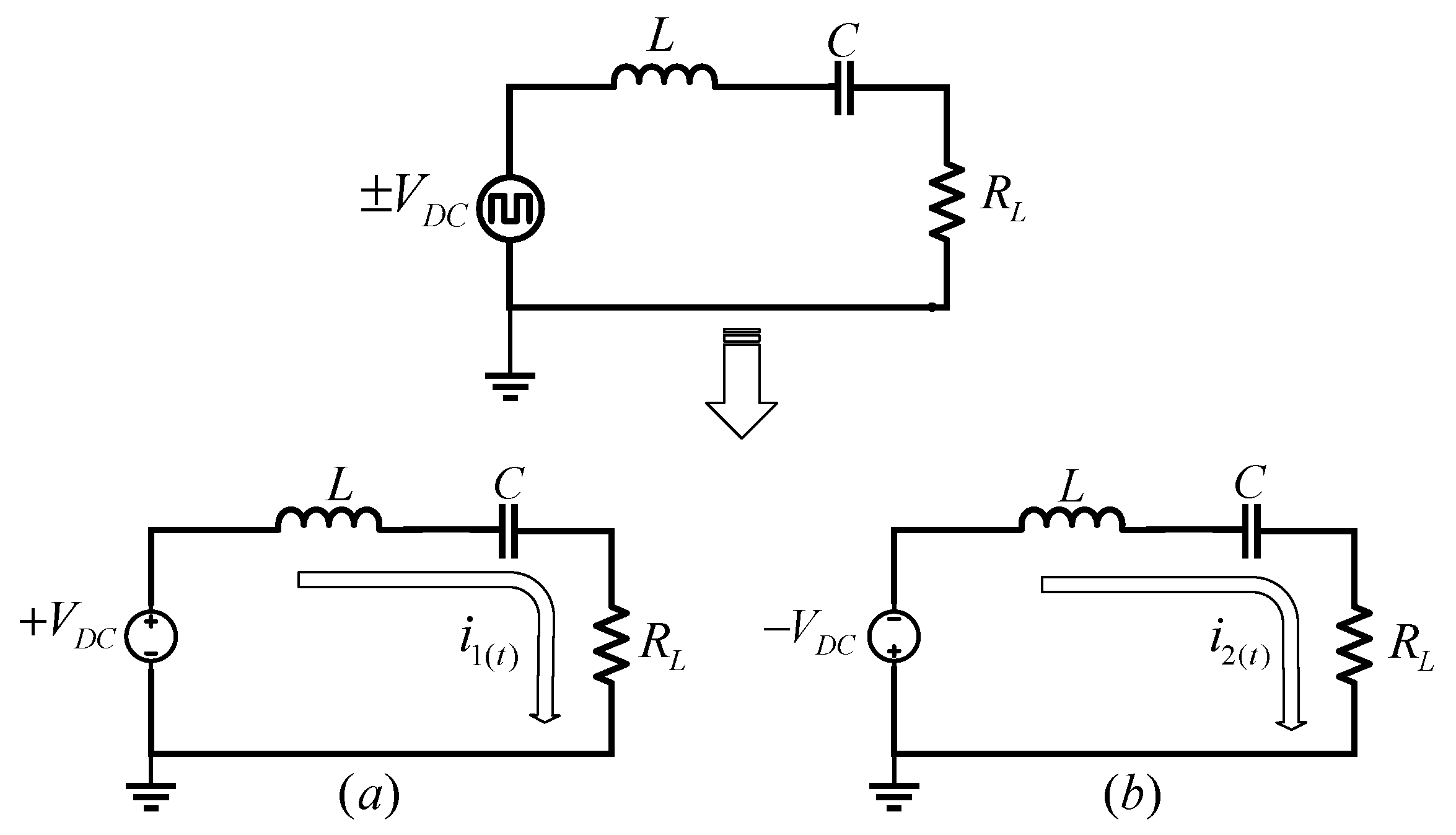
2.1. Determination of the Instantaneous Current with Underdamped Response Circulating in the Resonant Tank
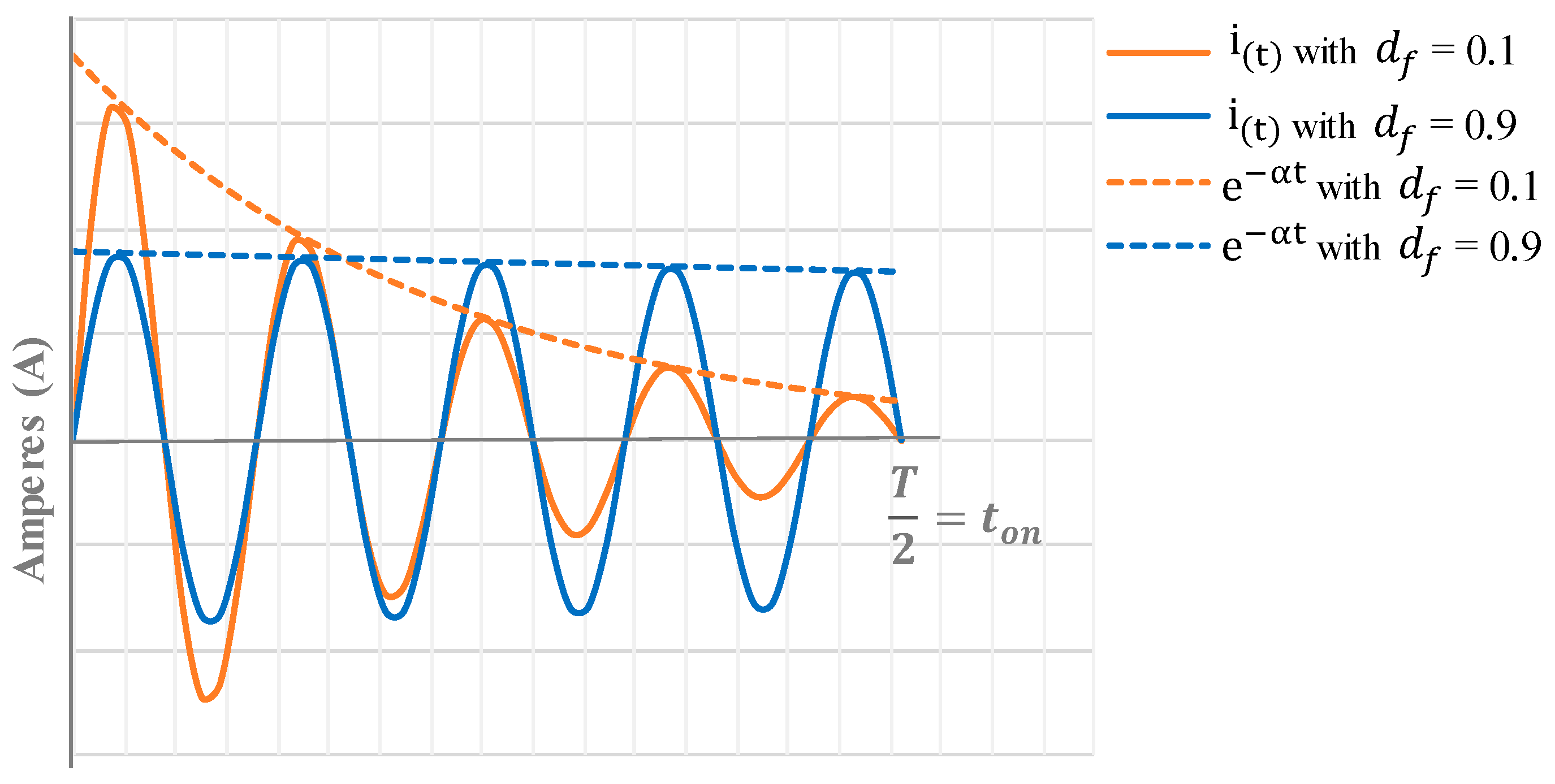
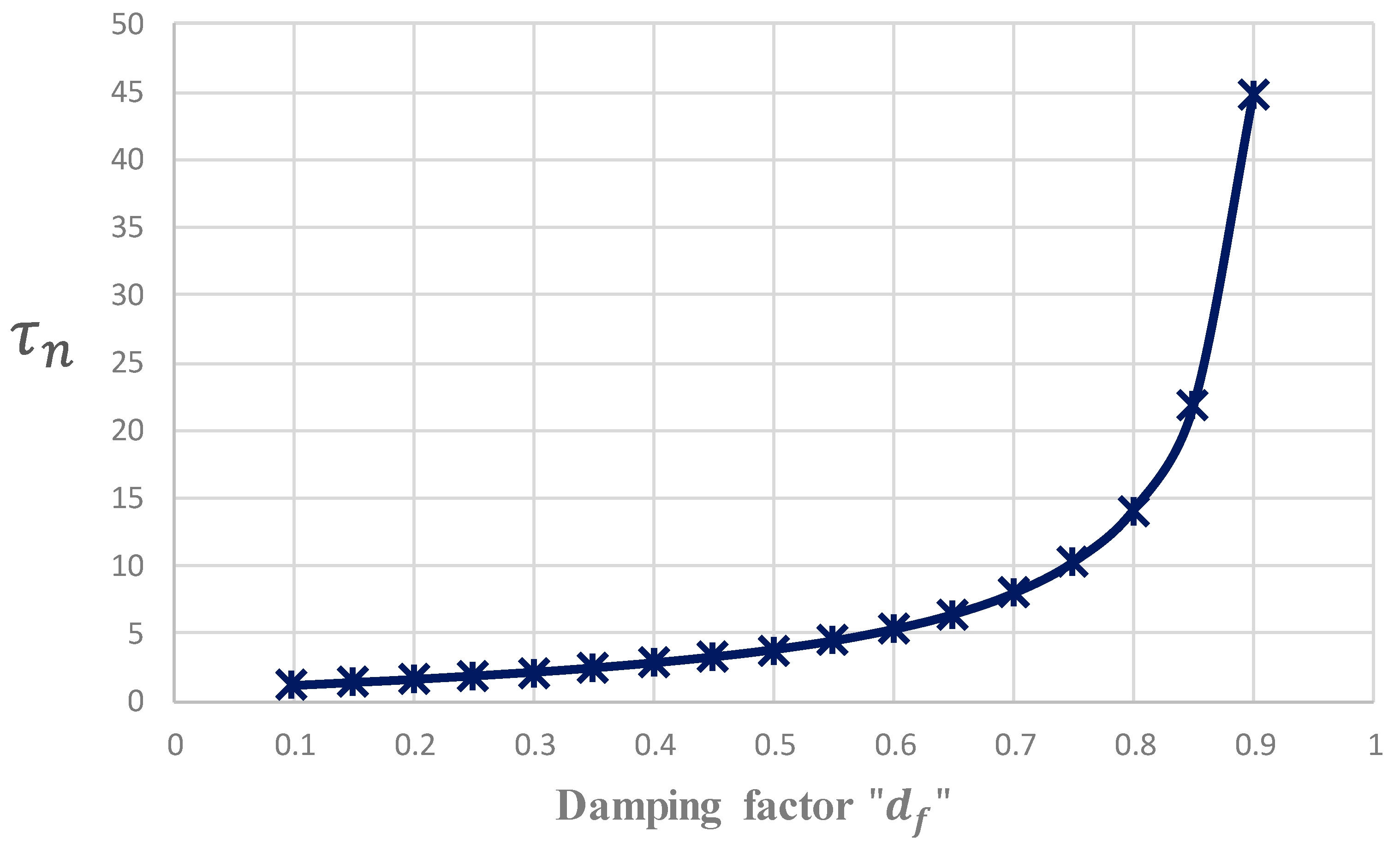
2.2. Determination of Parameters Defining the Underdamping Level and Waveform of the Instantaneous Current in the Resonant Tank
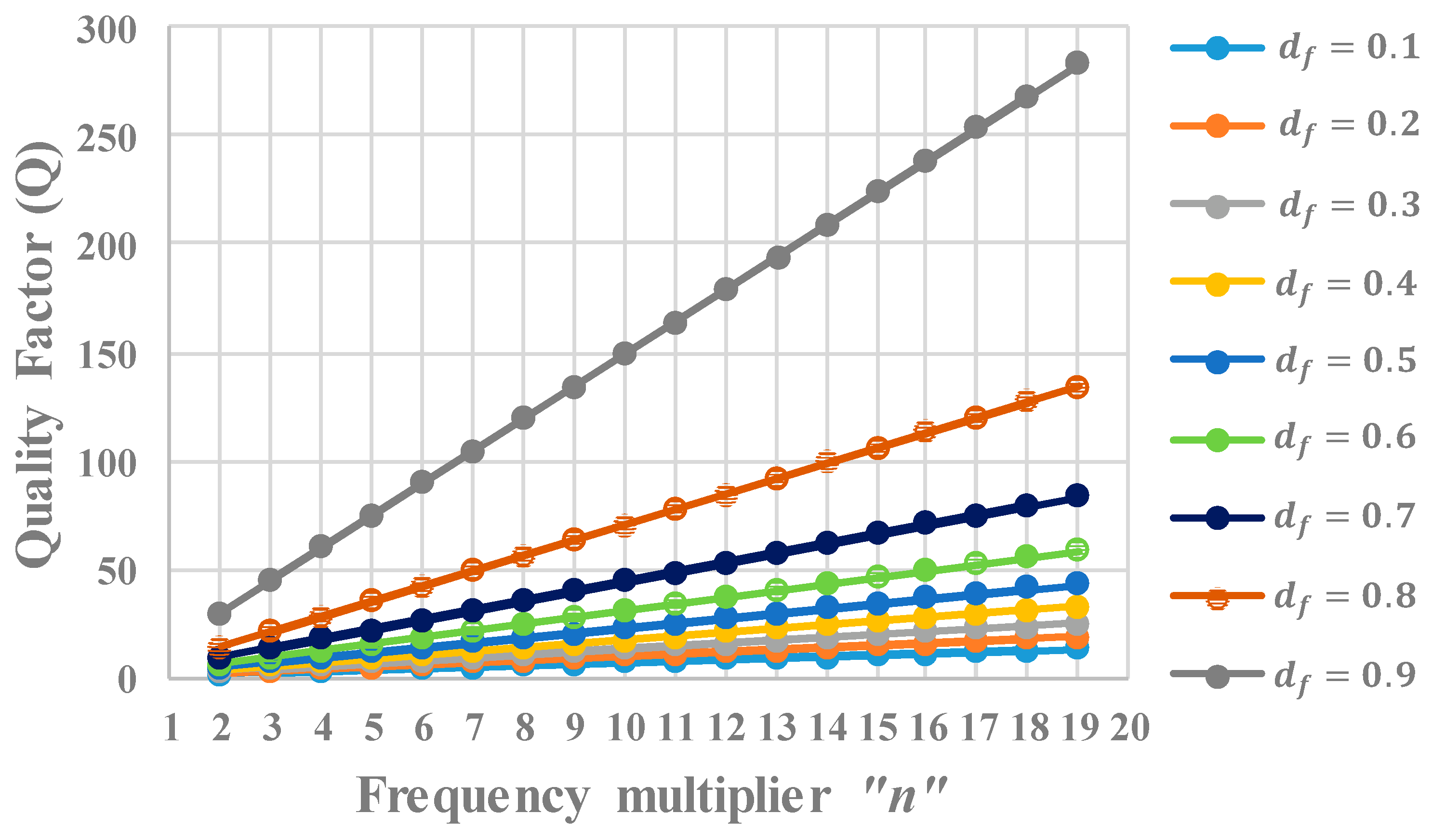
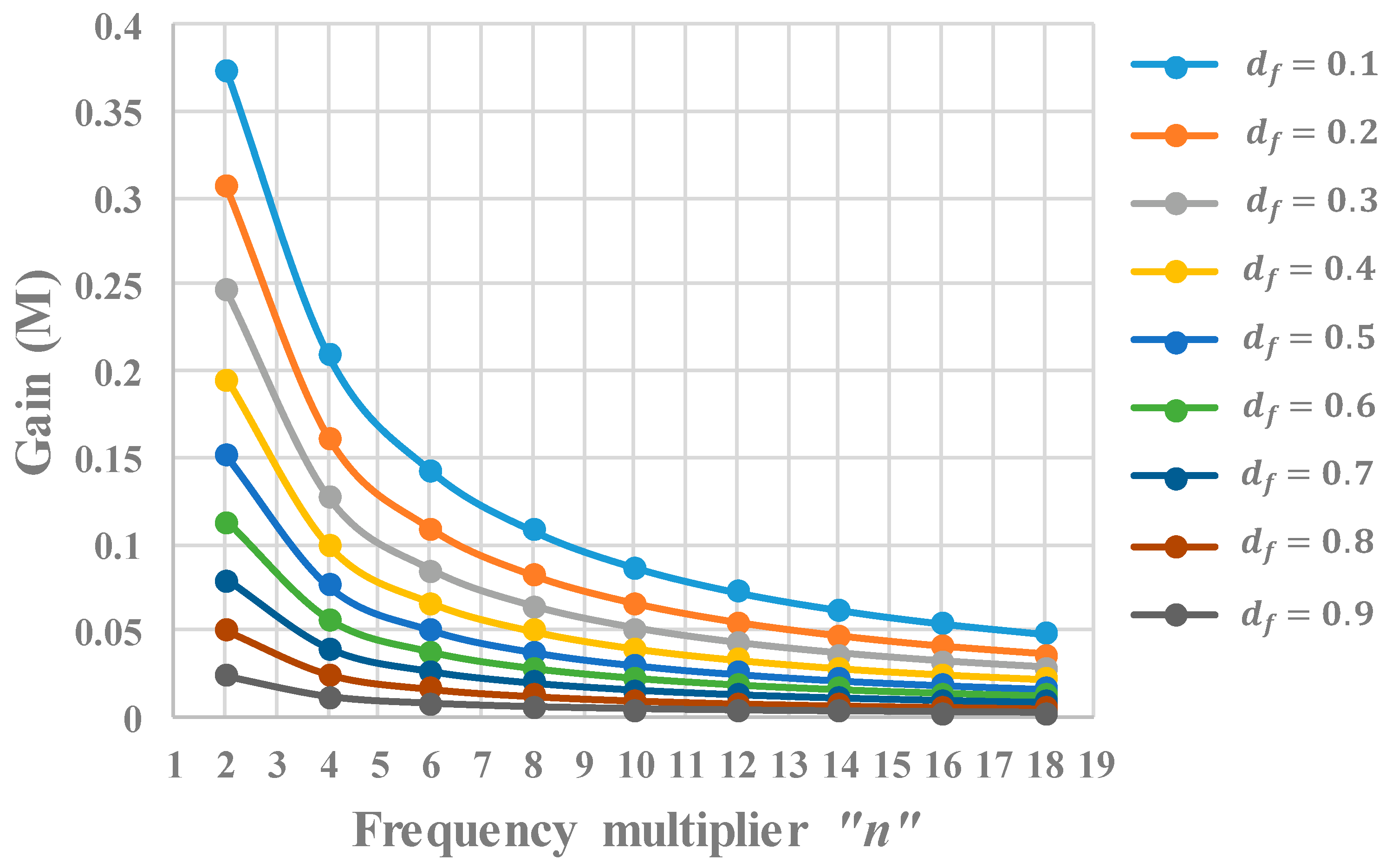
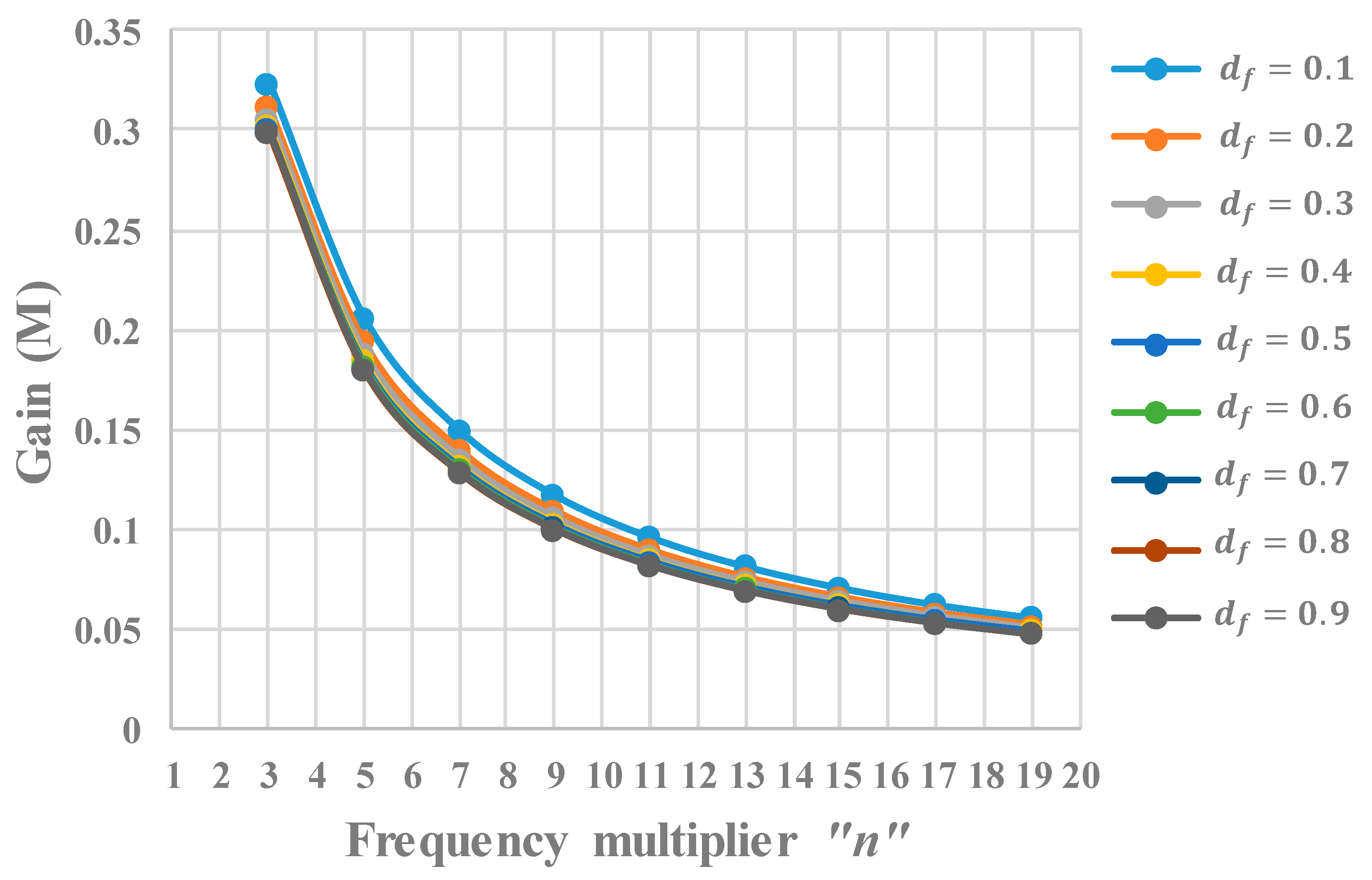
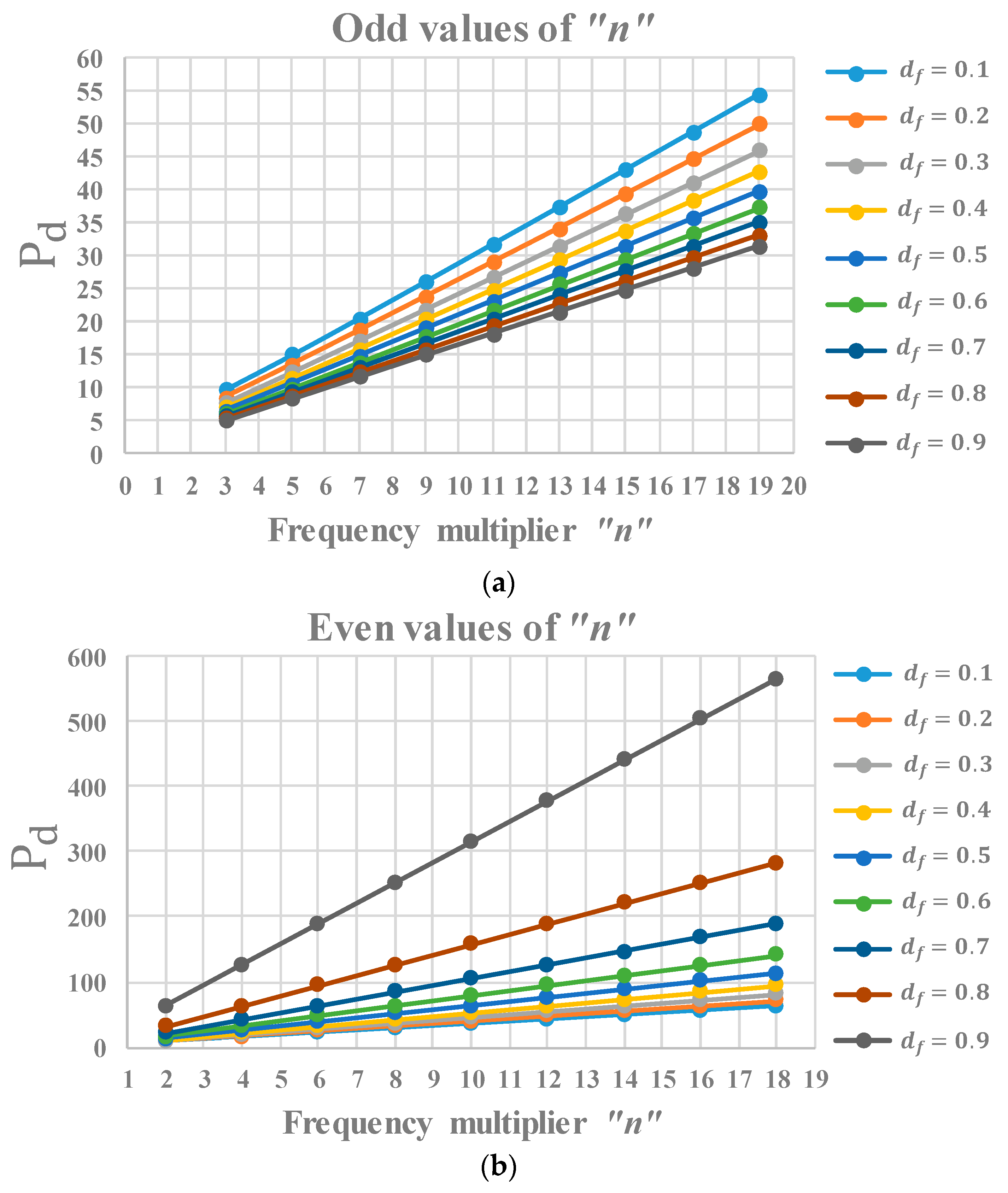
2.3. Determination of the Maximum Current in the Resonant Tank for Even and Odd Values of “n” with the Determination of Constant “c”
2.4. Determination of the Circuit Operating Parameters
3. Design Methodology and Simulation
3.1. Design Methodology
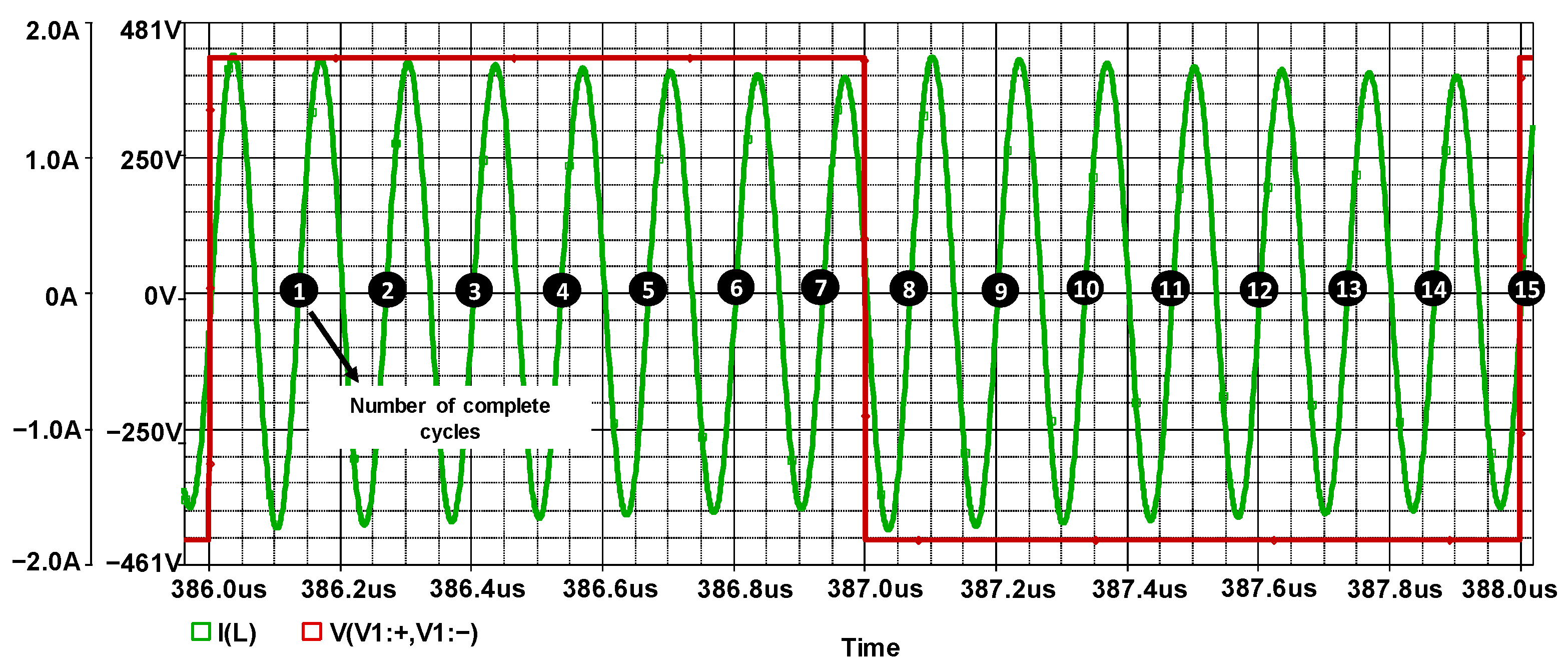
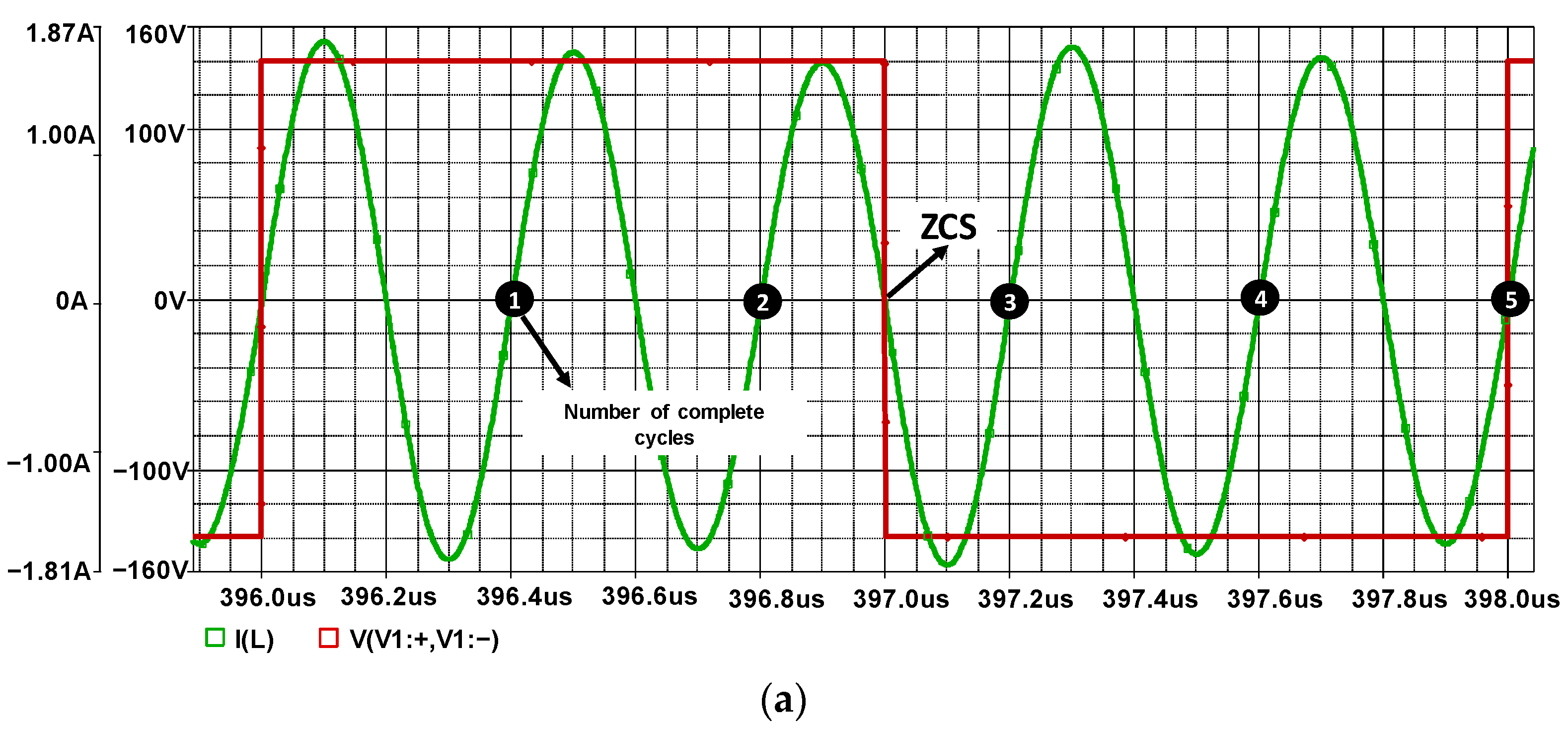
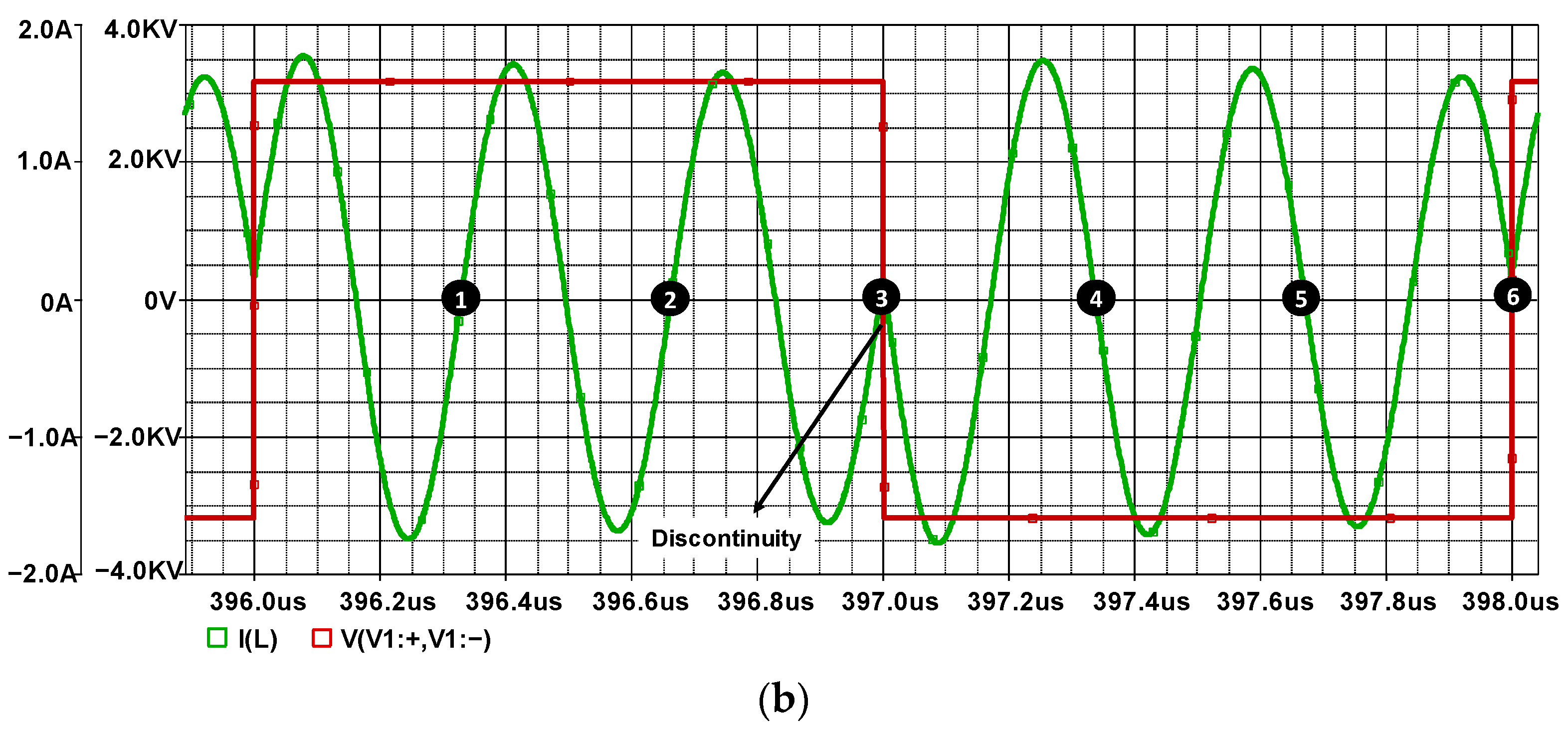
3.2. Simulation of the Circuit
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kshatri, S.S.; Dhillon, J.; Mishra, S.; Haghighi, A.T.; Hunt, J.D.; Patro, E.R. Comparative Reliability Assessment of Hybrid Si/SiC and Conventional Si Power Module Based PV Inverter Considering Mission Profile of India and Denmark Locations. Energies 2022, 15, 8612. [Google Scholar] [CrossRef]
- Alatai, S.; Salem, M.; Ishak, D.; Das, H.S.; Nazari, M.A.; Bughneda, A.; Kamarol, M. A Review on State-of-the-Art Power Converters: Bidirectional, Resonant, Multilevel Converters and Their Derivatives. Appl. Sci. 2021, 11, 10172. [Google Scholar] [CrossRef]
- İnci, M.; Büyük, M.; Demir, M.H.; İlbey, G. A review and research on fuel cell electric vehicles: Topologies, power electronic converters, energy management methods, technical challenges, marketing and future aspects. Renew. Sustain. Energy Rev. 2021, 137, 110648. [Google Scholar] [CrossRef]
- Chen, C.; Chen, Y.; Tan, Y.; Fang, J.; Luo, F.; Kang, Y. On the practical design of a high power density SiC single-phase uninterrupted power supply system. IEEE Trans. Ind. Inform. 2017, 13, 2704–2716. [Google Scholar] [CrossRef]
- Mahesh, M.; Kumar, K.V.; Abebe, M.; Udayakumar, L.; Mathankumar, M. A review on enabling technologies for high power density power electronic applications. Mater. Today Proc. 2021, 46, 3888–3892. [Google Scholar] [CrossRef]
- Baek, J.; Park, M.-H.; Kim, T.; Youn, H.-S. Modified power factor correction (PFC) control and printed circuit board (PCB) design for high-efficiency and high-power density on-board charger. Energies 2021, 14, 605. [Google Scholar] [CrossRef]
- Kwon, J.; Kim, R.-Y. High power density, high-voltage parallel resonant converter using parasitic capacitance on the secondary side of a transformer. Electronics 2021, 10, 1736. [Google Scholar] [CrossRef]
- Gu, L.; Zulauf, G.; Stein, A.; Kyaw, A.; Chen, T.; Davila, J.M.R. 6.78-MHz wireless power transfer with self-resonant coils at 95% DC–DC efficiency. IEEE Trans. Power Electron. 2020, 36, 2456–2460. [Google Scholar] [CrossRef]
- Shi, L.; Alou, P.; Oliver, J.A.; Cobos, J.A. A Novel Self-adaptive Wireless Power Transfer System to Cancel the Reactance of the Series Resonant Tank and Deliver More Power. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 4207–4211. [Google Scholar]
- Yoo, J.-S.; Gil, Y.-M.; Ahn, T.-Y. Steady-State Analysis and Optimal Design of an LLC Resonant Converter Considering Internal Loss Resistance. Energies 2022, 15, 8144. [Google Scholar] [CrossRef]
- Stojadinovic, N.; Dankovic, D.; Manic, I.; Davidovic, V.; Djoric-Veljkovic, S.; Golubovic, S. Impact of negative bias temperature instabilities on lifetime in p-channel power VDMOSFETs. In Proceedings of the 8th IEEE International Conference on Telecommunications in Modern Satellite, Cable and Broadcasting Services, Nis, Serbia, 26–28 September 2007; pp. 275–282. [Google Scholar]
- Djezzar, B.; Tahi, H.; Benabdelmoumene, A.; Chenouf, A. A new eye on NBTI-induced traps up to device lifetime using on the fly oxide trap method. In Proceedings of the 24th IEEE International Conference on Microelectronics (ICM), Algiers, Algeria, 16–20 December 2012; pp. 1–4. [Google Scholar]
- Tahi, H.; Tahanout, C.; Boubaaya, M.; Djezzar, B.; Merah, S.M.; Nadji, B.; Saoula, N. Experimental investigation of NBTI degradation in power VDMOS transistors under low magnetic field. IEEE Trans. Device Mater. Reliab. 2017, 17, 99–105. [Google Scholar] [CrossRef]
- Stojadinović, N.; Djorić-Veljković, S.; Davidović, V.; Golubović, S.; Stanković, S.; Prijić, A.; Prijić, Z.; Manić, I.; Danković, D. NBTI and irradiation related degradation mechanisms in power VDMOS transistors. Microelectron. Reliab. 2018, 88, 135–141. [Google Scholar] [CrossRef]
- Park, H.-P.; Kang, Y.; Kang, S.; Jung, J.-H. FPGA Controller Design for High-Frequency LLC Resonant Converters. IEEJ J. Ind. Appl. 2020, 9, 523–529. [Google Scholar] [CrossRef]
- Zhao, Y.; Xiao, Q.; Zhang, Z.; Zhao, X.; Lin, D. Research on ZVS Phase-Shifted Full-Bridge Broadband Inverter Based on Auxiliary Current Source. Energies 2022, 15, 8661. [Google Scholar] [CrossRef]
- Xu, S.; Wang, Z.; Chen, J.; Jiang, W. Research and Design of LC Series Resonant Wireless Power Transfer System with Modulation Control Method for Supercapacitor Charging in Linear Motion Systems. Energies 2022, 15, 6739. [Google Scholar] [CrossRef]
- Huang, J.; Wong, S.-C.; Liu, X.; Li, Z. Steady State Analysis of Wireless Power Transfer System with Rectifier-Load under DCM. In Proceedings of the 14th IEEE Conference on Industrial Electronics and Applications, Xi’an, China, 19–21 June 2019; pp. 462–467. [Google Scholar]
- Li, X.; Guo, L.; Lang, T.; Lu, D.; Alluhaybi, K.; Hu, H. Steady-State Characterization of LLC-Based Single-Stage AC/DC Converter Based on Numerical Analysis. IEEE Trans. Power Electron. 2021, 36, 9970–9983. [Google Scholar] [CrossRef]
- Shinoda, K.; Fujii, M.; Matsuo, M.; Suetsuga, T.; Mori, S. Idealized operation of Class DE frequency multipliers. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Atlanta, GA, USA, 15 May 1996; Volume 1, pp. 581–584. [Google Scholar]
- Zulinski, R.; Steadman, J. Idealized operation of class E frequency multipliers. IEEE Trans. Circuits Syst. 1986, 33, 1209–1218. [Google Scholar] [CrossRef]
- Inam, W.; Afridi, K.K.; Perreault, D.J. Variable frequency multiplier technique for high-efficiency conversion over a wide operating range. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 4, 335–343. [Google Scholar] [CrossRef]
- Li, R.T.; Vancu, M.-F.; Canales, F.; Aggeler, D. High performance dc-dc converter for wide voltage range operation. In Proceedings of the 7th International Power Electronics and Motion Control Conference, Harbin, China, 2–5 June 2012; Volume 2, pp. 1151–1158. [Google Scholar]
- Shinoda, K.; Fujii, M.; Koizumi, H.; Suetsugu, T.; Mori, S. Phase-controlled resonant dc/dc converter with Class E frequency multiplier. In Proceedings of INTELEC 95. In Proceedings of the 17th International Telecommunications Energy Conference, The Hague, The Netherlands, 29 October–1 November 1995; pp. 107–113. [Google Scholar]
- Gu, L.; Liang, W.; Praglin, M.; Chakraborty, S.; Rivas-Davila, J. A wide-input-range high-efficiency step-down power factor correction converter using a variable frequency multiplier technique. IEEE Trans. Power Electron. 2018, 33, 9399–9411. [Google Scholar] [CrossRef]
- Li, Y.; Meng, J.; Zhang, D.; Zhu, H. The Development of Frequency Tripler Based on Six-Anode Schottky Varactors. Micromachines 2021, 12, 1490. [Google Scholar] [CrossRef]
- Oh, K.-I.; Ko, G.-H.; Kim, G.-S.; Kim, J.-G.; Baek, D. A 17.8–34.8 GHz (64.6%) Locking Range Current-Reuse Injection-Locked Frequency Multiplier with Dual Injection Technique. Electronics 2021, 10, 1122. [Google Scholar] [CrossRef]
- Powell, J.; Viegas, C.; Sanghera, H.S.; Huggard, P.G.; Alderman, B. Comparing novel MMIC and hybrid circuit high efficiency GaAs Schottky diode mm-wave frequency doublers. Electronics 2020, 9, 1718. [Google Scholar] [CrossRef]
- Doo, J.; Kim, J.; Jeong, J. D-band frequency tripler module using anti-parallel diode pair and waveguide transitions. Electronics 2020, 9, 1201. [Google Scholar] [CrossRef]
- Jeong, J.; Choi, J.; Kim, J.; Choe, W. H-band INP HBT frequency tripler using the triple-push technique. Electronics 2020, 9, 2081. [Google Scholar] [CrossRef]
- Yao, J.; Li, M.; Yu, X.; Li, T.; Dai, Z. Analysis and Design of Class E Frequency Multiplier With Shunt Linear and Nonlinear Capacitances at Any Duty Cycle. IEEE Trans. Circuits Syst. II Express Briefs 2021, 69, 1827–1831. [Google Scholar] [CrossRef]
- Zaheri, R.; Moghani, J.S. A Modular Two-Stage High Step-Down DC-DC Converter Using Frequency Multiplier Circuit for Datacenter Applications. In Proceedings of the IEEE 12th Power Electronics, Drive Systems, and Technologies Conference (PEDSTC), Tabriz, Iran, 2–4 February 2021; pp. 1–5. [Google Scholar]
- Jia, P.; Guo, H.; Yuan, G.; Zhu, H.; Su, Z.; Guo, T. Prediction for the Overcurrent Value of the Three-Level LLC Resonant Converter in the Mode Switching Process. In Proceedings of the IEEE 24th International Conference on Electrical Machines and Systems (ICEMS), Gyeongju, Korea, 31 October–3 November 2021; pp. 211–2115. [Google Scholar]
- Sumi, F.H.; Dutta, L.; Sarker, F. Future with Wireless power transfer technology. J. Electr. Electron. Syst. 2018, 7, 1000279. [Google Scholar]
- Feng, J.; Li, Q.; Lee, F.C.; Fu, M. LCCL-LC Resonant Converter and Its Soft Switching Realization for Omnidirectional Wireless Power Transfer Systems. IEEE Trans. Power Electron. 2020, 36, 3828–3839. [Google Scholar] [CrossRef]
- Pahlavan, S.; Shooshtari, M.; Ashtiani, S.J. Star-Shaped Coils in the Transmitter Array for Receiver Rotation Tolerance in Free-Moving Wireless Power Transfer Applications. Energies 2022, 15, 8643. [Google Scholar] [CrossRef]
- Aydin, E.; Aydemir, M.T.; Aksoz, A.; el Baghdadi, M.; Hegazy, O. Inductive Power Transfer for Electric Vehicle Charging Applications: A Comprehensive Review. Energies 2022, 15, 4962. [Google Scholar] [CrossRef]
- Jha, R.K.; Kumar, A.; Prakash, S.; Jaiswal, S.; Bertoluzzo, M.; Kumar, A.; Joshi, B.P.; Forato, M. Modeling of the Resonant Inverter for Wireless Power Transfer Systems Using the Novel MVLT Method. Vehicles 2022, 4, 1277–1287. [Google Scholar] [CrossRef]
- Erickson, R.W.; Maksimovic, D. Fundamentals of Power Electronics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Robinson, J.C. An Introduction to Ordinary Differential Equations; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
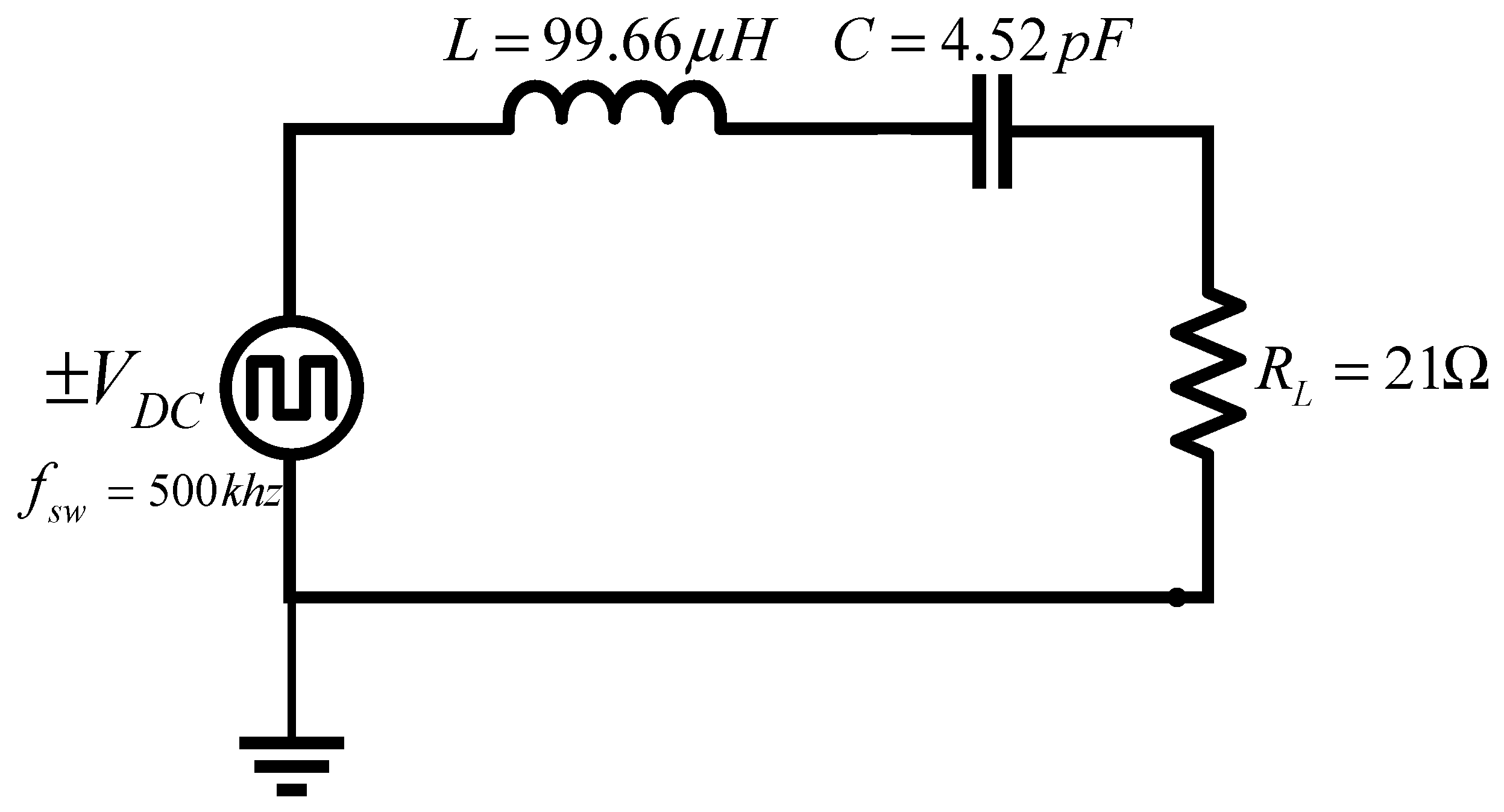
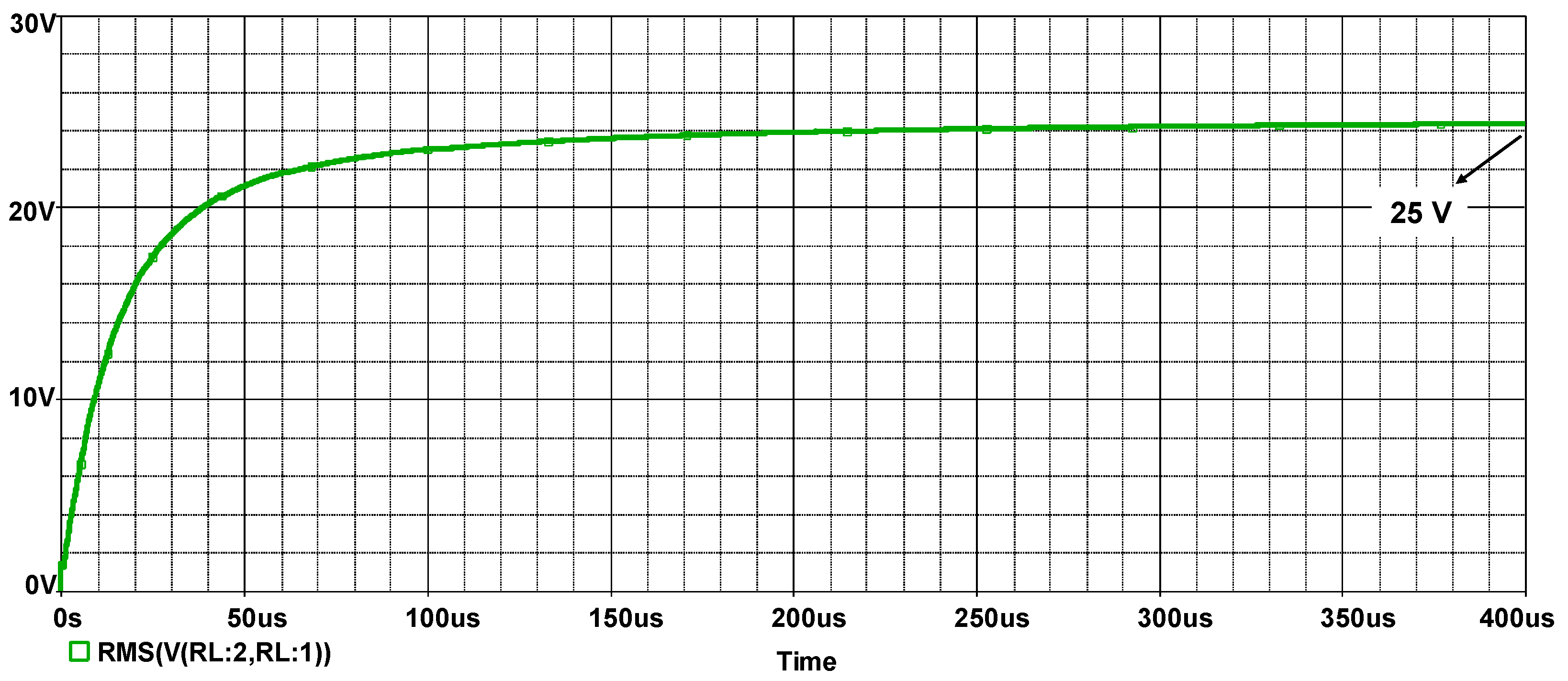
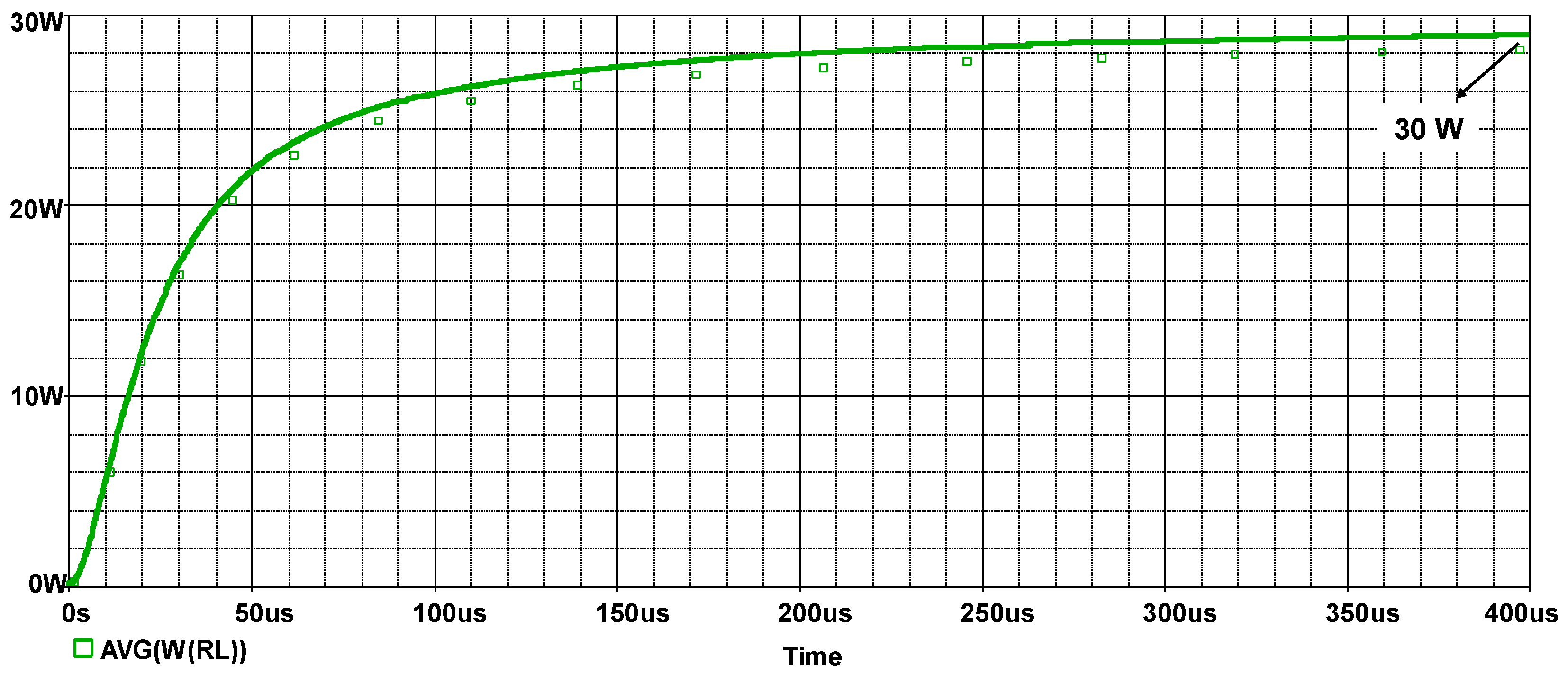
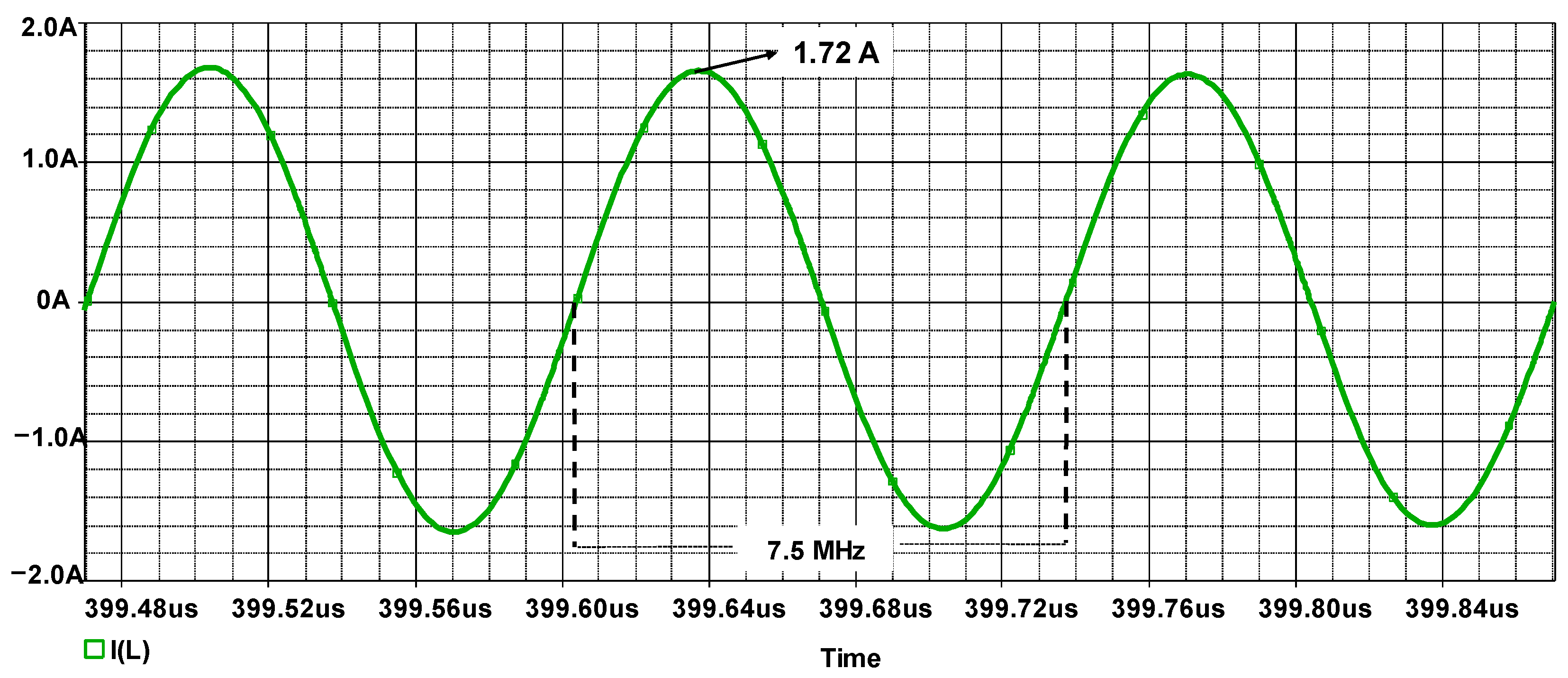
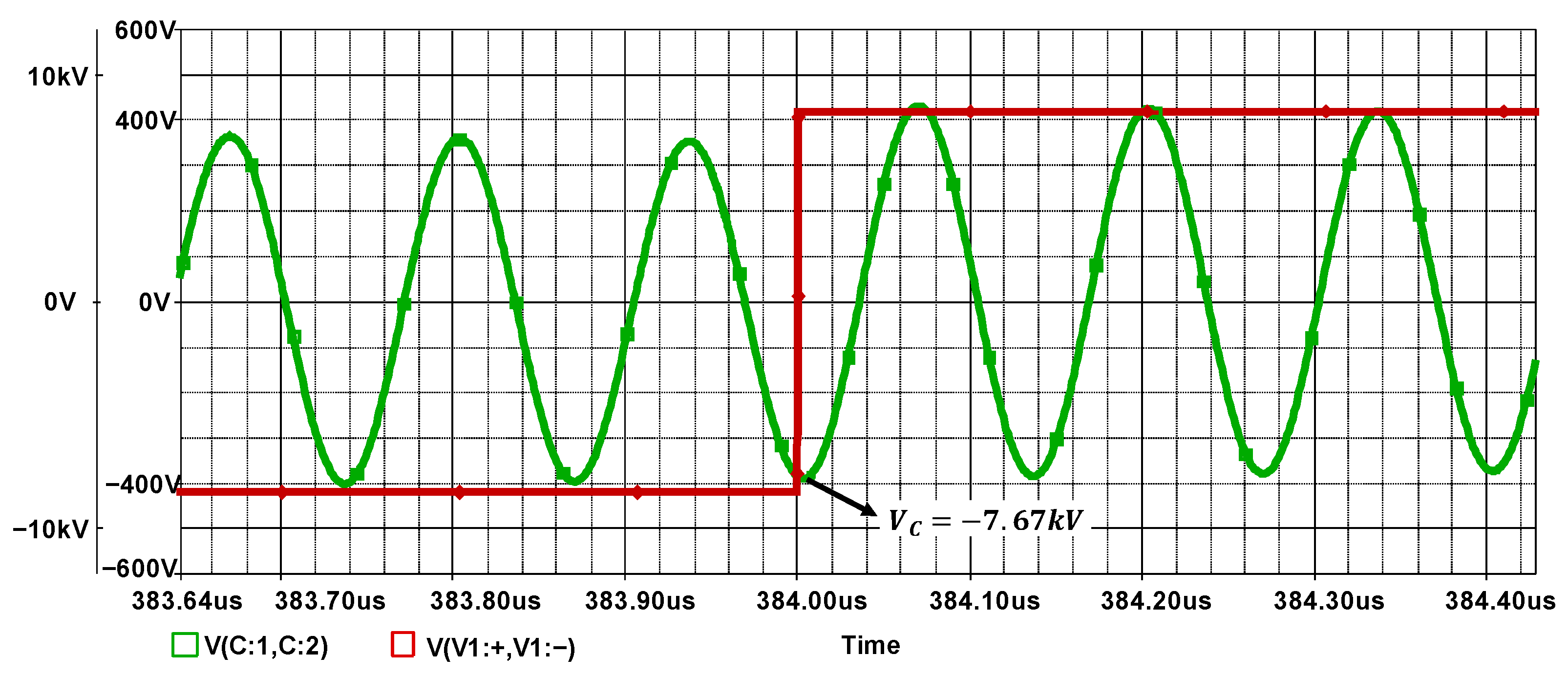

| Parameter | Description | Value |
|---|---|---|
| Po | Average output power | 30 Watts |
| Vout | RMS voltage at the load resistor | 25 Volts |
| fsw | Inverter switching frequency | 500 kHz |
| D | Duty cycle | 50% |
| n | Frequency multiplier | 15 |
| df | Damping factor | 0.9 |
| Parameter | Description | Equation | Value |
|---|---|---|---|
| RL | Load. | 21 Ω | |
| fo | Frequency of current in the resonant tank. | 7.5 MHz | |
| ωo | Angular frequency in the resonant tank. | 4.71 × 107 | |
| L | Inductor in the resonant tank. | 99.66 µH | |
| C | Capacitor in the resonant tank. | 4.52 pF | |
| a | Constant which defines the level of underdamping of the current in the resonant tank. | 447.26 | |
| Q | Quality factor. | 224 | |
| XC | Capacitive reactance. | 4696 Ω | |
| Codd | Constant that determines the voltage level in the resonant tank capacitor. | 18.99 | |
| b | Constant that determines the RMS current in the resonant tank. | 0.45 | |
| VDC | Input voltage. | 418 V | |
| Imax | Maximum current in the resonant tank | 1.78 A | |
| M | Gain of the circuit. | 0.060 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lara-Reyes, J.; Ponce-Silva, M.; Hernández-González, L.; DeLeón-Aldaco, S.E.; Cortés-García, C.; Ramirez-Hernandez, J. Series RLC Resonant Circuit Used as Frequency Multiplier. Energies 2022, 15, 9334. https://doi.org/10.3390/en15249334
Lara-Reyes J, Ponce-Silva M, Hernández-González L, DeLeón-Aldaco SE, Cortés-García C, Ramirez-Hernandez J. Series RLC Resonant Circuit Used as Frequency Multiplier. Energies. 2022; 15(24):9334. https://doi.org/10.3390/en15249334
Chicago/Turabian StyleLara-Reyes, Josué, Mario Ponce-Silva, Leobardo Hernández-González, Susana E. DeLeón-Aldaco, Claudia Cortés-García, and Jazmin Ramirez-Hernandez. 2022. "Series RLC Resonant Circuit Used as Frequency Multiplier" Energies 15, no. 24: 9334. https://doi.org/10.3390/en15249334
APA StyleLara-Reyes, J., Ponce-Silva, M., Hernández-González, L., DeLeón-Aldaco, S. E., Cortés-García, C., & Ramirez-Hernandez, J. (2022). Series RLC Resonant Circuit Used as Frequency Multiplier. Energies, 15(24), 9334. https://doi.org/10.3390/en15249334









