Modeling and Simulation of Silicon Solar Cells under Low Concentration Conditions
Abstract
1. Introduction
2. Model of Solar Cell
3. Extracting Parameters of Solar Cell
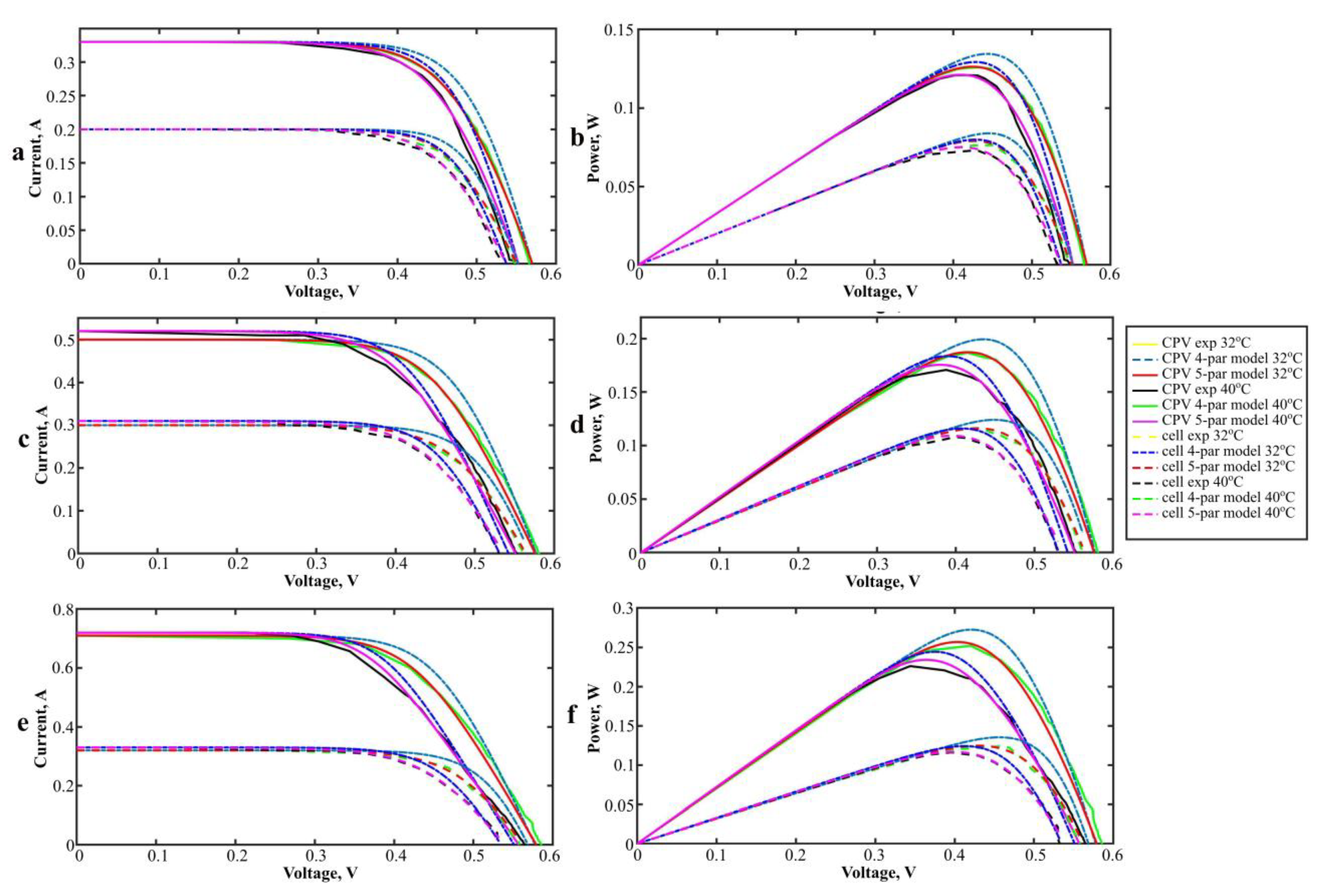
4. Modeling Silicon CPV Solar Cell Using Extracted Parameters
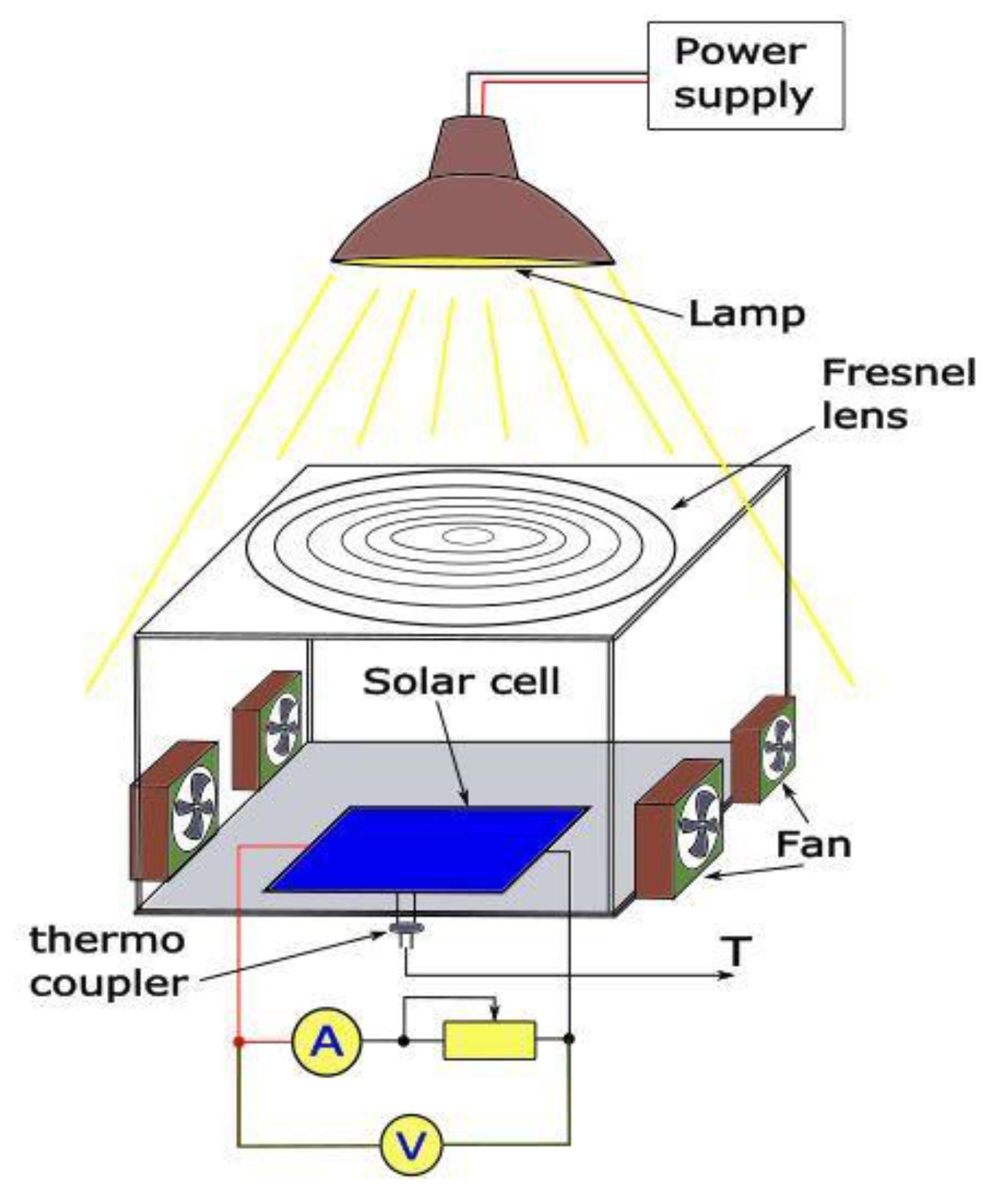
5. Silicon LCPV Cooling System
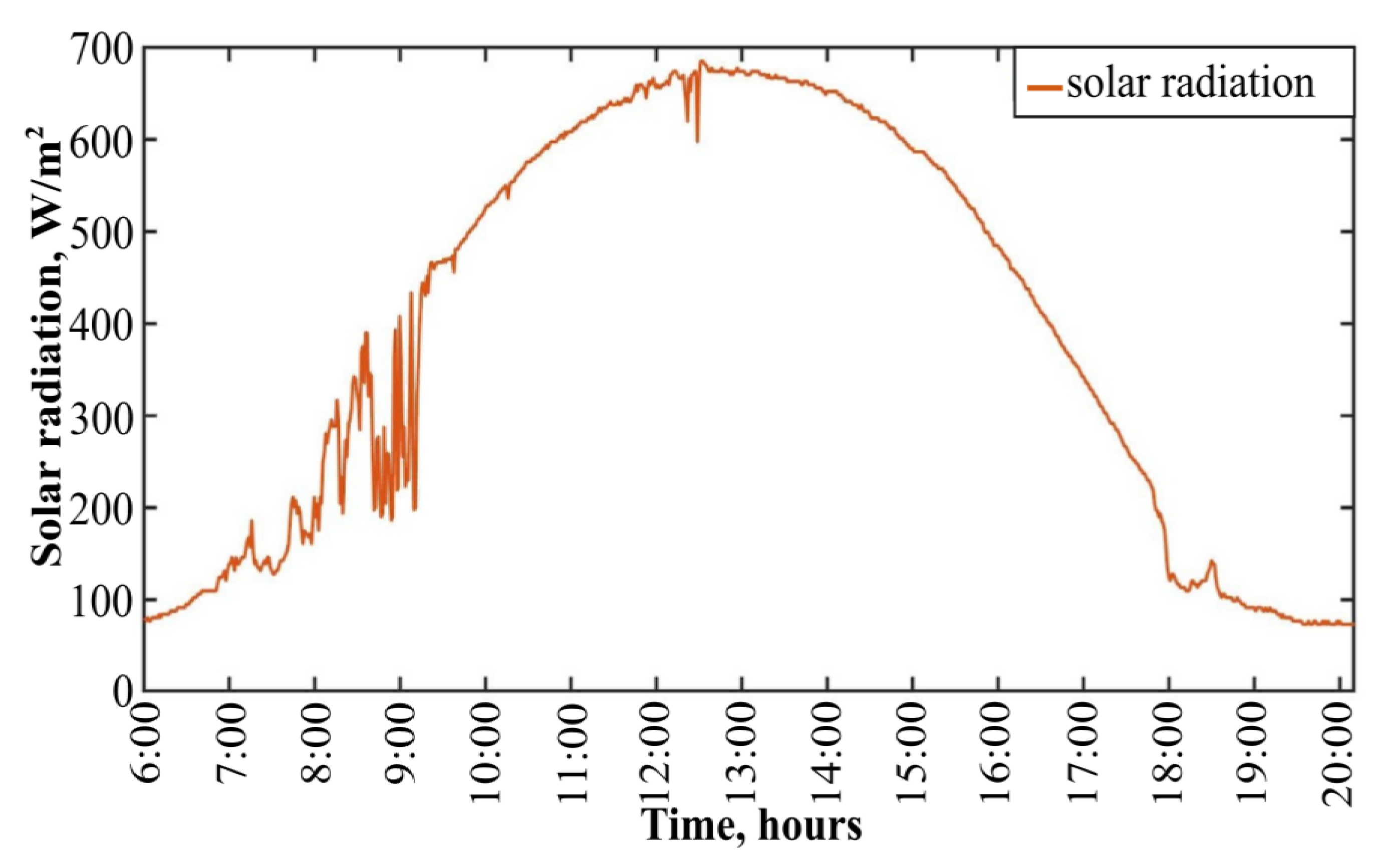
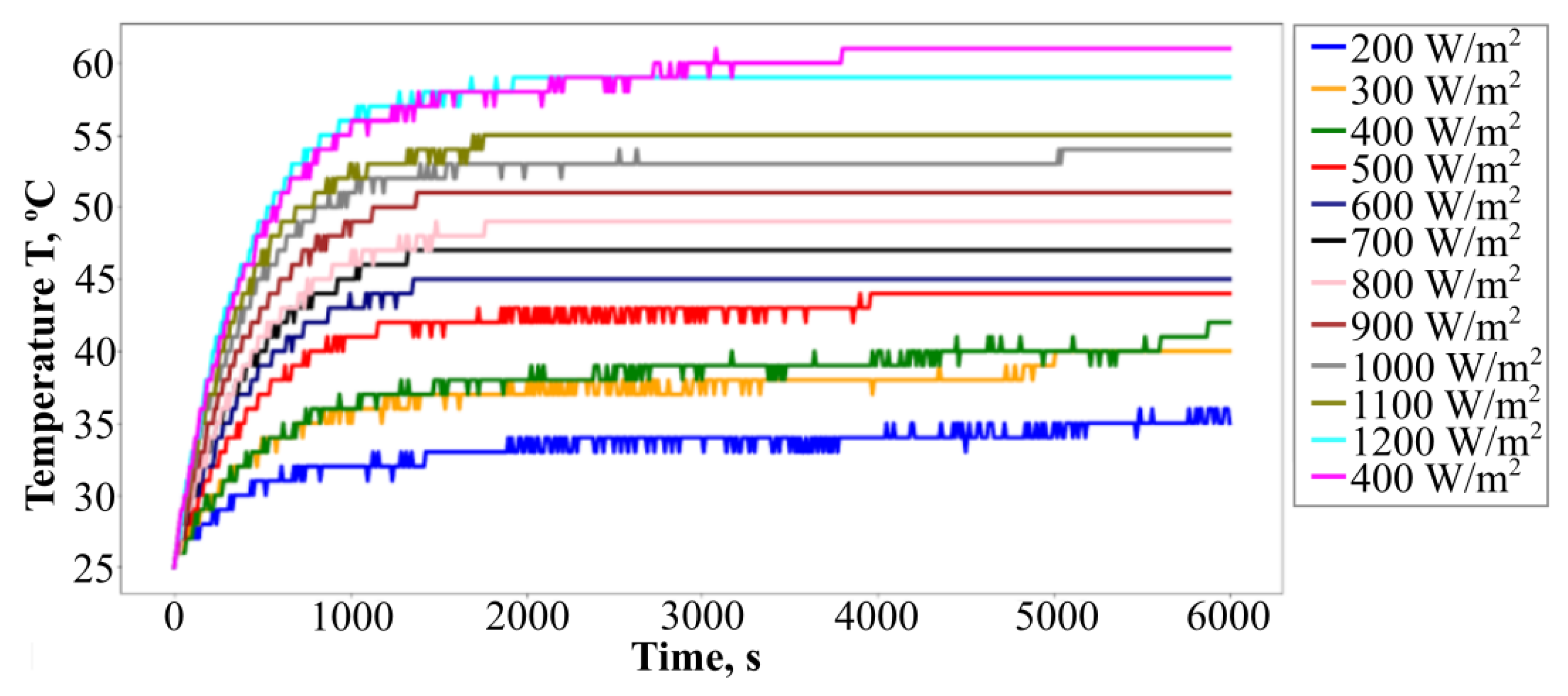
6. Results of Modeling Energy Generation and Temperature of Silicon LCPV Cell and Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Singh, R.; Kumar, S.; Gehlot, A.; Pachauri, R. An imperative role of sun trackers in photovoltaic technology: A review. Renew. Sustain. Energy Rev. 2018, 82, 3263–3278. [Google Scholar] [CrossRef]
- Kuttybay, N.; Saymbetov, A.; Mekhilef, S.; Nurgaliyev, M.; Tukymbekov, D.; Dosymbetova, G.; Svanbayev, Y. Optimized single-axis schedule solar tracker in different weather conditions. Energies 2020, 13, 5226. [Google Scholar] [CrossRef]
- Saymbetov, A.; Mekhilef, S.; Kuttybay, N.; Nurgaliyev, M.; Tukymbekov, D.; Meiirkhanov, A.; Svanbayev, Y. Dual-axis schedule tracker with an adaptive algorithm for a strong scattering of sunbeam. Sol. Energy 2021, 224, 285–297. [Google Scholar] [CrossRef]
- Sarvi, M.; Azadian, A. A comprehensive review and classified comparison of mppt algorithms in pv systems. Energy Syst. 2022, 13, 281–320. [Google Scholar] [CrossRef]
- Cristobal, A.; Vega, A.M.; López, A.L. (Eds.) Next Generation of Photovoltaics: New Concepts; Springer: Berlin/Heidelberg, Germany, 2012; Volume 165. [Google Scholar]
- Shanks, K.; Baig, H.; Singh, N.P.; Senthilarasu, S.; Reddy, K.S.; Mallick, T.K. Prototype fabrication and experimental investigation of a conjugate refractive reflective homogeniser in a cassegrain concentrator. Sol. Energy 2017, 142, 97–108. [Google Scholar] [CrossRef]
- Vossier, A.; Chemisana, D.; Flamant, G.; Dollet, A. Very high fluxes for concentrating photovoltaics: Considerations from simple experiments and modeling. Renew. Energy 2012, 38, 31–39. [Google Scholar] [CrossRef]
- Khamooshi, M.; Salati, H.; Egelioglu, F.; Hooshyar Faghiri, A.; Tarabishi, J.; Babadi, S. A review of solar photovoltaic concentrators. Int. J. Photoenergy 2014, 2014, 958521. [Google Scholar] [CrossRef]
- Wu, Y.; Eames, P.; Mallick, T.; Sabry, M. Experimental characterisation of a Fresnel lens photovoltaic concentrating system. Sol. Energy 2012, 86, 430–440. [Google Scholar] [CrossRef]
- Kumar, V.; Shrivastava, R.L.; Untawale, S.P. Fresnel lens: A promising alternative of reflectors in concentrated solar power. Renew. Sustain. Energy Rev. 2015, 44, 376–390. [Google Scholar] [CrossRef]
- Shanks, K.; Senthilarasu, S.; Mallick, T.K. Optics for concentrating photovoltaics: Trends, limits and opportunities for materials and design. Renew. Sustain. Energy Rev. 2016, 60, 394–407. [Google Scholar] [CrossRef]
- Jing, L.; Liu, H.; Wang, Y.; Xu, W.; Zhang, H.; Lu, Z. Design and optimization of Fresnel lens for high concentration photovoltaic system. Int. J. Photoenergy 2014, 2014, 539891. [Google Scholar] [CrossRef]
- Renno, C.; Petito, F.; Landi, G.; Neitzert, H.C. Experimental characterization of a concentrating photovoltaic system varying the light concentration. Energy Convers. Manag. 2017, 138, 119–130. [Google Scholar] [CrossRef]
- Shanks, K.; Ferrer-Rodriguez, J.P.; Fernández, E.F.; Almonacid, F.; Pérez-Higueras, P.; Senthilarasu, S.; Mallick, T. A> 3000 suns high concentrator photovoltaic design based on multiple Fresnel lens primaries focusing to one central solar cell. Sol. Energy 2018, 169, 457–467. [Google Scholar] [CrossRef]
- Chemisana, D. Building integrated concentrating photovoltaics: A review. Renew. Sustain. Energy Rev. 2011, 15, 603–611. [Google Scholar] [CrossRef]
- Xu, N.; Ji, J.; Sun, W.; Huang, W.; Li, J.; Jin, Z. Numerical simulation and experimental validation of a high concentration photovoltaic/thermal module based on point-focus Fresnel lens. Appl. Energy 2016, 168, 269–281. [Google Scholar] [CrossRef]
- Ghassan, Z.; Bernal-Agustín, J.L.; Fracastoro, G.V. High concentration photovoltaic systems applying III–V cells. Renew. Sustain. Energy Rev. 2009, 13, 2645–2652. [Google Scholar]
- Miller, N.; Patel, P.; Struempel, C.; Kerestes, C.; Aiken, D.; Sharps, P. Terrestrial concentrator four-junction inverted metamorphic solar cells with efficiency> 45%. In Proceedings of the 2014 IEEE 40th Photovoltaic Specialist Conference (PVSC), IEEE, Denver, CO, USA, 8–13 June 2014. [Google Scholar]
- Hornung, T.; Steiner, M.; Nitz, P. Estimation of the influence of Fresnel lens temperature on energy generation of a concentrator photovoltaic system. Sol. Energy Mater. Sol. Cells 2012, 99, 333–338. [Google Scholar] [CrossRef]
- Guter, W.; Schöne, J.; Philipps, S.P.; Steiner, M.; Siefer, G.; Wekkeli, A.; Welser, E.; Oliva, E.; Bett, A.W.; Dimroth, F. Current-matched triple-junction solar cell reaching 41.1% conversion efficiency under concentrated sunlight. Appl. Phys. Lett. 2009, 94, 223504. [Google Scholar] [CrossRef]
- Li, D.; Xuan, Y.; Yin, E.; Li, Q. Conversion efficiency gain for concentrated triple-junction solar cell system through thermal management. Renew. Energy 2018, 126, 960–968. [Google Scholar] [CrossRef]
- Karimi, F.; Xu, H.; Wang, Z.; Chen, J.; Yang, M. Experimental study of a concentrated PV/T system using linear Fresnel lens. Energy 2017, 123, 402–412. [Google Scholar] [CrossRef]
- Du, B.; Hu, E.; Kolhe, M. Performance analysis of water cooled concentrated photovoltaic (CPV) system. Renew. Sustain. Energy Rev. 2012, 16, 6732–6736. [Google Scholar] [CrossRef]
- Chemisana, D.; Ibáñez, M.; Rosell, J.I. Characterization of a photovoltaic-thermal module for Fresnel linear concentrator. Energy Convers. Manag. 2011, 52, 3234–3240. [Google Scholar] [CrossRef]
- Campbell, P.; Green, M.A. The limiting efficiency of silicon solar cells under concentrated sunlight. IEEE Trans. Electron Devices 1986, 33, 234–239. [Google Scholar] [CrossRef]
- Xing, Y.; Han, P.; Wang, S.; Liang, P.; Lou, S.; Zhang, Y.; Hu, S.; Zhu, H.; Zhao, C.; Mi, Y. A review of concentrator silicon solar cells. Renew. Sustain. Energy Rev. 2015, 51, 1697–1708. [Google Scholar] [CrossRef]
- Levi, D.H.; Green, M.A.; Hishikawa, Y.; Dunlop, E.D.; Hohl-Ebinger, J.; Ho-Baillie, A.W. Solar cell efficiency tables (version 51). Prog. Photovolt. 2017, 26, 1062–7995. [Google Scholar]
- Boumaaraf, H.; Talha, A.; Saidi, N.; Habireche, A. Experimental study of low-concentrator photovoltaic systems: Electrical and thermal. Electr. Eng. 2018, 100, 2569–2578. [Google Scholar] [CrossRef]
- Burhan, M.; Oh, S.J.; Chua, K.J.E.; Ng, K.C. Double lens collimator solar feedback sensor and master slave configuration: Development of compact and low cost two axis solar tracking system for CPV applications. Sol. Energy 2016, 137, 352–363. [Google Scholar] [CrossRef]
- Zsiborács, H.; Baranyai, N.H.; Vincze, A.; Weihs, P.; Schreier, S.F.; Gützer, C.; Pintér, G. The Impacts of Tracking System Inaccuracy on CPV Module Power. Processes 2020, 8, 1278. [Google Scholar] [CrossRef]
- Humada, A.M.; Hojabri, M.; Mekhilef, S.; Hamada, H.M. Solar cell parameters extraction based on single and double-diode models: A review. Renew. Sustain. Energy Rev. 2016, 56, 494–509. [Google Scholar] [CrossRef]
- Celik, A.N.; Acikgoz, N. Modelling and experimental verification of the operating current of mono-crystalline photovoltaic modules using four-and five-parameter models. Appl. Energy 2007, 84, 1–15. [Google Scholar] [CrossRef]
- Chan, D.S.H.; Phillips, J.R.; Phang, J.C.H. A comparative study of extraction methods for solar cell model parameters. Solid-State Electron. 1986, 29, 329–337. [Google Scholar] [CrossRef]
- Xiao, W.; Dunford, W.G.; Capel, A. A novel modeling method for photovoltaic cells. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No. 04CH37551), IEEE, Aachen, Germany, 20–25 June 2004; Volume 3. [Google Scholar]
- Ma, T.; Gu, W.; Shen, L.; Li, M. An improved and comprehensive mathematical model for solar photovoltaic modules under real operating conditions. Sol. Energy 2019, 184, 292–304. [Google Scholar] [CrossRef]
- Brano, V.L.; Orioli, A.; Ciulla, G.; Di Gangi, A. An improved five-parameter model for photovoltaic modules. Sol. Energy Mater. Sol. Cells 2010, 94, 1358–1370. [Google Scholar] [CrossRef]
- Brano, V.L.; Ciulla, G. An efficient analytical approach for obtaining a five parameters model of photovoltaic modules using only reference data. Appl. Energy 2013, 111, 894–903. [Google Scholar] [CrossRef]
- Haouari-Merbah, M.; Belhamel, M.; Tobias, I.; Ruiz, J. Extraction and analysis of solar cell parameters from the illuminated current–voltage curve. Sol. Energy Mater. Sol. Cells 2005, 87, 225–233. [Google Scholar] [CrossRef]
- Tivanov, M.; Patryn, A.; Drozdov, N.; Fedotov, A.; Mazanik, A. Determination of solar cell parameters from its current–voltage and spectral characteristics. Sol. Energy Mater. Sol. Cells 2005, 87, 457–465. [Google Scholar] [CrossRef]
- Chegaar, M.; Azzouzi, G.; Mialhe, P. Simple parameter extraction method for illuminated solar cells. Solid-State Electron. 2006, 50, 1234–1237. [Google Scholar] [CrossRef]
- Khan, F.; Baek, S.-H.; Kim, J.H. Intensity dependency of photovoltaic cell parameters under high illumination conditions: An analysis. Appl. Energy 2014, 133, 356–362. [Google Scholar] [CrossRef]
- Kaminski, A.; Marchand, J.; Laugier, A. I–V methods to extract junction parameters with special emphasis on low series resistance. Solid-State Electron. 1999, 43, 741–745. [Google Scholar] [CrossRef]
- Khan, F.; Baek, S.H.; Park, Y.; Kim, J.H. Extraction of diode parameters of silicon solar cells under high illumination conditions. Energy Convers. Manag. 2013, 76, 421–429. [Google Scholar] [CrossRef]
- Renno, C.; Perone, A. Experimental modeling of the optical and energy performances of a point-focus CPV system applied to a residential user. Energy 2021, 215, 119156. [Google Scholar] [CrossRef]










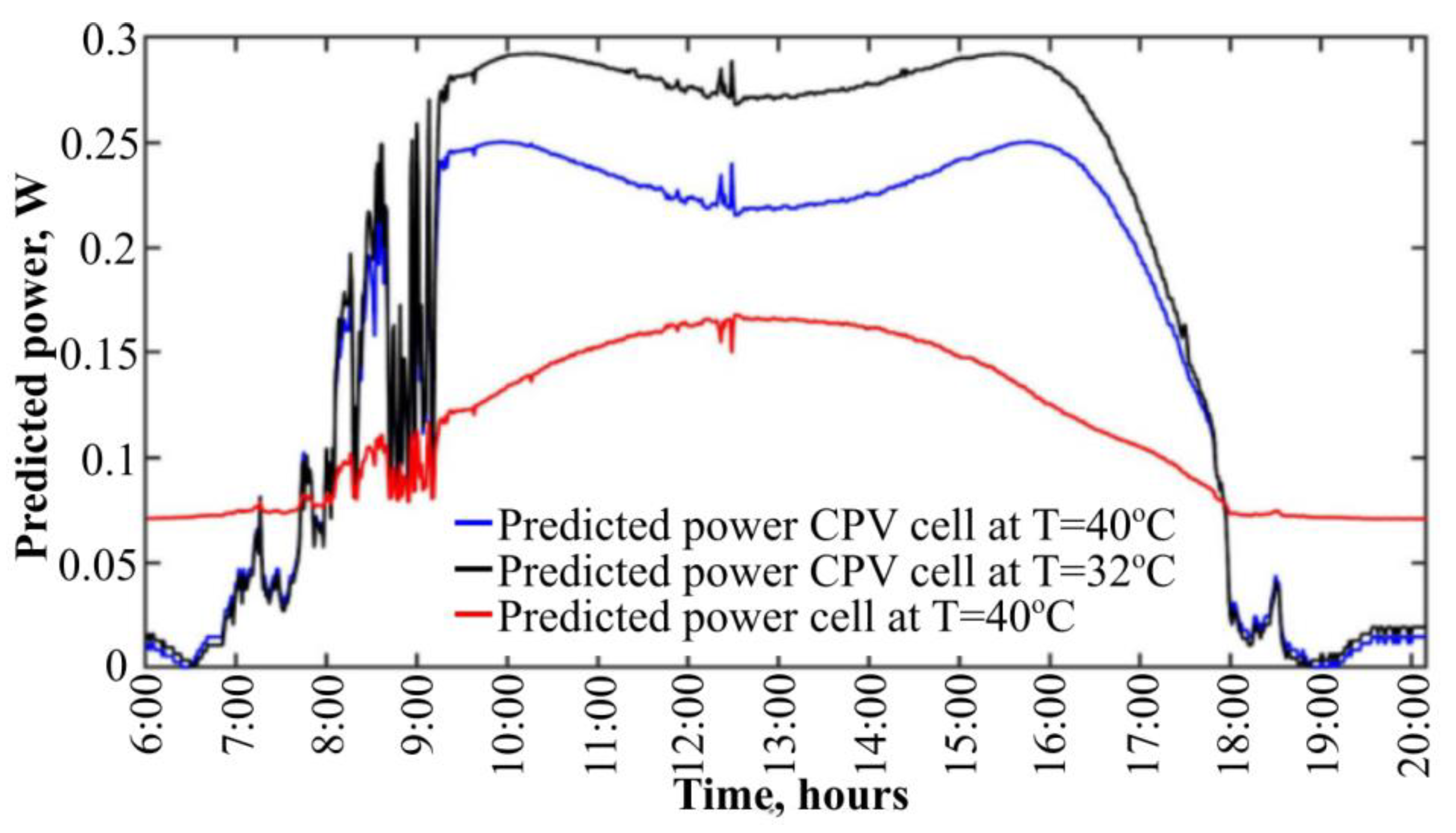


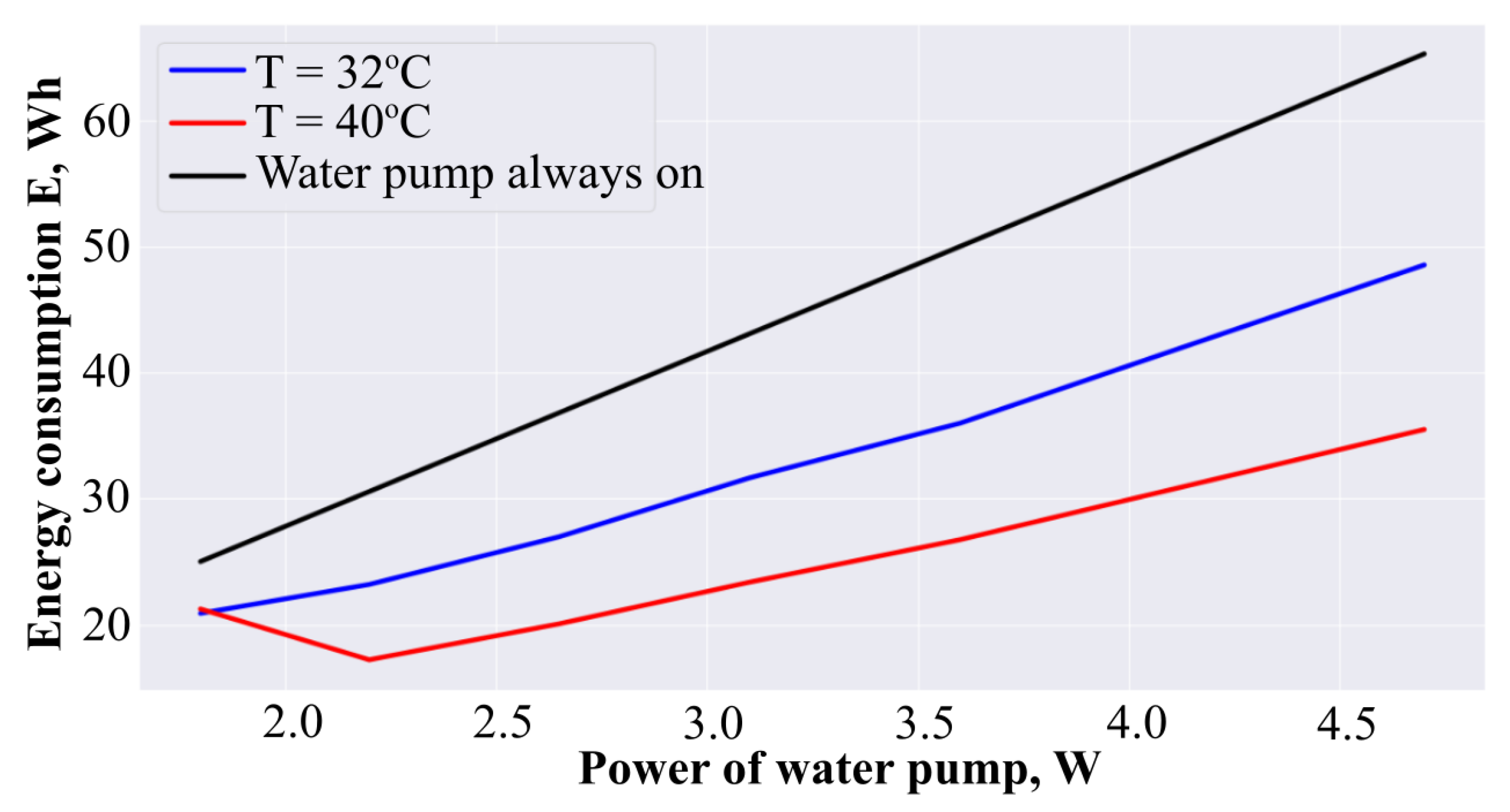
| MAE | MSE | RMSE | |
|---|---|---|---|
| 0.125 | 0.0879 | 0.2965 | 0.99896 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dosymbetova, G.; Mekhilef, S.; Saymbetov, A.; Nurgaliyev, M.; Kapparova, A.; Manakov, S.; Orynbassar, S.; Kuttybay, N.; Svanbayev, Y.; Yuldoshev, I.; et al. Modeling and Simulation of Silicon Solar Cells under Low Concentration Conditions. Energies 2022, 15, 9404. https://doi.org/10.3390/en15249404
Dosymbetova G, Mekhilef S, Saymbetov A, Nurgaliyev M, Kapparova A, Manakov S, Orynbassar S, Kuttybay N, Svanbayev Y, Yuldoshev I, et al. Modeling and Simulation of Silicon Solar Cells under Low Concentration Conditions. Energies. 2022; 15(24):9404. https://doi.org/10.3390/en15249404
Chicago/Turabian StyleDosymbetova, Gulbakhar, Saad Mekhilef, Ahmet Saymbetov, Madiyar Nurgaliyev, Ainur Kapparova, Sergey Manakov, Sayat Orynbassar, Nurzhigit Kuttybay, Yeldos Svanbayev, Isroil Yuldoshev, and et al. 2022. "Modeling and Simulation of Silicon Solar Cells under Low Concentration Conditions" Energies 15, no. 24: 9404. https://doi.org/10.3390/en15249404
APA StyleDosymbetova, G., Mekhilef, S., Saymbetov, A., Nurgaliyev, M., Kapparova, A., Manakov, S., Orynbassar, S., Kuttybay, N., Svanbayev, Y., Yuldoshev, I., Zholamanov, B., & Koshkarbay, N. (2022). Modeling and Simulation of Silicon Solar Cells under Low Concentration Conditions. Energies, 15(24), 9404. https://doi.org/10.3390/en15249404







