Energy Losses Related to Ring Pack Wear in Gasoline Car Engine
Abstract
:1. Introduction
2. Object and Methods
2.1. Tested Engine
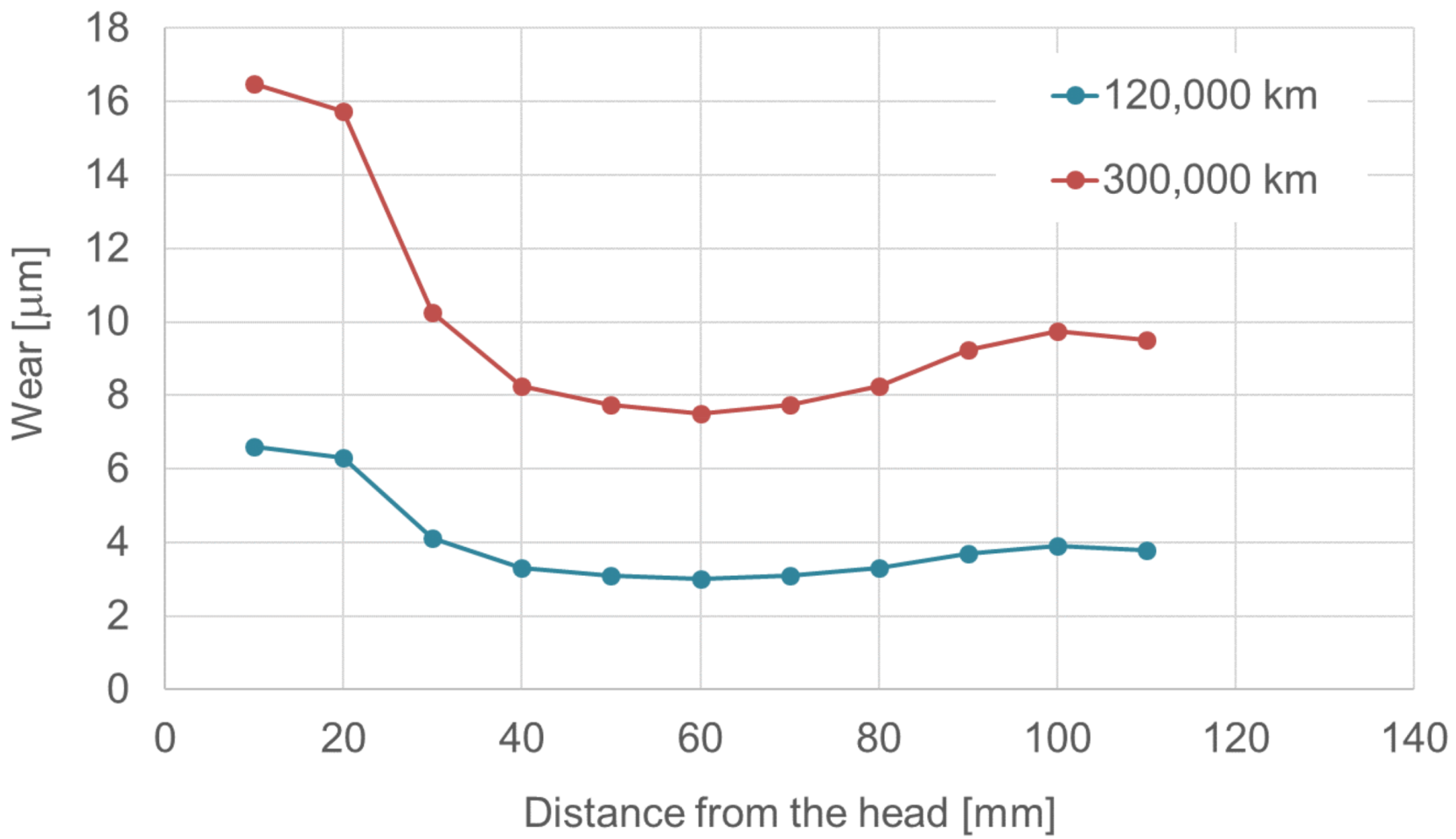
2.2. Determination of Wear
2.3. Dynamometer Tests
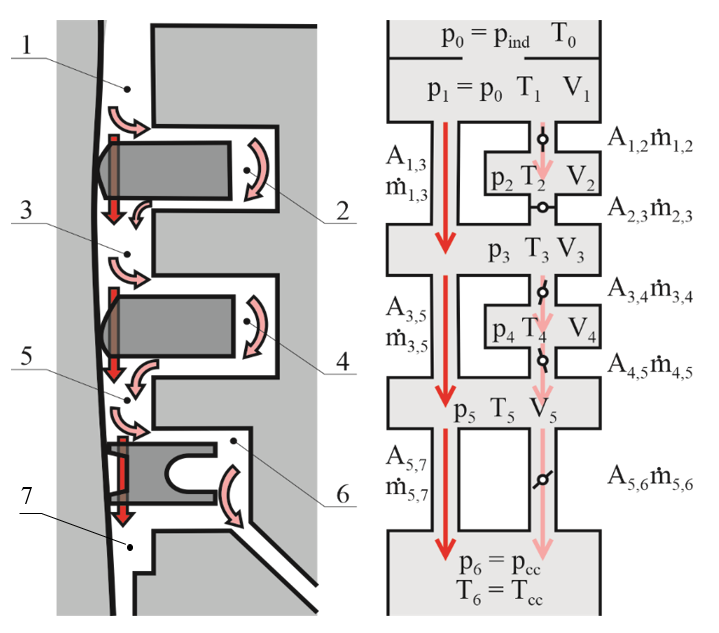
2.4. Model of the Ring-Pack
2.4.1. Model of Gas Flow
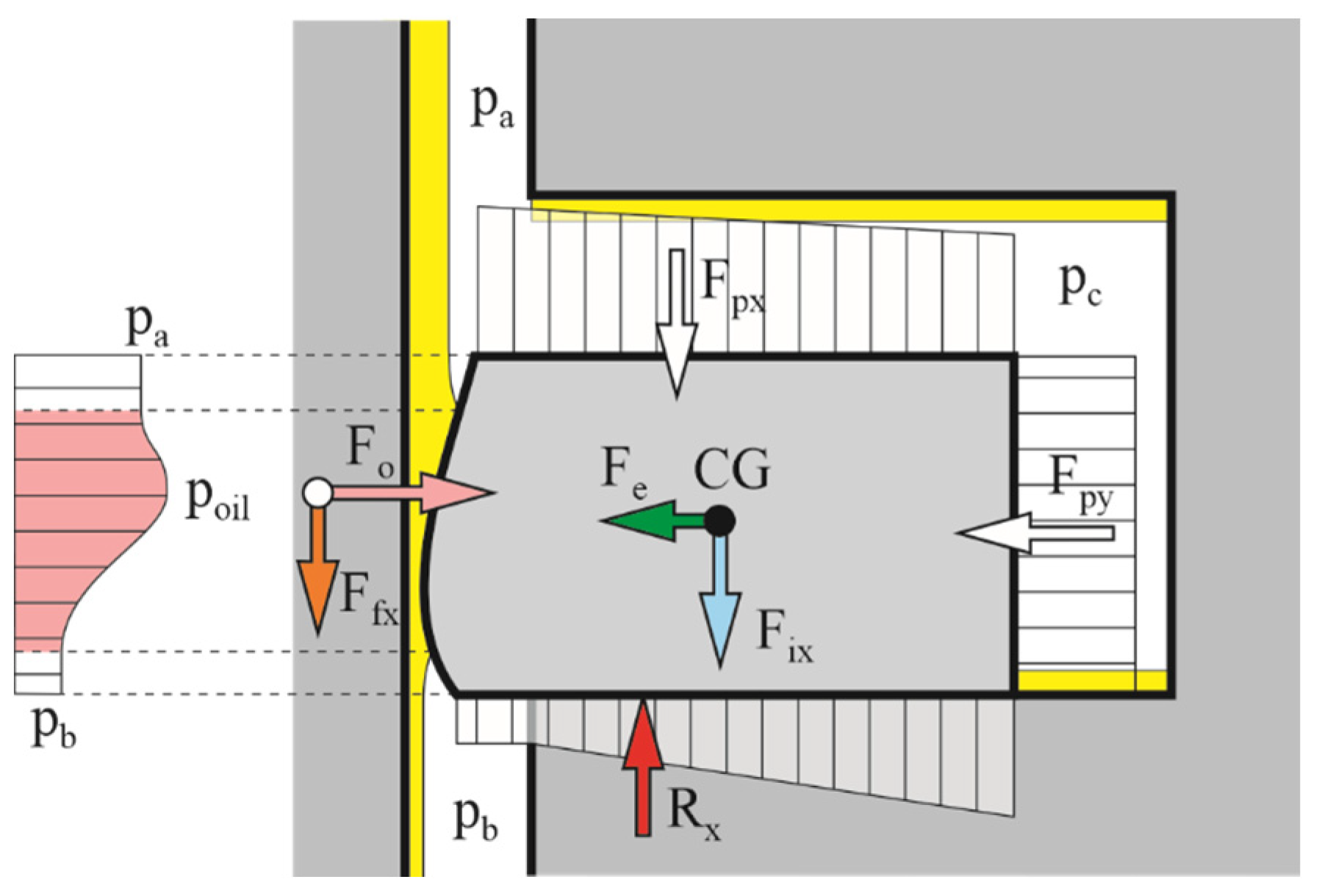
2.4.2. Model of the Ring Movements
2.4.3. Model of Oil Film
2.5. Simulations
2.6. Evaluation of Energy Losses Due to Blow-by and Ring Friction
3. Results and Discussion
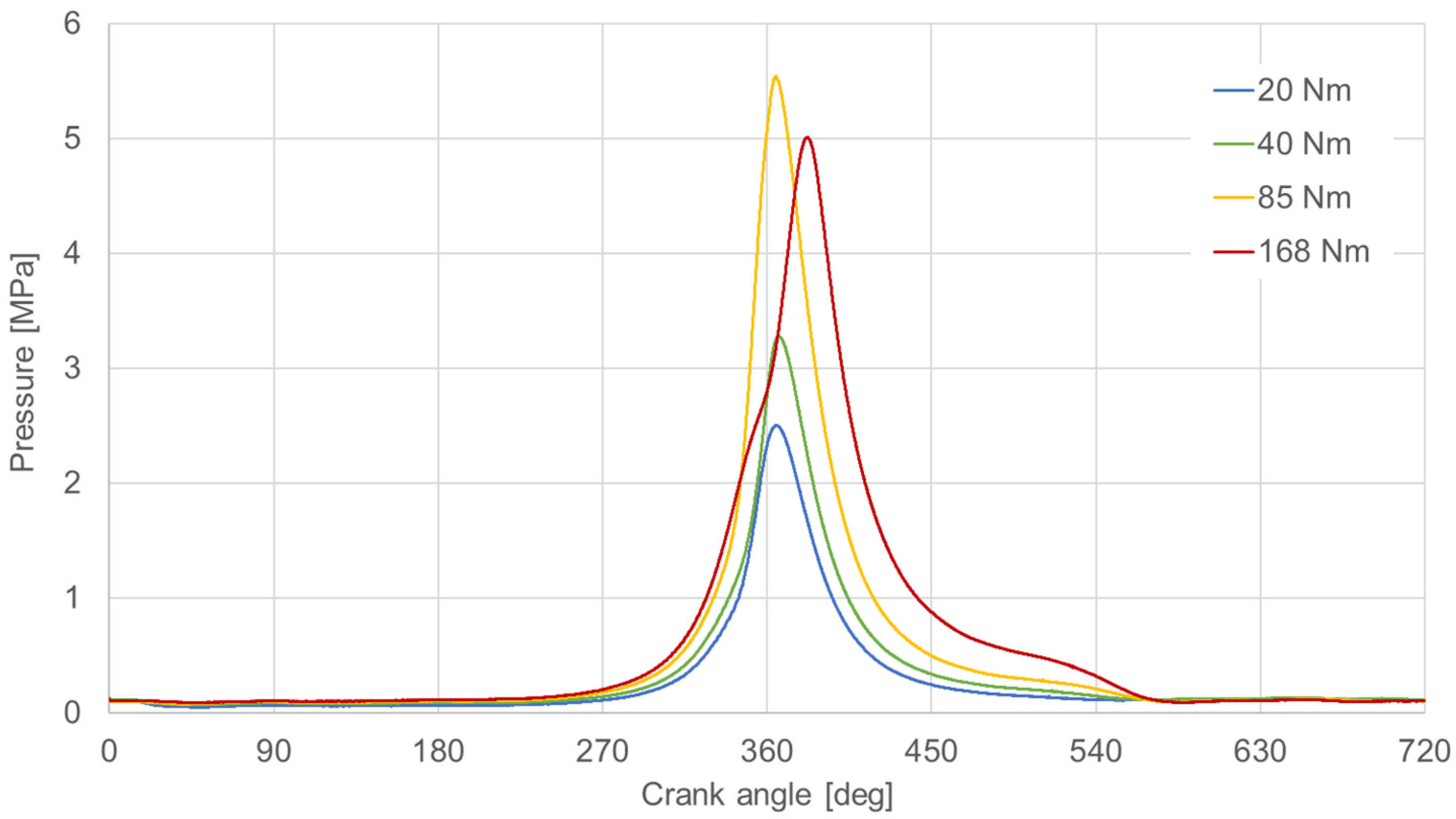
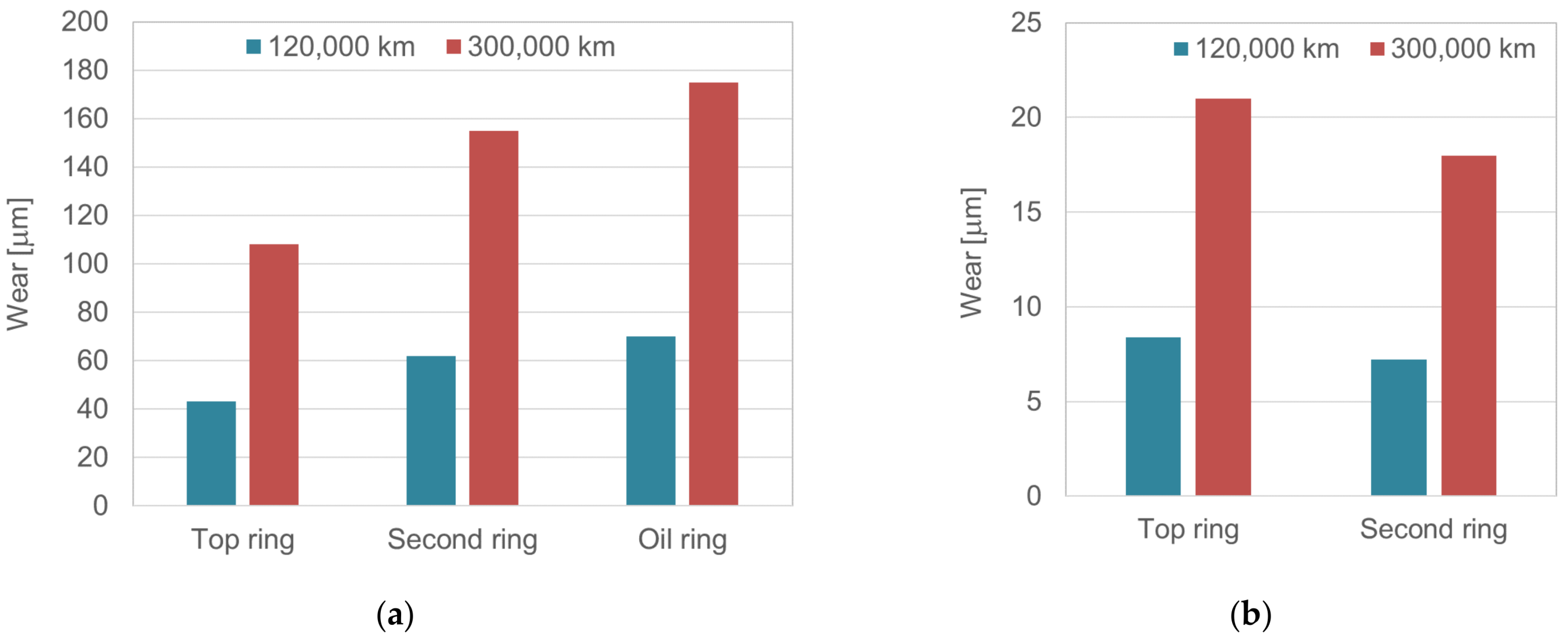
3.1. Indicated Pressure and Wear
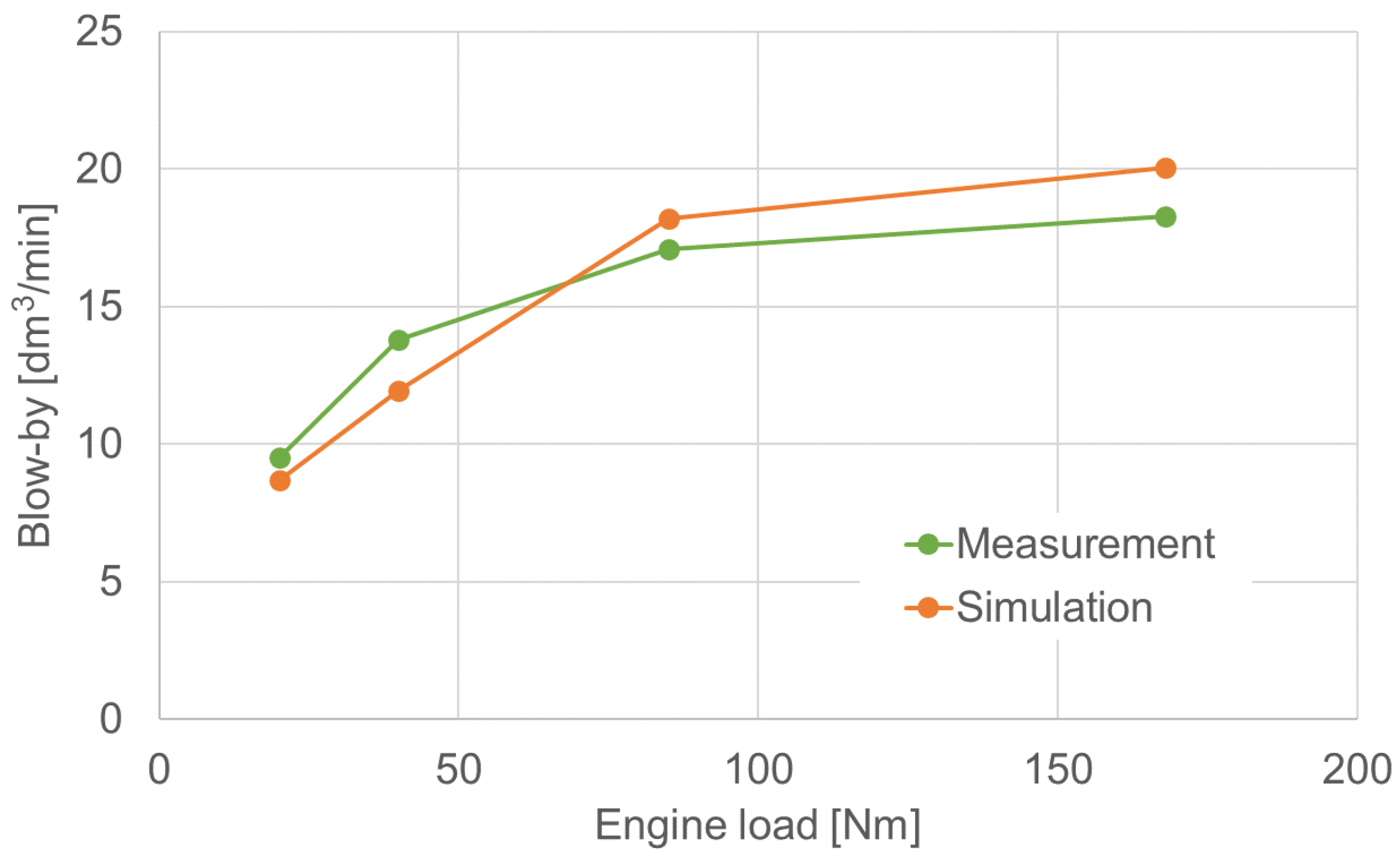
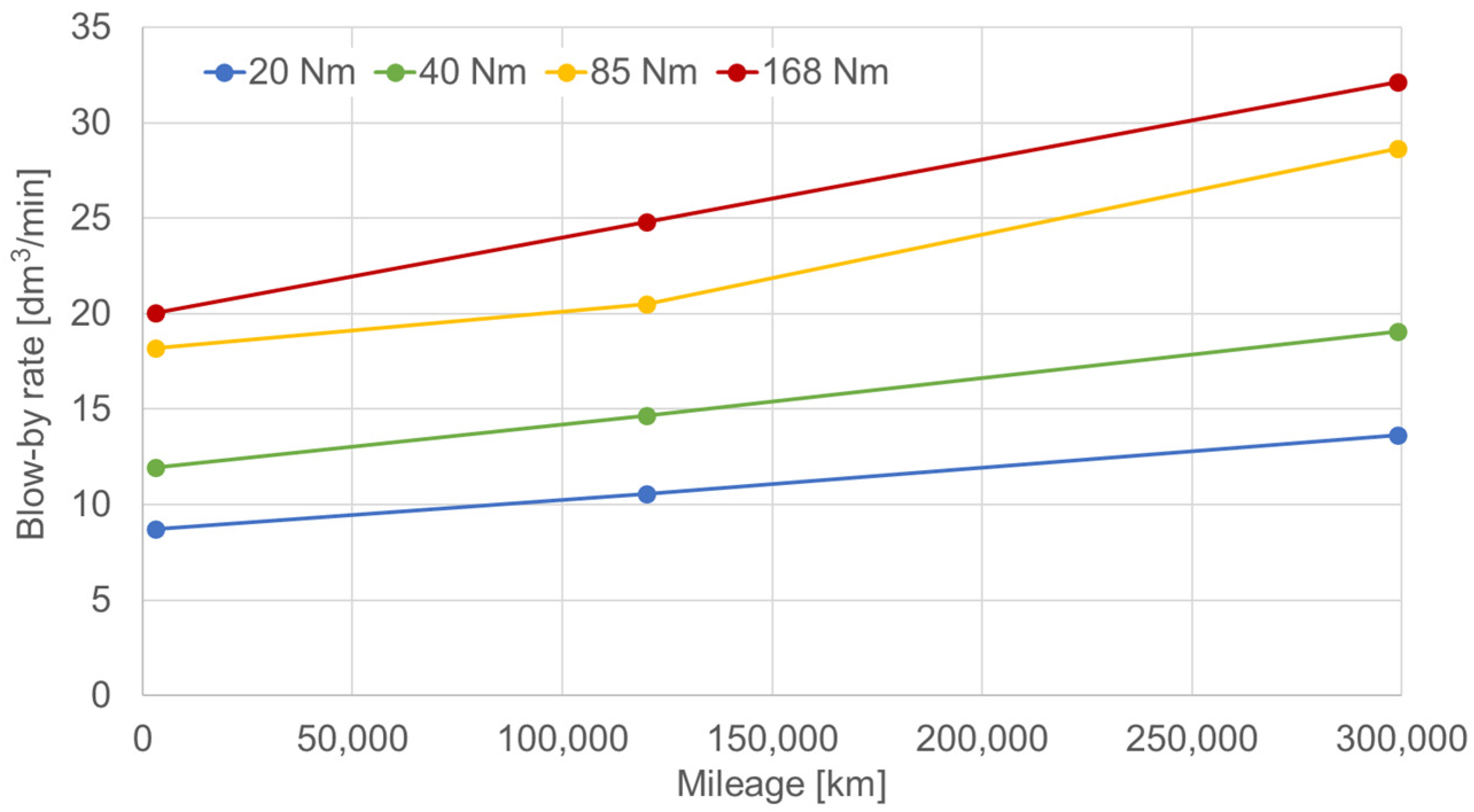
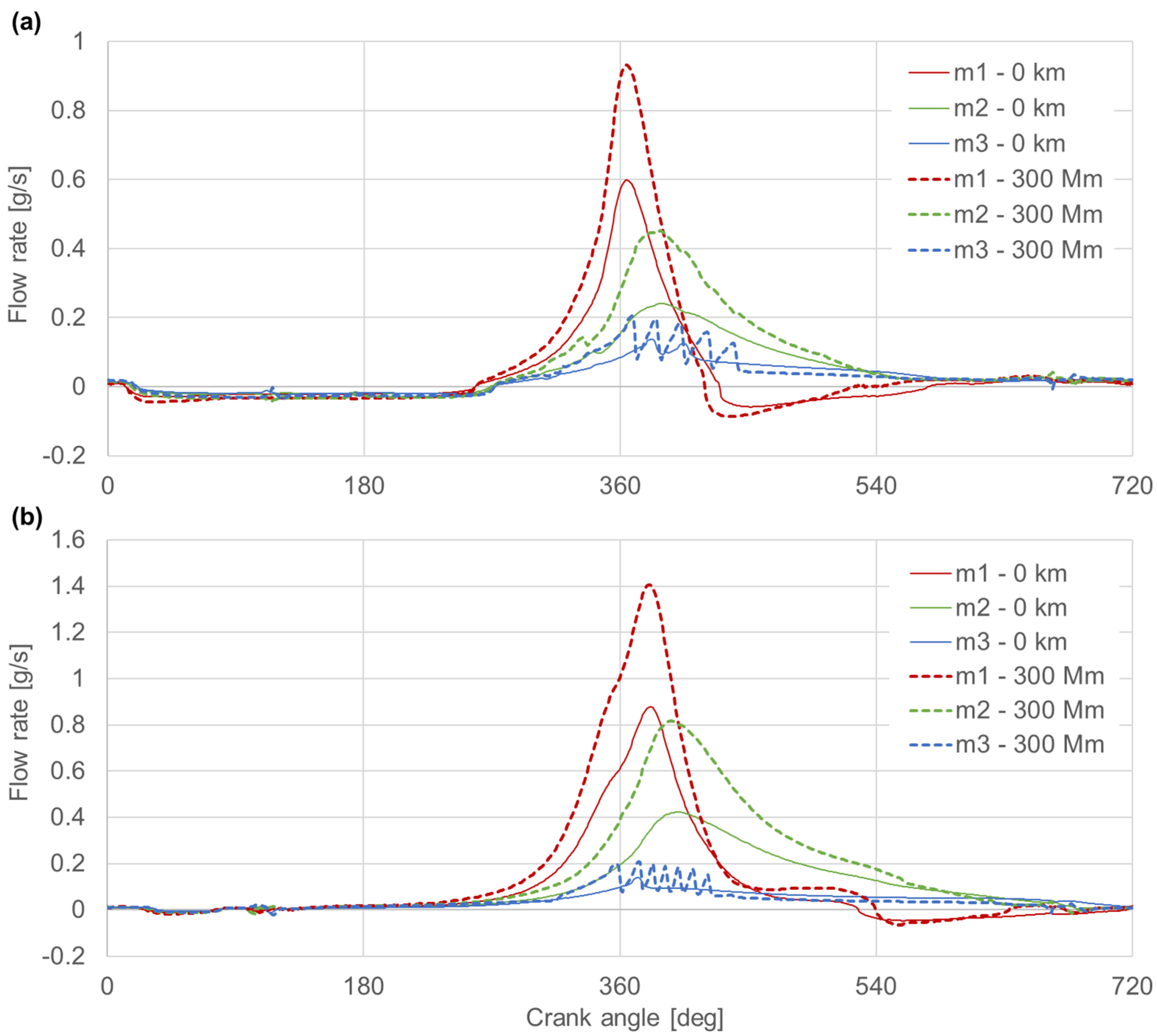
3.2. Blow-by Rate
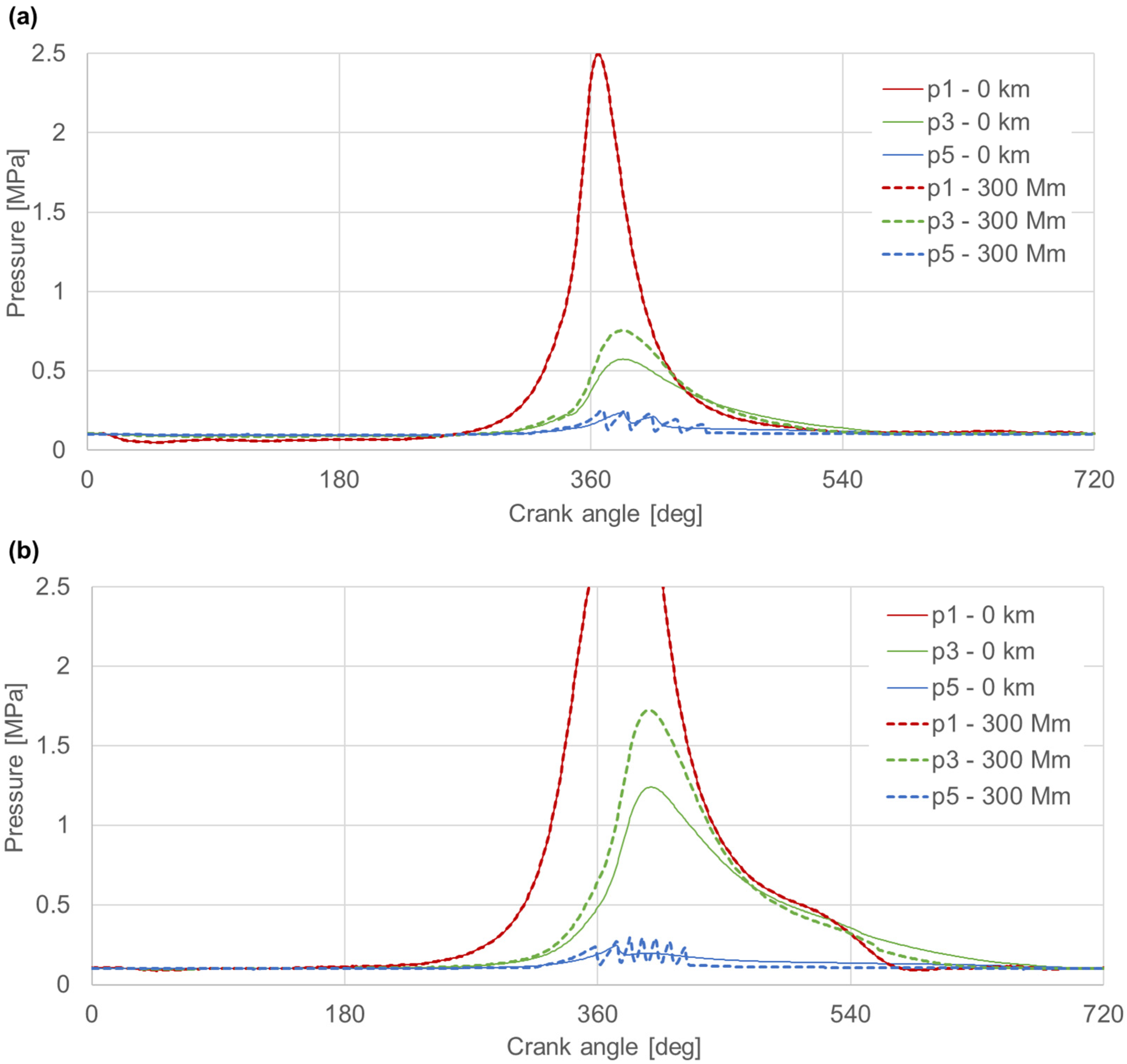
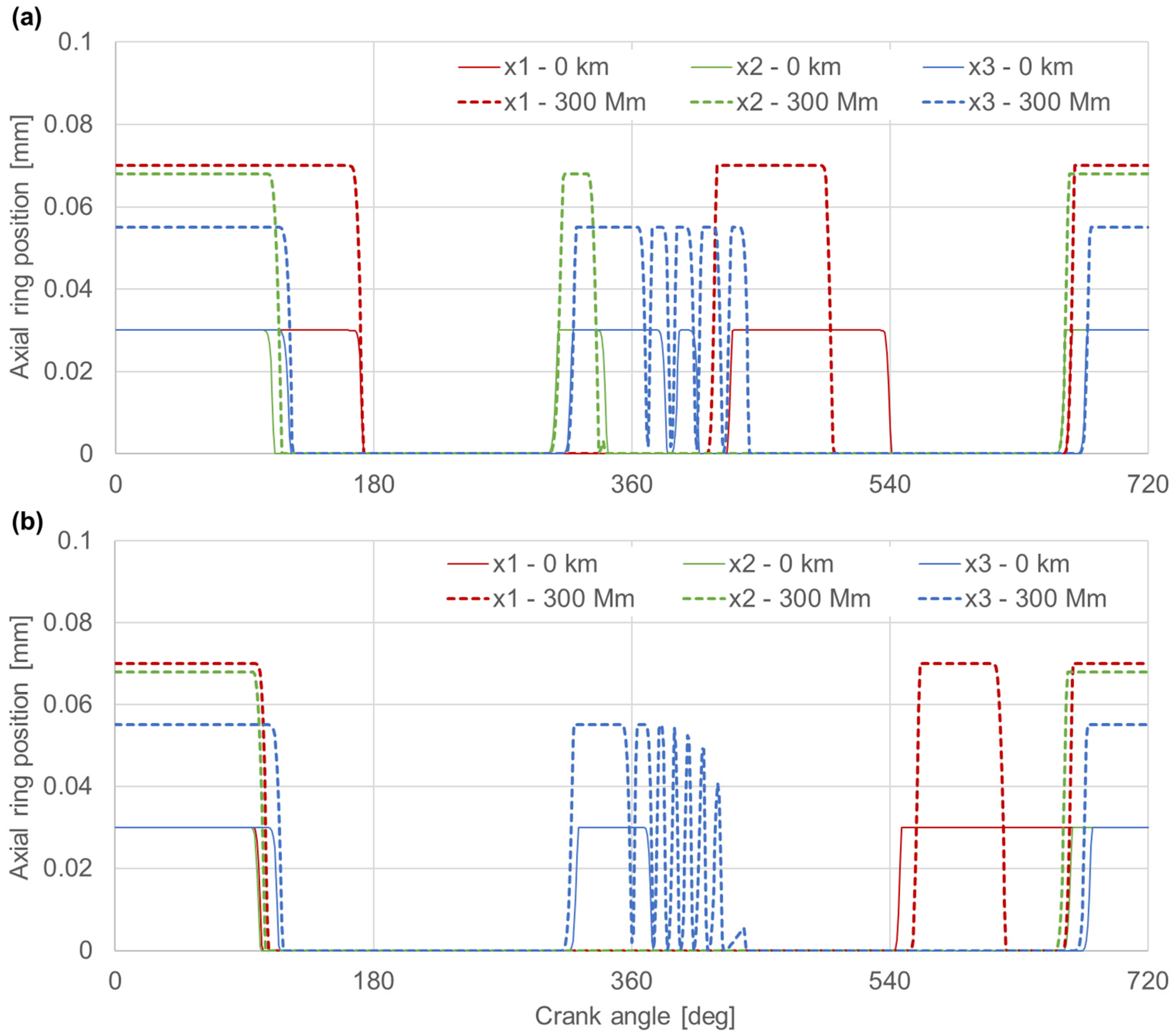
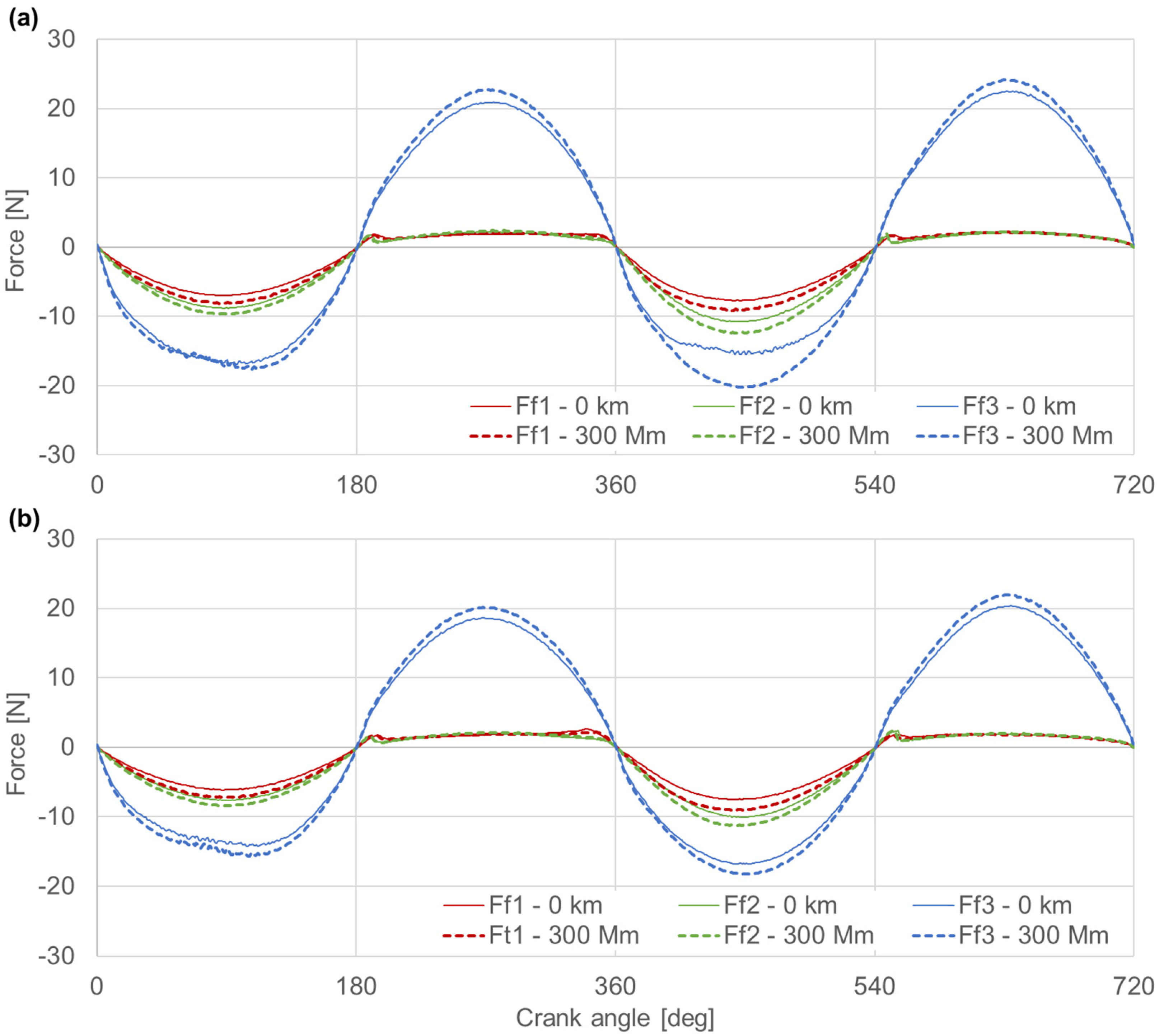
3.3. Instantaneous Values of Parameters Associated with the Work of the Ring Pack
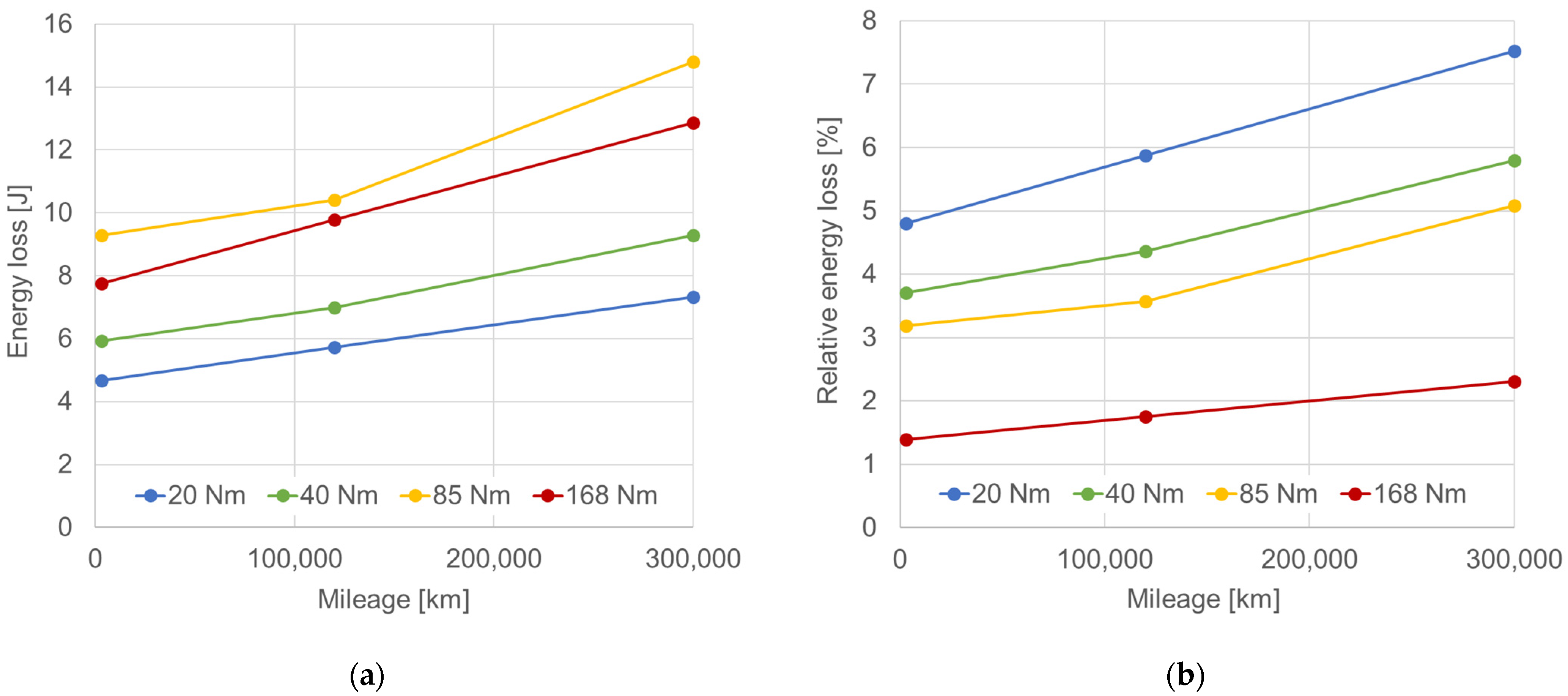
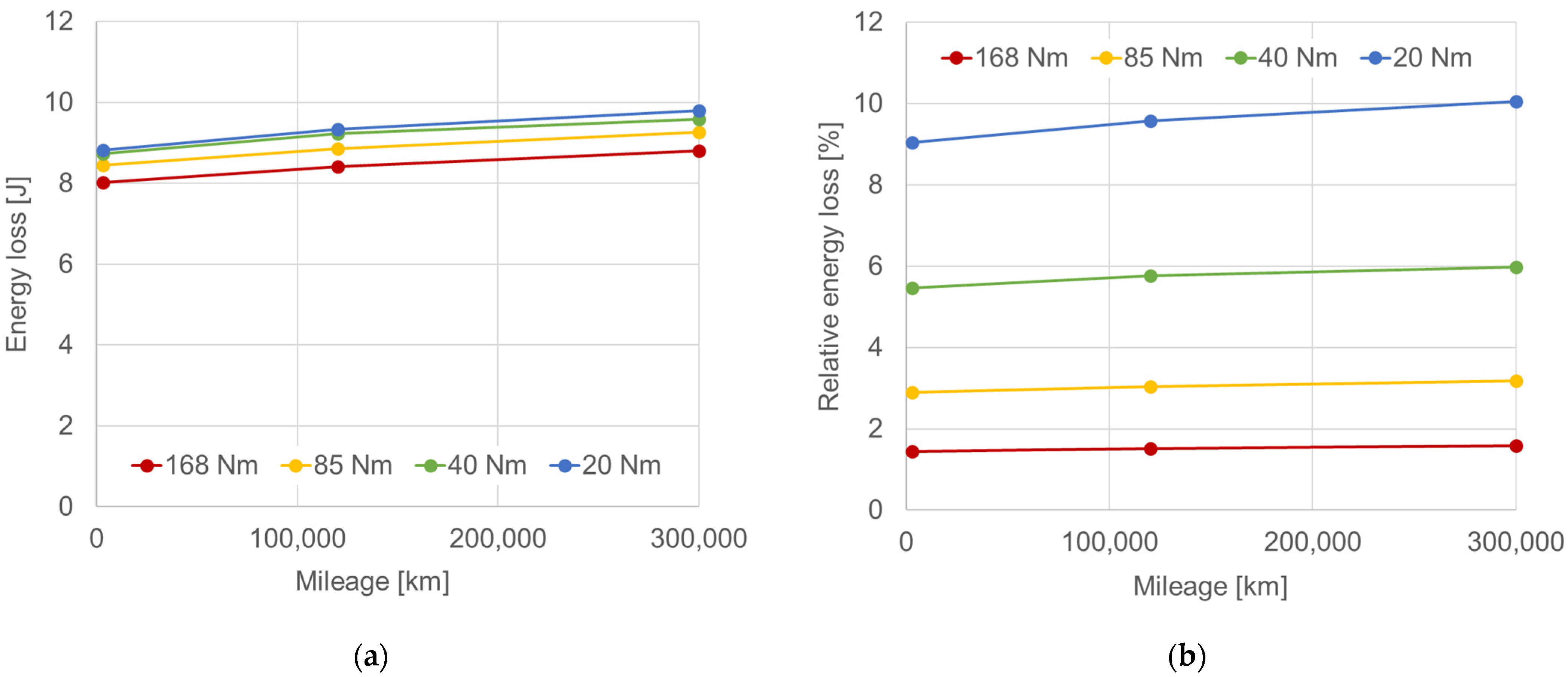
3.4. Effect of Wear on Energy Losses
4. Conclusions
- The energy losses due to blow-by are comparable to those due to friction of the rings, especially at low and medium engine loads;
- Engine wear significantly affects the blow-by related energy losses, but has little effect on friction losses;
- After a mileage of 300,000 km, the total share of both blow-by and friction losses in indicated work is higher than in the unworn engine from 1% at a high load to 4% at a low load. This will translate into the same increase in fuel consumption.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kalghatgi, G. Is It the End of Combustion and Engine Combustion Research? Should It Be? Transp. Eng. 2022, 10, 100142. [Google Scholar] [CrossRef]
- Holmberg, K.; Erdemir, A. The Impact of Tribology on Energy Use and CO2 Emission Globally and in Combustion Engine and Electric Cars. Tribol. Int. 2019, 135, 389–396. [Google Scholar] [CrossRef]
- Usman, A.; Park, C.W. Optimizing the Tribological Performance of Textured Piston Ring–Liner Contact for Reduced Frictional Losses in SI Engine: Warm Operating Conditions. Tribol. Int. 2016, 99, 224–236. [Google Scholar] [CrossRef]
- Orozco Lozano, W.; Fonseca-Vigoya, M.D.S.; Pabón-León, J. Study of the Kinematics and Dynamics of the Ring Pack of a Diesel Engine by Means of the Construction of CFD Model in Conjunction with Mathematical Models. Lubricants 2021, 9, 116. [Google Scholar] [CrossRef]
- Chong, W.W.F.; Ng, J.-H.; Rajoo, S.; Chong, C.T. Passenger Transportation Sector Gasoline Consumption Due to Friction in Southeast Asian Countries. Energy Convers. Manag. 2018, 158, 346–358. [Google Scholar] [CrossRef]
- Buberger, J.; Kersten, A.; Kuder, M.; Eckerle, R.; Weyh, T.; Thiringer, T. Total CO2-Equivalent Life-Cycle Emissions from Commercially Available Passenger Cars. Renew. Sustain. Energy Rev. 2022, 159, 112158. [Google Scholar] [CrossRef]
- Leach, F. A Negative Emission Internal Combustion Engine Vehicle? Atmos. Environ. 2023, 294, 119488. [Google Scholar] [CrossRef]
- Mamala, J.; Śmieja, M.; Prażnowski, K. Analysis of the Total Unit Energy Consumption of a Car with a Hybrid Drive System in Real Operating Conditions. Energies 2021, 14, 3966. [Google Scholar] [CrossRef]
- Paul, S.; Debnath, D.; Doloi, S.; Mohanty, S. Fractal Mathematics Applications for Wear Image Analysis of Engines Using Biofuels. Mater. Today: Proc. 2022, 66, 3784–3789. [Google Scholar] [CrossRef]
- Liu, Z.; Guo, Z.; Rao, X.; Xu, Y.; Sheng, C.; Yuan, C. A Comprehensive Review on the Material Performance Affected by Gaseous Alternative Fuels in Internal Combustion Engines. Eng. Fail. Anal. 2022, 139, 106507. [Google Scholar] [CrossRef]
- García, C.P.; Orjuela Abril, S.; León, J.P. Analysis of Performance, Emissions, and Lubrication in a Spark-Ignition Engine Fueled with Hydrogen Gas Mixtures. Heliyon 2022, 8, e11353. [Google Scholar] [CrossRef] [PubMed]
- Gracz, W.; Marcinkowski, D.; Golimowski, W.; Szwajca, F.; Strzelczyk, M.; Wasilewski, J.; Krzaczek, P. Multifaceted Comparison Efficiency and Emission Characteristics of Multi-Fuel Power Generator Fueled by Different Fuels and Biofuels. Energies 2021, 14, 3388. [Google Scholar] [CrossRef]
- Kindrachuk, M.; Volchenko, D.; Balitskii, A.; Abramek, K.F.; Volchenko, M.; Balitskii, O.; Skrypnyk, V.; Zhuravlev, D.; Yurchuk, A.; Kolesnikov, V. Wear Resistance of Spark Ignition Engine Piston Rings in Hydrogen-Containing Environments. Energies 2021, 14, 4801. [Google Scholar] [CrossRef]
- Grube, T.; Kraus, S.; Reul, J.; Stolten, D. Passenger Car Cost Development through 2050. Transp. Res. Part D Transp. Environ. 2021, 101, 103110. [Google Scholar] [CrossRef]
- Rokicki, T.; Bórawski, P.; Bełdycka-Bórawska, A.; Żak, A.; Koszela, G. Development of Electromobility in European Union Countries under COVID-19 Conditions. Energies 2021, 15, 9. [Google Scholar] [CrossRef]
- Razmjoo, A.; Ghazanfari, A.; Jahangiri, M.; Franklin, E.; Denai, M.; Marzband, M.; Astiaso Garcia, D.; Maheri, A. A Comprehensive Study on the Expansion of Electric Vehicles in Europe. Appl. Sci. 2022, 12, 11656. [Google Scholar] [CrossRef]
- Morfeldt, J.; Davidsson Kurland, S.; Johansson, D.J.A. Carbon Footprint Impacts of Banning Cars with Internal Combustion Engines. Transp. Res. Part D Transp. Environ. 2021, 95, 102807. [Google Scholar] [CrossRef]
- Kapsiz, M.; Durat, M.; Ficici, F. Friction and Wear Studies between Cylinder Liner and Piston Ring Pair Using Taguchi Design Method. Adv. Eng. Softw. 2011, 42, 595–603. [Google Scholar] [CrossRef]
- Xun, D.; Sun, X.; Liu, Z.; Zhao, F.; Hao, H. Comparing Supply Chains of Platinum Group Metal Catalysts in Internal Combustion Engine and Fuel Cell Vehicles: A Supply Risk Perspective. Clean. Logist. Supply Chain. 2022, 4, 100043. [Google Scholar] [CrossRef]
- Lieven, T.; Hügler, B. Did Electric Vehicle Sales Skyrocket Due to Increased Environmental Awareness While Total Vehicle Sales Declined during COVID-19? Sustainability 2021, 13, 13839. [Google Scholar] [CrossRef]
- Frieske, B.; Stieler, S. The “Semiconductor Crisis” as a Result of the COVID-19 Pandemic and Impacts on the Automotive Industry and Its Supply Chains. WEVJ 2022, 13, 189. [Google Scholar] [CrossRef]
- Hagman, J.; Stier, J.J. Selling Electric Vehicles: Experiences from Vehicle Salespeople in Sweden. Res. Transp. Bus. Manag. 2022, 45, 100882. [Google Scholar] [CrossRef]
- Manley, R.L.; Alonso, E.; Nassar, N.T. Examining Industry Vulnerability: A Focus on Mineral Commodities Used in the Automotive and Electronics Industries. Resour. Policy 2022, 78, 102894. [Google Scholar] [CrossRef]
- Severson, M.H.; Nguyen, R.T.; Ormerod, J.; Williams, S. An Integrated Supply Chain Analysis for Cobalt and Rare Earth Elements under Global Electrification and Constrained Resources. Resour. Conserv. Recycl. 2023, 189, 106761. [Google Scholar] [CrossRef]
- Teske, S.; Bratzel, S.; Tellermann, R.; Stephan, B.; Vargas, M. Net Zero: The Remaining Global Market Volume for Internal Combustion Engines in Light-Duty Vehicles under a 1.5 °C Carbon Budget Trajectory. Energies 2022, 15, 8037. [Google Scholar] [CrossRef]
- Ayetor, G.K.; Mbonigaba, I.; Sackey, M.N.; Andoh, P.Y. Vehicle Regulations in Africa: Impact on Used Vehicle Import and New Vehicle Sales. Transp. Res. Interdiscip. Perspect. 2021, 10, 100384. [Google Scholar] [CrossRef]
- Abo-Khalil, A.G.; Abdelkareem, M.A.; Sayed, E.T.; Maghrabie, H.M.; Radwan, A.; Rezk, H.; Olabi, A.G. Electric Vehicle Impact on Energy Industry, Policy, Technical Barriers, and Power Systems. Int. J. Thermofluids 2022, 13, 100134. [Google Scholar] [CrossRef]
- Holmberg, K.; Andersson, P.; Erdemir, A. Global Energy Consumption Due to Friction in Passenger Cars. Tribol. Int. 2012, 47, 221–234. [Google Scholar] [CrossRef]
- Ma, W.; Biboulet, N.; Lubrecht, A.A. Performance Evolution of a Worn Piston Ring. Tribol. Int. 2018, 126, 317–323. [Google Scholar] [CrossRef]
- Pabón León, J.A.; Rojas Suárez, J.P.; Orjuela Abril, M.S. Numerical Study of the Physical Processes of Gas Leakage in the Compression Ring in Diesel Engines. J. Phys. Conf. Ser. 2021, 2118, 012016. [Google Scholar] [CrossRef]
- Gao, L.; Cui, Y.; Xu, Z.; Fu, Y.; Liu, S.; Li, Y.; Hou, X. A Fully Coupled Tribo-Dynamic Model for Piston-Ring-Liner System. Tribol. Int. 2023, 178, 107998. [Google Scholar] [CrossRef]
- Baby, A.K.; Rajendrakumar, P.K.; Lawrence, K.D. Influence of Honing Angle on Tribological Behaviour of Cylinder Liner–Piston Ring Pair: Experimental Investigation. Tribol. Int. 2022, 167, 107355. [Google Scholar] [CrossRef]
- Kang, J.; Lu, Y.; Yang, X.; Zhao, X.; Zhang, Y.; Xing, Z. Modeling and Experimental Investigation of Wear and Roughness for Honed Cylinder Liner during Running-in Process. Tribol. Int. 2022, 171, 107531. [Google Scholar] [CrossRef]
- Chen, T.; Wang, L.; Xu, J.; Gao, T.; Qin, X.; Yang, X.; Cong, Q.; Jin, J.; Liu, C. Effect of Groove Texture on Deformation and Sealing Performance of Engine Piston Ring. Machines 2022, 10, 1020. [Google Scholar] [CrossRef]
- Grabon, W.; Pawlus, P.; Wos, S.; Koszela, W.; Wieczorowski, M. Effects of Honed Cylinder Liner Surface Texture on Tribological Properties of Piston Ring-Liner Assembly in Short Time Tests. Tribol. Int. 2017, 113, 137–148. [Google Scholar] [CrossRef]
- Zabala, B.; Igartua, A.; Fernández, X.; Priestner, C.; Ofner, H.; Knaus, O.; Abramczuk, M.; Tribotte, P.; Girot, F.; Roman, E.; et al. Friction and Wear of a Piston Ring/Cylinder Liner at the Top Dead Centre: Experimental Study and Modelling. Tribol. Int. 2017, 106, 23–33. [Google Scholar] [CrossRef]
- Wróblewski, P.; Rogólski, R. Experimental Analysis of the Influence of the Application of TiN, TiAlN, CrN and DLC1 Coatings on the Friction Losses in an Aviation Internal Combustion Engine Intended for the Propulsion of Ultralight Aircraft. Materials 2021, 14, 6839. [Google Scholar] [CrossRef] [PubMed]
- Tomanik, E.; Fujita, H.; Sato, S.; Paes, E.; Galvao, C.; Morais, P. Investigation of PVD Piston Ring Coatings With Different Lubricant Formulations. In Proceedings of the ICEF2017; Volume 2: Emissions Control Systems; Instrumentation, Controls, and Hybrids; Numerical Simulation; Engine Design and Mechanical Development, Seattle, WA, USA, 15 October 2017. [Google Scholar]
- Dubey, M.K.; Chaudhary, R.; Emmandi, R.; Seth, S.; Mahapatra, R.; Harinarain, A.K.; Ramakumar, S.S.V. Tribological Evaluation of Passenger Car Engine Oil: Effect of Friction Modifiers. Results Eng. 2022, 16, 100727. [Google Scholar] [CrossRef]
- Gamble, R.J.; Priest, M.; Taylor, C.M. Detailed Analysis of Oil Transport in the Piston Assembly of a Gasoline Engine. Tribol. Lett. 2003, 14, 147–156. [Google Scholar] [CrossRef]
- Kunt, M.A.; Calam, A.; Gunes, H. Analysis of the Effects of Lubricating Oil Viscosity and Engine Speed on Piston-Cylinder Liner Frictions in a Single Cylinder HCCI Engine by GT-SUITE Program. Proc. Inst. Mech. Eng. Part E: J. Process Mech. Eng. 2022, 09544089221132988. [Google Scholar] [CrossRef]
- Gołębiowski, W.; Zając, G.; Sarkan, B. Evaluation of the Impact of Tractor Field Works on Changes in Selected Elements of Engine Oils. Agric. Eng. 2022, 26, 1–12. [Google Scholar] [CrossRef]
- Lenauer, C.; Tomastik, C.; Wopelka, T.; Jech, M. Piston Ring Wear and Cylinder Liner Tribofilm in Tribotests with Lubricants Artificially Altered with Ethanol Combustion Products. Tribol. Int. 2015, 82, 415–422. [Google Scholar] [CrossRef]
- Fernandes, W.; Tomanik, E.; Moreira, H.; Cousseau, T.; Pintaude, G. Effect of Aged Oils on Ring-Liner Wear. SAE Int. J. Fuels Lubr. 2020, 13, 167–176. [Google Scholar] [CrossRef]
- Nikolakopoulos, P.; Mavroudis, S.; Zavos, A. Lubrication Performance of Engine Commercial Oils with Different Performance Levels: The Effect of Engine Synthetic Oil Aging on Piston Ring Tribology under Real Engine Conditions. Lubricants 2018, 6, 90. [Google Scholar] [CrossRef] [Green Version]
- Fang, C.; Meng, X.; Kong, X.; Zhao, B.; Huang, H. Transient Tribo-Dynamics Analysis and Friction Loss Evaluation of Piston during Cold- and Warm-Start of a SI Engine. Int. J. Mech. Sci. 2017, 133, 767–787. [Google Scholar] [CrossRef]
- Rahmani, R.; Rahnejat, H.; Fitzsimons, B.; Dowson, D. The Effect of Cylinder Liner Operating Temperature on Frictional Loss and Engine Emissions in Piston Ring Conjunction. Appl. Energy 2017, 191, 568–581. [Google Scholar] [CrossRef] [Green Version]
- Tomanik, E.; Profito, F.; Sheets, B.; Souza, R. Combined Lubricant–Surface System Approach for Potential Passenger Car CO2 Reduction on Piston-Ring-Cylinder Bore Assembly. Tribol. Int. 2020, 149, 105514. [Google Scholar] [CrossRef]
- Tormos, B.; Martín, J.; Pla, B.; Jiménez-Reyes, A.J. A Methodology to Estimate Mechanical Losses and Its Distribution during a Real Driving Cycle. Tribol. Int. 2020, 145, 106208. [Google Scholar] [CrossRef]
- Zhao, L.; Li, J.; Yang, Q.; Wang, Y.; Zhang, X.; Li, H.; Yang, Z.; Xu, D.; Liu, J. Study on Friction and Wear Properties of New Self-Lubricating Bearing Materials. Crystals 2022, 12, 834. [Google Scholar] [CrossRef]
- Venkateswara babu, P.; Syed, I.; BenBeera, S. Experimental Investigation on Effects of Positive Texturing on Friction and Wear Reduction of Piston Ring/Cylinder Liner System. Mater. Today Proc. 2020, 24, 1112–1121. [Google Scholar] [CrossRef]
- Fenske, G.; Erch, R.; Demas, N.; Eryilmaz, O.; De la Cinta, M.; Martin, L. Parasitic Energy Losses. Argonne Natl. Lab. US Dep. Energy 2009. [Google Scholar]
- Turnbull, R.; Dolatabadi, N.; Rahmani, R.; Rahnejat, H. An Assessment of Gas Power Leakage and Frictional Losses from the Top Compression Ring of Internal Combustion Engines. Tribol. Int. 2020, 142, 105991. [Google Scholar] [CrossRef]
- Koszalka, G.; Hunicz, J. Comparative Study of Energy Losses Related to the Ring Pack Operation in Homogeneous Charge Compression Ignition and Spark Ignition Combustion. Energy 2021, 235, 121388. [Google Scholar] [CrossRef]
- Richardson, D.E.; Krause, S.A. Predicted Effects of Cylinder Kit Wear on Blowby and Oil Consumption for Two Diesel Engines. J. Eng. Gas Turbines Power 1999, 122, 520–525. [Google Scholar] [CrossRef]
- Koszałka, G.; Guzik, M. Mathematical Model of Piston Ring Sealing in Combustion Engine. Pol. Marit. Res. 2015, 21, 66–78. [Google Scholar] [CrossRef] [Green Version]
- Priest, M.; Dowson, D.; Taylor, C.M. Theoretical Modelling of Cavitation in Piston Ring Lubrication. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2000, 214, 435–447. [Google Scholar] [CrossRef]
- Koszalka, G.; Suchecki, A. Durability Prediction of a Diesel Engine Piston-Rings-Cylinder Assembly on the Basis of Test Bench Results. SAE Tech. Pap. 2011. [Google Scholar] [CrossRef]
- Koszalka, G.; Suchecki, A. Changes in Performance and Wear of Small Diesel Engine during Durability Test. Combust. Engines 2015, 162, 34–40. [Google Scholar] [CrossRef]
- Koszałka, G. Predicting the Durability of the Piston-Rings-Cylinder Assembly of a Diesel Engine Using a Piston Ring Pack Model. Eksploat. I Niezawodn.-Maint. Reliab. 2011, 40–44. [Google Scholar]
| Parameter | Value |
|---|---|
| Displacement | 1995 cm3 |
| Nominal diameter of the bore | 84 mm |
| Stroke | 90 mm |
| Compression ratio | 12:1 |
| No of valves | 4 |
| Max power | 105 kW at 6000 rpm |
| Max torque | 190 Nm at 4500 rpm |
| Parameter | Top Ring | Second Ring | Oil Ring |
|---|---|---|---|
| Axial height(mm) | 1.20 | 1.5 | 2.0 |
| Radial thickness(mm) | 3.8 | 3.8 | 3.8 |
| Nominal ring end gap(mm) | 0.20 | 0.30 | 0.25 |
| Nominal ring side clearance(mm) | 0.03 | 0.03 | 0.03 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koszalka, G.; Krzaczek, P. Energy Losses Related to Ring Pack Wear in Gasoline Car Engine. Energies 2022, 15, 9570. https://doi.org/10.3390/en15249570
Koszalka G, Krzaczek P. Energy Losses Related to Ring Pack Wear in Gasoline Car Engine. Energies. 2022; 15(24):9570. https://doi.org/10.3390/en15249570
Chicago/Turabian StyleKoszalka, Grzegorz, and Paweł Krzaczek. 2022. "Energy Losses Related to Ring Pack Wear in Gasoline Car Engine" Energies 15, no. 24: 9570. https://doi.org/10.3390/en15249570
APA StyleKoszalka, G., & Krzaczek, P. (2022). Energy Losses Related to Ring Pack Wear in Gasoline Car Engine. Energies, 15(24), 9570. https://doi.org/10.3390/en15249570






