Control Method of Step Voltage Regulator on Distribution Lines with Distributed Generation
Abstract
:1. Introduction
2. SVR Voltage Control Method
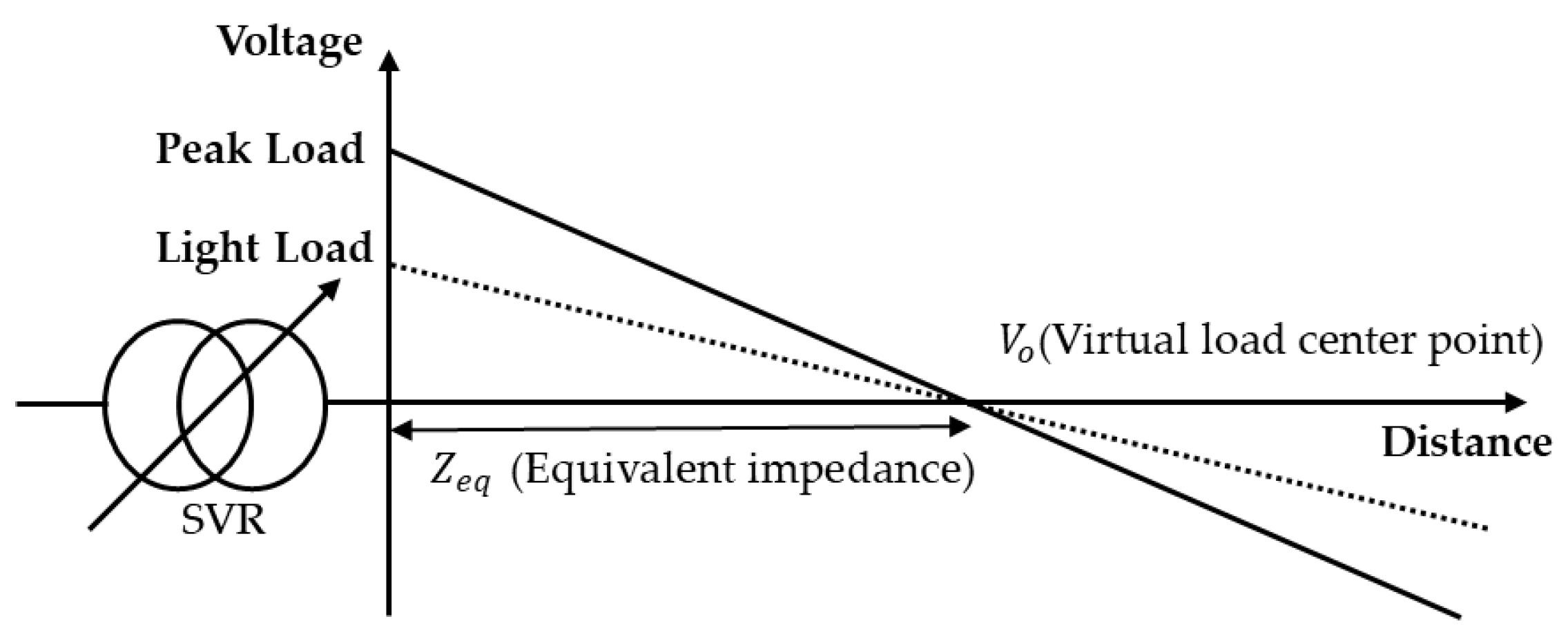
2.1. LDC Control
2.2. Constant Voltage Control Method
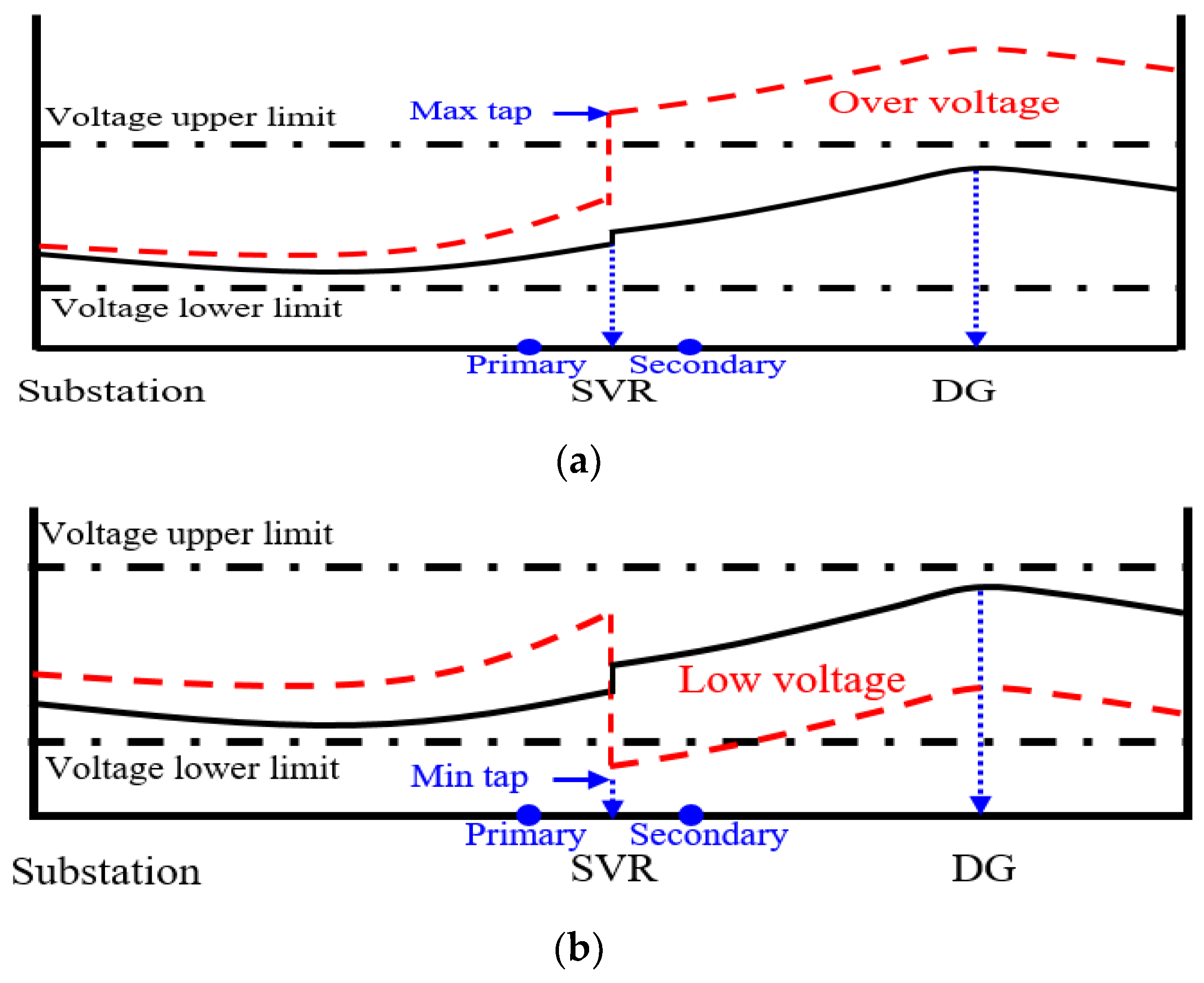
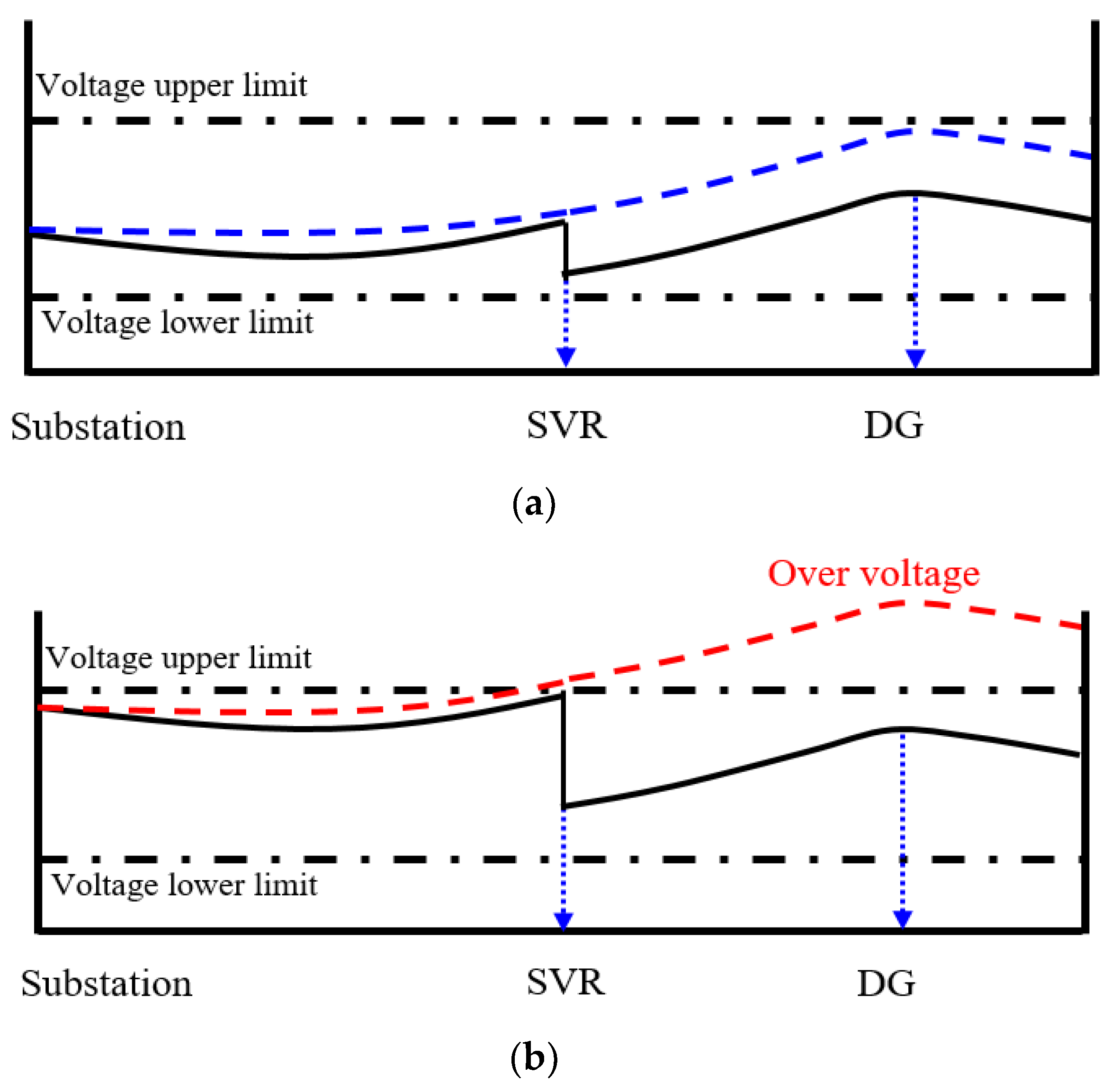
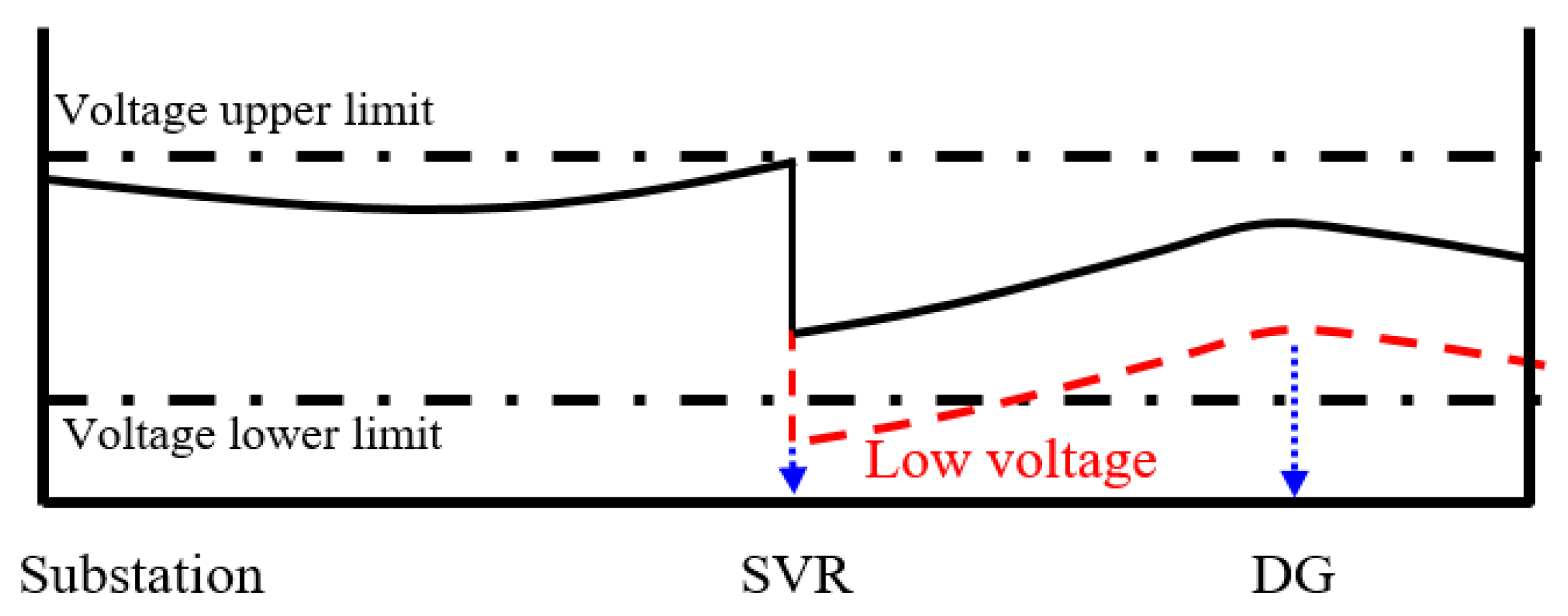
2.3. Reverse Power Flow Control
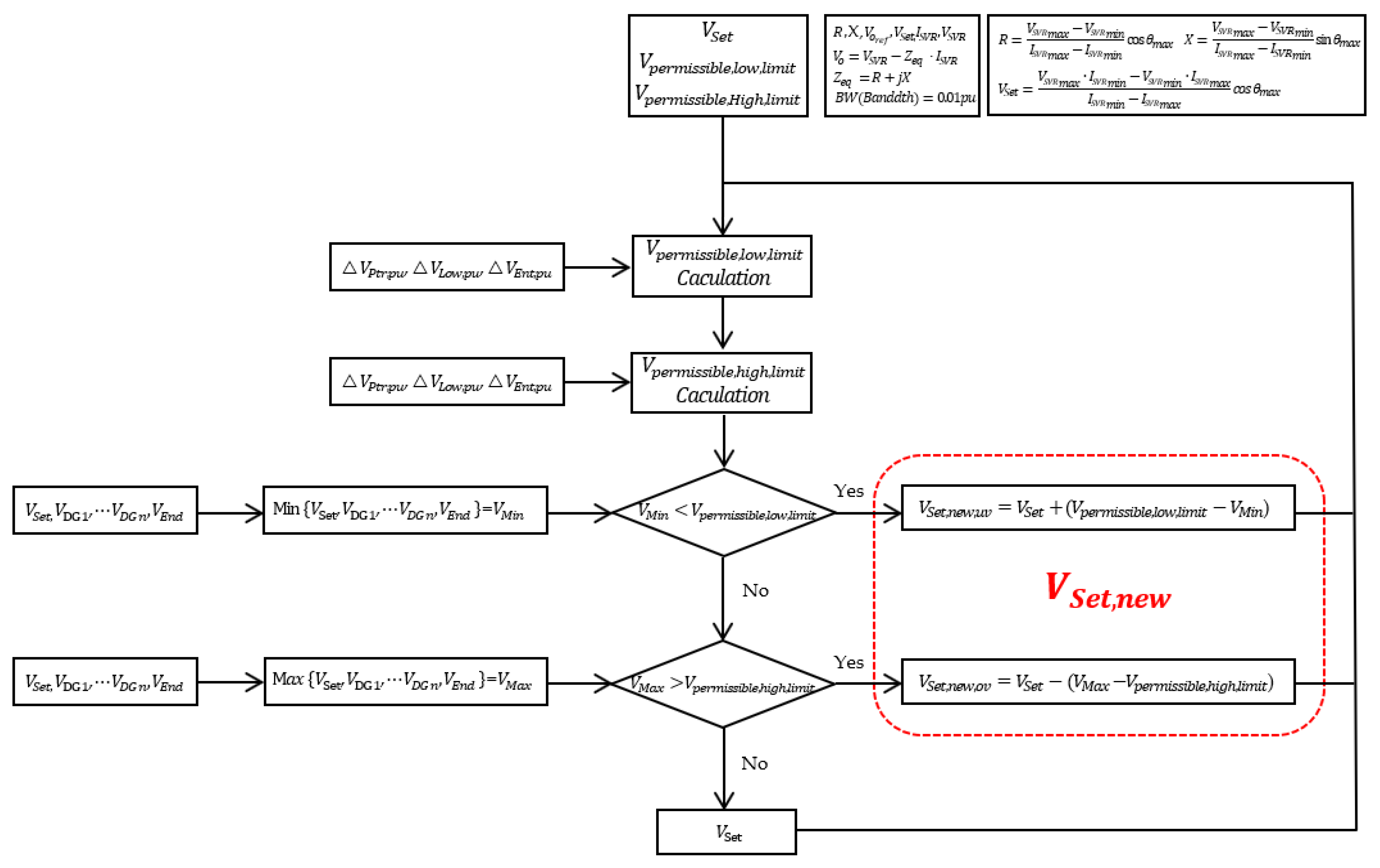
3. SVR Tap-Control Algorithm
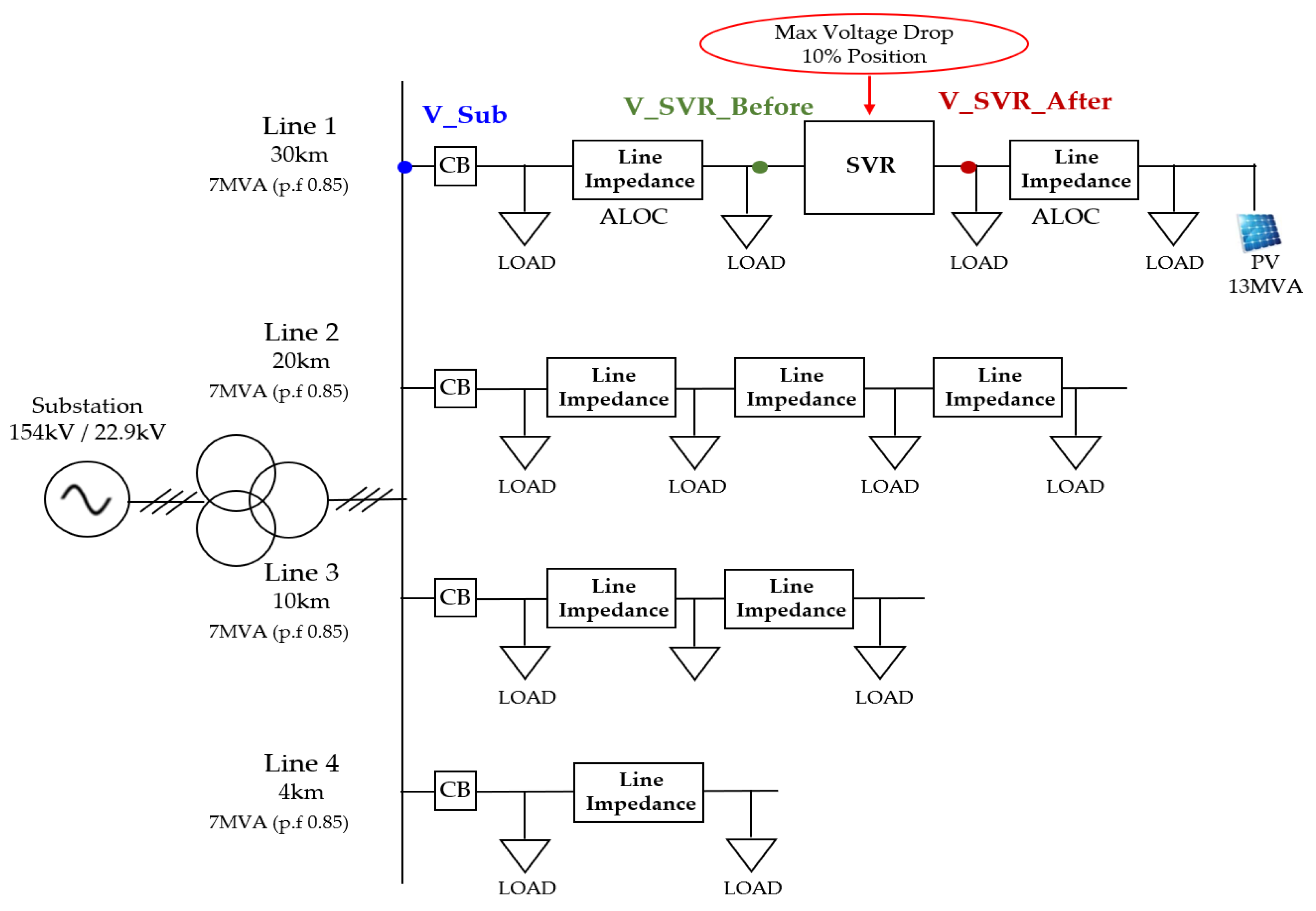
4. Simulation and Result
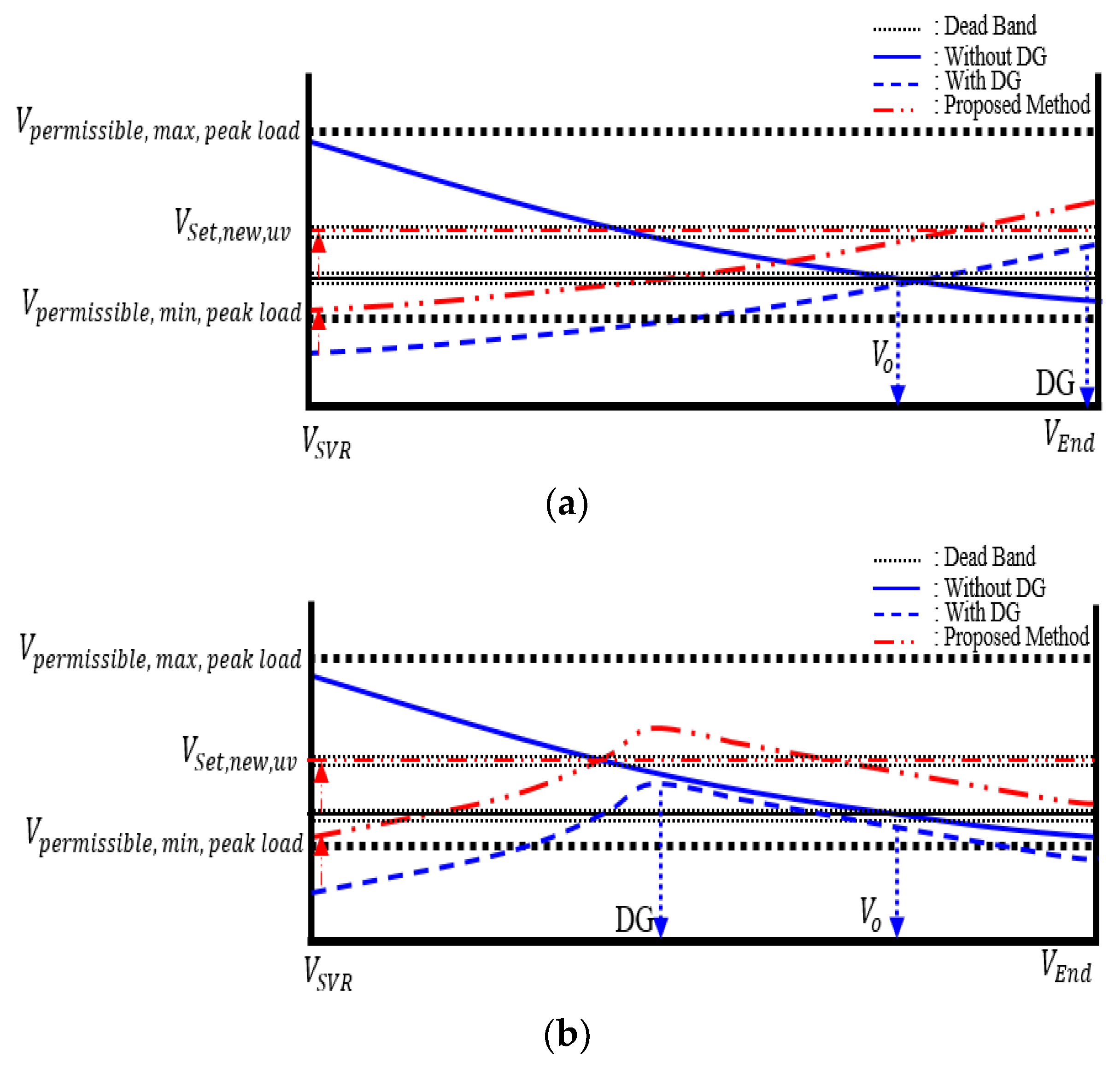
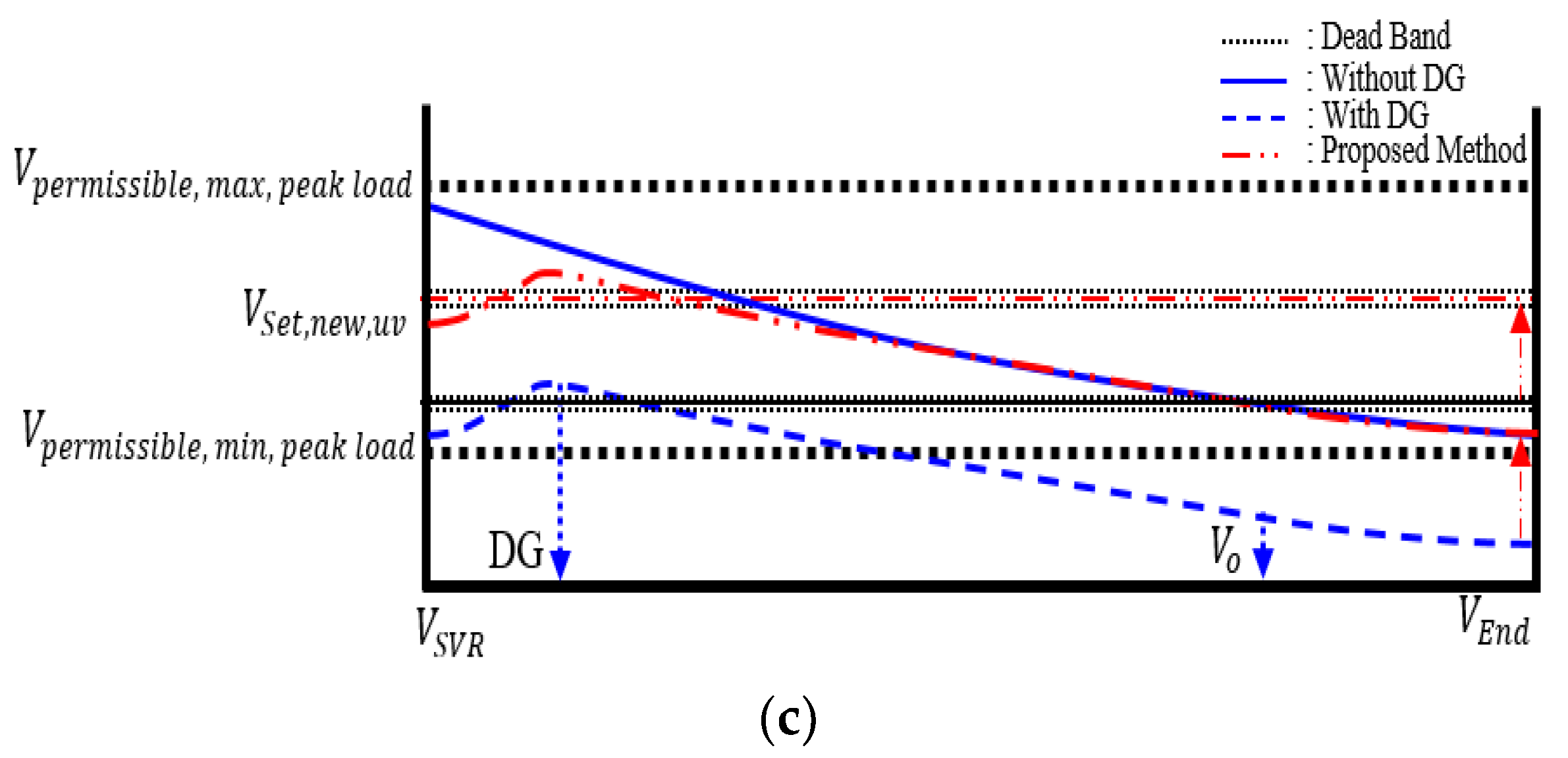
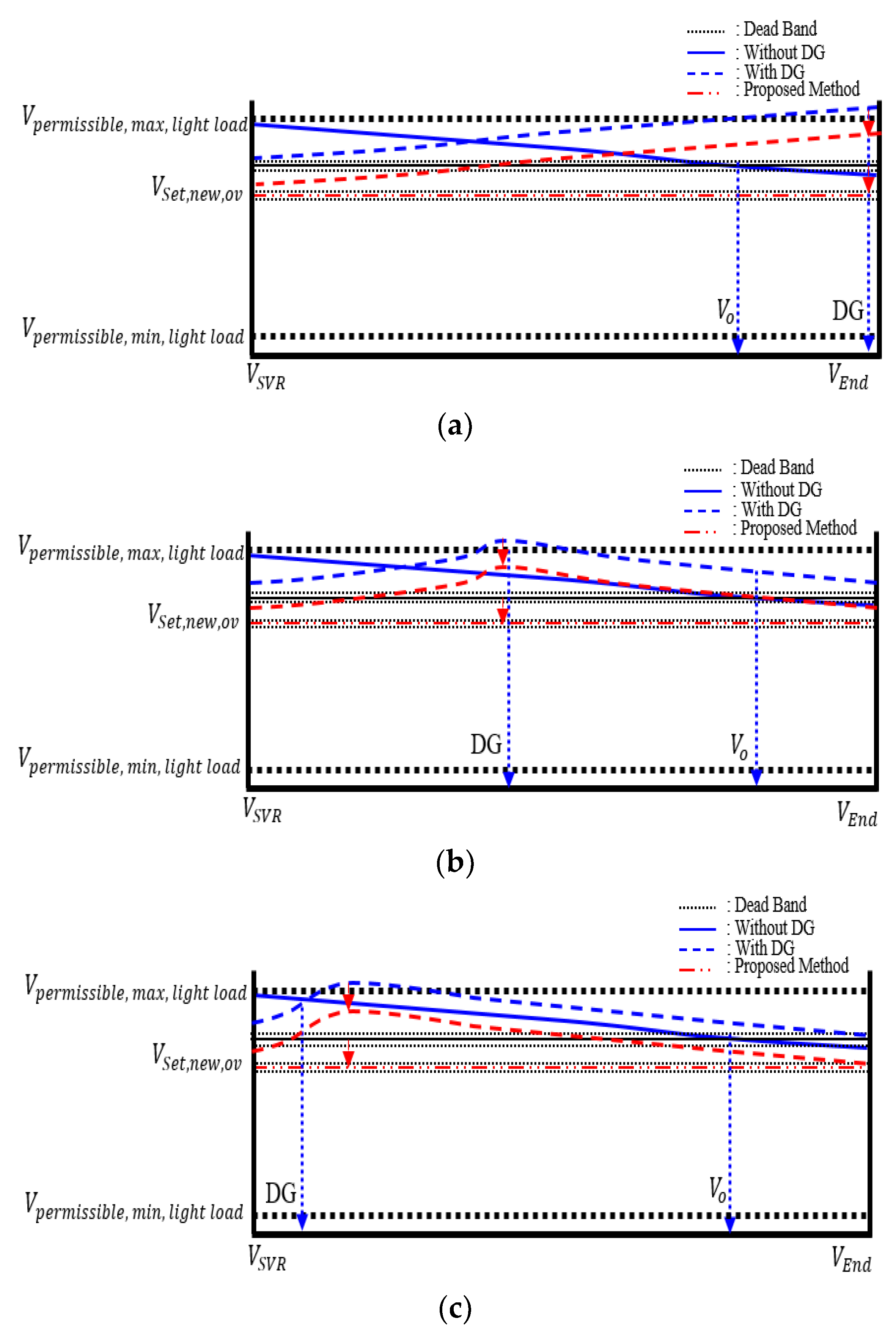
4.1. Simulation and Condition
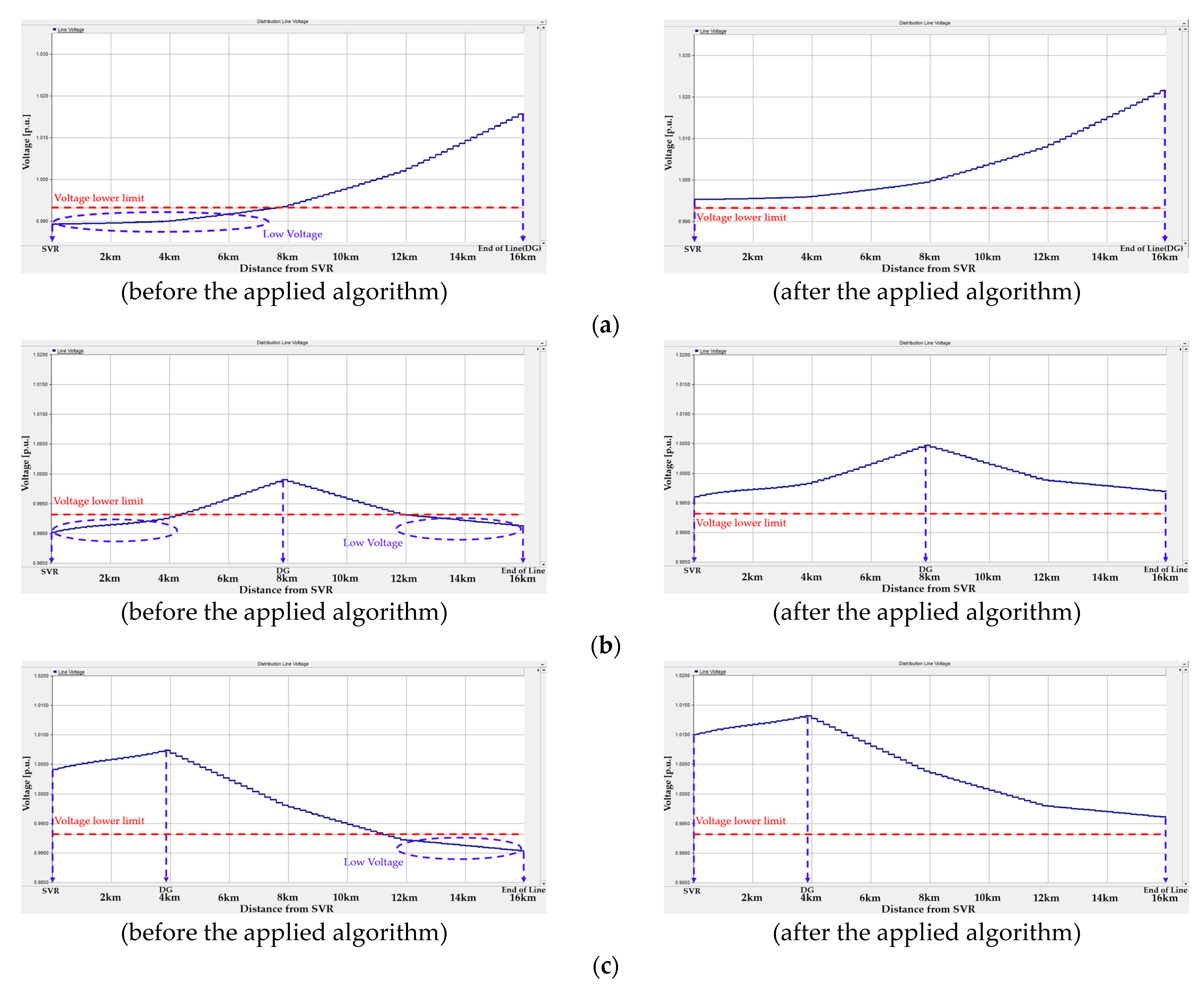
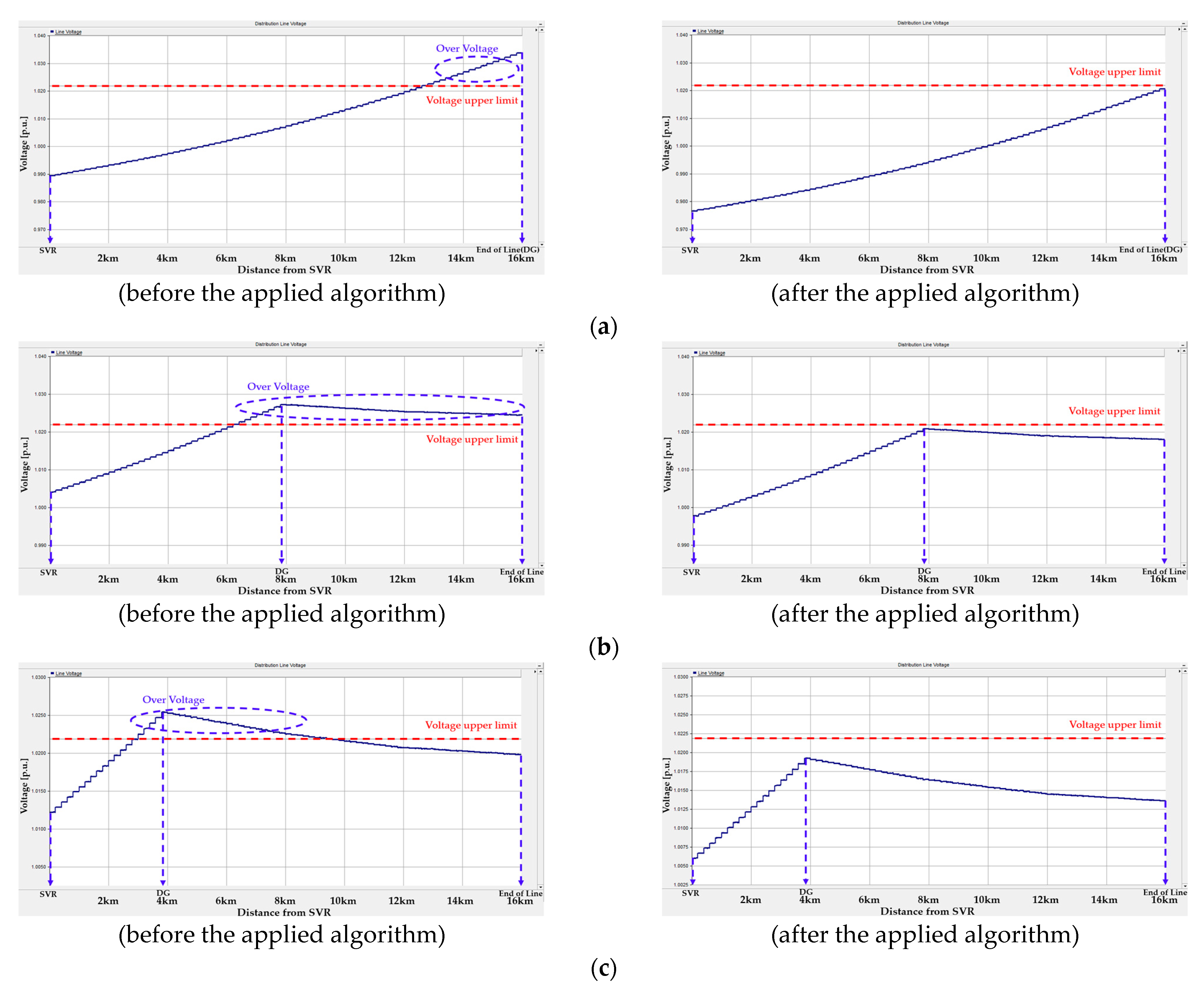
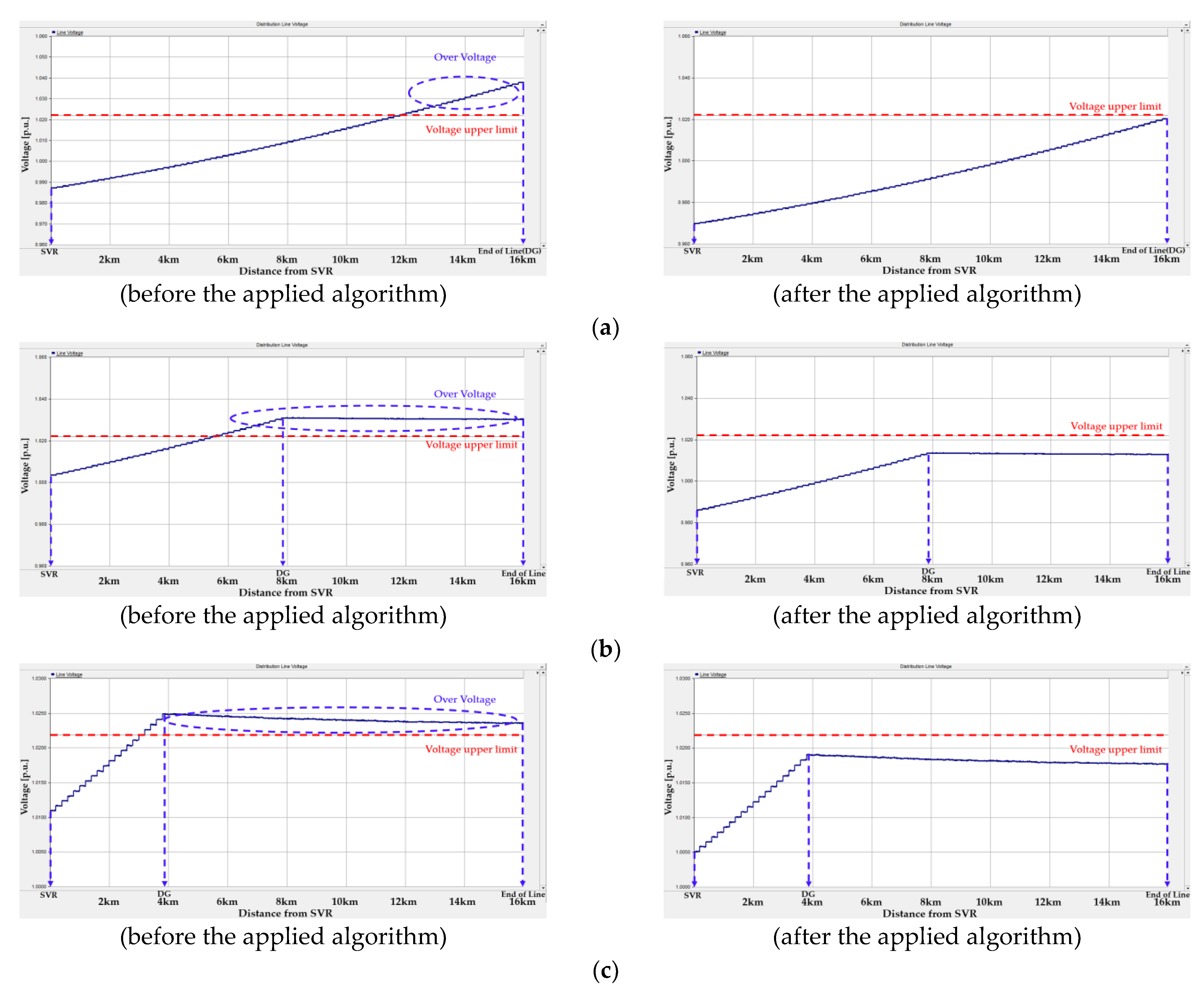
4.2. Simulation and Verification
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- IPCC. Summary for Policymakers. 2018. Available online: https://www.ipcc.ch/sr15/chapter/spm/ (accessed on 6 October 2018).
- Kraiczy, M.; AL Fakhri, L.; Braun, M. Local Voltage Support by Distributed Generation; IEA-PVPS T14-08; International Energy Agency: Paris, France, 2017. [Google Scholar]
- Mahmud, N.; Zahedi, A. Review of Control Strategies for Voltage Regulation of the Smart Distribution Network with High Penetration of Renewable Distributed Generation. Renew. Sustain. Energy Rev. 2016, 64, 582–595. [Google Scholar] [CrossRef]
- Hu, J.; Li, Z.; Zhu, J.; Guerrero, J. Voltage Stabilization. IEEE Ind. Electron. Mag. 2019, 13, 17–30. [Google Scholar] [CrossRef]
- IEEE-PES Task Force on Voltage Control for Smart Grids. Review of Challenges and Research Opportunities for Voltage Control in Smart Grids. IEEE Trans. Power Syst. 2019, 34, 2790–2801. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Guo, L.; Lu, C.; Chai, Y.; Gao, S.; Xu, B. A Fully Distributed Voltage Optimization Method for Distribution Networks Considering Integer Constraints of Step Voltage Regulators. IEEE Access 2019, 7, 60055–60066. [Google Scholar] [CrossRef]
- Sgouras, K.I.; Bouhouras, A.S.; Gkaidatzis, P.A.; Doukas, D.I.; Labridis, D.I. Impact of Reverse Power Flow on the Optimal Distributed Generation Placement Problem. IET Gener. Transm. Distrib. 2017, 11, 4626–4632. [Google Scholar] [CrossRef]
- NamKoong, W.; Jung, W.-W.; Shin, C.-H.; Hwang, P.-I.; Jang, G. Voltage Control of Distribution Networks to Increase their Hosting Capacity in South Korea. J. Electr. Eng. Technol. 2021, 16, 1305–1312. [Google Scholar] [CrossRef]
- Nagarajan, L.; Senthilkumar, M. Power Quality Improvement in Distribution System Based on Dynamic Voltage Restorer Using Rational Energy Transformative Optimization Algorithm. J. Electr. Eng. Technol. 2022, 17, 121–137. [Google Scholar] [CrossRef]
- Jahn, R.; Holt, M.; Rehtanz, C. Mitigation of Voltage Unbalances Using a Line Voltage Regulator. In Proceedings of the 2021 IEEE Madrid PowerTech, Madrid, Spain, 28 June 2021; pp. 1–6. [Google Scholar]
- Yan, R.; Li, Y.; Saha, T.K.; Wang, L.; Hossain, M.I. Modeling and Analysis of Open-Delta Step Voltage Regulators for Unbalanced Distribution Network with Photovoltaic Power Generation. IEEE Trans. Smart Grid 2018, 9, 2224–2234. [Google Scholar] [CrossRef] [Green Version]
- Nakadomari, A.; Shigenobu, R.; Senjyu, T. Optimal Control and Placement of Step Voltage Regulator for Voltage Unbalance Improvement and Loss Minimization in Distribution System. In Proceedings of the 2020 IEEE Region 10 Conference, Osaka, Japan, 16–19 November 2020; pp. 1013–1018. [Google Scholar]
- Liu, E.; Bebic, J. Distribution System Voltage Performance Analysis for High-Penetration Photovoltaics; NREL/SR-581-42298; National Renewable Energy Lab: Golden, CO, USA, 2008. [Google Scholar]
- Bai, F.; Yan, R.; Saha, T.K.; Eghbal, D. A New Remote Tap Position Estimation Approach for Open-Delta Step-Voltage Regulator in a Photovoltaic Integrated Distribution Network. IEEE Trans. Power Syst. 2018, 33, 4433–4443. [Google Scholar] [CrossRef] [Green Version]
- Ranamuka, D.; Agalgaonkar, A.P.; Muttaqi, K.M. Online Voltage Control in Distribution Systems with Multiple Voltage Regulating Devices. IEEE Trans. Sustain. Energy 2014, 5, 617–628. [Google Scholar] [CrossRef]
- Chamana, M.; Chowdhury, B.H.; Jahanbakhsh, F. Distributed Control of Voltage Regulating Devices in the Presence of High PV Penetration to Mitigate Ramp-Rate Issues. IEEE Trans. Smart Grid 2018, 9, 1086–1095. [Google Scholar] [CrossRef]
- Chamana, M.; Chowdhury, B.H. Optimal Voltage Regulation of Distribution Networks with Cascaded Voltage Regulators in the Presence of High PV Penetration. IEEE Trans. Sustain. Energy 2018, 9, 1427–1436. [Google Scholar] [CrossRef]
- Tonkoski, R.; Turcotte, D.; El-Fouly, T.H. Impact of high PV penetration on voltage profiles in residential neighborhoods. IEEE Trans. Sustain. Energy 2012, 3, 518–527. [Google Scholar] [CrossRef]
- Baran, M.E.; Wu, F.F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Power Eng. Rev. 1989, 4, 101–102. [Google Scholar] [CrossRef]
- Abrar Ahmed, C.; Vinod, K. DC-Microgrid Voltage Regulation using Dual Active Bridge based SVR. In Proceedings of the 2021 7th International Conference on Electrical Energy Systems (ICEES), Chennai, India, 11–13 February 2021; pp. 490–495. [Google Scholar]
- Short, T.A. Electric Power Distribution Handbook; CRC Press: New York, NY, USA, 2014; pp. 734–739. [Google Scholar]
- Wareham, D. Step Voltage Regulators, Cooper Power Systems by EATON. 2013. Available online: http://www.cscos.com/wp-content/uploads/NY1839-Eaton-Regulators-D.Wareham.pdf (accessed on 15 October 2022).
- Kajita, H.; Kanbe, A.; Fugawa, K.; Kadokura, S. Development of SVR Control System for Dispersed Power Supply; 2005 Aichi Electric Technical Report No.26; Aichi Electrical: Nagoya, Japan, 2005; pp. 10–16. (In Japanese) [Google Scholar]




| Index | Value | Remark |
|---|---|---|
| 154 kV Grid Source | ||
| Rated Power | 50 MVA | |
| Rated Voltage | 154 kV | |
| Rated Frequency | 60 Hz | |
| Positive Sequence %Z | 0.08 + j0.99 | 100 MVA Based |
| Zero Sequence %Z | 0.34 + j1.69 | |
| 3-Winding Transformer (154 kV / 22.9 kV / 6.6 kV) | ||
| Rated Power | 45/60 MVA | |
| Positive Sequence % | j15.97 | 45 MVA Based |
| Positive Sequence % | j6.69 | |
| Positive Sequence % | j25.38 | |
| Connection Type | ||
| Distribution Line (1 km, CNCV-W 325 ) | ||
| Positive Sequence %Z | 1.44 + j3.74 | 100 MVA Based |
| Zero Sequence %Z | 4.46 + j1.56 | |
| Distribution Line (1 km, ACSR 160/95 ) | ||
| Positive Sequence %Z | 5.23 + j11.62 | |
| Zero Sequence %Z | 13.65 + j34.2 | |
| Local Load | 5.95MW + 3.69Mvar | Lagging |
| Distribution Generation (22.9 kV) | ||
| Type of DG | PV | |
| DG Capacity | 13 MVA | |
| Transformer Connection | ||
| Positive Sequence %X | j0.05 | MVA Based |
| LDC’s Parameters at Substation OLTC | ||
| Equivalent Impedance | 1.3262 + j0.8143 | |
| Transmission reference voltage | 93.1007 V | 120 V Based |
| LDC’s Parameters at SVR | ||
| Equivalent Impedance | 19.1657 + j9.369 | |
| Transmission reference voltage | 103.8844 V | 120 V Based |
| At Peak Load | ||
| Feeder 1 Load Capacity before SVR | 3.3975 MVA | p.f. 0.8995 |
| Type 1: Feeder 1 Load Capacity after SVR | 2.718 MVA | |
| Type 2: Feeder 1 Load Capacity after SVR | 4.077 MVA | |
| Voltage Drop of Distribution Transformer | 1.913 | 230 V Based |
| Voltage Drop of Low-Voltage Line | 5.739 | |
| Voltage Drop of Customer Entrance | 1.913 | |
| High-Voltage Line Permissible Range | 0.9932 ~ 1.0505 p.u. | |
| At Light load | ||
| Feeder 1 Load Capacity before SVR | 0.849375 MVA | p.f. 0.8995 |
| Type 3: Feeder 1 Load Capacity after SVR | 0.6795 MVA | |
| Type 4: Feeder 1 Load Capacity after SVR | 0.3885 MVA | |
| Voltage Drop of Distribution Transformer | 0.4783 | 230 V Based |
| Voltage Drop of Low-Voltage Line | 1.4348 | |
| Voltage Drop of Customer Entrance | 0.4783 | |
| High-Voltage Line Permissible Range | 0.9216 ~ 1.0219 p.u. | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.-B.; Lee, M.-G.; Lee, J.-H.; Ryu, J.-C.; Choi, T.-S.; Park, M.-S.; Kim, J.-E. Control Method of Step Voltage Regulator on Distribution Lines with Distributed Generation. Energies 2022, 15, 9579. https://doi.org/10.3390/en15249579
Kim J-B, Lee M-G, Lee J-H, Ryu J-C, Choi T-S, Park M-S, Kim J-E. Control Method of Step Voltage Regulator on Distribution Lines with Distributed Generation. Energies. 2022; 15(24):9579. https://doi.org/10.3390/en15249579
Chicago/Turabian StyleKim, Jong-Bin, Min-Gu Lee, Jung-Hun Lee, Je-Chang Ryu, Tae-Seong Choi, Min-Su Park, and Jae-Eon Kim. 2022. "Control Method of Step Voltage Regulator on Distribution Lines with Distributed Generation" Energies 15, no. 24: 9579. https://doi.org/10.3390/en15249579
APA StyleKim, J.-B., Lee, M.-G., Lee, J.-H., Ryu, J.-C., Choi, T.-S., Park, M.-S., & Kim, J.-E. (2022). Control Method of Step Voltage Regulator on Distribution Lines with Distributed Generation. Energies, 15(24), 9579. https://doi.org/10.3390/en15249579








