Response Surface Methodology Analysis of Pyrolysis Reaction Rate Constants for Predicting Efficient Conversion of Bulk Plastic Waste into Oil and Gaseous Fuels
Abstract
1. Introduction
2. Statistical Prediction of Rate Constants
2.1. Execution of Design Expert
2.2. Validation of Model Significance
2.3. Selection of Predicted Rate Constants
3. Reaction Mechanism of HDPE
4. Implementation of MATLAB
4.1. Description of the Mathematical Model
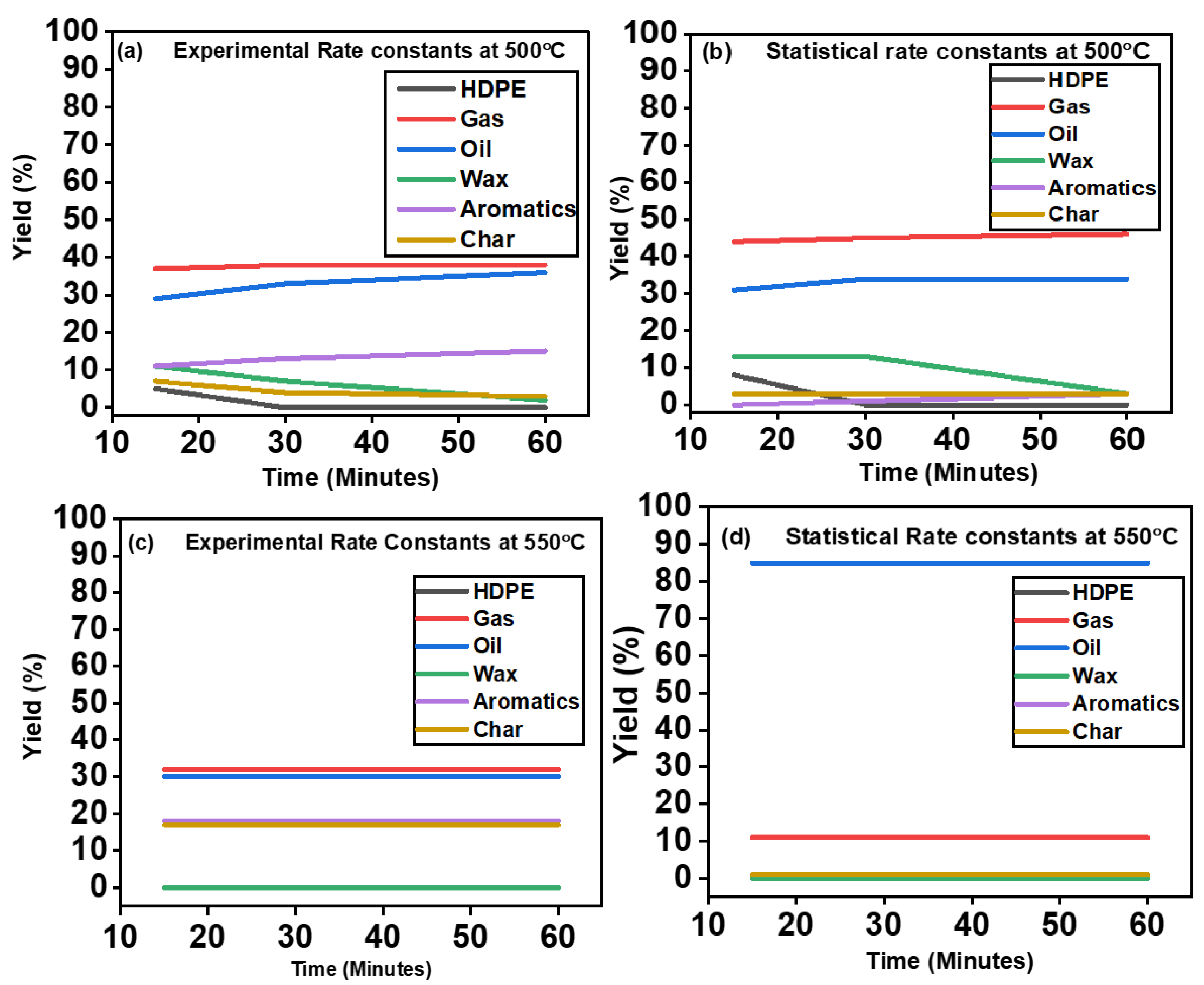
4.2. Effect of the Rate Constants and Conversion of HDPE into Species
5. Effects of Temperature and Time
6. Comparison with Literature
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tammaro, D.; Walker, C.; Lombardi, L.; Trommsdorff, U. Effect of extrudate swell on extrusion foam of polyethylene terephthalate. J. Cell. Plast. 2020, 57, 911–925. [Google Scholar] [CrossRef]
- Qureshi, M.S.; Oasmaa, A.; Pihkola, H.; Deviatkin, I.; Tenhunen, A.; Mannila, J.; Minkkinen, H.; Pohjakallio, M.; Laine-Ylijoki, J. Pyrolysis of plastic waste: Opportunities and challenges. J. Anal. Appl. Pyrolysis 2020, 152, 104804. [Google Scholar] [CrossRef]
- Tammaro, D.; Gatta, R.D.; Villone, M.M.; Maffettone, P.L. Continuous 3D Printing of Hierarchically Structured Microfoamed Objects. Adv. Eng. Mater. 2022, 24, 2101226. [Google Scholar] [CrossRef]
- Hassan, S.; Haq, I.I.U. Plastics: A brief review of its disasters and degradation techniques. Science 2019, 5, 100–102. [Google Scholar] [CrossRef]
- Jie, X.; Li, W.; Slocombe, D.; Gao, Y.; Banerjee, I.; Gonzalez-Cortes, S.; Yao, B.; AlMegren, H.; Alshihri, S.; Dilworth, J.; et al. Microwave-initiated catalytic deconstruction of plastic waste into hydrogen and high-value carbons. Nat. Catal. 2020, 3, 902–912. [Google Scholar] [CrossRef]
- Heller, M.C.; Mazor, M.H.; Keoleian, G.A. Plastics in the US: Toward a material flow characterization of production, markets, and end of life. Environ. Res. Lett. 2020, 15, 094034. [Google Scholar] [CrossRef]
- Kunwar, B.; Cheng, H.N.; Chandrashekaran, S.R.; Sharma, B.K. A review: Plastics to fuel. Renew. Sustain. Energy Rev. 2016, 54, 421–428. [Google Scholar] [CrossRef]
- Harussani, M.M.; Sapuan, S.M.; Rashid, U.; Khalina, A.; Ilyas, R.A. Pyrolysis of polypropylene plastic waste into carbonaceous char: Priority of plastic waste management amidst COVID-19 pandemic. Sci. Total Environ. 2022, 803, 149911. [Google Scholar] [CrossRef]
- Saebea, D.; Ruengrit, P.; Arpornwichanop, A.; Patcharavorachot, Y. Gasification of plastic waste for synthesis gas production. Energy Rep. 2020, 6, 202–207. [Google Scholar] [CrossRef]
- Domingo, M.J.; Bingwa, N.; Meijboom, R. Review of supported metal nanoparticles: Synthesis methodologies, advantages, and application as catalysts. J. Mater. Sci. 2020, 55, 6195–6241. [Google Scholar]
- Maqsood, T.; Dai, J.; Zhang, Y.; Guang, M.; Li, B. Pyrolysis of plastic species: A review of resources and products. J. Anal. Appl. Pyrolysis 2021, 159, 105295. [Google Scholar] [CrossRef]
- Arshad, H.; A Sulaiman, S.; Hussain, Z.; Naz, Y.; Basrawi, F. Microwave-assisted pyrolysis of plastic waste for the production of fuels: A review. MATEC Web Conf. 2017, 131, 02005. [Google Scholar] [CrossRef]
- Wirawan, R.P. Farizal Plastic Waste Pyrolysis Optimization to Produce Fuel Grade Using Factorial Design. E3S Web Conf. 2019, 125, 13005. [Google Scholar] [CrossRef]
- Joppert, N., Jr.; da Silva, A.A.; Marques, M.R. Enhanced diesel fuel fraction from waste high-density polyethylene and heavy gas oil pyrolysis using factorial design methodology. Waste Manag. 2015, 36, 166–176. [Google Scholar] [CrossRef] [PubMed]
- Pinto, F.; Paradela, F.; Gulyurtlu, I.; Ramos, A.M. Prediction of liquid yields from the pyrolysis of waste mixtures using response surface methodology. Fuel Process. Technol. 2013, 116, 271–283. [Google Scholar] [CrossRef]
- Inayat, M.; Sulaiman, S.A.; Inayat, A.; Shaik, N.B.; Gilal, A.R.; Shahbaz, M. Modeling and parametric optimization of air catalytic co-gasification of wood-oil palm fronds blend for clean syngas (H2+CO) production. Int. J. Hydrog. Energy 2021, 46, 30559–30580. [Google Scholar] [CrossRef]
- Ali, A.M.; Inayat, M.; Zahrani, A.A.; Shahzad, K.; Shahbaz, M.; Sulaiman, S.A.; Sadig, H. Process optimization and economic evaluation of air gasification of Saudi Arabian date palm fronds for H2-rich syngas using response surface methodology. Fuel 2022, 316, 123359. [Google Scholar] [CrossRef]
- Krishna, J.J.; Korobeinichev, O.P.; Vinu, R. Isothermal fast pyrolysis kinetics of synthetic polymers using analytical Pyroprobe. J. Anal. Appl. Pyrolysis 2019, 139, 48–58. [Google Scholar] [CrossRef]
- Harmon, R.E.; SriBala, G.; Broadbelt, L.J.; Burnham, A.K. Insight into Polyethylene and Polypropylene Pyrolysis: Global and Mechanistic Models. Energy Fuels 2021, 35, 6765–6775. [Google Scholar] [CrossRef]
- Senneca, O.; Tucciullo, T. Lumped Kinetics for Homogeneous Reactions of n-Hexadecane and n-Decene as Model Compounds for PE Pyrolysis Primary Tars. Energies 2020, 13, 5466. [Google Scholar] [CrossRef]
- Al-Salem, S.M.; Lettieri, P. Kinetic study of high density polyethylene (HDPE) pyrolysis. Chem. Eng. Res. Des. 2010, 88, 1599–1606. [Google Scholar] [CrossRef]
- Saunders, K.J. Organic Polymer Chemistry: An Introduction to the Organic Chemistry of Adhesives, Fibres, Paints, plastics and Rubbers; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Diaz-Silvarrey, L.S.; McMahon, A.; Phan, A.N. Benzoic acid recovery via waste poly(ethylene terephthalate) (PET) catalytic pyrolysis using sulphated zirconia catalyst. J. Anal. Appl. Pyrolysis 2018, 134, 621–631. [Google Scholar] [CrossRef]
- Bracco, P.; Costa, L.; Luda, M.P.; Billingham, N. A review of experimental studies of the role of free-radicals in polyethylene oxidation. Polym. Degrad. Stab. 2018, 155, 67–83. [Google Scholar] [CrossRef]
- Eidesen, H.; Khawaja, H.; Jackson, S. Simulation of the HDPE Pyrolysis Process. Int. J. Multiphysics 2018, 12, 79–88. [Google Scholar]
- Balboa, P. BalbiaPesific. 2004. Available online: http://www.balboapacific.com/Papers/HistoryOfPyrolysis.pdf (accessed on 3 November 2016).
- Debecker, D.P.; Le Bras, S.; Boissière, C.; Chaumonnot, A.; Sanchez, C. Aerosol processing: A wind of innovation in the field of advanced heterogeneous catalysts. Chem. Soc. Rev. 2018, 47, 4112–4155. [Google Scholar] [CrossRef]
- Norsk, k. Polymerisasjonskjemi. 2007. Available online: http://www.naturfag.no/artikkel/vis.html?tid=689055 (accessed on 18 November 2016).
- Alqarni, A.O.; Nabi RA, U.; Althobiani, F.; Naz, M.Y.; Shukrullah, S.; Khawaja, H.A.; Bou-Rabee, M.A.; Gommosani, M.E.; Abdushkour, H.; Irfan, M.; et al. Statistical Optimization of Pyrolysis Process for Thermal Destruction of Plastic Waste Based on Temperature-Dependent Activation Energies and Pre-Exponential Factors. Processes 2022, 10, 1559. [Google Scholar] [CrossRef]
- Nabi, R.A.U.; Naz, M.Y.; Shukrullah, S.; Ghamkhar, M.; Rehman, N.U.; Irfan, M.; Alqarni, A.O.; Legutko, S.; Kruszelnicka, I.; Ginter-Kramarczyk, D.; et al. Analysis of Statistically Predicted Rate Constants for Pyrolysis of High-Density Plastic Using R Software. Materials 2022, 15, 5910. [Google Scholar] [CrossRef]
- Piskulich, Z.A.; Thompson, W.H. Examining the role of different molecular interactions on activation energies and activation volumes in liquid water. J. Chem. Theory Comput. 2021, 17, 2659–2671. [Google Scholar] [CrossRef]
- Yang, J.; Rizkiana, J.; Widayatno, W.B.; Karnjanakom, S.; Kaewpanha, M.; Hao, X.; Abudula, A.; Guanac, G. Fast co-pyrolysis of low density polyethylene and biomass residue for oil production. Energy Convers. Manag. 2016, 120, 422–429. [Google Scholar] [CrossRef]
- Dewangan, A.; Pradhan, D.; Singh, R.K. Co-pyrolysis of sugarcane bagasse and low-density polyethylene: Influence of plastic on pyrolysis product yield. Fuel 2016, 185, 508–516. [Google Scholar] [CrossRef]
- Fan, L.; Chen, P.; Zhang, Y.; Liu, S.; Liu, Y.; Wang, Y.; Dai, L.; Ruan, R. Fast microwave-assisted catalytic co-pyrolysis of lignin and low-density polyethylene with HZSM-5 and MgO for improved bio-oil yield and quality. Bioresour. Technol. 2017, 225, 199–205. [Google Scholar] [CrossRef] [PubMed]
- Bu, Q.; Chen, K.; Xie, W.; Liu, Y.; Cao, M.; Kong, X.; Chu, Q.; Mao, H. Hydrocarbon rich bio-oil production, thermal behavior analysis and kinetic study of microwave-assisted co-pyrolysis of microwave-torrefied lignin with low density polyethylene. Bioresour. Technol. 2019, 291, 121860. [Google Scholar] [CrossRef] [PubMed]
- Akubo, K.; Nahil, M.A.; Williams, P.T. Aromatic fuel oils produced from the pyrolysis-catalysis of polyethylene plastic with metal-impregnated zeolite catalysts. J. Energy Inst. 2019, 92, 195–202. [Google Scholar] [CrossRef]
- Önal, E.; Uzun, B.B.; Pütün, A.E. An experimental study on bio-oil production from co-pyrolysis with potato skin and high-density polyethylene (HDPE). Fuel Processing Technol. 2012, 104, 365–370. [Google Scholar] [CrossRef]
- Al-Salem, S.M. Thermal pyrolysis of high-density polyethylene (HDPE) in a novel fixed bed reactor system for the production of high-value gasoline range hydrocarbons (HC). Process Saf. Environ. Prot. 2019, 127, 171–179. [Google Scholar] [CrossRef]
- Khan, M.Z.H.; Sultana, M.; Al-Mamun, M.R.; Hasan, M.R. Pyrolytic Waste Plastic Oil and Its Diesel Blend: Fuel Characterization. J. Environ. Public Health 2016, 2016, 1–6. [Google Scholar] [CrossRef]
- Rodríguez-Luna, L.; Bustos-Martínez, D.; Valenzuela, E. Two-step pyrolysis for waste HDPE valorization. Process Saf. Environ. Prot. 2021, 149, 526–536. [Google Scholar] [CrossRef]
- Park, K.B.; Choi, M.J.; Chae, D.Y.; Jung, J.; Kim, J.S. Separate two-step and continuous two-stage pyrolysis of a waste plastic mixture to produce a chlorine-depleted oil. Energy 2022, 244, 122583. [Google Scholar] [CrossRef]
- Sun, K.; Themelis, N.J.; Bourtsalas, A.; Huang, Q. Selective production of aromatics from waste plastic pyrolysis by using sewage sludge derived char catalyst. J. Clean. Prod. 2020, 268, 122038. [Google Scholar] [CrossRef]
- Demirbas, A. Pyrolysis of municipal plastic wastes for recovery of gasoline range hydrocarbons. J. Anal. Appl. Pyrolysis 2004, 72, 97–102. [Google Scholar] [CrossRef]
- Gardy, J.; Hassanpour, A.; Lai, X.; Cunliffe, A.; Rehan, M. The influence of blending process on the quality of rapeseed oil-used cooking oil biodiesels. Int. Sci. J. Environ. Sci. 2014, 3, 233–240. [Google Scholar]
- Islam, M.R.; Parveen, M.; Haniu, H.; Sarker, M.I. Innovation in pyrolysis technology for the management of scrap tire: A solution of Energy and Environment. Int. J. Environ. Sci. Dev. 2010, 1, 89–96. [Google Scholar] [CrossRef]
- Lee, S.; Yoshida, K.; Yoshikawa, K. Application of waste plastic pyrolysis oil in a direct injection diesel engine: For a small scale non-grid electrification. Energy Environ. Res. 2015, 5, 18–32. [Google Scholar] [CrossRef]

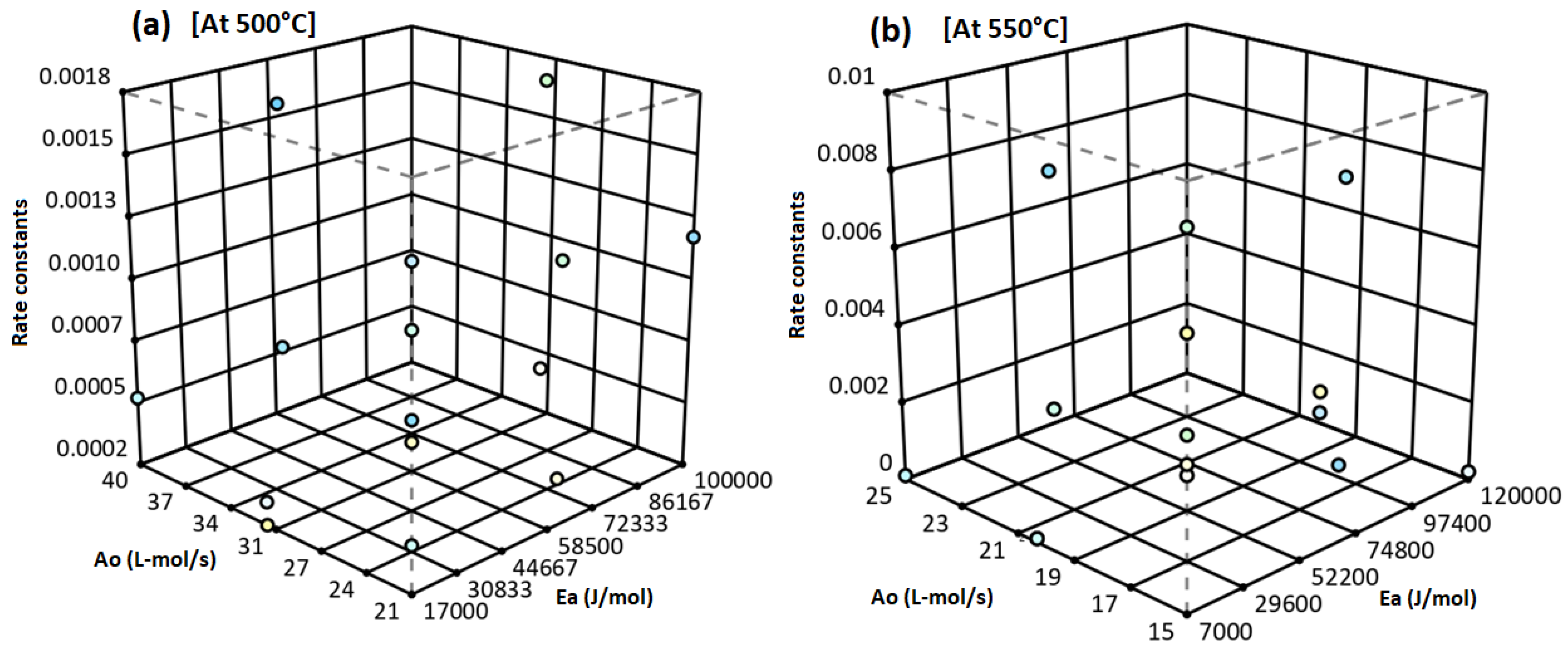
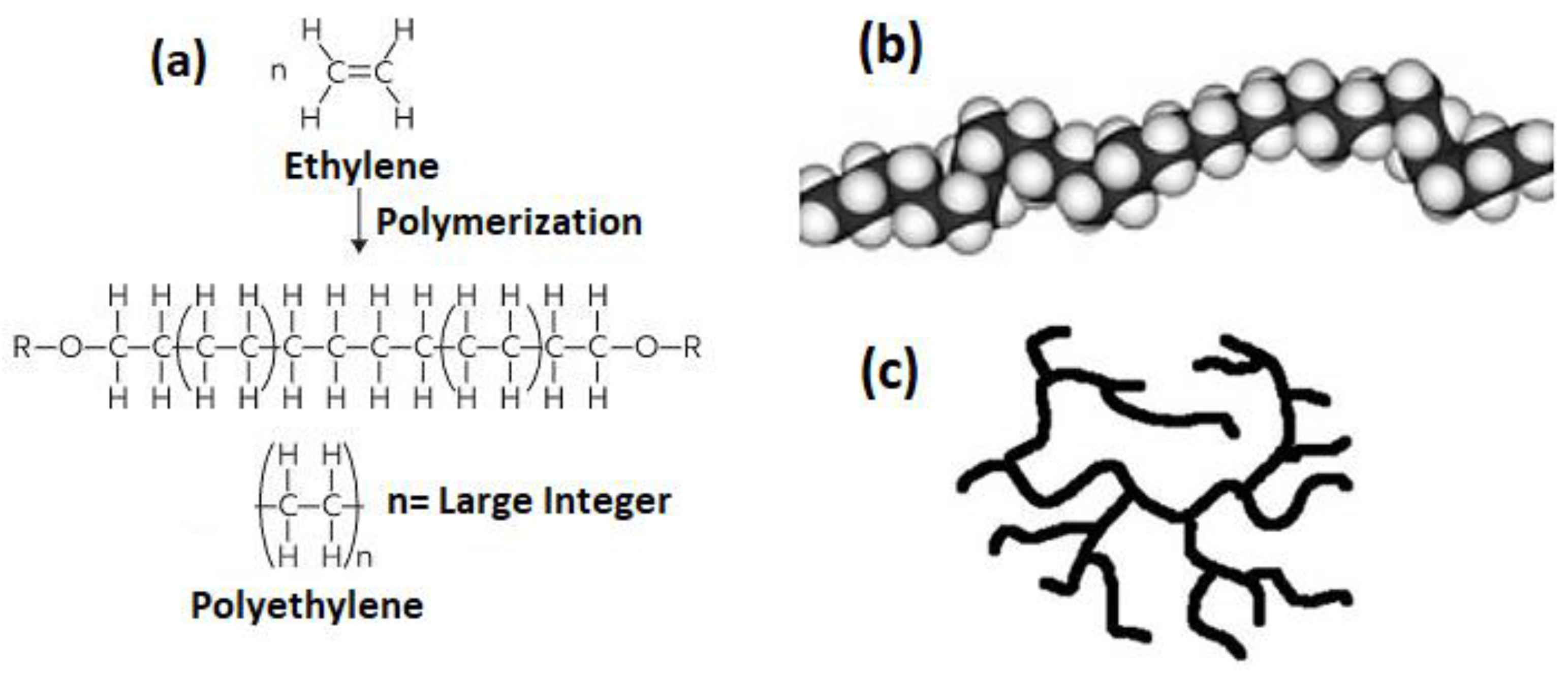


| Settings | 500 °C | 550 °C |
|---|---|---|
| Study Type | Response Surface | Response Surface |
| Design Type | Box–Behnken | Box–Behnken |
| Design Model | Quadratic | Quadratic |
| Build Time (ms) | 1.0000 | 2.00 |
| Subtype | Randomized | Randomized |
| Runs | 15 | 15 |
| Blocks | No Blocks | No Blocks |
| At 500 °C | ||||||||
|---|---|---|---|---|---|---|---|---|
| Factor | Units | Type | Minimum | Maximum | Coded Low | Coded High | Mean | Std. Dev. |
| A | J/mol | Numeric | 7000.00 | 1.200 × 105 | −1 ↔ 7000.00 | +1 ↔120,000 | 63,500.00 | 42,709.99 |
| B | L-mol/s | Numeric | 15.00 | 25.00 | −1 ↔ 15.00 | +1 ↔ 25.00 | 20.00 | 3.78 |
| C | C | Numeric | 500.00 | 600.00 | −1 ↔ 500.00 | +1 ↔ 600.00 | 550.00 | 37.80 |
| Resp. | Analysis | Min. | Max. | Mean | Std. Dev. | Ratio | Trans. | Model |
| R1 = kA | Polynomial | 0 | 0.0013 | 0.0004 | 0.0004 | Not applicable | None | Linear |
| At 550 °C | ||||||||
| A = Ea | J/mol | Numeric | 7000.00 | 1.500 × 105 | −1 ↔ 7000.00 | +1 ↔150,000 | 78,500.00 | 54,048.92 |
| B = Ao | L-mol/s | Numeric | 19.00 | 30.00 | −1 ↔ 19.00 | +1 ↔ 30.00 | 24.50 | 4.16 |
| C = T | °C | Numeric | 500.00 | 600.00 | −1 ↔ 500.00 | +1 ↔ 600.00 | 550.00 | 37.80 |
| Resp. | Analysis | Min. | Max. | Mean | Std. Dev. | Ratio | Trans. | Model |
| R2 = kB | Polynomial | 0.0001 | 0.009 | 0.0021 | 0.0033 | 90.00 | None | Quadratic |
| At 500 °C | |||||
|---|---|---|---|---|---|
| Source | Sum of Squares | Mean Square | F-Value | p-Value | |
| Model | 1.452 × 106 | 4.842 × 107 | 3.87 | 0.0411 | Significant |
| A-Ea | 7.200 × 107 | 7.200 × 107 | 5.75 | 0.0353 | |
| B-Ao | 2.812 × 107 | 2.812 × 107 | 2.25 | 0.1620 | |
| C-T | 4.512 × 107 | 4.512 × 107 | 3.61 | 0.0841 | |
| Residual | 1.377 × 106 | 1.252 × 107 | |||
| Lack of Fit | 1.290 × 106 | 1.434 × 107 | 3.31 | 0.2537 | Not significant |
| Pure Error | 8.667 × 108 | 2 | 4.333 × 108 | ||
| Cor Total | 2.829 × 106 | 14 | |||
| Adj. R2 = 0.5752 | Pred. R2 = 0.3651 | ||||
| At 550 °C | |||||
| Model | 0.0001 | 0.0000 | 6.13 | 0.0300 | Significant |
| A-Ea | 5.611 × 106 | 5.611 × 106 | 2.24 | 0.1950 | |
| B-Ao | 0.0000 | 0.0000 | 6.59 | 0.0502 | |
| C-T | 5.000 × 109 | 5.000 × 109 | 0.0020 | 0.9661 | |
| AB | 0.0000 | 0.0000 | 9.77 | 0.0261 | |
| AC | 9.000 × 108 | 9.000 × 108 | 0.0359 | 0.8572 | |
| BC | 0.0000 | 0.0000 | 18.43 | 0.0078 | |
| A2 | 4.434 × 106 | 4.434 × 106 | 1.77 | 0.2411 | |
| B2 | 0.0000 | 0.0000 | 14.64 | 0.0123 | |
| C2 | 2.854 × 106 | 2.854 × 106 | 1.14 | 0.3349 | |
| Residual | 0.0000 | 2.509 × 106 | |||
| Lack of Fit | 0.0000 | 3.966 × 106 | 12.27 | 0.0763 | Not significant |
| Pure Error | 6.467 × 107 | 3.233 × 107 | |||
| Cor Total | 0.0002 | ||||
| Adj. R2= −0.0859 | Pred. R2= −0.7746 | ||||
| At 500 °C | |||||
|---|---|---|---|---|---|
| Factor | Coefficient Estimate | Standard Error | 95% CI Low | 95% CI High | VIF |
| Intercept | 0.0004 | 0.0001 | 0.0002 | 0.0006 | |
| A-Ea | −0.0003 | 0.0001 | −0.0006 | −0.0000 | 1.0000 |
| B-Ao | 0.0002 | 0.0001 | −0.0001 | 0.0005 | 1.0000 |
| C-T | 0.0002 | 0.0001 | −0.0000 | 0.0005 | 1.0000 |
| At 550 °C | |||||
| Intercept | 0.0006 | 0.0009 | −0.0018 | 0.0029 | |
| A-Ea | −0.0008 | 0.0006 | −0.0023 | 0.0006 | 1.0000 |
| B-Ao | −0.0014 | 0.0006 | −0.0029 | 2.035 × 106 | 1.0000 |
| C-T | −0.0000 | 0.0006 | −0.0015 | 0.0014 | 1.0000 |
| AB | 0.0025 | 0.0008 | 0.0004 | 0.0045 | 1.0000 |
| AC | −0.0001 | 0.0008 | −0.0022 | 0.0019 | 1.0000 |
| BC | −0.0034 | 0.0008 | −0.0054 | −0.0014 | 1.0000 |
| A2 | −0.0011 | 0.0008 | −0.0032 | 0.0010 | 1.0000 |
| B2 | 0.0032 | 0.0008 | 0.0010 | 0.0053 | 1.0000 |
| C2 | 0.0009 | 0.0008 | −0.0012 | 0.0030 | 1.0000 |
| Experimentally Fixed Rate Constants | Statistically Predicted with Suggested Combination of Ea and Ao | ||||||
|---|---|---|---|---|---|---|---|
| At 500 °C | At 550 °C | ||||||
| 500 | 550 | Ea | Ao | kA | Ea | Ao | kB |
| k(1) = 0.0015 | k(1) = 0.008 | J/mol | L-mol/s | N/A | J/mol | L-mol/s | N/A |
| k(2) = 0.001 | k(2) = 0.0042 | 58,500 | 30.5 | k(1) = 0.0012 | 63,500 | 20 | k(1) = 0.0012 |
| k(3) = 0.0006 | k(3) = 0.0042 | 17,000 | 21 | k(2) = 0.0009 | 7000 | 15 | k(2) = 0.009 |
| k(4) = 0.0004 | k(4) = 0.0037 | 17,000 | 40 | k(3) = 0.0004 | 7000 | 25 | k(3) = 0.0001 |
| k(5) = 0.003 | k(5) = 0.0042 | 58,500 | 30.5 | k(4) = 0.00 | 120,000 | 15 | k(4) = 0.0002 |
| k(6) = 0.003 | k(6) = 0.0034 | 100,000 | 21 | k(5) = 0.0001 | 63,500 | 20 | k(5) = 0.0001 |
| k(7) = 0.0002 | k(7) = 0.0009 | 100,000 | 40 | k(6) = 0.000 | 63,500 | 20 | k(6) = 0.0004 |
| 58,500 | 30.5 | k(7) = 0.0001 | 120,000 | 25 | k(7) = 0.0012 | ||
| Time | HDPE | Gas | Oil | Wax | Aromatics | Char |
|---|---|---|---|---|---|---|
| Minutes | (%) | |||||
| Experimental at 500 °C | ||||||
| 15 | 5 | 37 | 29 | 11 | 11 | 7 |
| 30 | 0 | 38 | 33 | 7 | 13 | 4 |
| 60 | 0 | 38 | 36 | 2 | 15 | 3 |
| Statistical at 500 °C | ||||||
| 15 | 8 | 44 | 31 | 13 | 0 | 3 |
| 30 | 0 | 45 | 34 | 13 | 1 | 3 |
| 60 | 0 | 46 | 34 | 3 | 3 | 3 |
| Experimental at 550 °C | ||||||
| 15 | 0 | 32 | 30 | 0 | 18 | 17 |
| 30 | 0 | 32 | 30 | 0 | 18 | 17 |
| 60 | 0 | 32 | 30 | 0 | 18 | 17 |
| Statistical at 550 °C | ||||||
| 15 | 0 | 11 | 85 | 0 | 1 | 1 |
| 30 | 0 | 11 | 85 | 0 | 1 | 1 |
| 60 | 0 | 11 | 85 | 0 | 1 | 1 |
| Waste Type | Method | Temperature | Yield (%) | Reference |
|---|---|---|---|---|
| HDPE | Co-pyrolysis | 600 °C | 43.36 | [32] |
| LDPE | Co-pyrolysis | 500 °C | 52.75 | [33] |
| LDPE | Co-pyrolysis | 500 °C | 77.01 | [34] |
| LDPE | Co-pyrolysis | 250–320 °C | 80 | [35] |
| LDPE | Pyrolysis | 600 °C | 70 | [36] |
| HDPE | Pyrolysis | 330–490 °C | 76 | [37] |
| HDPE | Pyrolysis | 450–550 °C | 77 | [38] |
| HDPE | Two-step Pyrolysis | 730 °C | 80 | [39] |
| Mix | Pyrolysis | 800 °C | 53 | [40] |
| HDPE | Pyrolysis | 535–675 °C | 57 | [41] |
| PP, PE | Pyrolysis | 420 °C | 80 | [42] |
| HDPE | Pyrolysis | 500–550 °C | 85% | Current study |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Irfan, M.; Nabi, R.A.U.; Hussain, H.; Naz, M.Y.; Shukrullah, S.; Khawaja, H.A.; Rahman, S.; Ghanim, A.A.J.; Kruszelnicka, I.; Ginter-Kramarczyk, D.; et al. Response Surface Methodology Analysis of Pyrolysis Reaction Rate Constants for Predicting Efficient Conversion of Bulk Plastic Waste into Oil and Gaseous Fuels. Energies 2022, 15, 9594. https://doi.org/10.3390/en15249594
Irfan M, Nabi RAU, Hussain H, Naz MY, Shukrullah S, Khawaja HA, Rahman S, Ghanim AAJ, Kruszelnicka I, Ginter-Kramarczyk D, et al. Response Surface Methodology Analysis of Pyrolysis Reaction Rate Constants for Predicting Efficient Conversion of Bulk Plastic Waste into Oil and Gaseous Fuels. Energies. 2022; 15(24):9594. https://doi.org/10.3390/en15249594
Chicago/Turabian StyleIrfan, Muhammad, Rao Adeel Un Nabi, Hammad Hussain, Muhammad Yasin Naz, Shazia Shukrullah, Hassan Abbas Khawaja, Saifur Rahman, Abdulnoor A. J. Ghanim, Izabela Kruszelnicka, Dobrochna Ginter-Kramarczyk, and et al. 2022. "Response Surface Methodology Analysis of Pyrolysis Reaction Rate Constants for Predicting Efficient Conversion of Bulk Plastic Waste into Oil and Gaseous Fuels" Energies 15, no. 24: 9594. https://doi.org/10.3390/en15249594
APA StyleIrfan, M., Nabi, R. A. U., Hussain, H., Naz, M. Y., Shukrullah, S., Khawaja, H. A., Rahman, S., Ghanim, A. A. J., Kruszelnicka, I., Ginter-Kramarczyk, D., & Legutko, S. (2022). Response Surface Methodology Analysis of Pyrolysis Reaction Rate Constants for Predicting Efficient Conversion of Bulk Plastic Waste into Oil and Gaseous Fuels. Energies, 15(24), 9594. https://doi.org/10.3390/en15249594











