Consumer-Driven Demand-Side Management Using K-Mean Clustering and Integer Programming in Standalone Renewable Grid
Abstract
:1. Introduction
- A demand-side management algorithm is proposed to fulfil the energy gap between generation and consumer demand for standalone renewable energy systems;
- K-mean clustering is used to group the data based on two factors: probability of turning on a specific appliance at time t, and the priority number given by the consumer to that specific appliance;
- Linear integer programming is used to schedule the clusters of appliances based on the available power and state of charge of the battery system.
2. Mathematical Modeling of the Energy Sources
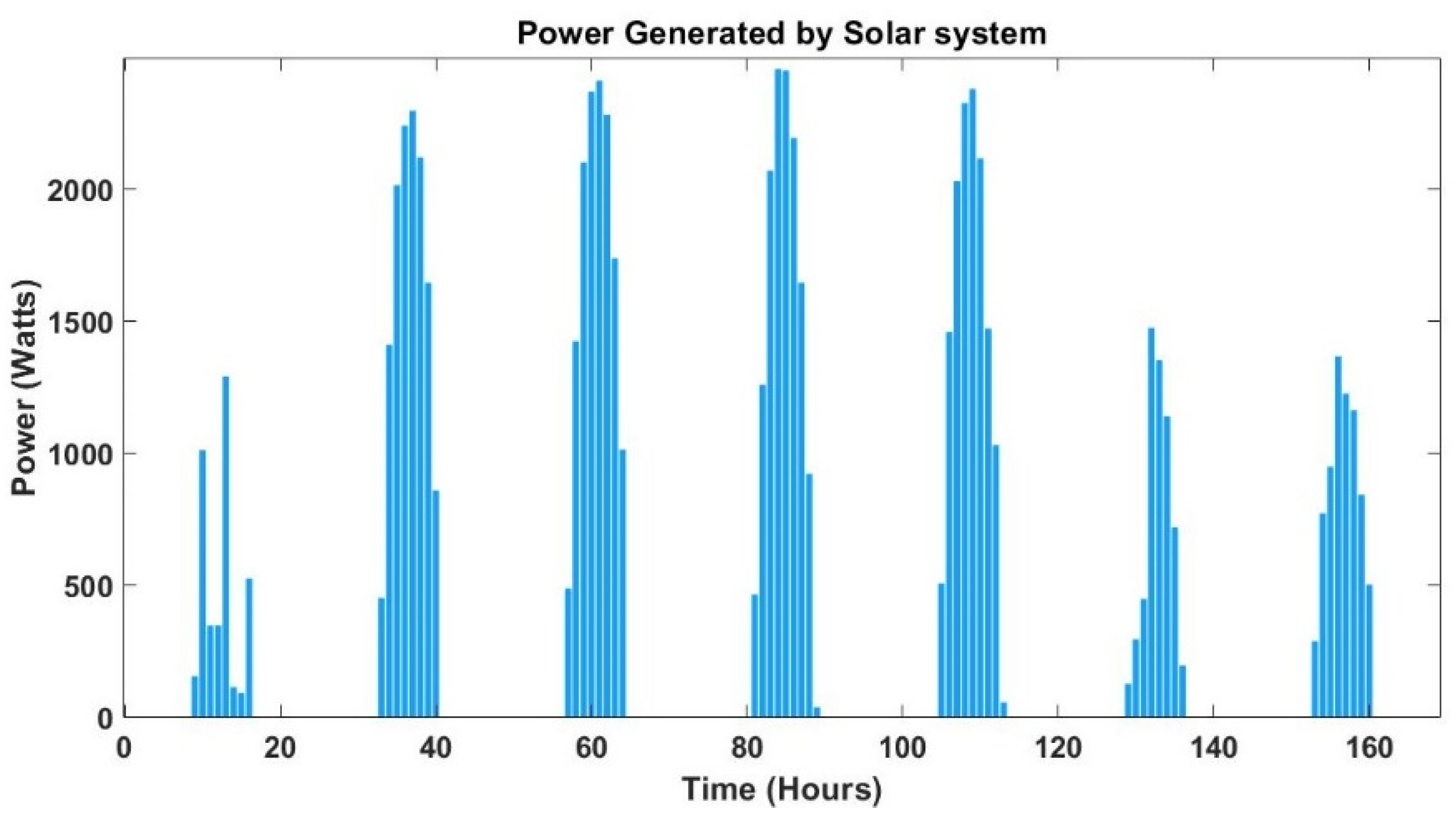
2.1. Solar Panels
2.2. Wind Farm
2.3. Battery Storage
- The SOC of the storage battery changes linearly, and the charging and discharging power are uniform;
- The charging and discharging efficiency of the battery is 100%.
2.4. Diesel Generator
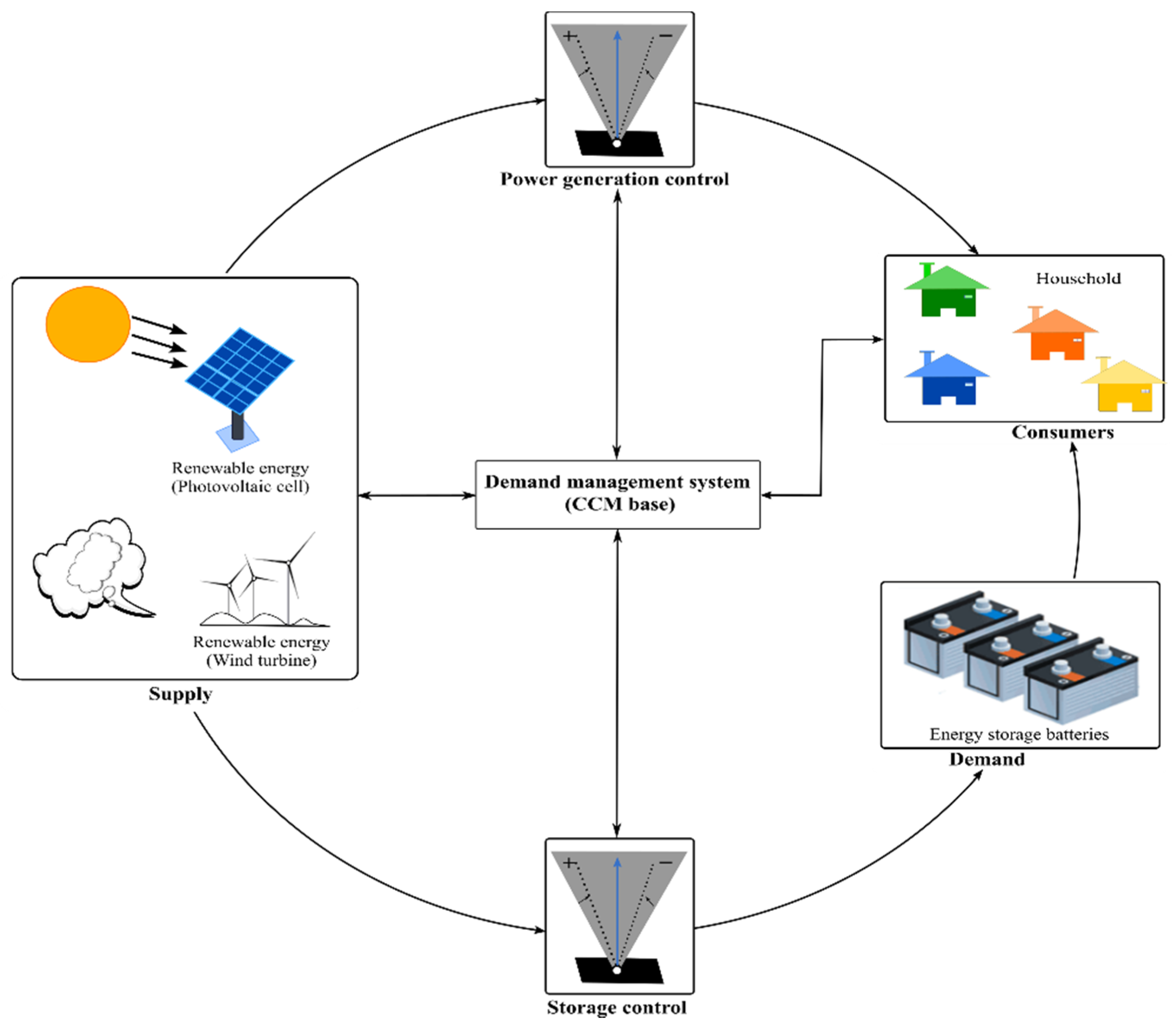
3. System Model and Problem Formulation
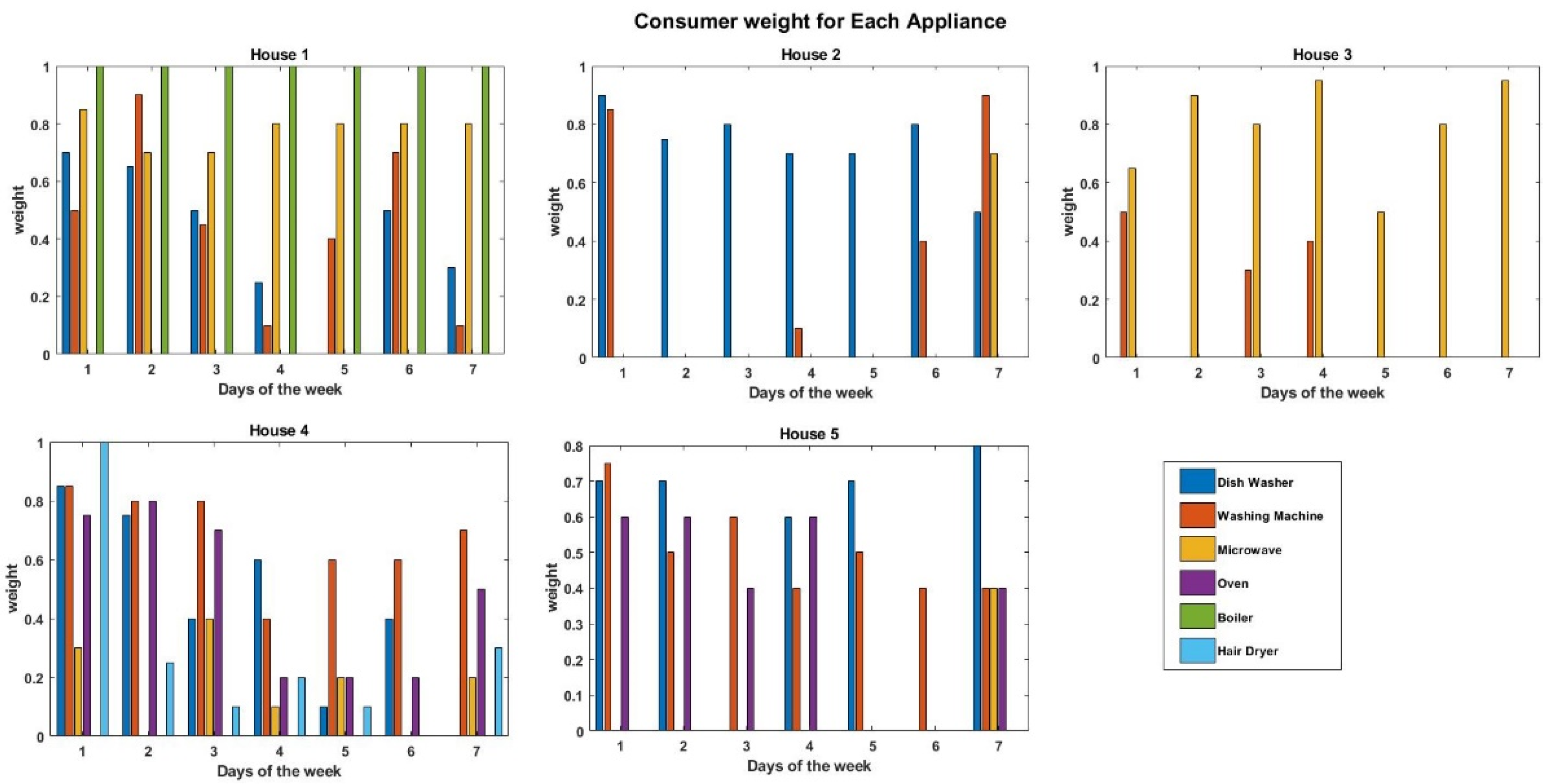
3.1. Probability Weights
3.2. K-Mean Clustering
| Algorithm 1: K-mean clustering algorithm |
| Input: Appliance data of each consumer |
| Initialize: select k number of clusters (Ck) with their centroid value Vk |
| Flag = 0 |
|
3.3. Battery Management System
3.4. Linear Integer Programming
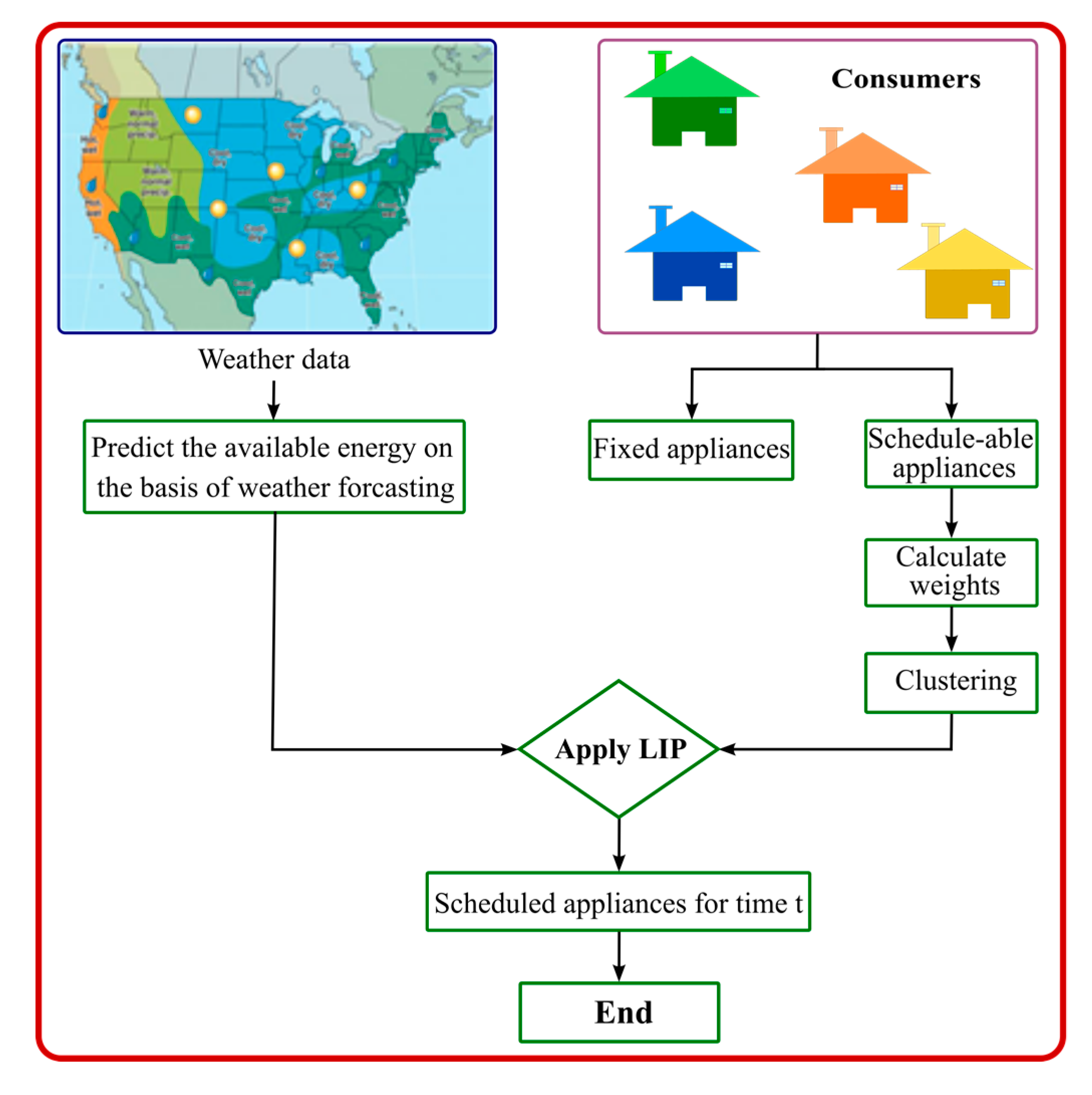
4. Proposed Demand Management System
| Algorithm 2: Categorization of Data |
| Input: Appliance consumption data of the community |
| Consumer appliance preference for weekdays. |
|
| Output: Consumer appliance data in the form of clusters. |
| Algorithm 3: Demand Management System Algorithm |
| Initialize: |
| Flag = 0 |
|
5. Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- IEA-World Energy Outlook 2004. ATW-Internationale Zeitschrift fur Kernenergie; OECD: Paris, France, 2004; Volume 49. [Google Scholar] [CrossRef]
- Alturki, F.; Al-Shamma’A, A.A.; Farh, H.M.H.; Alsharabi, K. Optimal sizing of autonomous hybrid energy system using supply-demand-based optimization algorithm. Int. J. Energy Res. 2021, 45, 605–625. [Google Scholar] [CrossRef]
- Birol, F. World energy outlook, Paris. Int. Energy Agency 2008, 23, 329. [Google Scholar]
- Ogunjuyigbe, A.; Ayodele, T.; Monyei, C. An intelligent load manager for PV powered off-grid residential houses. Energy Sustain. Dev. 2015, 26, 34–42. [Google Scholar] [CrossRef]
- Shezan, S.; Julai, S.; Kibria, M.; Ullah, K.; Saidur, R.; Chong, W.T.; Akikur, R. Performance analysis of an off-grid wind-PV (photovoltaic)-diesel-battery hybrid energy system feasible for remote areas. J. Clean. Prod. 2016, 125, 121–132. [Google Scholar] [CrossRef]
- Tong, S.; Fung, T.; Klein, M.P.; Weisbach, D.A.; Park, J.W. Demonstration of reusing electric vehicle battery for solar energy storage and demand side management. J. Energy Storage 2017, 11, 200–210. [Google Scholar] [CrossRef]
- Yazdaninejadi, A.; Hamidi, A.; Golshannavaz, S.; Aminifar, F.; Teimourzadeh, S. Impact of inverter-based DERs integration on protection, control, operation, and planning of electrical distribution grids. Electr. J. 2019, 32, 43–56. [Google Scholar] [CrossRef]
- Faraji, J.; Babaei, M.; Bayati, N.; A Hejazi, M. A comparative study between traditional backup generator systems and renewable energy based microgrids for power resilience enhancement of a local clinic. Electronics 2019, 8, 1485. [Google Scholar] [CrossRef] [Green Version]
- Basnet, S.M.; Aburub, H.; Jewell, W. Residential demand response program: Predictive analytics, virtual storage model and its optimization. J. Energy Storage 2019, 23, 183–194. [Google Scholar] [CrossRef]
- Mamun, A.; Narayanan, I.; Wang, D.; Sivasubramaniam, A.; Fathy, H. Multi-objective optimization of demand response in a datacenter with lithium-ion battery storage. J. Energy Storage 2016, 7, 258–269. [Google Scholar] [CrossRef] [Green Version]
- Khemakhem, S.; Rekik, M.; Krichen, L. Double layer home energy supervision strategies based on demand response and plug-in electric vehicle control for flattening power load curves in a smart grid. Energy 2019, 167, 312–324. [Google Scholar] [CrossRef]
- Setlhaolo, D.; Xia, X. Combined residential demand side management strategies with coordination and economic analysis. Int. J. Electr. Power Energy Syst. 2016, 79, 150–160. [Google Scholar] [CrossRef]
- Yalcintas, M.; Hagen, W.T.; Kaya, A. An analysis of load reduction and load shifting techniques in commercial and industrial buildings under dynamic electricity pricing schedules. Energy Build. 2015, 88, 15–24. [Google Scholar] [CrossRef]
- Manbachi, M.; Ordonez, M. AMI-Based Energy Management for Islanded AC/DC Microgrids Utilizing Energy Conservation and Optimization. IEEE Trans. Smart Grid 2019, 10, 293–304. [Google Scholar] [CrossRef]
- Soares, A.; Gomes, A.; Antunes, C.H.; Oliveira, C. A customized evolutionary algorithm for multiobjective management of residential energy resources. IEEE Trans. Ind. Inform. 2017, 13, 492–501. [Google Scholar] [CrossRef]
- Gudi, N.; Wang, L.; Devabhaktuni, V. A demand side management based simulation platform incorporating heuristic optimization for management of household appliances. Int. J. Electr. Power Energy Syst. 2012, 43, 185–193. [Google Scholar] [CrossRef]
- Cortés-Arcos, T.; Bernal-Agustín, J.L.; Dufo-López, R.; Lujano-Rojas, J.M.; Contreras, J. Multi-objective demand response to real-time prices (RTP) using a task scheduling methodology. Energy 2017, 138, 19–31. [Google Scholar] [CrossRef]
- Basit, A.; Sidhu, G.A.S.; Mahmood, A.; Gao, F. Efficient and Autonomous Energy Management Techniques for the Future Smart Homes. IEEE Trans. Smart Grid 2017, 8, 917–926. [Google Scholar] [CrossRef]
- Kleszcz-Szczyrba, R. ‘Pomagać soba̧’-Rozważania na temat czynników niespecyficznych w psychoterapii zwia̧zanych z osoba̧ psychoterapeuty. Psychoterapia 2010, 1, 61–72. [Google Scholar]
- Mohsenian-Rad, A.-H.; Wong, V.W.S.; Jatskevich, J.; Schober, R.; Leon-Garcia, A. Autonomous Demand-Side Management Based on Game-Theoretic Energy Consumption Scheduling for the Future Smart Grid. IEEE Trans. Smart Grid 2010, 1, 320–331. [Google Scholar] [CrossRef] [Green Version]
- Bharathi, C.; Rekha, D.; Vijayakumar, V. Genetic Algorithm Based Demand Side Management for Smart Grid. Wirel. Pers. Commun. 2017, 93, 481–502. [Google Scholar] [CrossRef]
- Mohseni, S.; Brent, A.C.; Burmester, D.; Browne, W.N. Lévy-flight moth-flame optimisation algorithm-based micro-grid equipment sizing: An integrated investment and operational planning approach. Energy AI 2021, 3, 100047. [Google Scholar] [CrossRef]
- Sheykhloei, B.; Abedinzadeh, T.; Mohammadian, L.; Mohammadi-Ivatloo, B. Optimal co-scheduling of distributed generation resources and natural gas network considering uncertainties. J. Energy Storage 2019, 21, 383–392. [Google Scholar] [CrossRef]
- Conejo, A.; Morales, J.; Baringo, L. Real-time demand response model. IEEE Trans. Smart Grid 2010, 1, 236–242. [Google Scholar] [CrossRef]
- Ayub, M.A.; Hassan, N.U.; Yuen, C. Hybrid Iterative Algorithm for Non-Intrusive Load Disaggregation. In Proceedings of the 2018 IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20–24 May 2018. [Google Scholar] [CrossRef]
- Rastegar, M.; Fotuhi-Firuzabad, M.; Aminifar, F. Load commitment in a smart home. Appl. Energy 2012, 96, 45–54. [Google Scholar] [CrossRef]
- Rastegar, M.; Fotuhi-Firuzabad, M.; Zareipour, H. Home energy management incorporating operational priority of appliances. Int. J. Electr. Power Energy Syst. 2016, 74, 286–292. [Google Scholar] [CrossRef]
- Eren, Y.; Küçükdemiral, I.B.; Üstoğlu, I. Introduction to Optimization; Butterworth–Heinemann: Oxford, UK, 2017. [Google Scholar]
- Khasanov, M.; Kamel, S.; Rahmann, C.; Hasanien, H.M.; Al-Durra, A. Optimal distributed generation and battery energy storage units integration in distribution systems considering power generation uncertainty. IET Gener. Transm. Distrib. 2021, 15, 3400–3422. [Google Scholar] [CrossRef]
- Tostado-Véliz, M.; Icaza-Alvarez, D.; Jurado, F. A novel methodology for optimal sizing photovoltaic-battery systems in smart homes considering grid outages and demand response. Renew. Energy 2021, 170, 884–896. [Google Scholar] [CrossRef]
- Wu, X.; Hu, X.; Teng, Y.; Qian, S.; Cheng, R. Optimal integration of a hybrid solar-battery power source into smart home nanogrid with plug-in electric vehicle. J. Power Sources 2017, 363, 277–283. [Google Scholar] [CrossRef] [Green Version]
- Arévalo, P.; Tostado-Véliz, M.; Jurado, F. A novel methodology for comprehensive planning of battery storage systems. J. Energy Storage 2021, 37, 102456. [Google Scholar] [CrossRef]
- Xu, J.Y.W. Power disturbance data analytics–new application of power quality monitoring data. Proc. CSEE 2013, 33, 93–101. [Google Scholar]
- Mohassel, R.R.; Fung, A.; Mohammadi, F.; Raahemifar, K. A survey on Advanced Metering Infrastructure. Int. J. Electr. Power Energy Syst. 2014, 63, 473–484. [Google Scholar] [CrossRef] [Green Version]
- Tu, C.; He, X.; Shuai, Z.; Jiang, F. Big data issues in smart grid–A review. Renew. Sustain. Energy Rev. 2017, 79, 1099–1107. [Google Scholar] [CrossRef]
- Semeraro, L.; Crisostomi, E.; Franco, A.; Landi, A.; Raugi, M.; Tucci, M.; Giunta, G. Electrical load clustering: The Italian case. In Proceedings of the IEEE PES Innovative Smart Grid Technologies, Istanbul, Turkey, 2 January 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Benítez, I.; Quijano, A.; Diez, J.L.; Delgado, I. Dynamic clustering segmentation applied to load profiles of energy consumption from Spanish customers. Int. J. Electr. Power Energy Syst. 2014, 55, 437–448. [Google Scholar] [CrossRef]
- Li, R.; Gu, C.; Li, F.; Shaddick, G.; Dale, M. Development of Low Voltage Network Templates—Part I: Substation Clustering and Classification. IEEE Trans. Power Syst. 2015, 30, 3036–3044. [Google Scholar] [CrossRef]
- Gulbinas, R.; Khosrowpour, A.; Taylor, J. Segmentation and Classification of Commercial Building Occupants by Energy-Use Efficiency and Predictability. IEEE Trans. Smart Grid 2015, 6, 1414–1424. [Google Scholar] [CrossRef]
- Ma, S.; Geng, H.; Yang, G.; Pal, B.C. Clustering-Based Coordinated Control of Large-Scale Wind Farm for Power System Frequency Support. IEEE Trans. Sustain. Energy 2018, 9, 1555–1564. [Google Scholar] [CrossRef]
- Mahela, O.P.; Shaik, A.G. Power quality recognition in distribution system with solar energy penetration using S -transform and Fuzzy C-means clustering. Renew. Energy 2017, 106, 37–51. [Google Scholar] [CrossRef]
- Khan, H.; Wang, X.; Liu, H. Missing value imputation through shorter interval selection driven by Fuzzy C-Means clustering. Comput. Electr. Eng. 2021, 93, 107230. [Google Scholar] [CrossRef]
- Kumar, K.P.; Saravanan, B. Day ahead scheduling of generation and storage in a microgrid considering demand Side management. J. Energy Storage 2019, 21, 78–86. [Google Scholar] [CrossRef]
- Ogunjuyigbe, A.; Ayodele, T.; Oladimeji, O. Management of loads in residential buildings installed with PV system under intermittent solar irradiation using mixed integer linear programming. Energy Build. 2016, 130, 253–271. [Google Scholar] [CrossRef]
- Babaei, M.; Azizi, E.; Beheshti, M.T.; Hadian, M. Data-Driven load management of stand-alone residential buildings including renewable resources, energy storage system, and electric vehicle. J. Energy Storage 2020, 28, 101221. [Google Scholar] [CrossRef]
- El-Bidairi, K.S.; Nguyen, H.D.; Jayasinghe, S.; Mahmoud, T.S.; Penesis, I. A hybrid energy management and battery size optimization for standalone microgrids: A case study for Flinders Island, Australia. Energy Convers. Manag. 2018, 175, 192–212. [Google Scholar] [CrossRef]
- Weather Forecast Data, Canada. Available online: https://ottawa.weatherstats.ca/ (accessed on 29 December 2021).
- Kelly, J.; Knottenbelt, W. The UK-DALE dataset, domestic appliance-level electricity demand and whole-house demand from five UK homes. Sci. Data 2015, 2, 150007. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Makonin, S.; Ellert, B.; Bajić, I.V.; Popowich, F. Electricity, water, and natural gas consumption of a residential house in Canada from 2012 to 2014. Sci. Data 2016, 3, 1–12. [Google Scholar] [CrossRef] [Green Version]
- National Weather Service. Available online: https://www.weather.gov/ddc/avewind (accessed on 29 December 2021).

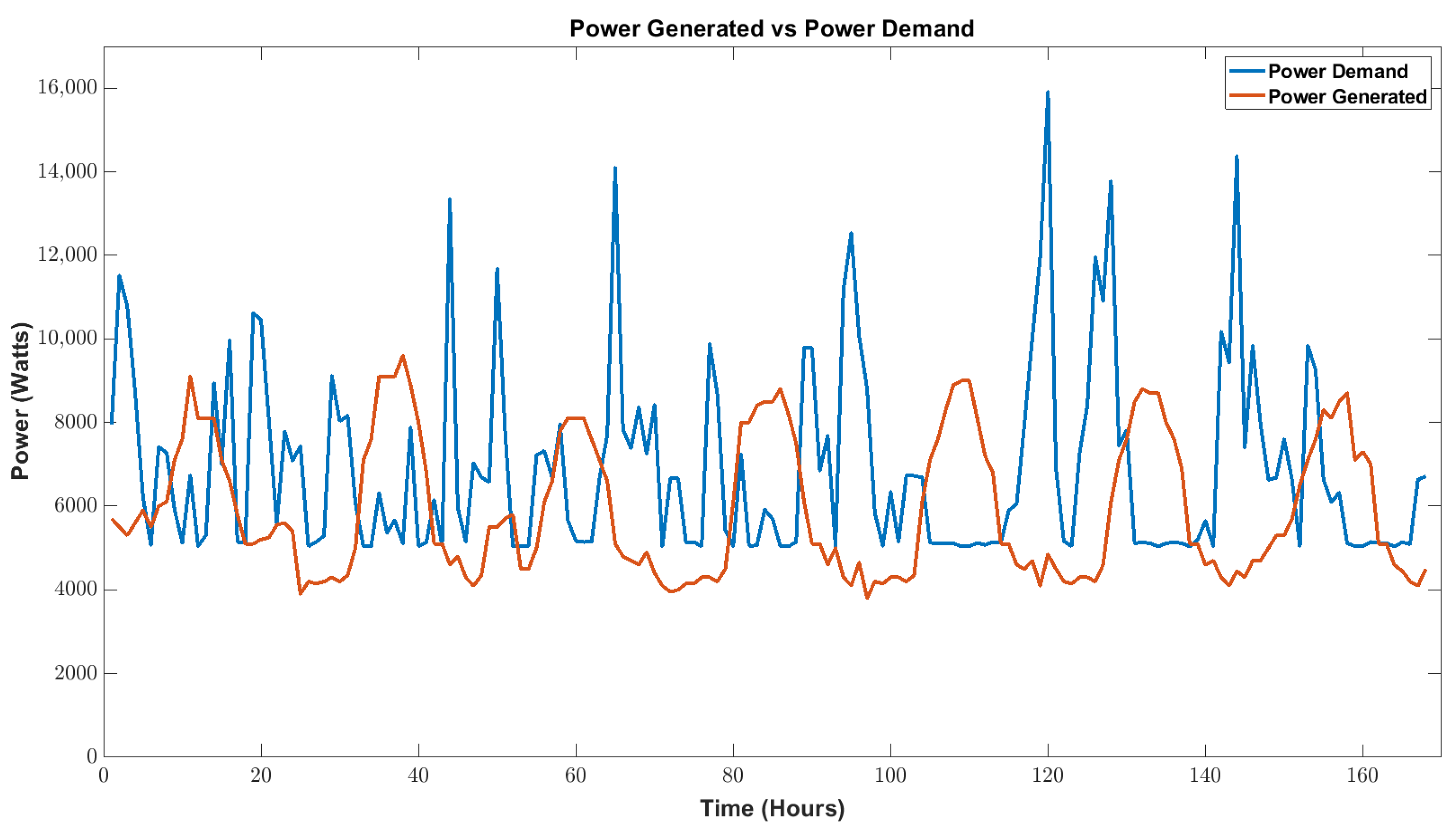
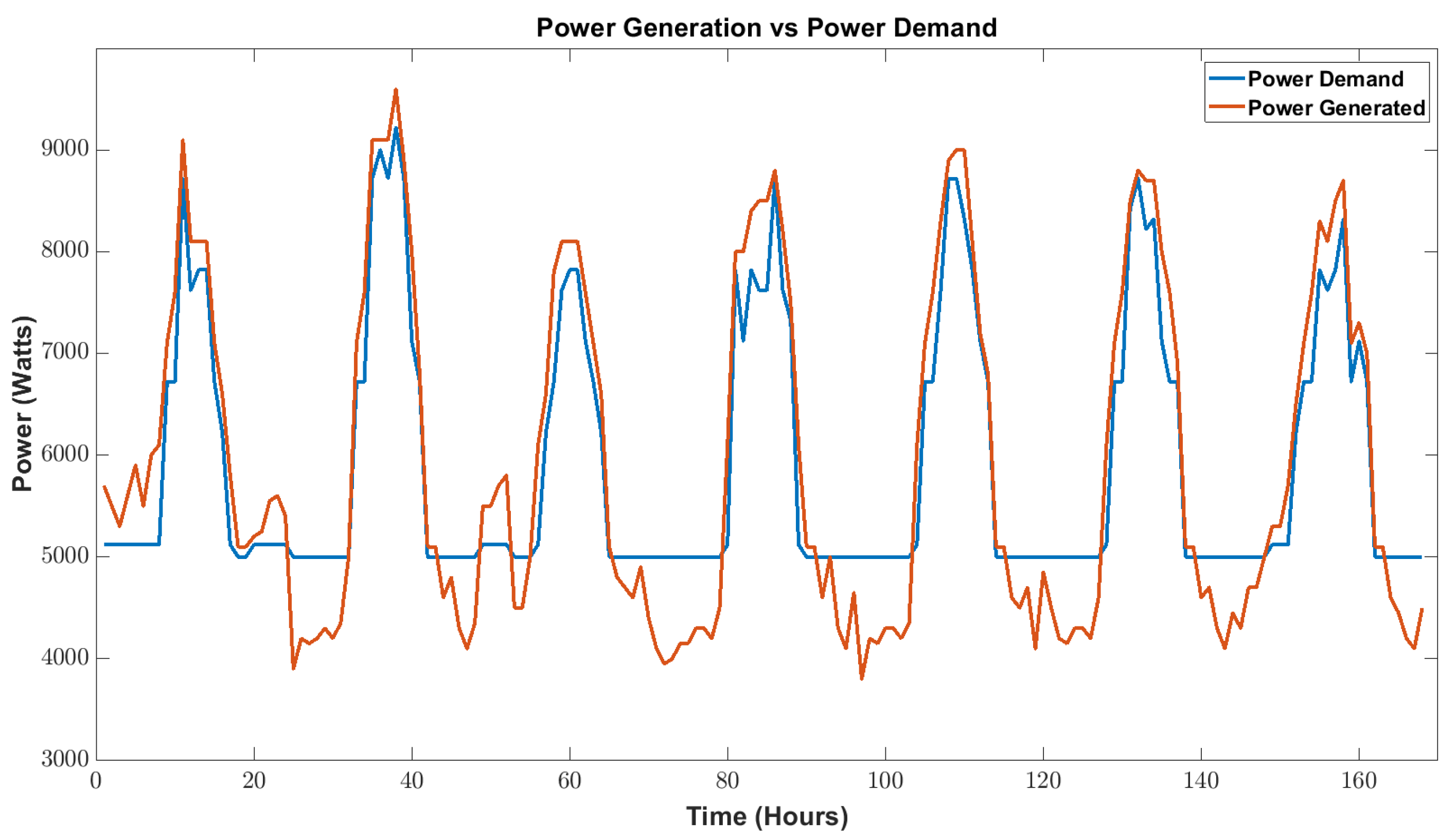

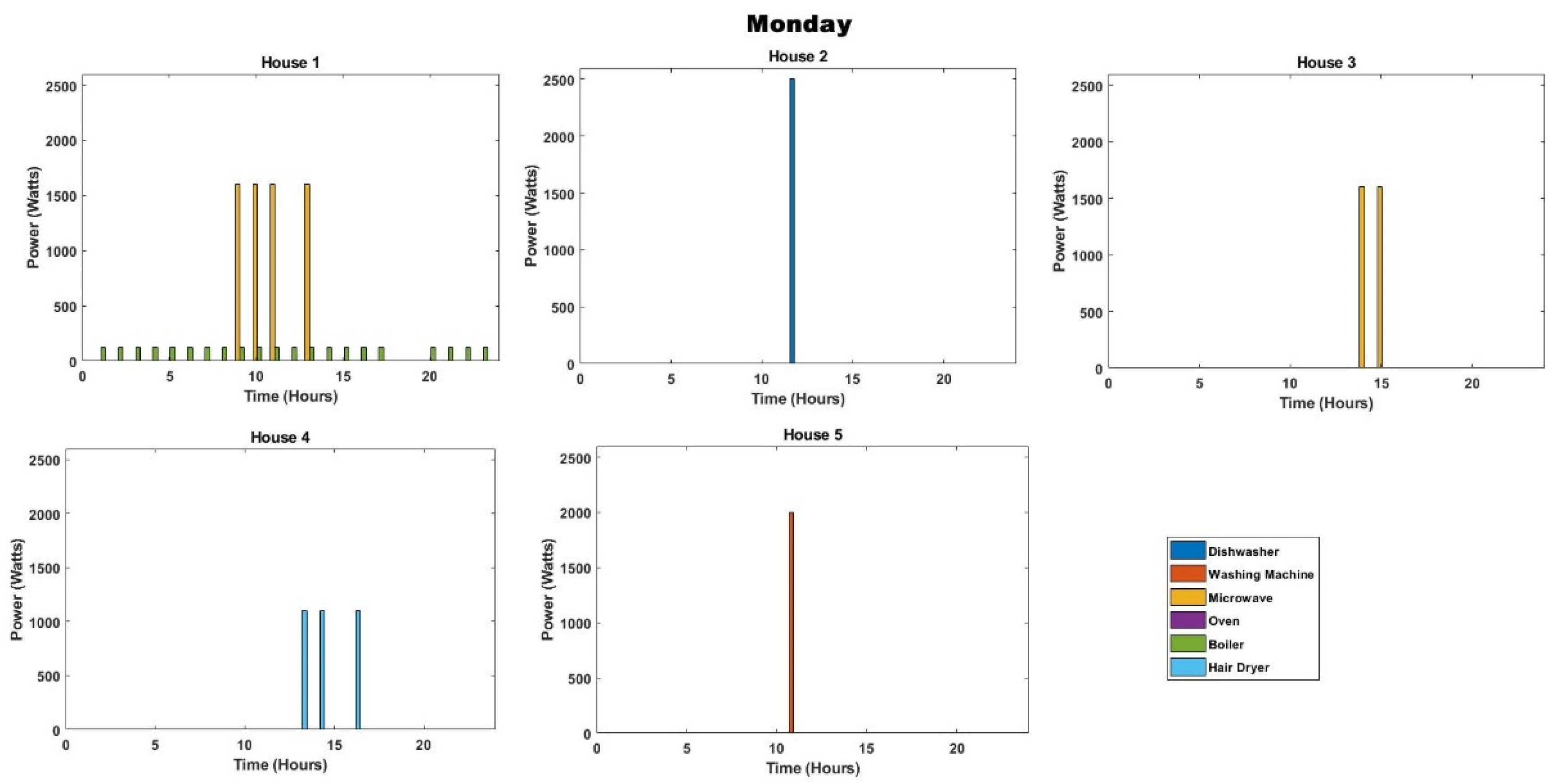

| House | Boiler | DW | Micro | WM | HD | Oven |
|---|---|---|---|---|---|---|
| 1 | ✓ | ✓ | ✓ | ✓ | ||
| 2 | ✓ | ✓ | ||||
| 3 | ✓ | ✓ | ||||
| 4 | ✓ | ✓ | ✓ | ✓ | ✓ | |
| 5 | ✓ | ✓ | ✓ |
| Appliance | Power Rating (watts) |
|---|---|
| Dish Washer (DW) | 2500 |
| Washing Machine (WM) | 2000 |
| Microwave (micro) | 1600 |
| Oven | 2200 |
| Boiler | 120 |
| Hair Dryer (HD) | 1100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ayub, M.A.; Khan, H.; Peng, J.; Liu, Y. Consumer-Driven Demand-Side Management Using K-Mean Clustering and Integer Programming in Standalone Renewable Grid. Energies 2022, 15, 1006. https://doi.org/10.3390/en15031006
Ayub MA, Khan H, Peng J, Liu Y. Consumer-Driven Demand-Side Management Using K-Mean Clustering and Integer Programming in Standalone Renewable Grid. Energies. 2022; 15(3):1006. https://doi.org/10.3390/en15031006
Chicago/Turabian StyleAyub, Muhammad Ahsan, Hufsa Khan, Jianchun Peng, and Yitao Liu. 2022. "Consumer-Driven Demand-Side Management Using K-Mean Clustering and Integer Programming in Standalone Renewable Grid" Energies 15, no. 3: 1006. https://doi.org/10.3390/en15031006
APA StyleAyub, M. A., Khan, H., Peng, J., & Liu, Y. (2022). Consumer-Driven Demand-Side Management Using K-Mean Clustering and Integer Programming in Standalone Renewable Grid. Energies, 15(3), 1006. https://doi.org/10.3390/en15031006







