Evaluation of an Additional Generator on the Economic Effect Based on a Load Sharing Optimization of Medium-Speed/High-Speed Diesel Generators in a Microgrid
Abstract
1. Introduction
- Evaluation of the economic effects of the mixed operation of medium- and high-speed reciprocating engine generators;
- Establishment of a method to accurately approximate non-linear fuel consumption curves from the low range to the high range and optimize them with MIP;
- The proposal of a method to reduce the operating costs of independent MGs that is effective even when the balance between the generator unit configuration and demand changes.
- The proposal of a method to strengthen the resilience of independent MG power plants that cannot receive power support from other sources.
2. Operation of the Diesel Generators in Microgrid
2.1. Assumed Microgrid Conditions
- Located in remote areas such as remote islands;
- The power demand is dominated by consumer use, and large-scale consumers such as the manufacturing industry shall not be there;
- Not connected to other grids, and power is not supplied to nor received from outside;
- Multiple medium-speed generators of several hundred to 2000 kW supply power are used;
- The operation of the generator is controlled to minimize the sum of fuel and maintenance costs;
- The unplanned withdrawal due to unit failure, etc., shall be taken into account for stable power supply.
2.2. Conventional Concept of the Diesel Generators Operation
2.3. Proposal of New Generator Operation Method
2.4. Characteristics of Medium and High-Speed Diesel Generators
3. Optimization Model for Generator Operation
3.1. Features of Modeling
3.2. Objective Function
3.3. Modeling of Conventional Load Sharing Method
3.4. Modeling of Optimal Load Sharing
4. Simulation Results and Discussion
4.1. Micro Grid Power Demand and Generator Assumptions
4.2. Case Setting
4.3. Example Results with Only Medium-Speed Diesel Generators
4.3.1. Conventional Operation (Case 0)
4.3.2. Optimal Operation Case (Case 1)
4.4. The Results of Operation with Additional High-Speed DG
4.4.1. Conventional Operation (Case 2)
4.4.2. Optimal Operation Case (Case 3)
4.4.3. Effect of Adding a High-Speed DG
5. Conclusions
5.1. Results Analysis
5.2. Evaluation for the Optimization of Load Sharing
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Nomenclature
| Index | ||
| Group of Generator units except . | ||
| Hours | 1 to 24 | |
| Generator units | 1 to 6 | |
| The unit number of the maximum capacity | ||
| Month | 1 to 12 | |
| Load factor [%], an integer from | to 100 | |
| Day types | Weekday, Saturday, and Holiday | |
| Variables and parameters | ||
| Minimum operating load factor [%] | ||
| Annual fuel cost [JPY] | ||
| Maintenance cost [JPY] | ||
| Annual operating cost [JPY] | ||
| Number of days for each day type of the target month | ||
| Power demand [kW] | ||
| Rated output of each power generation facility [kW] | ||
| The power generation efficiency of each power generation facility with the load factor [%] as a variable | ||
| Load factor of each power generation facility [%] | ||
| Operating state at each time as binary | ||
| Power generation output [kW] | ||
| Fuel unit price per calorifique value [JPY/kW-h] | ||
| Maintenance unit price [JPY/kWh] | ||
| A variable of function | ||
| η | The uneven performance of the medium-speed DGs | |
| Definitions | ||
| Lower-load operation | operation in load factor less than 50 percent | |
References
- Landbrain Co., Ltd. Survey Report on the Potential of All-Energy Renewable Energy Projects on Small Remote Islands Mar. 2014. Available online: https://www.pref.okinawa.jp/site/shoko/seisaku/kiban/syoukiboritoukoubo/documents/h25houkokusyo1_4.pdf (accessed on 25 October 2021).
- Sasaki, H.; Seino, M.; Hashimoto, N.; Sakata, I. Off-Grid Electrification Scenarios for Rural Electrification in Myanmar. 2018. Available online: https://energypedia.info/wiki/Publication_-_Off-Grid_Electrification_Scenarios_for_Rural_Electrification_in_Myanmar (accessed on 7 October 2021).
- Dulău, L.I.; Bică, D. Optimization of generation cost in a microgrid. Procedia Manuf. 2018, 22, 703–708. [Google Scholar] [CrossRef]
- He, L.; Lu, Z.; Pan, L.; Zhao, H.; Li, X.; Zhang, J. Optimal Economic and Emission Dispatch of a Microgrid with a Combined Heat and Power System. Energies 2019, 12, 604. [Google Scholar] [CrossRef]
- Togawa, T.; Dou, Y.; Oba, M.; Nemoto, K.; Nakumura, S.; Fujii, M. Desing and Standards for Distributed Energy System in the Inter-Mountainous Area. J. Jpn. Soc. Civ. Eng. Ser. G Environ. Res. 2017, 73, I_107–I_119. [Google Scholar] [CrossRef][Green Version]
- Kannengießer, T.; Hoffmann, M.; Kotzur, L.; Stenzel, P.; Schuetz, F.; Peters, K.; Nykamp, S.; Stolten, D.; Robinius, M. Reducing Computational Load for Mixed Integer Linear Programming: An Example for a District and an Island Energy System. Energies 2019, 12, 2825. [Google Scholar] [CrossRef]
- Gildenhuys, T.; Zhang, L.; Ye, X.; Xia, X. Optimization of the Operational Cost and Environmental Impact of a Multi-Microgrid System. Energy Procedia 2019, 158, 3827–3832. [Google Scholar] [CrossRef]
- Ito, K.; Yokoyama, R. A Planning Method for Optimal Operation of Cogeneration Systems: Part 1-Methodological Study. J. Trans. Soc. Heat. Air-Cond. Sanit. Eng. Jpn. 1990, 15, 59–67. (In Japanese) [Google Scholar]
- Chiba, R.; Tanahashi, Y.; Nishiwaki, O.; Tanaka, H. Study on Optimization of Control Parameters for Generator Operation with Multiple Units in a Combined Generator System. J. Trans. Soc. Heat. Air-Cond. Sanit. Eng. Jpn. 2018, 43, 11–19. (In Japanese) [Google Scholar]
- Pang, C.; Mohsenzadeh, A.; Haghifam, M. Determining optimal forming of flexible microgrids in the presenceof demand response in smart distribution systems. IEEE Syst. J. 2017, 12, 3315–3323. [Google Scholar]
- Ghiasi, M.; Niknam, T.; Dehghani, M.; Siano, P.; Alhelou, H.H.; Al-Hinai, A. Optimal Multi-Operation Energy Management in Smart Microgrids in the Presence of RESs Based on Multi-Objective Improved DE Algorithm: Cost-Emission Based Optimization. Appl. Sci. 2021, 11, 3661. [Google Scholar] [CrossRef]
- Koguma, Y.; Inamura, A. Mathematical Optimization Model and Algorithm for Energy System Configuration and Operation. J. IHI Technol. 2019, 59, 24–35. (In Japanese) [Google Scholar]
- Shinji, T.; Kumagai, K.; Akisawa, A.; Kashiwagi, T.; Fujita, G. Study on Generator Dispatching Considering Partial Load Efficiency of GT under a Daily Load Curve in Microgrids. J. Jpn. Inst. Energy 2011, 90, 654–659. [Google Scholar] [CrossRef][Green Version]
- Watanabe, I.; Sagai, S.; Tokoro, K.; Komatsu, H.; Higo, T. Development of Demand and Supply Operation Simulator Considering the Output Fluctuation of Renewable Energy—Prototype Development of Demand and Supply Planning Function. J. Cent. Res. Inst. Electr. Power Ind. 2014, R13013, 1–19. (In Japanese) [Google Scholar]
- Tomita, Y. Glossary 64th Theme: Economic Load Allocation (ELD). IEEJ Trans. Power Energy 2016, 136, NL7_9. [Google Scholar]
- Japan Cogeneration Center. New Edition Cogeneration Comprehensive Manual 2003; Japan Cogeneration Center: Tokyo Japan, 2003. (In Japanese) [Google Scholar]
- Kojima, T.; Fukuta, Y. Microgrid System for Isolated Islands. Fuji Electr. J. 2011, 84, 188–193. [Google Scholar]
- Lavrik, A.; Zhukovskiy, Y.; Tcvetkov, P. Optimizing the Size of Autonomous Hybrid Microgrids with Regard to Load Shifting. Energies 2021, 14, 5059. [Google Scholar] [CrossRef]
- The Chugoku Electric Power Company, Incorporated. Demonstration project of hybrid storage battery system in Oki Islands. J. Inst. Electr. Install. Eng. Jpn. 2018, 38, 57–58. (In Japanese) [Google Scholar]
- Okinawa Enetech Co., Inc. Improving Plant Efficiency by Improving the Operation of Power Plants. JICA Report. 2014. Available online: https://openjicareport.jica.go.jp/pdf/12229035_02.pdf (accessed on 25 October 2021).
- Committee Secretariat on Coordination and Demand-Supply Balance Evaluation, etc. Examination of Technical Issues and Countermeasures for Renewable Energy Main Power Source. Organization for Cross-Regional Coordination of Transmission Operators, Japan. 2020. Available online: https://www.occto.or.jp/iinkai/chouseiryoku/2020/ (accessed on 25 October 2021).
- Mitsubishi Research Institute, Inc. Recognition of the Current Situation Regarding Power Storage Systems. Ministry of Economy, Trade and Industry. 2020. Available online: https://www.meti.go.jp/shingikai/energy_environment/storage_system/pdf/001_05_00.pdf (accessed on 25 October 2021).
- Hirota, S.; Kanoh, M.; Hara, T. Lithium-ion Battery System for Smart Grid. Hitachi Chemical Technical Report 2014 No.57. Available online: https://www.mc.showadenko.com/japanese/report/057/57.pdf (accessed on 25 October 2021).
- U.S. Environmental Protection Agency Combined Heat and Power Partnership. Catalog of CHP Technologies Section 2. Technology Characterization Reciprocating Internal Combustion Engines. 2015. Available online: http://www.gossengineering.com/wp-content/uploads/2017/03/CATALOG-OF-CHP-TECHNOLOGIES.pdf (accessed on 25 October 2021).
- Yamano, S.; Nakaya, T.; Ikegami, T.; Nakayama, M.; Akisawa, A. Optimization modeling of mixed gas engine types with different maintenance spans and costs: Case study OF CCHP to evaluate optimal gas engine operations and combination of the types. Energy 2021, 222, 119823. [Google Scholar] [CrossRef]
- Kohler. Model: 800REOZM. 2018. Available online: https://www.kohlerpower.sg/onlinecatalog/pdf/800REOZM.pdf (accessed on 25 October 2021).
- Daihatsu Diesel Mfg. Co., Ltd. Guaranteed Fuel Consumption Curve at Site List No. PC-160610-001Z; Daihatsu Diesel Mfg. Co., Ltd.: Osaka, Japan, 2016. [Google Scholar]
- Horii, S.; Ito, K.; Pak, P.S.; Suzuki, Y. Optimal planning of gas turbine co-generation plants based on mixed-integer linear programming. Int. J. Energy Res. 1987, 11, 507–518. [Google Scholar] [CrossRef]
- Tomofuji, D.; Akisawa, A. Effect of Introducing Gas Engine Cogeneration in Non-Residential Building Considering Regional Characteristics—Study on Energy Saving, Securing BCP Power Supply, and Demand Response. J. Jpn. Soc. Energy Resour. 2018, 39, 1–10. [Google Scholar]
- Generac Power Systems, Inc. White Paper Total Cost of Ownership Diesel vs. Gas Generators. 2017, p. 3. Available online: https://gensetservices.com/wp-content/uploads/2017/11/TCO-_diesel_vs_natural_gas_generators.pdf (accessed on 25 October 2021).
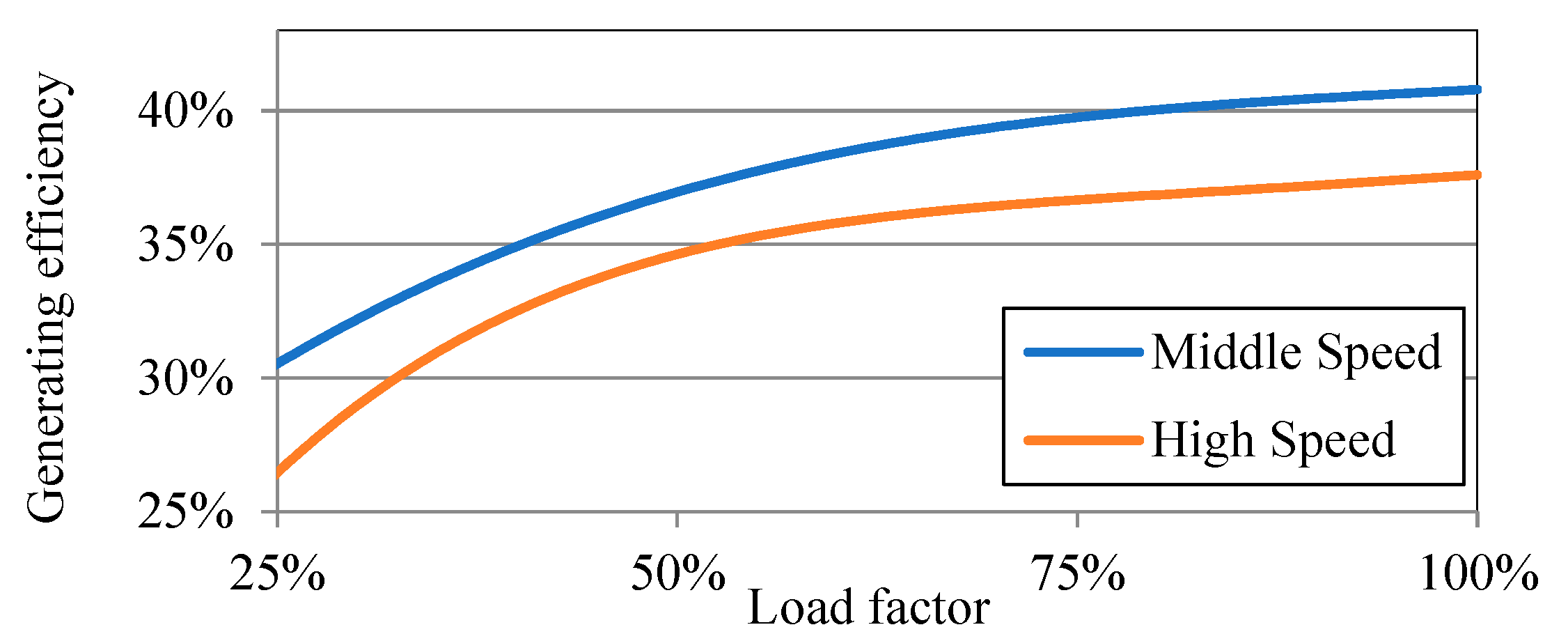

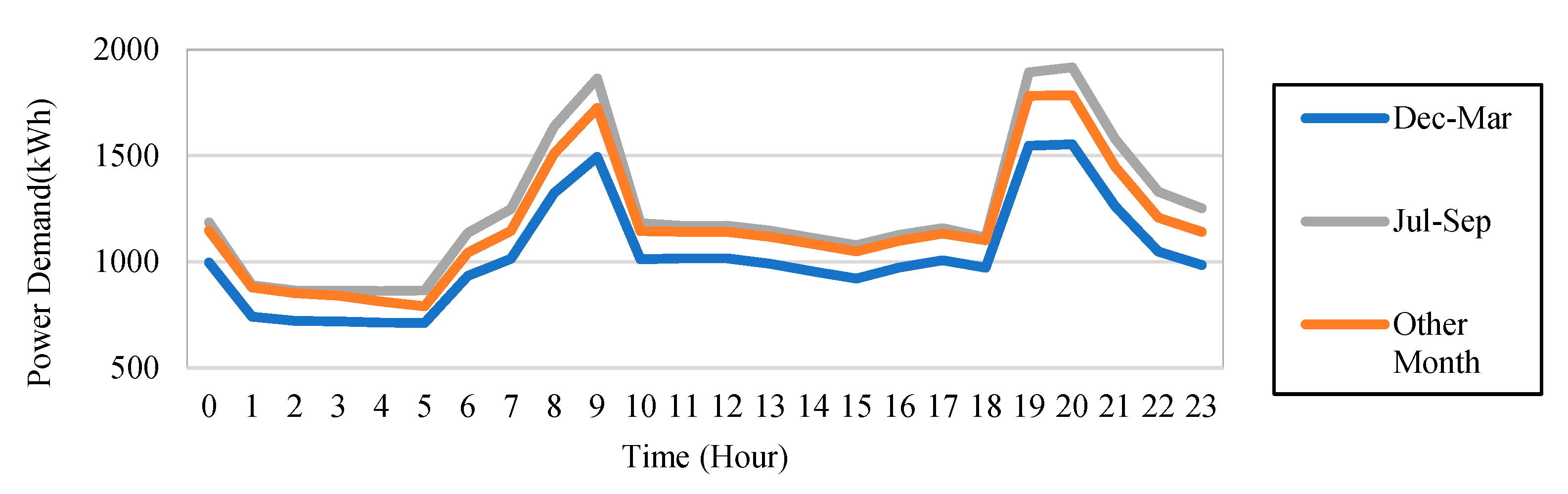
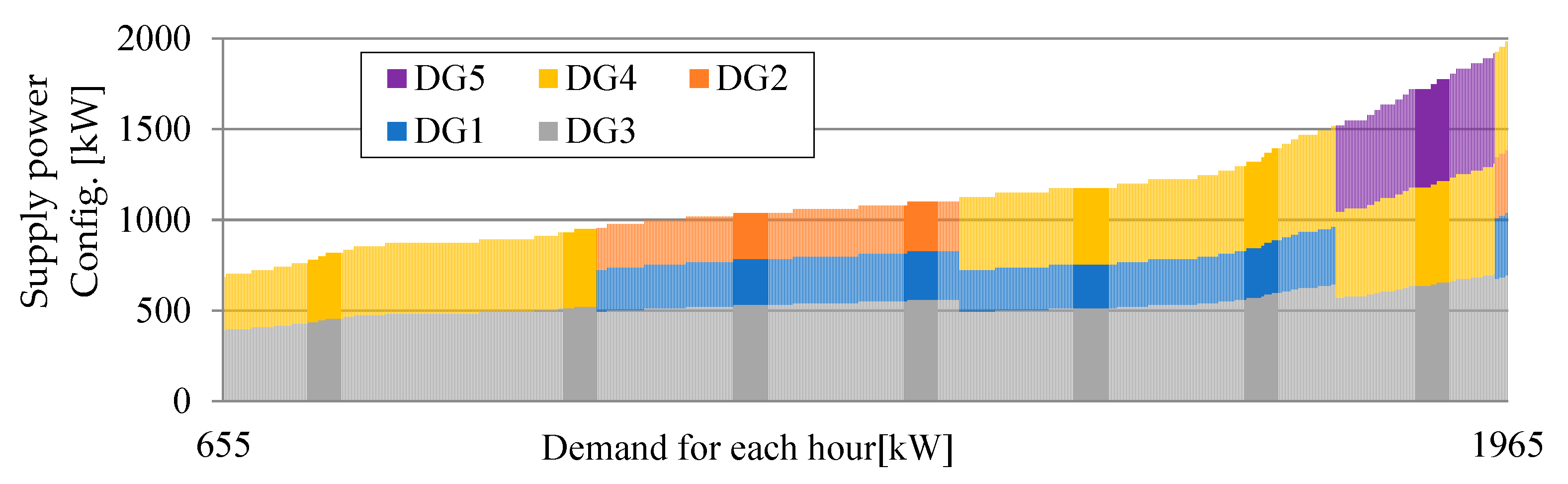




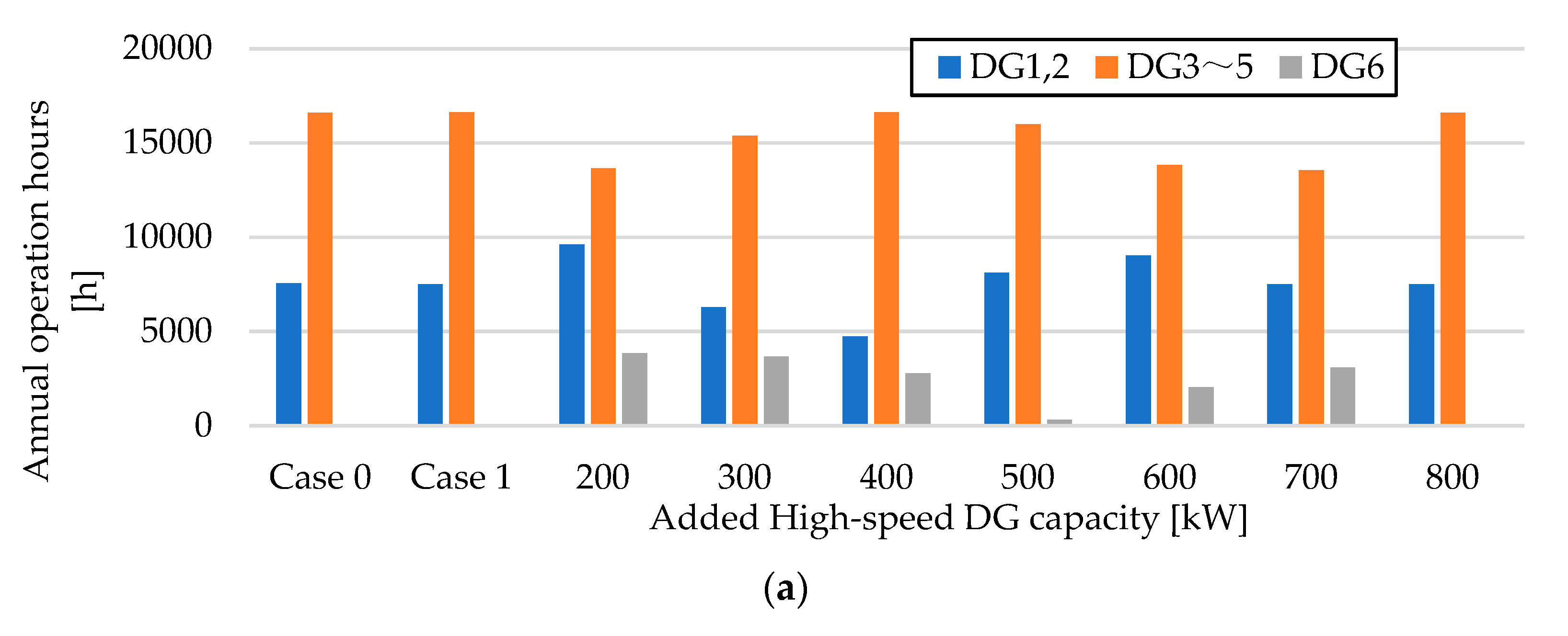
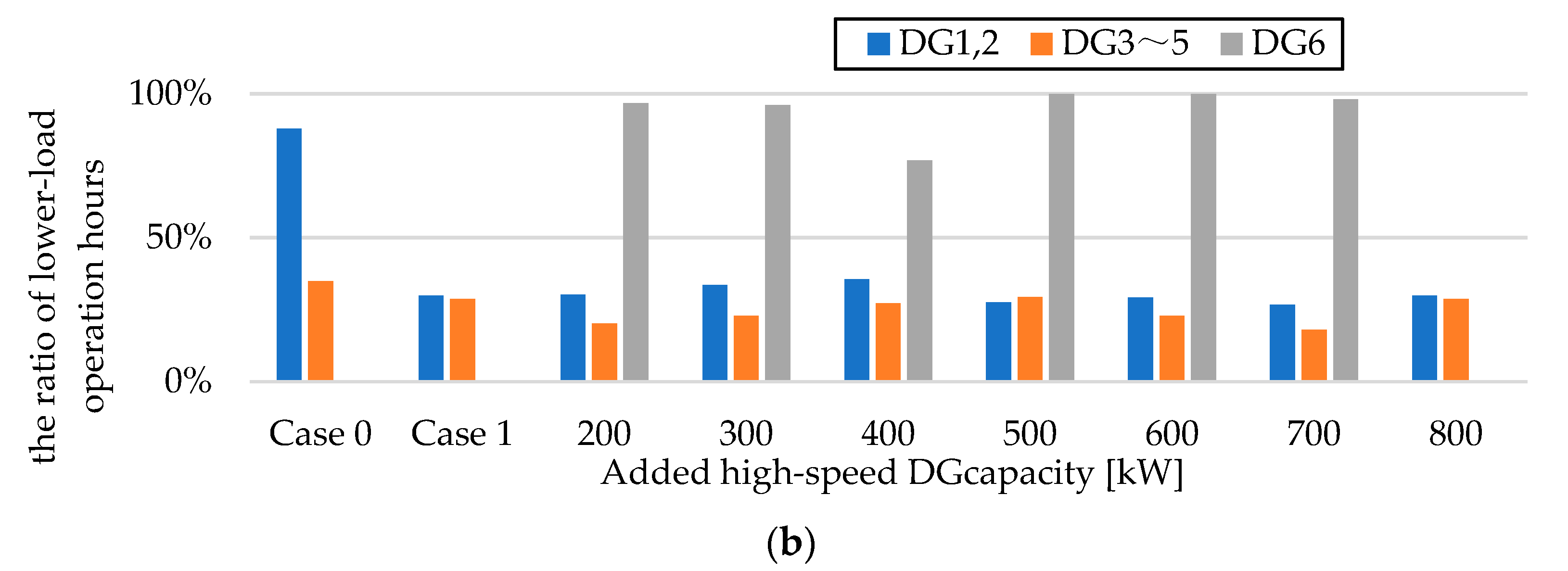
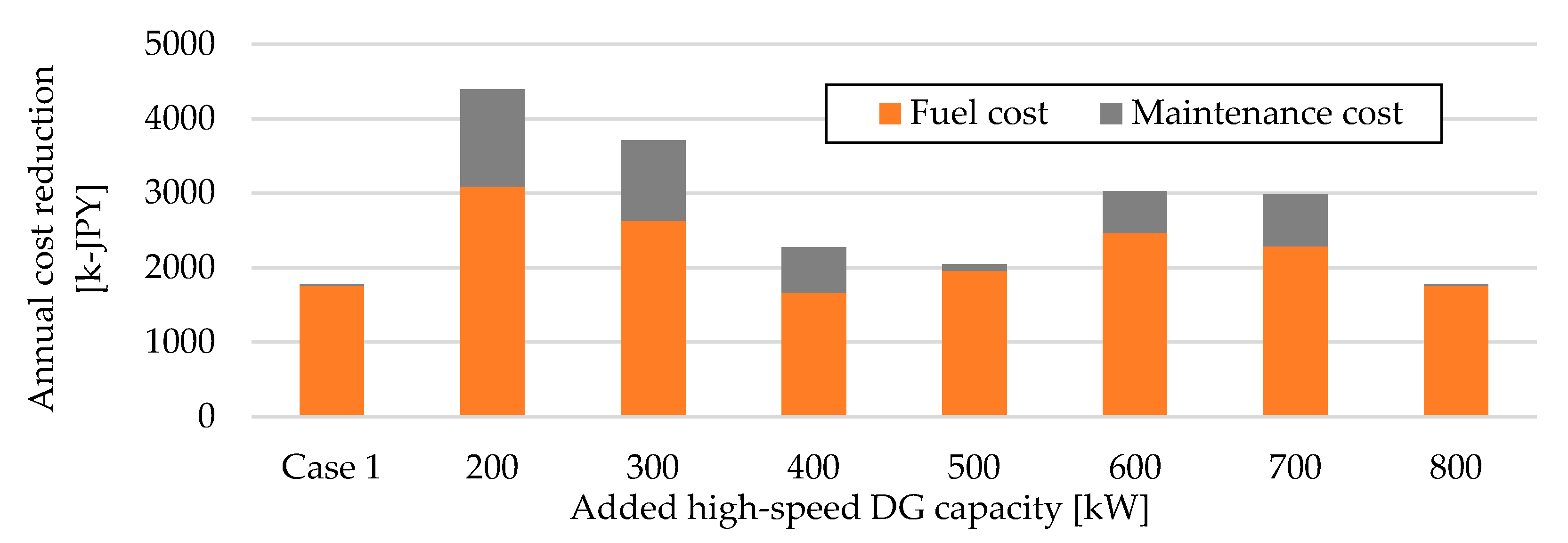
| Load Factor | Medium-Speed DG | High-Speed DG |
|---|---|---|
| 100% | 40.8% | 37.6% |
| 75% | 39.8% | 36.7% |
| 50% | 37.0% | 34.6% |
| 25% | 30.5% | 26.5% |
| Building Type | Floor Space [m2] |
| Offices | 2000 |
| Stores | 3000 |
| Clinics | 2100 |
| Residences and Hostels | 40,000 |
| Total | 47,100 |
| Engine Type | |||
|---|---|---|---|
| Middle speed | 1,2 | 550 | 2.2 |
| 3,4,5 | 950 | 2.0 | |
| High Speed | 6 | 500 | 2.5 |
| 501 | 2.4 |
| Case | Operation | Medium-Speed DG (Units) | High-Speed DG (Units) |
|---|---|---|---|
| Case 0 | Conventional | 5 | 0 |
| Case 1 | Optimized | 5 | 0 |
| Case 2 | Conventional | 5 | 1 |
| Case 3 | Optimized | 5 | 1 |
|
Operation Pattern | Supply Ability [kW] | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 1900∼2050 | 1 | 1 | 1 | 1 | 0 | 3000 |
| 2 | 1500∼1900 | 0 | 0 | 1 | 1 | 1 | 2850 |
| 3 | 1100∼1500 | 1 | 0 | 1 | 1 | 0 | 2450 |
| 4 | 950∼1100 | 1 | 1 | 1 | 0 | 0 | 2050 |
| 5 | 550∼950 | 0 | 0 | 1 | 1 | 0 | 1900 |
| Annual Operation [h] | Annual Operation, Less than 50% load [h] | Average Load Factor | |
|---|---|---|---|
| 1∼2 | 7544 | 6634 | 46.8% |
| 3∼5 | 16,604 | 5798 | 51.8% |
| Operation Pattern | Supply Ability [kW] | |||||||
|---|---|---|---|---|---|---|---|---|
| (a) The 5 units of medium-speed + 200 kW the high-speed DG | ||||||||
| 1 | 1900∼2050 | 1 | 1 | 1 | 1 | 0 | 0 | 3000 |
| 2 | 1700∼1900 | 0 | 0 | 1 | 1 | 1 | 0 | 2850 |
| 3 | 1500∼1700 | 1 | 0 | 1 | 1 | 0 | 1 | 2650 |
| 4 | 1300∼1500 | 1 | 0 | 1 | 1 | 0 | 0 | 2450 |
| 5 | 1150∼1300 | 1 | 1 | 1 | 0 | 0 | 1 | 2250 |
| 6 | 1100∼1150 | 0 | 0 | 1 | 1 | 0 | 1 | 2100 |
| 7 | 950∼1100 | 1 | 1 | 1 | 0 | 0 | 0 | 2050 |
| 8 | 750∼950 | 0 | 0 | 1 | 1 | 0 | 0 | 1900 |
| 9 | 550∼750 | 1 | 0 | 1 | 0 | 0 | 1 | 1700 |
| (b) The 5 units of medium-speed + 500 kW the high-speed DG | ||||||||
| 1 | 2000∼2050 | 1 | 1 | 1 | 1 | 0 | 0 | 3000 |
| 2 | 1900∼2000 | 1 | 0 | 1 | 1 | 0 | 1 | 2950 |
| 3 | 1600∼1900 | 0 | 0 | 1 | 1 | 1 | 0 | 2850 |
| 4 | 1500∼1600 | 1 | 1 | 1 | 0 | 0 | 1 | 2550 |
| 5 | 1450∼1500 | 1 | 0 | 1 | 1 | 0 | 0 | 2450 |
| 6 | 1100∼1450 | 0 | 0 | 1 | 1 | 0 | 1 | 2400 |
| 7 | 1050∼1100 | 1 | 1 | 1 | 0 | 0 | 0 | 2050 |
| 8 | 1050∼1050 | 1 | 0 | 1 | 0 | 0 | 1 | 2000 |
| 9 | 550∼950 | 0 | 0 | 1 | 1 | 0 | 0 | 1900 |
| (c) The 5 units of medium-speed + 800 kW the high-speed DG | ||||||||
| 1 | 1900∼2050 | 1 | 1 | 1 | 1 | 0 | 0 | 3000 |
| 2 | 1750∼1900 | 0 | 0 | 1 | 1 | 1 | 0 | 2850 |
| 3 | 1500∼1750 | 0 | 0 | 1 | 1 | 0 | 1 | 2700 |
| 4 | 1350∼1500 | 1 | 0 | 1 | 1 | 0 | 0 | 2450 |
| 5 | 1100∼1350 | 1 | 0 | 1 | 0 | 0 | 1 | 2300 |
| 6 | 950∼1100 | 1 | 1 | 1 | 0 | 0 | 0 | 2050 |
| 7 | 800∼950 | 0 | 0 | 1 | 1 | 0 | 0 | 1900 |
| 8 | 550∼800 | 0 | 0 | 1 | 0 | 0 | 1 | 1750 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamano, S.; Akisawa, A. Evaluation of an Additional Generator on the Economic Effect Based on a Load Sharing Optimization of Medium-Speed/High-Speed Diesel Generators in a Microgrid. Energies 2022, 15, 1007. https://doi.org/10.3390/en15031007
Yamano S, Akisawa A. Evaluation of an Additional Generator on the Economic Effect Based on a Load Sharing Optimization of Medium-Speed/High-Speed Diesel Generators in a Microgrid. Energies. 2022; 15(3):1007. https://doi.org/10.3390/en15031007
Chicago/Turabian StyleYamano, Shuhei, and Atsushi Akisawa. 2022. "Evaluation of an Additional Generator on the Economic Effect Based on a Load Sharing Optimization of Medium-Speed/High-Speed Diesel Generators in a Microgrid" Energies 15, no. 3: 1007. https://doi.org/10.3390/en15031007
APA StyleYamano, S., & Akisawa, A. (2022). Evaluation of an Additional Generator on the Economic Effect Based on a Load Sharing Optimization of Medium-Speed/High-Speed Diesel Generators in a Microgrid. Energies, 15(3), 1007. https://doi.org/10.3390/en15031007





