Optimized Design of Laminated Busbar for Large-Capacity Back-to-Back Converters
Abstract
:1. Introduction
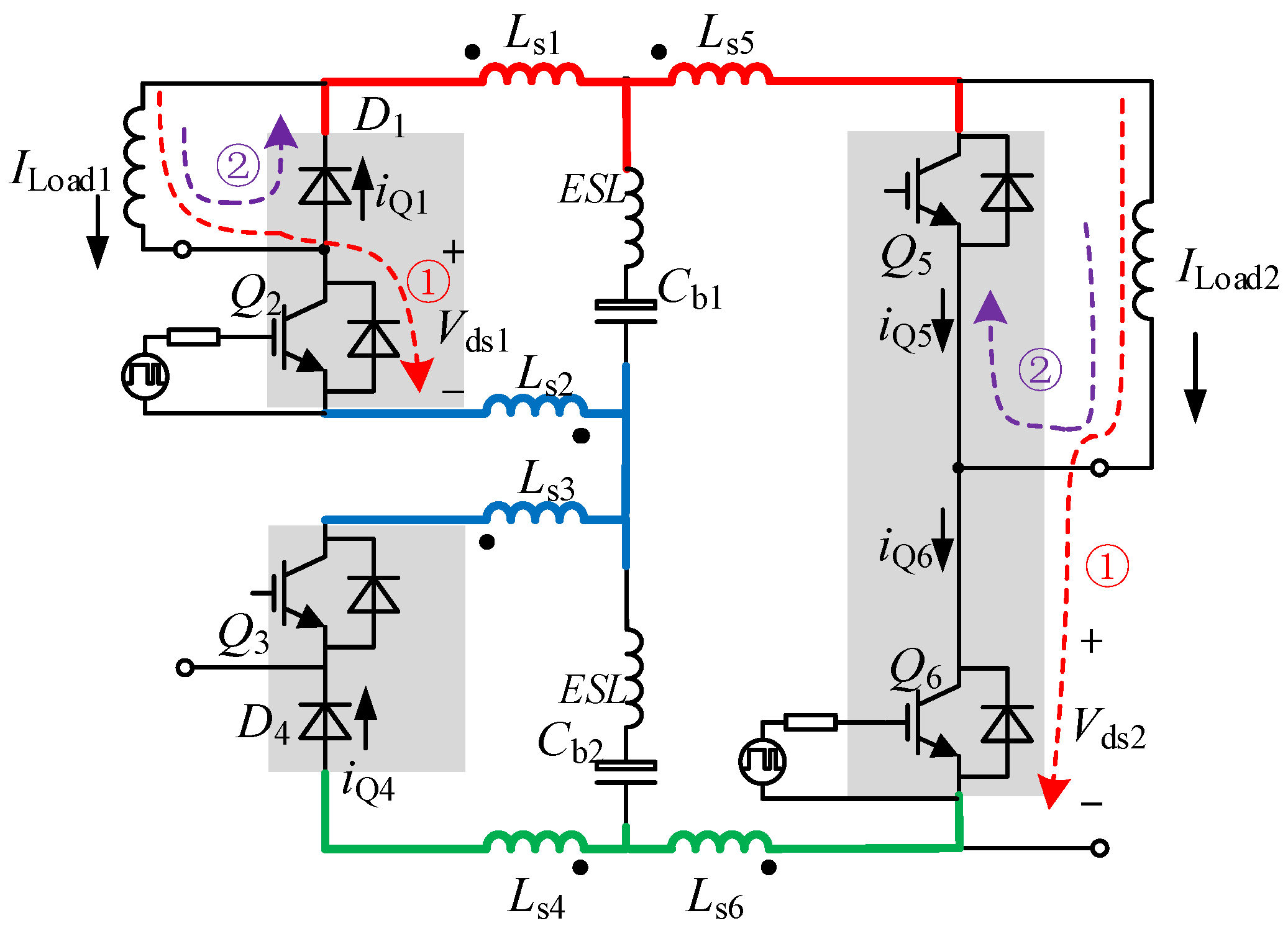
2. Circuit Topology and Commutation Loop Analysis
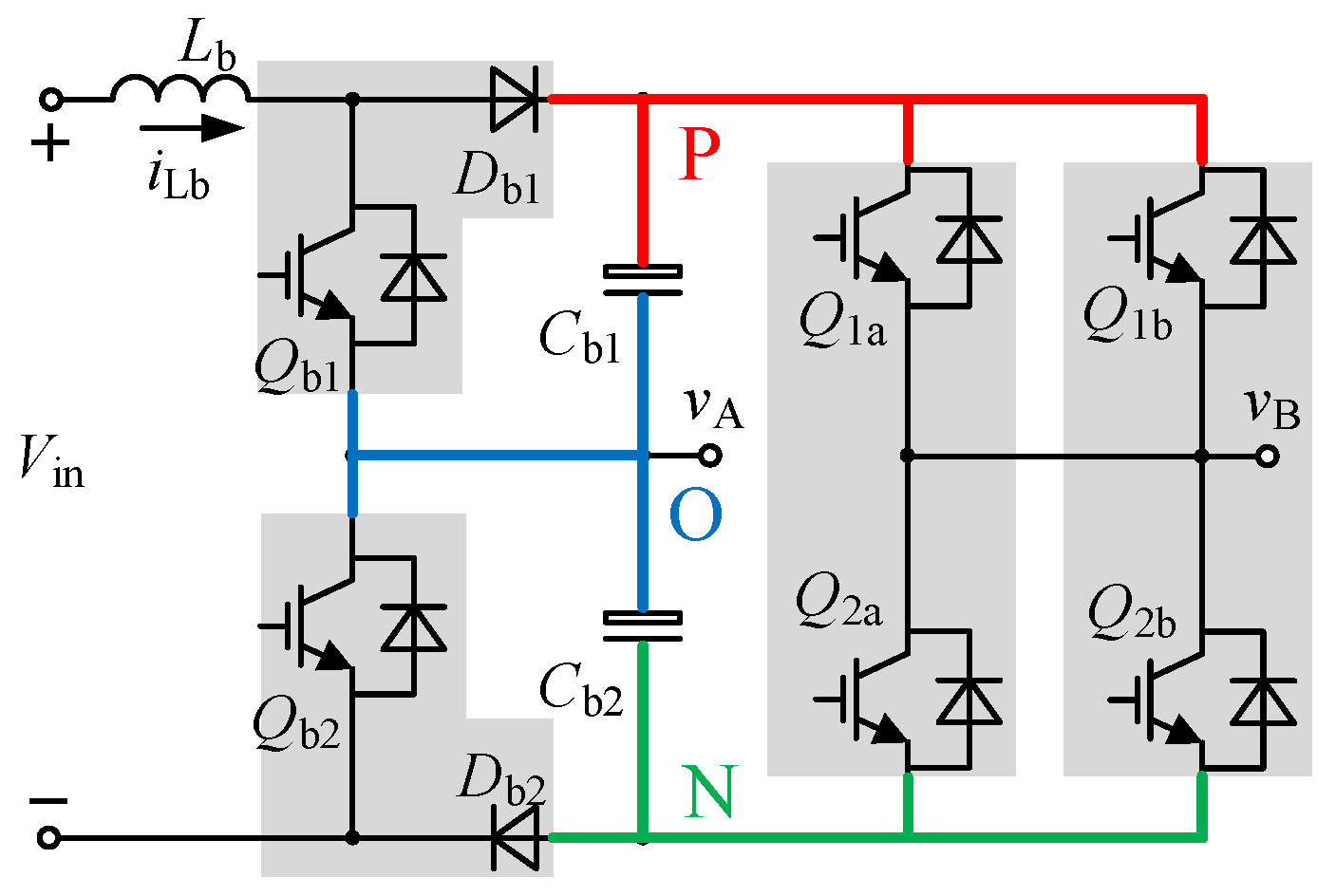
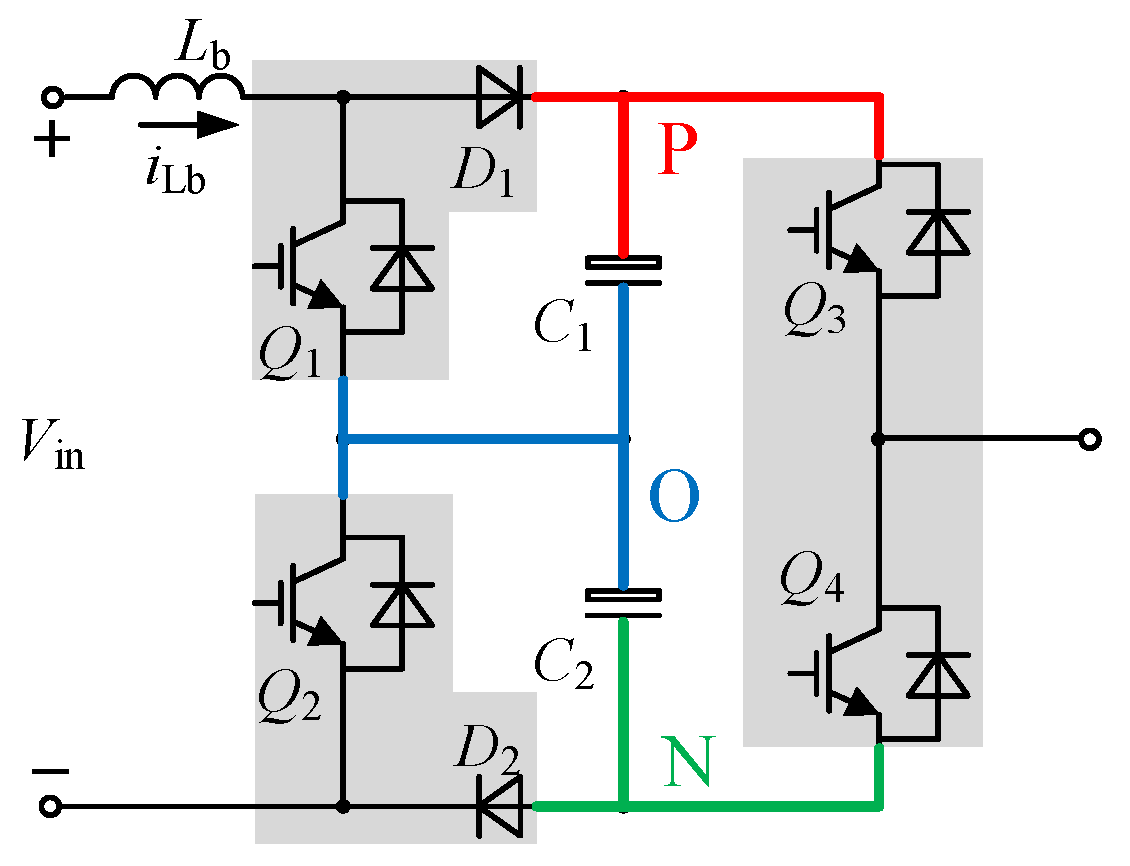
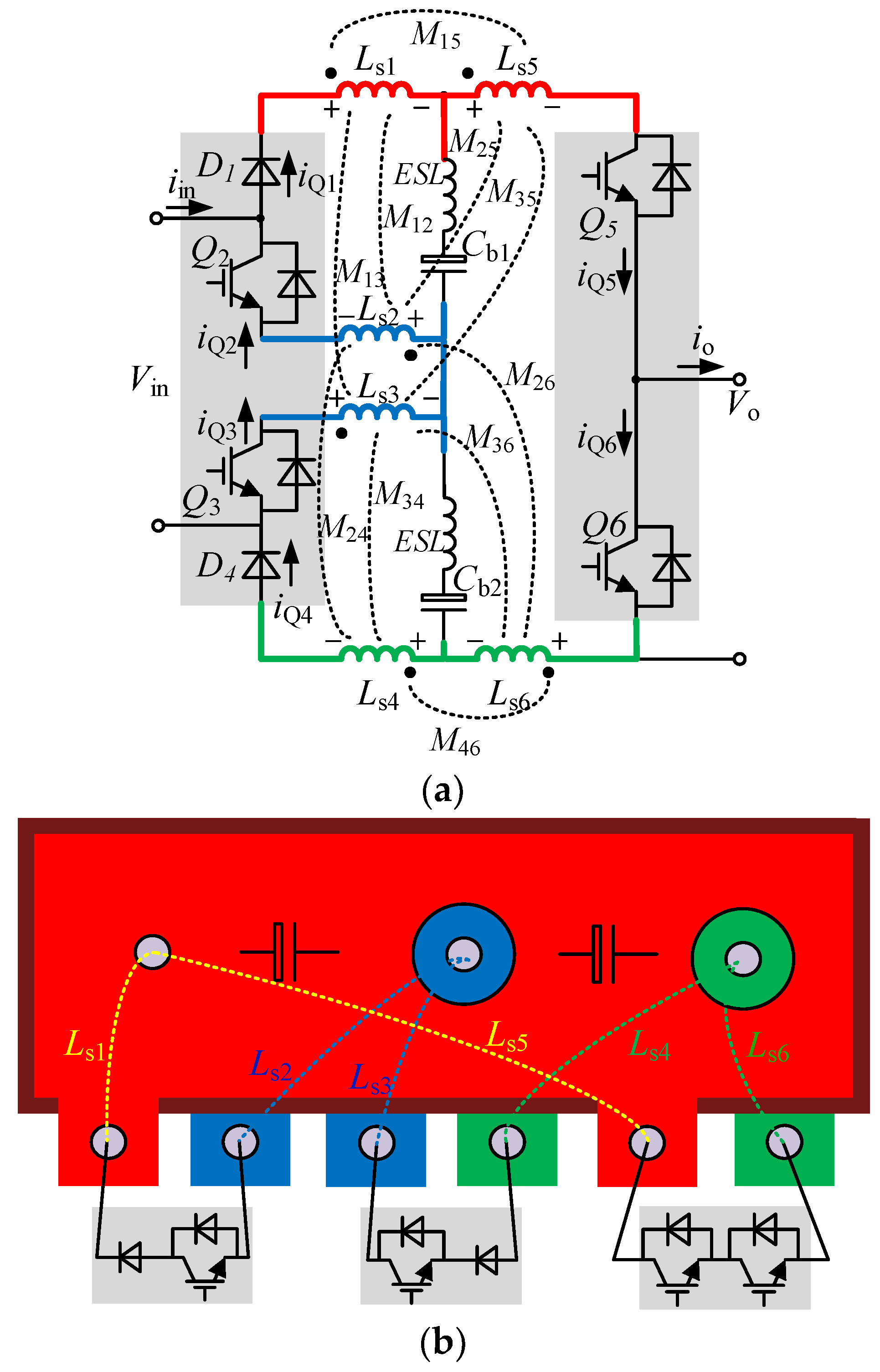
2.1. Auxiliary Power Supply Circuit Topology
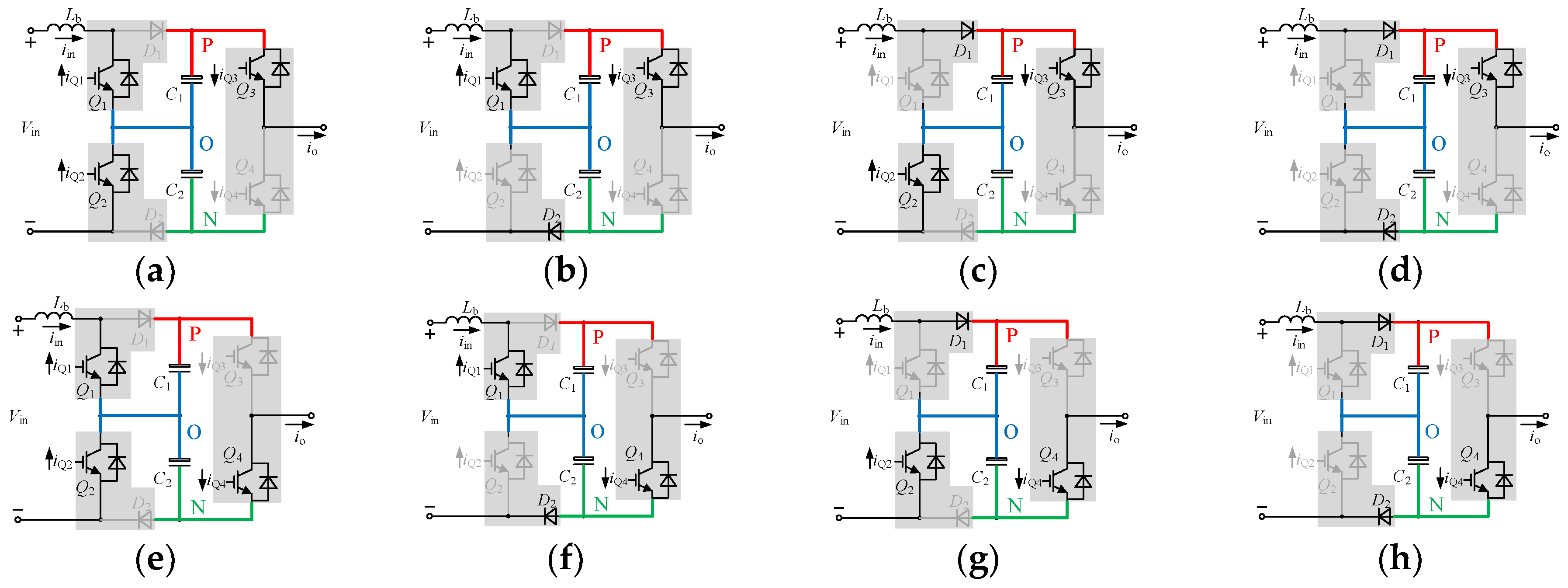
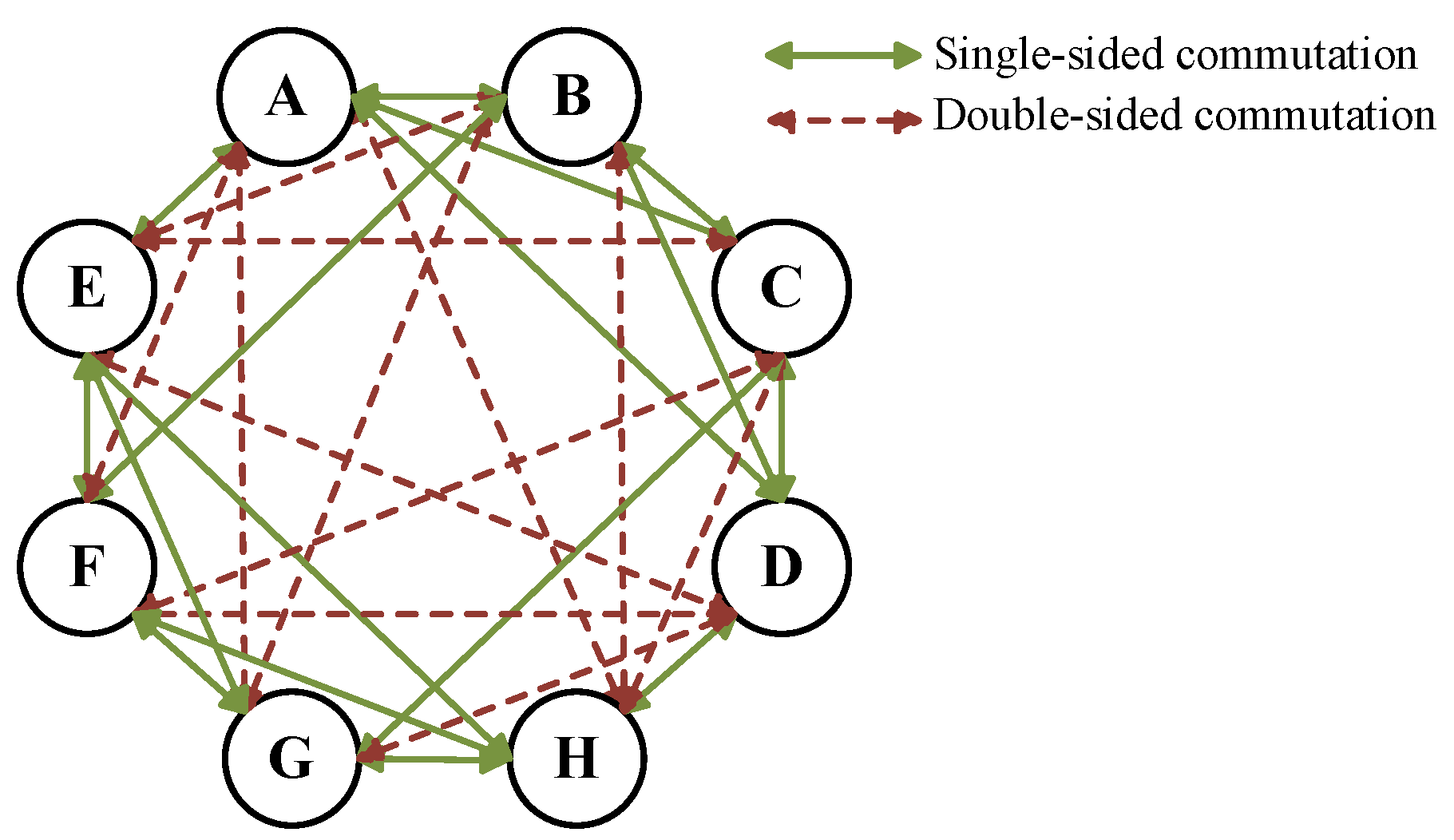
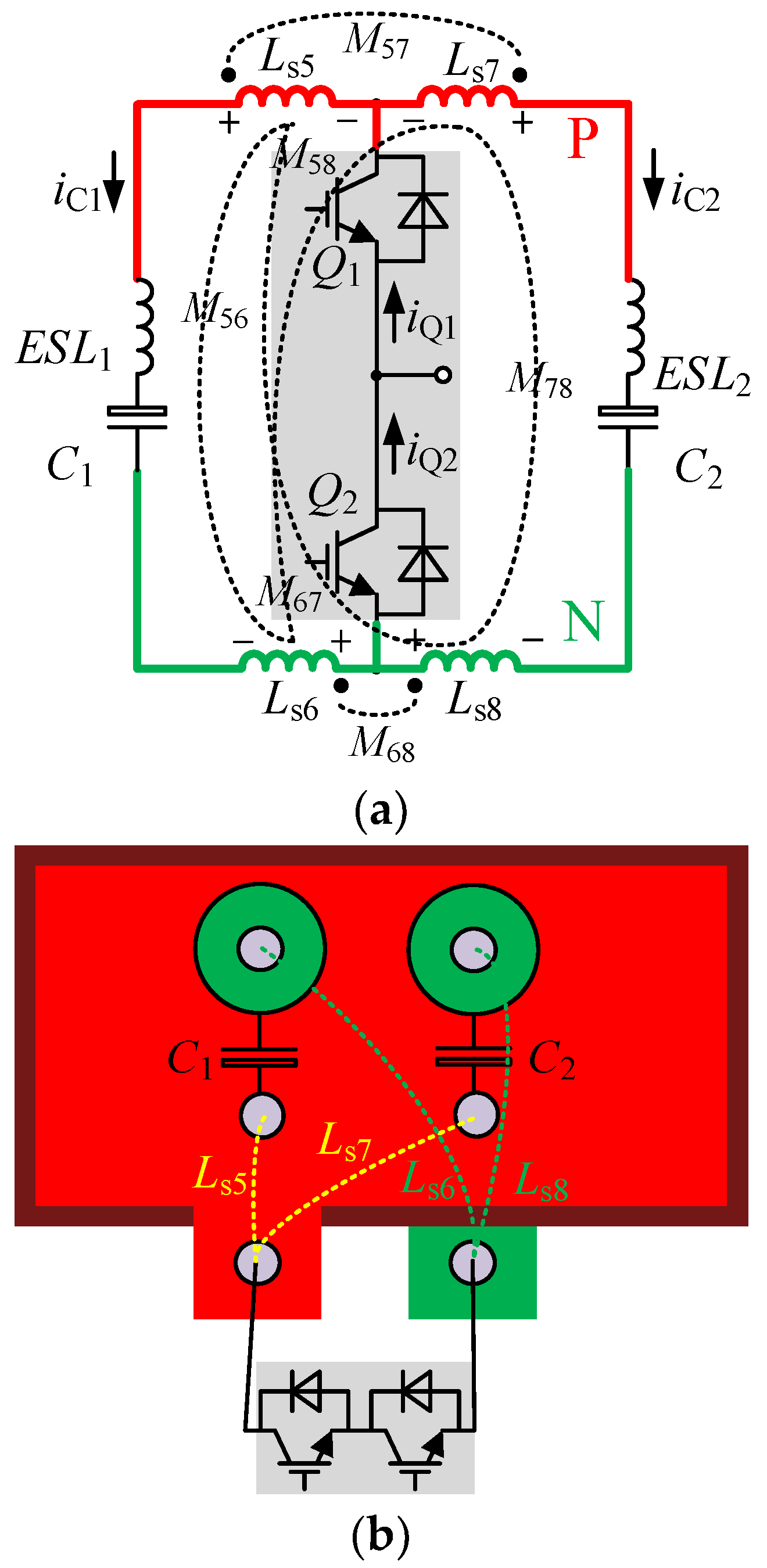
2.2. Circuit Loop Analysis
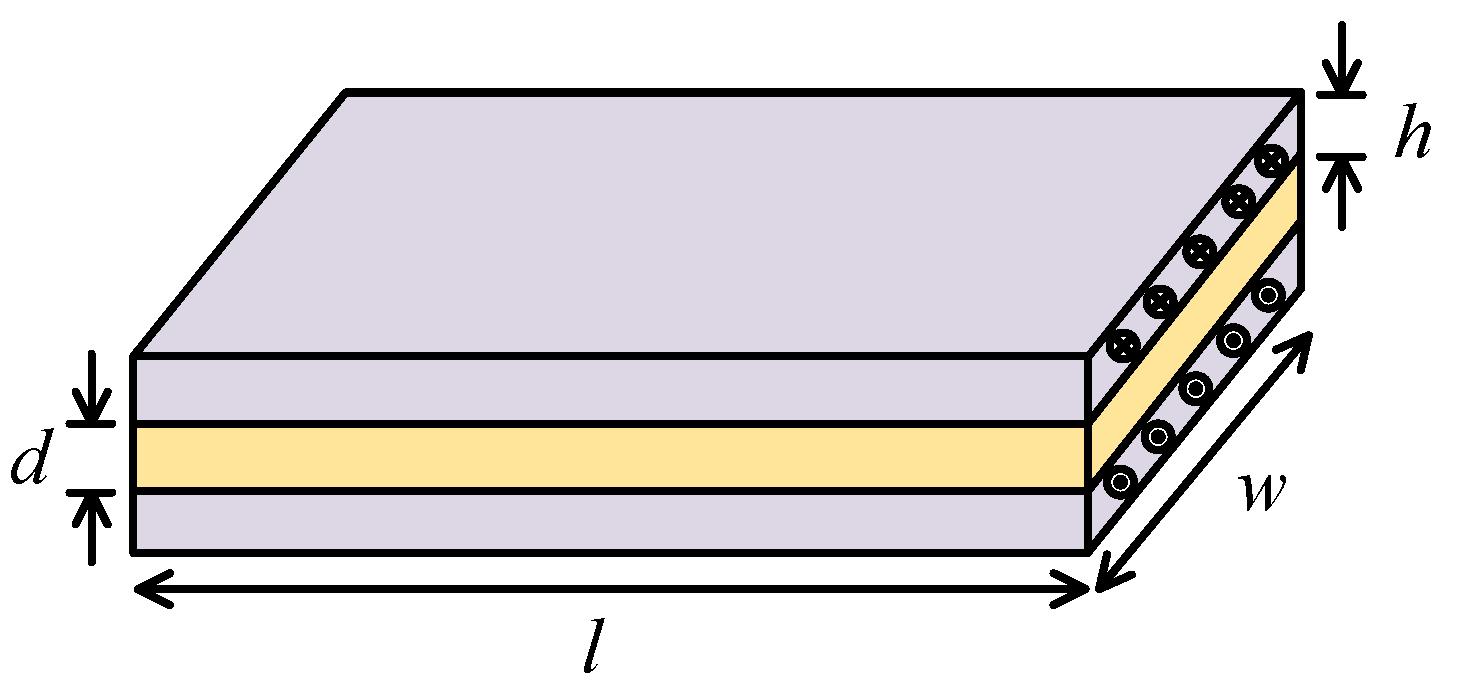
3. Analysis of Stray Inductance of Multi-Layer Busbar
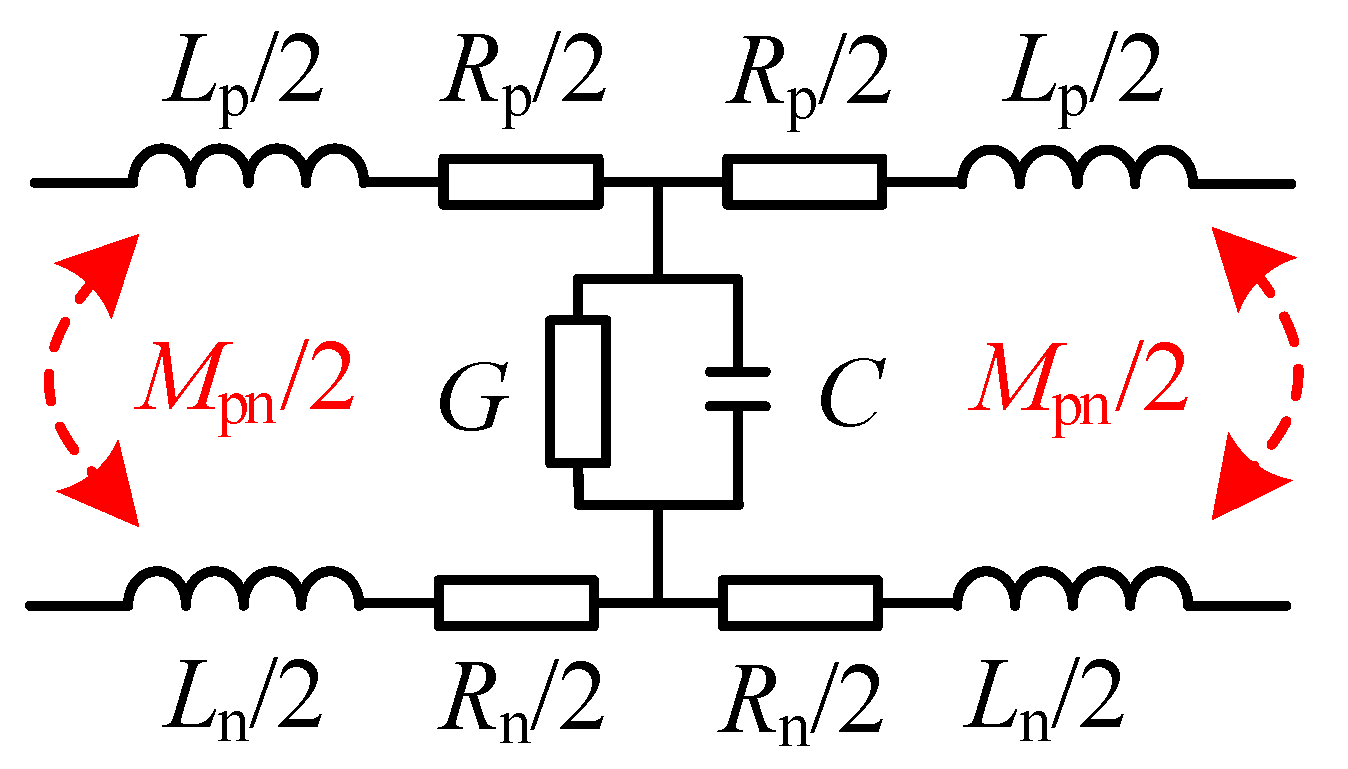
3.1. Stray Inductance Theory of Laminated Busbars
3.2. Relationship between Switch Voltage Stress and Stray Inductance in Back-to-Back Converters
3.3. Analysis of Parallel Model of Multi-Bus Capacitors
3.4. Relationship between Connection Point Spacing and Stray Inductance
3.5. Optimization Principle of Laminated Busbar
- (1)
- Reduce the stray inductance of the current flow loop at this side, which is consistent with the conventional way of improving the characteristics of the laminated busbar, and reduce the surrounding area of the current circuit as much as possible so that the self-inductance and mutual inductance cancel each other to reduce the switching voltage spike;
- (2)
- Reduce the stray inductance caused by the mutual inductance between the two sides of the flow loops and minimizing the overlapping area of the two-sides flow loops via the unique laminated busbar optimization mode of the common DC bus back-to-back converter;
- (3)
- Select a laminated busbar with multiple bus capacitors in parallel to reduce the stray inductance of the commutation loop, considering the length of the laminated busbar and the number of power modules.
4. Design and Verification
4.1. Optimal Design and Simulation of Laminated Busbar
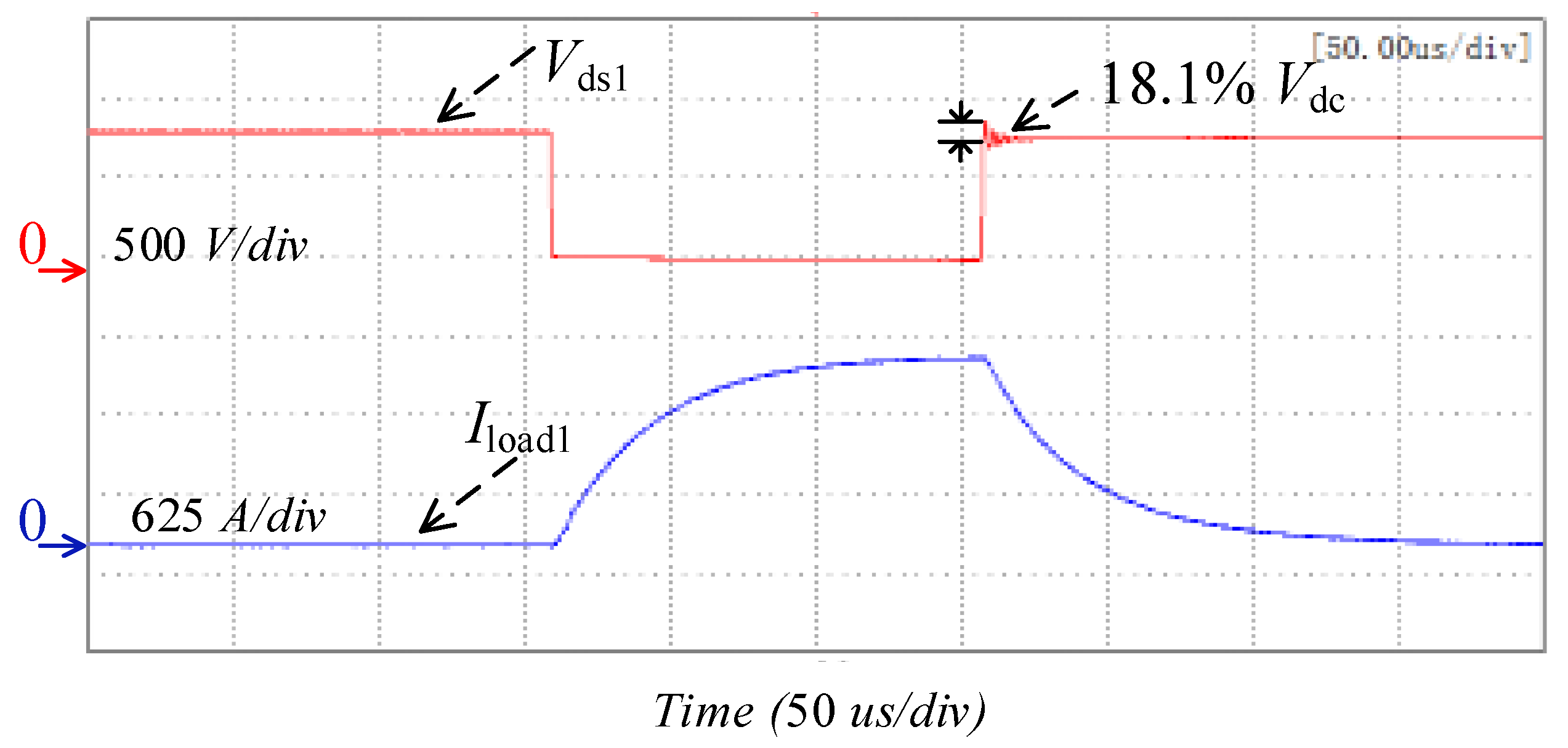
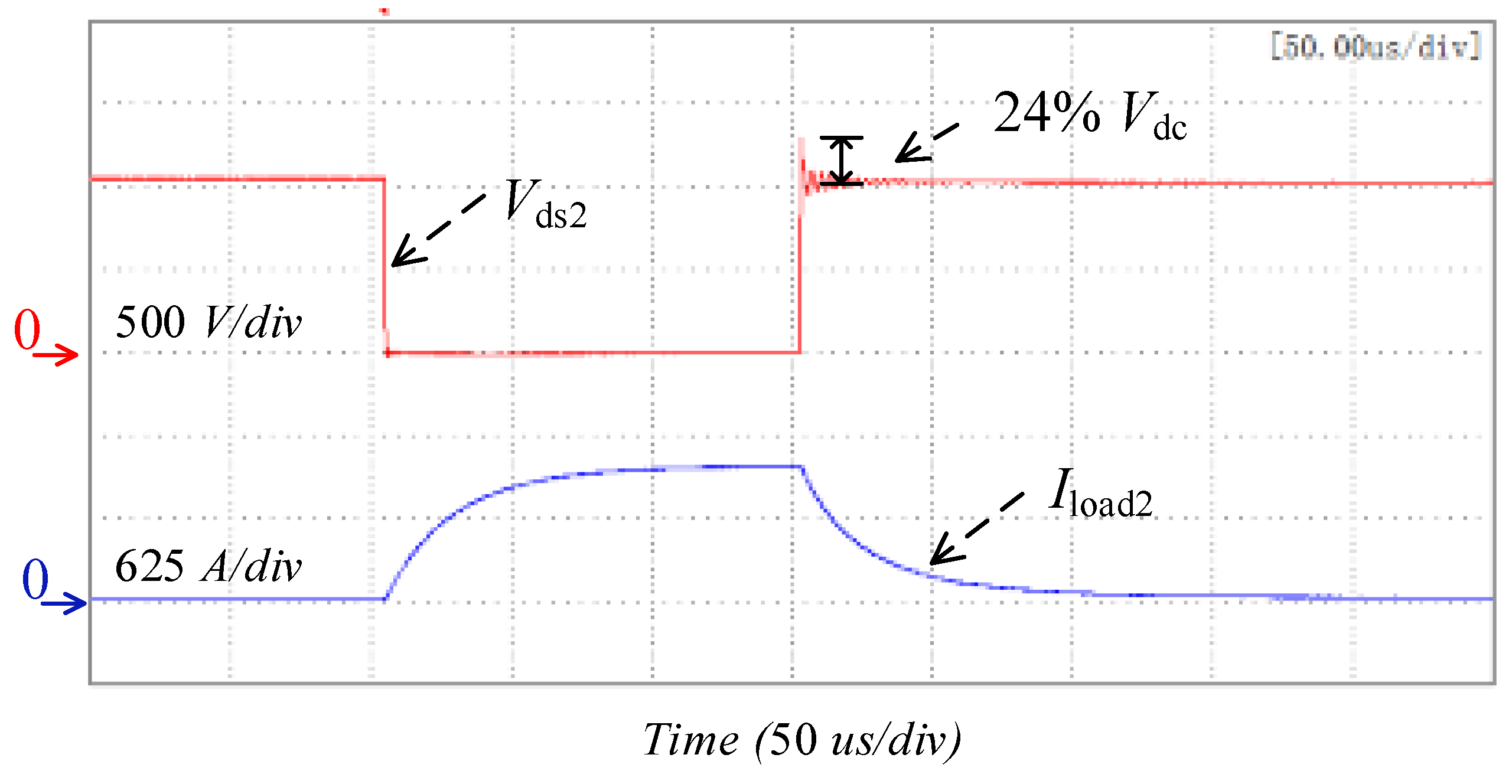
4.2. Dynamic Characteristic Test
5. Conclusions and Future Work
- (1)
- It establishes the coupled inductance model of the laminated busbar of the back-to-back converter and gives measures to improve the voltage stress of the power device: reduce the enclosing area of the current flow loop so that the self-inductance and mutual inductance cancel each other; reduce the two overlap areas of the one-side flow loops; and reduce the mutual inductance between the flow loops on both sides;
- (2)
- An optimized design structure of laminated busbars suitable for large-capacity, back-to-back converters is given.
- (3)
- A set of 180 kW train high frequency auxiliary power converters is designed, and the pulse experiment verifies the safety and reliability of the theoretical analysis.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schiestl, M.; Marcolini, F.; Incurvati, M.; Capponi, F.G.; Starz, R.; Caricchi, F.; Rodriguez, A.S.; Wild, L. Development of a High Power Density Drive System for Unmanned Aerial Vehicles. IEEE Trans. Power Electron. 2020, 36, 3159–3171. [Google Scholar] [CrossRef]
- Lee, H.; Smet, V.; Tummala, R. A Review of SiC Power Module Packaging Technologies: Challenges, Advances, and Emerging Issues. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 239–255. [Google Scholar] [CrossRef]
- Chen, J.; Du, X.; Luo, Q.; Zhang, X.; Sun, P.; Zhou, L. A Review of Switching Oscillations of Wide Bandgap Semiconductor Devices. IEEE Trans. Power Electron. 2020, 35, 13182–13199. [Google Scholar] [CrossRef]
- Dongye, Z.; Qi, L.; Liu, K.; Wei, X.; Cui, X. Coupled Inductance Model of Full-Bridge Modules in Hybrid High Voltage Direct Current Circuit Breakers. IEEE Trans. Ind. Electron. 2019, 67, 10315–10324. [Google Scholar] [CrossRef]
- Wang, K.; Wang, L.; Yang, X.; Zeng, X.; Chen, W.; Li, H. A Multiloop Method for Minimization of Parasitic Inductance in GaN-Based High-Frequency DC–DC Converter. IEEE Trans. Power Electron. 2017, 32, 4728–4740. [Google Scholar] [CrossRef]
- Moorthy, R.S.K.; Aberg, B.; Olimmah, M.; Yang, L.; Rahman, D.; Lemmon, A.N.; Yu, W.; Husain, I.; Sree, K.R. Estimation, Minimization, and Validation of Commutation Loop Inductance for a 135-kW SiC EV Traction Inverter. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 286–297. [Google Scholar] [CrossRef]
- Xie, Y.; Bingyang, L.; Hongkeng, Z.; Jiwen, W.; Kangping, W.; Xu, Y.; Laily, W. Optimization of Laminated Busbar for Three-Level NPC Topology Using SiC Module. In Proceedings of the 2020 IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia), Nanjing, China, 29 November–2 December 2020; pp. 302–307. [Google Scholar]
- Zhang, N.; Wang, S.; Zhao, H. Develop Parasitic Inductance Model for the Planar Busbar of an IGBT H Bridge in a Power Inverter. IEEE Trans. Power Electron. 2015, 30, 6924–6933. [Google Scholar] [CrossRef]
- Wang, J.; Shaolin, Y.; Zhang, X. Effect of key physical structures on the laminated bus bar inductance. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 3689–3694. [Google Scholar]
- Geng, C.; He, F.; Zhang, J.; Hu, H. Partial Stray Inductance Modeling and Measuring of Asymmetrical Parallel Branches on the Bus-Bar of Electric Vehicles. Energies 2017, 10, 1519. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Liu, C.; Wang, M.; Si, Y.; Liu, Y.; Lei, Q. High-Efficiency High-Power-Density CLLC Resonant Converter with Low-Stray-Capacitance and Well-Heat-Dissipated Planar Transformer for EV On-Board Charger. IEEE Trans. Power Electron. 2020, 35, 10831–10851. [Google Scholar] [CrossRef]
- Plesca, A. Thermal Analysis of Busbars from a High Current Power Supply System. Energies 2019, 12, 2288. [Google Scholar] [CrossRef] [Green Version]
- Liang, Z.; Hu, S.; Wang, M.; He, X. DC-Link Busbar Network Design and Evaluation Method for the Large-Capacity Power Electronic Converter. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 4137–4145. [Google Scholar] [CrossRef]
- Liu, B.; Li, W.; Meng, D.; Diao, L.; Ma, Y.; Qiu, T.; Diao, L. Low-stray inductance optimized design for power circuit of SiC-MOSFET-Based inverter. IEEE Access 2020, 8, 20749–20758. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, S. Parasitic Inductance Modeling and Reduction for Wire-Bonded Half-Bridge SiC Multichip Power Modules. IEEE Trans. Power Electron. 2021, 36, 5892–5903A. [Google Scholar] [CrossRef]
- Deshpande, A.; Luo, F. Multilayer busbar design for a Si IGBT and SiC MOSFET hybrid switch based 100 kW three-level T-type PEBB. In Proceedings of the 2017 IEEE 5th Workshop on Wide Bandgap Power Devices and Applications (WiPDA), Albuquerque, NM, USA, 30 October–1 November 2017; pp. 20–24. [Google Scholar]
- Zou, G.; Zhao, Z.; Yuan, L. Study on DC busbar structure considering stray inductance for the back-to-back IGBT-based converter. In Proceedings of the 2013 Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 17–21 March 2013; pp. 1213–1218. [Google Scholar]
- Liu, B.; Ren, R.; Jones, E.A.; Gui, H.; Zhang, Z.; Chen, R.; Wang, F.; Costinett, D. Effects of Junction Capacitances and Commutation Loops Associated with Line-Frequency Devices in Three-Level AC/DC Converters. IEEE Trans. Power Electron. 2018, 34, 6155–6170. [Google Scholar] [CrossRef]
- Gui, H.; Chen, R.; Zhang, Z.; Niu, J.; Tolbert, L.M.; Wang, F.; Costinett, D.; Blalock, B.J.; Choi, B.B. Methodology of Low Inductance Busbar Design for Three-Level Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 3468–3478. [Google Scholar] [CrossRef]
- Yuan, Z.; Peng, H.; Deshpande, A.; Narayanasamy, B.; Emon, A.I.; Luo, F.; Chen, C. Design and Evaluation of Laminated Busbar for Three-Level T-Type NPC Power Electronics Building Block With Enhanced Dynamic Current Sharing. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 395–406. [Google Scholar] [CrossRef]
- Smirnova, L.; Juntunen, R.; Murashko, K.; Musikka, T.; Pyrhonen, J. Thermal Analysis of the Laminated Busbar System of a Multilevel Converter. IEEE Trans. Power Electron. 2015, 31, 1479–1488. [Google Scholar] [CrossRef]
- Mehrabadi, N.R.; Cvetkovic, I.; Wang, J.; Burgos, R.; Boroyevich, D. Busbar design for SiC-based H-bridge PEBB using 1.7 kV, 400 a SiC MOSFETs operating at 100 kHz. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–7. [Google Scholar]
- Nguyen, T.V.; Wong, R.K.W.; Hegde, C. Benefits of Jointly Training Autoencoders: An Improved Neural Tangent Kernel Analysis. IEEE Trans. Inf. Theory 2021, 67, 4669–4692. [Google Scholar] [CrossRef]
- Fan, S.; Hsu, C.Y.; Jen, C.H.; Chen, C.L.; Juan, L.-T. Defective wafer detection using a denoising autoencoder for semiconductor manufacturing processes. Adv. Eng. Inform. 2020, 46, 101166. [Google Scholar] [CrossRef]

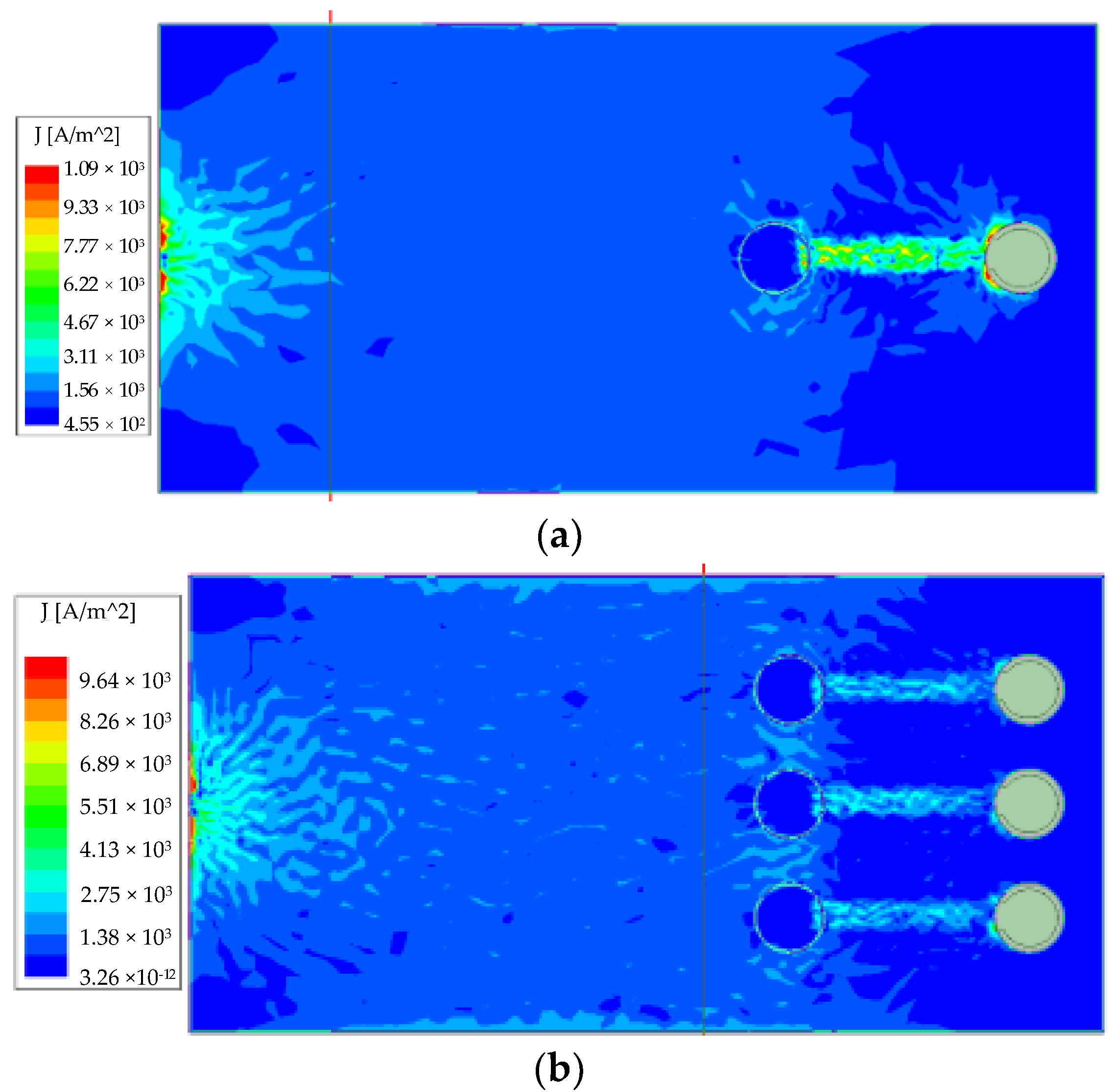
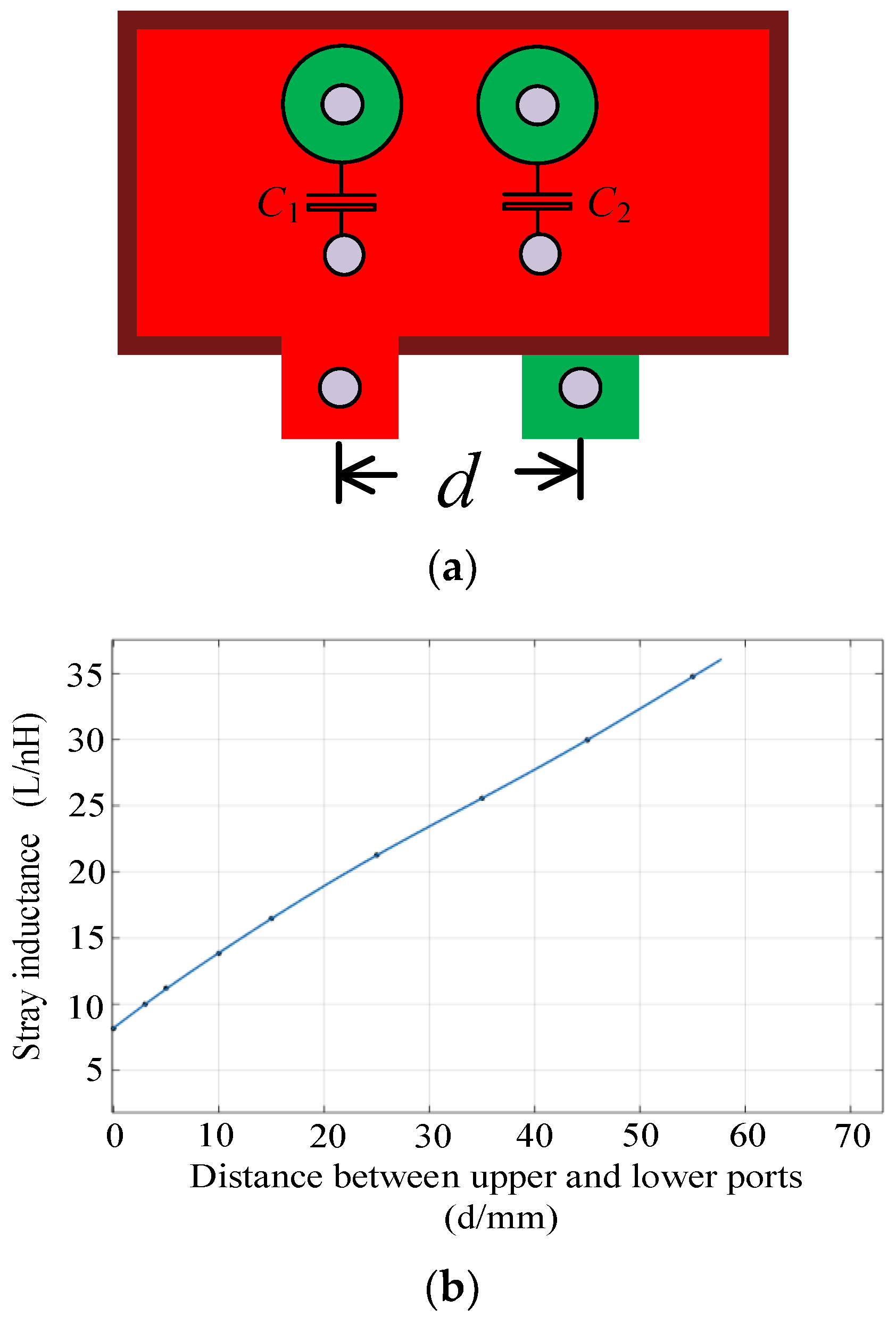


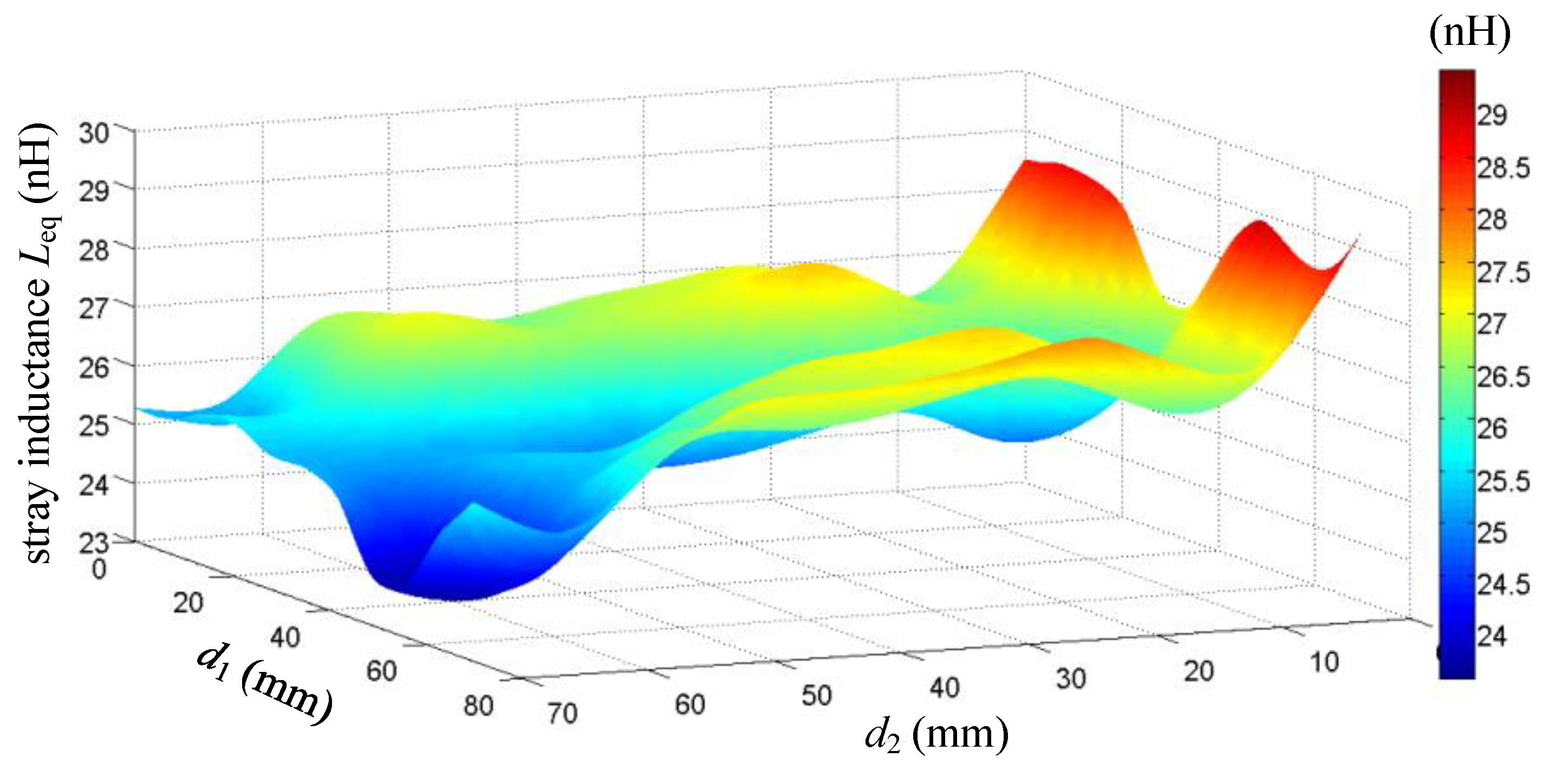

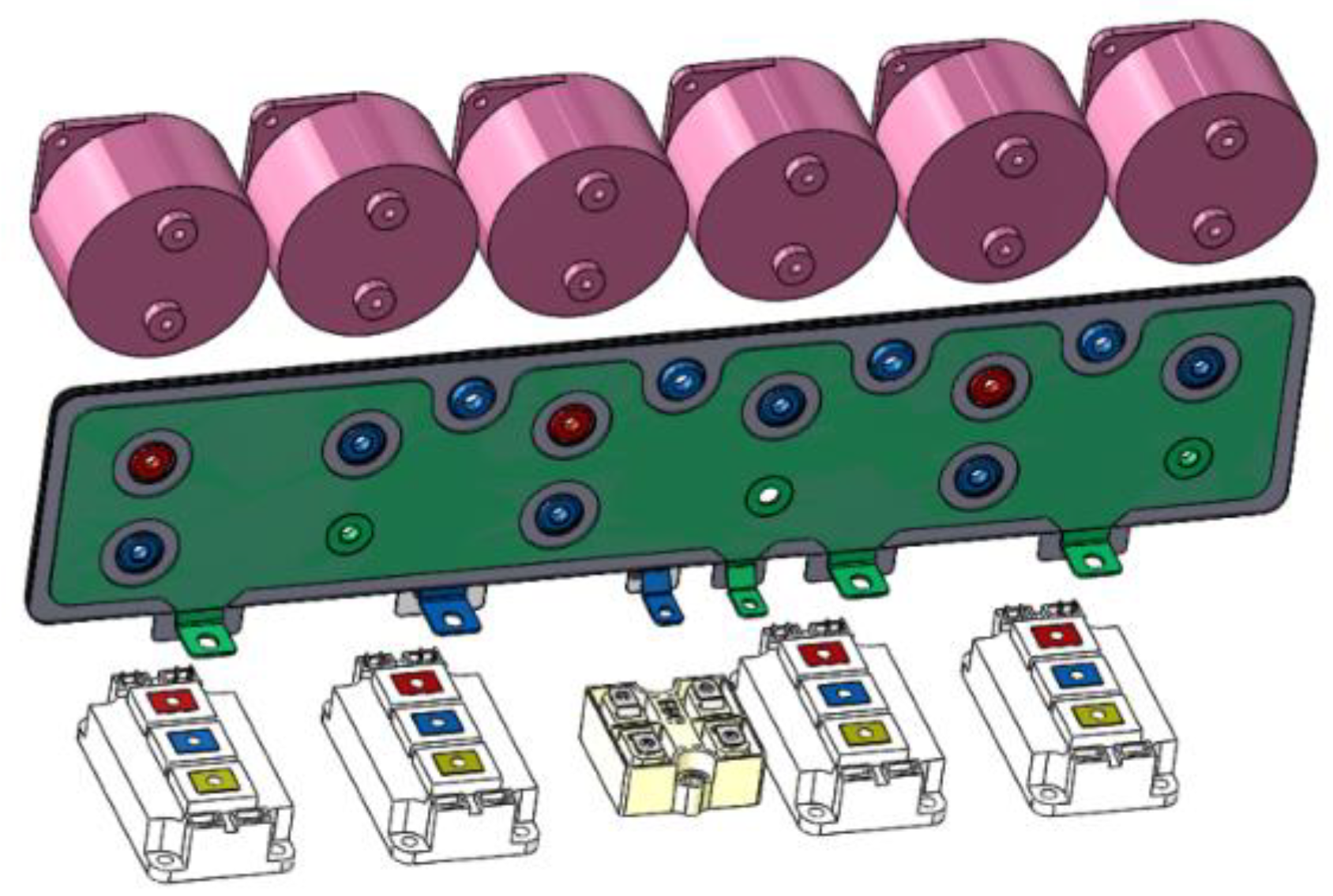

| Parameter | Value |
|---|---|
| Length of busbar | 160 mm |
| Width of busbar | 80 mm |
| Thickness of busbar | 1 mm |
| Radius of calculation region circle | 140 mm |
| Radius of bus capacitor | 6 mm |
| Parameter | Value |
|---|---|
| D1, Q2 | SKM400GAL125 |
| Q3, D4 | SKM400GAR125 |
| Q5, Q6 | SKM400GB176D |
| Time of Pulse Width | 150 us |
| Maximum load test current | 1000 A |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, M.; Wang, N.; Wang, Z. Optimized Design of Laminated Busbar for Large-Capacity Back-to-Back Converters. Energies 2022, 15, 774. https://doi.org/10.3390/en15030774
Xu M, Wang N, Wang Z. Optimized Design of Laminated Busbar for Large-Capacity Back-to-Back Converters. Energies. 2022; 15(3):774. https://doi.org/10.3390/en15030774
Chicago/Turabian StyleXu, Mingxia, Ninghui Wang, and Zhipeng Wang. 2022. "Optimized Design of Laminated Busbar for Large-Capacity Back-to-Back Converters" Energies 15, no. 3: 774. https://doi.org/10.3390/en15030774
APA StyleXu, M., Wang, N., & Wang, Z. (2022). Optimized Design of Laminated Busbar for Large-Capacity Back-to-Back Converters. Energies, 15(3), 774. https://doi.org/10.3390/en15030774





