Nonlinear Hierarchical Easy-to-Implement Control for DC MicroGrids
Abstract
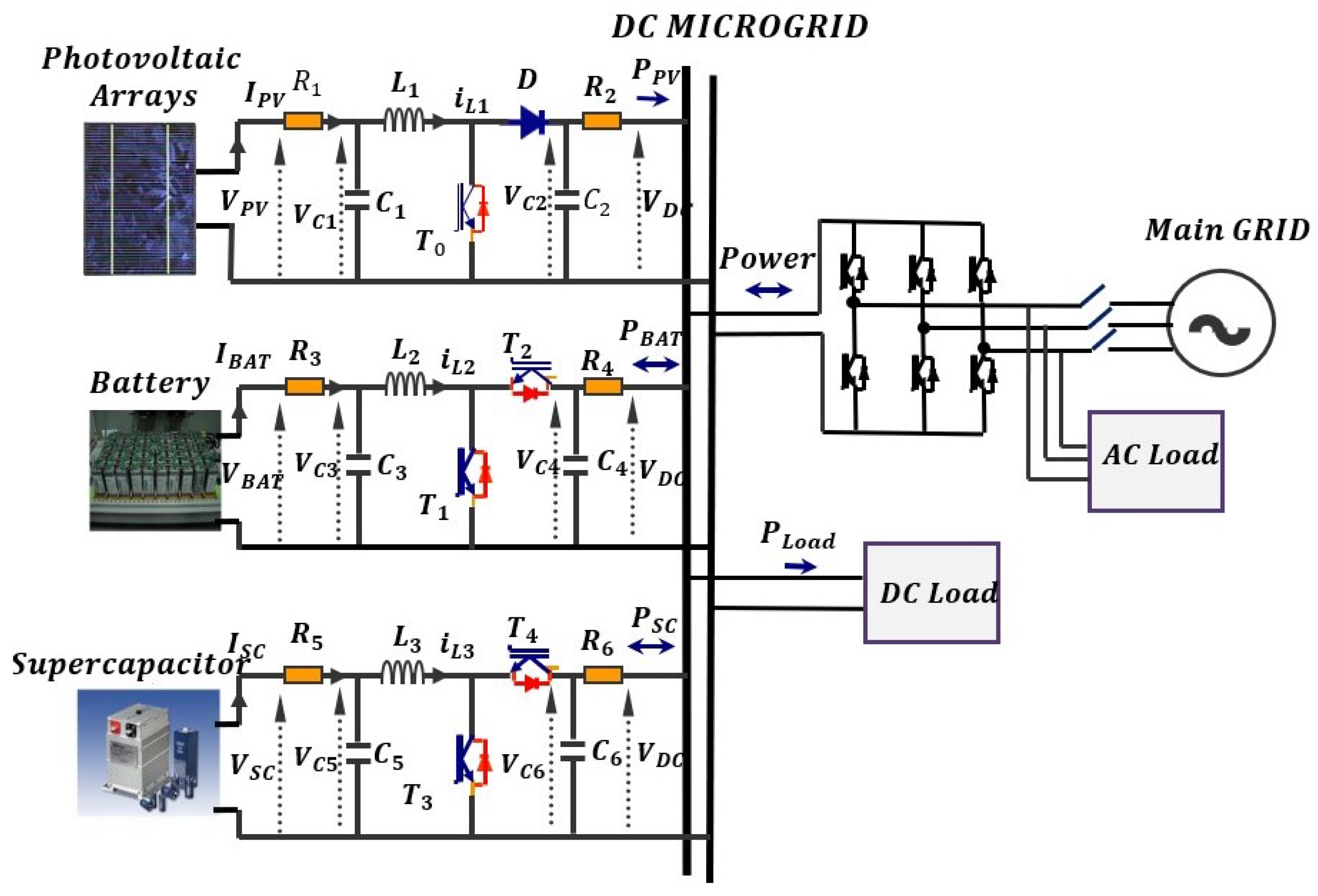
:1. DC MicroGrid Model
1.1. PV System Modeling
1.1.1. Solar Array
1.1.2. DC/DC Boost Converter
1.2. Storage System
1.2.1. Battery Model
1.2.2. Supercapacitor
1.2.3. Bidirectional Boost Converters
1.3. Interconnected Model
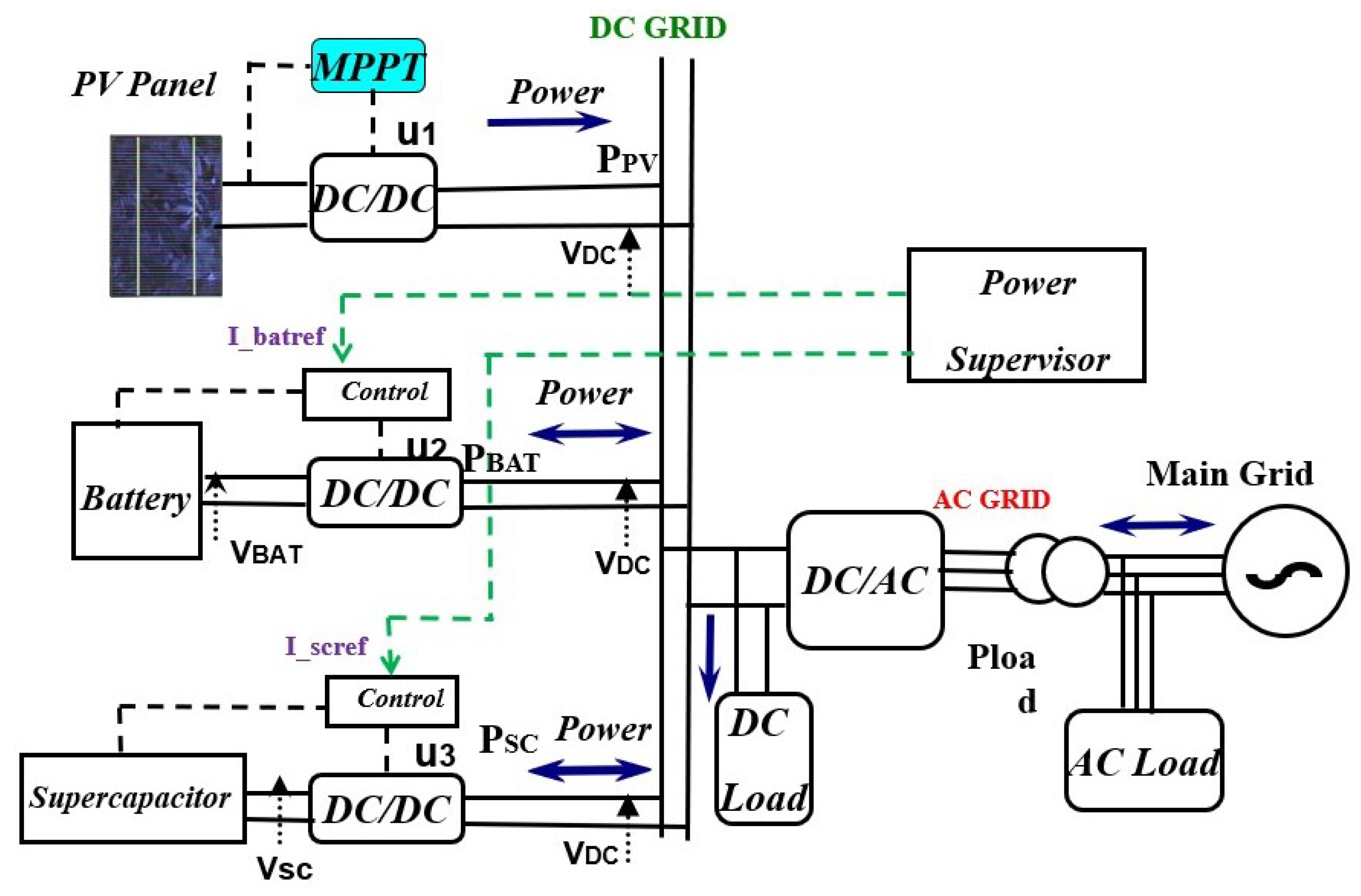
2. DC MicroGrid Control Strategy
2.1. High Level Controller for PV Array Source
2.2. High Level Controller for Storage System
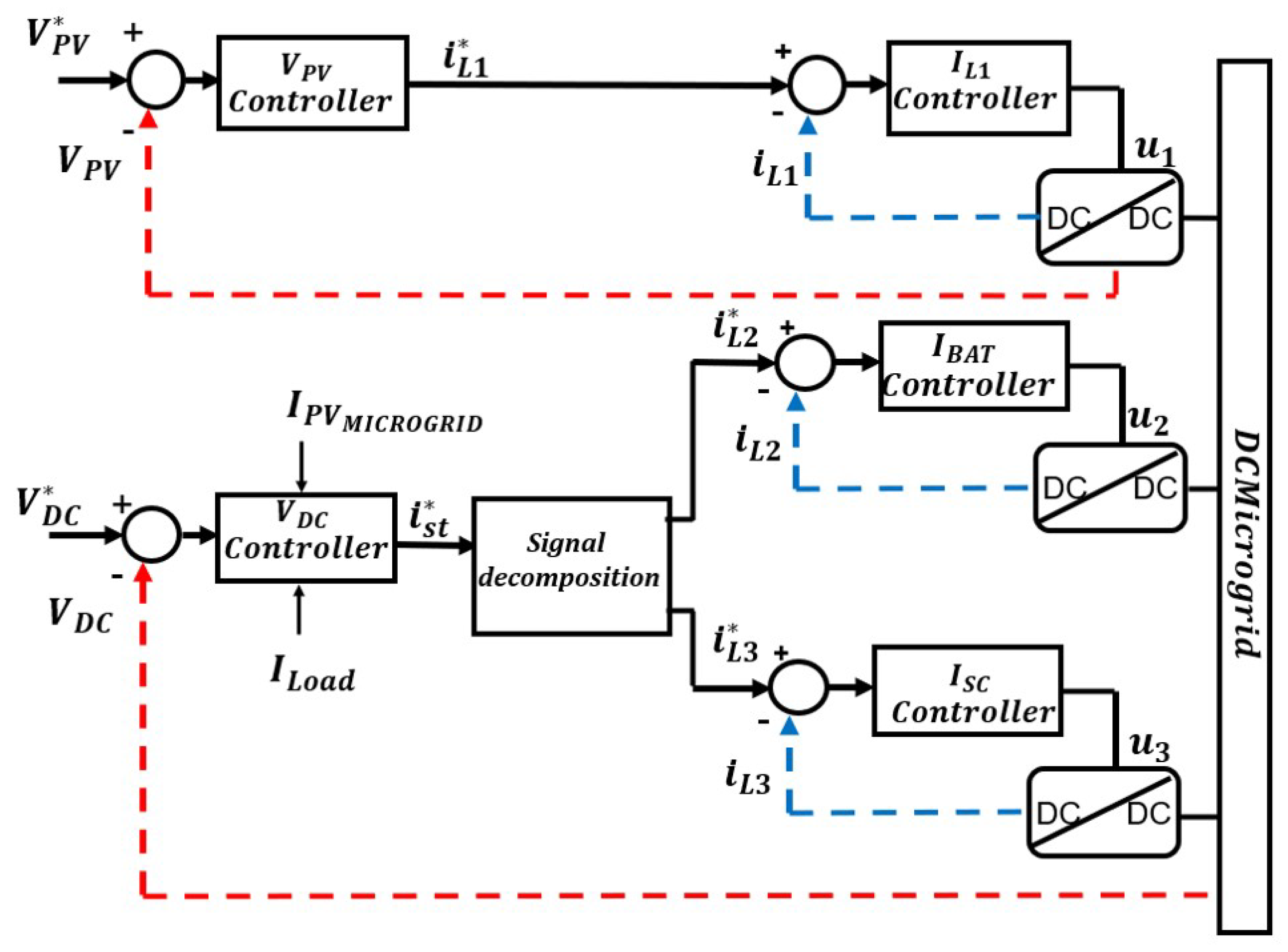
3. Local Control Level
3.1. Storage System Control
3.1.1. Battery Control Law
3.1.2. Supercapacitor Control Law
3.2. PV System Control
4. Stability Study of the Interconnected System
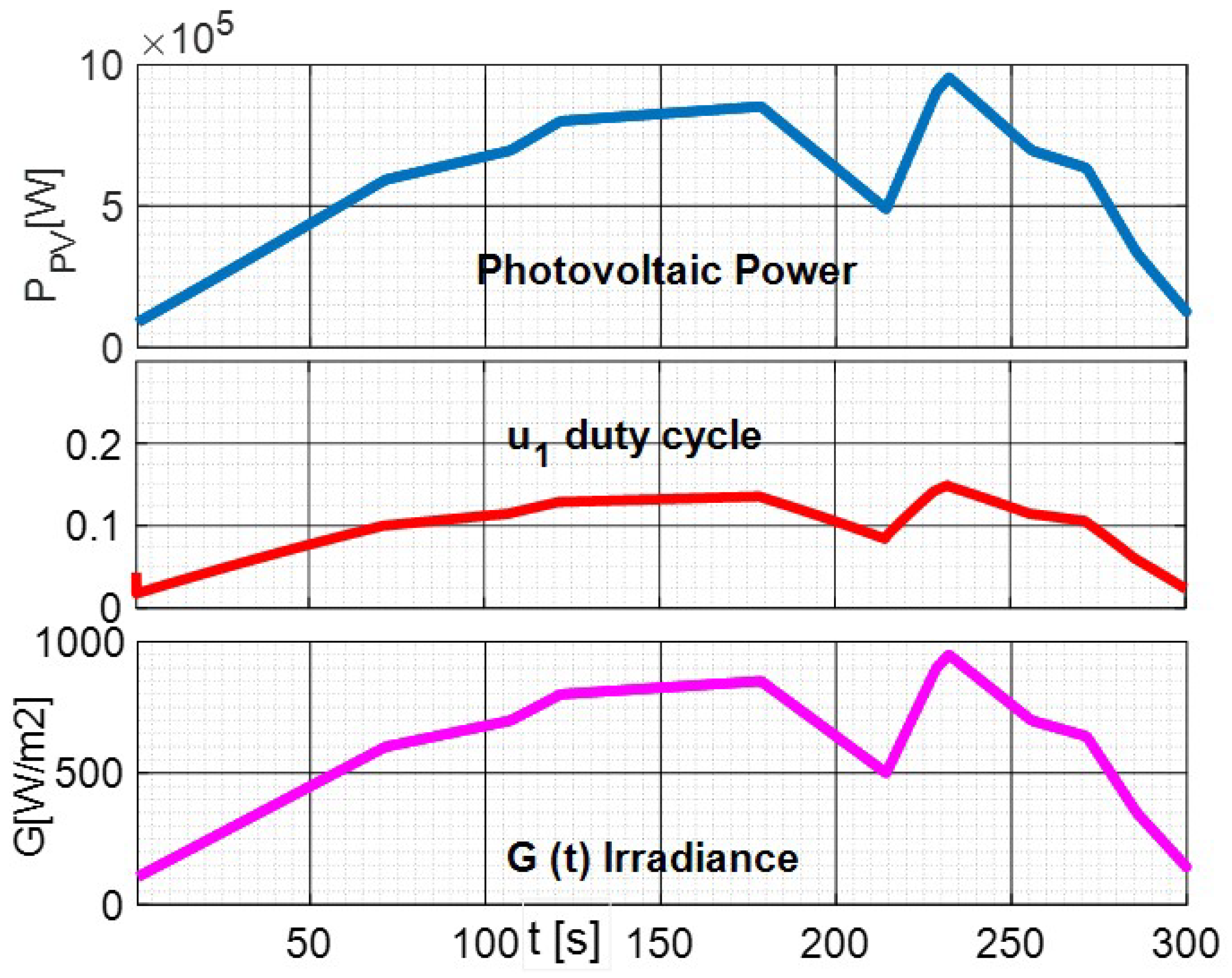
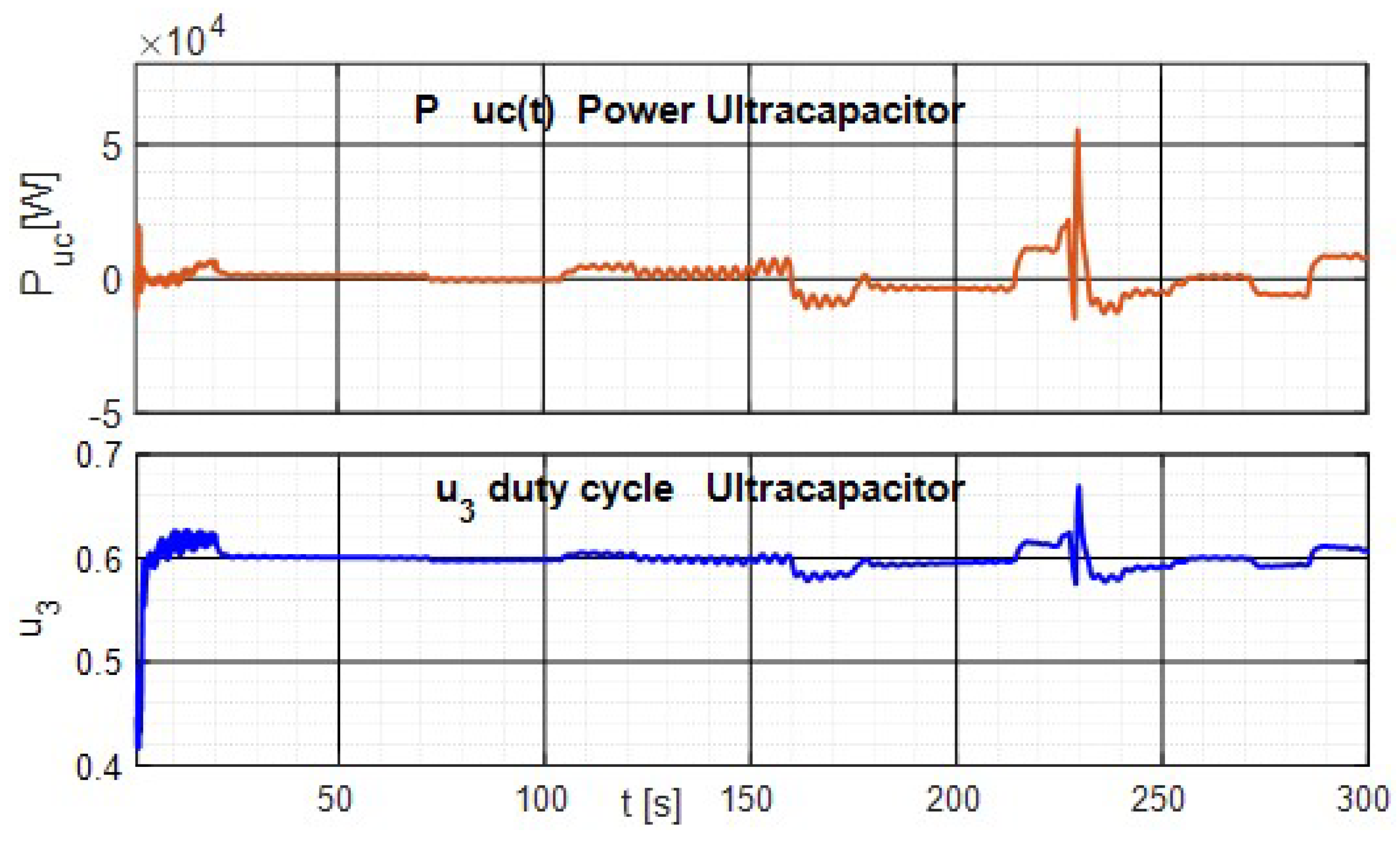
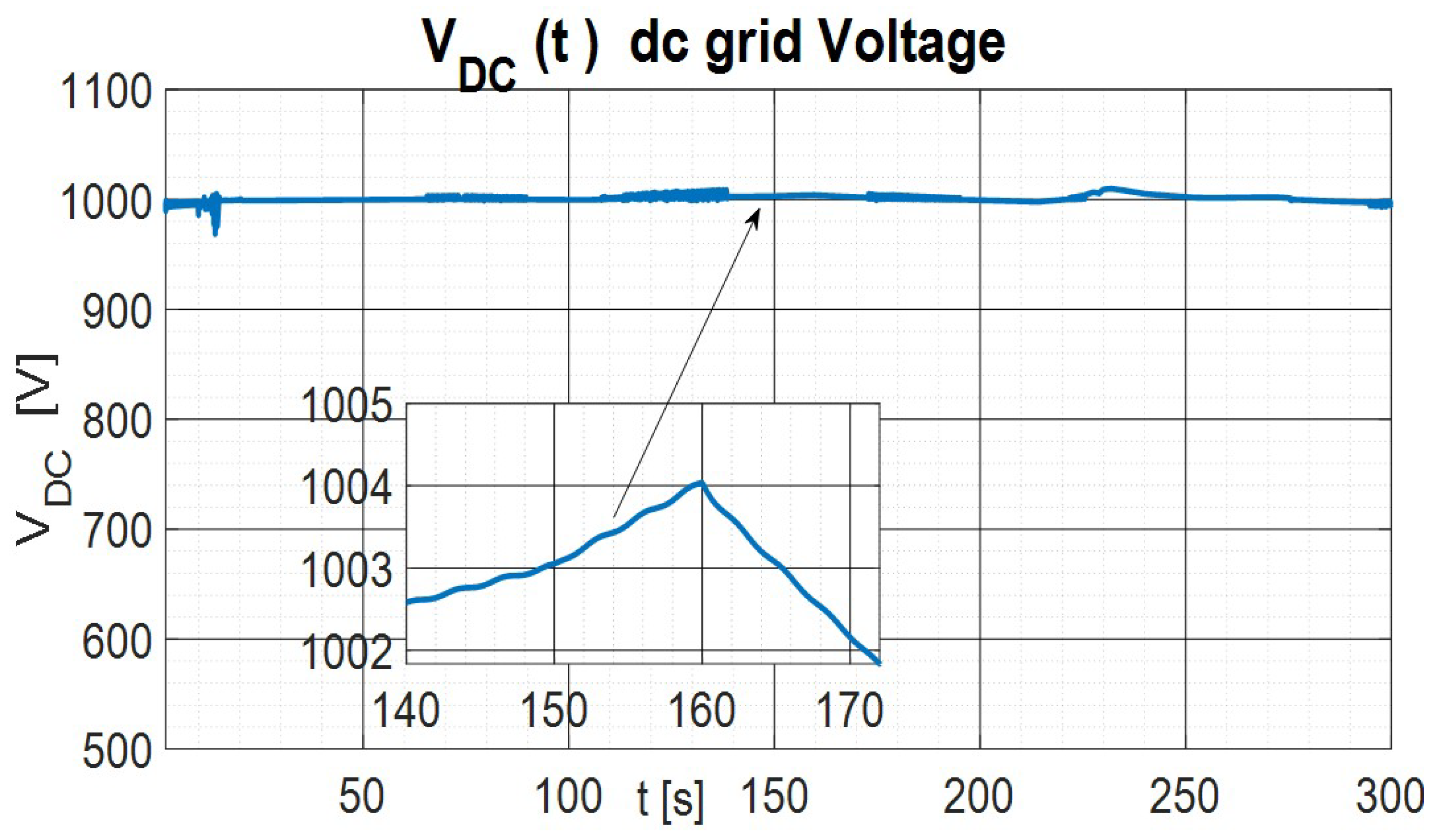
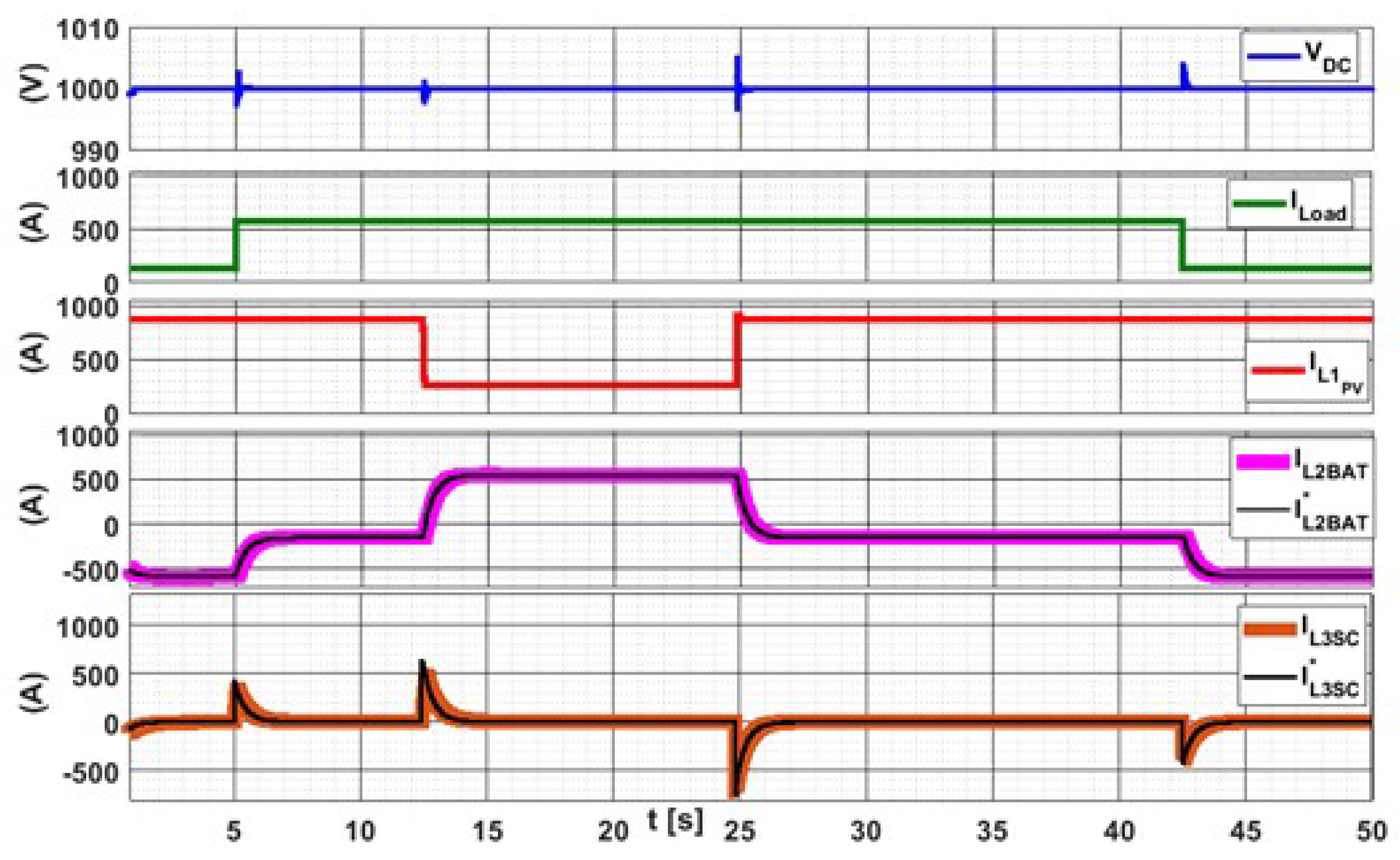
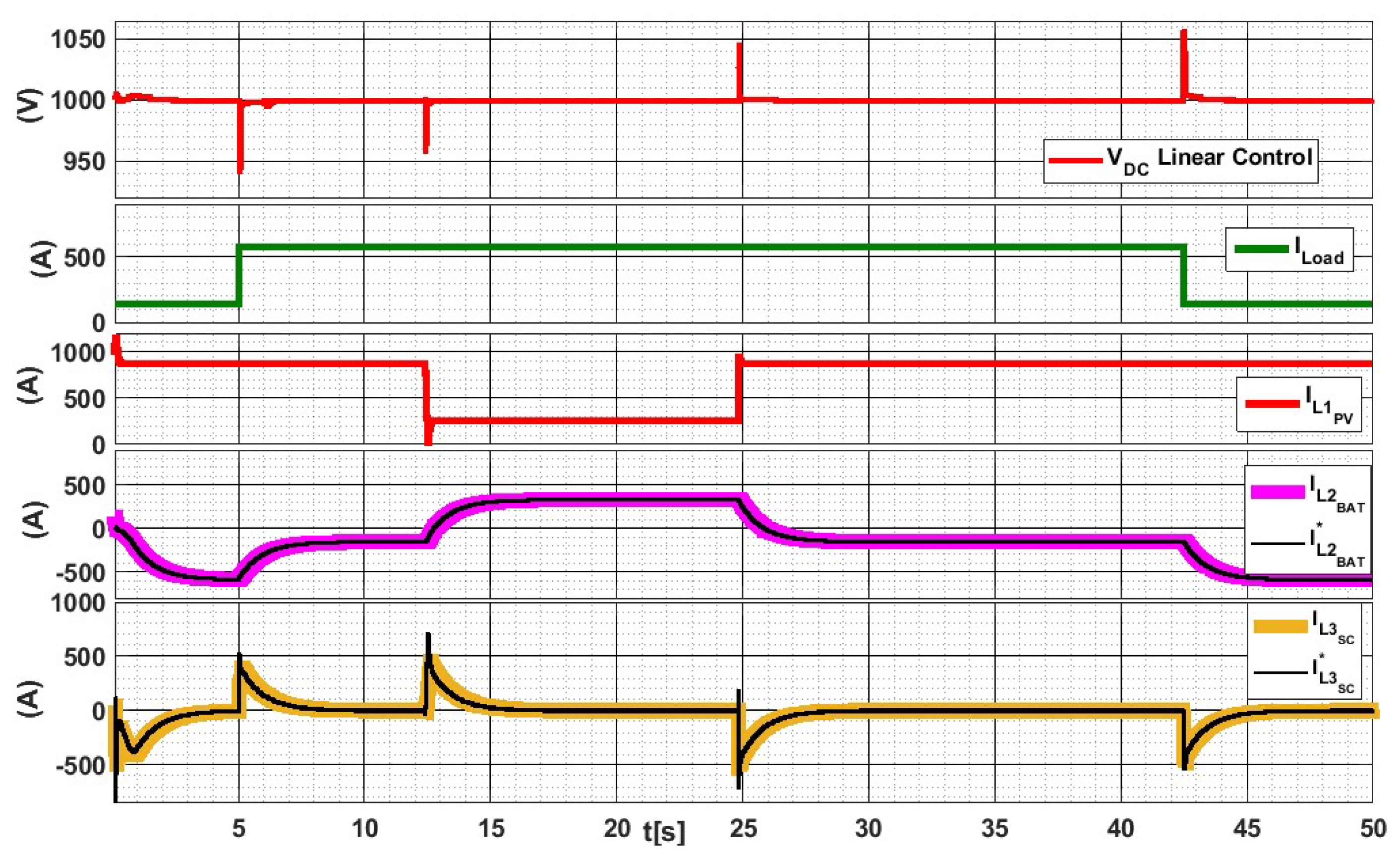
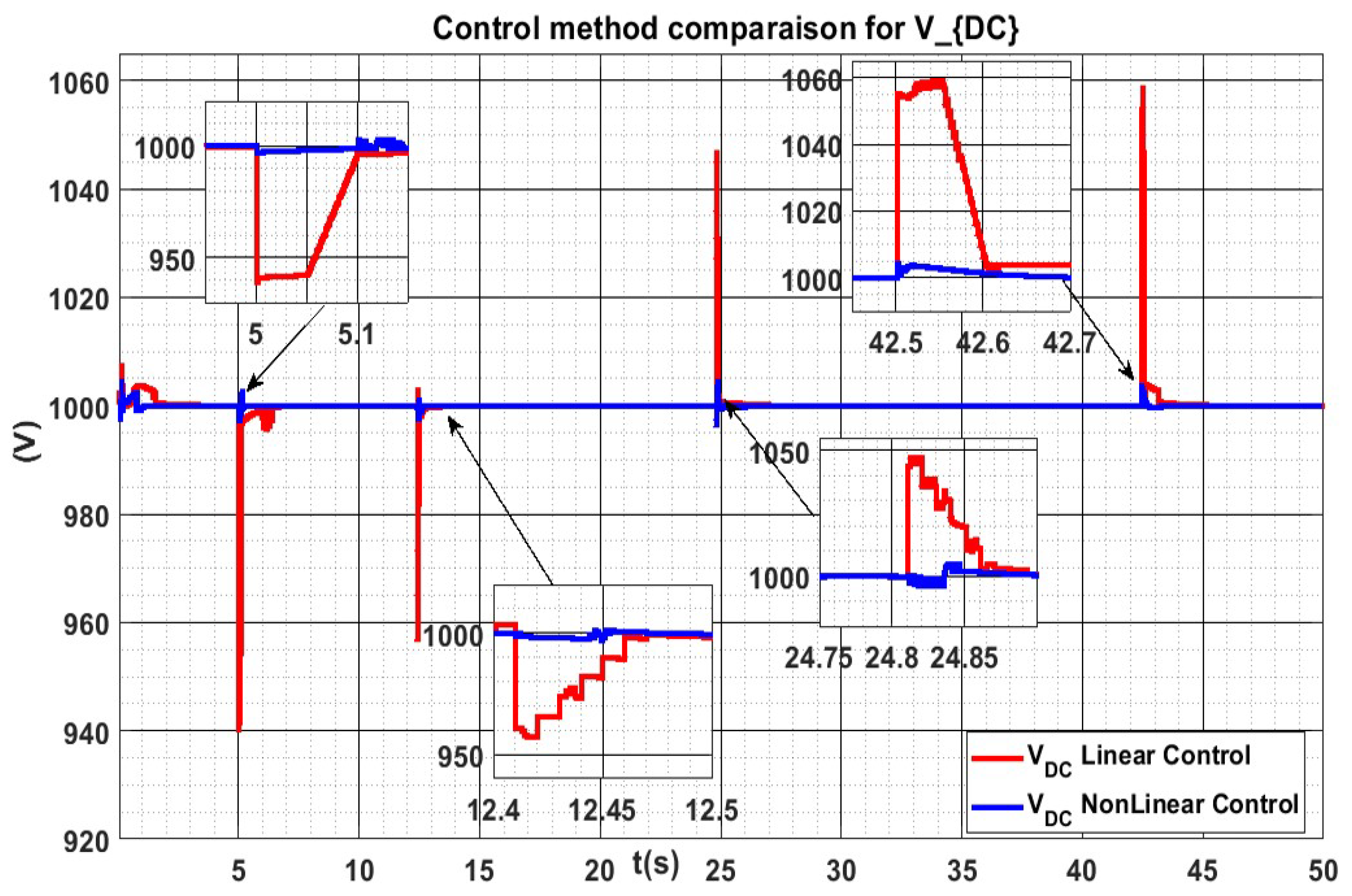
5. Simulation Results
Comparison with PI Control
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Output current of solar cell | |
| Output power of solar cell | |
| Terminal voltage of PV cell | |
| Output current of the battery | |
| Output voltage of the battery | |
| Output power of the battery | |
| Output current of the super capacitor | |
| Output voltage of the super capacitor | |
| Output power of the super capacitor | |
| Output power of the DC microgrid | |
| T | Cell’s reference Temperature |
| G | Solar irradiation |
| State of charge of battery | |
| , | internal resistances of DC/DC converter for the PV |
| , | resistances of DC/DC converter for the PV |
| inductance for the boost converter for the PV | |
| capacitance of DC/DC converter for the PV | |
| , | Voltage of capacitance and of DC/DC converter for the PV |
| current of inductance for the boost converter for the PV | |
| , | internal resistances of DC/DC converter for the battery |
| , | resistances of DC/DC converter for the battery |
| inductance for the boost converter for the battery | |
| capacitance of DC/DC converter for the battery | |
| , | Voltage of capacitance and of DC/DC converter for the battery |
| current of inductance for the boost converter for the battery | |
| , | internal resistances of DC/DC converter for the super capacitor |
| , | resistances of DC/DC converter for the super capacitor |
| inductance for the boost converter for the super capacitor | |
| capacitance of DC/DC converter for the super capacitor | |
| , | Voltage of capacitance and of DC/DC converter for the super capacitor |
| current of inductance for the boost converter for the super capacitor | |
| DC-link capacitance of DC micro grid | |
| f | Frequency of the AC grid |
| cutoff frequency for the filter | |
| … | positive tuning gains parameters |
| , and | Duties cycle of DC/DC converter |
References
- Hatziargyriou, N. Microgrids: Architectures and Control; John Wiley and Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Bevrani, H.; Francois, B.; Ise, T. Microgrid Dynamics and Control; John Wiley and Sons Inc.: Hoboken, NJ, USA, 2017. [Google Scholar]
- Ongaro, F.; Saggini, S.; Mattavelli, P. Li-Ion Battery-Supercapacitor Hybrid Storage System for a Long Lifetime, Photovoltaic-Based Wireless Sensor Network. IEEE Trans. Power Electron. 2012, 27, 3944–3952. [Google Scholar] [CrossRef]
- Tahim, A.P.N.; Pagano, D.J.; Lenz, E.; Stramosk, V. Modeling and Stability Analysis of Islanded DC Microgrids under Droop Control. IEEE Trans. Power Electron. 2015, 30, 4597–4607. [Google Scholar] [CrossRef]
- Dulout, J.; Jammes, B.; Seguier, L.; Alonso, C. Control and design of a hybrid energy storage system. In Proceedings of the 2015 17th European Conference on Power Electronics and Applications (EPE 15 ECCE-Europe), Geneva, Switzerland, 8–10 September 2015; pp. 1–9. [Google Scholar]
- O’Keeffe, D.; Riverso, S.; Albiol-Tendillo, L.; Lightbody, G. Distributed Hierarchical Droop Control of Boost Converters in DC Microgrids. In Proceedings of the 28th IEEE Irish Signals & Systems Conference, Killarney, Ireland, 20–21 June 2017. [Google Scholar]
- Liang, C.; Zhang, Y.; Ji, X.; Meng, X.; An, Y.; Yao, Q. DC Bus Voltage Sliding-mode Control for a DC Microgrid Based on Linearized Feedback. In Proceedings of the 2019 Chinese Automation Congress (CAC), Hangzhou, China, 22–24 November 2019; pp. 5380–5384. [Google Scholar] [CrossRef]
- Kollimalla, S.K.; Mishra, M.K.; Narasamma, N.L. Design and Analysis of Novel Control Strategy for Battery and Supercapacitor Storage System. IEEE Trans. Sustain. Energy 2014, 5, 1137–1144. [Google Scholar] [CrossRef]
- Ferreira, R.A.F.; Barbosa, P.G.; Braga, H.A.; Ferreira, A.A. Analysis of non-linear adaptive voltage droop control method applied to a grid connected DC microgrid. In Proceedings of the 2013 Brazilian Power Electronics Conference, Gramado, Brazil, 27–31 October 2013; pp. 1067–1074. [Google Scholar] [CrossRef]
- Chen, Y.; Damm, G.; Benchaib, A.; Netto, M.; Lamnabhi-Lagarrigue, F. Control Induced Explicit Time-Scale Separation to Attain DC Voltage Stability for a VSC-HVDC Terminal. IFAC Proc. Vol. 2014, 47, 540–545. [Google Scholar] [CrossRef] [Green Version]
- Iovine, A.; Siad, S.B.; Damm, G.; De Santis, E.; Di Benedetto, M.D. Nonlinear Control of a DC MicroGrid for the Integration of Photovoltaic Panels. IEEE Trans. Autom. Sci. Eng. 2017, 14, 524–535. [Google Scholar] [CrossRef] [Green Version]
- Siad, S.B.; Malkawi, A.; Damm, G.; Lopes, L.; Dol, L.G. Nonlinear control of a DC MicroGrid for the integration of distributed generation based on different time scales. Int. J. Electr. Power Energy Syst. 2019, 111, 93–100. [Google Scholar] [CrossRef] [Green Version]
- Siad, S.; Damm, G.; Dol, L.G.; Bernardinis, A.d. Design and Control of a DC Grid for Railway Stations. In Proceedings of the PCIM Europe 2017, International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Shanghai, China, 27–29 June 2017; pp. 1–8. [Google Scholar]
- Guerrero, J.M.; Loh, P.C.; Lee, T.; Chandorkar, M. Advanced Control Architectures for Intelligent Microgrids—Part II: Power Quality, Energy Storage, and AC/DC Microgrids. IEEE Trans. Ind. Electron. 2013, 60, 1263–1270. [Google Scholar] [CrossRef] [Green Version]
- Carrizosa, M.J.; Navas, F.D.; Damm, G.; Lamnabhi-Lagarrigue, F. Optimal power flow in multi-terminal HVDC grids with offshore wind farms and storage devices. Int. J. Electr. Power Energy Syst. 2015, 65, 291–298. [Google Scholar] [CrossRef]
- Carrizosa, M.J.; Arzandé, A.; Navas, F.D.; Damm, G.; Vannier, J. A control strategy for multi-terminal DC grids with renewable production and storage devices. IEEE Trans. Sustain. Energy 2018, 9, 930–939. [Google Scholar] [CrossRef]
- Siad, S. DC MicroGrids Control for Renewable Energy Integration. Ph.D. Thesis, University Evry, Évry-Courcouronnes, France, 2019. [Google Scholar]
- Iovine, A.; Siad, S.; Damm, G.; De Santis, E.; Di Benedetto, M.D. Nonlinear Control of an AC-connected DC MicroGrid. In Proceedings of the 42nd Annual Conference of the IEEE Industrial Electronics Society—IECON 2016, Florence, Italy, 24–27 October 2016. [Google Scholar]
- Iovine, A.; Carrizosa, M.J.; Damm, G.; Alou, P. Nonlinear Control for DC MicroGrids enabling Efficient Renewable Power Integration and Ancillary Services for AC grids. IEEE Trans. Power Syst. 2019, 34, 5136–5146. [Google Scholar] [CrossRef]
- Iovine, A.; Rigaut, T.; Damm, G.; De Santis, E.; Di Benedetto, M.D. Power management for a DC MicroGrid integrating renewables and storages. Control Eng. Pract. 2019, 85, 59–79. [Google Scholar] [CrossRef]
- Benchaib, A. Advanced Control of AC/DC Power Networks: System of Systems Approach Based on Spatio-Temporal Scales; Wiley-ISTE: London, UK, 2015. [Google Scholar]
- Lee, J.; Han, B.; Choi, N. DC micro-grid operational analysis with detailed simulation model for distributed generation. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 12–16 September 2010; pp. 3153–3160. [Google Scholar]
- Krajacic, G.; Duic, N.; Mathiesen, B.V.; Carvalho, M.G. Smart energy storages for integration of renewable in 100% independent energy systems. Chem. Eng. Trans. 2010, 21, 391–396. [Google Scholar]
- Yahya, A.M.; Mahmoud, A.; Youm, L. Etude et modellisation d’un generateur photovoltaique. Rev. Energ. Renouvelables 2008, 11, 473–483. [Google Scholar]
- Sera, D.; Teodorescu, R.; Hantschel, J.; Knoll, M. Optimized Maximum Power Point Tracker for fast changing environmental conditions. In Proceedings of the 2008 IEEE International Symposium on Industrial Electronics, Cambridge, UK, 30 June–2 July 2008; pp. 2401–2407. [Google Scholar]
- Xiao, W. A Modified Adaptive Hill Climbing Maximum Power Point Tracking (MPPT) Control Method for Photovoltaic Power Systems. Ph.D. Thesis, University of British Columbia Library, Vancouver, BC, Canada, 2003. [Google Scholar]
- Bacha, S.; Munteanu, I.; Bratcu, A.I. Power Electronic Converters Modeling and Control: With Case Studies; Advanced Textbooks in Control and Signal Processing; Springer: London, UK, 2013. [Google Scholar]
- Merdassi, A.; Gerbaud, L.; Seddik, B. General Average Modelling for Power Electronics Systems: Automatic Building Approach. In Proceedings of the 9th International Conference on Modeling and Simulation of Electric Machines, Converters and Systems, Quebec, QC, Canada, 26–28 May 2008. [Google Scholar]
- Merdassi, A. La Modellisation Automatique Pour l’Electronique de Puissance; Editions Universitaires Europeennes: Chisinau, Moldova, 2010. [Google Scholar]
- Sanders, S.R.; Noworolski, J.M.; Liu, X.Z.; Verghese, G.C. Generalized averaging method for power conversion circuits. IEEE Trans. Power Electron. 1991, 6, 251–259. [Google Scholar] [CrossRef] [Green Version]
- Barton, J.; Infield, D. Energy storage and its use with intermittent renewable energy. IEEE Trans. Energy Convers. 2004, 19, 441–448. [Google Scholar] [CrossRef]
- Bhatia, R.S.; Singh, B.; Jain, D.K.; Jain, S.P. Battery Energy Storage System Based Power Conditioner for Improved Performance of Hybrid Power Generation. In Proceedings of the 2008 Joint International Conference on Power System Technology and IEEE Power India Conference, New Delhi, India, 12–15 October 2008; pp. 1–6. [Google Scholar]
- Gergaud, O.; Robin, G.; Multon, B.; Ahmed, H. Energy Modeling of a Lead-Acid Battery within Hybrid Wind/Photovoltaic Systems. In Proceedings of the European Power Electronic Conference 2003, Toulouse, France, 2–4 September 2003. [Google Scholar]
- Vairamohan, B. State of Charge Estimation for Batteries. Master’s Thesis, University of Tennessee, Knoxville, TN, USA, 2002. [Google Scholar]
- Miller, J.M.; Nebrigic, D.; Everett, M. Ultra Capacitor Distributed Model Equivalent Circuit for Power Electronic Circuit Simulation; Ansoft Leading Insights Workshop; Maxwell Technologies Inc.: San diego, CA, USA, 2006. [Google Scholar]
- Lifshitz, D.; Weiss, G. Optimal control of a capacitor-type energy storage system. IEEE Trans. Autom. Control 2015, 60, 216–220. [Google Scholar] [CrossRef]
- Odo, P. A Comparative Study of Single-phase Non-isolated Bidirectional dc-dc Converters Suitability for Energy Storage Application in a dc Microgrid. In Proceedings of the 2020 IEEE 11th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Dubrovnik, Croatia, 28 September–1 October 2020; pp. 391–396. [Google Scholar] [CrossRef]
- Sun, J.; Lin, W.; Hong, M.; Loparo, K.A. Voltage Regulation of DC-Microgrid with PV and Battery. IEEE Trans. Smart Grid 2020, 11, 4662–4675. [Google Scholar] [CrossRef]
- Adhikari, S.; Li, F. Coordinated V-f and P-Q Control of Solar Photovoltaic Generators with MPPT and Battery Storage in Microgrids. IEEE Trans. Smart Grid 2014, 5, 1270–1281. [Google Scholar] [CrossRef]
- Manandhar, U.; Ukil, A.; Gooi, H.B.; Tummuru, N.R.; Kollimalla, S.K.; Wang, B.; Chaudhari, K. Energy Management and Control for Grid Connected Hybrid Energy Storage System under Different Operating Modes. IEEE Trans. Smart Grid 2019, 10, 1626–1636. [Google Scholar] [CrossRef]
- Chen, Y.; Jiménez Carrizosa, M.; Damm, G.; Lamnabhi-Lagarrigue, F.; Li, M.; Li, Y. Control-Induced Time-Scale Separation for Multiterminal High-Voltage Direct Current Systems Using Droop Control. IEEE Trans. Control Syst. Technol. 2019, 28, 967–983. [Google Scholar] [CrossRef]
- Fei, Y.; Zhuang, J.; Li, G.; Yao, L.; Yang, B. Research on the dual-terminal ring topology-based dc microgrid system. J. Eng. 2018, 2019, 3255–3258. [Google Scholar] [CrossRef]
- Kumar, D.; Zare, F.; Ghosh, A. DC Microgrid Technology: System Architectures, AC Grid Interfaces, Grounding Schemes, Power Quality, Communication Networks, Applications, and Standardizations Aspects. IEEE Access 2017, 5, 12230–12256. [Google Scholar] [CrossRef]
- Khalil, H. Nonlinear Systems; Pearson: London, UK, 2002. [Google Scholar]
- Jin, Y.; Xu, J.; Zhou, G.; Mi, C. Small-signal modeling and analysis of improved digital peak current control of boost converter. In Proceedings of the 2009 IEEE 6th International Power Electronics and Motion Control Conference, Wuhan, China, 17–20 May 2009; pp. 326–330. [Google Scholar]
- Tang, W.; Lee, F.C.; Ridley, R.B. Small-signal modeling of average current-mode control. IEEE Trans. Power Electron. 1993, 8, 112–119. [Google Scholar] [CrossRef]
- Sun, J.; Bass, R.M. Modeling and practical design issues for average current control. In Proceedings of the Fourteenth Annual Applied Power Electronics Conference and Exposition (APEC ’99), Dallas, TX, USA, 14–18 March 1999; Volume 2, pp. 980–986. [Google Scholar]
- Cherati, S.M.; Azli, N.A.; Ayob, S.M.; Mortezaei, A. Design of a current mode PI controller for a single-phase PWM inverter. In Proceedings of the 2011 IEEE Applied Power Electronics Colloquium (IAPEC), Johor Bahru, Malaysia, 18–19 April 2011; pp. 180–184. [Google Scholar]
- Dixon, L.H. Average Current Mode Control of Switching Power Supplies. In Unitrode Power Supply Design Seminar Manual; Unitrode Corporation: Merrimack, MA, USA, 1990. [Google Scholar]
- Khalid, M. A Review on the Selected Applications of Battery-Supercapacitor Hybrid Energy Storage Systems for Microgrids. Energies 2019, 12, 4559. [Google Scholar] [CrossRef] [Green Version]
- Kollimalla, S.K.; Mishra, M.K.; Ukil, A.; Gooi, H.B. DC Grid Voltage Regulation Using New HESS Control Strategy. IEEE Trans. Sustain. Energy 2017, 8, 772–781. [Google Scholar] [CrossRef]
- Manandhar, U.; Tummuru, N.R.; Kollimalla, S.K.; Ukil, A.; Beng, G.H.; Chaudhari, K. Validation of Faster Joint Control Strategy for Battery- and Supercapacitor-Based Energy Storage System. IEEE Trans. Ind. Electron. 2018, 65, 3286–3295. [Google Scholar] [CrossRef]





| 0.1 F | |||||
| 0.01 F | |||||
| 0.1 F | |||||
| 0.01 F | |||||
| 0.1 F | |||||
| 0.01 F | |||||
| 0.0033 H | 0.0033 H | 0.0033 H | |||
| 1000 V | 1 MW | 1000 V | |||
| 500 V | 500 V | 1000 V |
| Steps | Peak | Peak | Settling | Settling |
|---|---|---|---|---|
| Overshoot | Overshoot | Time | Time | |
| Linear | Nonlinear | Linear | Nonlinear | |
| Control [V] | Control [V] | Control [s] | Control [s] | |
| s | ||||
| s | ||||
| s | 48 | 4 | ||
| s | 58 | 4 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siad, S.B.; Iovine, A.; Damm, G.; Galai-Dol, L.; Netto, M. Nonlinear Hierarchical Easy-to-Implement Control for DC MicroGrids. Energies 2022, 15, 969. https://doi.org/10.3390/en15030969
Siad SB, Iovine A, Damm G, Galai-Dol L, Netto M. Nonlinear Hierarchical Easy-to-Implement Control for DC MicroGrids. Energies. 2022; 15(3):969. https://doi.org/10.3390/en15030969
Chicago/Turabian StyleSiad, Sabah B., Alessio Iovine, Gilney Damm, Lilia Galai-Dol, and Mariana Netto. 2022. "Nonlinear Hierarchical Easy-to-Implement Control for DC MicroGrids" Energies 15, no. 3: 969. https://doi.org/10.3390/en15030969
APA StyleSiad, S. B., Iovine, A., Damm, G., Galai-Dol, L., & Netto, M. (2022). Nonlinear Hierarchical Easy-to-Implement Control for DC MicroGrids. Energies, 15(3), 969. https://doi.org/10.3390/en15030969








