Recovery of Trains’ Braking Energy in a Railway Micro-Grid Devoted to Train plus Electric Vehicle Integrated Mobility
Abstract
:1. Introduction
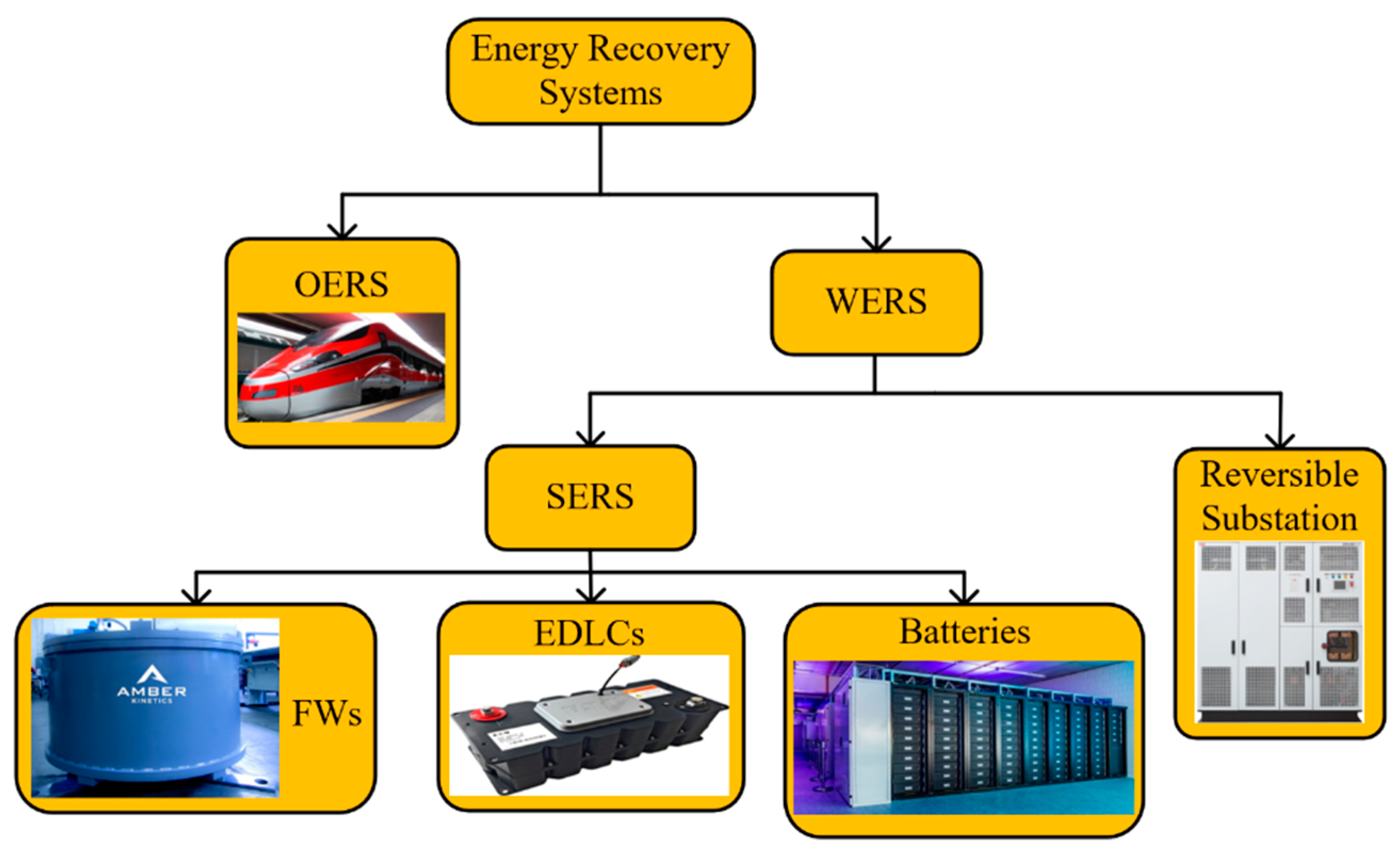
2. Energy Recovery Systems for Train Regenerative Braking
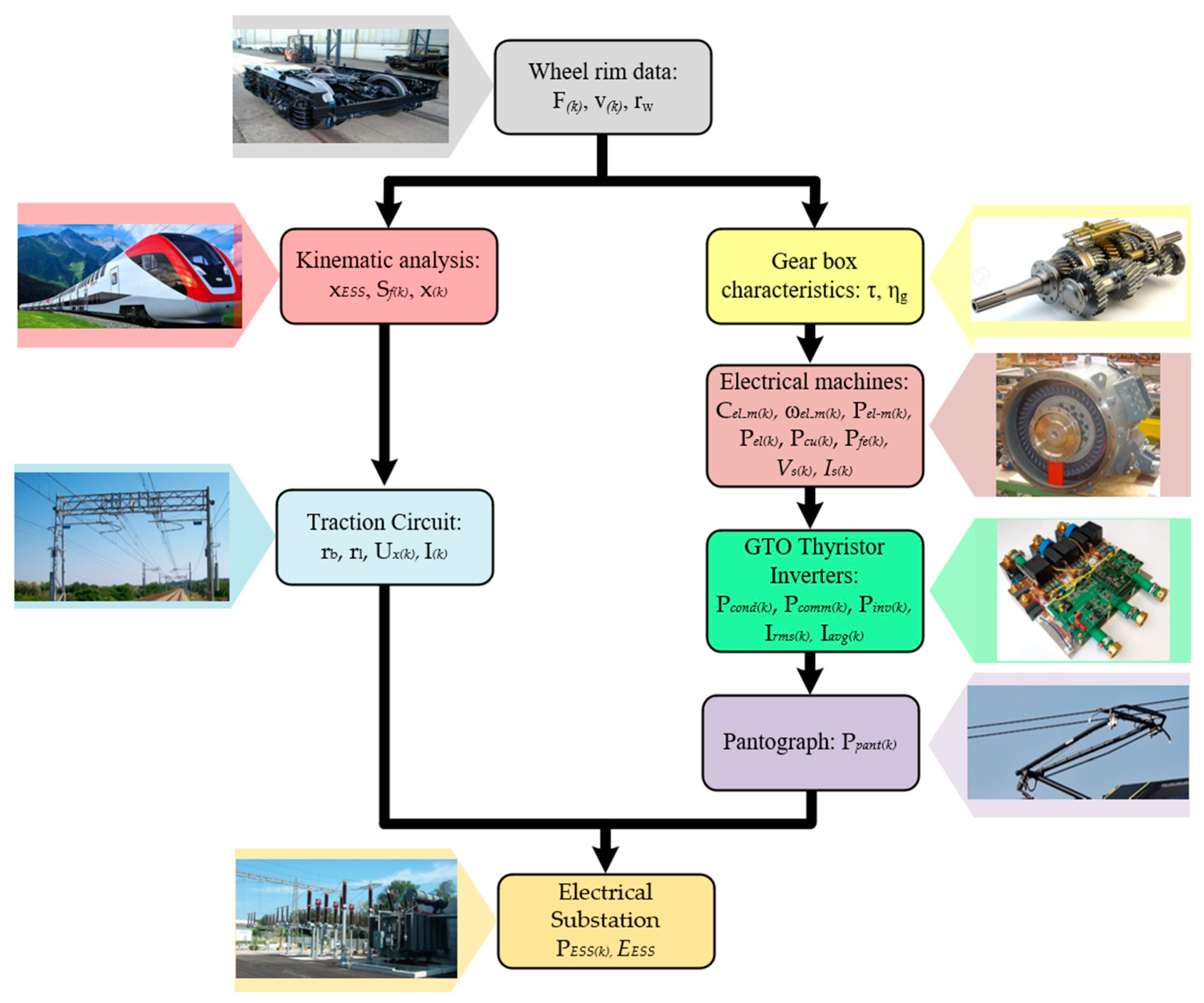
3. Estimating the Energy Recovery from the Timetable of a Railway Station
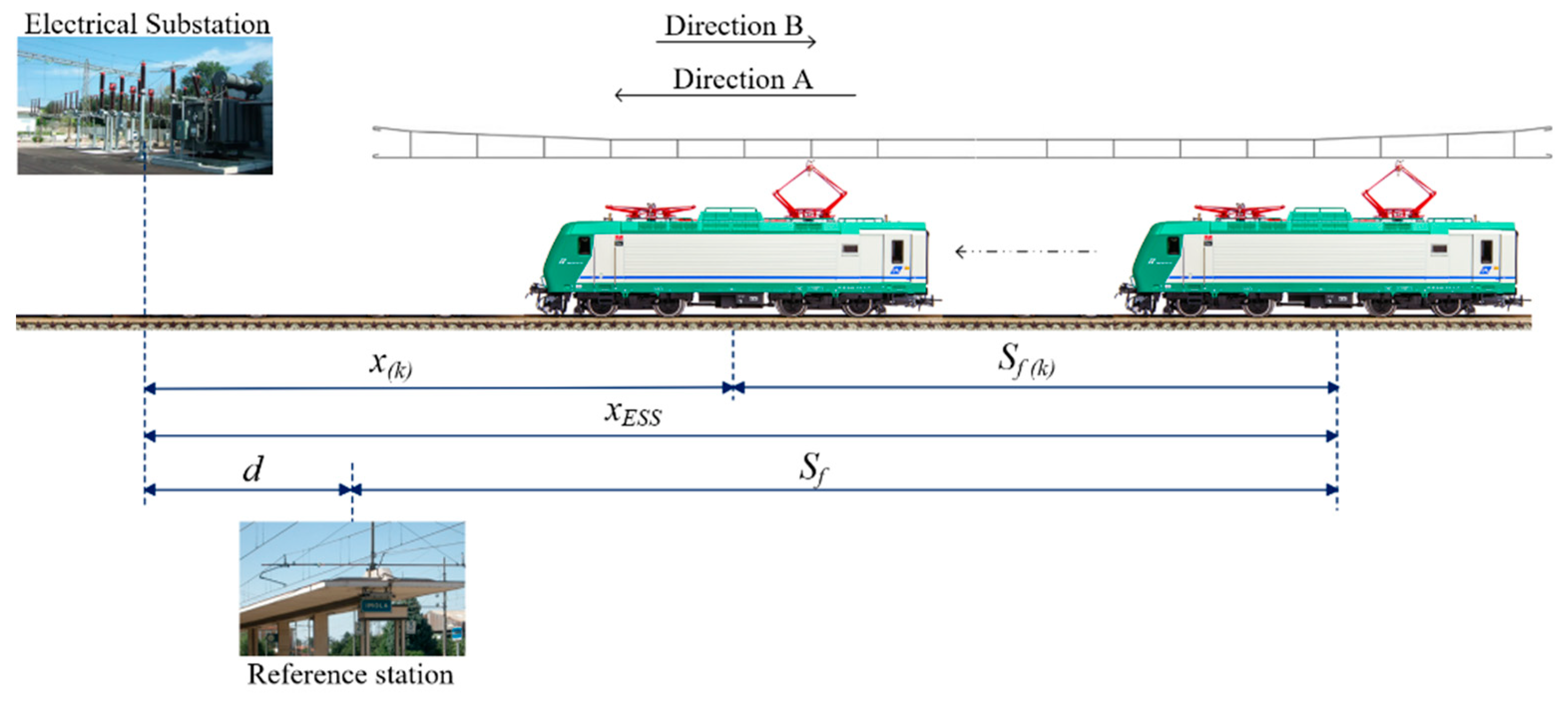
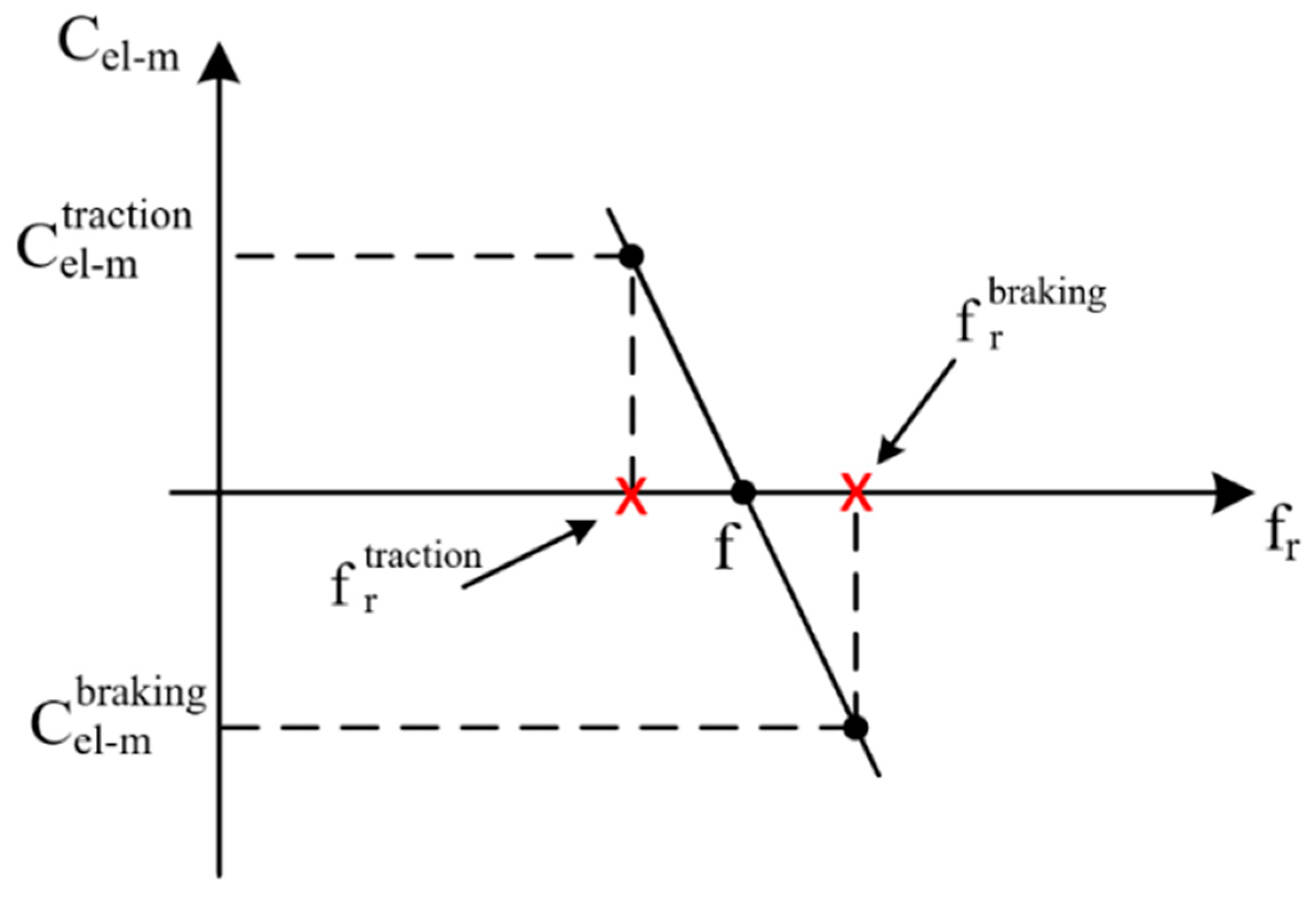
Modelling the Braking Transient for Arriving Trains
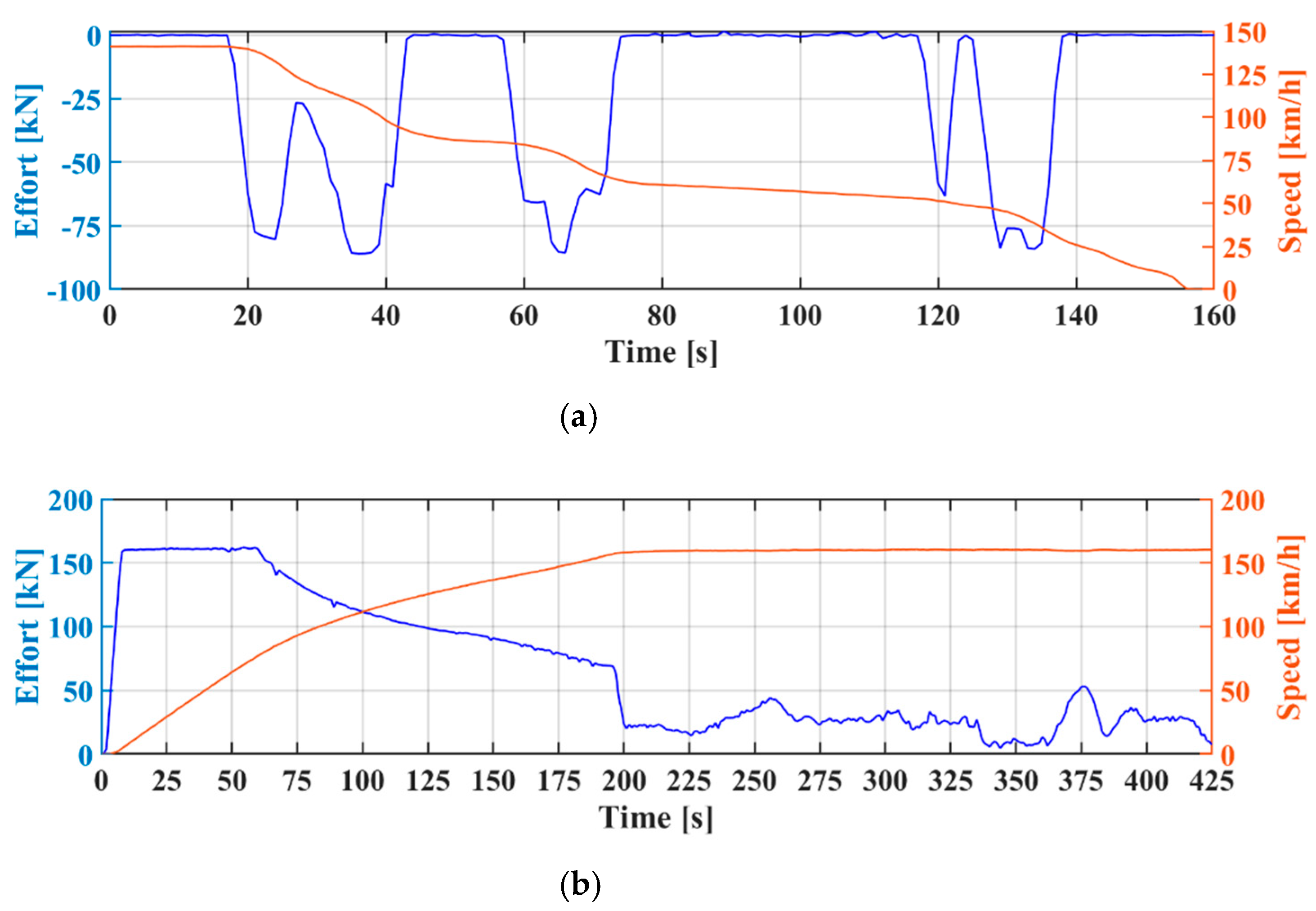
4. Case of Study: Imola Railway Station
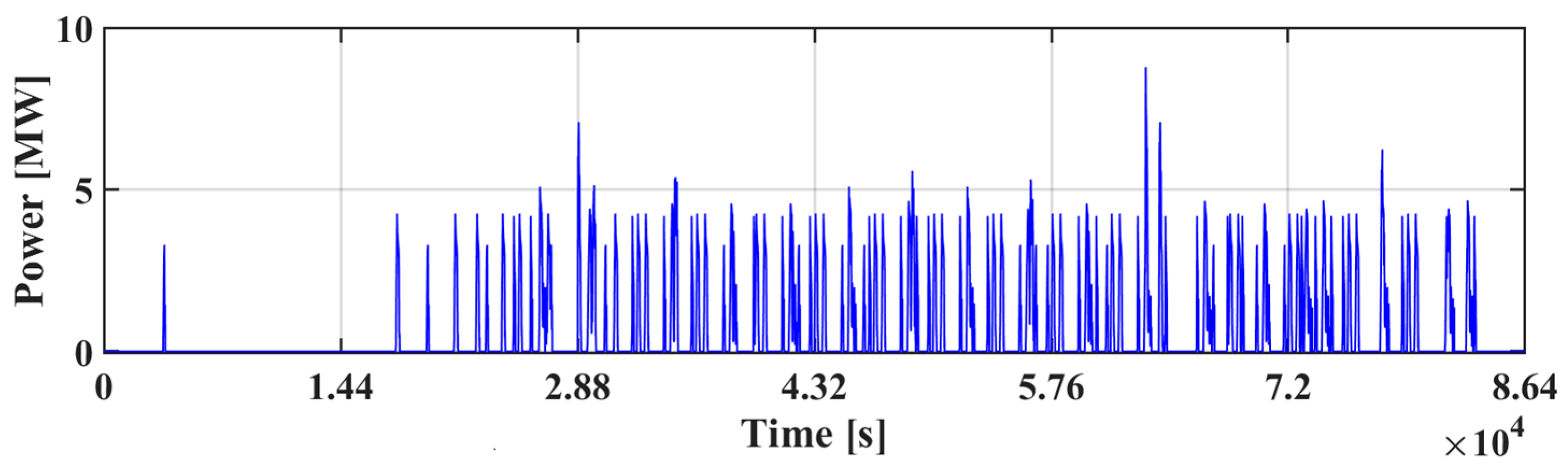
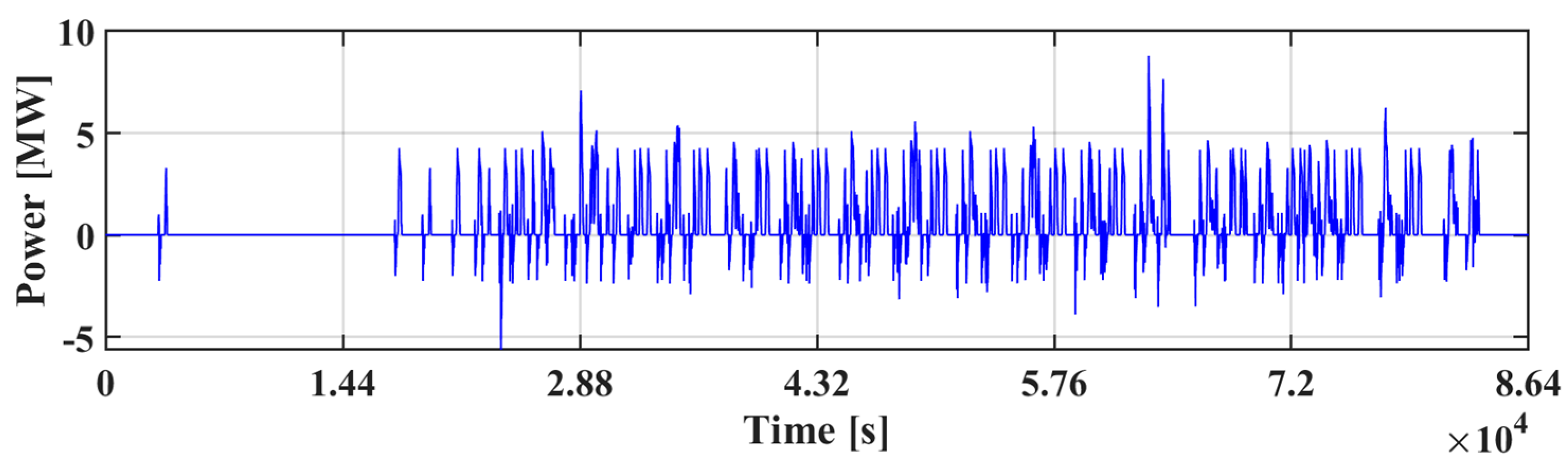
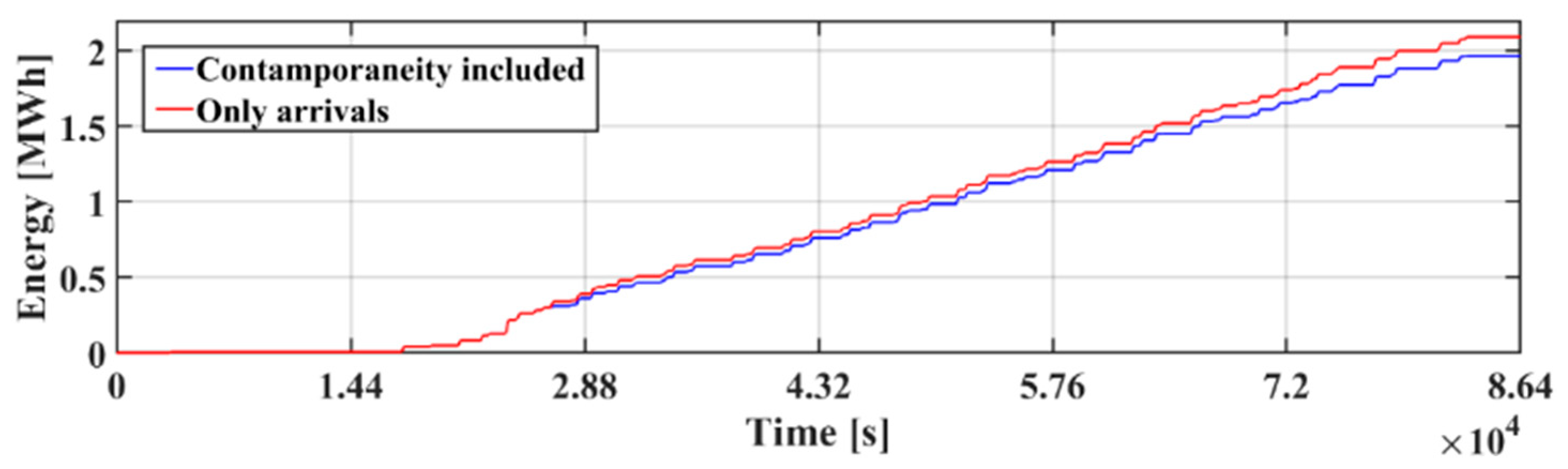
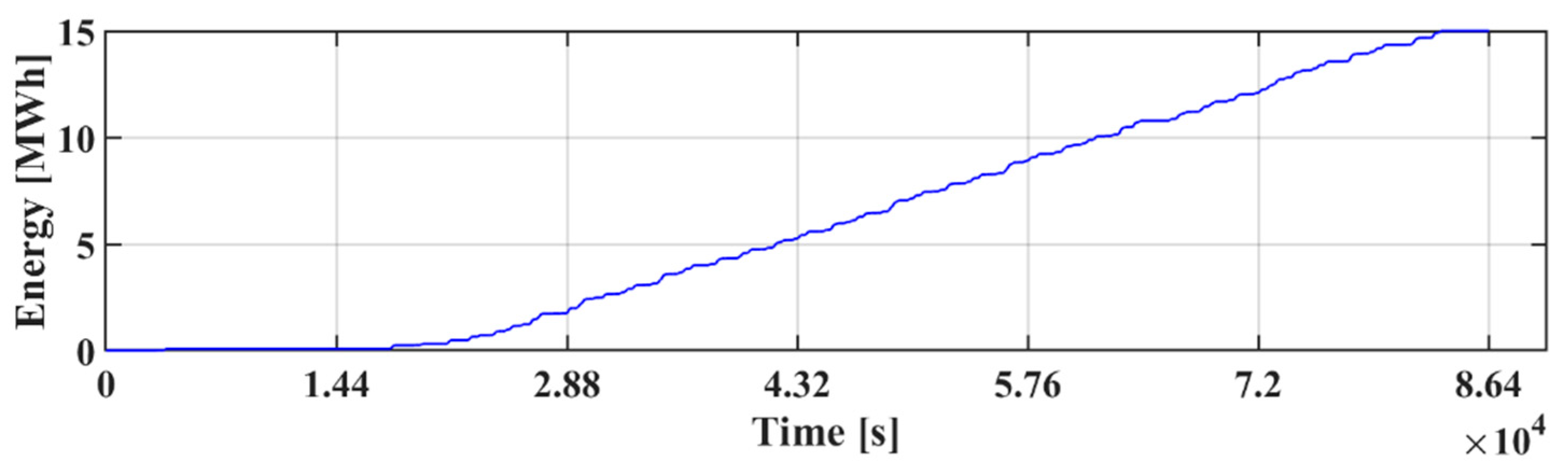
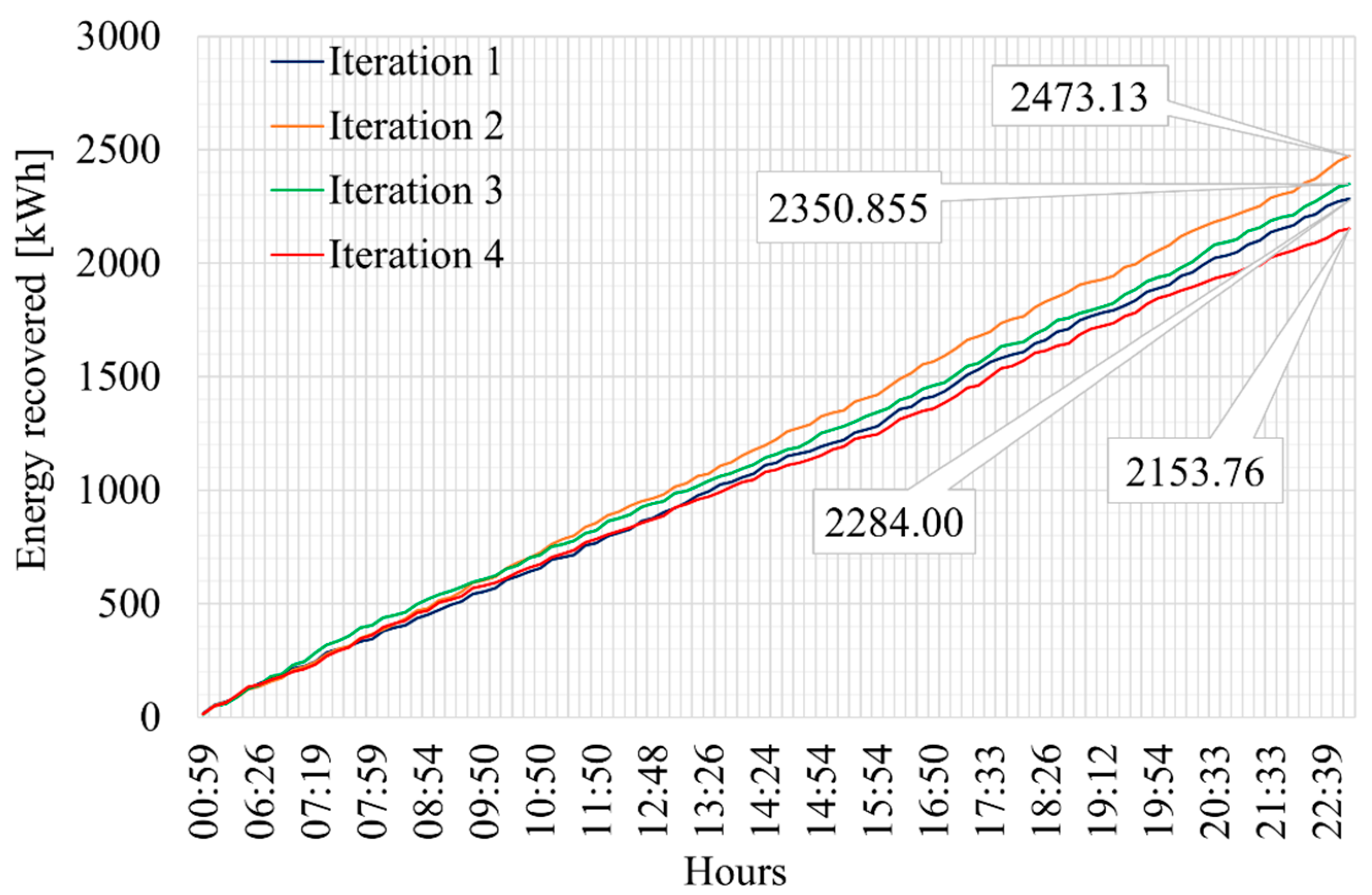
5. Discussion of Results
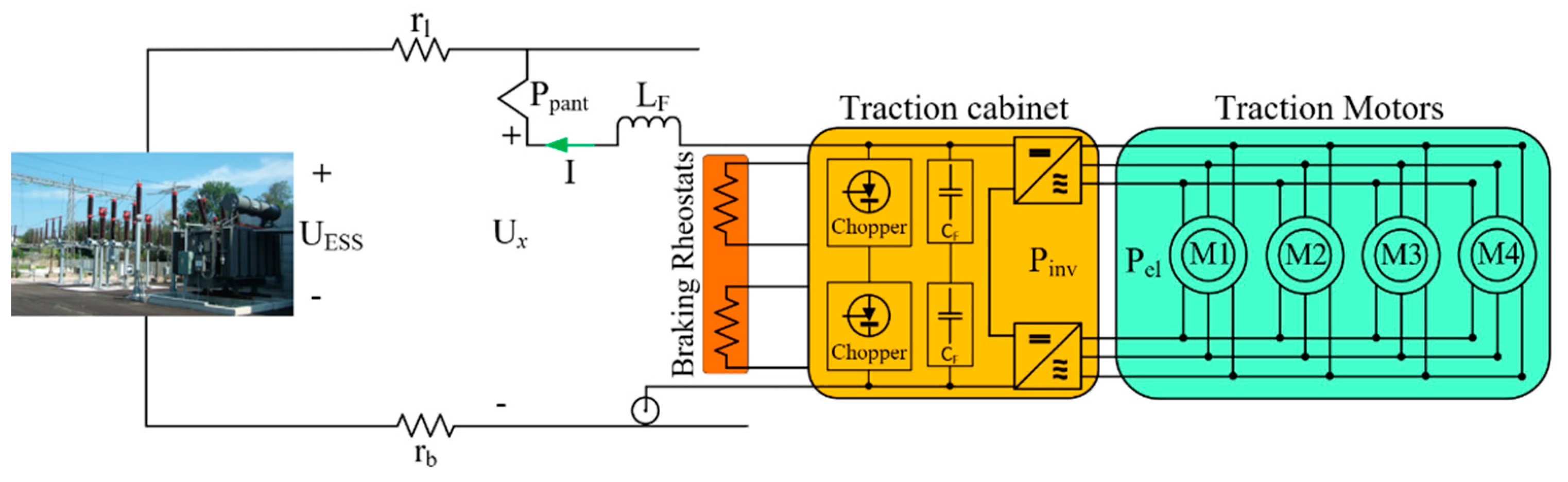
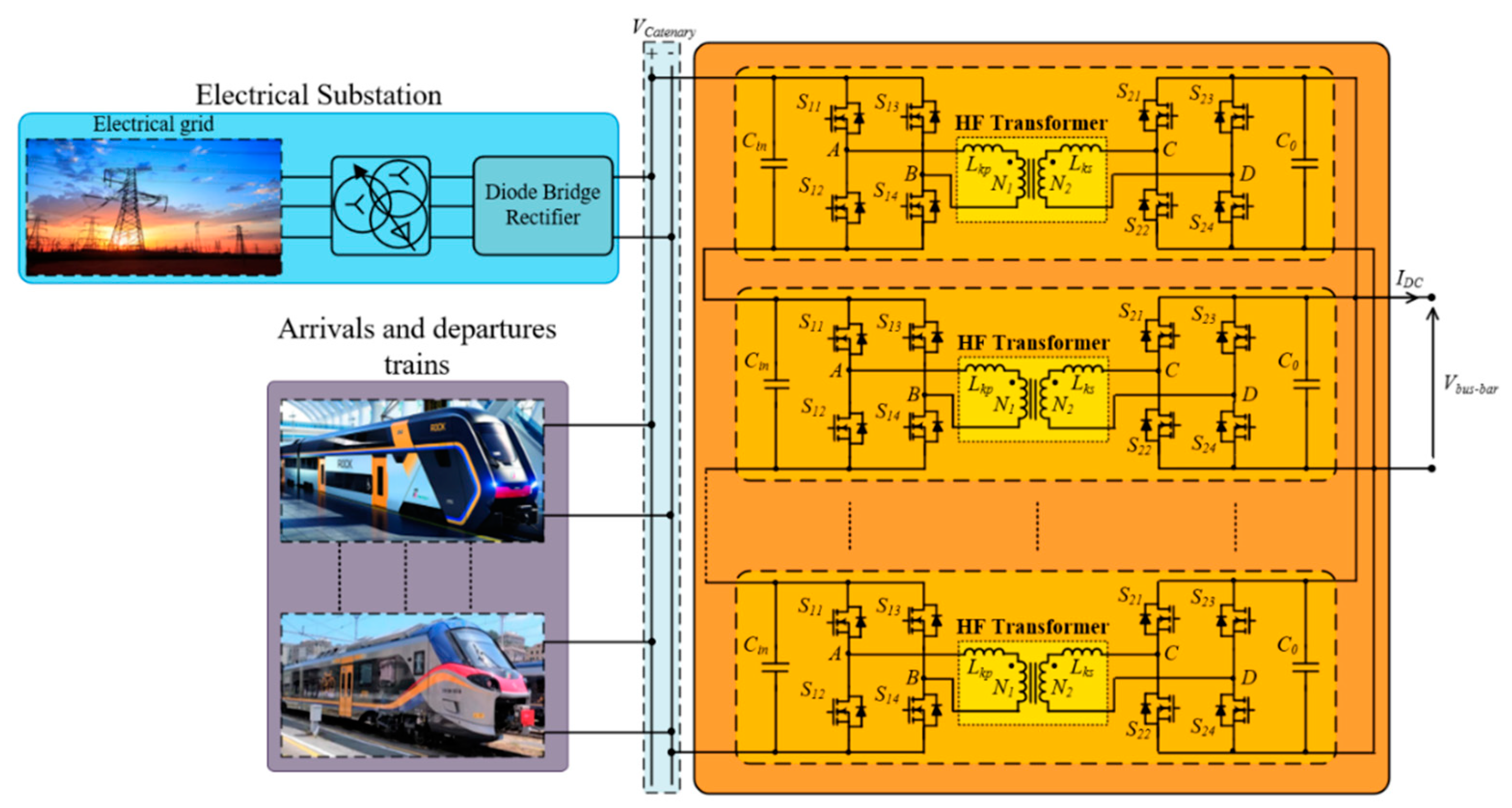
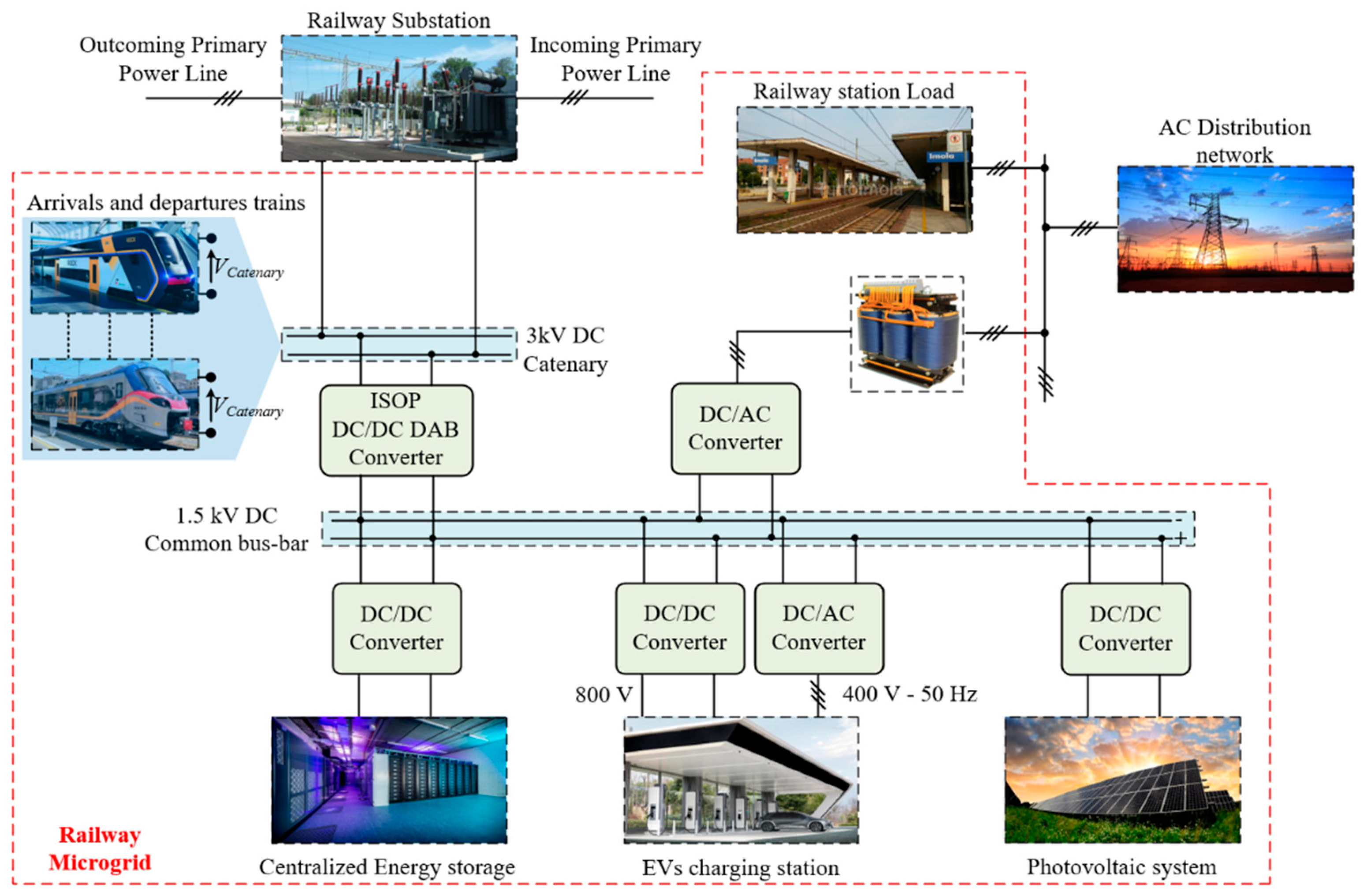
6. Architecture of the Railways DC Micro-Grid
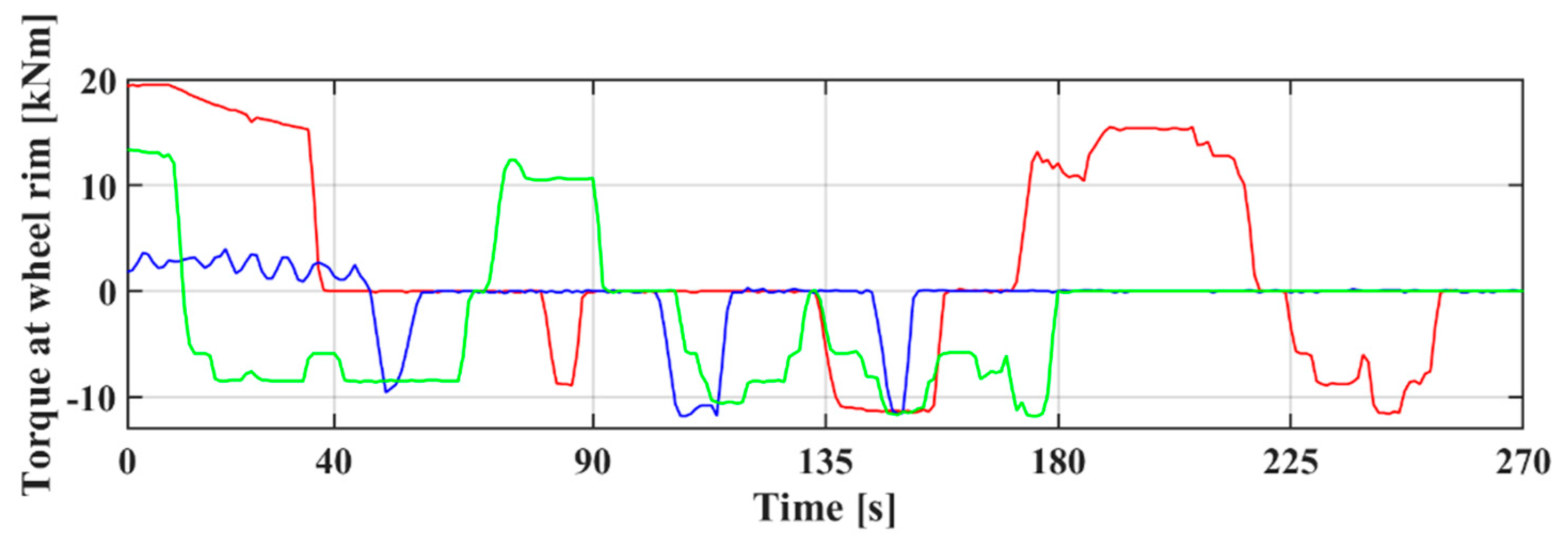
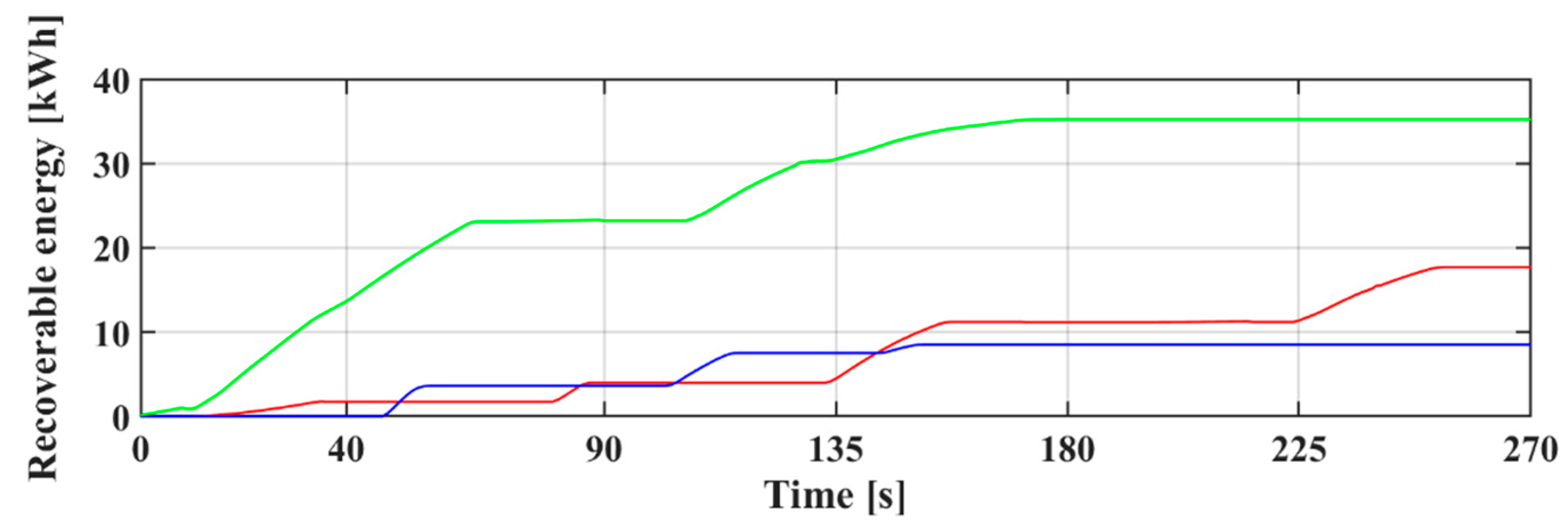
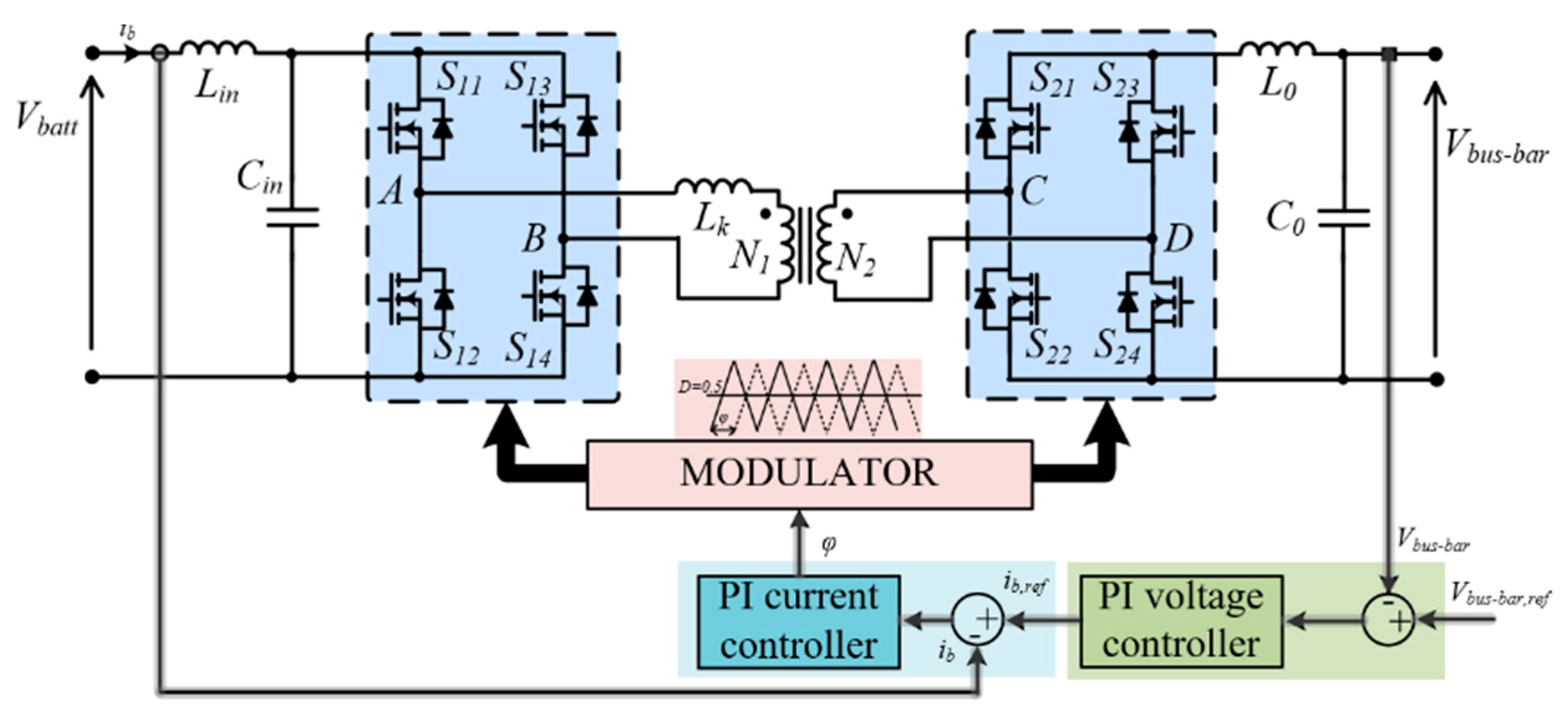
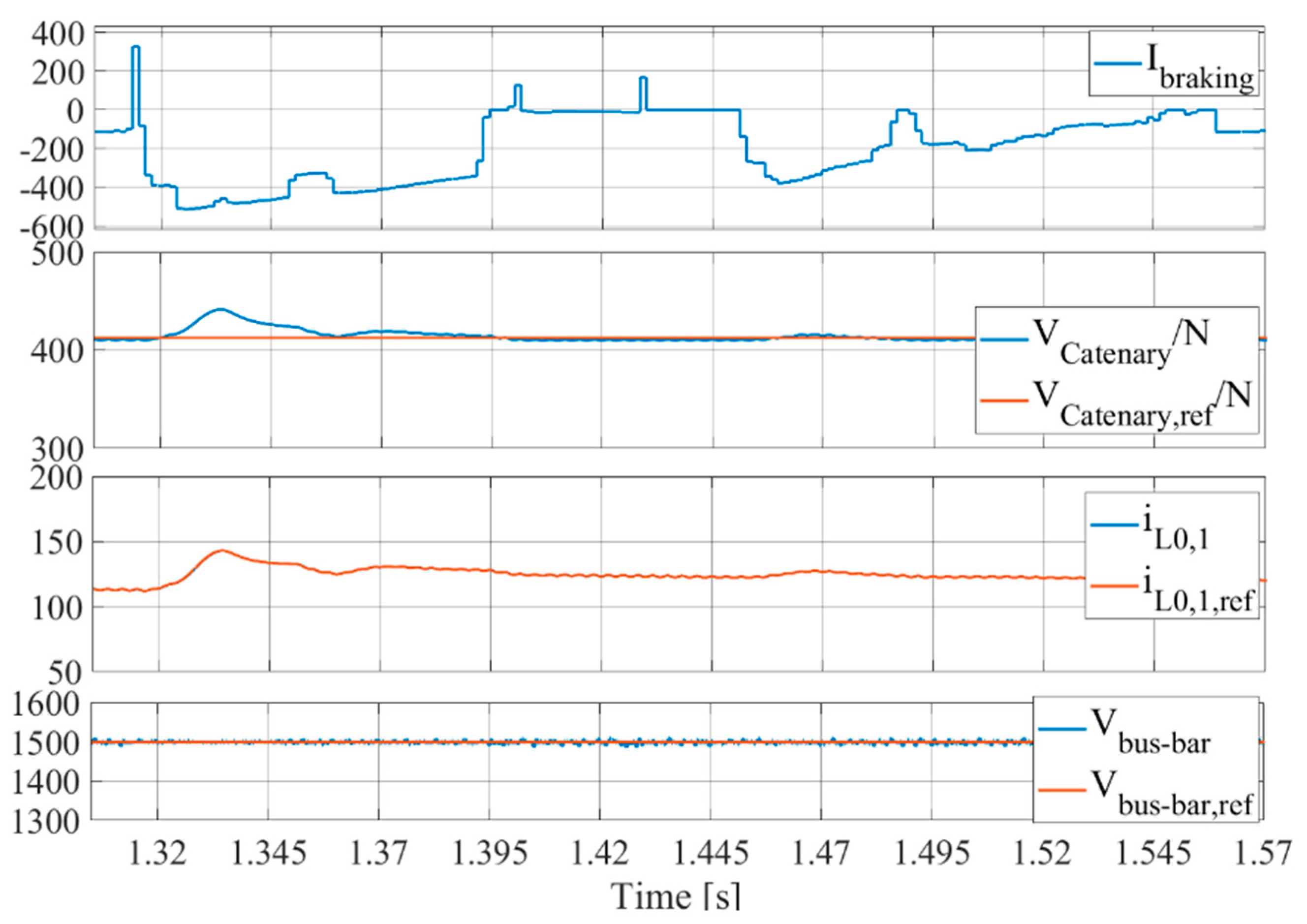
7. Dynamic Control of the Micro-Grid DC Voltage during Train Braking Transients
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Cel-m(k) | electromagnetic torque (Nm) | I(k) | current at the train’s pantograph (A) |
| d | distance from electrical substation and the station (m) | Id,ave (k) | average value of the diode current (A) |
| dbot(k) | bottom switch’s duty cycles | Id,rms(k) | RMS value of the diode current (A) |
| dtop(k) | top switch’s duty cycles | Is(k) | stator current (A) |
| Eag(k) | EMF induced by the airgap flux (V) | Isw,ave(k) | average value of the switching current (A) |
| Eavg | average energy loss in switch (J) | Isw,rms(k) | RMS value of the switching current (A) |
| Err | average energy loss in diode (J) | Ir(k) | RMS value of rotor current (A) |
| F(k) | effort applied at the wheel rim (N) | kC | machine constant |
| f(k) | machine supply frequency (Hz) | Lk | leakage inductance (H) |
| fr(k) | rotor electrical frequency (Hz) | M(k) | modulation depth |
| fsl(k) | slip frequency (Hz) | n | turn ratio |
| fsw | switching frequency (Hz) | N | Number of cells |
| is(k) | fundamental harmonic of the inverter output phase current (A) | Nm | twin asynchronous machines |
| p | machine pair of poles | t(k) | time (s) |
| Pcu,r(k) | power loss in rotor winding (W) | Udc(k) | DC voltage at inverter input terminals (V) |
| Pcu,s(k) | power loss in stator winding (W) | UESS | ESS supply voltage (V) |
| Pel(k) | electrical power (W) | Us(k) | RMS phase voltage (V) |
| Pel-m(k) | mechanical power at the electrical machine’s output shaft (W) | Ux,(k) | voltage at the train’s pantograph (V) |
| Pfe(k) | iron loss (W) | v(k) | train speed (km/h) |
| Pcond,d | diode’s conduction losses (W) | Vbus-bar | DC common bus-bar voltage (V) |
| Pcond,sw | switches’ conduction losses (W) | Vcatenary | catenary voltage (V) |
| Ploss,comm | commutation losses (W) | Vd,o | diode forward voltage (V) |
| Ppant(k) | electrical power at train pantograph (W) | Vsw,o | switch forward voltage (V) |
| rl | contact line resistance (mΩ/km) | x(k) | train position with respect to electrical substation (m) |
| rd | diode on-state resistance (Ω) | xESS | starting train position with respect to electrical substation (m) |
| rb | track resistance (mΩ/km) | ηg | mechanical gear efficiency |
| rsw | switch on-state resistance (Ω) | τ | gear ratio |
| rw | radius wheel (m) | φ(k) | lagging angle (rad) |
| Sf(k) | space covered by the (m) | φN | phase shift angle (rad) |
| Sf | space covered by the train during braking or acceleration transient (m) | ωel-m(k) | rotor speed (rad/s) |
References
- Martínez-Navarro, A.; Cloquell-Ballester, V.A.; Segui-Chilet, S. Photovoltaic Electric Scooter Charger Dock for the Development of Sustainable Mobility in Urban Environments. IEEE Access 2020, 8, 169486–169495. [Google Scholar] [CrossRef]
- Liberto, C.; Valenti, G.; Orchi, S.; Lelli, M.; Nigro, M.; Ferrara, M. The Impact of Electric Mobility Scenarios in Large Urban Areas: The Rome Case Study. IEEE Trans. Intell. Transp. Syst. 2018, 19, 3540–3549. [Google Scholar] [CrossRef]
- Dik, A.; Omer, S.; Boukhanouf, R. Electric Vehicles: V2G for Rapid, Safe, and Green EV Penetration. Energies 2022, 15, 803. [Google Scholar] [CrossRef]
- Available online: https://www.sbb.ch/it/clientela-aziendale/gestione-globale-mobilita/offerte-mobilita/greenclass-clienti-commerciale.html (accessed on 17 September 2021).
- Kaleybar, H.J.; Brenna, M.; Foiadelli, F. EV Charging Station Integrated with Electric Railway System Powering by Train Regenerative Braking Energy. In Proceedings of the 2020 IEEE Vehicle Power and Propulsion Conference (VPPC), Gijon, Spain, 18 November–16 December 2020; pp. 1–6. [Google Scholar]
- Menicanti, S.; Di Benedetto, M.; Lidozzi, A.; Solero, L.; Crescimbini, F. Recovery of Train Braking Energy in 3 kV DC Railway Systems: A case of study. In Proceedings of the 2020 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Sorrento, Italy, 24–26 June 2020; pp. 589–594. [Google Scholar]
- Alfieri, L.; Battistelli, L.; Pagano, M. Energy efficiency strategies for railway application: Alternative solutions applied to a real case study. IET Electr. Syst. Transp. 2018, 8, 122–129. [Google Scholar] [CrossRef]
- Clerici, A.; Tironi, E.; Dezza, F.C. Multiport converters and ESS on 3kV DC railway lines: Case study for braking energy savings. In 2016 IEEE 16th International Conference on Environment and Electrical Engineering (EEEIC); IEEE: Piscataway, NJ, USA, 2016; pp. 1–6. [Google Scholar]
- Tian, Z.; Zhang, G.; Zhao, N.; Hillmansen, S.; Tricoli, P.; Roberts, C. Energy Evaluation for DC Railway Systems with Inverting Substations. In Proceedings of the 2018 IEEE International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Nottingham, UK, 7–9 November 2018; pp. 1–6. [Google Scholar]
- Tian, Z.; Chen, M.; Weston, P.; Hillmansen, S.; Zhao, N.; Roberts, C.; Chen, L. Energy evaluation of the power network of a DC railway system with regenerating trains. IET Electr. Syst. Transp. 2015, 6, 41–49. [Google Scholar] [CrossRef]
- González-Gil, A.; Palacin, R.; Batty, P. Sustainable urban rail systems: Strategies and technologies for optimal management of regenerative braking energy. Energy Convers. Manag. 2013, 75, 374–388. [Google Scholar] [CrossRef] [Green Version]
- Ratniyomchai, T.; Hillmansen, S.; Tricoli, P. Recent developments and applications of energy storage devices in electrified railways. IET Electr. Syst. Transp. 2014, 4, 9–20. [Google Scholar] [CrossRef]
- Teymourfar, R.; Asaei, B.; Iman-Eini, H.; Fard, R.N. Stationary super-capacitor energy storage system to save regenerative braking energy in a metro line. Energy Convers. Manag. 2012, 56, 206–214. [Google Scholar] [CrossRef]
- Ratniyomchai, T.; Hillmansen, S.; Tricoli, P. Optimal capacity and positioning of stationary supercapacitors for light rail vehicle systems. In Proceedings of the 2014 International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Ischia, Italy, 18–20 June 2014; pp. 807–812. [Google Scholar]
- Calderaro, V.; Galdi, V.; Graber, G.; Piccolo, A. Optimal siting and sizing of stationary supercapacitors in a metro network using PSO. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015; pp. 2680–2685. [Google Scholar]
- LaMedica, R.; Ruvio, A.; Tobia, M.; Buffarini, G.G.; Carones, N. A Preliminary Techno-Economic Comparison between DC Electrification and Trains with On-Board Energy Storage Systems. Energies 2020, 13, 6702. [Google Scholar] [CrossRef]
- Ciccarelli, F.; Di Noia, L.P.; Rizzo, R. Integration of Photovoltaic Plants and Supercapacitors in Tramway Power Systems. Energies 2018, 11, 410. [Google Scholar] [CrossRef] [Green Version]
- Khodaparastan, M.; Mohamed, A. A study on super capacitor wayside connection for energy recuperation in electric rail systems. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar]
- Ciccarelli, F.; Iannuzzi, D.; Spina, I. Comparison of energy management control strategy based on wayside ESS for LRV application. In Proceedings of the IECON 2013—39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 1548–1554. [Google Scholar]
- Ovalle, A.; Pouget, J.; Bacha, S.; Gerbaud, L.; Vinot, E.; Sonier, B. Energy storage sizing methodology for mass-transit direct-current wayside support: Application to French railway company case study. Appl. Energy 2018, 230, 1673–1684. [Google Scholar] [CrossRef]
- Iannuzzi, D.; Pagano, E.; Tricoli, P. The Use of Energy Storage Systems for Supporting the Voltage Needs of Urban and Suburban Railway Contact Lines. Energies 2013, 6, 1802–1820. [Google Scholar] [CrossRef] [Green Version]
- Iannuzzi, D.; Lauria, D.; Tricoli, P. Optimal design of stationary supercapacitors storage devices for light electrical transportation systems. Optim. Eng. 2012, 13, 1–16. [Google Scholar] [CrossRef]
- Yang, Z.; Yang, Z.; Xia, H.; Lin, F.; Zhu, F. Supercapacitor State Based Control and Optimization for Multiple Energy Storage Devices Considering Current Balance in Urban Rail Transit. Energies 2017, 10, 520. [Google Scholar] [CrossRef]
- Iannuzzi, D.; Ciccarelli, F.; Lauria, D. Stationary ultracapacitors storage device for improving energy saving and voltage profile of light transportation networks. Transp. Res. Part C Emerg. Technol. 2012, 21, 321–337. [Google Scholar] [CrossRef]
- Battistelli, L.; Ciccarelli, F.; Lauria, D.; Proto, D. Optimal design of DC electrified railway stationary storage system. In Proceedings of the 2009 International Conference on Clean Electrical Power, Capri, Italy, 9–11 June 2009; pp. 739–745. [Google Scholar]
- Killer, A.; Armstorfer, A.; Díez, A.E.; Biechl, H. Ultracapacitor assisted regenerative braking in metropolitan railway systems. In Proceedings of the 2012 IEEE Colombian Intelligent Transportation Systems Symposium (CITSS), Bogota, Colombia, 30 August 2012; pp. 1–6. [Google Scholar]
- Ciccarelli, F.; Iannuzzi, D.; Kondo, K.; Fratelli, L. Line-Voltage Control Based on Wayside Energy Storage Systems for Tramway Networks. IEEE Trans. Power Electron. 2015, 31, 884–899. [Google Scholar] [CrossRef]
- Amiryar, M.E.; Pullen, K.R. A Review of Flywheel Energy Storage System Technologies and Their Applications. Appl. Sci. 2017, 7, 286. [Google Scholar] [CrossRef] [Green Version]
- Hayashiya, H. Recent Trend of Regenerative Energy Utilization in Traction Power Supply System in Japan. Urban Rail Transit 2017, 3, 183–191. [Google Scholar] [CrossRef] [Green Version]
- Hayashiya, H.; Iino, Y.; Takahashi, H.; Kawahara, K.; Yamanoi, T.; Sekiguchi, T.; Sakaguchi, H.; Sumiya, A.; Kon, S. Review of regenerative energy utilization in traction power supply system in Japan: Applications of energy storage systems in d.c. traction power supply system. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 3918–3923. [Google Scholar]
- Hayashiya, H.; Abe, S.; Iino, Y.; Nakao, K.; Hino, M.; Ikarashi, H.; Nemoto, H.; Kawatsu, H.; Kato, T. Proposal of a novel control method of Li-ion battery system for regenerative energy utilization in traction power supply system. In Proceedings of the 2016 IEEE International Power Electronics and Motion Control Conference (PEMC), Varna, Bulgaria, 25–28 September 2016; pp. 298–303. [Google Scholar]
- Ceraolo, M.; Lutzemberger, G. Stationary and on-board storage systems to enhance energy and cost efficiency of tramways. J. Power Sources 2014, 264, 128–139. [Google Scholar] [CrossRef]
- Bae, C.H. A simulation study of installation locations and capacity of regenerative absorption inverters in DC 1500V electric railways system. Simul. Model. Pract. Theory 2008, 17, 829–838. [Google Scholar] [CrossRef]
- Gelman, V. Braking energy recuperation. IEEE Veh. Technol. Mag. 2009, 4, 82–89. [Google Scholar] [CrossRef]
- Hayashiya, H.; Nakao, Y.; Aoki, Y.; Kobayashi, S.; Ogihara, M. Comparison between energy storage system and regenerative inverter in D.C. traction power supply system for regenerative energy utilization. In Proceedings of the 2017 19th European Conference on Power Electronics and Applications (EPE’17 ECCE Europe), Warsaw, Poland, 11–14 September 2017; pp. 1–7. [Google Scholar]
- Zhang, G.; Tian, Z.; Du, H.; Liu, Z. A Novel Hybrid DC Traction Power Supply System Integrating PV and Reversible Converters. Energies 2018, 11, 1661. [Google Scholar] [CrossRef] [Green Version]
- Berringer, K.; Marvin, J.; Perruchoud, P. Semiconductor power losses in AC inverters. In Proceedings of the IAS ’95. Conference Record of the 1995 IEEE Industry Applications Conference Thirtieth IAS Annual Meeting, Orlando, FL, USA, 8–12 October 1995; Volume 1, pp. 882–888. [Google Scholar]
- di Benedetto, M.; Lidozzi, A.; Solero, L.; Crescimbini, F.; Grbovi’c, P.J. High-Performance 3-Phase 5-Level E-Type Multilevel–Multicell Converters for Microgrids. Energies 2021, 14, 843. [Google Scholar] [CrossRef]
- Di Benedetto, M.; Lidozzi, A.; Solero, L.; Crescimbini, F.; Bifaretti, S. Hardware design of SiC-based Four-Port DAB Converter for Fast Charging Station. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 1231–1238. [Google Scholar]
- di Benedetto, M.; Lidozzi, A.; Solero, L.; Crescimbini, F.; Grbović, P.J. Five-Level E-Type Inverter for Grid-Connected Applications. IEEE Trans. Ind. Appl. 2018, 54, 5536–5548. [Google Scholar] [CrossRef]




| Mass | 72 t |
| Maximum power | 3000 kW |
| Maximum hourly power | 3500 kW |
| Max Traction effort | 200 kN |
| Drive axles (2 bogies) | 4 |
| Max braking effort | 85 kN |
| Power Supply | 1.5–3 kV DC |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Menicanti, S.; di Benedetto, M.; Marinelli, D.; Crescimbini, F. Recovery of Trains’ Braking Energy in a Railway Micro-Grid Devoted to Train plus Electric Vehicle Integrated Mobility. Energies 2022, 15, 1261. https://doi.org/10.3390/en15041261
Menicanti S, di Benedetto M, Marinelli D, Crescimbini F. Recovery of Trains’ Braking Energy in a Railway Micro-Grid Devoted to Train plus Electric Vehicle Integrated Mobility. Energies. 2022; 15(4):1261. https://doi.org/10.3390/en15041261
Chicago/Turabian StyleMenicanti, Stefano, Marco di Benedetto, Davide Marinelli, and Fabio Crescimbini. 2022. "Recovery of Trains’ Braking Energy in a Railway Micro-Grid Devoted to Train plus Electric Vehicle Integrated Mobility" Energies 15, no. 4: 1261. https://doi.org/10.3390/en15041261
APA StyleMenicanti, S., di Benedetto, M., Marinelli, D., & Crescimbini, F. (2022). Recovery of Trains’ Braking Energy in a Railway Micro-Grid Devoted to Train plus Electric Vehicle Integrated Mobility. Energies, 15(4), 1261. https://doi.org/10.3390/en15041261








