Linear Quadratic Regulator and Fuzzy Control for Grid-Connected Photovoltaic Systems
Abstract
:1. Introduction
- (a)
- Weather factors such as the temperature and solar radiation;
- (b)
- Hardware factors such as power electronic devices and system loads.
- Stand-alone mode;
- Grid-connected mode.
- Management of several combined systems;
- Regulation of each power stage or system.
- tracking the maximum power point (MPP);
- minimizing the harmonics, which usually cause negative effects on the power grid and devices;
- maintaining the DC-link voltage within a desired range;
- keeping the unity power factor (PF) at the output of the filter [10].
2. PV Grid-Connected System Modeling
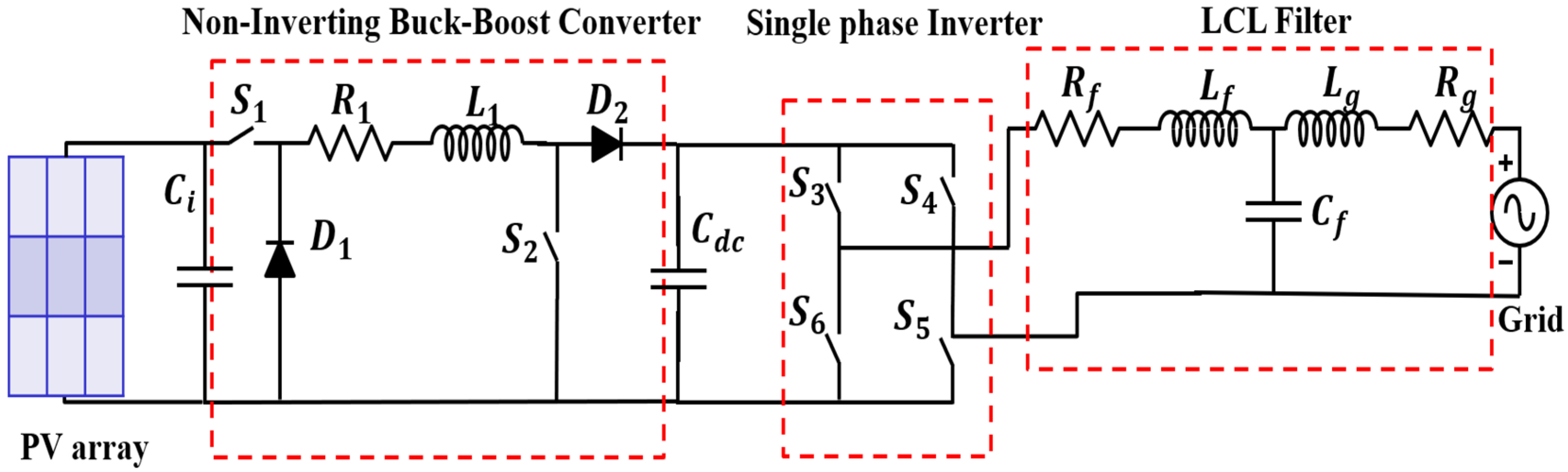
2.1. System Description
2.2. PV Panel Model
2.3. Modeling of Converters
3. Control System Design
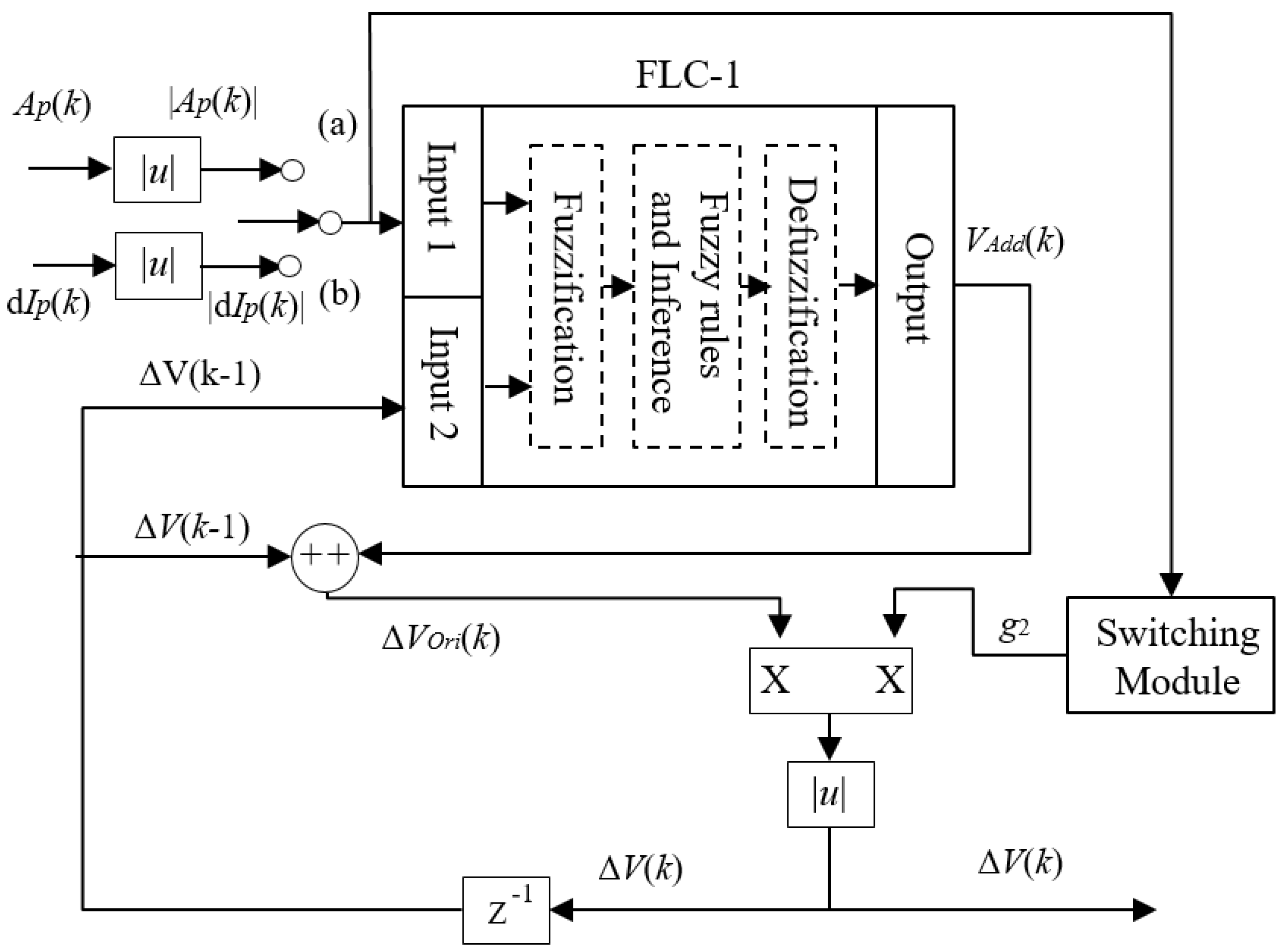
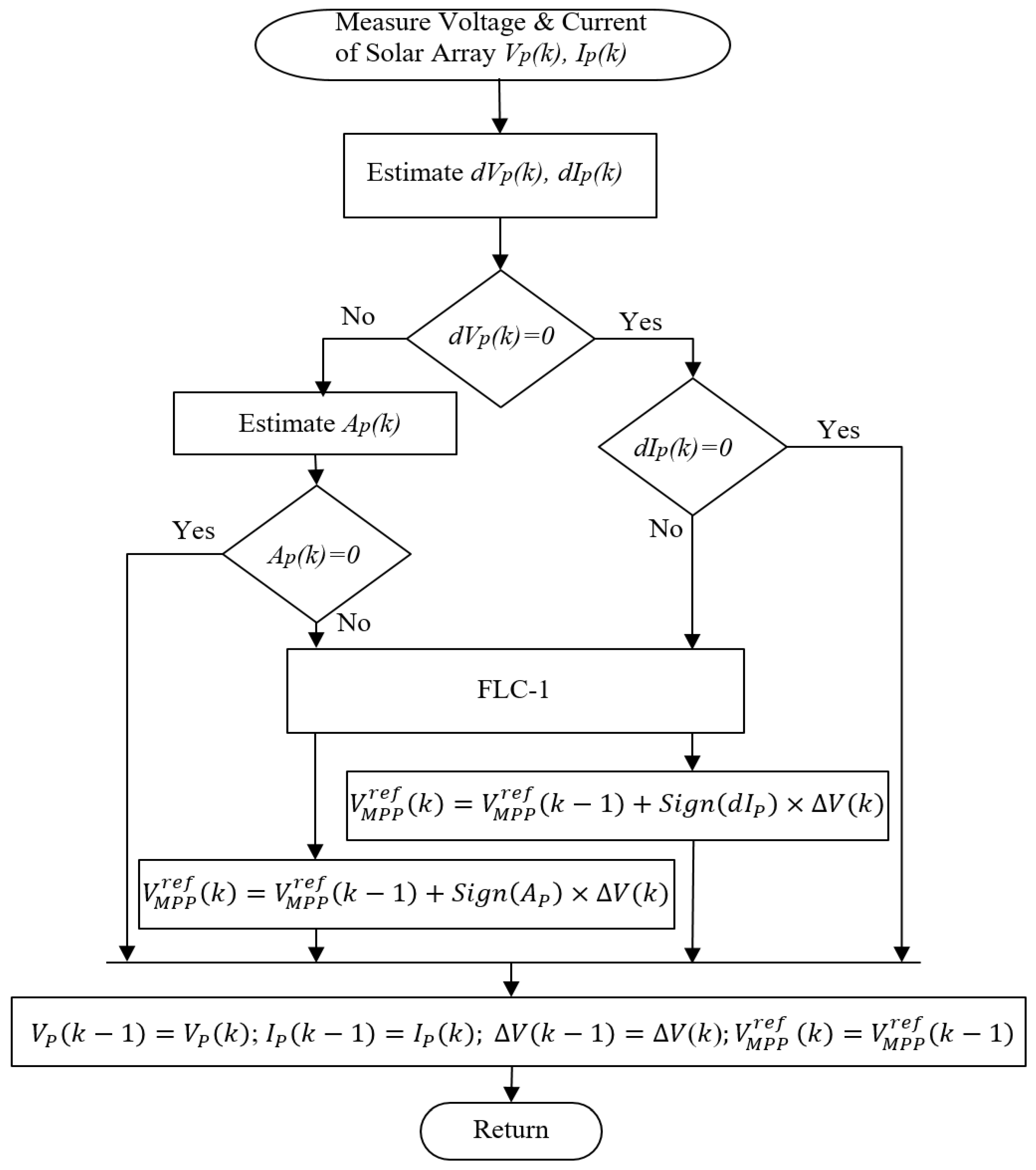
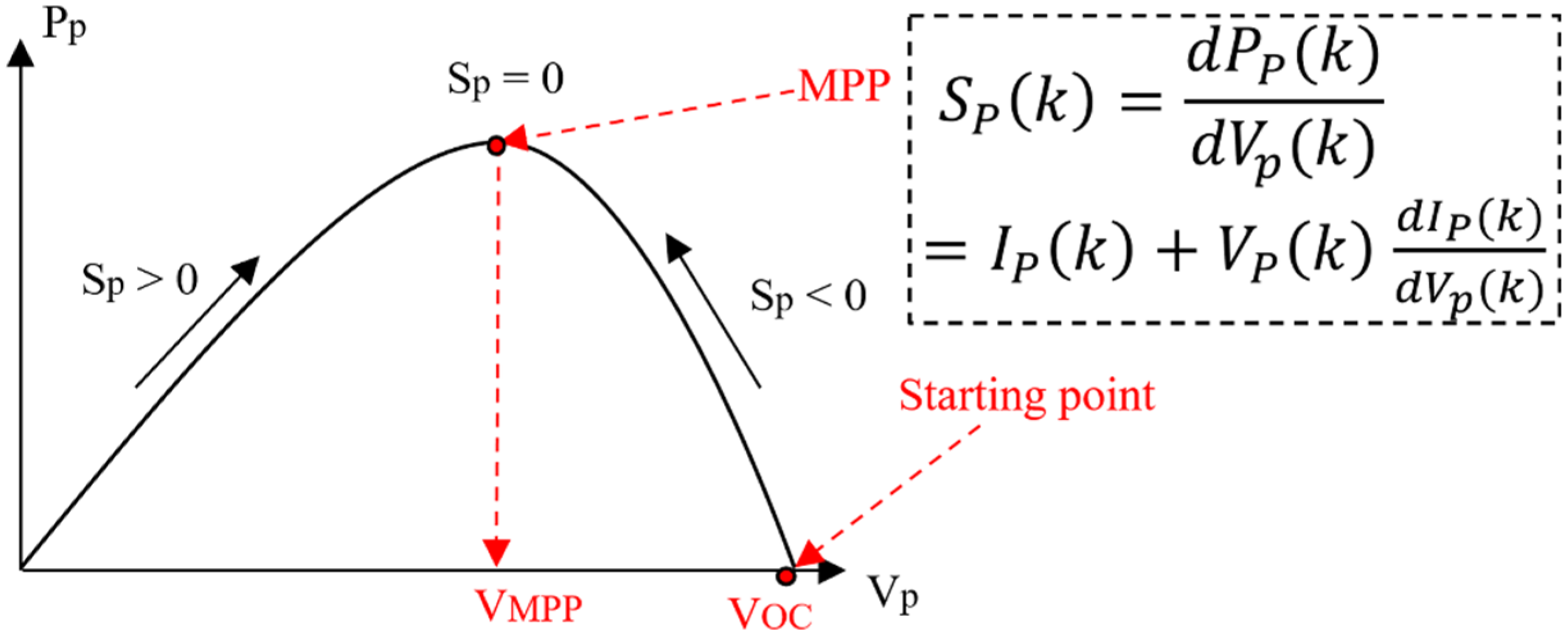
3.1. The MPPT Controller Module
3.1.1. FLC-1
- |Ap(k)|—the absolute value of a modified slope of the power–voltage (P-V) curve as expressed in (2). This equation also includes a pre-scaling module Gp(k), as shown in (3);
- |dIp(k)|—the change in the current of PV panels in absolute value.
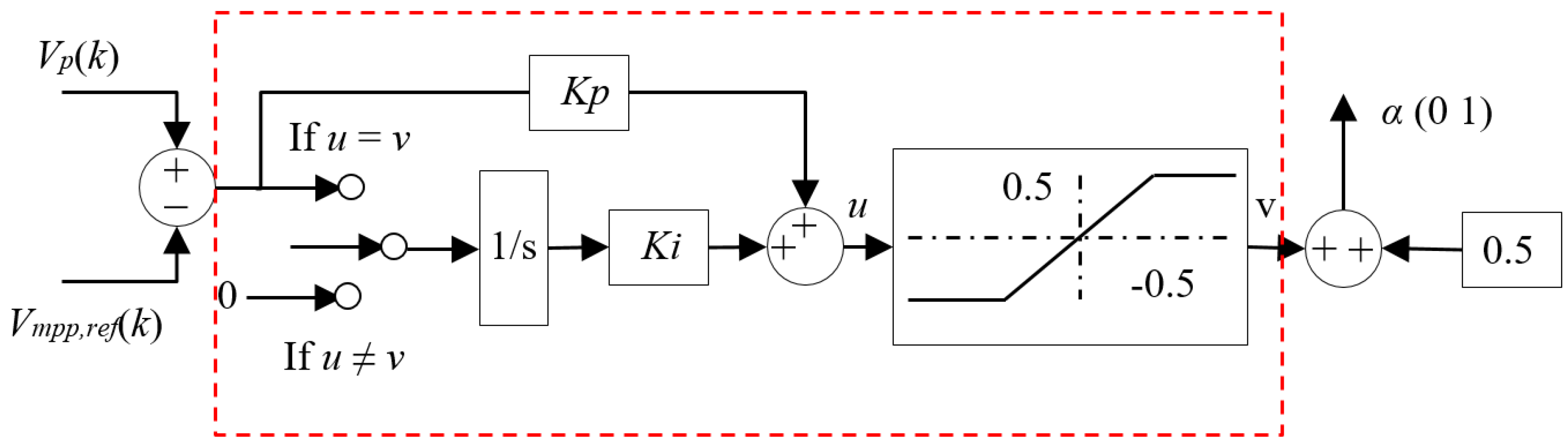
3.1.2. PI-1 Controller
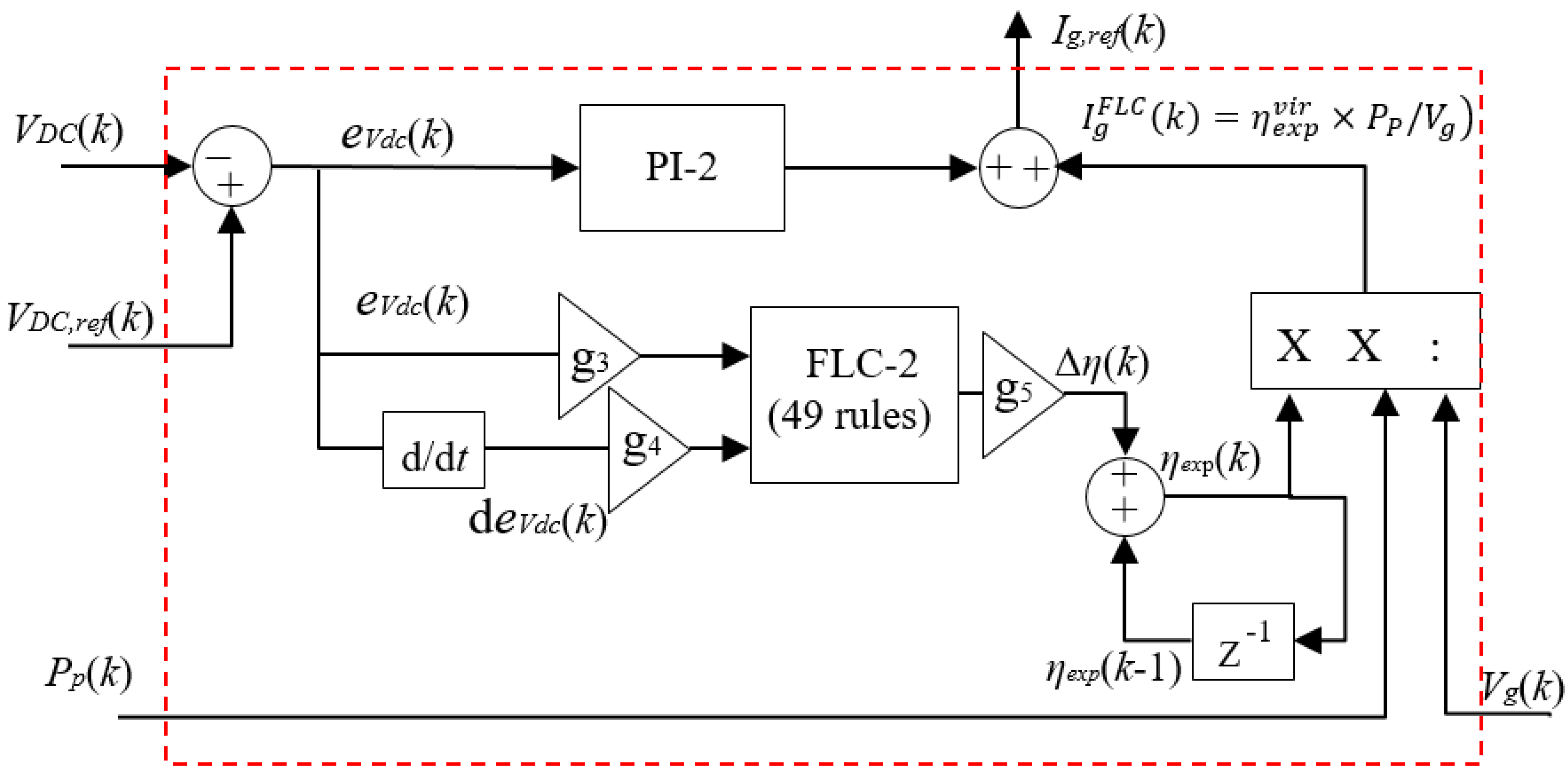
3.2. DC Link Voltage Regulator Module
- —the efficiency of the buck-boost DC-DC converter can be estimated theoretically as a ratio value of the DC link power and the output power of PV array ;
- —the efficiency of the DC-AC inverter can be estimated theoretically as a ratio value of the output power of the inverter and the DC link power ;
- = —the overall efficiency of the grid-connected PV system.
- (k)—error between desired and present DC link voltage;
- (k)—change in error.
- Δ(k)—step in efficiency, added to the “virtual efficiency” to reach the desired value:
3.3. Current Controller Module
4. Simulation Results
4.1. Simulation 1: Constant Module Temperature
4.2. Simulation 2: Constant Solar Irradiation
5. Comparison between LQR and Backstepping Approaches
5.1. Simulation 1: Constant Module Temperature
5.2. Simulation 2: Constant Solar Irradiation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Torquato, R.; Arguello, A.; Freitas, W. Practical Chart for Harmonic Resonance Assessment of DFIG-Based Wind Parks. IEEE Trans. Power Deliv. 2020, 35, 2233–2242. [Google Scholar] [CrossRef]
- Thao, N.G.M.; Uchida, K.; Kofuji, K.; Jintsugawa, T.; Nakazawa, C. A comprehensive analysis study about harmonic resonances in megawatt grid-connected wind farms. In Proceedings of the 2014 International Conference on Renewable Energy Research and Application (ICRERA), Milwaukee, WI, USA, 19–22 October 2014; pp. 387–394. [Google Scholar]
- Alajmi, B.N.; Ahmed, K.H.; Finney, S.J.; Williams, B.W. Fuzzy-Logic-Control Approach of a Modified Hill-Climbing Method for Maximum Power Point in Microgrid Standalone Photovoltaic System. IEEE Trans. Power Electron. 2011, 26, 1022–1030. [Google Scholar] [CrossRef]
- Kottas, T.L.; Boutalis, Y.S.; Karlis, A.D. New Maximum Power Point Tracker for PV Arrays Using Fuzzy Controller in Close Cooperation with Fuzzy Cognitive Networks. IEEE Trans. Energy Convers. 2006, 21, 793–803. [Google Scholar] [CrossRef]
- Hamidia, F.; Abbadi, A.; Boucherit, M.S. Maximum Power Point Tracking Control of Photovoltaic Generation Based on Fuzzy Logic. In International Conference in Artificial Intelligence in Renewable Energetic Systems; Springer: Cham, Switzerland, 2018; pp. 197–205. [Google Scholar] [CrossRef]
- Menniti, D.; Pinnarelli, A.; Brusco, G. Implementation of a novel fuzzy-logic based MPPT for grid-connected photovoltaic generation system. In Proceedings of the 2011 IEEE Trondheim PowerTech, Trondheim, Norway, 19–23 June 2011. [Google Scholar] [CrossRef]
- Yang, B.; Li, W.; Zhao, Y.; He, X. Design and Analysis of a Grid-Connected Photovoltaic Power System. IEEE Trans. Power Electron. 2009, 25, 992–1000. [Google Scholar] [CrossRef]
- El Fadil, H.; Giri, F.; Guerrero, J. Grid-connected of photovoltaic module using nonlinear control. In Proceedings of the 2012 3rd IEEE International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Aalborg, Denmark, 25–28 June 2012; pp. 119–124. [Google Scholar] [CrossRef] [Green Version]
- Wai, R.-J.; Wang, W.-H. Grid-Connected Photovoltaic Generation System. IEEE Trans. Circuits Syst. I Regul. Pap. 2008, 55, 953–964. [Google Scholar] [CrossRef]
- Reddy, D.; Ramasamy, S. A fuzzy logic MPPT controller based three phase grid-tied solar PV system with improved CPI voltage. In Proceedings of the 2017 Innovations in Power and Advanced Computing Technologies (I-PACT), Vellore, India, 21–22 April 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Kumar, J.; Rathor, B.; Bahrani, P. Fuzzy and P amp; O MPPT techniques for stabilized the efficiency of solar PV system. In Proceedings of the 2018 International Conference on Computing, Power and Communication Technologies (GUCON), Greater Noida, India, 28–29 September 2018; pp. 259–264. [Google Scholar] [CrossRef]
- Kumar, B.P.; Winston, D.P.; Christabel, S.C.; Venkatanarayanan, S. Implementation of a switched PV technique for rooftop 2 kW solar PV to enhance power during unavoidable partial shading conditions. J. Power Electron. 2017, 17, 1600–1610. [Google Scholar] [CrossRef]
- Andrew-Cotter, J.; Uddin, M.N.; Amin, I.K. Particle swarm optimization based adaptive neuro-fuzzy inference system for MPPT control of a three-phase grid-connected photovoltaic system. In Proceedings of the 2019 IEEE International Electric Machines & Drives Conference (IEMDC), San Diego, CA, USA, 12–15 May 2019; pp. 2089–2094. [Google Scholar] [CrossRef]
- Arulkumar, K.; Palanisamy, K.; Vijayakumar, D. Recent advances and control techniques in grid connected Pv system—A review. Int. J. Renew. Energy Res. 2016, 6, 1037–1049. [Google Scholar]
- Mukundan, N.; Singh, Y.; Naqvi, S.B.Q.; Singh, B.; Pychadathil, J. Multi-Objective Solar Power Conversion System with MGI Control for Grid Integration at Adverse Operating Conditions. IEEE Trans. Sustain. Energy 2020, 11, 2901–2910. [Google Scholar]
- Alturki, F.A.; Omotoso, H.O.; Al-Shamma’A, A.A.; Farh, H.M.H.; Alsharabi, K. Novel Manta Rays Foraging Optimization Algorithm Based Optimal Control for Grid-Connected PV Energy System. IEEE Access 2020, 8, 187276–187290. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Teodorescu, R.; Liserre, M.; Timbus, A.V. Overview of Control and Grid Synchronization for Distributed Power Generation Systems. IEEE Trans. Ind. Electron. 2006, 53, 1398–1409. [Google Scholar] [CrossRef] [Green Version]
- Teodorescu, R.; Blaabjerg, F.; Liserre, M.; Loh, P.C. Proportional-resonant controllers and filters for grid-connected voltage-source converters. IET Proc. Electr. Power Appl. 2006, 153, 750–762. [Google Scholar] [CrossRef] [Green Version]
- Wu, G.R.; Dewan, R.; Slemon, S.B. Analysis of a PWM AC to DC Voltage Source Converter under the Predicted Current Control with a Fixed Switching Frequency. IEEE Trans. Ind. Appl. 1991, 27, 756–764. [Google Scholar] [CrossRef]
- Zhang, K.; Kang, Y.; Xiong, J.; Chen, J. Direct repetitive control of SPWM inverter for UPS purpose. IEEE Trans. Power Electron. 2003, 18, 784–792. [Google Scholar] [CrossRef]
- Singh, B.; Jain, V. TOCF Based Control for Optimum Operation of a Grid Tied Solar PV System. IEEE Trans. Energy Convers. 2020, 35, 1171–1181. [Google Scholar] [CrossRef]
- Shan, Y.; Hu, J.; Guerrero, J.M. A Model Predictive Power Control Method for PV and Energy Storage Systems with Voltage Support Capability. IEEE Trans. Smart Grid 2019, 11, 1018–1029. [Google Scholar] [CrossRef]
- Manoharan, M.S.; Ahmed, A.; Park, J.-H. An Improved Model Predictive Controller for 27-Level Asymmetric Cascaded Inverter Applicable in High-Power PV Grid-Connected Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 4395–4405. [Google Scholar] [CrossRef]
- Mahfuz-Ur-Rahman, A.M.; Islam, R.; Muttaqi, K.M.; Sutanto, D. Model Predictive Control for a New Magnetic Linked Multilevel Inverter to Integrate Solar Photovoltaic Systems with the Power Grids. IEEE Trans. Ind. Appl. 2020, 56, 7145–7155. [Google Scholar] [CrossRef]
- Mansour, A.M.; Arafa, O.M.; Marei, M.I.; Abdelsalam, I.; Aziz, G.A.A.; Sattar, A.A. Hardware-in-the-Loop Testing of Seamless Interactions of Multi-Purpose Grid-Tied PV Inverter Based on SFT-PLL Control Strategy. IEEE Access 2021, 9, 123465–123483. [Google Scholar] [CrossRef]
- Verma, A.; Singh, B. CAPSA Based Control for Power Quality Correction in PV Array Integrated EVCS Operating in Standalone and Grid Connected Modes. IEEE Trans. Ind. Appl. 2020, 57, 1789–1800. [Google Scholar] [CrossRef]
- Sarita, K.; Kumar, S.; Vardhan, A.S.S.; Elavarasan, R.M.; Saket, R.K.; Shafiullah, G.M.; Hossain, E. Power Enhancement with Grid Stabilization of Renewable Energy-Based Generation System Using UPQC-FLC-EVA Technique. IEEE Access 2020, 8, 207443–207464. [Google Scholar] [CrossRef]
- Thao, N.G.M.; Uchida, K. Control the photovoltaic grid-connected system using fuzzy logic and backstepping approach. In Proceedings of the 2013 9th Asian Control Conference ASCC, Istanbul, Turkey, 23–26 June 2013; pp. 1–8. [Google Scholar] [CrossRef]
- Katir, H.; Abouloifa, A.; Noussi, K.; Lachkar, I.; El Aroudi, A.; Aourir, M.; El Otmani, F.; Giri, F. Fault Tolerant Backstepping Control for Double-Stage Grid-Connected Photovoltaic Systems Using Cascaded H-Bridge Multilevel Inverters. IEEE Control Syst. Lett. 2021, 6, 1406–1411. [Google Scholar] [CrossRef]
- Liserre, M.; Blaabjerg, F.; Hansen, S. Design and Control of an LCL-Filter-Based Three-Phase Active Rectifier. IEEE Trans. Ind. Appl. 2005, 41, 1281–1291. [Google Scholar] [CrossRef]
- Sun, W.; Chen, Z.; Wu, X. Intelligent optimize design of LCL filter for three-phase voltage-source PWM rectifier. In Proceedings of the 2009 IEEE 6th International Power Electronics and Motion Control Conference, Wuhan, China, 17–20 May 2009; pp. 970–974. [Google Scholar] [CrossRef]
- Li, X.-L.; Park, J.-G.; Shin, H.-B. Comparison and Evaluation of Anti-Windup PI Controllers. J. Power Electron. 2011, 11, 45–50. [Google Scholar] [CrossRef] [Green Version]
- Thao, N.G.M.; Uchida, K.; Nguyen-Quang, N. An Improved Incremental Conductance-Maximum Power Point Tracking Algorithm Based on Fuzzy Logic for Photovoltaic Systems. SICE J. Control. Meas. Syst. Integr. 2014, 7, 122–131. [Google Scholar] [CrossRef] [Green Version]
- Thao, N.G.M.; Dat, M.T.; Binh, T.C.; Phuc, N.H. PID-fuzzy logic hybrid controller for grid-connected photovoltaic inverters. In Proceedings of the International Forum on Strategic Technology, Ulsan, Korea, 13–15 October 2010; pp. 140–144. [Google Scholar] [CrossRef]
- Zeb, K.; Khan, I.; Uddin, W.; Khan, M.A.; Sathishkumar, P.; Busarello, T.D.C.; Ahmad, I.; Kim, H.J. A Review on Recent Advances and Future Trends of Transformerless Inverter Structures for Single-Phase Grid-Connected Photovoltaic Systems. Energies 2018, 11, 1968. [Google Scholar] [CrossRef] [Green Version]
- Figueredo, R.S.; De Carvalho, K.C.M.; Ama, N.R.N.; Matakas, L. Leakage current minimization techniques for single-phase transformerless grid-connected PV inverters—An overview. In Proceedings of the 2013 Brazilian Power Electronics Conference, Gramado, Brazil, 27–31 October 2013; pp. 517–524. [Google Scholar] [CrossRef]
- Hedayati, M.H.; John, V. EMI and ground leakage current reduction in single-phase grid-connected power converter. IET Power Electron. 2017, 10, 938–944. [Google Scholar] [CrossRef]
- Figueredo, R.S.; Matakas, L. Integrated Common and Differential Mode Filter With Capacitor-Voltage Feedforward Active Damping for Single-Phase Transformerless PV Inverters. IEEE Trans. Power Electron. 2019, 35, 7058–7072. [Google Scholar] [CrossRef]
- Liu, Y.; Lai, C.-M. LCL Filter Design with EMI Noise Consideration for Grid-Connected Inverter. Energies 2018, 11, 1646. [Google Scholar] [CrossRef] [Green Version]
- Niyomsatian, K.; Vanassche, P.; Gyselinck, J.J.C.; Sabariego, R.V. Active-Damping Virtual Circuit Control for Grid-Tied Converters with Differential-Mode and Common-Mode Output Filters. IEEE Trans. Power Electron. 2020, 35, 7583–7595. [Google Scholar] [CrossRef]



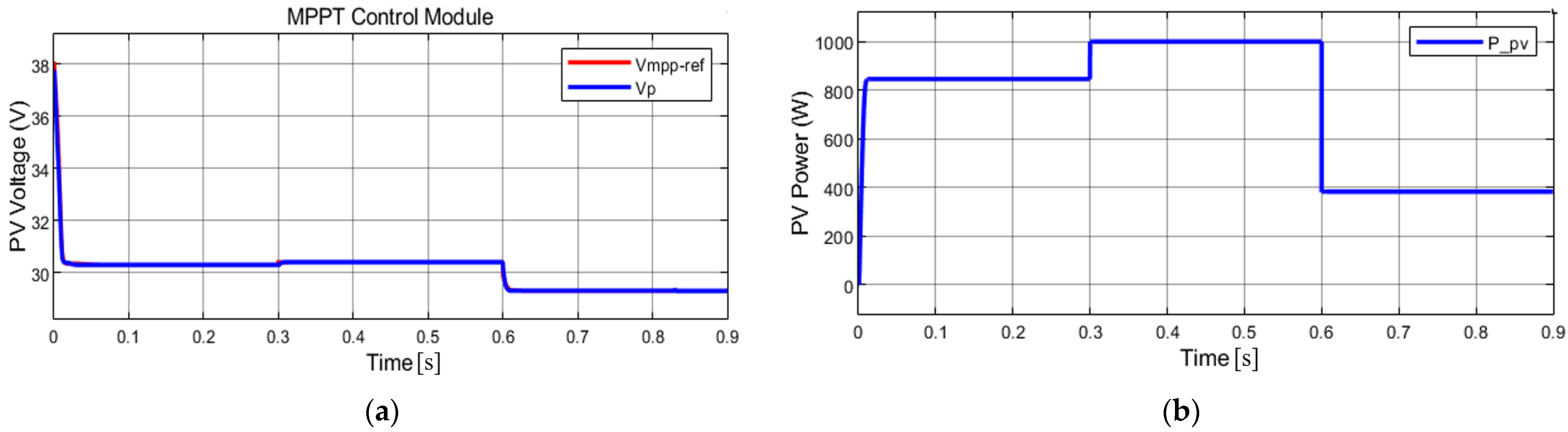

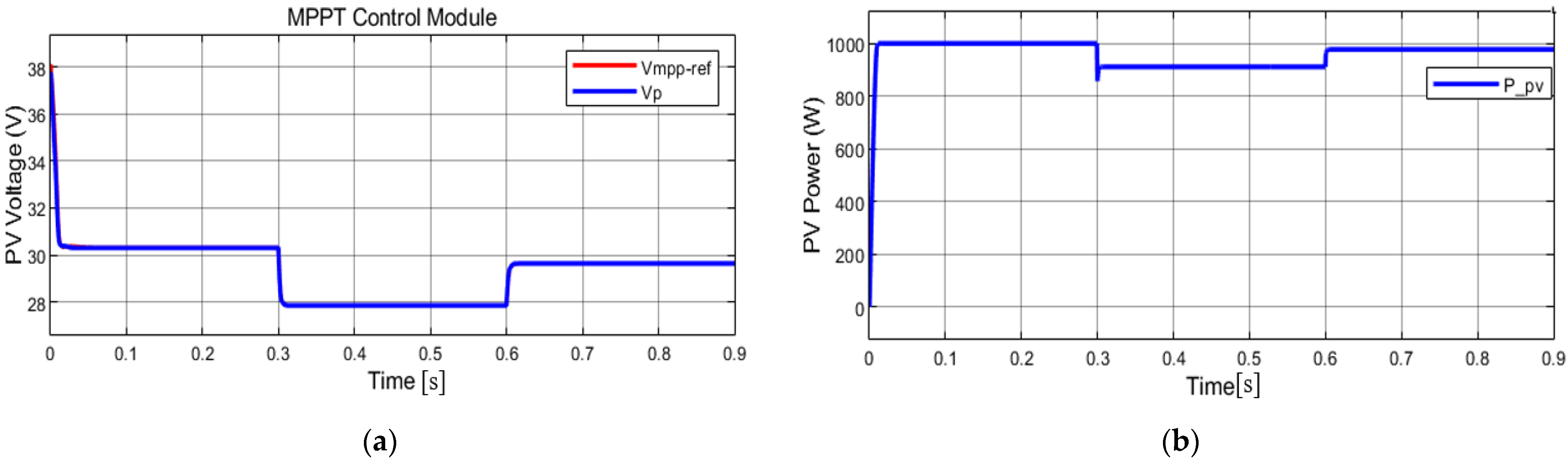

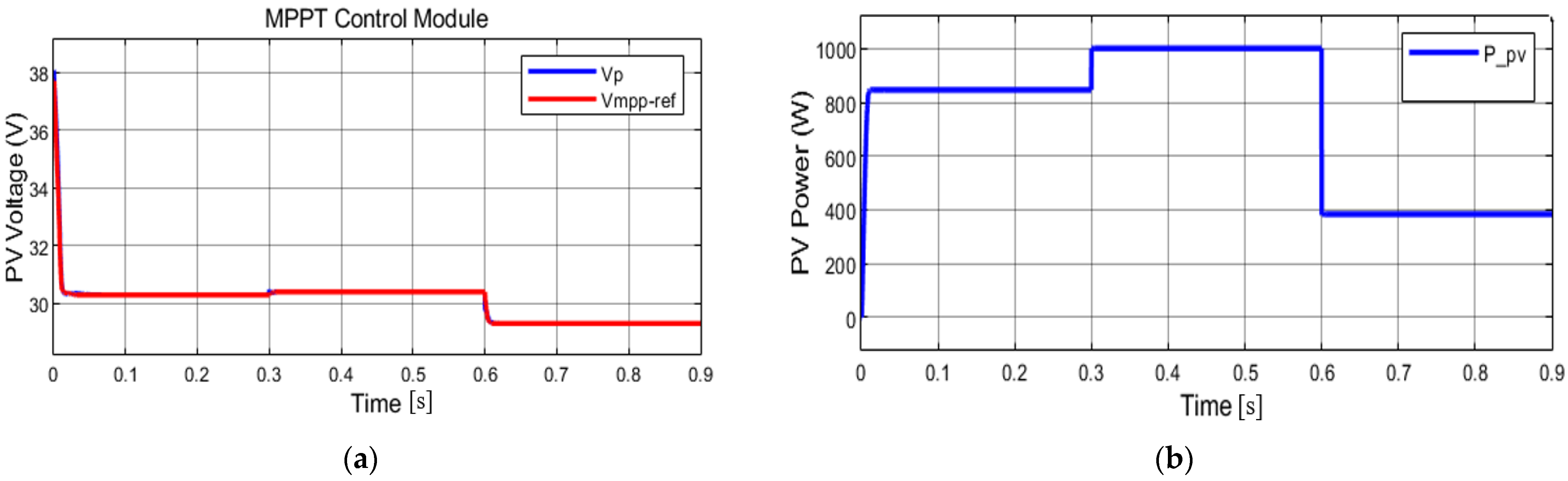
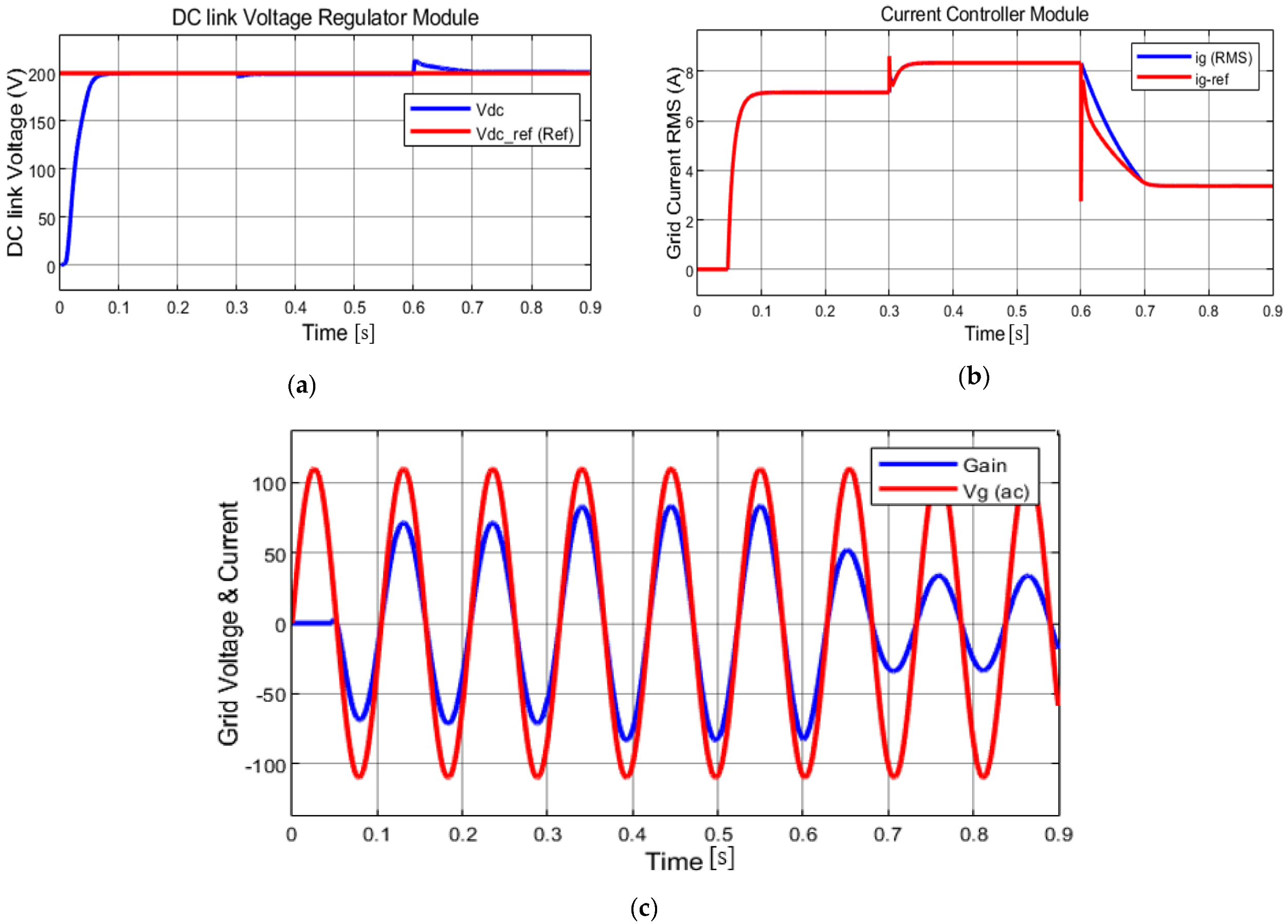

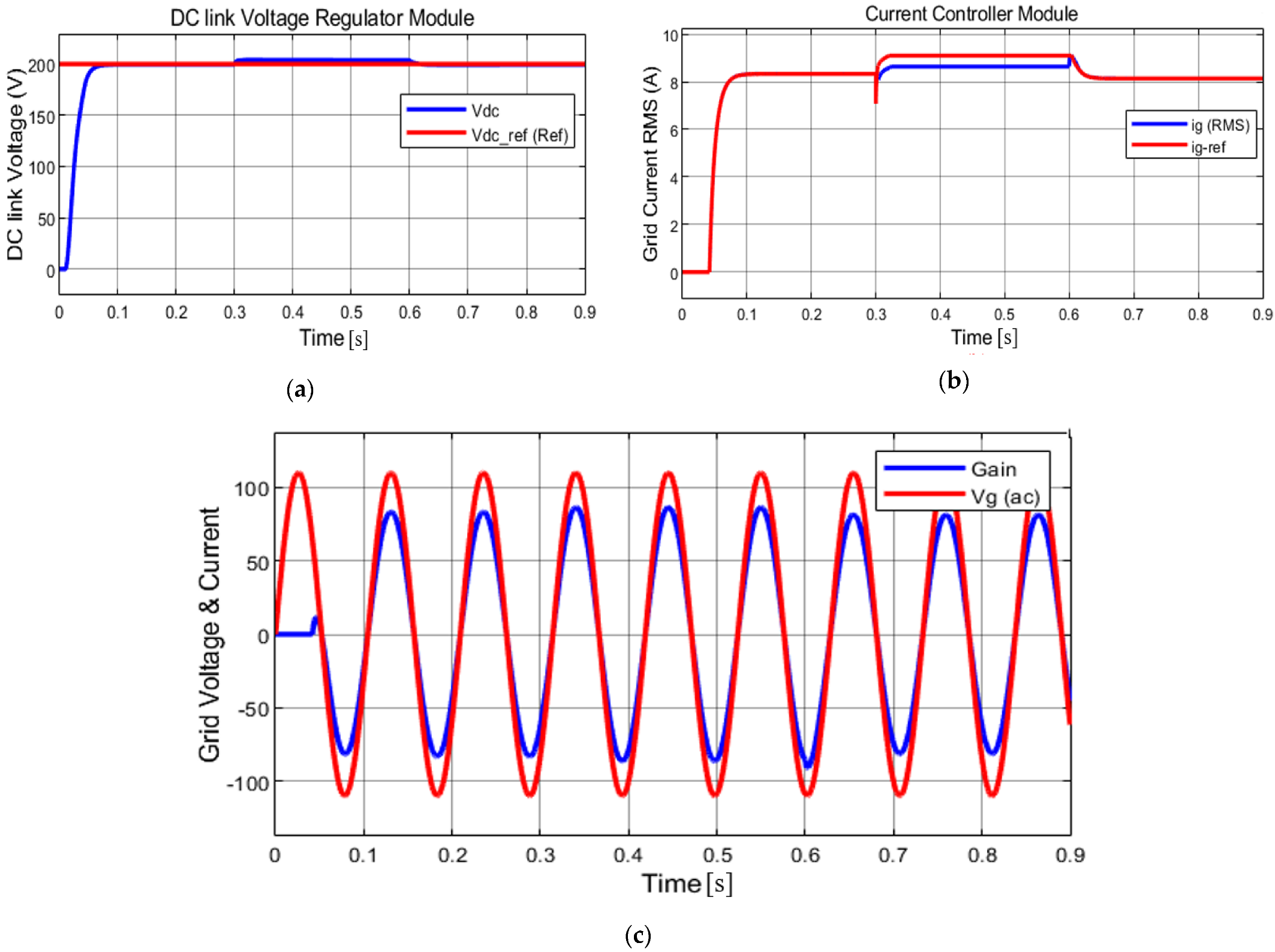
| MPPs | M1 | M2 | M3/M4 | M5 | M6 |
|---|---|---|---|---|---|
| Vp (V) | 29.3 | 30.32 | 30.4 | 29.8 | 28.04 |
| PP,panel (W) | 95.9 | 211.7 | 250 | 244.8 | 225.7 |
| PP,array (W) | 383.6 | 846.8 | 1000 | 979.2 | 912.8 |
| Variable | Symbol in Figure 1 | Averaged Variable in (1) |
|---|---|---|
| PV array voltage | Vp | x1 |
| Current through the inductor L1 | iL1 | x2 |
| DC link voltage | VDC | x3 |
| Input current of the LCL filter | if | x4 |
| Voltage on the capacitor Cf | VCf | x5 |
| RMS value of the electric grid current | ig | x6 |
| Control signal of the non-inverting buck-boost DC-DC converter | αp {0,1} | α (0,1) |
| Control signal of the single-phase DC-AC inverter | βp {−1,0,1} | β [−1,1] |
| PV array current | Ip | Īp |
| RMS value of the electric grid voltage | Vg | Vg |
| If the Input Is |AP(k)| | If the Input Is |dIP(k)| | |
|---|---|---|
| |AP(k)| > 0.1 | |AP(k) ≤ 0.1 | g2 = 1 (where every value of |dIP(k)|) |
| g2 = 0.25 | g2 = 0.1 | |
| Vadd(k) | |Ap(k)| or |dIp(k)| | |||||
|---|---|---|---|---|---|---|
| VS | SM | ME | LA | VL | ||
| ΔV(k−1) | VS | ZE | PZ | PS | PL | PL |
| SM | NZ | ZE | PZ | PM | PL | |
| ME | NS | NZ | ZE | PS | PM | |
| LA | NM | NS | NZ | PZ | PS | |
| VL | NL | NM | NS | ZE | PZ | |
| Δη(k) | eVdc(k) | |||||||
|---|---|---|---|---|---|---|---|---|
| NL | NM | NS | ZE | PS | PM | PL | ||
| deVdc(k) | NL | PU | PU | PL | PL | PM | PS | ZE |
| NM | PU | PU | PL | PM | PS | ZE | NS | |
| NS | PU | PL | PM | PS | ZE | NS | NM | |
| ZE | PL | PM | PS | ZE | NS | NM | NL | |
| PS | PM | PS | ZE | NS | NM | NL | NU | |
| PM | PS | ZE | NS | NM | NL | NU | NU | |
| PL | ZE | NS | NM | NL | NL | NU | NU | |
| Control Methods | The Current Controller Module Using the LQR in This Paper | The Introduced PID-Fuzzy Hybrid Controller in [34] |
|---|---|---|
| Design and computational complexity |
|
|
| Field of application in power systems |
|
|
| Control objectives, performance, and effectiveness |
|
|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mukhatov, A.; Thao, N.G.M.; Do, T.D. Linear Quadratic Regulator and Fuzzy Control for Grid-Connected Photovoltaic Systems. Energies 2022, 15, 1286. https://doi.org/10.3390/en15041286
Mukhatov A, Thao NGM, Do TD. Linear Quadratic Regulator and Fuzzy Control for Grid-Connected Photovoltaic Systems. Energies. 2022; 15(4):1286. https://doi.org/10.3390/en15041286
Chicago/Turabian StyleMukhatov, Azamat, Nguyen Gia Minh Thao, and Ton Duc Do. 2022. "Linear Quadratic Regulator and Fuzzy Control for Grid-Connected Photovoltaic Systems" Energies 15, no. 4: 1286. https://doi.org/10.3390/en15041286
APA StyleMukhatov, A., Thao, N. G. M., & Do, T. D. (2022). Linear Quadratic Regulator and Fuzzy Control for Grid-Connected Photovoltaic Systems. Energies, 15(4), 1286. https://doi.org/10.3390/en15041286








