Stress Coupling Analysis and Failure Damage Evaluation of Wind Turbine Blades during Strong Winds
Abstract
:1. Introduction
2. Materials and Methods
2.1. Theories
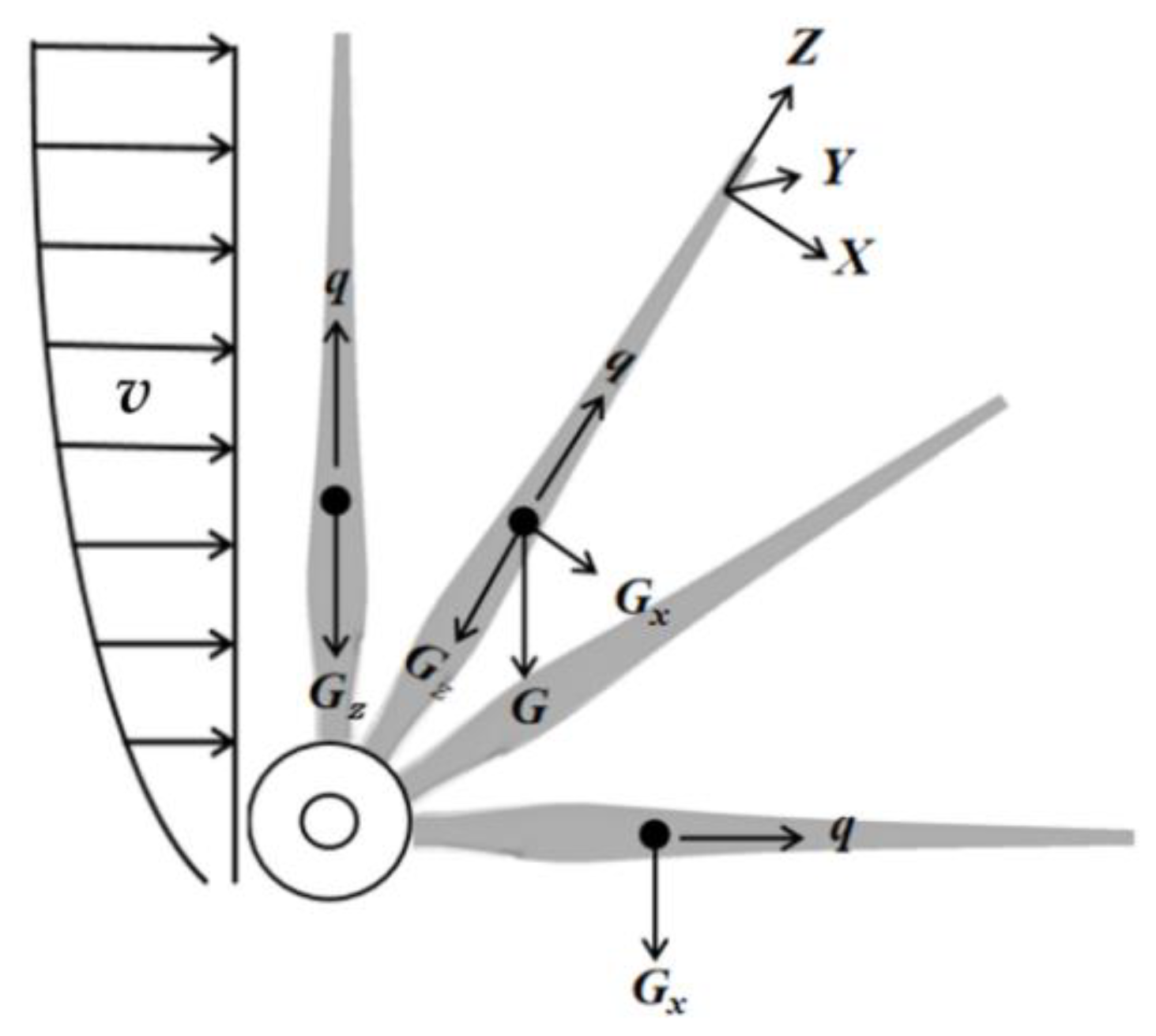
2.1.1. Fluid–Solid Coupling Control Equation
2.1.2. Theoretical Basis of the Turbulence Model
2.1.3. Sliding Mesh Theory
2.2. Physical Model and Numerical Settings
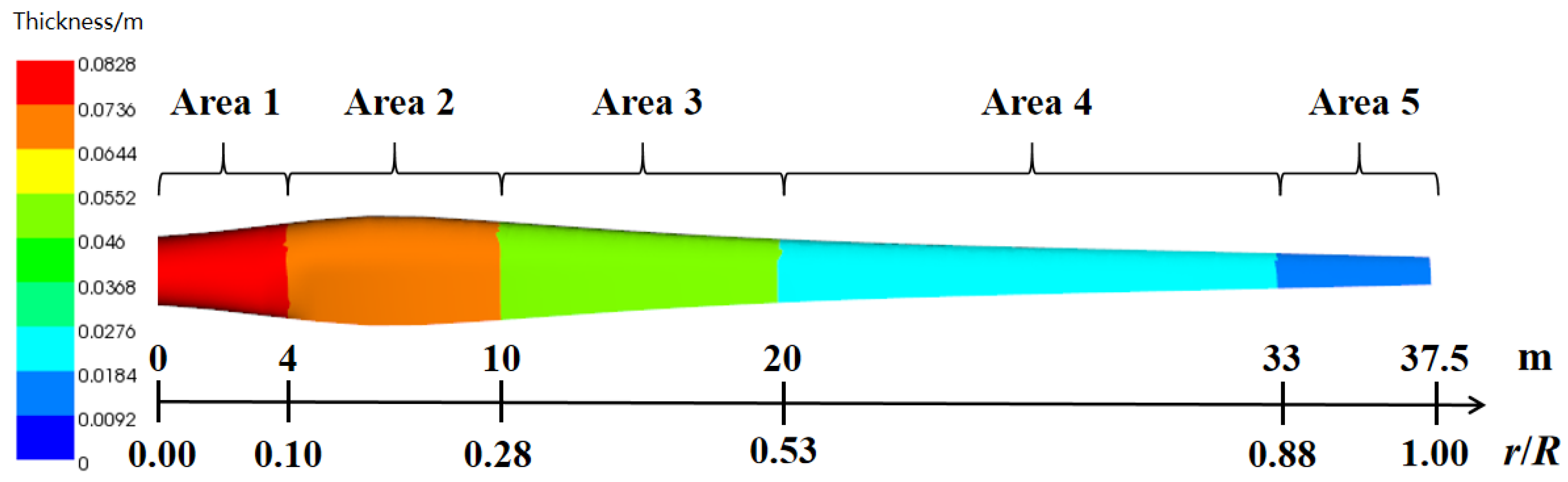
2.2.1. Physical Model
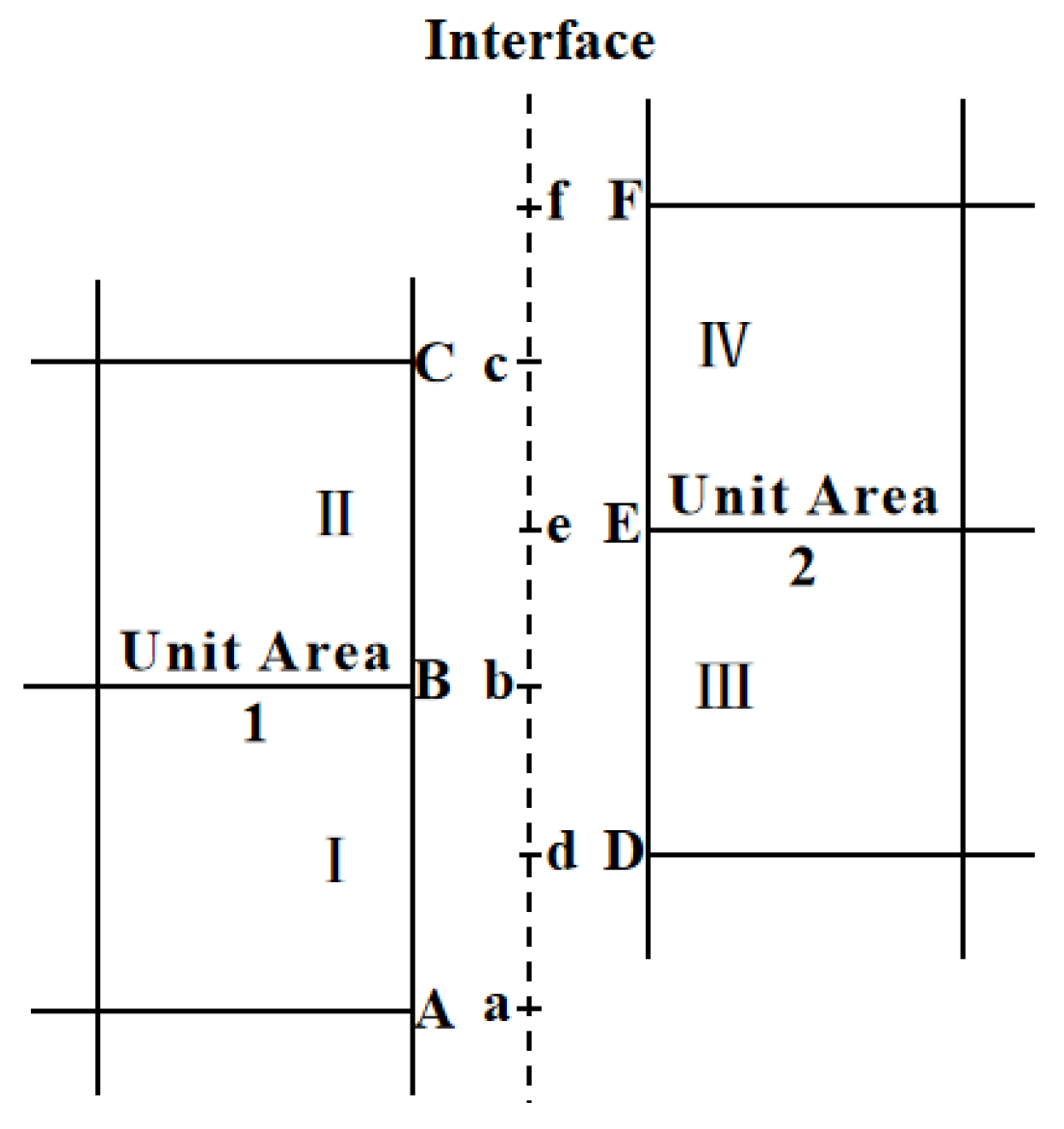
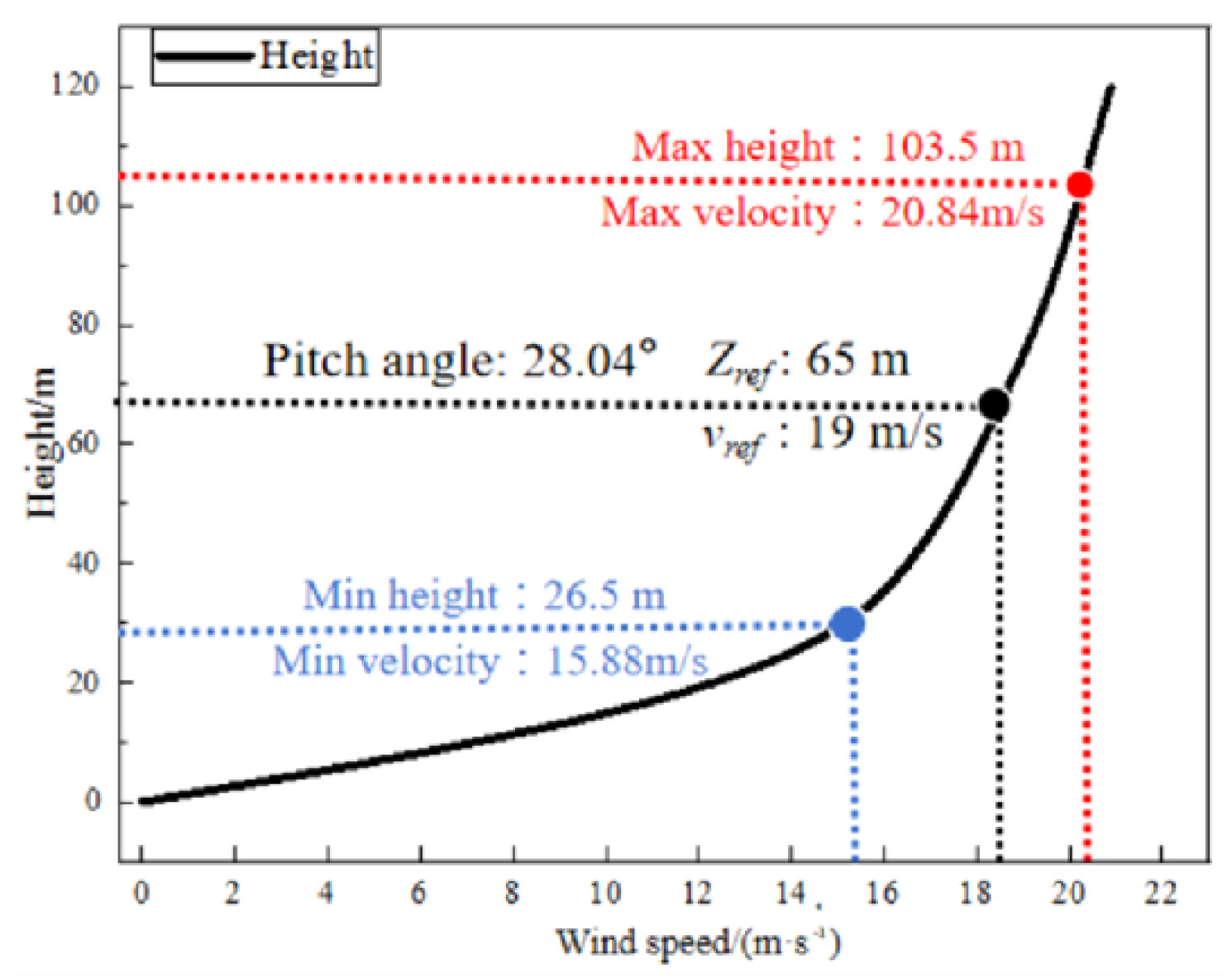
2.2.2. Boundary Conditions
3. Results and Discussion
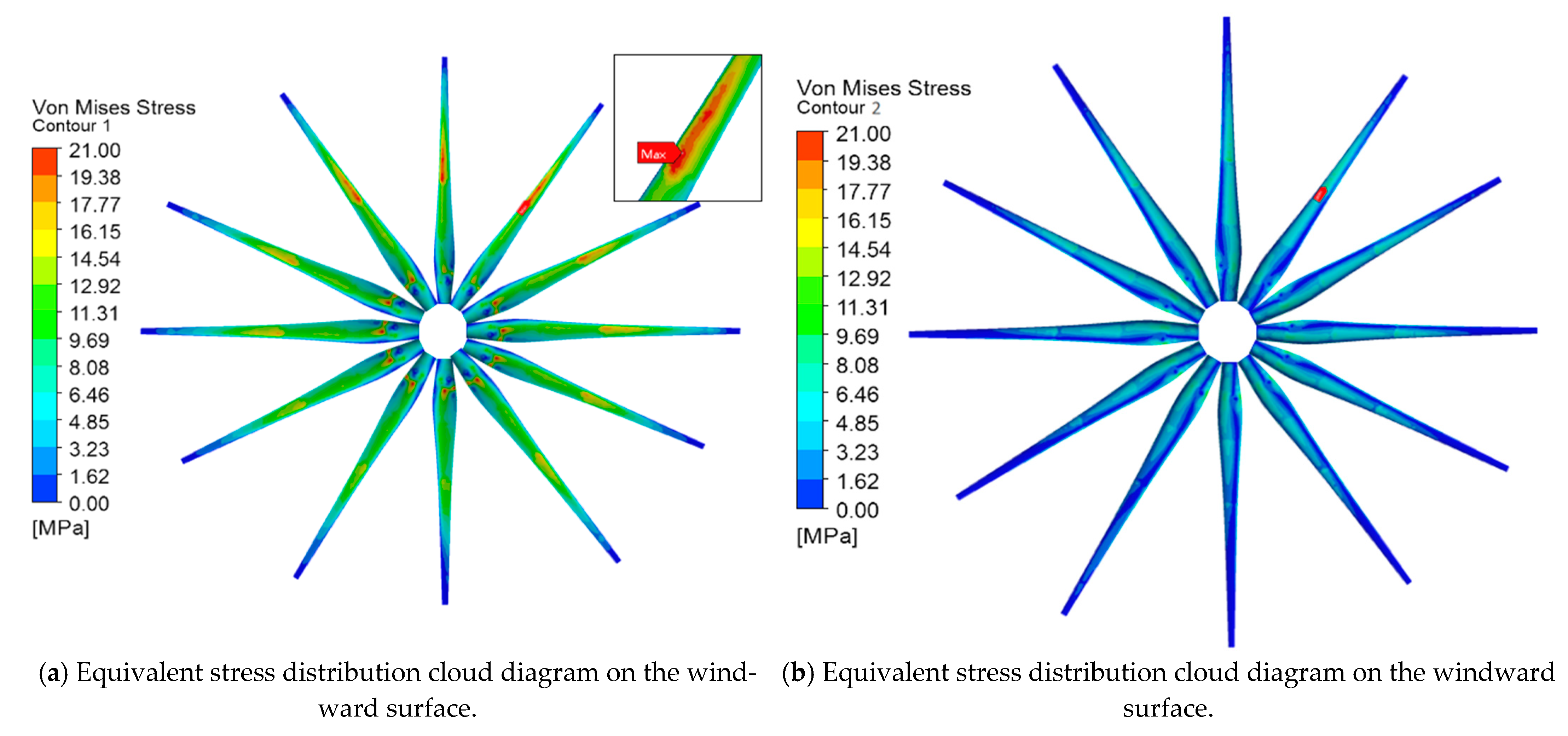
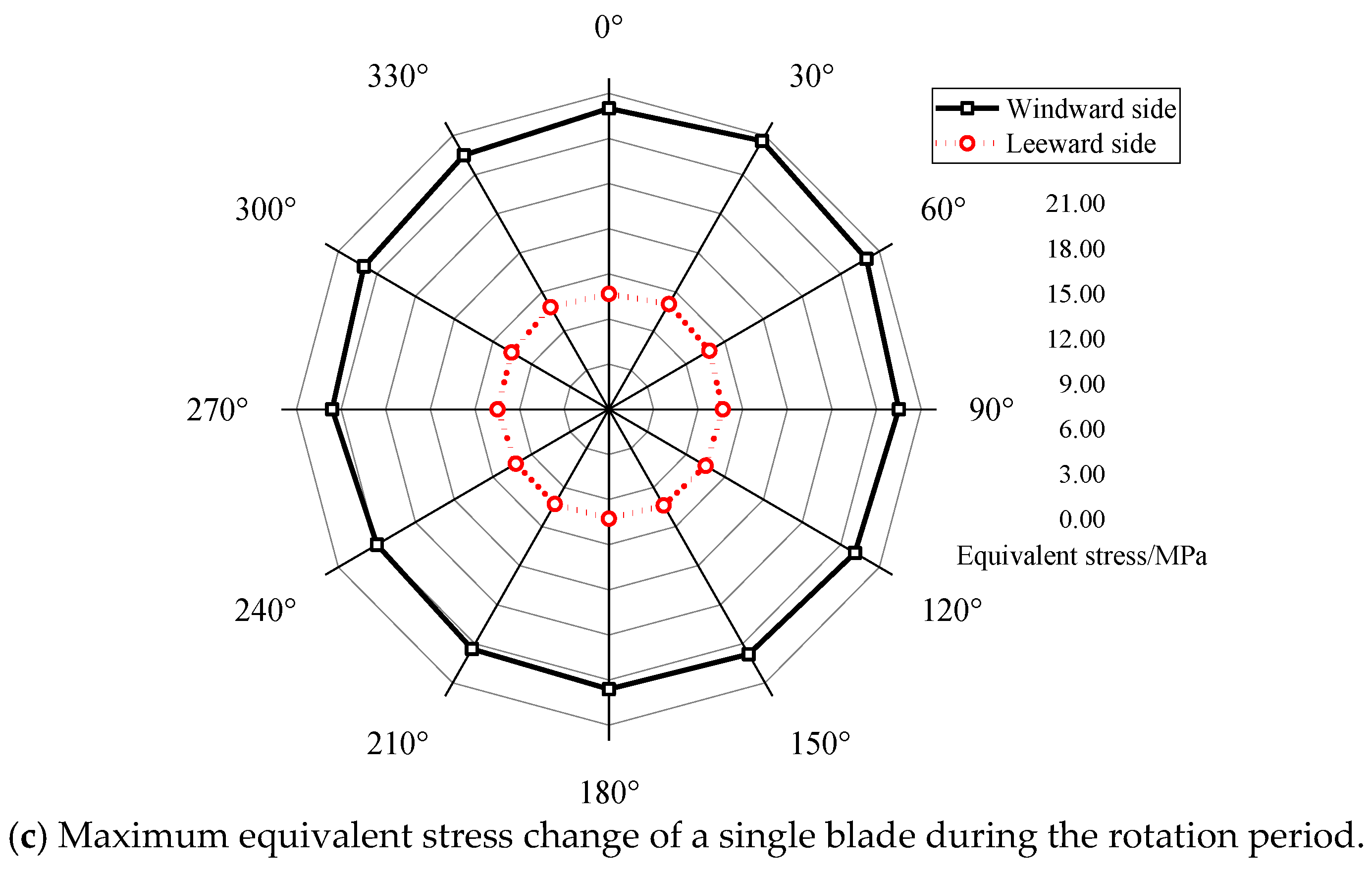
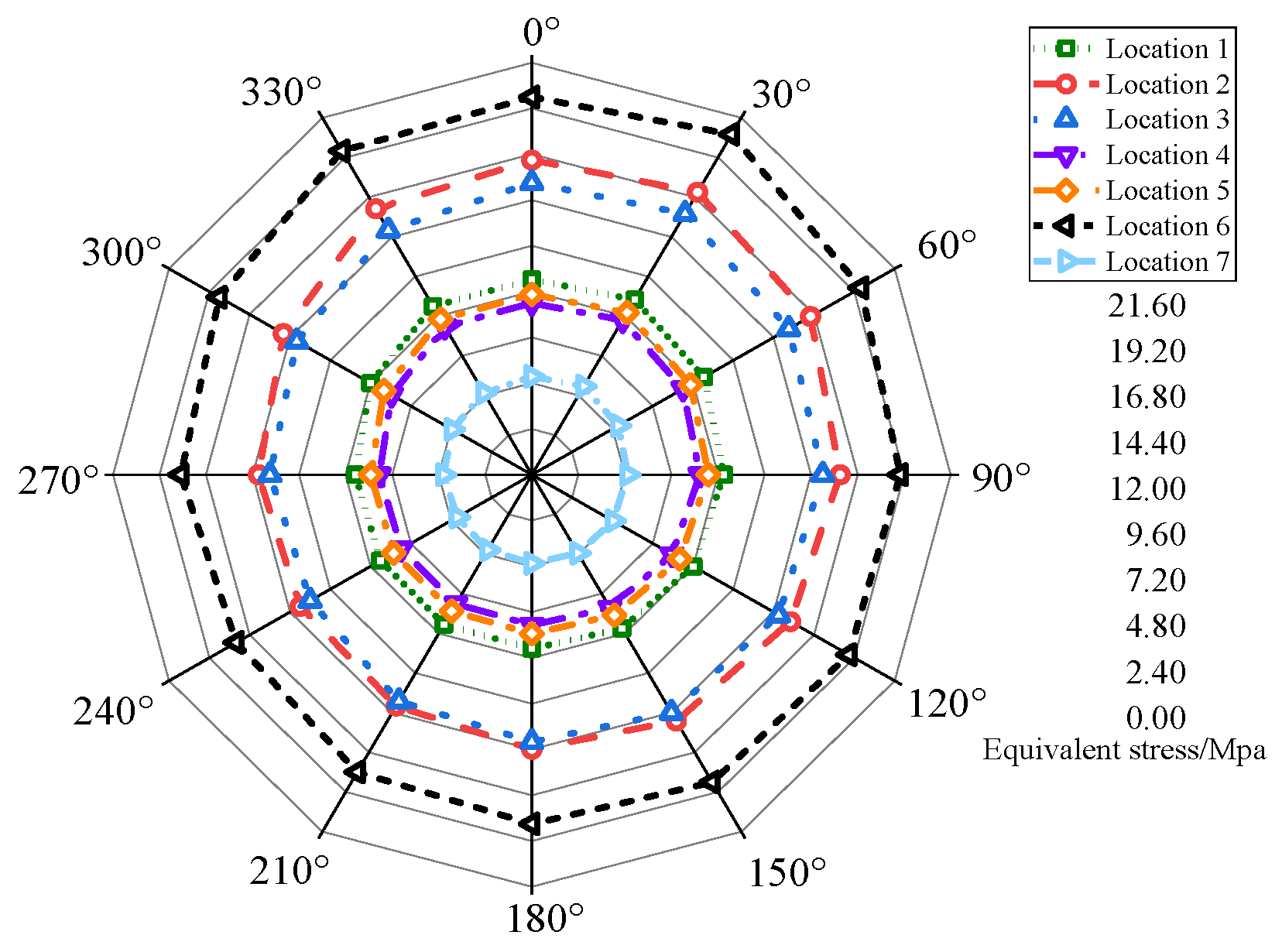
3.1. Analysis of the Blade Equivalent Stress under Different Azimuth Angles
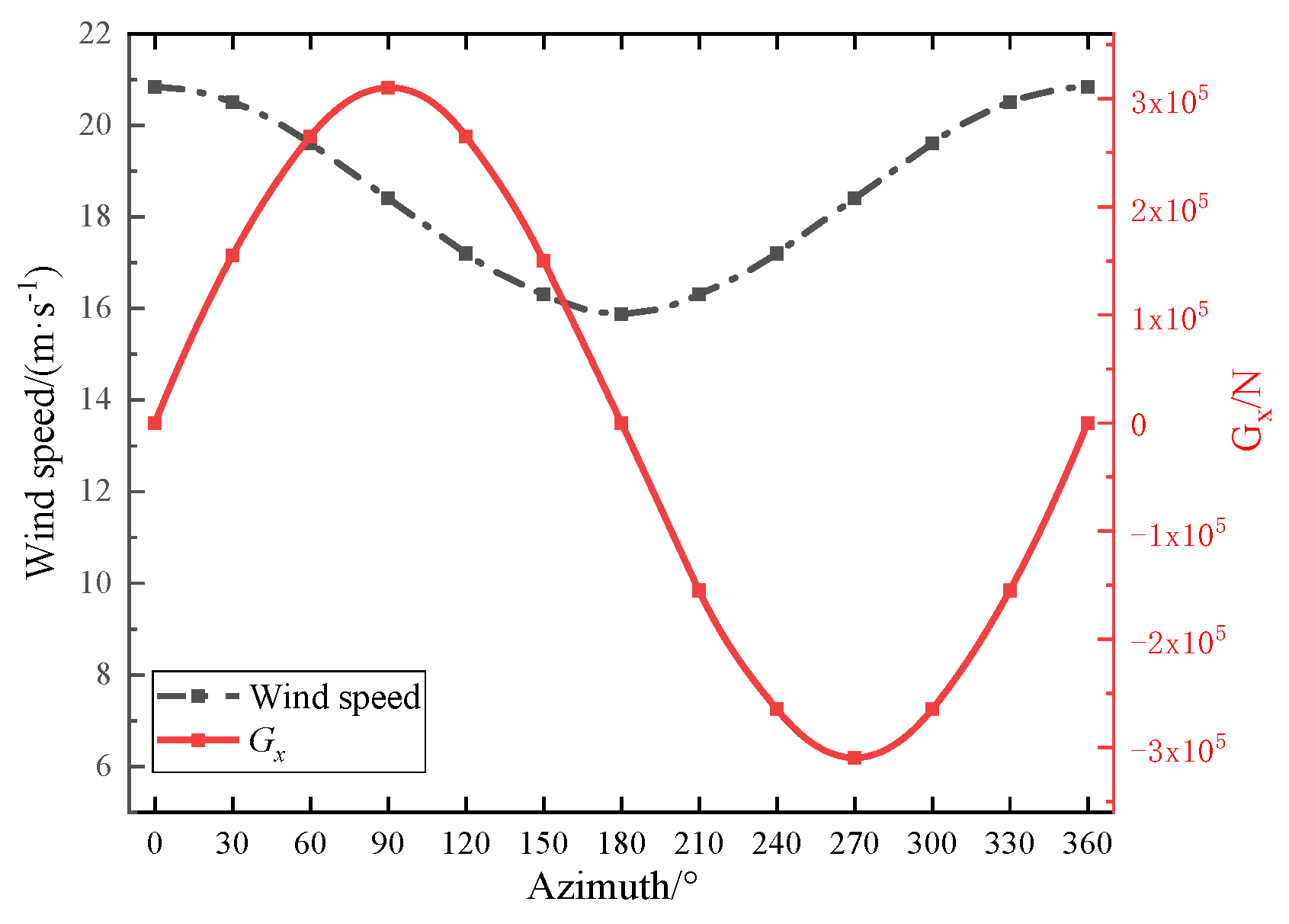
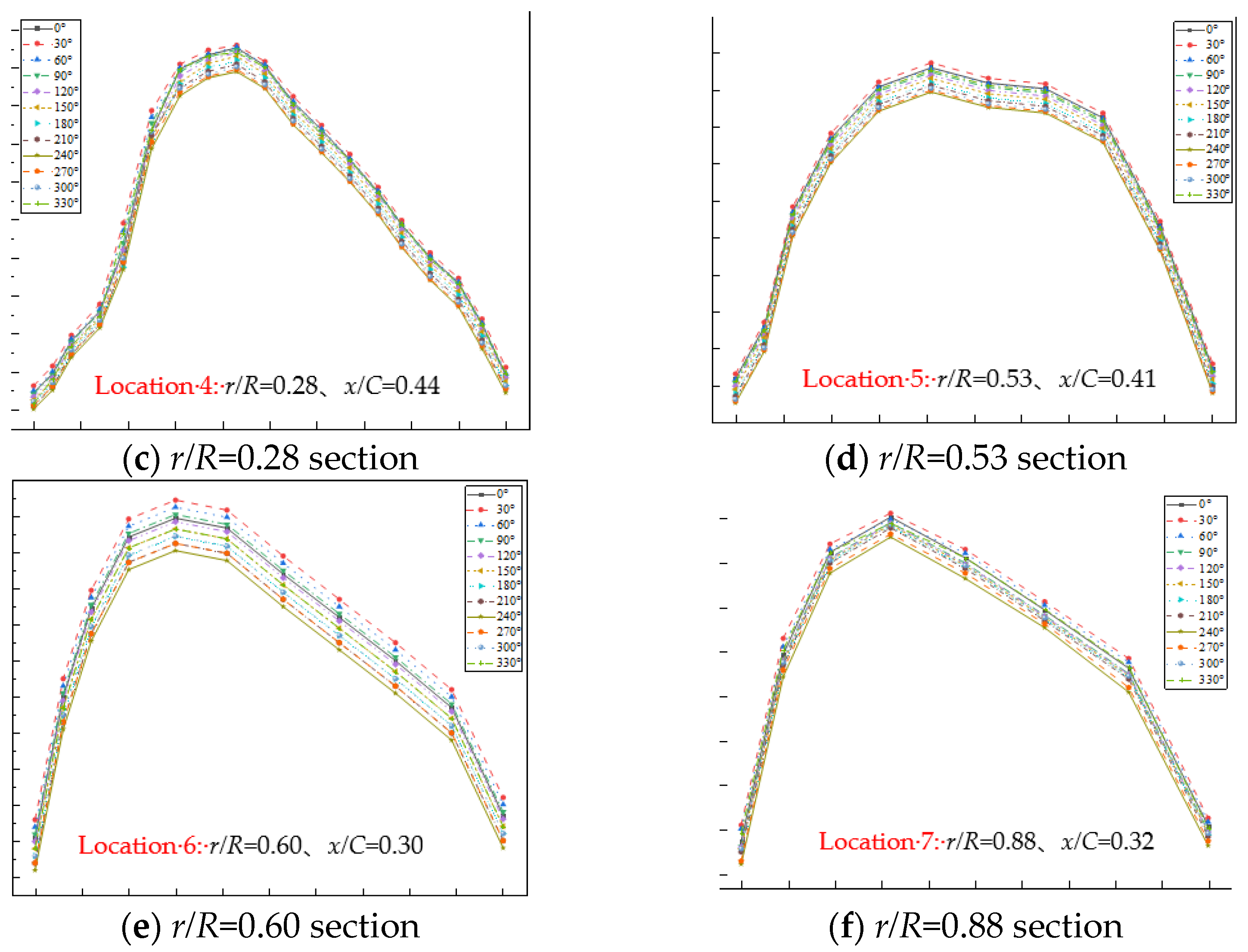
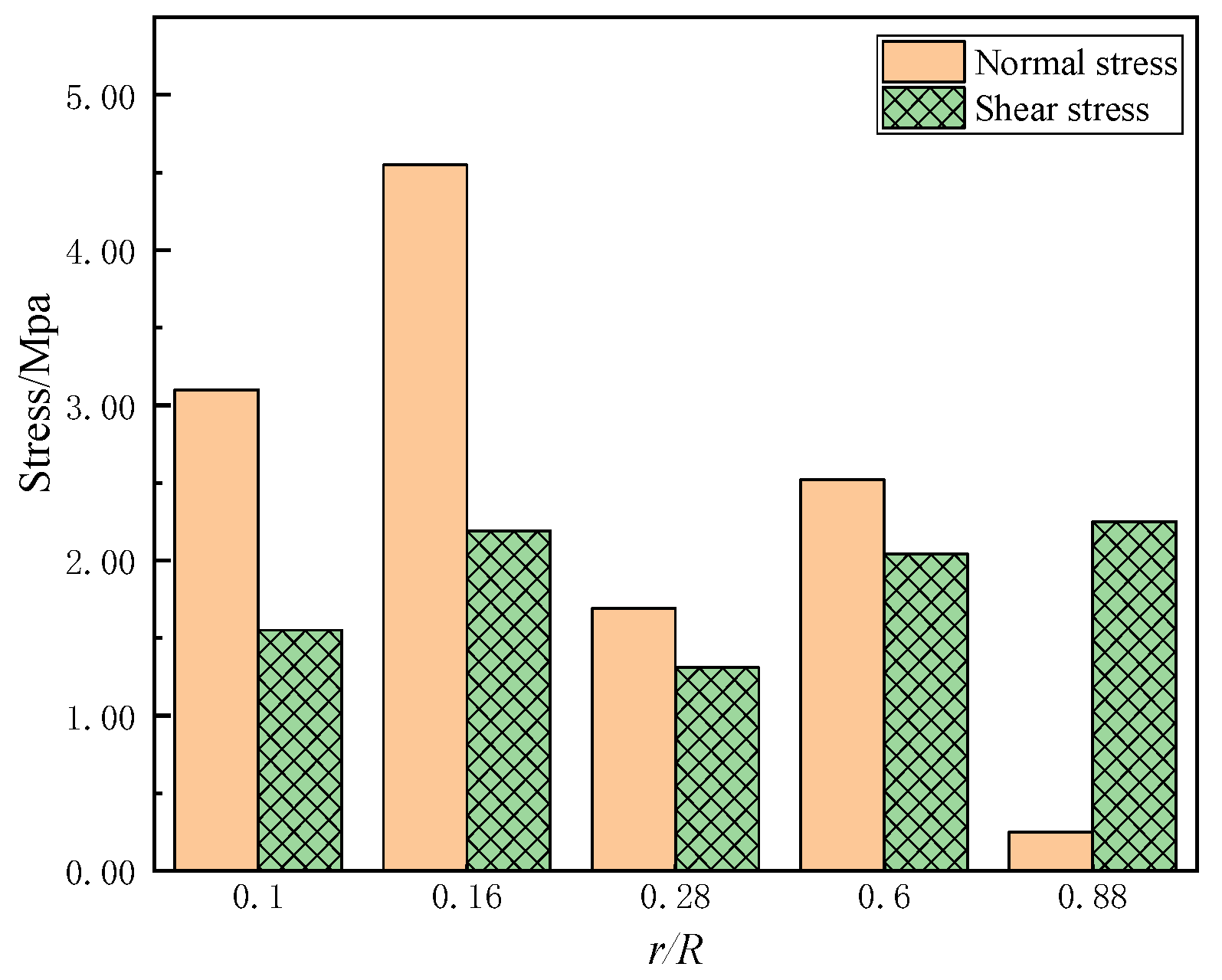
3.2. Load Analysis of a Typical Blade Failure Area
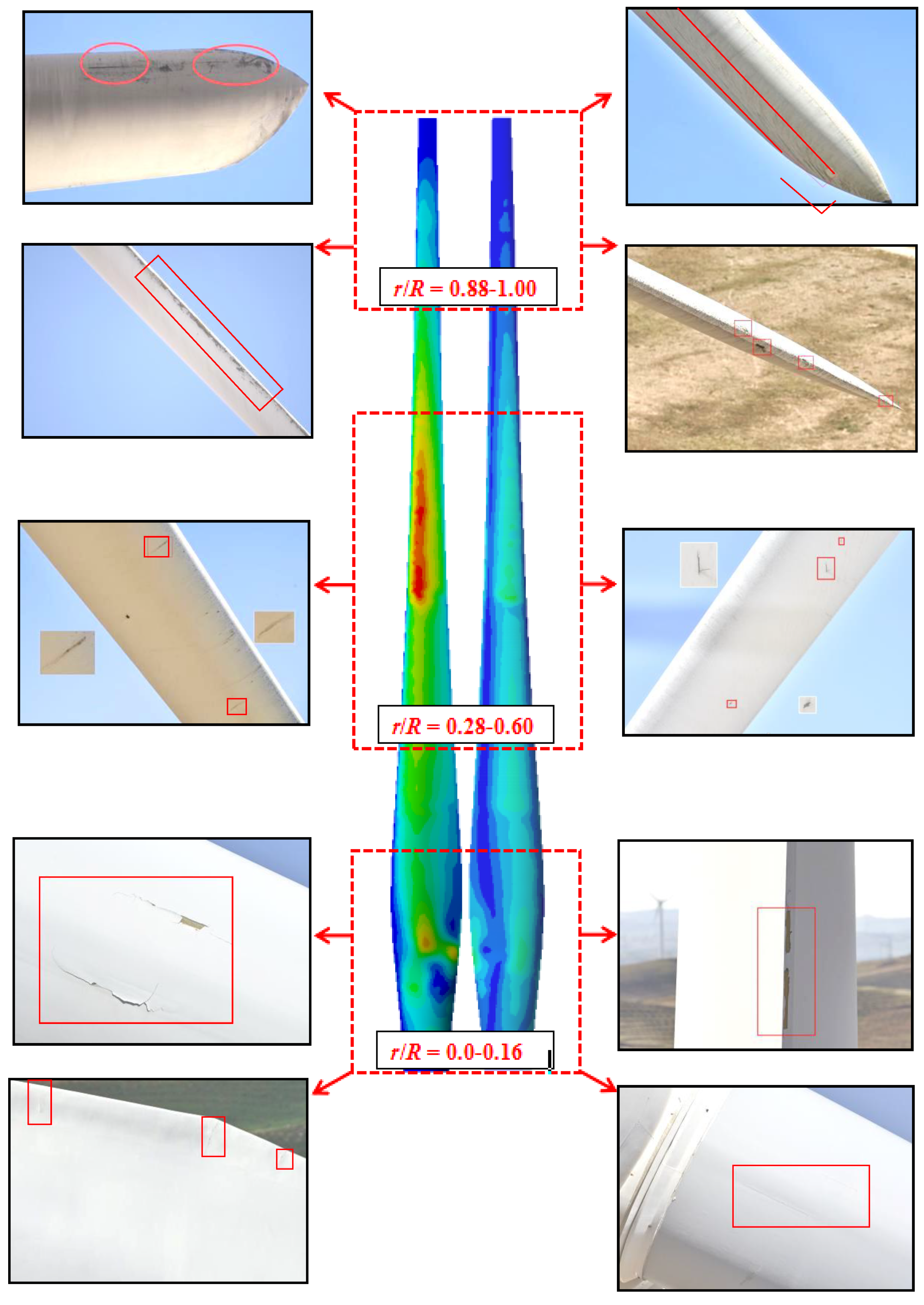
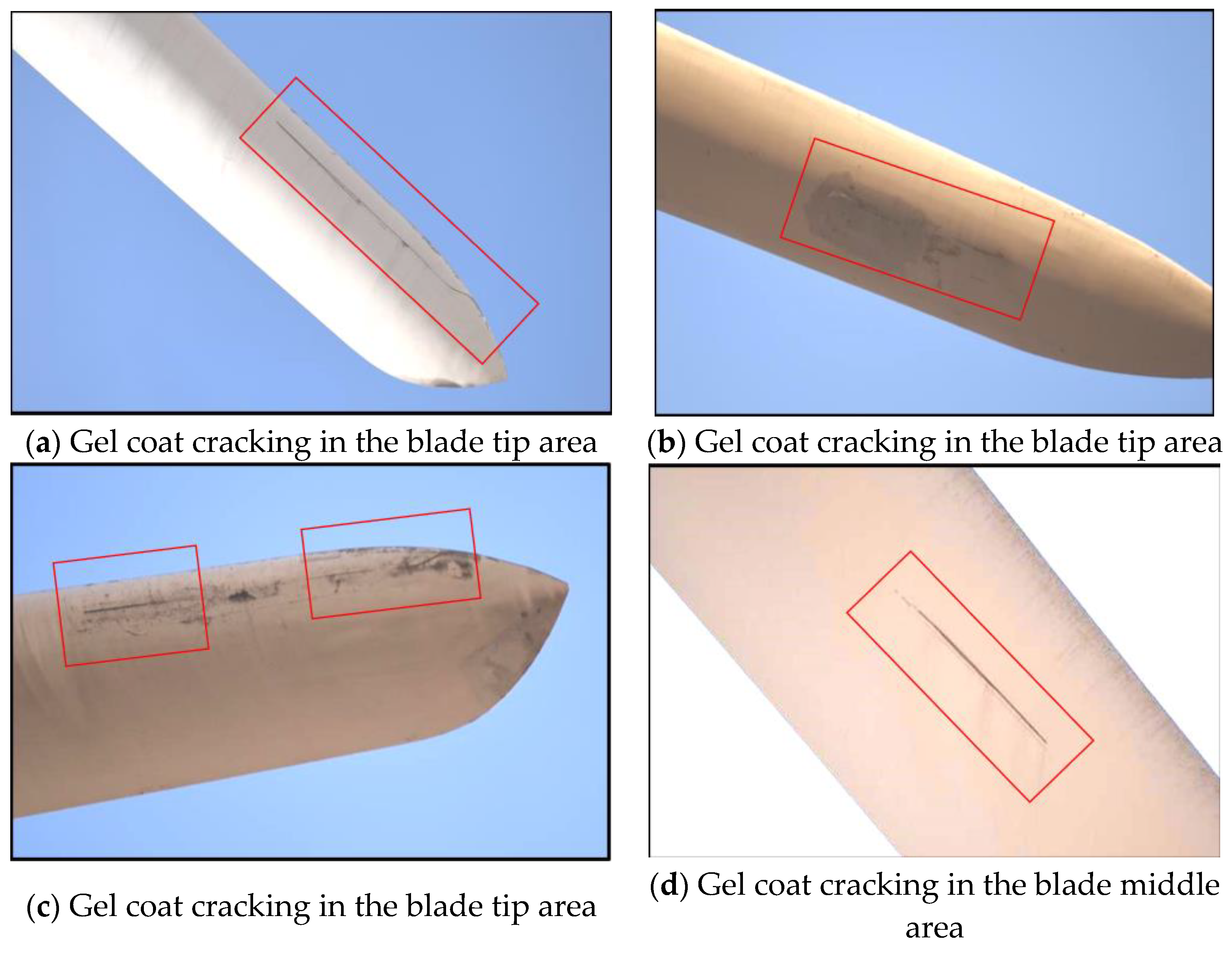
3.3. Research and Investigations of Failure and Damage of the Typical Area Outside the Blade
4. Conclusions
- The maximum stress of the blade near a 30° azimuth angle is 20.6 MPa. This is because the resultant force on the blade is the largest when the azimuth angle is 30°. By having an azimuth angle of 30° there are obvious equivalent stress peaks in the six sections of the blade, and the most vulnerable position is r/R = 0.60 and x/C = 0.30. The maximum stress value of the blade under strong wind conditions is 28.09% of the allowable stress. Theoretically, the blade structure is safe.
- When considering the UAV’s inspection of 132 wind turbines in the wind farm, 2145 failure images of the blades were collected. The damaged images account for 24.45% of the total number of images (i.e., paint peeling and oil pollution are the most frequent failure types at the end of the wind farm’s service, which appear 1988 times and account for 22.29% of the total number of image samples). The rest include scratches, cracks, bulges, gel coat cracks and so on, which resulted in a total of 192 photos.
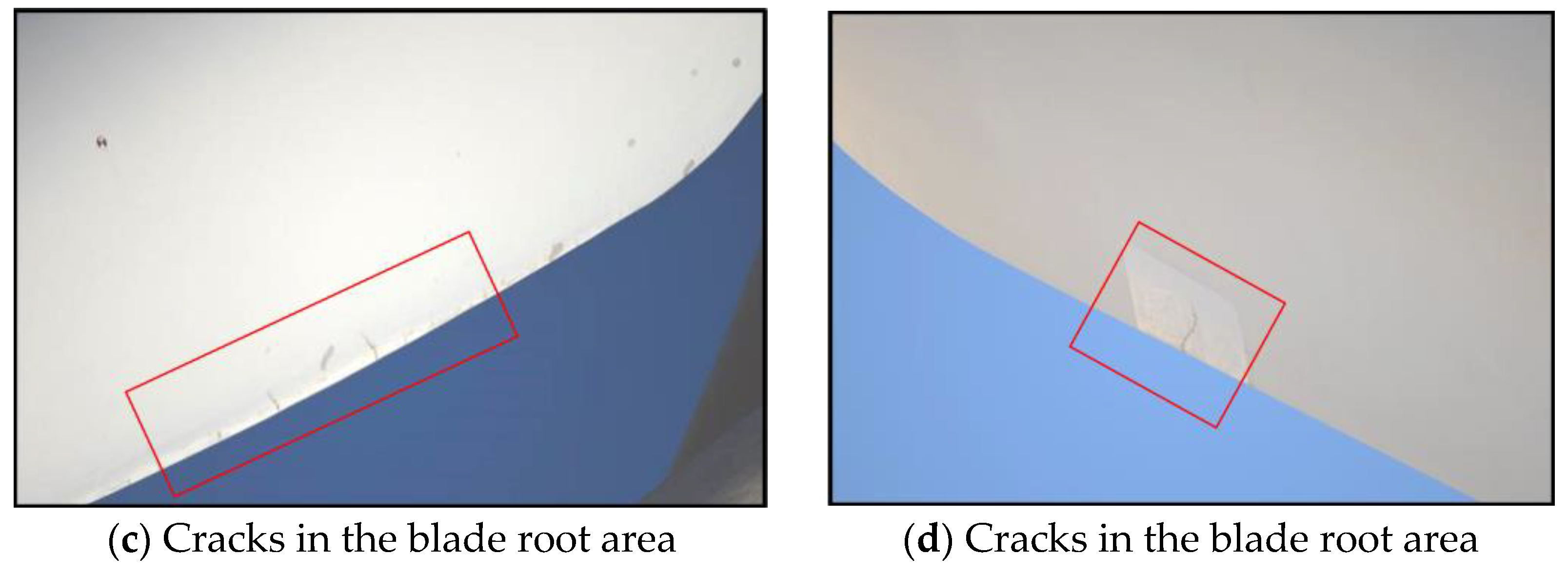
- Cracks appeared 49 times in total, with more occurrences at the root of the blade, 43 times with a frequency of 87.75%, respectively. There were three occurrences along the middle of the blade, with a frequency of 10.20%; and there were fewer occurrences at the tip of the blade, which occurred only once and the probability was 2.05%. Therefore, the main failure mode of the blade tip is gel coat cracking, the root of the blade is mainly cracked, and gel coat cracking and cracking in the blade occur, but the frequency is low.
- It was determined that the actual damage position of the blade is mostly near the stress concentration area that is calculated by the numerical simulation. The damage failure mode can confirm the force characteristics of the blade. These results can provide guidance for drone inspections.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ACP | ANSYS Composite PrepPost |
| α | the wind shear coefficient |
| E | Elastic Modulus |
| FRP | Fiber-reinforced plastic |
| G | Shear modulus |
| G | Gravity |
| x | Chord length along chordwise |
| C | Chord length |
| r | Blade length along spanwise |
| R | Blade length |
| UDF | User-Defined Function |
| v | Poisson’s ratio |
| v | Wind speed |
| Gz | Spanwise component of gravity |
| Gx | Gravity along the blade rotation direction |
| vref | Known wind speed at Zref |
| Zref | Height at the center of the hub |
| q | Centrifugal force load |
| θ | Azimuth angle |
References
- Santo, G.; Peeters, M.; Van Paepegem, W.; Degroote, J. Dynamic load and stress analysis of a large horizontal axis wind turbine using full scale fluid-structure interaction simulation. Renew. Energy 2019, 140, 212–226. [Google Scholar] [CrossRef]
- Zhu, J.; Cai, X.; Pan, P.; Gu, R.R. Static and Dynamic Characteristics Study of Wind Turbine Blade. Adv. Mater. Res. 2012, 433-440, 438–443. [Google Scholar] [CrossRef]
- Fernandez, G.; Usabiaga, H.; Vandepitte, D. An efficient procedure for the calculation of the stress distribution in a wind turbine blade under aerodynamic loads. J. Wind Eng. Ind. Aerodyn. 2018, 172, 42–54. [Google Scholar] [CrossRef]
- Jiang, X.; Gao, Z.; Wang, J.; Bai, Y.; Yan, M.; Wang, X. Experiment on correlation of wind turbine strain and tower vibration. J. Drain. Irrig. Mach. Eng. 2017, 35, 685. [Google Scholar]
- Kim, H.-I.; Han, J.-H.; Bang, H.-J. Real-time deformed shape estimation of a wind turbine blade using distributed fiber Bragg grating sensors. Wind Energy 2014, 17, 1455–1467. [Google Scholar] [CrossRef]
- Zhang, J.; Guo, L.; Wu, H.; Zhou, A.; Hu, D.; Ren, J. The influence of wind shear on vibration of geometrically nonlinear wind turbine blade under fluid–structure interaction. Ocean Eng. 2014, 84, 14–19. [Google Scholar] [CrossRef]
- Cheng, Y.; Xue, Z.; Jiang, T.; Wang, W.; Wang, Y. Numerical simulation on dynamic response of flexible multi-body tower blade coupling in large wind turbine. Energy 2018, 152, 601–612. [Google Scholar] [CrossRef]
- Zhang, J.P.; Li, D.L.; Liu, Y.; Wu, H.L.; Ren, J.X.; Pan, W.G. Dynamic Response Analysis of Large Wind Turbine Blade Based on Davenport Wind Speed Model. Adv. Mater. Res. 2011, 347-353, 2330–2336. [Google Scholar] [CrossRef]
- Zhou, B.; Wang, X.; Zheng, C.; Cao, J.; Zou, P. Finite Element Analysis for the Web Offset of Wind Turbine Blade. IOP Conf. Ser. Earth Environ. Sci. 2017, 63, 12011. [Google Scholar] [CrossRef] [Green Version]
- Choudhury, S.; Sharma, T.; Shukla, K. Effect of orthotropy ratio of the shear web on the aero-elasticity and torque generation of a hybrid wind turbine blade. Renew. Energy 2017, 113, 1378–1387. [Google Scholar] [CrossRef]
- Dimitrov, N.; Natarajan, A.; Kelly, M. Model of wind shear conditional on turbulence and its impact on wind turbine loads. Wind Energy 2014, 18, 1917–1931. [Google Scholar] [CrossRef]
- Ageze, M.B.; Hu, Y.; Wu, H. Comparative Study on Uni- and Bi-Directional Fluid Structure Coupling of Wind Turbine Blades. Energies 2017, 10, 1499. [Google Scholar] [CrossRef] [Green Version]
- Zhu, R.-S.; Zhao, H.-L.; Peng, J.-Y.; Li, J.-P.; Wang, S.-Q.; Zhao, H. Numerical Investigation on Fluid-structure Coupling of 3 MW Wind Turbine Blades. Int. J. Green Energy 2015, 13, 241–247. [Google Scholar] [CrossRef]
- Bae, S.-Y.; Kim, Y.-H. Structural design and analysis of large wind turbine blade. Mod. Phys. Lett. B 2019, 33, 1940032. [Google Scholar] [CrossRef]
- Ullah, H.; Ullah, B.; Riaz, M.; Iqbal, M.; Badshah, A. Structural Analysis of a Large Composite Wind Turbine Blade under Extreme Loading. In 2018 International Conference on Power Generation Systems and Renewable Energy Technologies, Islamabad, Pakistan, 10–12 September 2018; IEEE: Piscataway, NJ, USA, 2018. [Google Scholar]
- Shen, X.; Zhu, X.; Du, Z. Wind turbine aerodynamics and loads control in wind shear flow. Energy 2011, 36, 1424–1434. [Google Scholar] [CrossRef]
- Fu, B.; Zhao, J.; Li, B.; Yao, J.; Teifouet, A.R.M.; Sun, L.; Wang, Z. Fatigue reliability analysis of wind turbine tower under random wind load. Struct. Saf. 2020, 87, 101982. [Google Scholar] [CrossRef]
- Guo, S.; Li, Y.; Chen, W. Analysis on dynamic interaction between flexible bodies of large-sized wind turbine and its response to random wind loads. Renew. Energy 2020, 163, 123–137. [Google Scholar] [CrossRef]
- Wang, H.; Ke, S.T.; Wang, T.G.; Zhu, S.Y. Typhoon-induced vibration response and the working mechanism of large wind turbine considering multi-stage effects. Renew. Energy 2020, 153, 740–758. [Google Scholar] [CrossRef]
- Boujleben, A.; Ibrahimbegovic, A.; Lefrançois, E. An efficient computational model for fluid-structure interaction in application to large overall motion of wind turbine with flexible blades. Appl. Math. Model. 2020, 77, 392–407. [Google Scholar] [CrossRef]
- Peeters, M.; Santo, G.; Degroote, J.; Van Paepegem, W. Comparison of Shell and Solid Finite Element Models for the Static Certification Tests of a 43 m Wind Turbine Blade. Energies 2018, 11, 1346. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Quant, R.; Kolios, A. Fluid structure interaction modelling of horizontal-axis wind turbine blades based on CFD and FEA. J. Wind Eng. Ind. Aerodyn. 2016, 158, 11–25. [Google Scholar] [CrossRef] [Green Version]
- Tran, T.; Kim, D.; Song, J. Computational Fluid Dynamic Analysis of a Floating Offshore Wind Turbine Experiencing Platform Pitching Motion. Energies 2014, 7, 5011–5026. [Google Scholar] [CrossRef]
- Steijl, R.; Barakos, G. Sliding mesh algorithm for CFD analysis of helicopter rotor-fuselage aerodynamics. Int. J. Numer. Methods Fluids 2008, 58, 527–549. [Google Scholar] [CrossRef]
- Tian, K.; Song, L.; Jiao, X.; Feng, R.; Chen, Y.; Tian, R. Aeroelastic stability analysis and failure damage evaluation of wind turbine blades under variable conditions. Energy Sources Part A Recover. Util. Environ. Eff. 2021, 1–18. [Google Scholar] [CrossRef]
- Song, L.; Li, Q.; Chen, W.; Qin, P.; Huang, H.H.; Yuncheng, H. Wind characteristics of a strong typhoon in marine surface boundary layer. Wind Struct. 2012, 15, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Mao, Y.; Wang, S.; Yu, D.; Zhao, J. Automatic image detection of multi-type surface defects on wind turbine blades based on cascade deep learning network. Intell. Data Anal. 2021, 25, 463–482. [Google Scholar] [CrossRef]
- Xu, D.; Wen, C.; Liu, J. Wind turbine blade surface inspection based on deep learning and UAV-taken images. J. Renew. Sustain. Energy 2019, 11, 053305. [Google Scholar] [CrossRef]
- Toft, H.S.; Branner, K.; Berring, P.; Sorensen, J.D. Defect distribution and reliability assessment of wind turbine blades. Eng. Struct. 2011, 33, 171–180. [Google Scholar] [CrossRef]





| Name | Specifications | Name | Specifications |
|---|---|---|---|
| Airfoil | Provided by manufacturer | Rated power P/MW | 1.5 |
| Number of blades /N | 3 | Rated speed n/rpm | 19.8 |
| Hub center height H/m | 65 | Rated wind speed v/m·s−1 | 12 |
| Hub diameter d/m | 2 | Rated tip speed ratio λ | 8.5 |
| Wind wheel diameter D/m | 77 | Cut-in wind speed v/m·s−1 | 3 |
| Wind wheel quality m/t | 30.1 | Cut-out wind speed v/m·s−1 | 25 |
| Material | Elastic Modulus/MPa | Poisson’s Ratio | Shear Modulus/MPa | ||||||
|---|---|---|---|---|---|---|---|---|---|
| E11 | E22 | E33 | v12 | v23 | v13 | G12 | G23 | G13 | |
| FRP | 39,000 | 8600 | 8600 | 0.28 | 0.47 | 0.28 | 3800 | 2930 | 3800 |
| Wind Speed | Grid Numbers/Ten Thousand | |||||||
|---|---|---|---|---|---|---|---|---|
| 3.6 m/s | 340 | 430 | 520 | 620 | 700 | 850 | 900 | 1070 |
| Maximum pressure/Pa | 164 | 165 | 167 | 169 | 172 | 175 | 175 | 175 |
| 19 m/s | 340 | 430 | 520 | 620 | 700 | 850 | 900 | 1070 |
| Maximum pressure/Pa | 1573 | 1587 | 1604 | 1624 | 1646 | 1674 | 1674 | 1674 |
| 21.1 m/s | 340 | 430 | 520 | 620 | 700 | 850 | 900 | 1070 |
| Maximum pressure/Pa | 1618 | 1643 | 1668 | 1694 | 1720 | 1743 | 1743 | 1743 |
| Wind Speed | Grid Numbers/Ten Thousand | |||||||
|---|---|---|---|---|---|---|---|---|
| 19 m/s | 75 | 81 | 90 | 98 | 105 | 109 | 109 | 109 |
| Maximum Equivalent stress /Mpa | 19.2 | 19.5 | 19.7 | 20.3 | 20.6 | 20.6 | 20.6 | 20.6 |
| Maximum displacement/m | 0.56 | 0.58 | 0.59 | 0.61 | 0.63 | 0.63 | 0.63 | 0.63 |
| Location | Failure Location | Max Equivalent Stress/MPa | Azimuth Angle of the Maximum Equivalent Stress |
|---|---|---|---|
| Location 1 | r/R = 0.10 x/C = 0.53 | 10.60 | Around 30° |
| Location 2 | r/R = 0.16 x/C = 0.52 | 17.10 | Around 30° |
| Location 3 | r/R = 0.16 x/C = 0.88 | 15.80 | Around 30° |
| Location 4 | r/R = 0.28 x/C = 0.44 | 9.36 | Around 30° |
| Location 5 | r/R = 0.53 x/C = 0.41 | 9.74 | Around 30° |
| Location 6 | r/R = 0.60 x/C = 0.30 | 20.60 | Around 30° |
| Location 7 | r/R = 0.88 x/C = 0.32 | 5.28 | Around 30° |
| Location | |
|---|---|
| Location 1 | 14.45% |
| Location 2 | 23.32% |
| Location 3 | 21.55% |
| Location 4 | 12.76% |
| Location 5 | 13.28% |
| Location 6 | 28.09% |
| Location 7 | 7.20% |
| Damage Types Caused by Stress | Gel Coat Cracking | Cracks |
|---|---|---|
| Damage numbers | 58 | |
| Damage type numbers | 9 | 49 |
| Frequency | 15.52% | 84.48% |
| Damage Types | Gel Coat Cracking | Cracks | ||
|---|---|---|---|---|
| Typical area | Number | Frequency | Number | Frequency |
| Blade root r/R = 0.00–0.16 | 0 | 0.00% | 43 | 87.75% |
| Blade middle r/R = 0.28–0.60 | 2 | 22.22% | 5 | 10.20% |
| Blade tip r/R = 0.28–0.60 | 7 | 77.78% | 1 | 2.05% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, K.; Song, L.; Chen, Y.; Jiao, X.; Feng, R.; Tian, R. Stress Coupling Analysis and Failure Damage Evaluation of Wind Turbine Blades during Strong Winds. Energies 2022, 15, 1339. https://doi.org/10.3390/en15041339
Tian K, Song L, Chen Y, Jiao X, Feng R, Tian R. Stress Coupling Analysis and Failure Damage Evaluation of Wind Turbine Blades during Strong Winds. Energies. 2022; 15(4):1339. https://doi.org/10.3390/en15041339
Chicago/Turabian StyleTian, Kangqi, Li Song, Yongyan Chen, Xiaofeng Jiao, Rui Feng, and Rui Tian. 2022. "Stress Coupling Analysis and Failure Damage Evaluation of Wind Turbine Blades during Strong Winds" Energies 15, no. 4: 1339. https://doi.org/10.3390/en15041339
APA StyleTian, K., Song, L., Chen, Y., Jiao, X., Feng, R., & Tian, R. (2022). Stress Coupling Analysis and Failure Damage Evaluation of Wind Turbine Blades during Strong Winds. Energies, 15(4), 1339. https://doi.org/10.3390/en15041339





