Reliability Assessment under High Penetration of EVs including V2G Strategy
Abstract
:1. Introduction
- We propose a new mechanism for reliability assessment for the distribution networks under high penetration of BEVs, including V2G mode, using a dynamic stochastic BEV consumption model.
- We study the effects of different charging strategies, such as the uncontrolled charging strategy, controlled unidirectional strategy, and controlled bidirectional strategy as well as the impact of penetration of BEVs on the reliability of the power system.
- Various reliability indices, such as the Loss of Load Expectation (LOLE), Loss of Energy Expectation (LOEE), Loss of Load Frequency (LOLF), Energy Not Served per Interruption (ENSPI), System Average Interruption Frequency Index (SAIFI), and System Average Interruption Duration Index (SAIDI), are computed under different charging strategies to assess the impact of these strategies on the reliability of the power system.
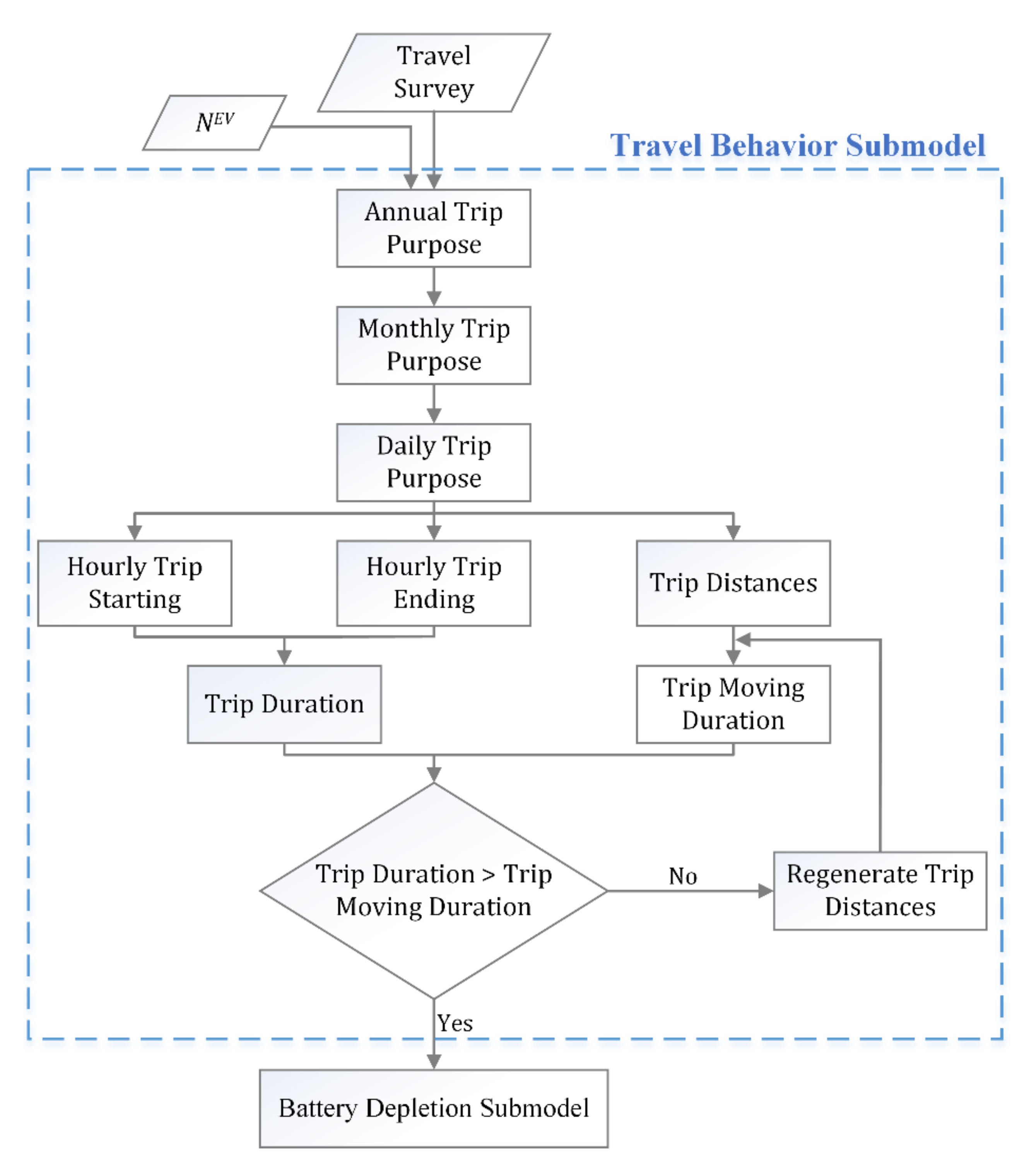
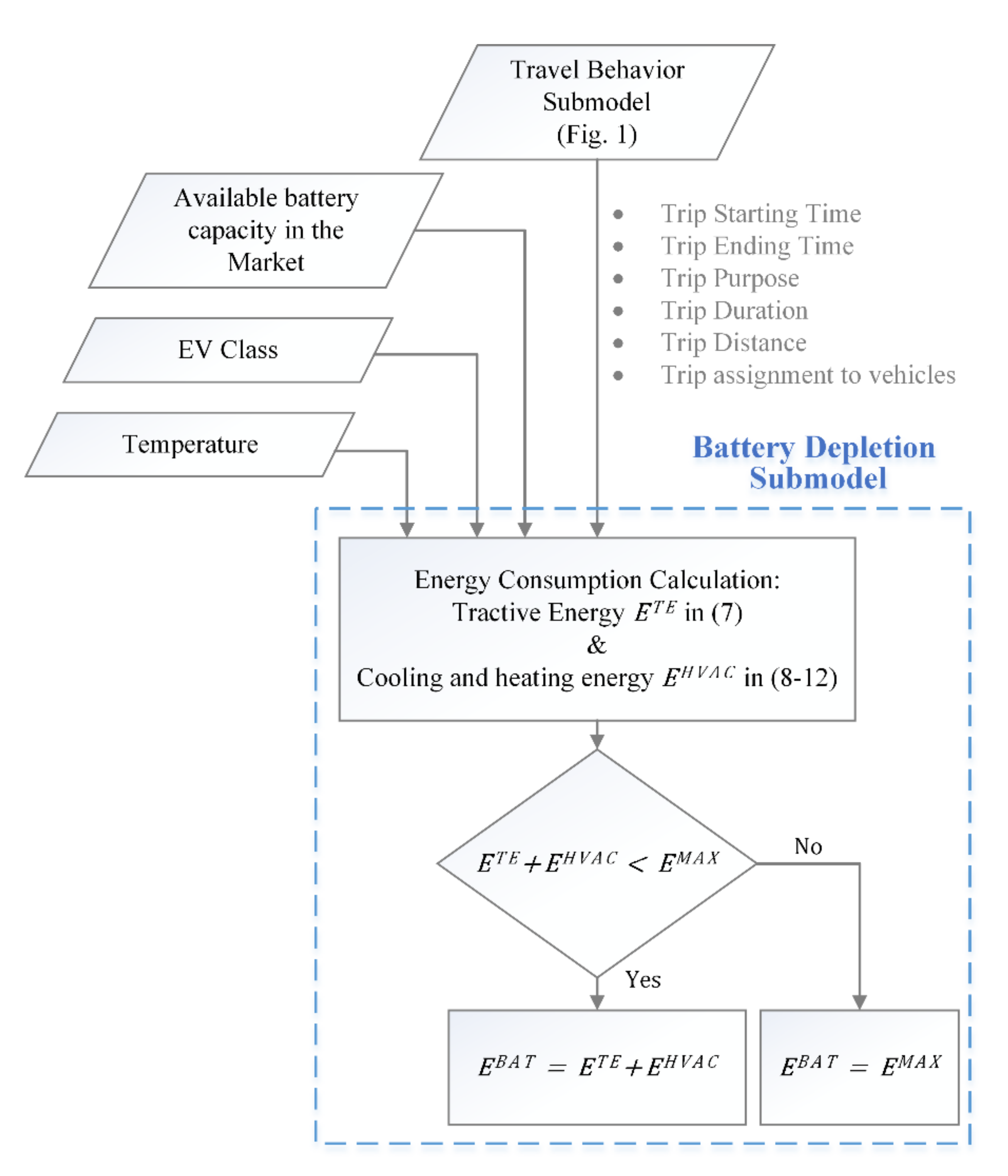
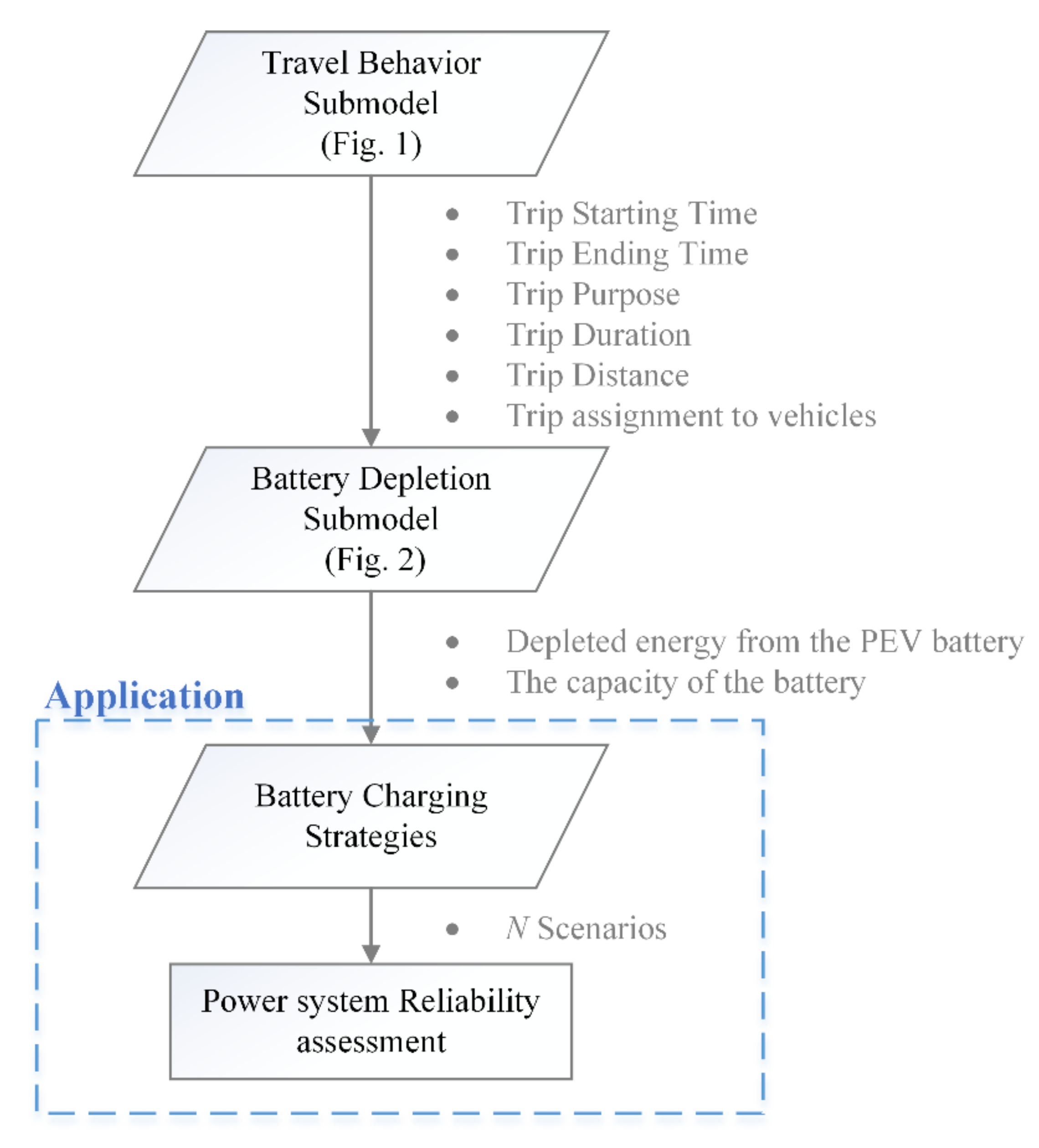
2. Dynamic Stochastic BEV Consumption Model
2.1. Travel Behavior Submodel
2.2. Battery Depletion Submodel
3. Reliability Assessment under Different Strategies
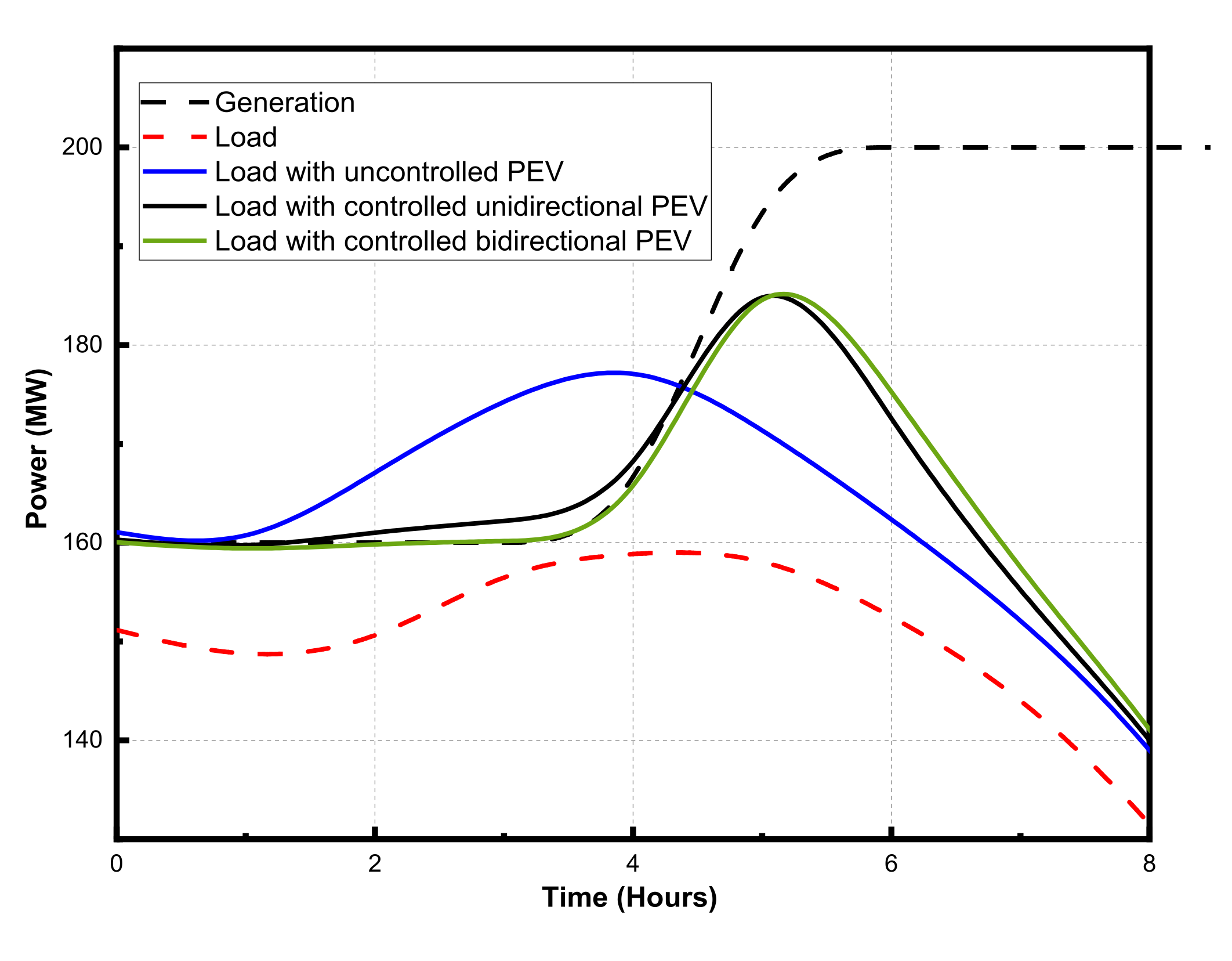
- Uncontrolled G2V charging strategy [32], where the power flow is only unidirectional from the grid to the BEV. The BEVs start charging once plugged into the charger without supervision.
- Controlled G2V charging strategy [33], where the power flow is still in one direction from the grid to the BEV. However, the EV chargers accept external control signals to enable/disable the charging process and control the level of charging. This external control signal can be sent by the BEV owner, the utility, or a third party subject to appropriate contracts or agreements.
- Controlled Bidirectional Strategy [34], where the power flow may be in two directions, G2V or V2G. The BEV may discharge to the grid during load peak periods, which can help enhance the power system reliability and stability as well as relief congestions.
- Indirect Controlled Bidirectional Strategy [35]; in this strategy, the power flow can be in both directions. The advantage of this approach is that smart coordination can be used to determine the optimal periods of charging to decrease the energy cost in addition to the advantages of the controlled bidirectional strategy, where the charging is indirectly affected by energy prices.
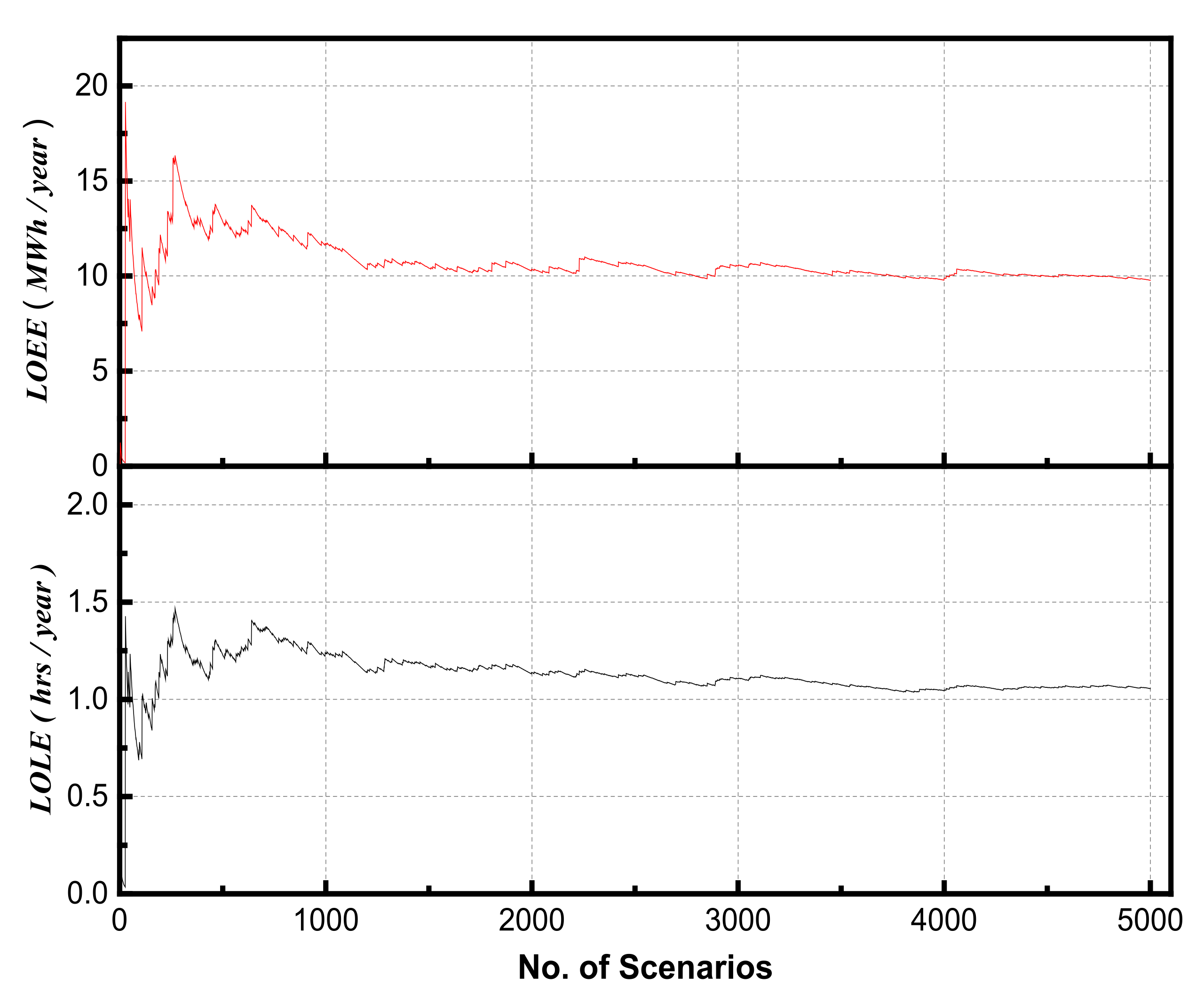
4. Simulation Results
4.1. Uncontrolled Charging
4.2. Controlled Charging
4.3. Controlled Charging/Discharging
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mokhtar, M.; Shaaban, M.F.; Zeineldin, H.; El-Saadany, E.F. Optimal Operation of Virtual Charging Systems for Plug-In Electric Vehicles. IEEE Syst. J. 2022. [Google Scholar] [CrossRef]
- Mokhtar, M.; Shaaban, M.F.; Zeineldin, H.; El-Saadany, E.F. A Customer-Centered Smart Charging Strategy Considering Virtual Charging System. IEEE Access 2021, 9, 117993–118004. [Google Scholar] [CrossRef]
- Moghaddam, Z.; Ahmad, I.; Habibi, D.; Phung, Q.V. Smart charging strategy for electric vehicle charging stations. IEEE Trans. Transp. Electrif. 2018, 4, 76–88. [Google Scholar] [CrossRef]
- Shafiee, S.; Fotuhi-Firuzabad, M.; Rastegar, M. Investigating the impacts of plug-in hybrid electric vehicles on power distribution systems. IEEE Trans. Smart Grid 2013, 4, 1351–1360. [Google Scholar] [CrossRef]
- Shalaby, A.A.; Shaaban, M.F.; Mokhtar, M.; Zeineldin, H.H.; El-Saadany, E.F. Optimal Day-ahead Operation for a PV-based Battery Swapping Station for Electric Vehicles. In Proceedings of the 2021 6th International Symposium on Environment-Friendly Energies and Applications (EFEA), Sofia, Bulgaria, 24–26 March 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Darabi, Z.; Ferdowsi, M. An event-based simulation framework to examine the response of power grid to the charging demand of plug-in hybrid electric vehicles. IEEE Trans. Ind. Inform. 2014, 10, 313–322. [Google Scholar] [CrossRef]
- Malhotra, A.; Binetti, G.; Davoudi, A.; Schizas, I.D. Distributed power profile tracking for heterogeneous charging of electric vehicles. IEEE Trans. Smart Grid 2017, 8, 2090–2099. [Google Scholar] [CrossRef]
- Shaaban, M.F.; Atwa, Y.M.; El-Saadany, E.F. PEVs modeling and impacts mitigation in distribution networks. IEEE Trans. Power Syst. 2013, 28, 1122–1131. [Google Scholar] [CrossRef]
- Mouli, G.R.C.; Kaptein, J.; Bauer, P.; Zeman, M. Implementation of dynamic charging and V2G using Chademo and CCS/Combo DC charging standard. In Proceedings of the 2016 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 27–29 June 2016; pp. 1–6. [Google Scholar]
- Fadlullah, Z.M.; Quan, D.M.; Kato, N.; Stojmenovic, I. GTES: An optimized game-theoretic demand-side management scheme for smart grid. IEEE Syst. J. 2014, 8, 588–597. [Google Scholar] [CrossRef]
- Geng, B.; Mills, J.K.; Sun, D. Two-stage charging strategy for plug-in electric vehicles at the residential transformer level. IEEE Trans. Smart Grid 2013, 4, 1442–1452. [Google Scholar] [CrossRef]
- Han, S.; Han, S.; Sezaki, K. Development of an optimal vehicle-to-grid aggregator for frequency regulation. IEEE Trans. Smart Grid 2010, 1, 65–72. [Google Scholar]
- Tan, J.; Wang, L. Integration of plug-in hybrid electric vehicles into residential distribution grid based on two-layer intelligent optimization. IEEE Trans. Smart Grid 2014, 5, 1774–1784. [Google Scholar] [CrossRef]
- Negarestani, S.; Fotuhi-Firuzabad, M.; Rastegar, M.; Rajabi-Ghahnavieh, A. Optimal sizing of storage system in a fast charging station for plug-in hybrid electric vehicles. IEEE Trans. Transp. Electrif. 2016, 2, 443–453. [Google Scholar] [CrossRef]
- Richardson, P.; Flynn, D.; Keane, A. Impact assessment of varying penetrations of electric vehicles on low voltage distribution systems. In Proceedings of the IEEE PES General Meeting, Providence, RI, USA, 25–29 July 2010; pp. 1–6. [Google Scholar]
- Al-Ogaili, A.S.; Hashim, T.J.T.; Rahmat, N.A.; Ramasamy, A.K.; Marsadek, M.B.; Faisal, M.; Hannan, M.A. Review on scheduling, clustering, and forecasting strategies for controlling electric vehicle charging: Challenges and recommendations. IEEE Access 2019, 7, 128353–128371. [Google Scholar] [CrossRef]
- Hou, K.; Xu, X.; Jia, H.; Yu, X.; Jiang, T.; Zhang, K.; Shu, B. A Reliability Assessment Approach for Integrated Transportation and Electrical Power Systems Incorporating Electric Vehicles. IEEE Trans. Smart Grid 2018, 9, 88–100. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhu, Y.; Wang, Z.; Su, Y.; Li, C. Reliability Assessment of Distribution Network and Electric Vehicle Considering Quasi-Dynamic Traffic Flow and Vehicle-to-Grid. IEEE Access 2019, 7, 131201–131213. [Google Scholar] [CrossRef]
- Farzin, H.; Moeini-Aghtaie, M.; Fotuhi-Firuzabad, M. Reliability studies of distribution systems integrated with electric vehicles under battery-exchange mode. IEEE Trans. Power Del. 2016, 31, 2473–2482. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, M.; Zeng, B.; Wu, L.; Zhang, J. Analyzing the impacts of electric vehicle charging on distribution system reliability. In Proceedings of the IEEE PES Innovative Smart Grid Technologies, Tianjin, China, 21–24 May 2012; pp. 1–6. [Google Scholar]
- Mozafar, M.R.; Amini, M.H.; Moradi, M.H. Innovative appraisement of smart grid operation considering large-scale integration of electric vehicles enabling V2G and G2V systems. Electr. Power Syst. Res. 2018, 154, 245–256. [Google Scholar] [CrossRef]
- Xu, N.Z.; Chung, C.Y. Reliability evaluation of distribution sys-tems including vehicle-to-home and vehicle-to-grid. IEEE Trans. Power Syst. 2016, 31, 759–768. [Google Scholar] [CrossRef]
- Kamruzzaman, M.; Benidris, M. Reliability-Based Metrics to Quantify the Maximum Permissible Load Demand of Electric Vehicles. IEEE Trans. Ind. Appl. 2019, 55, 3365–3375. [Google Scholar] [CrossRef]
- Rana, R.; Prakash, S.; Mishra, S. Energy management of electric vehicle integrated home in a time-of-day regime. IEEE Trans. Transp. Electrif. 2018, 4, 804–816. [Google Scholar] [CrossRef]
- Cheng, L.; Chang, Y.; Lin, J.; Singh, C. Power system reliability assessment with electric vehicle integration using battery exchange mode. IEEE Trans. Sustain. Energy 2013, 4, 1034–1042. [Google Scholar] [CrossRef]
- Cheng, L.; Chang, Y.; Wu, Q.; Lin, W.; Singh, C. Evaluating charging service reliability for plug-in EVs from the distribution network aspect. IEEE Trans. Sustain. Energy 2014, 5, 1287–1296. [Google Scholar] [CrossRef]
- Xu, N.Z.; Chung, C.Y. Well-being analysis of generating systems considering electric vehicle charging. IEEE Trans. Power Syst. 2014, 29, 2311–2320. [Google Scholar] [CrossRef]
- Department of Transportation. National Travel Survey 2009; Department of Transportation: London, UK, 2009.
- Shojaei, S.; McGordon, A.; Robinson, S.; Marco, J. Improving the performance attributes of plug-in hybrid electric vehicles in hot climates through key-off battery cooling. Energies 2017, 10, 2058. [Google Scholar] [CrossRef] [Green Version]
- Neubauer, J.; Wood, E. Thru-life impacts of driver aggression, climate, cabin thermal management, and battery thermal management on battery electric vehicle utility. J. Power Sources 2014, 259, 262–275. [Google Scholar] [CrossRef]
- Guan, T.; Sun, S.; Gao, Y.; Du, C.; Zuo, P.; Cui, Y.; Zhang, L.; Yin, G. The effect of elevated temperature on the accelerated aging of LiCoO2/mesocarbon microbeads batteries. Appl. Energy 2016, 177, 1–10. [Google Scholar] [CrossRef]
- Mukherjee, J.C.; Gupta, A. A review of charge scheduling of electric vehicles in smart grid. IEEE Syst. J. 2015, 9, 1541–1553. [Google Scholar] [CrossRef]
- Wu, D.; Ke, X.; Radhakrishnan, N.; Reiman, A. Optimization methods for evaluating PEV charging considering customer behavior. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018; pp. 1–5. [Google Scholar]
- Kisacikoglu, M.C.; Kesler, M.; Tolbert, L.M. Single-phase on-board bidirectional PEV charger for V2G reactive power operation. IEEE Trans. Smart Grid 2015, 6, 767–775. [Google Scholar] [CrossRef]
- Yusuf, J.; Ula, S. Impact of building loads on cost optimization strategy for a plug-in electric vehicle operation. In Proceedings of the 2019 IEEE Transportation Electrification Conference and Expo (ITEC), Detroit, MI, USA, 19–21 June 2019; pp. 1–5. [Google Scholar]
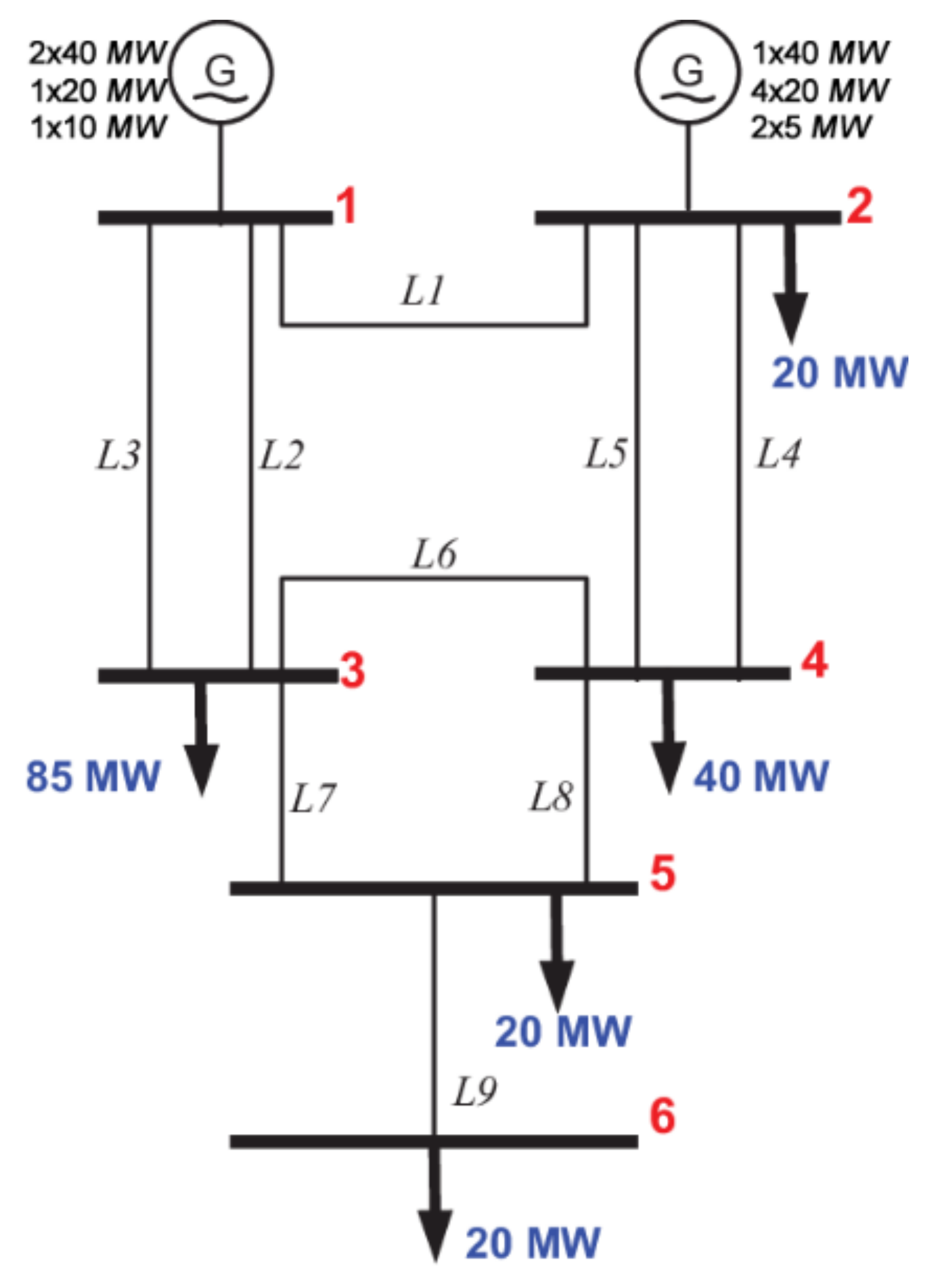
- Bertling, L.; Bangalore, P.; Tuan, L.A. On the use of reliability test systems: A literature survey. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011. [Google Scholar]


| Purpose | Purpose | ||
|---|---|---|---|
| 1 | Commuting | 6 | Business |
| 2 | Education | 7 | Escort education |
| 3 | Shopping | 8 | Other escort and personal business |
| 4 | Visit friends | 9 | Holiday trip |
| 5 | Day trip | 10 | Others (entertainment, public activity, etc.) |
| Fitted pdf | Parameters | Fitted pdf | Parameters | ||||
|---|---|---|---|---|---|---|---|
| 1 | Lognormal | 3.27 | = 1.02 | 6 | Lognormal | 3.02 | = 1.32 |
| 2 | Weibull | = 111.75 | = 1.27 | 7 | Weibull | = 83.81 | = 0.93 |
| 3 | Lognormal | 2.48 | = 1.16 | 8 | Weibull | = 176.47 | = 2.67 |
| 4 | Lognormal | 2.16 | = 1.38 | 9 | Weibull | = 79.63 | = 1.19 |
| 5 | Lognormal | 2.76 | = 1.18 | 10 | Lognormal | 3.42 | = 1.29 |
| BEV Penetration | Reliability Indices | Charger Rating = 7.2 kW | Charger Rating = 9.6 kW | ||||
|---|---|---|---|---|---|---|---|
| Uncontrolled | Unidirectional | Bidirectional | Uncontrolled | Unidirectional | Bidirectional | ||
| 0 % | LOLE (h/yr) | 1.0562 | |||||
| LOEE (MWh/yr) | 9.7788 | ||||||
| LOLF (int./yr) | 0.2078 | ||||||
| ENSPI (MWh/int.) | 47.058 | ||||||
| SAIFI (int./cu.) | 0.1154 | ||||||
| SAIDI (h/cu.) | 0.5283 | ||||||
| 20% | LOLE (h/yr) | 1.7882 | 1.88 | 0.8818 | 1.8728 | 1.96 | 0.884 |
| LOEE (MWh/yr) | 17.3736 | 10.8958 | 6.5947 | 18.046 | 11.1448 | 6.1485 | |
| LOLF (int./yr) | 0.4352 | 0.4228 | 0.1974 | 0.4538 | 0.4482 | 0.2138 | |
| ENSPI (MWh/int.) | 39.9209 | 25.7706 | 33.4076 | 39.7663 | 24.8657 | 28.75 | |
| SAIFI (int./cu.) | 0.2489 | 0.136 | 0.0706 | 0.2473 | 0.1392 | 0.0668 | |
| SAIDI (h/cu.) | 0.9391 | 0.589 | 0.3565 | 0.9755 | 0.6024 | 0.3323 | |
| 40% | LOLE (h/yr) | 2.9652 | 3.209 | 1.11 | 3.1912 | 3.4398 | 1.1558 |
| LOEE (MWh/yr) | 32.265 | 13.1856 | 5.3179 | 34.6965 | 14.2084 | 4.929 | |
| LOLF (int./yr) | 0.8222 | 0.8170 | 0.3706 | 0.8122 | 0.8204 | 0.4134 | |
| ENSPI (MWh/int.) | 39.243 | 16.139 | 14.3495 | 42.7191 | 17.3189 | 11.923 | |
| SAIFI (int./cu.) | 0.5249 | 0.1823 | 0.0627 | 0.5105 | 0.1973 | 0.0624 | |
| SAIDI (h/cu.) | 1.7441 | 0.7127 | 0.2875 | 1.8775 | 0.768 | 0.2664 | |
| 60% | LOLE (h/yr) | 5.9982 | 6.26 | 1.581 | 6.7096 | 6.9426 | 1.6984 |
| LOEE (MWh/yr) | 63.3742 | 18.468 | 4.8154 | 70.3812 | 21.535 | 4.6879 | |
| LOLF (int./yr) | 2.016 | 2.014 | 0.7138 | 2.0284 | 2.0622 | 0.779 | |
| ENSPI (MWh/int.) | 31.4356 | 9.1698 | 6.7461 | 34.6979 | 10.4427 | 6.0178 | |
| SAIFI (int./cu.) | 1.2168 | 0.3149 | 0.0655 | 1.1635 | 0.3664 | 0.0722 | |
| SAIDI (h/cu.) | 3.4256 | 0.9983 | 0.2603 | 3.8044 | 1.1641 | 0.2534 | |
| Base Case | 20% Increase in MTTR | 20% Decrease in MTTR | 20% Increase in MTTF | 20% Decrease in MTTF | 20% Increase in MTTR & MTTF | 20% Decrease in MTTR & MTTF | |
|---|---|---|---|---|---|---|---|
| LOLE | 1.0562 | 1.6780 | 0.6166 | 0.5854 | 1.7692 | 1.0178 | 0.9846 |
| LOEE | 9.7788 | 15.4054 | 5.0921 | 4.5251 | 16.6511 | 9.037 | 9.6237 |
| LOLF | 0.2078 | 0.3240 | 0.1328 | 0.1282 | 0.3500 | 0.202 | 0.2006 |
| ENSPI | 47.058 | 47.5475 | 38.3433 | 35.2971 | 47.5745 | 44.7376 | 47.9745 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mokhtar, M.; Shaaban, M.F.; Ismail, M.H.; Sindi, H.F.; Rawa, M. Reliability Assessment under High Penetration of EVs including V2G Strategy. Energies 2022, 15, 1585. https://doi.org/10.3390/en15041585
Mokhtar M, Shaaban MF, Ismail MH, Sindi HF, Rawa M. Reliability Assessment under High Penetration of EVs including V2G Strategy. Energies. 2022; 15(4):1585. https://doi.org/10.3390/en15041585
Chicago/Turabian StyleMokhtar, Mohamed, Mostafa F. Shaaban, Mahmoud H. Ismail, Hatem F. Sindi, and Muhyaddin Rawa. 2022. "Reliability Assessment under High Penetration of EVs including V2G Strategy" Energies 15, no. 4: 1585. https://doi.org/10.3390/en15041585
APA StyleMokhtar, M., Shaaban, M. F., Ismail, M. H., Sindi, H. F., & Rawa, M. (2022). Reliability Assessment under High Penetration of EVs including V2G Strategy. Energies, 15(4), 1585. https://doi.org/10.3390/en15041585








