Electric Vehicle Battery Storage Concentric Intelligent Home Energy Management System Using Real Life Data Sets
Abstract
:1. Introduction
2. State of the Art Literature Review
Our Contribution
- 1.
- Most significantly, this paper is written keeping in view a call from a special issue of Energies on the subject “Demand Side Management of Distributed and Uncertain Flexibilities”, utilizing real-life yearly data sets of household demands, EV driving patterns, and EV battery (dis)charging patterns to demonstrate the actual iEMS capabilities of the proposed system model. To the best of our knowledge, this is the first paper written introducing energy management system strategy by utilizing the above mentioned explicit data sets.
- 2.
- Introducing a comprehensive converter-based nanogrid model. This model combines real-world data sets and operating limitations for conventional and renewable energy power sources. The model also includes lifespan deterioration of the EV storage’s capacity given in Appendix B. Data sets are re-processed (i.e., Appendix A) to be used in MATLAB.
- 3.
- Adopting a two-stage co-simulation framework to implement a multi-time scale iEMS and control strategy. A robust decision-based operation strategy is proposed to utilize the least expensive energy supply sources and to maximize the consumer’s satisfaction level.
- 4.
- Proposing a computationally efficient mixed integer rule-based sliding horizon dynamical algorithm to tackle the prediction uncertainties and to make cost effective scheduling decisions for supply sources. In addition, comparing daily and seasonal scheduling decisions for various supply sources in the first stage.
3. System Architecture
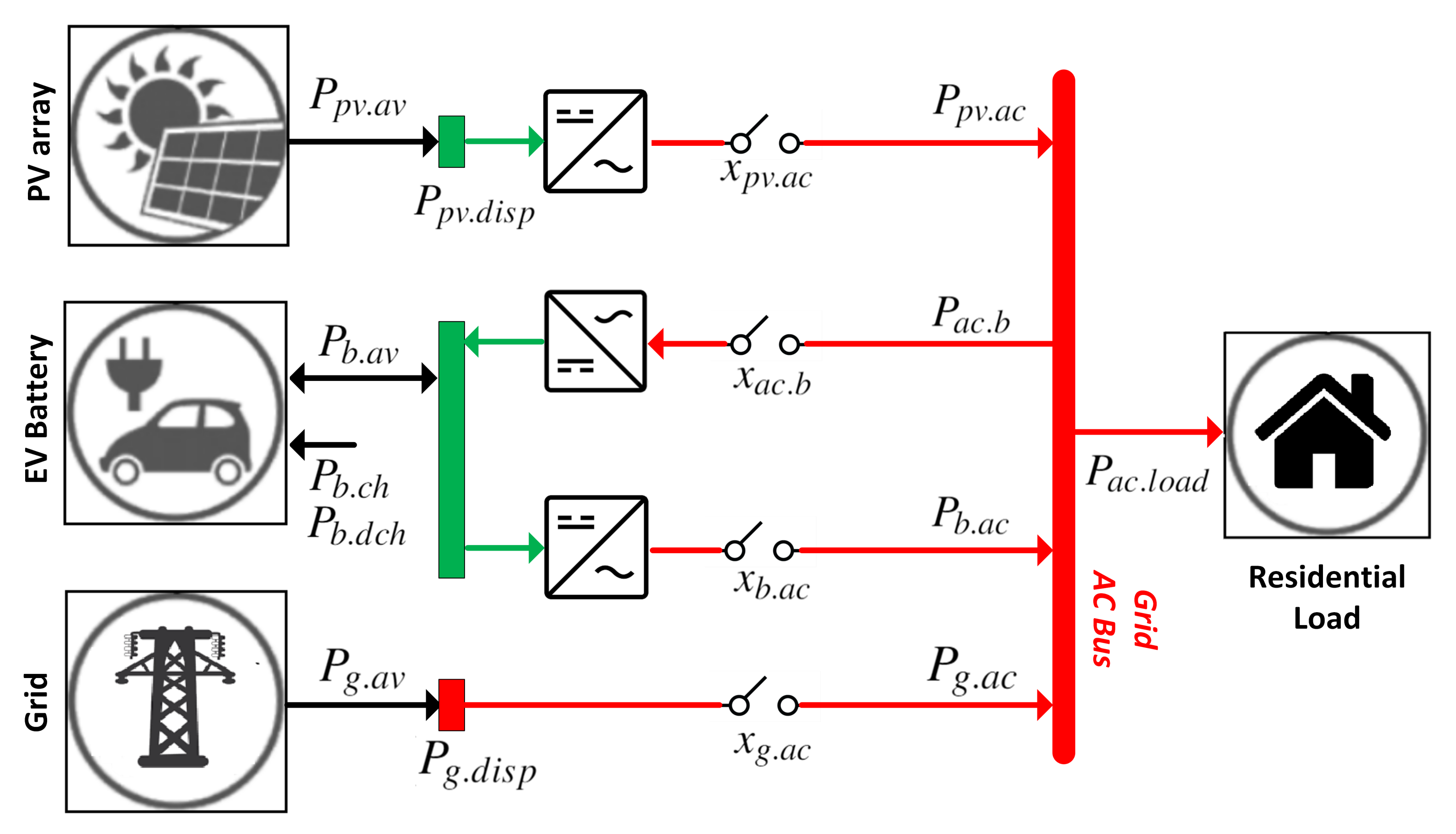
3.1. Home Area Power Network Architecture
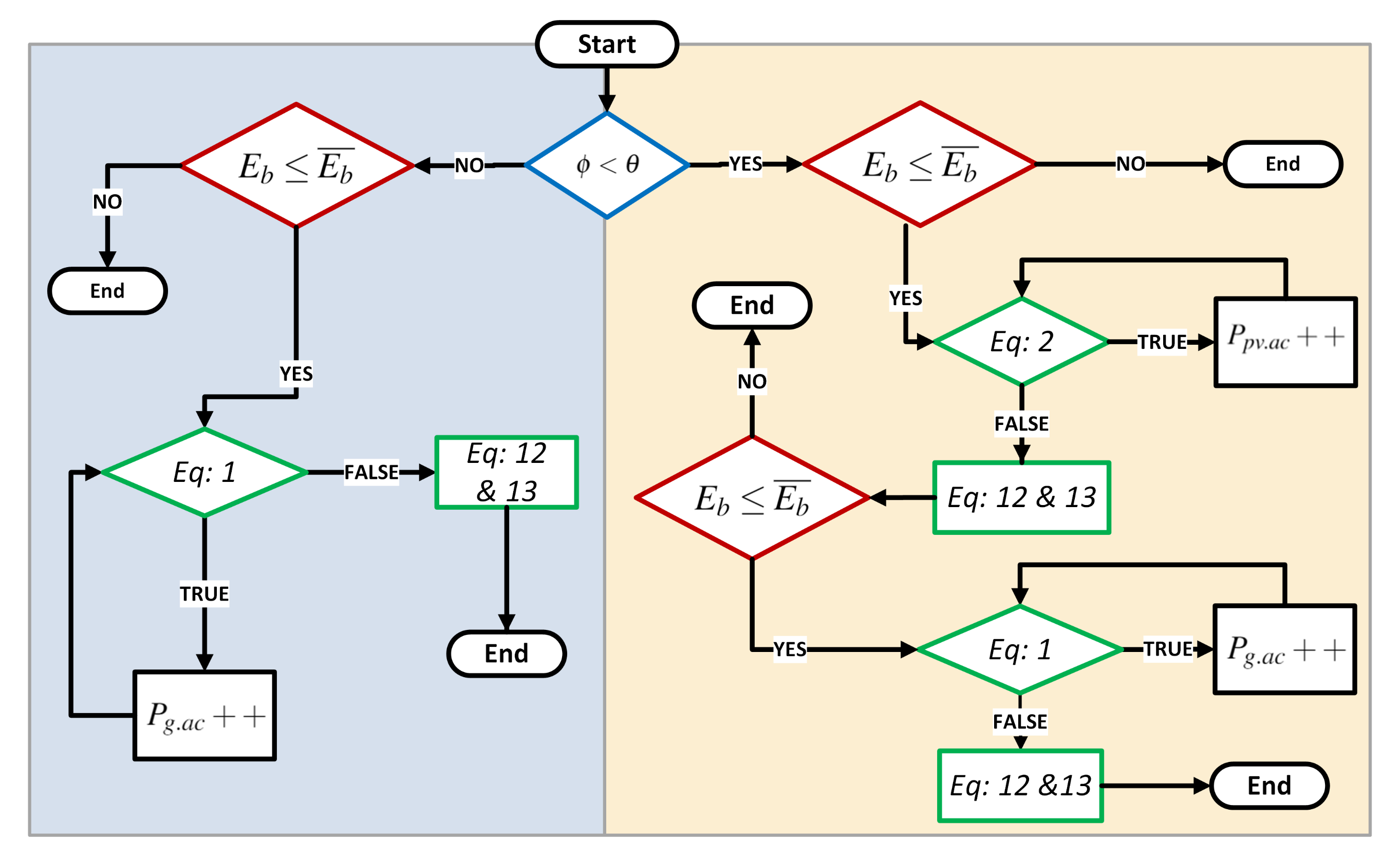
3.2. Battery Degradation Model
3.3. Entities Cost Modeling
4. Problem Formulation & Numerical Solution
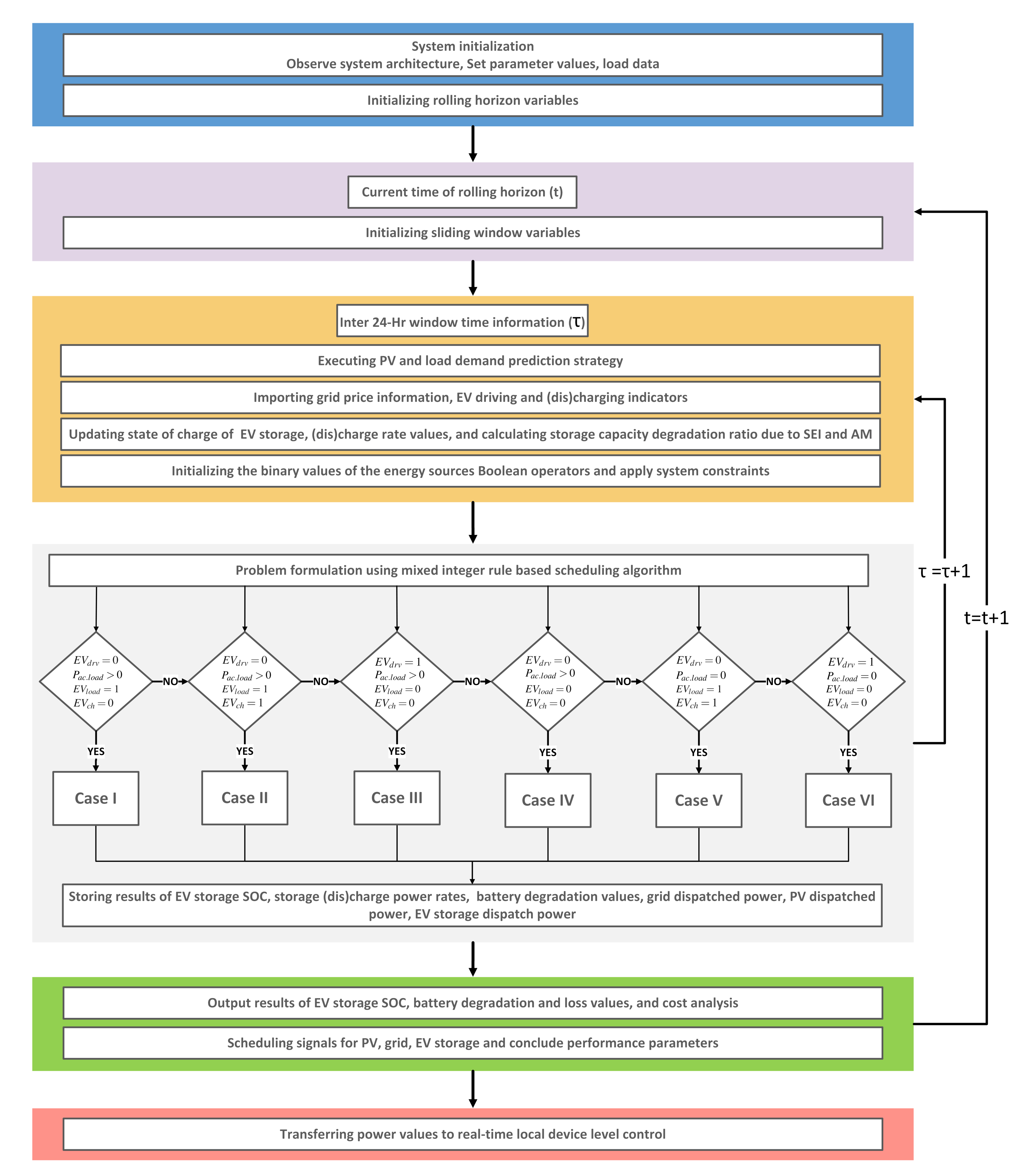
4.1. Algorithms and Implementation
- 1.
- Scheme 1: Conventional rule-based strategy involves only the EV storage and grid energy supply (Conv-EG).
- 2.
- Scheme 2: Conventional model predictive rule-based strategy involves PV supply along with EV storage and grid energy supply (Conv-PEG).
- 3.
- Scheme 3: Proposed Model predictive intelligent energy management system (MP-iEMS).
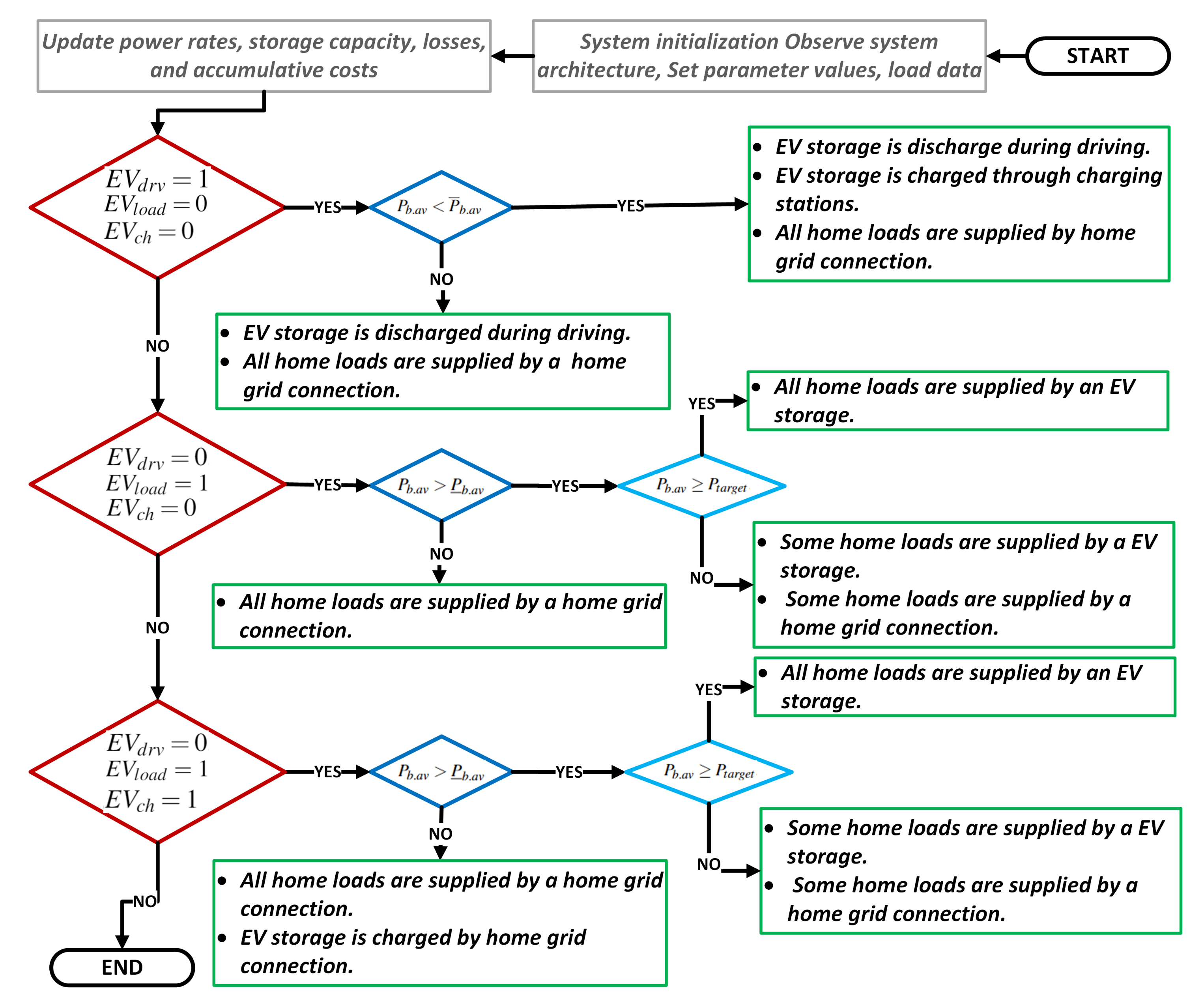
4.1.1. Scheme 1: Conv-EG
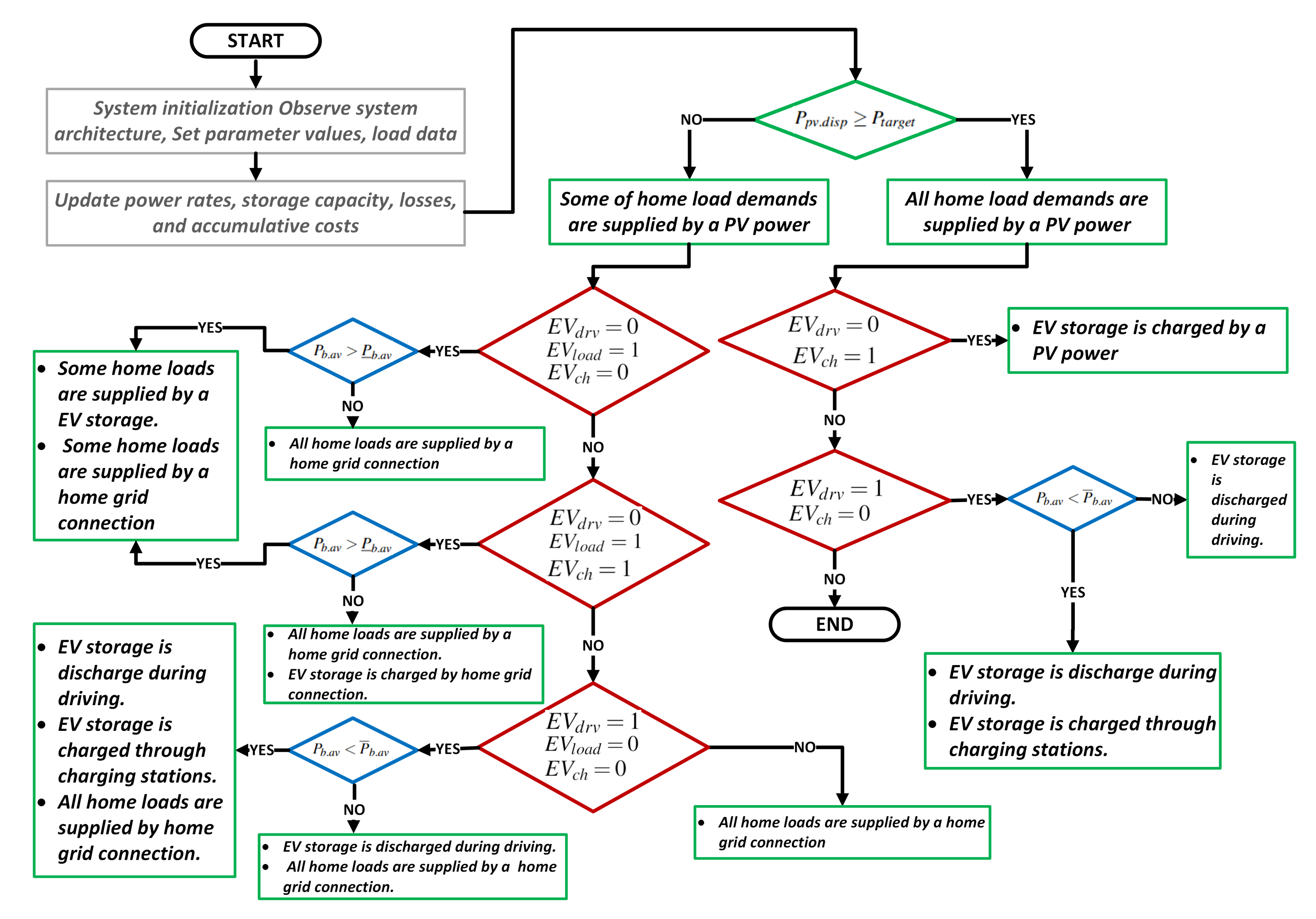
4.1.2. Scheme 2: Conv-PEG
4.1.3. Scheme 3: MP-iEMS
- 1.
- Case 1: & & & :
- 2.
- Case 2: & & & :
- 3.
- Case 3: & & & :
- 4.
- Case 4: & & & :
- 5.
- Case 5: & & & :
- 6.
- Case 6: & & & :
Case I
Case II
Case III
Case IV
Case V
Case VI
4.2. Evaluation Indices
PV Utilization Factor ()
PV Penetration Level ()
Grid Utilization Factor ()
Grid Penetration Level ()
EV Storage Utilization Factor ()
EV Storage Penetration Level ()
Degree of Self-Sufficiency ()
5. Case Study & Simulation Results
5.1. Data Preparation
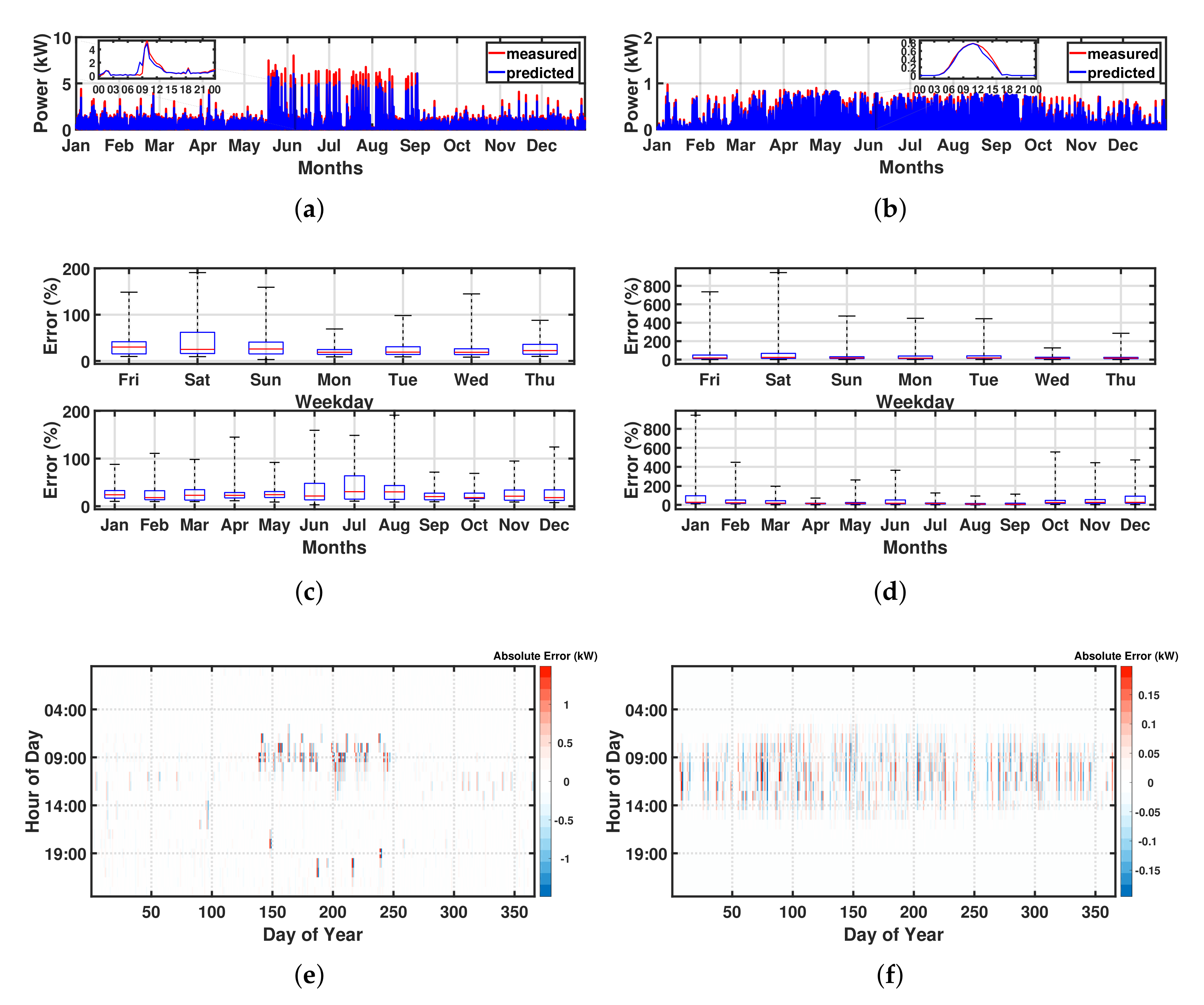
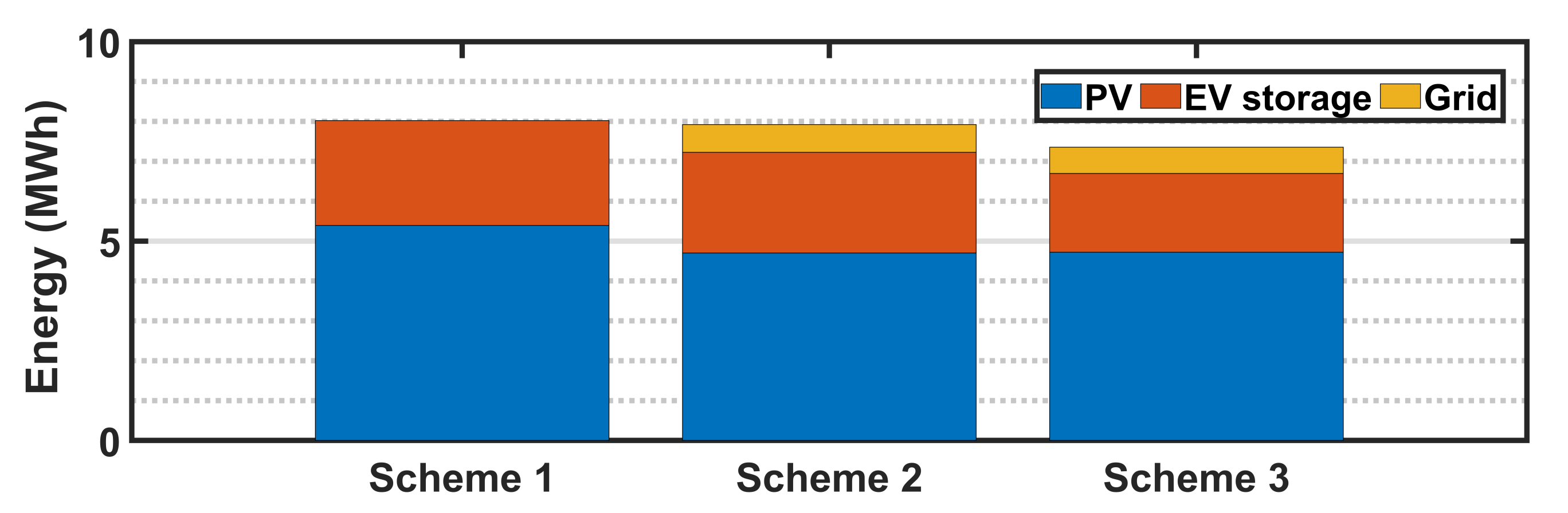
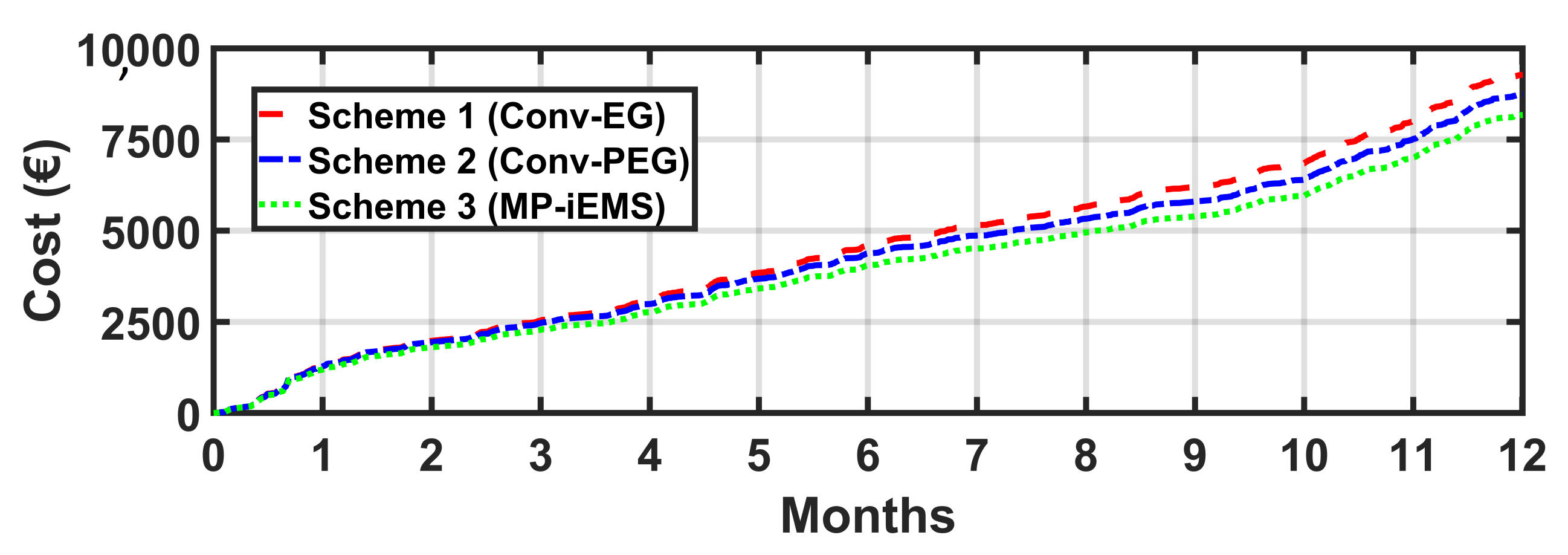
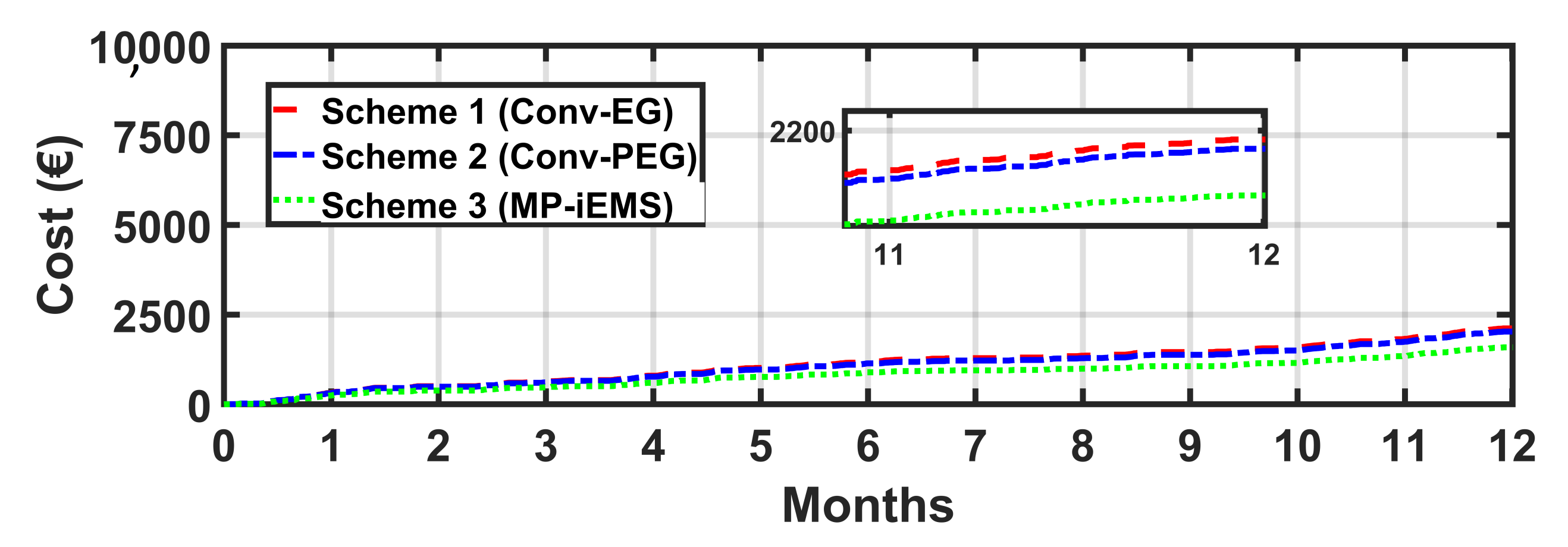
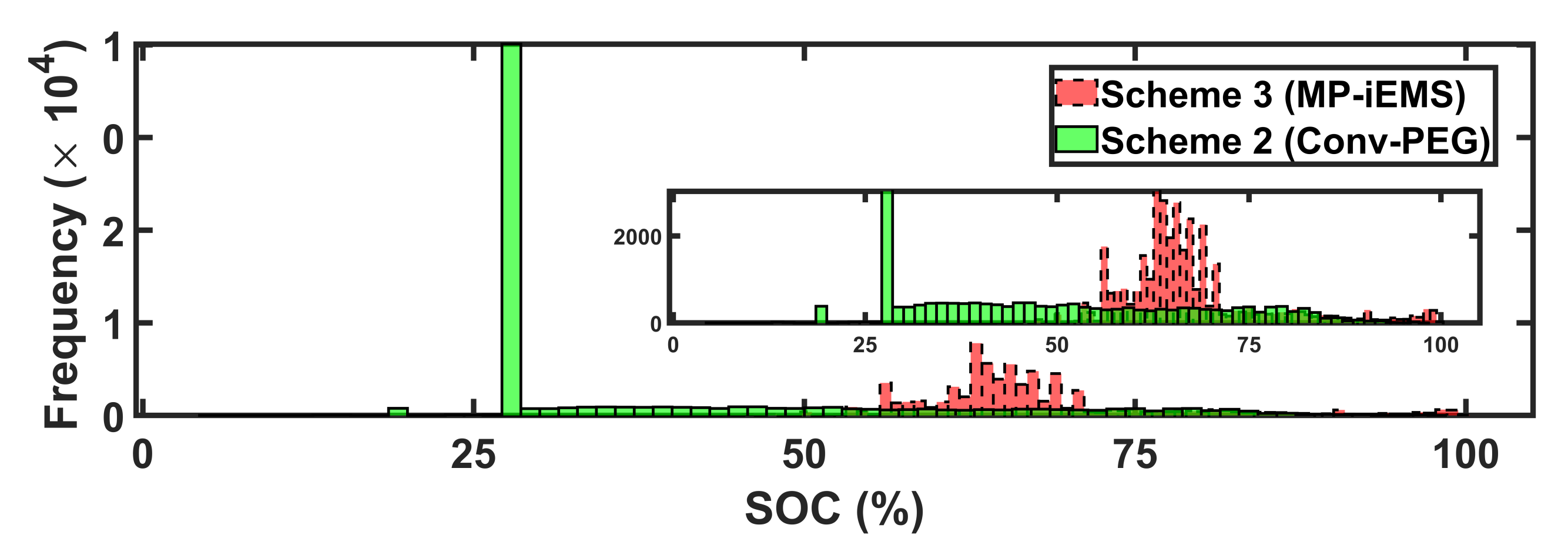
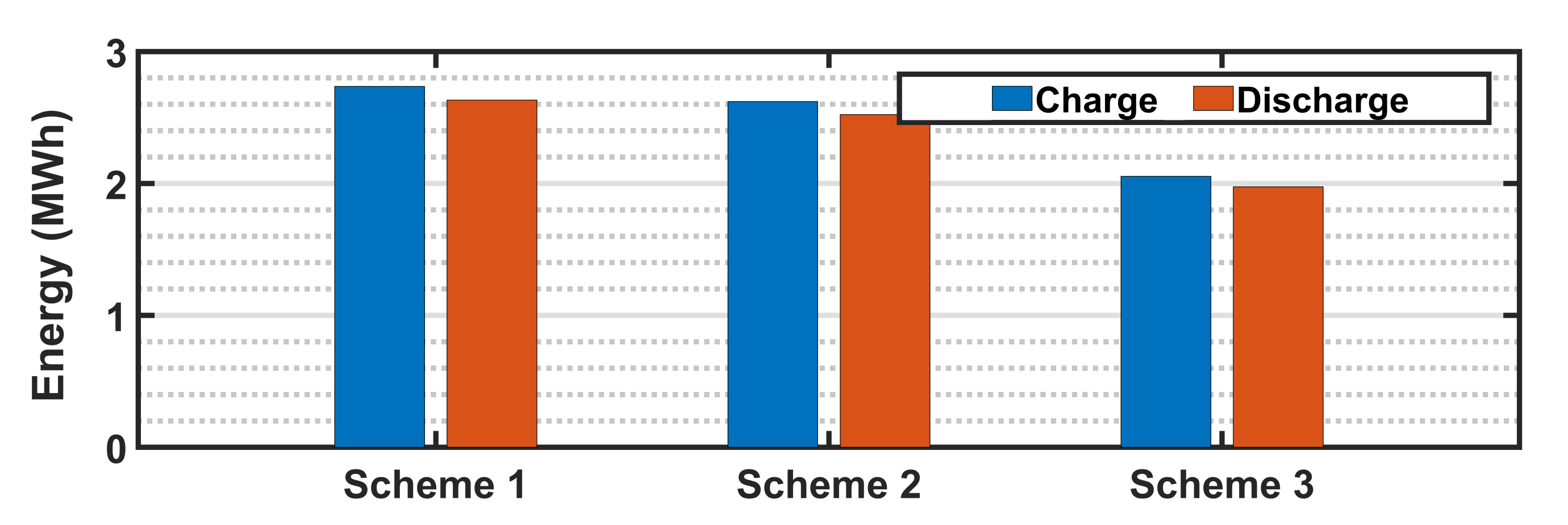
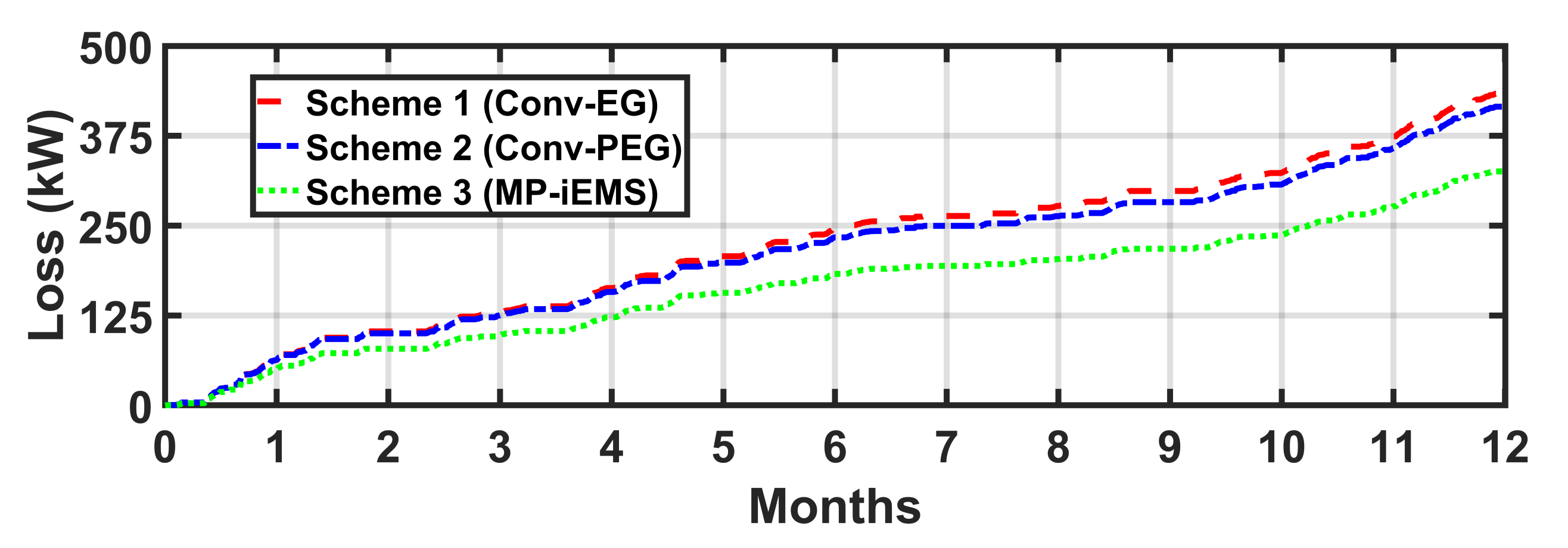
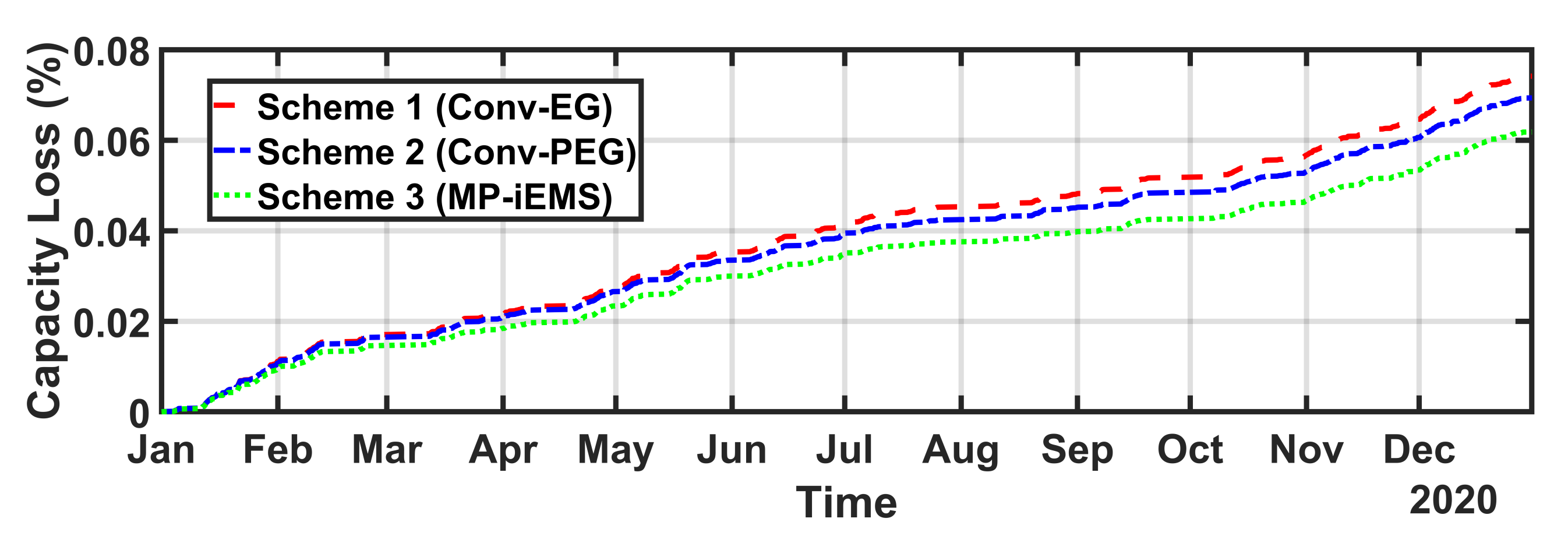
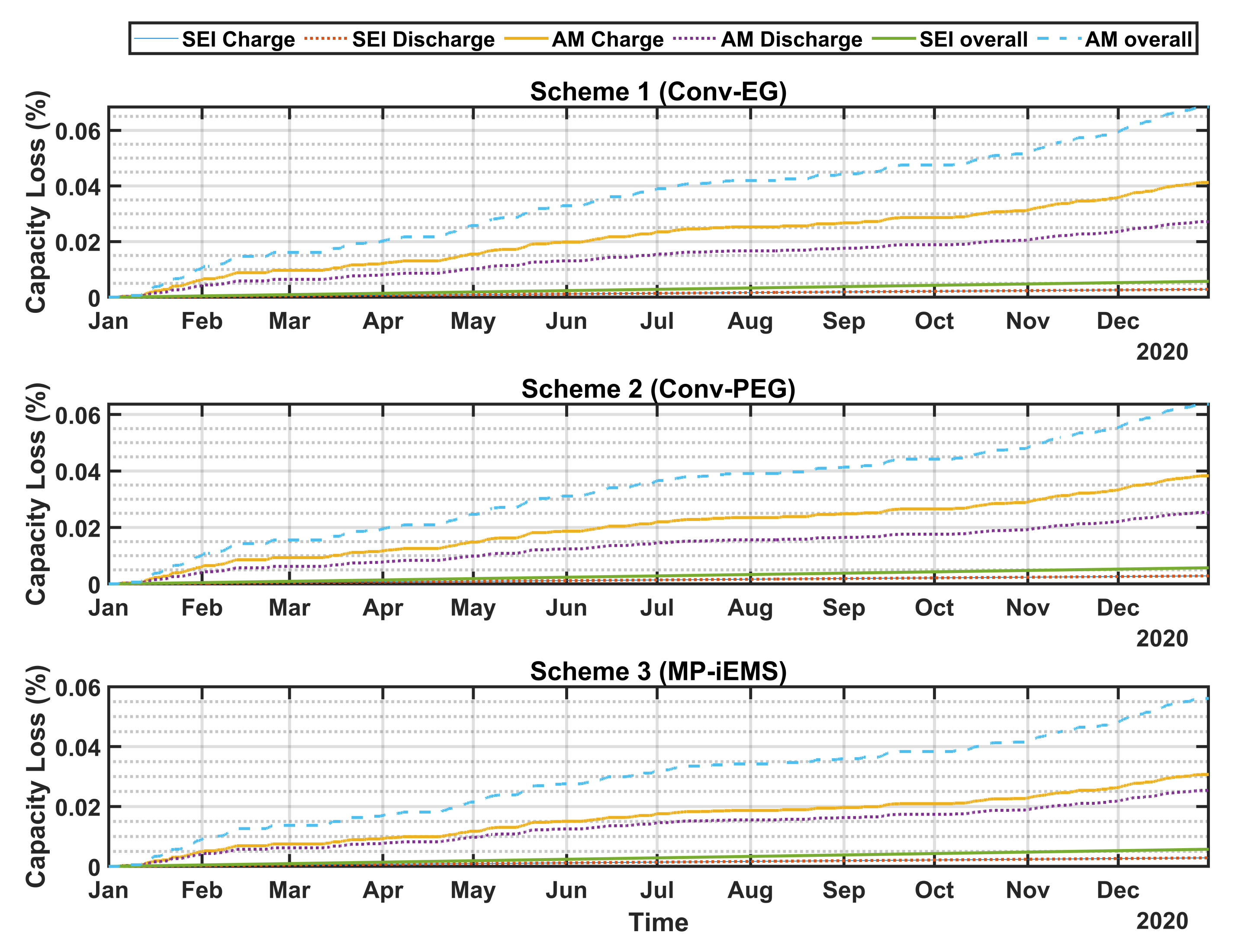
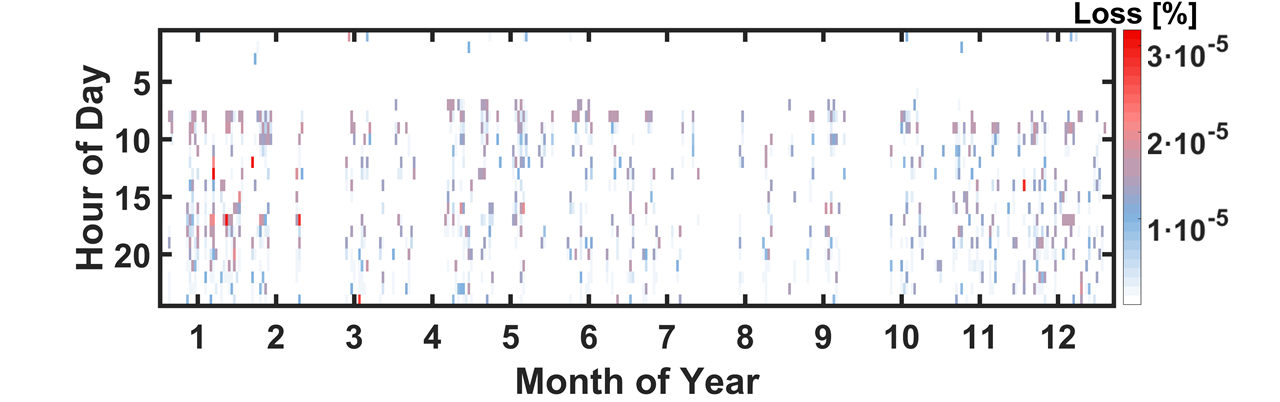
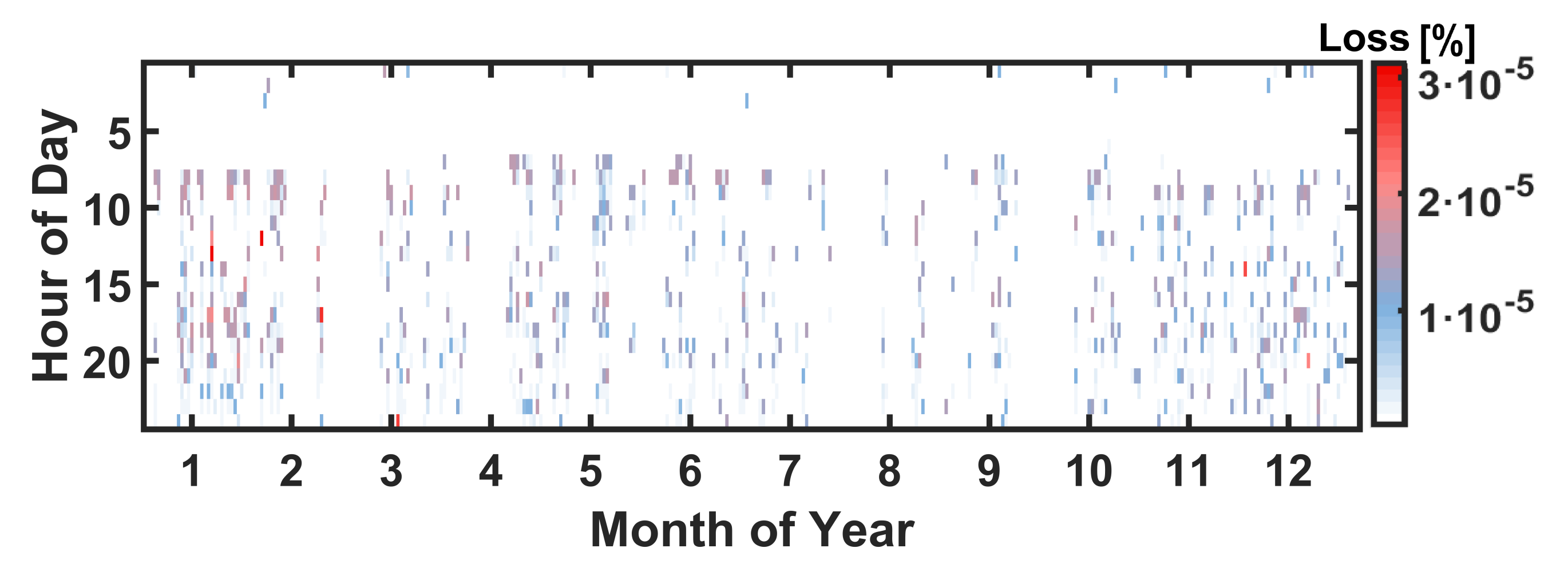
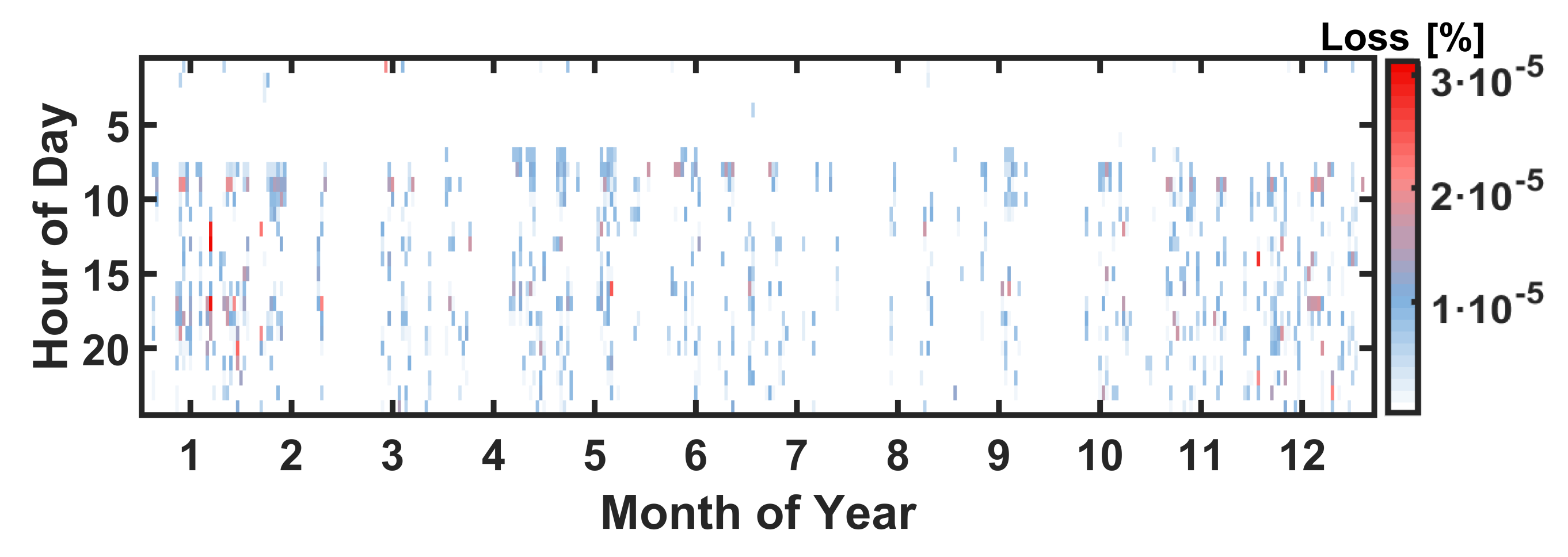
5.2. Comparative Analysis of Power Scheduling Schemes
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Data Preparation

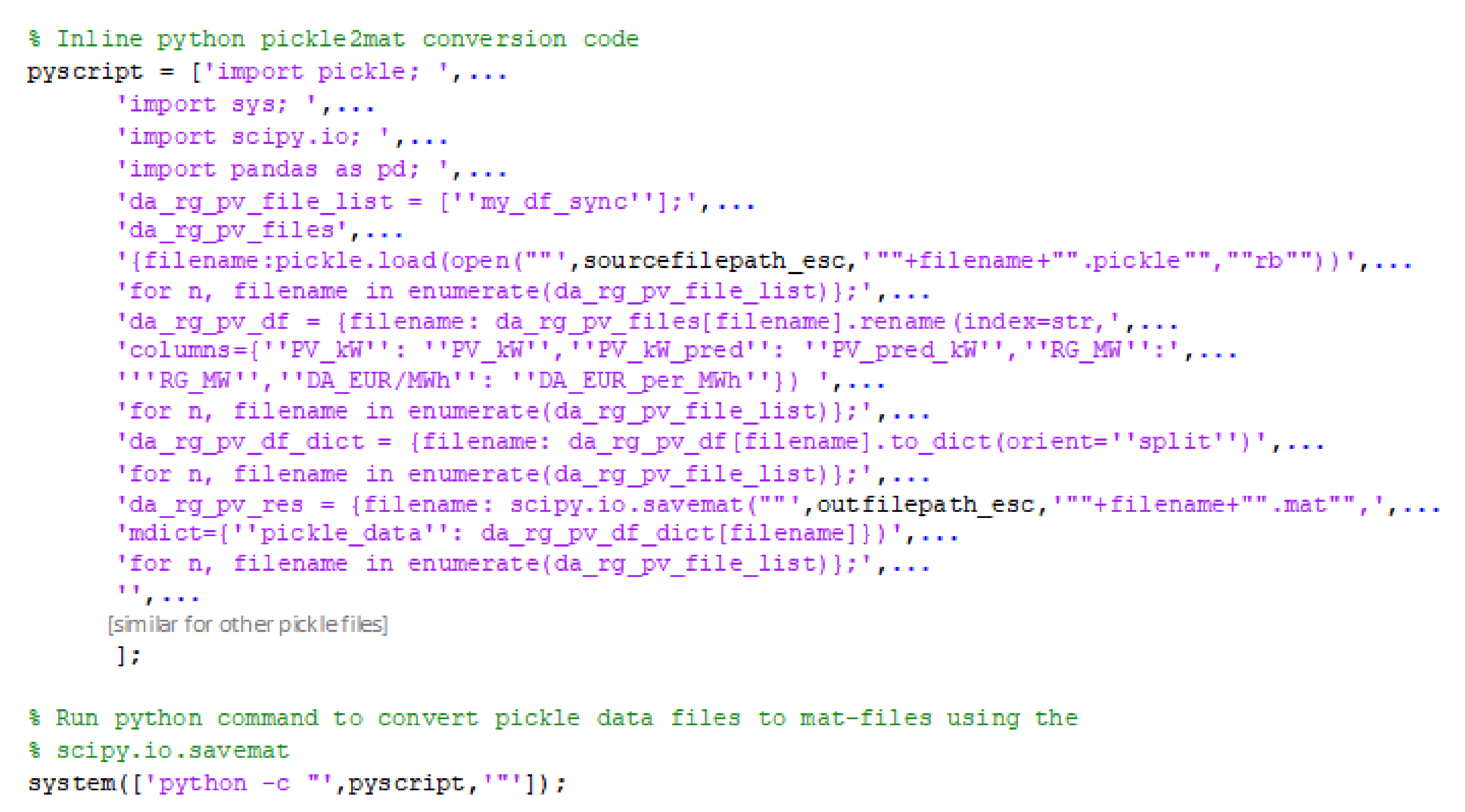
- Fast charging between 0–35% of SOC and;
- Decreased charging between 35–100% of SOC.
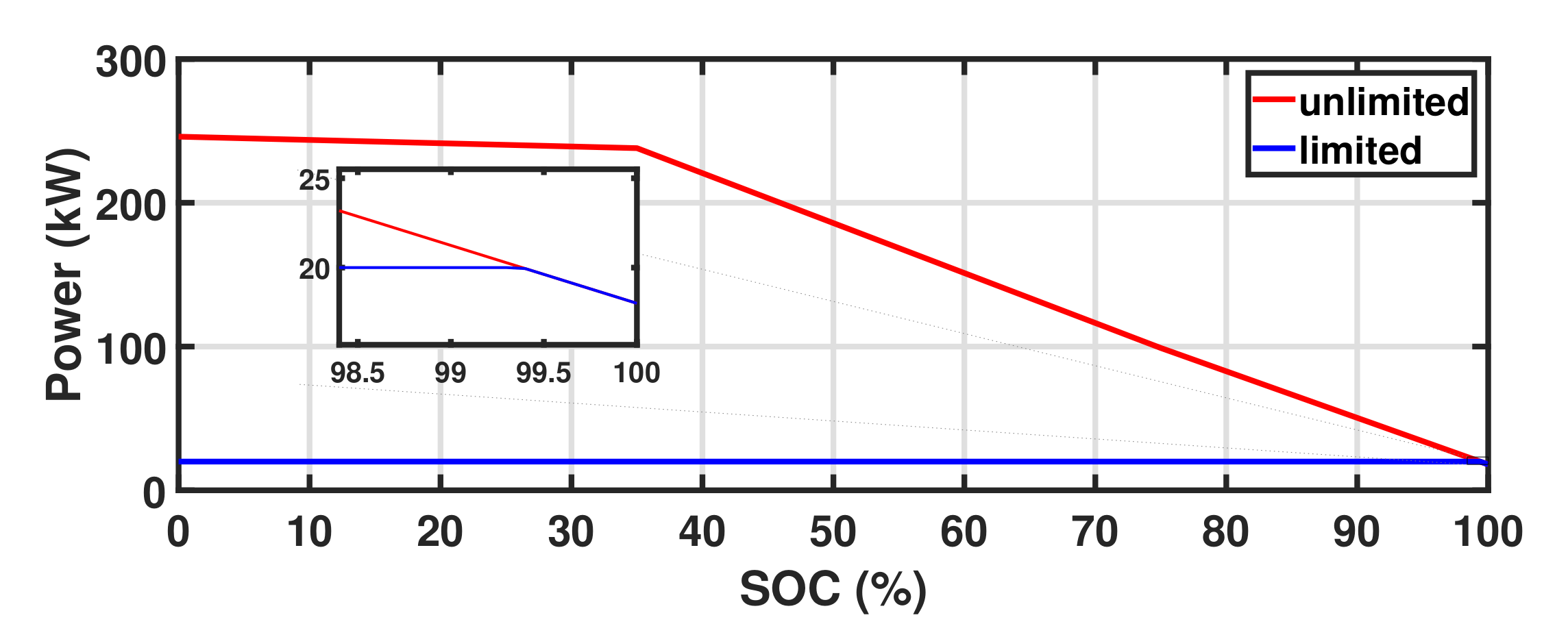
Appendix B. Battery Degradation Model
References
- U.S. Energy Information Administration. An Assessment of Energy Technologies and Research Opportunities. In Energy Inf. Adm.; 2020. Available online: www.eia.gov/tools/faqs/faq.php?id=86&t=1 (accessed on 15 January 2022).
- Javaid, N.; Hafeez, G.; Iqbal, S.; Alrajeh, N.; Alabed, M.S.; Guizani, M. Energy Efficient Integration of Renewable Energy Sources in the Smart Grid for Demand Side Management. IEEE Access 2018, 6, 77077–77096. [Google Scholar] [CrossRef]
- Ryu, K.S.; Kim, D.J.; Ko, H.; Boo, C.J.; Kim, J.; Jin, Y.G.; Kim, H.C. MPC Based Energy Management System for Hosting Capacity of PVs and Customer Load with EV in Stand-Alone Microgrids. Energies 2021, 14, 4041. [Google Scholar] [CrossRef]
- Li, T.; Dong, M. Residential Energy Storage Management With Bidirectional Energy Control. IEEE Trans. Smart Grid 2019, 10, 3596–3611. [Google Scholar] [CrossRef] [Green Version]
- Burmester, D.; Rayudu, R.; Seah, W.; Akinyele, D. A review of nanogrid topologies and technologies. Renew. Sustain. Energy Rev. 2017, 67, 760–775. [Google Scholar] [CrossRef]
- Minhas, D.M.; Frey, G. Rolling Horizon Based Time-Triggered Distributed Control for AC/DC Home Area Power Network. IEEE Trans. Ind. Appl. 2021, 57, 4021–4032. [Google Scholar] [CrossRef]
- Betancur, D.; Duarte, L.F.; Revollo, J.; Restrepo, C.; Díez, A.E.; Isaac, I.A.; López, G.J.; González, J.W. Methodology to Evaluate the Impact of Electric Vehicles on Electrical Networks Using Monte Carlo. Energies 2021, 14, 1300. [Google Scholar] [CrossRef]
- Elmeligy, M.M.; Shaaban, M.F.; Azab, A.; Azzouz, M.A.; Mokhtar, M. A Mobile Energy Storage Unit Serving Multiple EV Charging Stations. Energies 2021, 14, 2969. [Google Scholar] [CrossRef]
- Yoo, Y.; Al-Shawesh, Y.; Tchagang, A. Coordinated Control Strategy and Validation of Vehicle-to-Grid for Frequency Control. Energies 2021, 14, 2530. [Google Scholar] [CrossRef]
- Minhas, D.M.; Frey, G. Modeling and Optimizing Energy Supply and Demand in Home Area Power Network (HAPN). IEEE Access 2020, 8, 2052–2072. [Google Scholar] [CrossRef]
- Ran, X.; Leng, S. Enhanced Robust Index Model for Load Scheduling of a Home Energy Local Network With a Load Shifting Strategy. IEEE Access 2019, 7, 19943–19953. [Google Scholar] [CrossRef]
- Ali, A.Y.; Hussain, A.; Baek, J.W.; Kim, H.M. Optimal Operation of Networked Microgrids for Enhancing Resilience Using Mobile Electric Vehicles. Energies 2021, 14, 142. [Google Scholar] [CrossRef]
- Liao, J.T.; Huang, H.W.; Yang, H.T.; Li, D. Decentralized V2G/G2V Scheduling of EV Charging Stations by Considering the Conversion Efficiency of Bidirectional Chargers. Energies 2021, 14, 962. [Google Scholar] [CrossRef]
- Ustun, T.S.; Hussain, S.M.S.; Kikusato, H. IEC 61850-Based Communication Modeling of EV Charge-Discharge Management for Maximum PV Generation. IEEE Access 2019, 7, 4219–4231. [Google Scholar] [CrossRef]
- Abdalla, M.A.A.; Min, W.; Mohammed, O.A.A. Two-Stage Energy Management Strategy of EV and PV Integrated Smart Home to Minimize Electricity Cost and Flatten Power Load Profile. Energies 2020, 13, 6387. [Google Scholar] [CrossRef]
- Wu, J.; Wei, Z.; Li, W.; Wang, Y.; Li, Y.; Sauer, D.U. Battery Thermal- and Health-Constrained Energy Management for Hybrid Electric Bus Based on Soft Actor-Critic DRL Algorithm. IEEE Trans. Ind. Inform. 2021, 17, 3751–3761. [Google Scholar] [CrossRef]
- Zeiselmair, A.; Köppl, S. Constrained Optimization as the Allocation Method in Local Flexibility Markets. Energies 2021, 14, 3932. [Google Scholar] [CrossRef]
- Khan, S.U.; Mehmood, K.K.; Haider, Z.M.; Rafique, M.K.; Khan, M.O.; Kim, C.H. Coordination of Multiple Electric Vehicle Aggregators for Peak Shaving and Valley Filling in Distribution Feeders. Energies 2021, 14, 352. [Google Scholar] [CrossRef]
- Nishimwe H., H.L.F.; Yoon, S.-G. Combined Optimal Planning and Operation of a Fast EV-Charging Station Integrated with Solar PV and ESS. Energies 2021, 14, 3152. [Google Scholar] [CrossRef]
- Alrumayh, O.; Bhattacharya, K. Flexibility of Residential Loads for Demand Response Provisions in Smart Grid. IEEE Trans. Smart Grid 2019, 10, 6284–6297. [Google Scholar] [CrossRef]
- Zhou, L.; Zhang, Y.; Lin, X.; Li, C.; Cai, Z.; Yang, P. Optimal Sizing of PV and BESS for a Smart Household Considering Different Price Mechanisms. IEEE Access 2018, 6, 41050–41059. [Google Scholar] [CrossRef]
- Ouramdane, O.; Elbouchikhi, E.; Amirat, Y.; Sedgh Gooya, E. Optimal Sizing and Energy Management of Microgrids with Vehicle-to-Grid Technology: A Critical Review and Future Trends. Energies 2021, 14, 4166. [Google Scholar] [CrossRef]
- Salvatti, G.A.; Carati, E.G.; Cardoso, R.; da Costa, J.P.; Stein, C.M.d.O. Electric Vehicles Energy Management with V2G/G2V Multifactor Optimization of Smart Grids. Energies 2020, 13, 1191. [Google Scholar] [CrossRef] [Green Version]
- Yu, L.; Jiang, T.; Zou, Y. Online Energy Management for a Sustainable Smart Home With an HVAC Load and Random Occupancy. IEEE Trans. Smart Grid 2019, 10, 1646–1659. [Google Scholar] [CrossRef] [Green Version]
- Moon, S.; Lee, J. Multi-Residential Demand Response Scheduling With Multi-Class Appliances in Smart Grid. IEEE Trans. Smart Grid 2018, 9, 2518–2528. [Google Scholar] [CrossRef]
- Shahab, M.; Wang, S.; Junejo, A.K. Improved Control Strategy for Three-Phase Microgrid Management with Electric Vehicles Using Multi Objective Optimization Algorithm. Energies 2021, 14, 1146. [Google Scholar] [CrossRef]
- Von Bonin, M.; Dörre, E.; Al-Khzouz, H.; Braun, M.; Zhou, X. Impact of Dynamic Electricity Tariff and Home PV System Incentives on Electric Vehicle Charging Behavior: Study on Potential Grid Implications and Economic Effects for Households. Energies 2022, 15, 1079. [Google Scholar] [CrossRef]
- Al-Quraan, A.; Al-Qaisi, M. Modelling, Design and Control of a Standalone Hybrid PV-Wind Micro-Grid System. Energies 2021, 14, 4849. [Google Scholar] [CrossRef]
- Wang, L.; Wu, Z.; Cao, C. Integrated Optimization of Routing and Energy Management for Electric Vehicles in Delivery Scheduling. Energies 2021, 14, 1762. [Google Scholar] [CrossRef]
- Minhas, D.M.; Frey, G. Two-Stage Multi-time Scale Energy Management Control framework for Home Area Power Network. In Proceedings of the 2020 IEEE International Conference on Environment and Electrical Engineering and 2020 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I CPS Europe), Madrid, Spain, 9–12 June 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhao, J.; Wang, X.; Tong, L.; Jiang, H.; Zhou, J. Distribution Network Hierarchically Partitioned Optimization Considering Electric Vehicle Orderly Charging with Isolated Bidirectional DC-DC Converter Optimal Efficiency Model. Energies 2021, 14, 1614. [Google Scholar] [CrossRef]
- Minhas, D.M.; Frey, G. Optimal Scheduling of Energy Supply Entities in Home Area Power Network. In Proceedings of the 2019 6th International Conference on Control, Decision and Information Technologies (CoDIT), Paris, France, 23–26 April 2019; pp. 732–737. [Google Scholar] [CrossRef]
- Trinh, P.H.; Chung, I.Y. Optimal Control Strategy for Distributed Energy Resources in a DC Microgrid for Energy Cost Reduction and Voltage Regulation. Energies 2021, 14, 992. [Google Scholar] [CrossRef]
- Wu, J.; Wei, Z.; Liu, K.; Quan, Z.; Li, Y. Battery-Involved Energy Management for Hybrid Electric Bus Based on Expert-Assistance Deep Deterministic Policy Gradient Algorithm. IEEE Trans. Veh. Technol. 2020, 69, 12786–12796. [Google Scholar] [CrossRef]
- Savard, C.; Iakovleva, E.; Ivanchenko, D.; Rassõlkin, A. Accessible Battery Model with Aging Dependency. Energies 2021, 14, 3493. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhao, D.; Li, X.; Wang, D. Control-Limited Adaptive Dynamic Programming for Multi-Battery Energy Storage Systems. IEEE Trans. Smart Grid 2019, 10, 4235–4244. [Google Scholar] [CrossRef]
- Hao, H.; Wu, D.; Lian, J.; Yang, T. Optimal Coordination of Building Loads and Energy Storage for Power Grid and End User Services. IEEE Trans. Smart Grid 2018, 9, 4335–4345. [Google Scholar] [CrossRef]
- Hu, J.; He, H.; Wei, Z.; Li, Y. Disturbance-Immune and Aging-Robust Internal Short Circuit Diagnostic for Lithium-Ion Battery. IEEE Trans. Ind. Electron. 2022, 69, 1988–1999. [Google Scholar] [CrossRef]
- Wikner, E.; Thiringer, T. Extending battery lifetime by avoiding high SOC. Appl. Sci. 2018, 8, 1825. [Google Scholar] [CrossRef] [Green Version]
- Jin, X.; Vora, A.; Hoshing, V.; Saha, T.; Shaver, G.; García, R.E.; Wasynczuk, O.; Varigonda, S. Physically-based reduced-order capacity loss model for graphite anodes in Li-ion battery cells. J. Power Sources 2017, 342, 750–761. [Google Scholar] [CrossRef] [Green Version]
- Neon Neue Energieökonomik GmbH. Open Power System Data. 2021. Available online: https://data.open-power-system-data.org/time_series/ (accessed on 18 February 2021).
- Feldman, D.; Ramasamy, V.; Fu, R.; Ramdas, A.; Desai, J.; Margolis, R. U.S. Solar Photovoltaic Systemand Energy Storage CostBenchmark: Q1 2020; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2020. [Google Scholar]
- Rheinberger, K.; DSM-Data. GitHub Repository. 2021. Available online: https://github.com/klaus-rheinberger/DSM-data (accessed on 18 February 2021).
- ENTSO-E. Transparency Platform. 2021. Available online: https://transparency.entsoe.eu/ (accessed on 18 February 2021).
- European Commission, Joint Research Centre. PVGIS—Photovoltaic Geographical Information System. 2021. Available online: https://re.jrc.ec.europa.eu/pvg_tools/en/tools.html (accessed on 18 February 2021).
- EA Technology. My Electric Avenue. 2021. Available online: https://eatechnology.com/americas/resources/projects/my-electric-avenue-data-download/ (accessed on 18 February 2021).
- Commission for Energy Regulation. CER Smart Metering Project-Electricity Customer Behaviour Trial, 2009–2010, 1st Edition, Irish Social Science Data Archive, SN: 0012-00. 2021. Available online: https://www.ucd.ie/issda/data/commissionforenergyregulationcer/ (accessed on 18 February 2021).
- MATLAB. Version 9.9 (R2020b); The MathWorks Inc.: Natick, MA, USA, 2020. [Google Scholar]
- Hösl, N.; Teulings, T. Open EV Data. 2021. Available online: https://github.com/chargeprice/open-ev-data (accessed on 18 February 2021).








| Ref #. | Objectives | Technique(s) | Scheduling Entities | Dynamic EV Charging | Battery Degradation | Cost Reduction | Energy Balancing | Limitation(s) | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Grid | PV | EV | ||||||||
| [3] | According to this study, using battery storage for PV and EV hosting capacity optimization as well as grid voltage maintenance was critical. | Model Predictive Control | ✓ | ✓ | ✓ | ✗ | ✗ | ✓ | ✗ | The case study is fictitious. It was confirmed that the generation of DG and PVs exceeds the consumption of the load and EV charging and that the ESS maintains all bus voltages within the permitted limit. |
| [22] | The purpose of this study is to propose a methodology for simulating plug-in electric vehicle charging in order to quantify the impact of this type of load on power systems. | Monte Carlo Simulation | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | ✓ | The proposed technique focused on transmission networks and provides a deterministic representation of the EV charge distribution across the network. It made no reference to any real-world data collection. |
| [23] | Dynamic programming is used to govern the charging (G2V) and discharging of the storage device (V2G) in order to extend the life of the battery and minimizing grid reliance. | Adaptive Dynamic Programming | ✓ | ✓ | ✓ | ✓ | ✗ | ✗ | ✓ | The model was confined to battery storage alone and did not include specific information about load needs. Additionally, constraint functions that do not have an exact model of the device were estimated. |
| [24] | The author discussed the challenge of minimizing the total of energy and thermal discomfort costs. The suggested system stabilized developing queues for indoor temperature control, electric car charging, and energy storage. | Lyapunov Optimization | ✓ | ✓ | ✓ | ✗ | ✗ | ✓ | ✓ | The energy demand model was limited in scope since it examines only thermal loads. Additionally, the algorithm was incapable of addressing the issue of peak forms. |
| [25] | Maximizing the utility sums of residential customers while keeping energy consumption costs in check is explored in this article. It is decentralized, but it protected the residents’ private information at the same time. | Generalized Benders Decomposition algorithm | ✓ | ✓ | ✗ | ✗ | ✗ | ✓ | ✗ | The technique might not operate successfully if the homes’ demand information is inaccurate. It also did not address the peak-to-average power demand ratio (PAR). |
| [20] | A two-stage optimization approach is devised, in which peak reduction signals are discovered and their flexibility provision determined by aggregating individual users’ energy use histories. | Mixed Integer Linear Programming | ✓ | ✓ | ✗ | ✗ | ✓ | ✓ | ✗ | This study made no allowance for incentives for postponing loading or for the penalty cost associated with reducing customer suffering. |
| [26] | The control method outlined in this work is intended to address power factor concerns associated with EV charging stations while still allowing for full PV generation. | Optimal Dynamic Programming | ✓ | ✓ | ✓ | ✗ | ✗ | ✓ | ✗ | The effort was done to boost the power factor. The battery management system was designed to adjust only the power factor, ignoring the demand- supply balance and ignoring real-world data. |
| [27] | This study examines the influence of dynamic energy pricing and home PV system incentives on EV charging behavior, grid load, and household economics. | Mixed Integter Linear Programming | ✓ | ✓ | ✓ | ✓ | ✗ | ✓ | ✗ | The battery deterioration model outlined in this study is critical to the model’s success. Realistic information about the actions of prosumers was also not included. |
| [15] | The suggested technique uses time-of-use pricing, time-varying residential power demand, solar generating profiles, and EV specifications to reduce electricity prices and flatten the load curve. | Rule Based Optimization | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | ✓ | The battery degradation model is an important factor in this study’s model. However, realistic data sets on prosumer actions were not included in the investigation. |
| [28] | The PV produced more energy than needed to meet load demands and charge the batteries. Battery discharge happens when PV panel output falls short of load needs. The controller prevented over(dis)charging. | Fuzzy Logic Design | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ✓ | The focus of this paper was solely on the supply and demand for energy. Cost reduction and customer satisfaction were not adequately addressed. |
| Parameters | Value | Parameters | Value | Parameters | Value |
|---|---|---|---|---|---|
| 20 kW | 15 min | ||||
| 110 kWh | 1 s | ||||
| 120 kWh | [42] | 130 $/MWh | Figure A4 | ||
| 1 kWh | [42] | 201 $/MWh | Figure A4 |
| Parameters | Value | Unit | Parameters | Value | Unit |
|---|---|---|---|---|---|
| 6684.8 | 39,146 | J/mol | |||
| 1.368 | 1/Ah | 39,500 | J/mol | ||
| R | 8.314 | J/K·mol | - | ||
| F | 96,485.3 | C/mol | - |
| Scheme/Parameters | |||||||
|---|---|---|---|---|---|---|---|
| Scheme 1: (Conv-EG) | 0 | 0.0307 | 0.9597 | 0 | 0.8598 | 0.4198 | 0.1402 |
| Scheme 2: (Conv-PEG) | 0.6634 | 0.0268 | 0.9598 | 0.1129 | 0.7639 | 0.4098 | 0.2361 |
| Scheme 3: (MP-iEMS) | 0.6272 | 0.0269 | 0.9579 | 0.1175 | 0.8447 | 0.3533 | 0.1553 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Minhas, D.M.; Meiers, J.; Frey, G. Electric Vehicle Battery Storage Concentric Intelligent Home Energy Management System Using Real Life Data Sets. Energies 2022, 15, 1619. https://doi.org/10.3390/en15051619
Minhas DM, Meiers J, Frey G. Electric Vehicle Battery Storage Concentric Intelligent Home Energy Management System Using Real Life Data Sets. Energies. 2022; 15(5):1619. https://doi.org/10.3390/en15051619
Chicago/Turabian StyleMinhas, Daud Mustafa, Josef Meiers, and Georg Frey. 2022. "Electric Vehicle Battery Storage Concentric Intelligent Home Energy Management System Using Real Life Data Sets" Energies 15, no. 5: 1619. https://doi.org/10.3390/en15051619
APA StyleMinhas, D. M., Meiers, J., & Frey, G. (2022). Electric Vehicle Battery Storage Concentric Intelligent Home Energy Management System Using Real Life Data Sets. Energies, 15(5), 1619. https://doi.org/10.3390/en15051619








