Virtual Sensor Using a Super Twisting Algorithm Based Uniform Robust Exact Differentiator for Electric Vehicles
Abstract
:1. Introduction
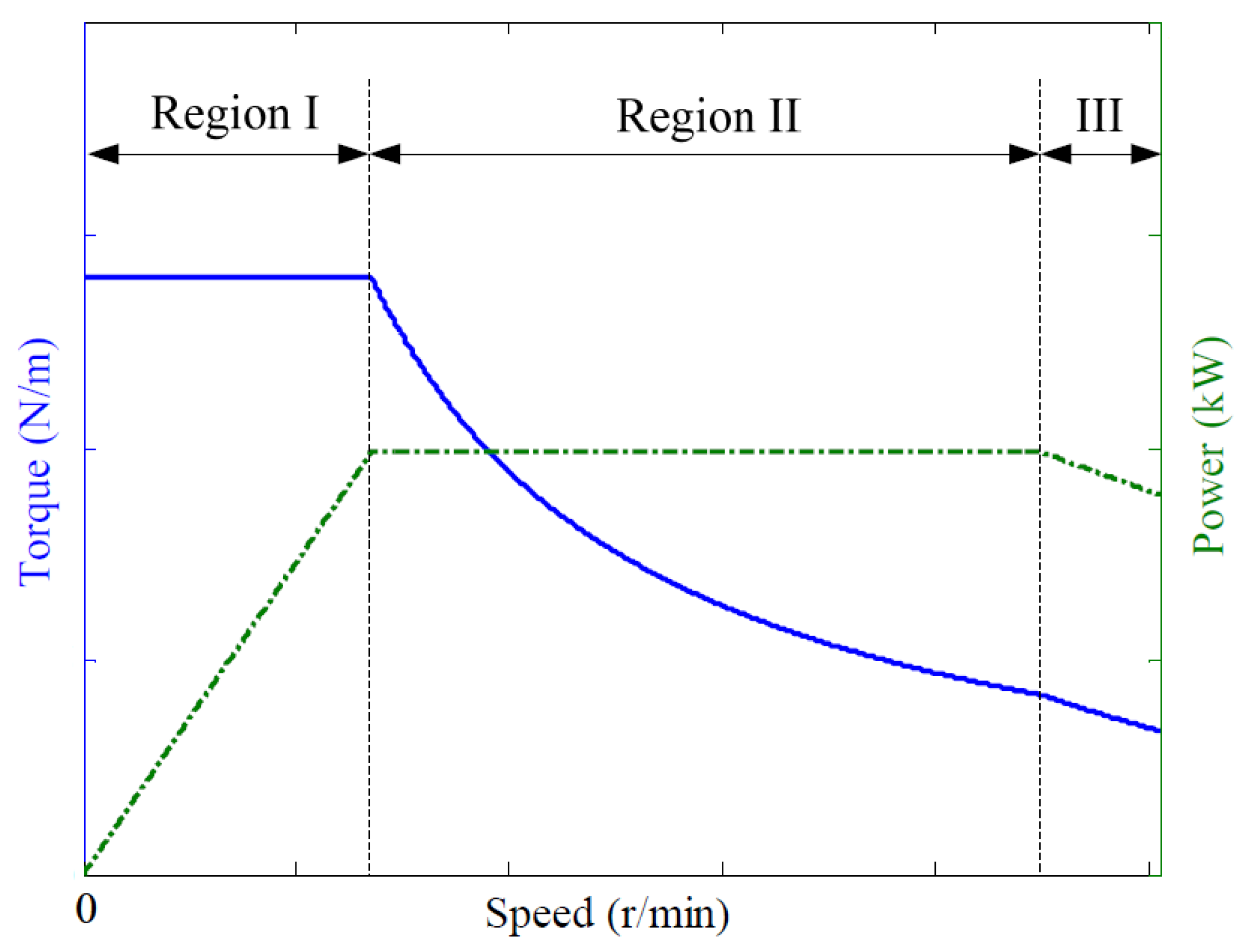
1.1. Electrified Powertrain
- Being unable to meet the road loads in all operating conditions;
- Aging (Reduced life span);
- Inefficient powertrain operations or high power loss.
1.2. Related Work
1.3. Major Contributions
2. EV-Based IPMSM Dynamics
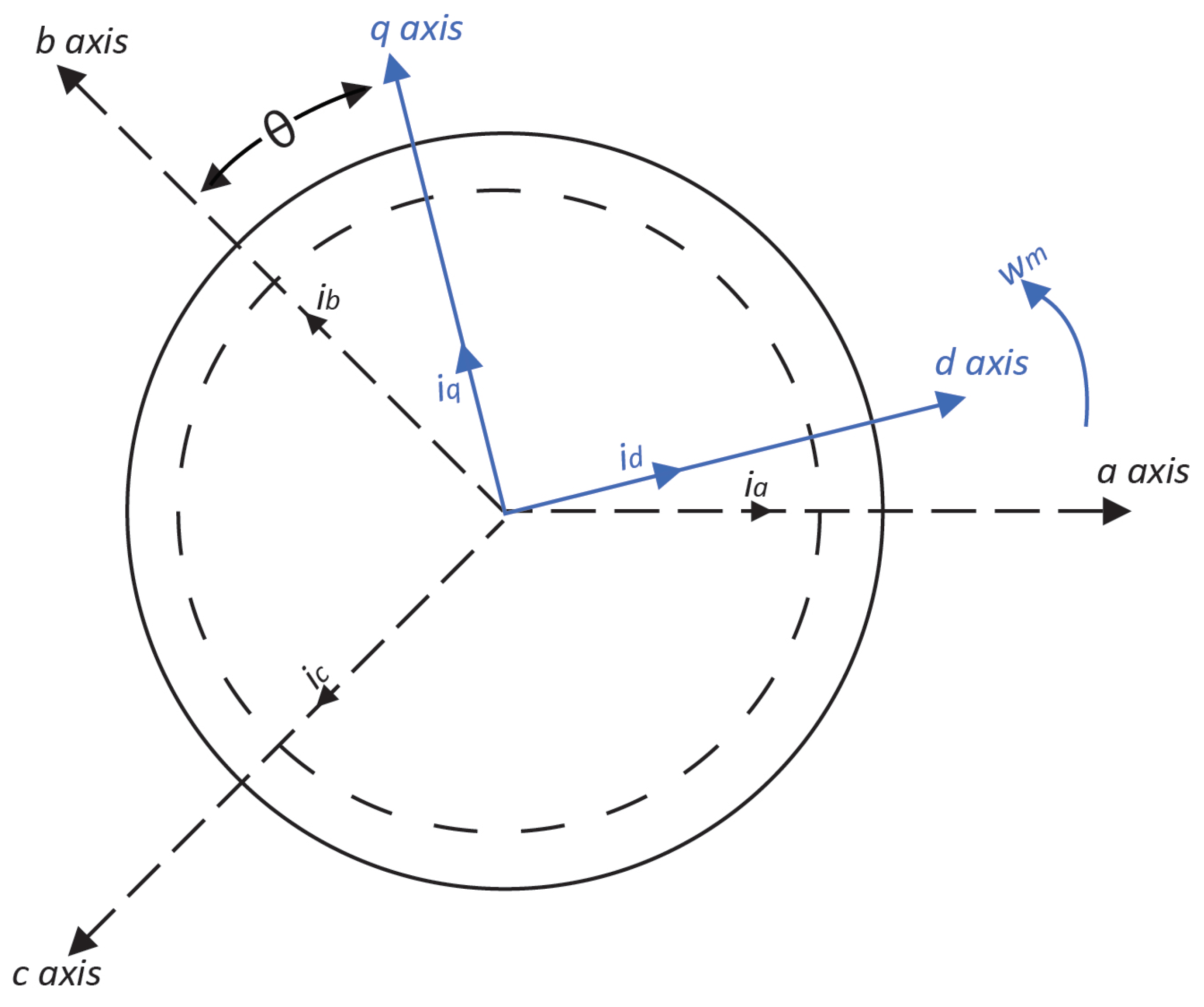
2.1. IPMSM Mathematical Modelling
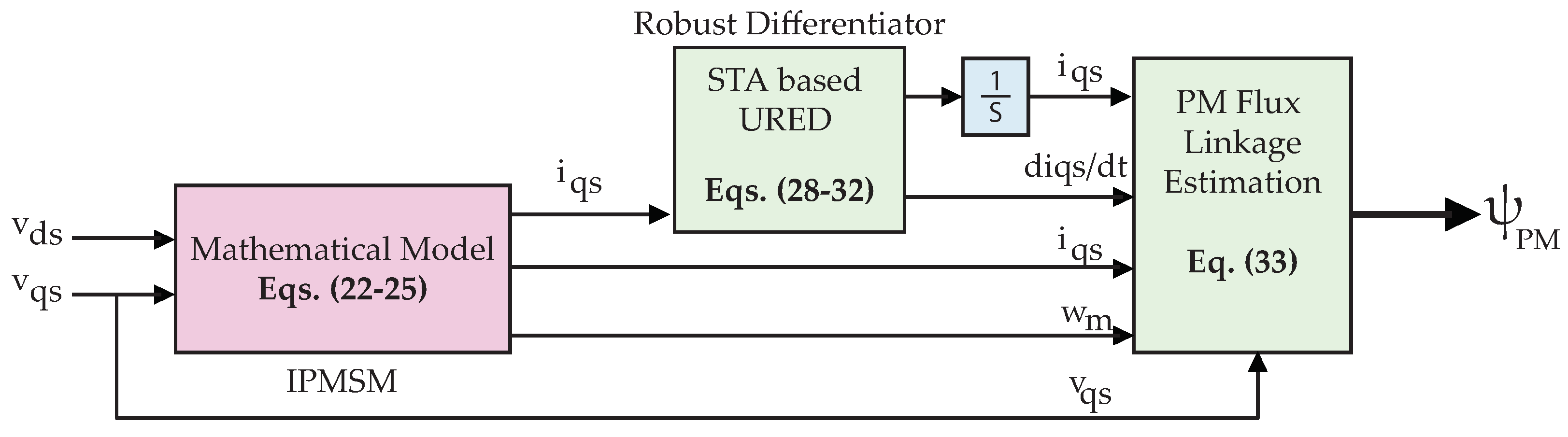
3. Virtual Sensor Development Strategy
4. Simulation Experiments
4.1. Simulator Design
4.2. Estimating/Sensing of an Immeasurable Parameter
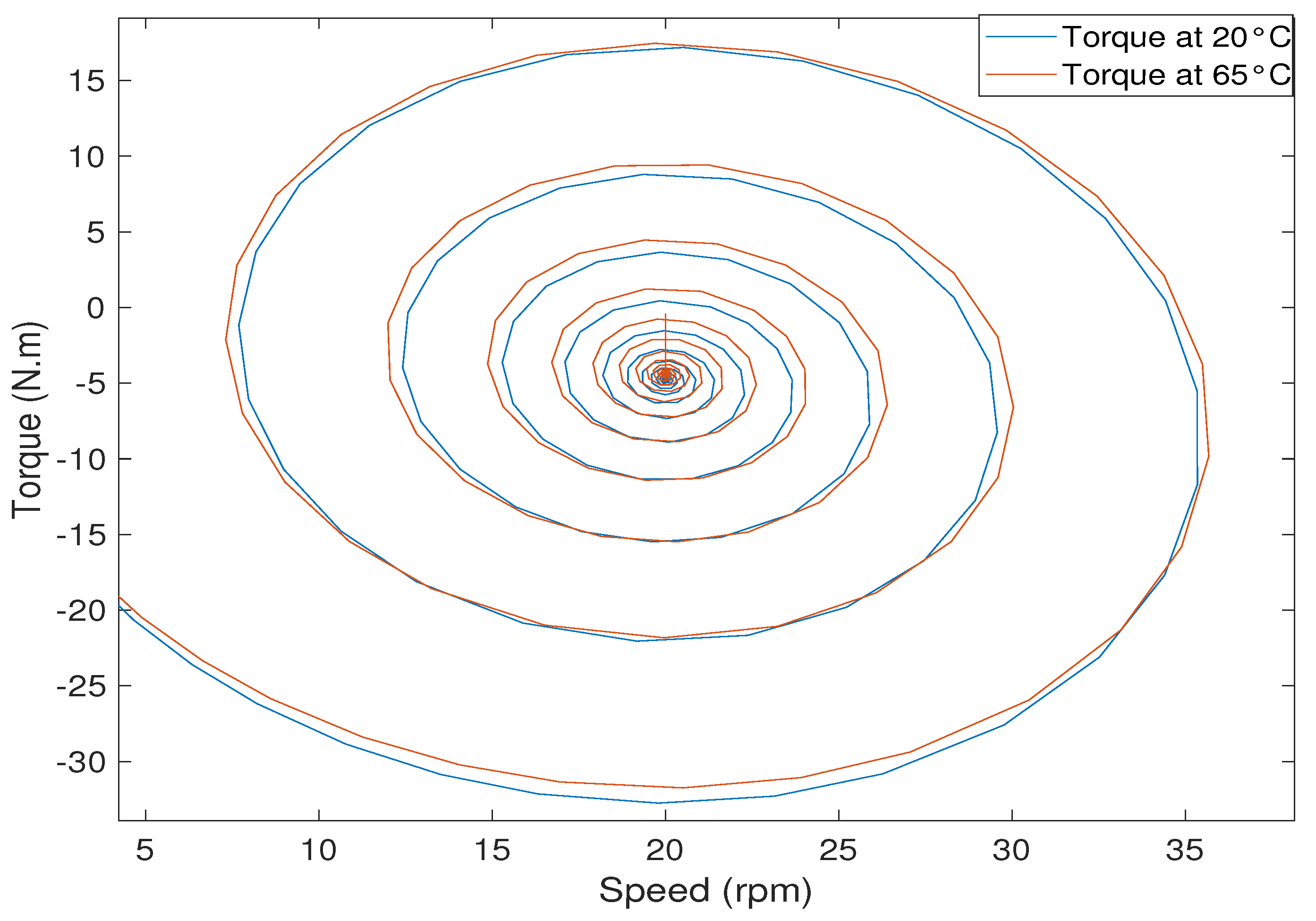
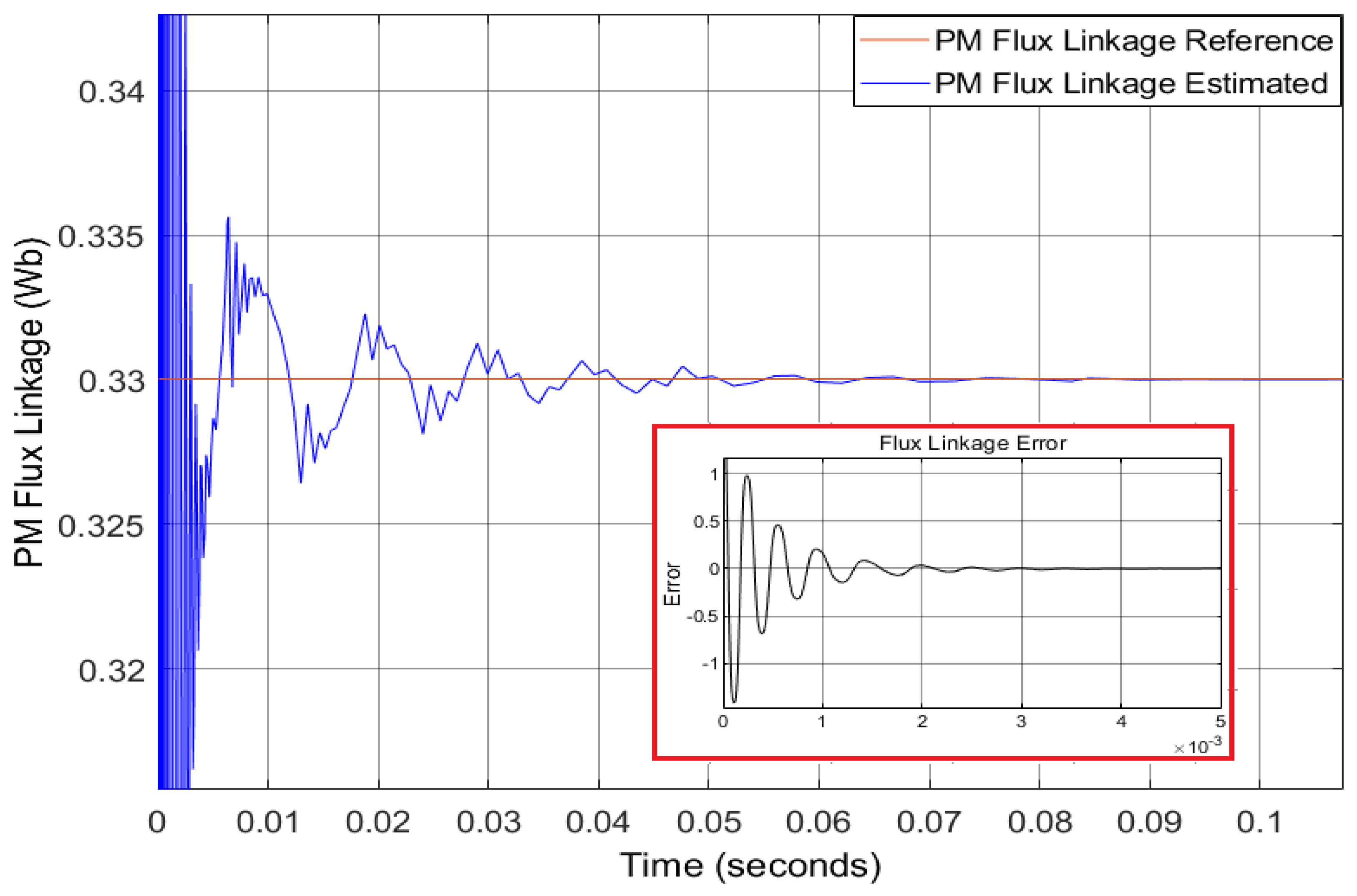
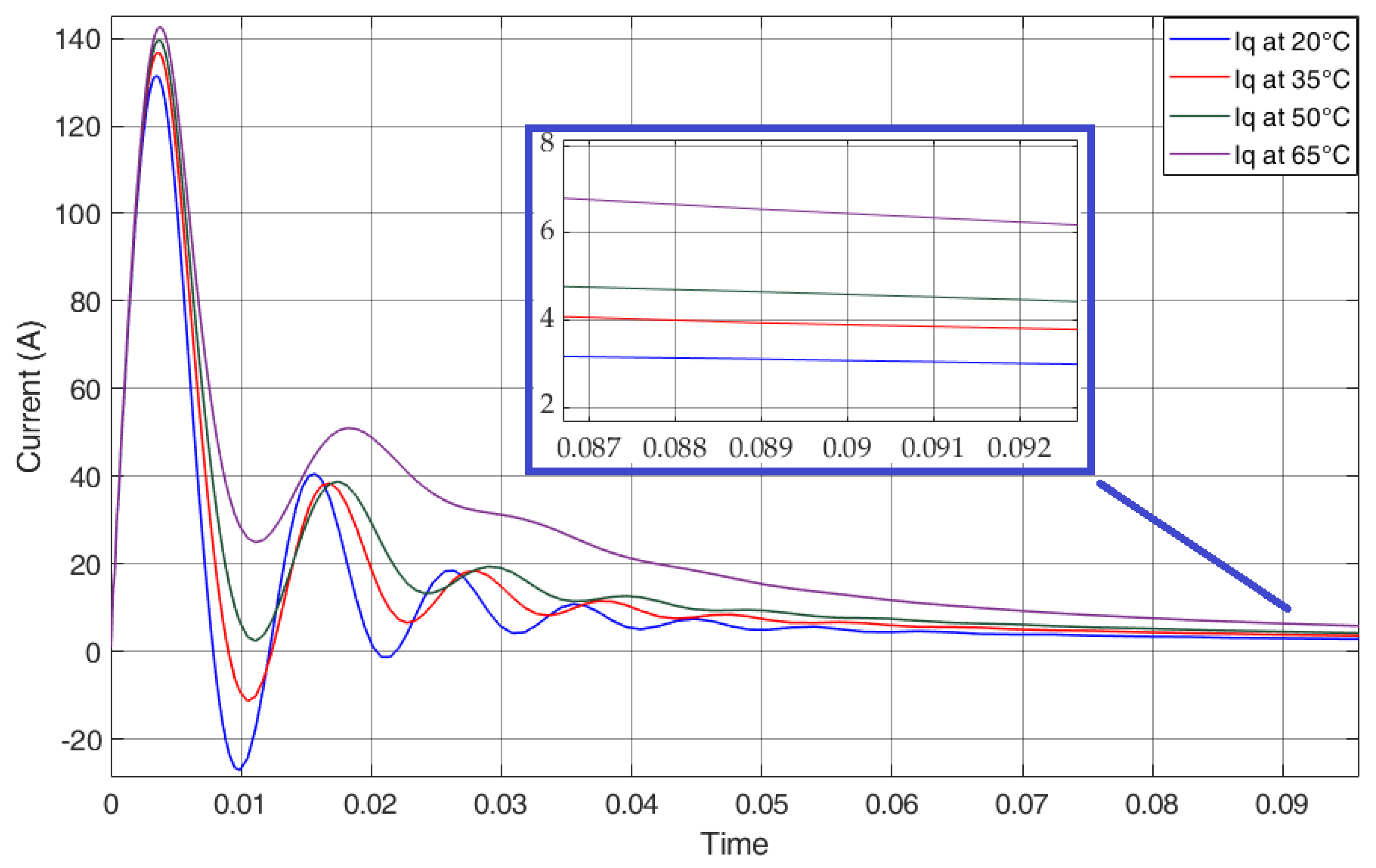
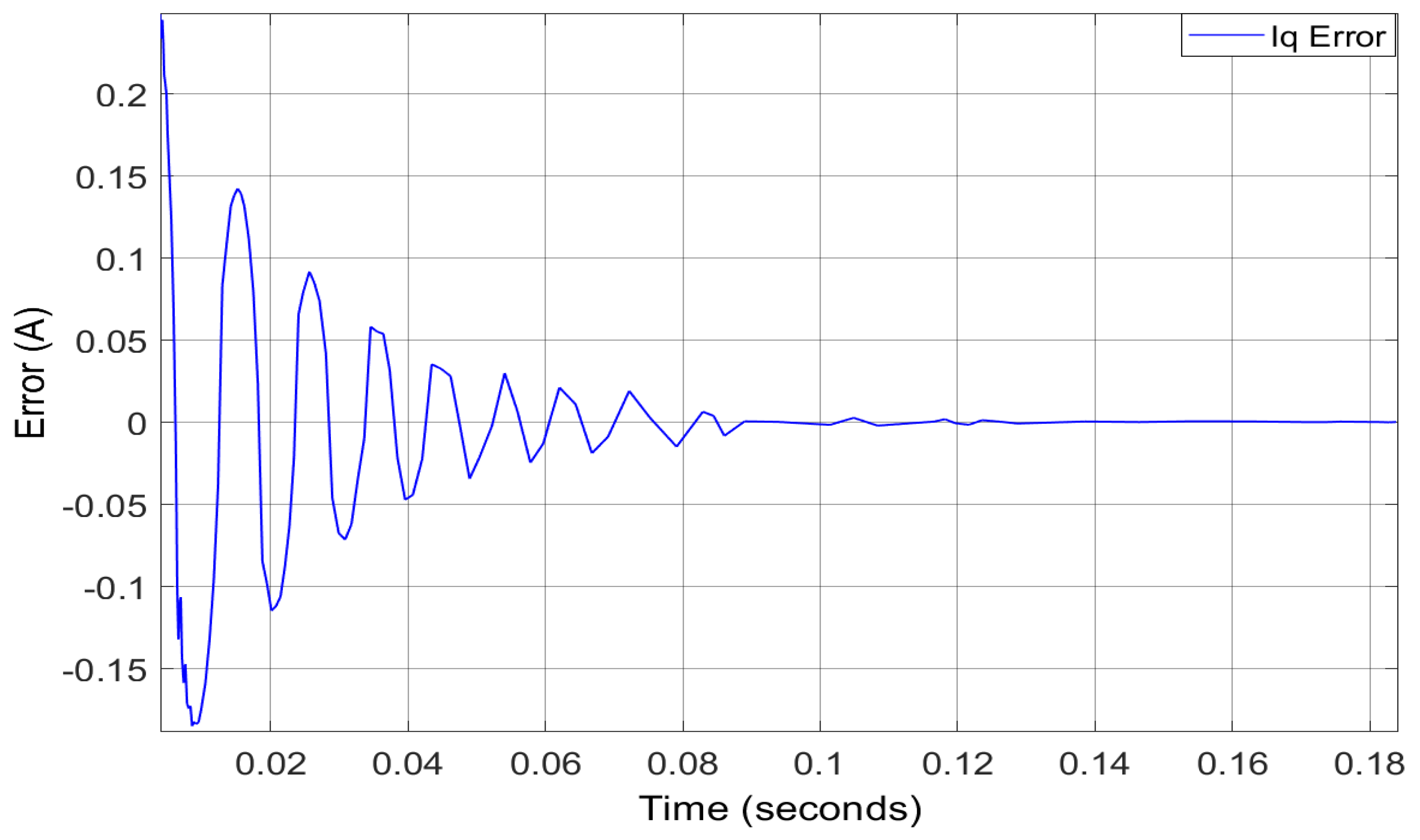
- Case 1:The PM flux linkage is estimated to be at a nominal temperature of 20 C. There is no change in stator resistance. The settling time remains less than 0.09 s and the convergence error remains close to zero.
- Case 2:As the operating temperature of IPMSM-based electrified powertrain increases to 35 C, the stator resistance value increases around . Therefore, PM flux linkage decreases, and the decrease is estimated to . The settling time remains less than 0.09 s, and the convergence error remains close to zero.
- Case 3:With the increase of operating temperature of IPMSM-based electrified powertrain to 50 C, the stator resistance value increases around . The proposed virtual sensor is still able to detect decreased PM flux linkage. The estimated value from the figure can be seen to be . The settling time still remains less than 0.09 s and the convergence error remains close to zero.
- Case 4:The stator resistance value increases with the increase of operating temperature of IPMSM-based electrified powertrain to 65 C. The PM flux linkage decreases, and the decrease is still correctly detected and estimated to be . The settling time remains less than 0.09 s, and the convergence error remains close to zero.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| EV | Electric Vehicles |
| OEMs | Original Equipment Manufacture |
| PMSM | Permanent Magnet Synchronous Motor |
| IPMSM | Interior Permanent Magnet Synchronous Motor |
| SPMSM | Surface Mounted Permanent Magnet Synchronous Motor |
| PM | Permanent Magnet |
| SMO | Sliding Mode Observer |
| HOSM | Higher Order Sliding Mode Observer |
| STA | Super Twisting Algorithm |
| URED | Uniform Robust Exact Differentiator |
| WLTP | Worldwide harmonized Light vehicle Test Procedures |
| , | Intrinsic Coercivity and Remanence |
| Field Current | |
| , | Stator and Mutual Inductance |
| Leakage Inductance | |
| , | Average value and Variation in value of magnetizing Inductance |
| Stator Voltages in d and q-axis in V | |
| , | Stator flux in d and q-frame in |
| , | Stator currents in A |
| Stator Resistance in | |
| p | Poles pair |
| Angle between rotating and stationary reference frame | |
| Rotor position | |
| Rotor mechanical speed in | |
| , | Inductances of stator in H |
| Permanent Magnet flux linkage at operating temperature in | |
| J | Moment of inertia in |
| Load torque in | |
| B | Viscous damping constant |
| Magnet remanence at operating temperature | |
| , T | Nominal and operating temperature |
| Permanent Magnet flux linkage at nominal temperature in | |
| A | Area passed by magnetic flux linkage at and T |
| Difference between PM flux linkage at operating and nominal temperature | |
| Temperature coefficient of remanence, which is not constant but changes with temperature | |
| , | Rolling and downgrade resistance force |
| , | Viscous frictional and Aerodynamics drag force |
| Tractive force | |
| Gear ratio | |
| Wheel radius | |
| m | Vehicle mass |
References
- Bilgin, B.; Magne, P.; Malysz, P.; Yang, Y.; Pantelic, V.; Preindl, M.; Korobkine, A.; Jiang, W.; Lawford, M.; Emadi, A. Making the case for electrified transportation. IEEE Trans. Transp. Electrif. 2015, 1, 4–17. [Google Scholar] [CrossRef]
- Ehsani, M.; Gao, Y.; Longo, S.; Ebrahimi, K. Modern Electric, Hybrid Electric, and Fuel Cell Vehicles; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Liu, C. Emerging electric machines and drives—An overview. IEEE Trans. Energy Convers. 2018, 33, 2270–2280. [Google Scholar] [CrossRef]
- Rind, S.J.; Ren, Y.; Hu, Y.; Wang, J.; Jiang, L. Configurations and control of traction motors for electric vehicles: A review. Chin. J. Electr. Eng. 2017, 3, 1–17. [Google Scholar]
- Li, S.; Sarlioglu, B.; Jurkovic, S.; Patel, N.R.; Savagian, P. Analysis of temperature effects on performance of interior permanent magnet machines for high variable temperature applications. IEEE Trans. Ind. Appl. 2017, 53, 4923–4933. [Google Scholar] [CrossRef]
- Wilson, S.D.; Stewart, P.; Taylor, B.P. Methods of resistance estimation in permanent magnet synchronous motors for real-time thermal management. IEEE Trans. Energy Convers. 2010, 25, 698–707. [Google Scholar] [CrossRef] [Green Version]
- Bilgin, O.; Kazan, F.A. The effect of magnet temperature on speed, current and torque in PMSMs. In Proceedings of the 2016 XXII International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 4–7 September 2016; pp. 2080–2085. [Google Scholar]
- Li, S.; Sarlioglu, B.; Jurkovic, S.; Patel, N.R.; Savagian, P. Comparative analysis of torque compensation control algorithms of interior permanent magnet machines for automotive applications considering the effects of temperature variation. IEEE Trans. Transp. Electrif. 2017, 3, 668–681. [Google Scholar] [CrossRef]
- Hanif, A.; Ahmed, Q.; Bhatti, A.I.; Rizzoni, G. A Unified Control Framework for Traction Machine Drive Using Linear Parameters Varying-Based Field-Oriented Control. J. Dyn. Syst. Meas. Control 2020, 142, 101006. [Google Scholar] [CrossRef]
- Maughan, C.V.; Reschovsky, J.M. Advances in motor and generator rotor health. In Proceedings of the 2010 IEEE International Symposium on Electrical Insulation, San Diego, CA, USA, 6–9 June 2010; pp. 1–4. [Google Scholar]
- Fan, J.; Zhang, C.; Wang, Z.; Dong, Y.; Nino, C.; Tariq, A.; Strangas, E. Thermal analysis of permanent magnet motor for the electric vehicle application considering driving duty cycle. IEEE Trans. Magn. 2010, 46, 2493–2496. [Google Scholar] [CrossRef]
- Reigosa, D.D.; Briz, F.; García, P.; Guerrero, J.M.; Degner, M.W. Magnet temperature estimation in surface PM machines using high-frequency signal injection. IEEE Trans. Ind. Appl. 2010, 46, 1468–1475. [Google Scholar] [CrossRef]
- Wang, T.; Huang, J.; Ye, M.; Chen, J.; Kong, W.; Kang, M.; Yu, M. An EMF observer for PMSM sensorless drives adaptive to stator resistance and rotor flux linkage. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 7, 1899–1913. [Google Scholar] [CrossRef]
- Rafaq, M.S.; Jung, J.W. A comprehensive review of state-of-the-art parameter estimation techniques for permanent magnet synchronous motors in wide speed range. IEEE Trans. Ind. Inform. 2019, 16, 4747–4758. [Google Scholar] [CrossRef]
- Rafaq, M.S.; Mohammed, S.A.Q.; Jung, J.W. Online multiparameter estimation for robust adaptive decoupling PI controllers of an IPMSM drive: Variable regularized APAs. IEEE/ASME Trans. Mechatron. 2019, 24, 1386–1395. [Google Scholar] [CrossRef]
- Urbanski, K.; Janiszewski, D. Sensorless control of the permanent magnet synchronous motor. Sensors 2019, 19, 3546. [Google Scholar] [CrossRef] [Green Version]
- Pei, G.; Liu, J.; Li, L.; Du, P.; Pei, L.; Hu, Y. MRAS based online parameter identification for PMSM considering VSI nonlinearity. In Proceedings of the 2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 4–7 November 2018; pp. 1–7. [Google Scholar]
- Sun, X.; Wu, M.; Lei, G.; Guo, Y.; Zhu, J. An improved model predictive current control for PMSM drives based on current track circle. IEEE Trans. Ind. Electron. 2020, 68, 3782–3793. [Google Scholar] [CrossRef]
- Lee, J.; Ha, J.I. Temperature estimation of PMSM using a difference-estimating feedforward neural network. IEEE Access 2020, 8, 130855–130865. [Google Scholar] [CrossRef]
- Avdeev, A.; Osipov, O. PMSM identification using genetic algorithm. In Proceedings of the 2019 26th International Workshop on Electric Drives: Improvement in Efficiency of Electric Drives (IWED), Moscow, Russia, 30 January–2 February 2019; pp. 1–4. [Google Scholar]
- Sun, X.; Zhang, Y.; Lei, G.; Guo, Y.; Zhu, J. An improved deadbeat predictive stator flux control with reduced-order disturbance observer for in-wheel PMSMs. IEEE/ASME Trans. Mechatron. 2021. [Google Scholar] [CrossRef]
- Yao, Y.; Huang, Y.; Peng, F.; Dong, J. Position sensorless drive and online parameter estimation for surface-mounted pmsms based on adaptive full-state feedback control. IEEE Trans. Power Electron. 2019, 35, 7341–7355. [Google Scholar] [CrossRef] [Green Version]
- Vu, N.T.T. A Nonlinear State Observer for Sensorless Speed Control of IPMSM. J. Control. Autom. Electr. Syst. 2020, 31, 1087–1096. [Google Scholar] [CrossRef]
- Young, K.D.; Utkin, V.I.; Ozguner, U. A control engineer’s guide to sliding mode control. IEEE Trans. Control Syst. Technol. 1999, 7, 328–342. [Google Scholar] [CrossRef] [Green Version]
- Bensalem, Y.; Kouzou, A.; Abbassi, R.; Jerbi, H.; Kennel, R.; Abdelrahem, M. Sliding-Mode-Based Current and Speed Sensors Fault Diagnosis for Five-Phase PMSM. Energies 2022, 15, 71. [Google Scholar] [CrossRef]
- Sun, X.; Cao, J.; Lei, G.; Guo, Y.; Zhu, J. A robust deadbeat predictive controller with delay compensation based on composite sliding-mode observer for PMSMs. IEEE Trans. Power Electron. 2021, 36, 10742–10752. [Google Scholar] [CrossRef]
- Liang, Y.W.; Ting, L.W.; Lin, L.G. Study of reliable control via an integral-type sliding mode control scheme. IEEE Trans. Ind. Electron. 2011, 59, 3062–3068. [Google Scholar] [CrossRef]
- Sun, G.; Wu, L.; Kuang, Z.; Ma, Z.; Liu, J. Practical tracking control of linear motor via fractional-order sliding mode. Automatica 2018, 94, 221–235. [Google Scholar] [CrossRef]
- Huang, S.; Wu, G.; Rong, F.; Zhang, C.; Huang, S.; Wu, Q. Novel predictive stator flux control techniques for PMSM drives. IEEE Trans. Power Electron. 2018, 34, 8916–8929. [Google Scholar] [CrossRef] [Green Version]
- Yu, X.; Kaynak, O. Sliding-mode control with soft computing: A survey. IEEE Trans. Ind. Electron. 2009, 56, 3275–3285. [Google Scholar]
- Mohd Zaihidee, F.; Mekhilef, S.; Mubin, M. Robust speed control of PMSM using sliding mode control (SMC)—A review. Energies 2019, 12, 1669. [Google Scholar] [CrossRef] [Green Version]
- Levant, A. Robust exact differentiation via sliding mode technique. Automatica 1998, 34, 379–384. [Google Scholar] [CrossRef]
- Levant, A. Higher-order sliding modes, differentiation and output-feedback control. Int. J. Control 2003, 76, 924–941. [Google Scholar] [CrossRef]
- Zafari, Y.; Shoja-Majidabad, S. Second-order terminal sliding mode control of five-phase IPMSM with super twisting observer under demagnetisation fault. Int. J. Model. Identif. Control 2020, 34, 127–136. [Google Scholar] [CrossRef]
- Cruz-Zavala, E.; Moreno, J.A.; Fridman, L.M. Uniform robust exact differentiator. IEEE Trans. Autom. Control 2011, 56, 2727–2733. [Google Scholar] [CrossRef]
- Yang, Z.; Shang, F.; Brown, I.P.; Krishnamurthy, M. Comparative study of interior permanent magnet, induction, and switched reluctance motor drives for EV and HEV applications. IEEE Trans. Transp. Electrif. 2015, 1, 245–254. [Google Scholar] [CrossRef]
- Fang, L.; Qin, S.; Xu, G.; Li, T.; Zhu, K. Simultaneous optimization for hybrid electric vehicle parameters based on multi-objective genetic algorithms. Energies 2011, 4, 532–544. [Google Scholar] [CrossRef]
- Pohl, L.; Buchta, L. H∞ tuning technique for PMSM cascade PI control structure. In Proceedings of the 2016 6th IEEE International Conference on Control System, Computing and Engineering (ICCSCE), Penang, Malaysia, 25–27 November 2016; pp. 119–124. [Google Scholar]
- Lee, Y.; Lee, S.H.; Chung, C.C. LPV H∞ Control with Disturbance Estimation for Permanent Magnet Synchronous Motors. IEEE Trans. Ind. Electron. 2017, 65, 488–497. [Google Scholar]
- Alizadeh Pahlavani, M.R.; Damroodi, H. LPV Control for speed of permanent magnet synchronous motor (PMSM) with PWM Inverter. J. Electr. Comput. Eng. Innov. 2016, 4, 185–193. [Google Scholar]
- Lee, H.; Lee, Y.; Shin, D.; Chung, C.C. H∞ control based on LPV for load torque compensation of PMSM. In Proceedings of the 2015 15th International Conference on Control, Automation and Systems (ICCAS), Busan, Korea, 13–16 October 2015; pp. 1013–1018. [Google Scholar]
- Hwang, H.; Lee, Y.; Shin, D.; Chung, C.C. H2 control based on LPV for speed control of permanent magnet synchronous motors. In Proceedings of the 2014 14th International Conference on Control, Automation and Systems (ICCAS 2014), Gyeonggi-do, Korea, 22–25 October 2014; pp. 922–927. [Google Scholar]
- Youssef, H.; Zazi Malika, M.R. Modeling and Robust H∞ Control of a Synchronous Machine with a Salient Rotor. Int. J. Adv. Res. Sci. Eng. Technol. 2016, 3, 1332–1340. [Google Scholar]
- Yang, Z.; Chai, Y.; Yin, H.; Tao, S. LPV model based sensor fault diagnosis and isolation for permanent magnet synchronous generator in wind energy conversion systems. Appl. Sci. 2018, 8, 1816. [Google Scholar] [CrossRef] [Green Version]
- Quang, N.P.; Dittrich, J.A. Vector Control of Three-Phase AC Machines; Springer: Berlin/Heidelberg, Germany, 2008; Volume 2. [Google Scholar]
- Tabbache, B.; Benbouzid, M.E.H.; Kheloui, A.; Bourgeot, J.M. Virtual-sensor-based maximum-likelihood voting approach for fault-tolerant control of electric vehicle powertrains. IEEE Trans. Veh. Technol. 2012, 62, 1075–1083. [Google Scholar] [CrossRef] [Green Version]


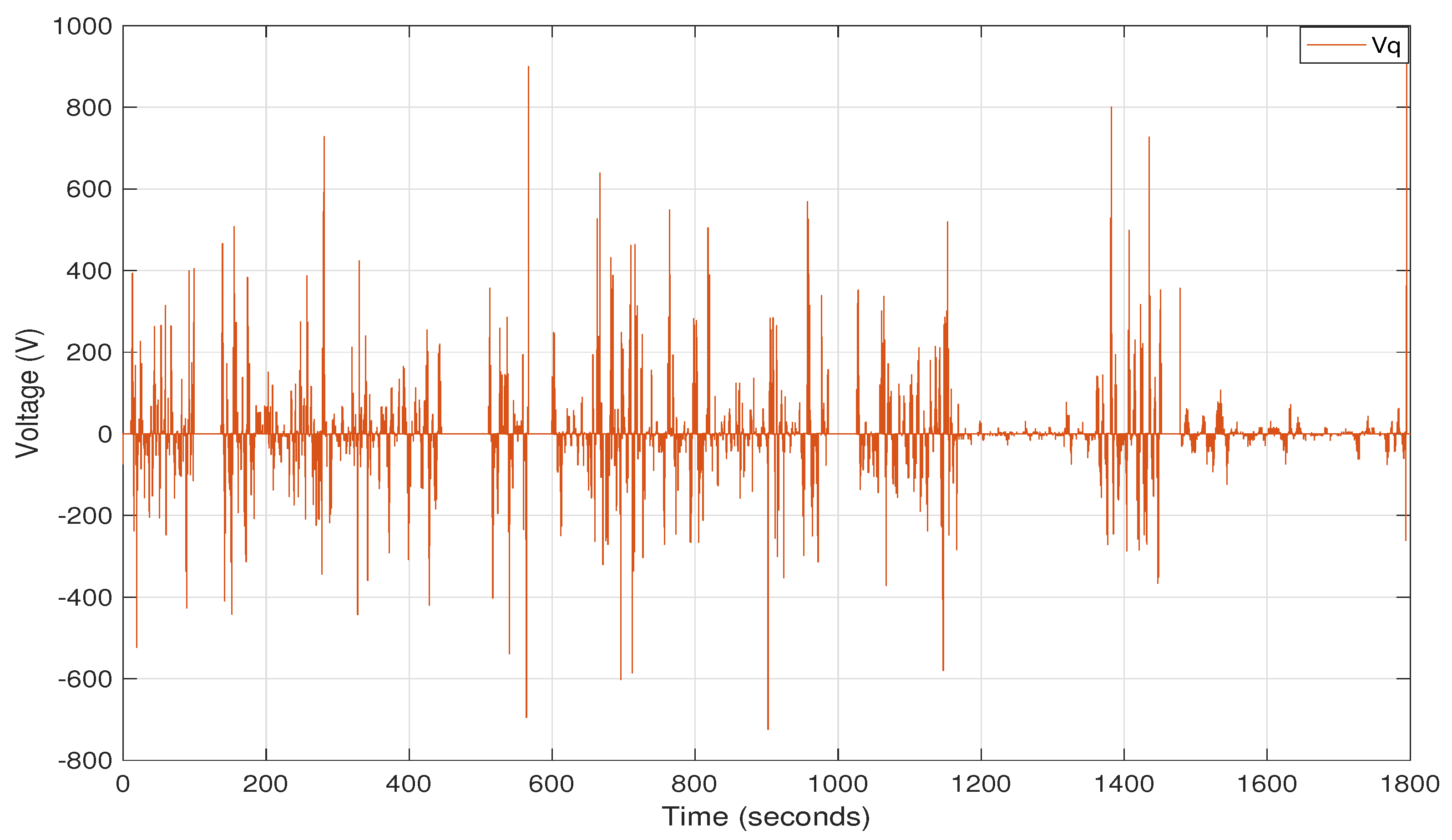
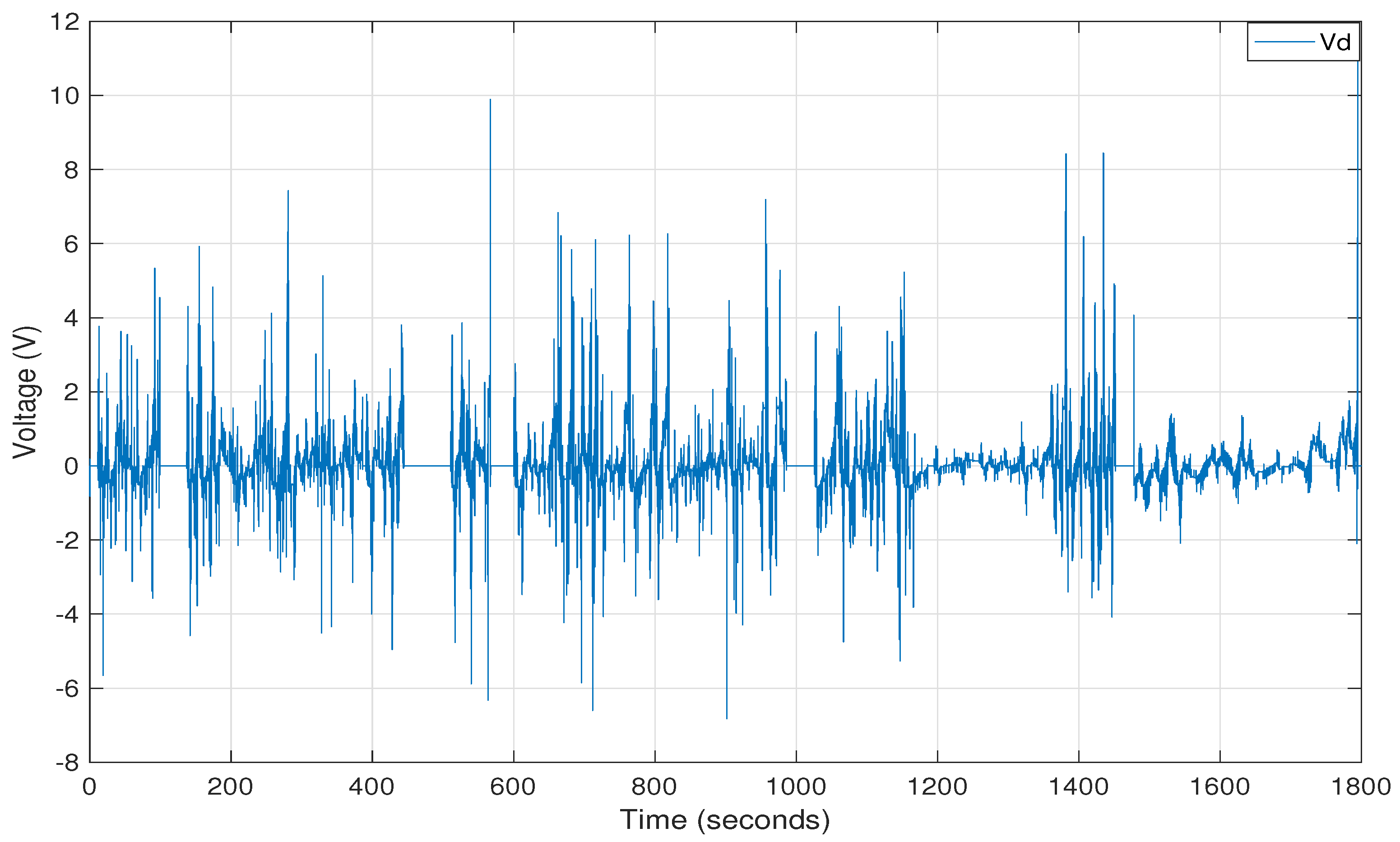


| Parameters [Units] | Symbol | Value |
|---|---|---|
| Power [kW] | P | 3 |
| Nominal Torque [Nm] | 20 | |
| Stator Resistance [] | 0.5 | |
| Inductance in q-axis [H] | 0.005 | |
| Inductance in d-axis [H] | 0.0035 | |
| Flux Linkage [Wb] | 0.33 | |
| Pole pairs | p | 3 |
| Inertia [Kgm] | J | 0.004 |
| Viscous Damping | B | 0.0028 |
| Vehicle Data | ||
| Gear ratio | 6 | |
| Wheel radius [m] | 0.3 | |
| Vehicle mass [kg] | m | 750 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muazzam, H.; Ishak, M.K.; Hanif, A.; Uppal, A.A.; Bhatti, A.; Isa, N.A.M. Virtual Sensor Using a Super Twisting Algorithm Based Uniform Robust Exact Differentiator for Electric Vehicles. Energies 2022, 15, 1773. https://doi.org/10.3390/en15051773
Muazzam H, Ishak MK, Hanif A, Uppal AA, Bhatti A, Isa NAM. Virtual Sensor Using a Super Twisting Algorithm Based Uniform Robust Exact Differentiator for Electric Vehicles. Energies. 2022; 15(5):1773. https://doi.org/10.3390/en15051773
Chicago/Turabian StyleMuazzam, Hassam, Mohamad Khairi Ishak, Athar Hanif, Ali Arshad Uppal, AI Bhatti, and Nor Ashidi Mat Isa. 2022. "Virtual Sensor Using a Super Twisting Algorithm Based Uniform Robust Exact Differentiator for Electric Vehicles" Energies 15, no. 5: 1773. https://doi.org/10.3390/en15051773
APA StyleMuazzam, H., Ishak, M. K., Hanif, A., Uppal, A. A., Bhatti, A., & Isa, N. A. M. (2022). Virtual Sensor Using a Super Twisting Algorithm Based Uniform Robust Exact Differentiator for Electric Vehicles. Energies, 15(5), 1773. https://doi.org/10.3390/en15051773








