A Multiobjective Fractional Programming for a CHP System Operation Optimization Based on Energy Intensity
Abstract
:1. Introduction
2. Case study
2.1. Overview of Studied Region
2.2. The Description of CHP System
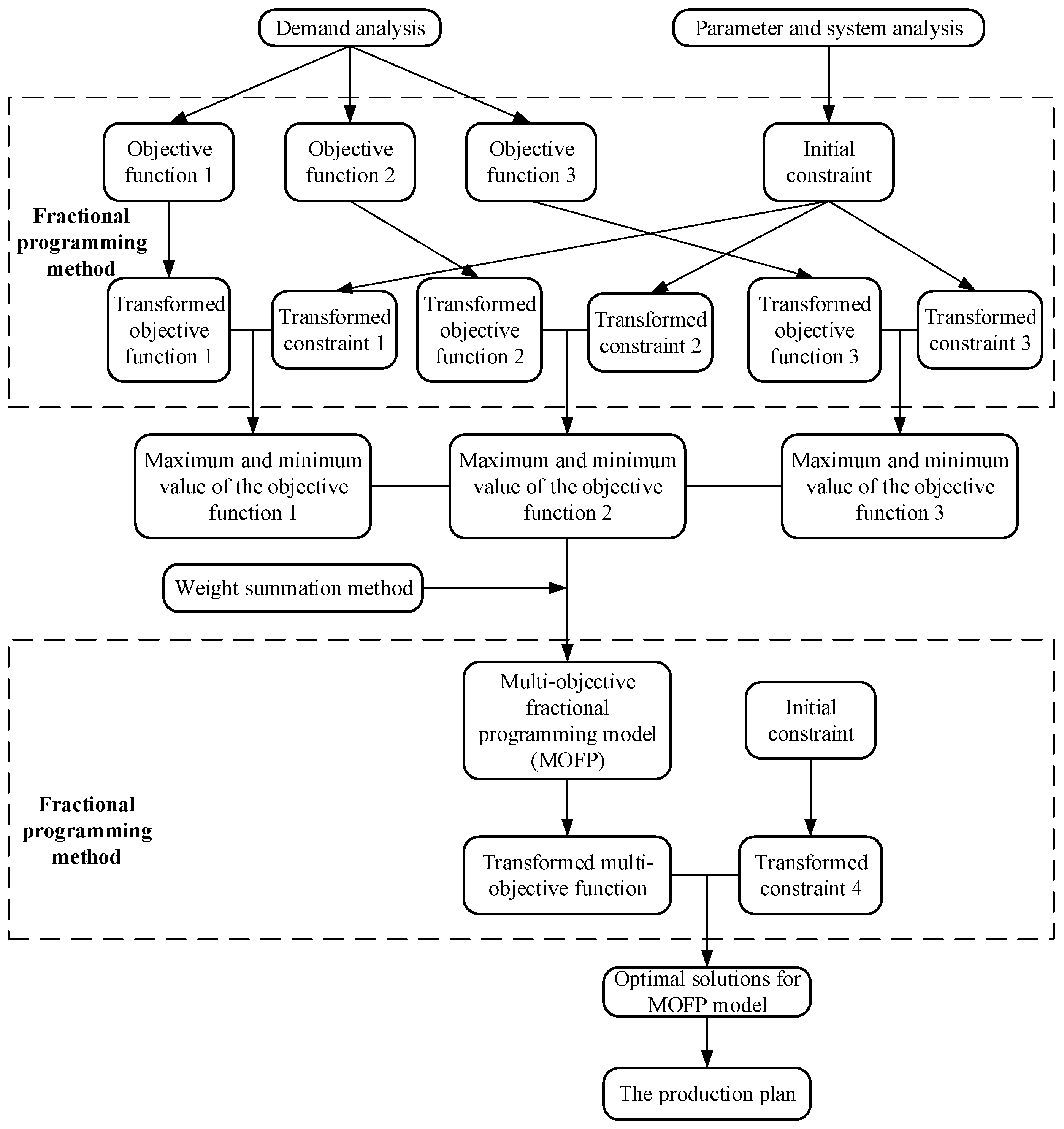
3. Formulation and Solution of MOFP Model for Operational Management of CHP System
3.1. Objective Functions
3.2. Subject to
4. Results Analysis and Discussion
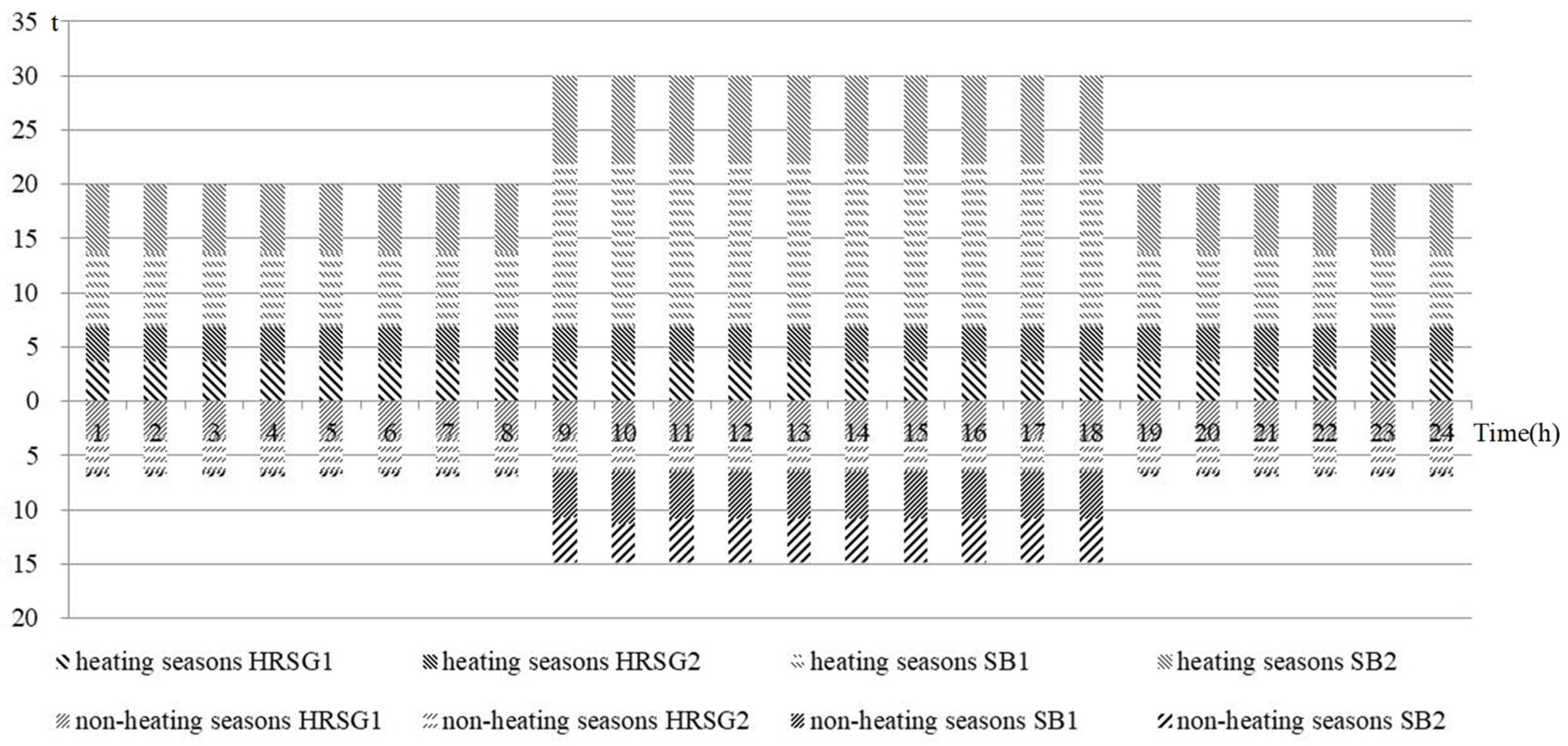
4.1. Result Analysis
4.2. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| c | different atmospheric pollutants, (c = 1 for SO2, c = 2 for NOX, c = 3 for CO2) |
| dce | daily operation cost of HRSG (RMB) |
| dcf | daily operation cost of SB (RMB) |
| dct | daily operation cost of GT (RMB) |
| dec | daily environmental cost (RMB) |
| dw | daily cost of water consumption (RMB) |
| ec | emission coefficient (kg/106 m3) |
| ep | the time-of-use electricity price (RMB) |
| EI | the new integrated objective function |
| f(t) | total consumption amounts of natural gas corresponding to unit benefits |
| g(t) | total consumption amounts of electricity power corresponding to unit benefits |
| Gam | inlet flow of compressor (kg/s) |
| Cpa | specific heat at constant pressure (J/kg.K) |
| GP | total system revenues in that day (RMB) |
| h(t) | total consumption amounts of water corresponding to unit benefits |
| hce | the operation cost of HRSG per hour (RMB) |
| hcf | the operation cost of SB per hour (RMB) |
| hct | the operation cost of GT per hour (RMB) |
| hece | the electricity power consumption of HRSG per hour (kW/h) |
| hecf | the electricity power consumption of SB per hour (kW/h) |
| hect | the electricity power consumption of GT per hour (kW/h) |
| het | the electricity production of GT per hour (kW) |
| hetmax | the maximum power generation of GT, kW |
| hgcf | the natural gas consumption of SB per hour (m3/h) |
| hgct | the natural gas consumption of GT per hour (m3/h) |
| hse | the steam production from HRSG per hour (t) |
| hsemax | regulated maximum steam provision amount |
| hsf | the steam production from SB erper hour (t/h) |
| hsfmax | the rated power of SBs |
| hst | the heat generated by GT per hour (t/h) |
| hw | the consumption cost of water caused by devices utilization (RMB) |
| I | total number of devices |
| ps | the unit price of steam (RMB/t) |
| png | the price of nature gas (RMB/m3) |
| Qg | the calorific value of natural gas |
| t (t = 1, 2, …, T) | the index of time periods (h) |
| Δt | operational time (s) |
| T | total number of time periods |
| T1 | inlet temperature of compressor (°C) |
| T2 | outlet temperature of compressor (°C) |
| TC | total system cost in that day (RMB) |
| TCE | total consumption amounts of electricity power (kW) |
| TCG | total consumption amounts of natural gas (m3) |
| TWC | total consumption amounts of water (t) |
| Vc | the charge for pollutant c discharge (RMB/kg) |
| wp | the water price (RMB/t) |
| αGT1 and βGT1 | coefficients of fit function describing the relationship between excess heat and natural gas consumption |
| αGT2 and βGT2 | the coefficients of fit function that represents the relationship between power generation and natural gas consumption |
| αHRSG and βHRSG | coefficients of fit function that represents the relationship between the power consumption and steam production |
| aSB1 and bSB1 | the coefficients of fit function describing the relationship between the power consumption and steam production |
| αSB2 | empirical coefficient of thermal power conversion of SB |
| Λ | conversion coefficient of water vapor and water |
| ρ | density of natural gas (kg/m3) |
| η1 | efficiency of HRSG |
| η2 | efficiency of SBs |
| τ1, τ2 and τ3 | the intermediate variables, respectively |
References
- Mohn, K. The gravity of status quo: A review of IEA’s World Energy Outlook. Econ. Energy Environ. Policy 2020, 9, 63–81. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, Q.; Wang, Z.; Jermsittiparsert, K.; Shafiee, M. A new optimized configuration for capacity and operation improvement of CCHP system based on developed owl search algorithm. Energy Rep. 2020, 6, 315–324. [Google Scholar] [CrossRef]
- Tan, Z.-F.; Zhang, H.-J.; Shi, Q.-S.; Song, Y.-H.; Ju, L.-W. Multi-objective operation optimization and evaluation of large-scale NG distributed energy system driven by gas-steam combined cycle in China. Energy Build. 2014, 76, 572–587. [Google Scholar] [CrossRef]
- Jing, Y.-Y.; Bai, H.; Wang, J. Multi-objective optimization design and operation strategy analysis of BCHP system based on life cycle assessment. Energy 2012, 37, 405–416. [Google Scholar] [CrossRef]
- Wang, J.; Yang, Y.; Sui, J.; Jin, H. Multi-objective energy planning for regional natural gas distributed energy: A case study. J. Nat. Gas Sci. Eng. 2016, 28, 418–433. [Google Scholar] [CrossRef]
- Zhao, F.; Zhang, C.H.; Sun, B. Initiative Optimization Operation Strategy and Multi-objective Energy Management Method for Combined Cooling Heating and Power. IEEE-CAA J. Autom. Sin. 2016, 3, 385–393. [Google Scholar]
- Zheng, C.; Wu, J.; Zhai, X.; Wang, R. Impacts of feed-in tariff policies on design and performance of CCHP system in different climate zones. Appl. Energy 2016, 175, 168–179. [Google Scholar] [CrossRef] [Green Version]
- Luo, X.; Zhu, Y.; Liu, J.; Liu, Y. Design and analysis of a combined desalination and standalone CCHP (combined cooling heating and power) system integrating solar energy based on a bi-level optimization model. Sustain. Cities Soc. 2018, 43, 166–175. [Google Scholar] [CrossRef]
- Luo, Z.; Wu, Z.; Li, Z.; Cai, H.; Li, B.; Gu, W. A two-stage optimization and control for CCHP microgrid energy management. Appl. Therm. Eng. 2017, 125, 513–522. [Google Scholar] [CrossRef]
- Yang, G.; Zhai, X. Optimal design and performance analysis of solar hybrid CCHP system considering influence of building type and climate condition. Energy 2019, 174, 647–663. [Google Scholar] [CrossRef]
- Yang, G.; Zhai, X. Optimization and performance analysis of solar hybrid CCHP systems under different operation strategies. Appl. Therm. Eng. 2018, 133, 327–340. [Google Scholar] [CrossRef]
- Wang, J.; Lu, Z.; Li, M.; Lior, N.; Li, W. Energy, exergy, exergoeconomic and environmental (4E) analysis of a distributed generation solar-assisted CCHP (combined cooling, heating and power) gas turbine system. Energy 2019, 175, 1246–1258. [Google Scholar] [CrossRef]
- Zhu, H.; Huang, G. SLFP: A stochastic linear fractional programming approach for sustainable waste management. Waste Manag. 2011, 31, 2612–2619. [Google Scholar] [CrossRef] [PubMed]
- Charles, V.; Dutta, D. Identification of redundant objective functions in multi-objective stochastic fractional programming problems. Asia-Pac. J. Oper. Res. 2006, 23, 155–170. [Google Scholar] [CrossRef]
- Shen, K.; Yu, W. Fractional Programming for Communication Systems—Part I: Power Control and Beamforming. IEEE Trans. Signal Process. 2018, 66, 2616–2630. [Google Scholar] [CrossRef] [Green Version]
- Klačková, I.; Zajačko, I.; Lenhard, R.; Gritsuk, I.; Wiecek, D. Simulation of wood biomass combustion in hot water boiler. IOP Conf. Ser. Mater. Sci. Eng. 2020, 776, 012033. [Google Scholar] [CrossRef]
- Zhong, Y.F.; Yan, W.D. Research on modeling and simulation of a micro gas turbine based on MATLAB. Power Equip. 2019, 33, 325–330. [Google Scholar]
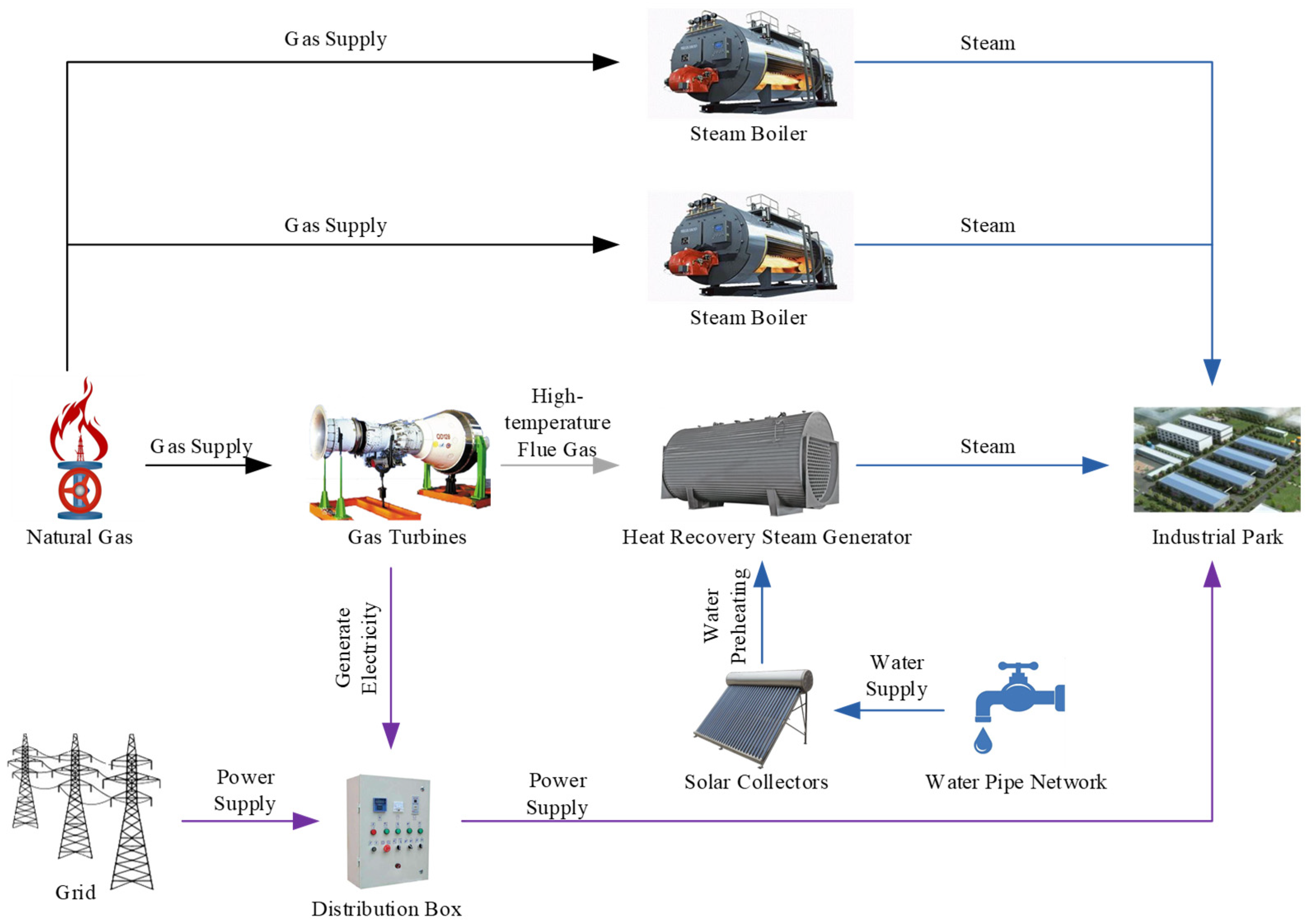

| Main Machines | |||||
|---|---|---|---|---|---|
| GTs | Note | HRSGs | SBs | ||
| Rated speed | 26,000 r/min | / | Production | 6 t/h | 15 t/h |
| Generating output | 1850 kW | Ambient temperature: 5 °C | Rated steam pressure | 1.25 MPa | 1.25 MPa |
| 171 kW | Ambient temperature: 15 °C | Rated steam temperature | 193.4 °C | 193.4 | |
| Efficiency | 24.4% | Ambient temperature: 5 °C | Economizer feed temperature | 104 °C | 104 °C |
| 23.6% | Ambient temperature: 15 °C | Blowdown rate | 2% | 2% | |
| Natural gas consumption | 742 Nm3/h | Ambient temperature: 5 °C | Inlet flue gas temperature | 570 °C | / |
| 709 Nm3/h | Ambient temperature: 15 °C | Gas mass flow | 9.09 kg/s | / | |
| Exhaust temperature | 570 °C | Ambient temperature: 5 °C | Exhaust temperature | <100 °C | ~137 °C |
| 578 °C | Ambient temperature: 15 °C | Efficiency | ~75% | ~93.4% | |
| Gas mass flow | 9.09 kg/s | Ambient temperature: 5 °C | Heating area | / | 286.19 m2 |
| 8.73 kg/s | Ambient temperature: 15 °C | Energy consumption | / | 1038 Nm3/h | |
| Time | Heating Seasons | Nonheating Seasons | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Energy Consumption | Economic Efficiency | Energy Consumption | Economic Efficiency | |||||||
| Gas (m3) | Power (kW) | Water (t) | Cost (RMB) | Profit (RMB) | Gas (m3) | Power (kW) | Water (t) | Cost (RMB) | Profit (RMB) | |
| 1 | 1066.27 | 231.79 | 22.27 | 4205.69 | 3099.71 | 166.94 | 182.60 | 9.20 | 873.79 | 2999.41 |
| 2 | 1066.27 | 231.79 | 22.27 | 4205.69 | 3099.71 | 166.94 | 182.60 | 9.20 | 873.79 | 2999.41 |
| 3 | 1066.27 | 231.79 | 22.27 | 4205.69 | 3099.71 | 166.94 | 182.60 | 9.20 | 873.79 | 2999.41 |
| 4 | 1066.27 | 231.79 | 22.27 | 4205.69 | 3099.71 | 166.94 | 182.60 | 9.20 | 873.79 | 2999.41 |
| 5 | 1066.27 | 231.79 | 22.27 | 4205.69 | 3099.71 | 166.94 | 182.60 | 9.20 | 873.79 | 2999.41 |
| 6 | 1066.27 | 231.79 | 22.27 | 4205.69 | 3099.71 | 166.94 | 182.60 | 9.20 | 873.79 | 2999.41 |
| 7 | 1066.27 | 231.79 | 22.27 | 4205.69 | 3099.71 | 166.94 | 182.60 | 9.20 | 873.79 | 2999.41 |
| 8 | 1066.27 | 231.79 | 22.27 | 4205.69 | 3099.71 | 166.94 | 182.60 | 9.20 | 873.79 | 2999.41 |
| 9 | 1768.37 | 269.89 | 32.27 | 6803.35 | 3102.05 | 728.62 | 213.08 | 17.20 | 2951.92 | 3001.28 |
| 10 | 1768.37 | 269.89 | 32.27 | 6884.32 | 4073.78 | 728.62 | 213.08 | 17.20 | 3015.84 | 3963.96 |
| 11 | 1768.37 | 269.89 | 32.27 | 6884.32 | 4073.78 | 728.62 | 213.08 | 17.20 | 3015.84 | 3963.96 |
| 12 | 1768.37 | 269.89 | 32.27 | 6884.32 | 4073.78 | 728.62 | 213.08 | 17.20 | 3015.84 | 3963.96 |
| 13 | 1768.37 | 269.89 | 32.27 | 6884.32 | 4073.78 | 728.62 | 213.08 | 17.20 | 3015.84 | 3963.96 |
| 14 | 1768.37 | 269.89 | 32.27 | 6884.32 | 4073.78 | 728.62 | 213.08 | 17.20 | 3015.84 | 3963.96 |
| 15 | 1768.37 | 269.89 | 32.27 | 6884.32 | 4073.78 | 728.62 | 213.08 | 17.20 | 3015.84 | 3963.96 |
| 16 | 1768.37 | 269.89 | 32.27 | 6884.32 | 4073.78 | 728.62 | 213.08 | 17.20 | 3015.84 | 3963.96 |
| 17 | 1768.37 | 269.89 | 32.27 | 6884.32 | 4073.78 | 728.62 | 213.08 | 17.20 | 3015.84 | 3963.96 |
| 18 | 1768.37 | 269.89 | 32.27 | 6938.29 | 4721.61 | 728.62 | 213.08 | 17.20 | 3058.46 | 4605.74 |
| 19 | 1066.27 | 231.79 | 22.27 | 4321.58 | 4738.32 | 166.94 | 182.60 | 9.20 | 965.09 | 4619.11 |
| 20 | 1066.27 | 231.79 | 22.27 | 4321.58 | 4738.32 | 166.94 | 182.60 | 9.20 | 965.09 | 4619.11 |
| 21 | 1066.27 | 231.79 | 22.27 | 4321.58 | 4738.32 | 166.94 | 182.60 | 9.20 | 965.09 | 4619.11 |
| 22 | 1066.27 | 231.79 | 22.27 | 4275.22 | 4082.88 | 166.94 | 182.60 | 9.20 | 928.57 | 3971.23 |
| 23 | 1066.27 | 231.79 | 22.27 | 4275.22 | 4082.88 | 166.94 | 182.60 | 9.20 | 928.57 | 3971.23 |
| 24 | 1066.27 | 231.79 | 22.27 | 4275.22 | 4082.88 | 166.94 | 182.60 | 9.20 | 928.57 | 3971.23 |
| aggregate | 32,611.48 | 5943.92 | 634.47 | 128,252.07 | 91,675.23 | 9623.43 | 4687.23 | 300.74 | 42,808.33 | 89,085.07 |
| Heating Seasons | |||
| Objective Functions | Traditional Model | MOFP Model | Gap |
| f(x) | 48,023,330,907.09 | 48,023,329,663.71 | 1243.3895 |
| g(x) | 8,752,958,259.86 | 8,752,958,133.22 | 126.6447 |
| h(x) | 981,030,925.43 | 981,030,911.24 | 14.1943 |
| EI | −0.00334281 | −0.01208454 | 0.0087 |
| A Year | |||
| Objective Functions | Traditional Model | MOFP Model | Gap |
| f(x) | 72,869,132,006.15 | 72,869,131,089.21 | 916.9460 |
| g(x) | 20,854,468,697.71 | 20,854,468,730.08 | −32.3698 |
| h(x) | 1,796,291,165.26 | 1,796,291,161.78 | 3.4822 |
| EI | 7537.9899 | 7537.9899 | 0.000031 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Meng, N.; Wang, X.; Tan, J.; Li, W. A Multiobjective Fractional Programming for a CHP System Operation Optimization Based on Energy Intensity. Energies 2022, 15, 1965. https://doi.org/10.3390/en15061965
Xu Y, Meng N, Wang X, Tan J, Li W. A Multiobjective Fractional Programming for a CHP System Operation Optimization Based on Energy Intensity. Energies. 2022; 15(6):1965. https://doi.org/10.3390/en15061965
Chicago/Turabian StyleXu, Ye, Na Meng, Xu Wang, Junyuan Tan, and Wei Li. 2022. "A Multiobjective Fractional Programming for a CHP System Operation Optimization Based on Energy Intensity" Energies 15, no. 6: 1965. https://doi.org/10.3390/en15061965






