Development and Experimental Implementation of Active Tilt Control System Using a Servo Motor Actuator for Narrow Tilting Electric Vehicle
Abstract
1. Introduction
- A DTC controller is developed using state feedback control with pole placement design technique. Unlike the PD controller proposed in [1], a derivative term is not used. The proposed controller is less sensitive against noise.
- The state feedback controller is improved by combination with a first order reference model. In this way, further reduction in actuator torque and perceived acceleration can be achieved.
- Detailed design inputs for the servo motor actuator and tilt control are studied.
- DTC configuration given in this study has a servo motor having 400 W rated power at 24 or 48 V DC input. The proposed configuration can achieve tilting up to 8 m/s vehicle speed without exceeding motor’s continuous torque.
- Simulation and experimental verification on a three-wheeled electric vehicle are carried out.
- Section 1 provides a review of the state of the art, summarizes technological problems, and compares the hydraulic and servo motor actuators.
- Section 2 describes the application methodology of the servo motor in the DTC system. Control modes of the servo motor, critical design inputs, and integration into the tilt controller are studied. A prototype vehicle configuration and control configuration is described. Section 2 can also be considered as the conceptual design phase of this study.
- Section 3 describes the design of the tilt controller and state feedback control law by pole placement design technique. Simulation results in Matlab–Simulink are presented.
- Section 4 presents the software implementation steps and experimental results.
- Section 5 presents the conclusions and possible future tasks.
1.1. Brief Review of the State of the Art in Tilt Control Technology
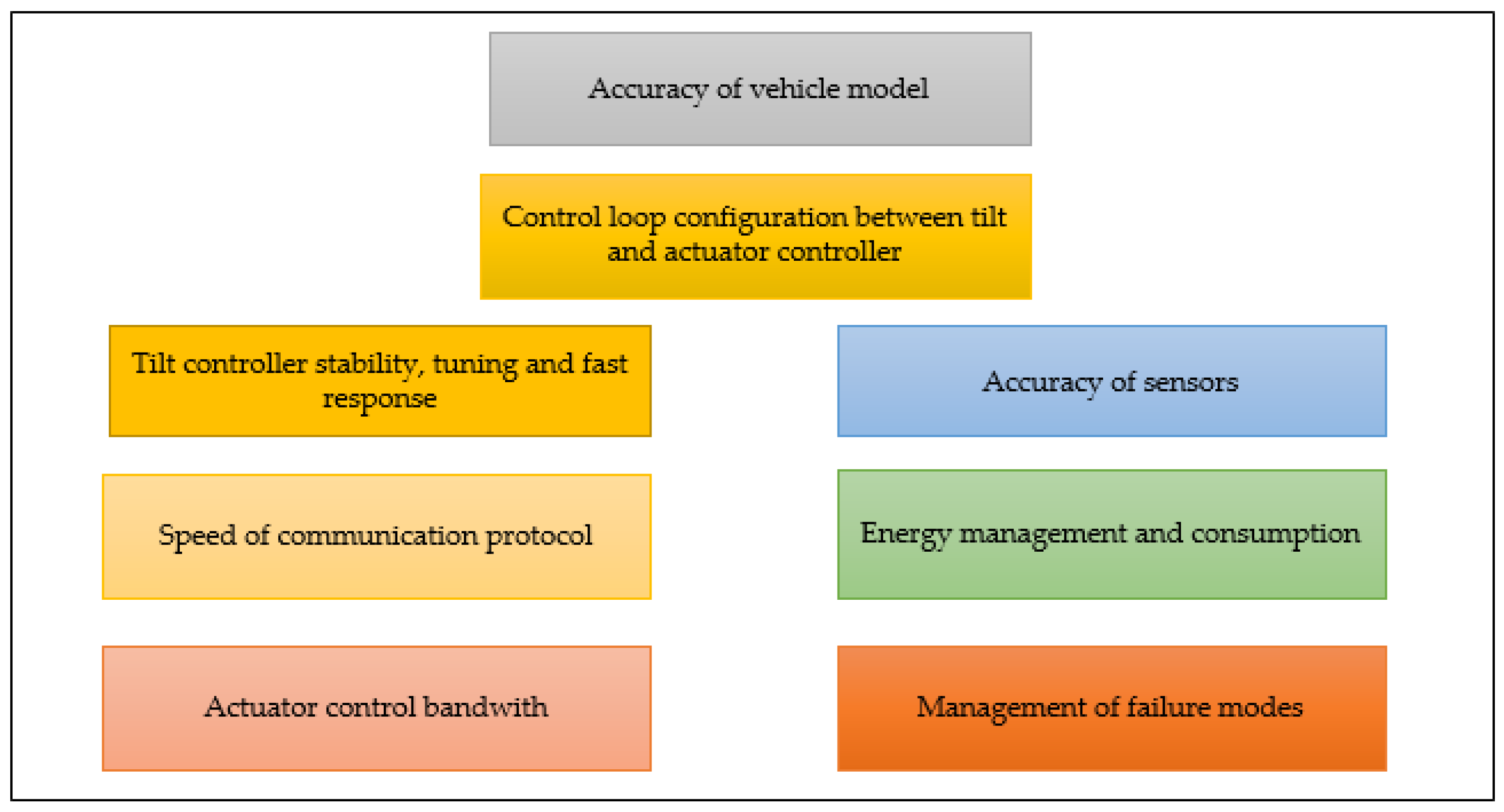
1.2. Summary of Technological Problems
- (1)
- Stability control
- Speed limitations of DTC and STC methods: Model changeover and bumpless transfer are problems of the combined DTC–STC method. Using a DTC and STC combination requires separate actuator design, high computation effort, and extra cost.
- Limited stability margin of PID and PD controllers: Instability or performance degradation may occur in the case of variation of vehicle mass, roll inertia, suspension stiffness, and vehicle speed.
- Performance of tilt controller in discrete form for a given sampling time: A designed tilt controller may require high sampling time for the required performance. In this case, it should be verified that the actuator controller should also respond, i.e., have the required bandwidth to respond to the tilt controller. Performance of model predictive controller changes at different sampling times. In [27], varying sampling time for the MPC method is proposed for vehicle control applications. In [28], a discrete form of MPC with low sampling time is studied for power converter application.
- (2)
- Energy consumption
- Energy consumption should be analysed and compared for hydraulic and servo motor actuators. Power and energy consumption and available battery energy for the next tilting motion are critical for driver’s safety and system reliability.
- (3)
- Vehicle modeling
- Modeling of nonlinear effects such as sideslip angle and tire modeling: Tilting on slippery roads and operation at high speedsrequire a nonlinear vehicle model.
- (4)
- Functional safety
- Failure of sensors, actuator or software related reliability problems.
- (5)
- Energy management
- To improve energy management of the tilt control system, early warnings and a driver assistant system are needed to inform the driver on the possibility of the next tilting movement, considering available battery energy.
1.3. Actuator Types in Tilt Control
- (1)
- Torque and power derating of the servo motor due to temperature and battery voltage variation;
- (2)
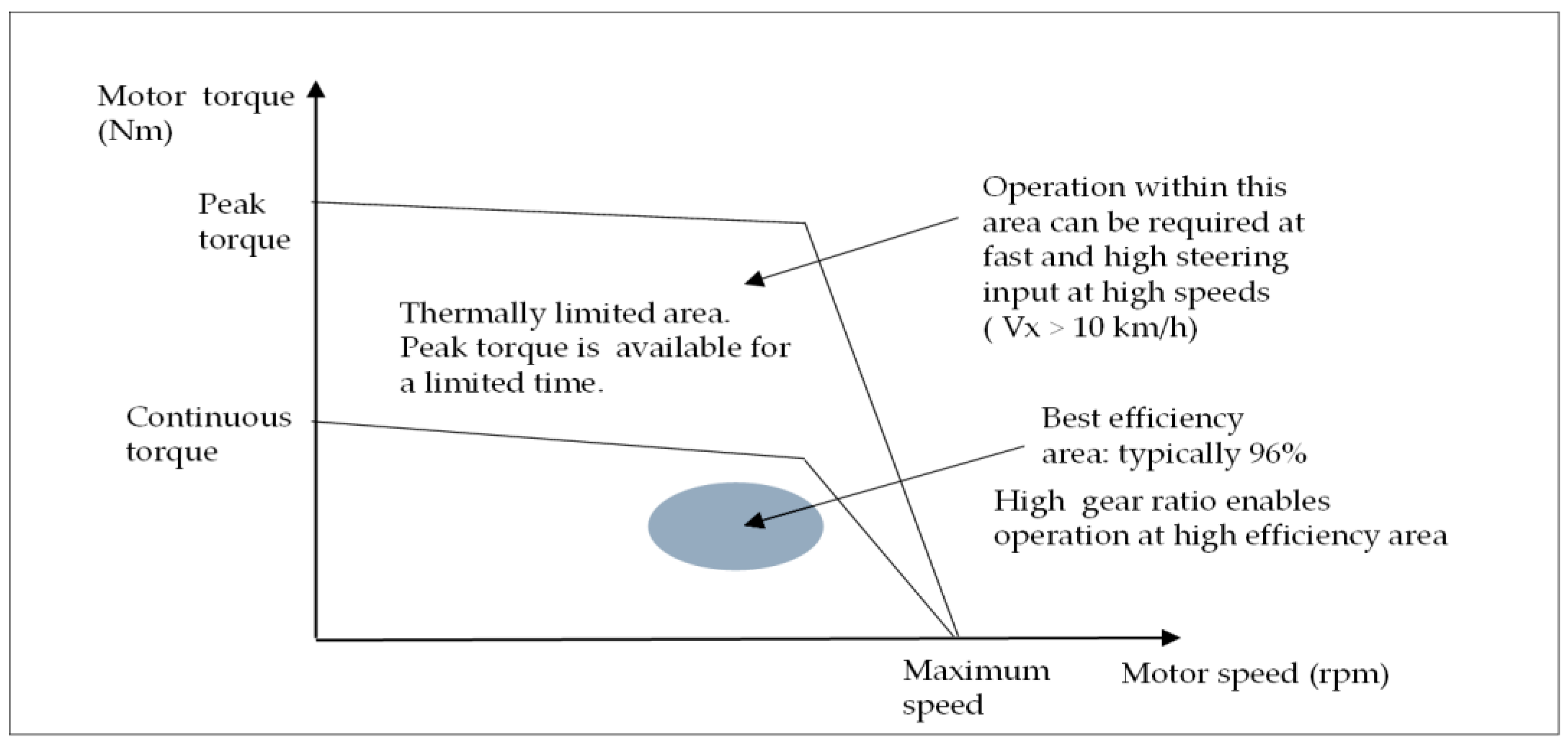
- Limited duration of operation at maximum peak torque which is typically between 0 and 5 s. Duration of operation between continuous torque and maximum peak torque curves varies depending on the motor thermal condition as shown in Figure 2. This constraint is the most critical one when operating at high vehicle speeds above 10 km/h. Therefore, reduction of peak torque is the most critical design criteria. If servo motor can be coupled with a gearbox having high gear ratio, operation within the thermally limited area can be avoided.
1.3.1. Comparison of Hydraulic and Servo Motor Actuators
- Dual actuator topology for right and left suspensions can be easily integrated;
- Fewer parameters and simple operation for integration;
- High damping provides higher comfort during tilting motion.
- Less efficiency;
- Slow torque dynamics;
- Gearbox cannot be used as applied in servo motor, which increases hydraulic actuator torque rating;
- Internal speed control loop is not a standard loop for hydraulic actuators;
- More components;
- More audible noise;
- Low temperature causes increase of viscosity, which causes vibration, noise, and wear of internal pump parts;
- Performance variation at high and low temperatures.
- Torque linearity within defined temperature limits (typically between 0 and 40 degrees);
- Fast torque response can compensate for system delays in the DTC method;
- Fewer moving components;
- Minimum maintenance;
- Monitoring capability of motor and MCU parameters such as estimated torque, power and temperature etc;
- High system efficiency >85%;
- High accuracy of positioning and speed control;
- Enabling configuration of motor control parameters such as tuning of speed, position control loops, ramp profiles (linear, S-ramp to reduce jerk), torque monitoring and limitation;
- Electrically safe operation up to 60 V DC;
- Electrical motor can be coupled with required gearbox to increase tilt torque.
- Less damping than hydraulic actuator;
- Limited duration of operation at peak torque due to thermal limit of electric motors;
- Torque derating above 40°.
2. Application Methodology
- 24 or 48 V battery supply for servo motor controller;
- Operating the motor at efficient points;
- Ratio of load to motor inertia and selection of gear ratio of gearbox as design parameter;
- Duty cycle and requested maximum torque should match with servo motor torque-speed curve shown in Figure 2.
- PM motors have a cogging torque problem that affects the tilting comfort and also can cause positioning errors [34]. In the case of using a gearbox with high gear ratio, cogging torque is amplified and may cause discomfort at the driver side and vibration through the vehicle body. Therefore, the servo motor should have minimum cogging torque.
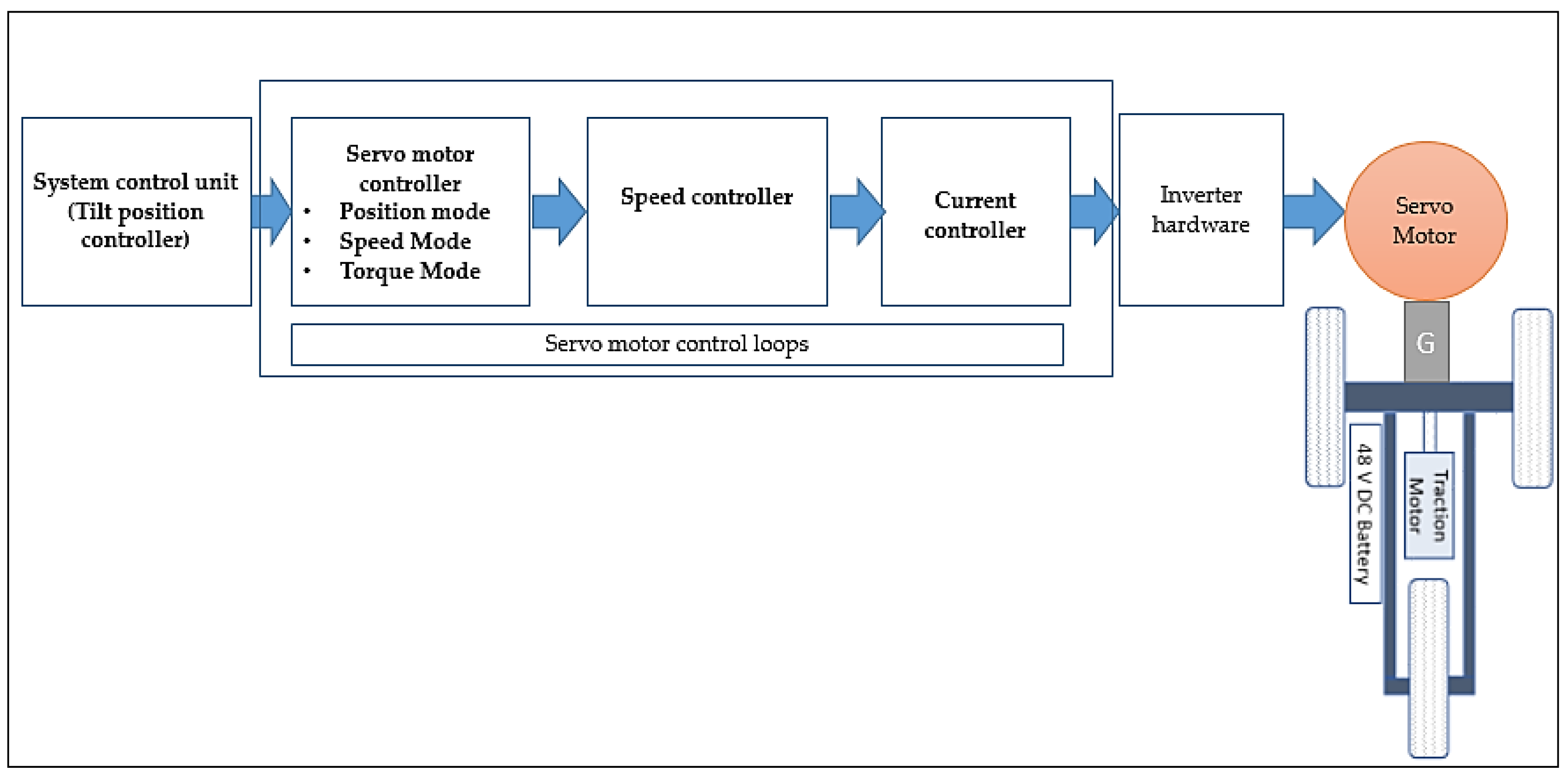
2.1. Selection of Control Mode of Servo Motor Controller
- Current controller: 62.5…125 µs;
- Speed controller: 62.5…500 µs;
- Position controller: 500 µs…4 ms;
2.1.1. Torque Control Mode
2.1.2. Speed Control Mode
2.1.3. Position Control Mode
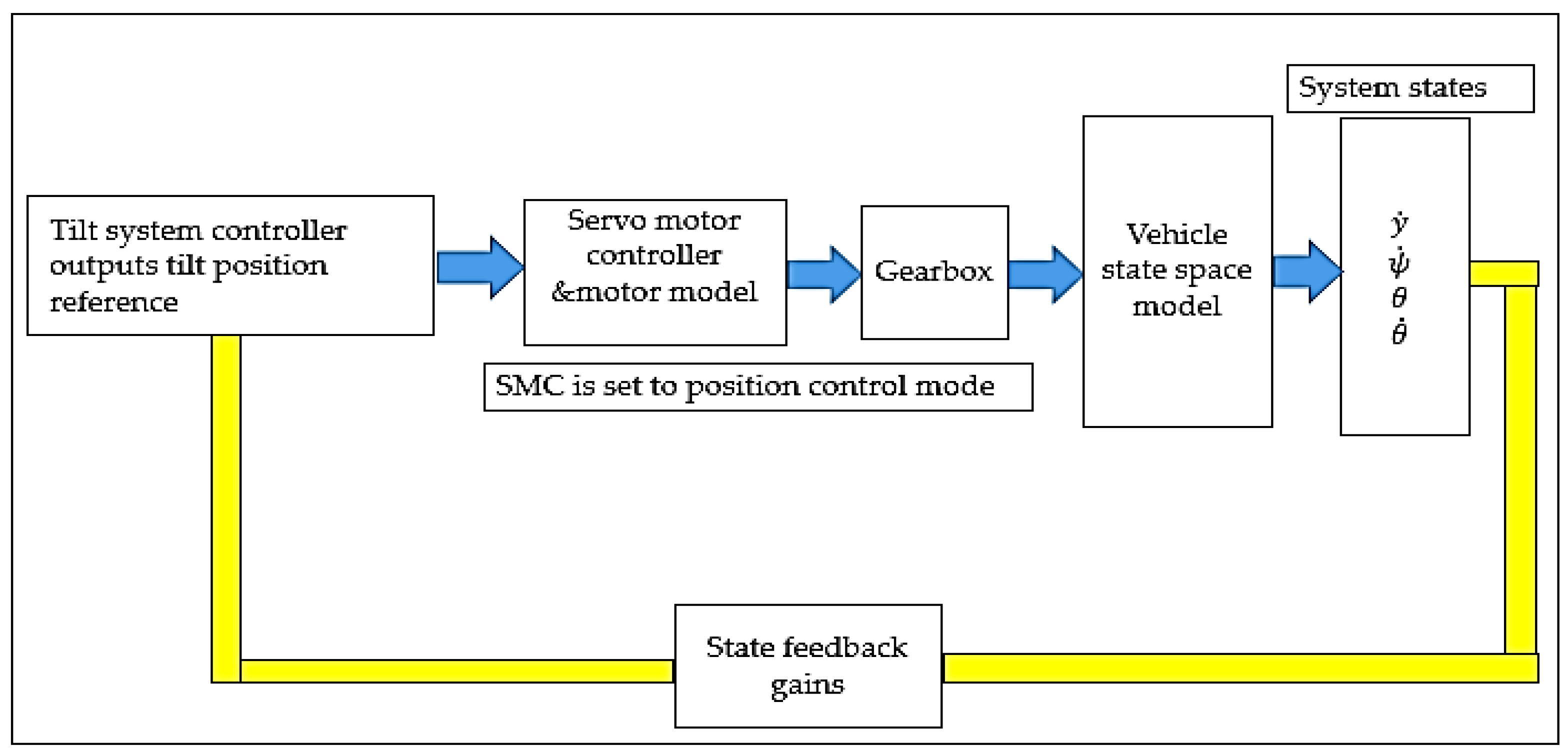
2.2. Interactions between Tilt System and Servo Motor Actuator
- There are transient and steady-state components of lateral acceleration, as given in Equation (1) [11].
- 2.
- In order to produce a tilt control reference, reliable and practically realizable methods and signals are required for stable operation. Lateral translation acceleration is used in PD control [1,11], and lateral vehicle speed is used as a state variable in state feedback by H2 optimal control in [16]. Both of these variables are difficult to measure or estimate in a reliable manner. In order to produce faster torque response without using or , an alternative method is proposed in Section 3.1.5.
- 3.
- Actuator dynamics and low stiffness of tilting system: Very fast actuator response can cause oscillations during tilting because suspension and tire elasticity exhibit a flexible system with low rigidity. Although the fast torque response is desired to reduce the perceived acceleration, the actuator should not cause oscillations through the tire suspension system. A similar problem occurs in electric vehicles, which is known as electric drive-train oscillations [36].
- 4.
- Ratio of load to motor inertia: The roll inertia of NTV about the roll axis can be around 80 kg∙m2 range [11,16]. In case the three wheeled vehicle is used for logistic applications, it can have additional payload, and hence roll (tilt) inertia will increase further. Servo motor in this study has 0. 34 kg∙cm2 rotor inertia [37]. In servo motor applications, there is a limitation for the load-to-motor inertia ratio [38]. The most practical way of providing the limitation is to use a gearbox.
2.3. Definition of Servo Motor Operating Points and Actuator Gear Ratio
- A servo motor with higher torque and lower speed range: This type of servo motor requires a lower gearbox ratio. Large motor diameter is the main concern. Efficient operating points may not be provided at low speeds.
- A servo motor with lower torque and higher speed range: This type of servo motor requires a gearbox with higher gear ratio. The motor can be operated at higher speed and hence at higher efficiency area.
2.4. Prototype Vehicle Configuration and Proposed Control Configuration
2.4.1. Vehicle Configuration
- Three-wheeled electric NTV, one front wheel and two rear wheels as shown in Figure 4;
- Maximum steering angle 45 degrees;
- Traction system has an electric motor and Li-ion battery at 48 V DC;
- Tilt actuator system and control modules are supplied by separate 24 V DC;
- Tilt actuator system has separate system control unit.
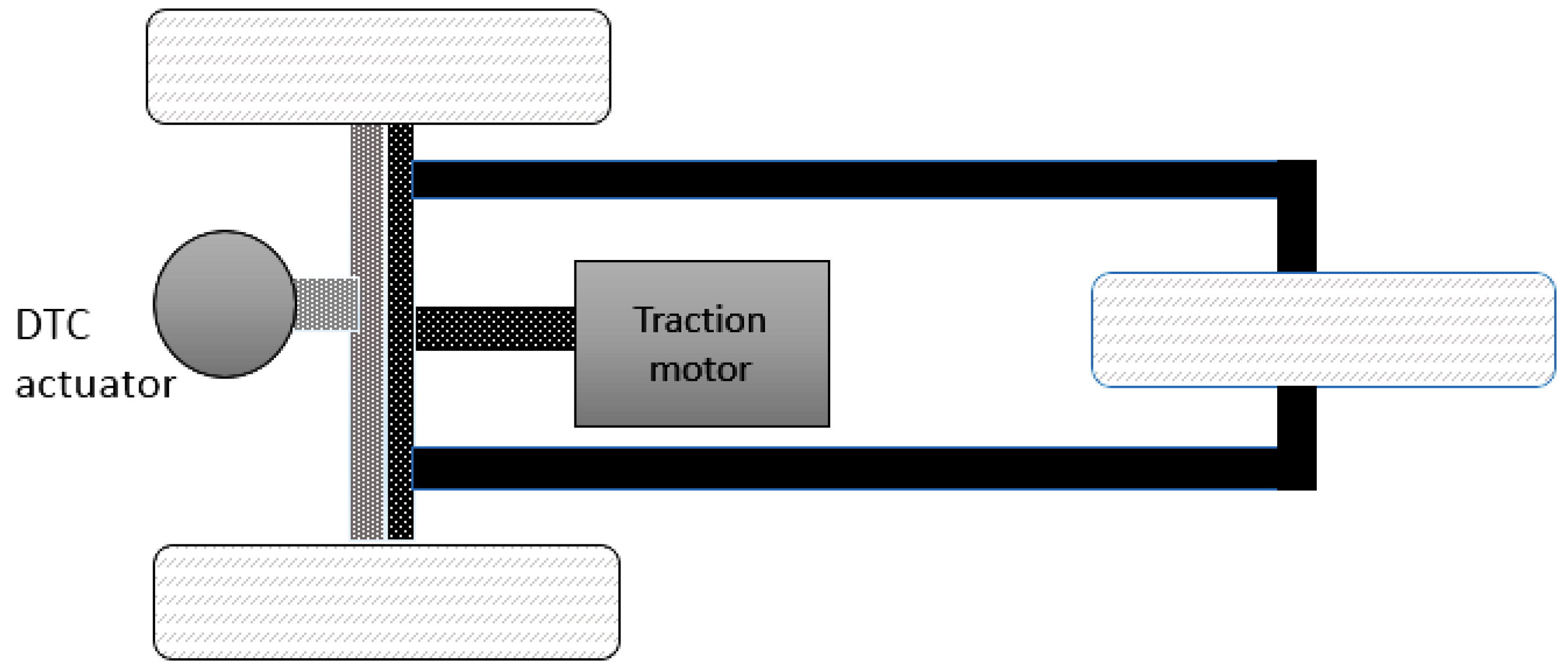
2.4.2. DTC Mechanism and Actuator Layout
2.4.3. Proposed Control Loop Configuration
3. Design and Simulation
3.1. Controller Design
3.1.1. Mathematical Model of a Three-Wheeled Vehicle
3.1.2. Controllability and Observability
3.1.3. Pole Placement Design Considering Minimum Input Power
- Steady state power should be constant or zero in a perfectly coordinated turn. This property of tilt control can also be interpreted by the stability law of the Lyapunov’s direct method which states that zero energy consumed by a mechanical system corresponds to an equilibrium state whereas instability is related to continuously increasing mechanical energy [45].
- As shown in simulations, the yaw rate and tilt angle feedback terms perform a rampwise action similar to integral action that ramps the actual value to the control reference [46]. Therefore, the actuator control model has no need for an integrator. In most state-of-art studies, a proportional derivative controller is used.
- Tilting speed is the derivative of the tilting position and its effect as a state feedback is similar to the derivative term in PD control.
- Gain applied to lateral speed is set to zero. This is due to the complexity of estimation of lateral speed and variation in estimation error. The requested stability can also be provided by ignoring it. Lateral speed and yaw rate have similar changes. Detailed simulations are given in [16]. Moreover, estimation error and noise of lateral speed can yield inaccurate results which can risk the stability in practical experiments. Proper settings of gains applied to yaw rate, tilt position and speed can compensate for the absence of lateral speed feedback. Lateral speed estimation methods and simulation results are studied in [47].
3.1.4. Simplified Model of Servo Motor Controller and Control Input
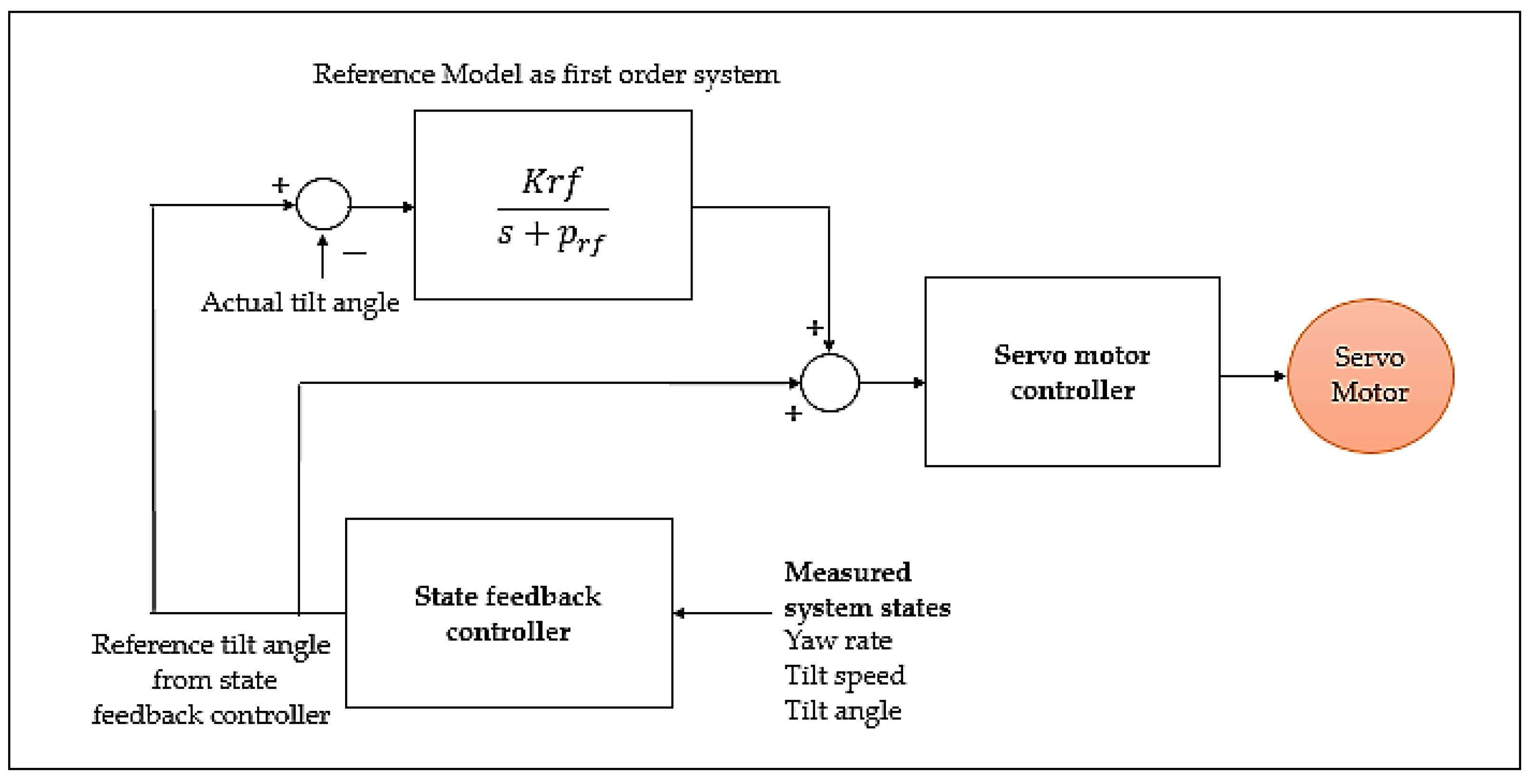
3.1.5. Improvement of State Feedback Control with Reference Model Concept
3.2. Simulation
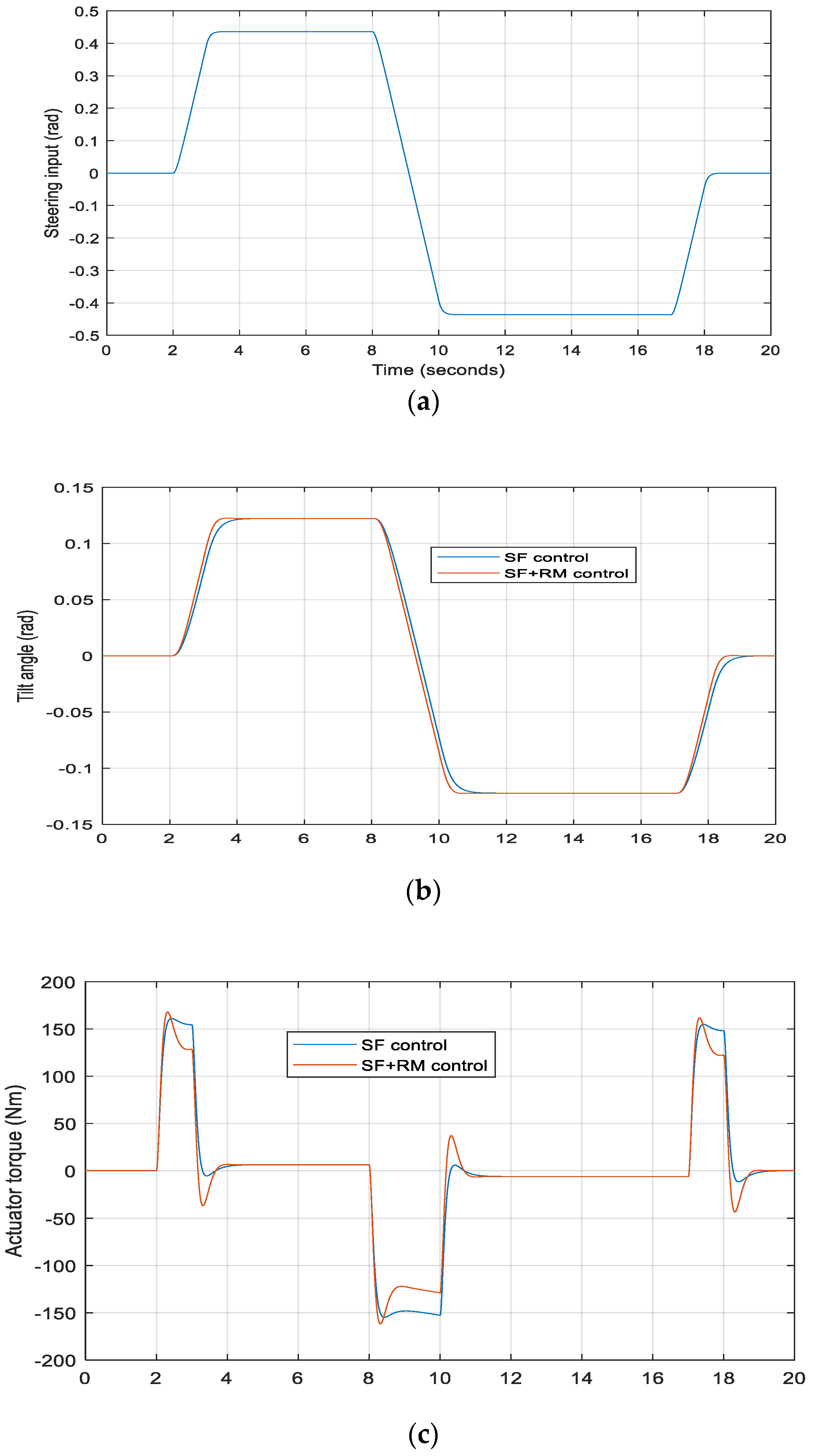
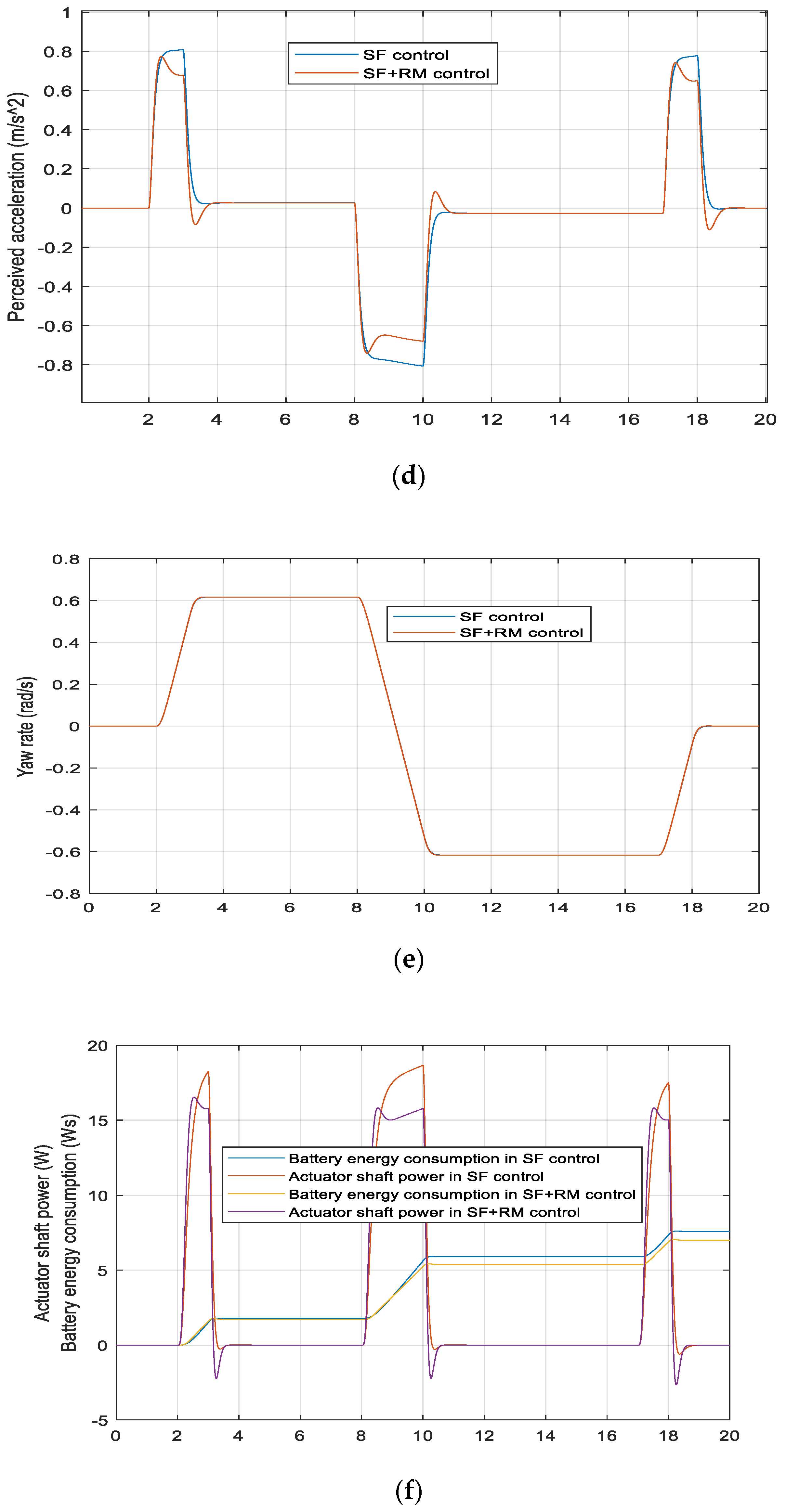
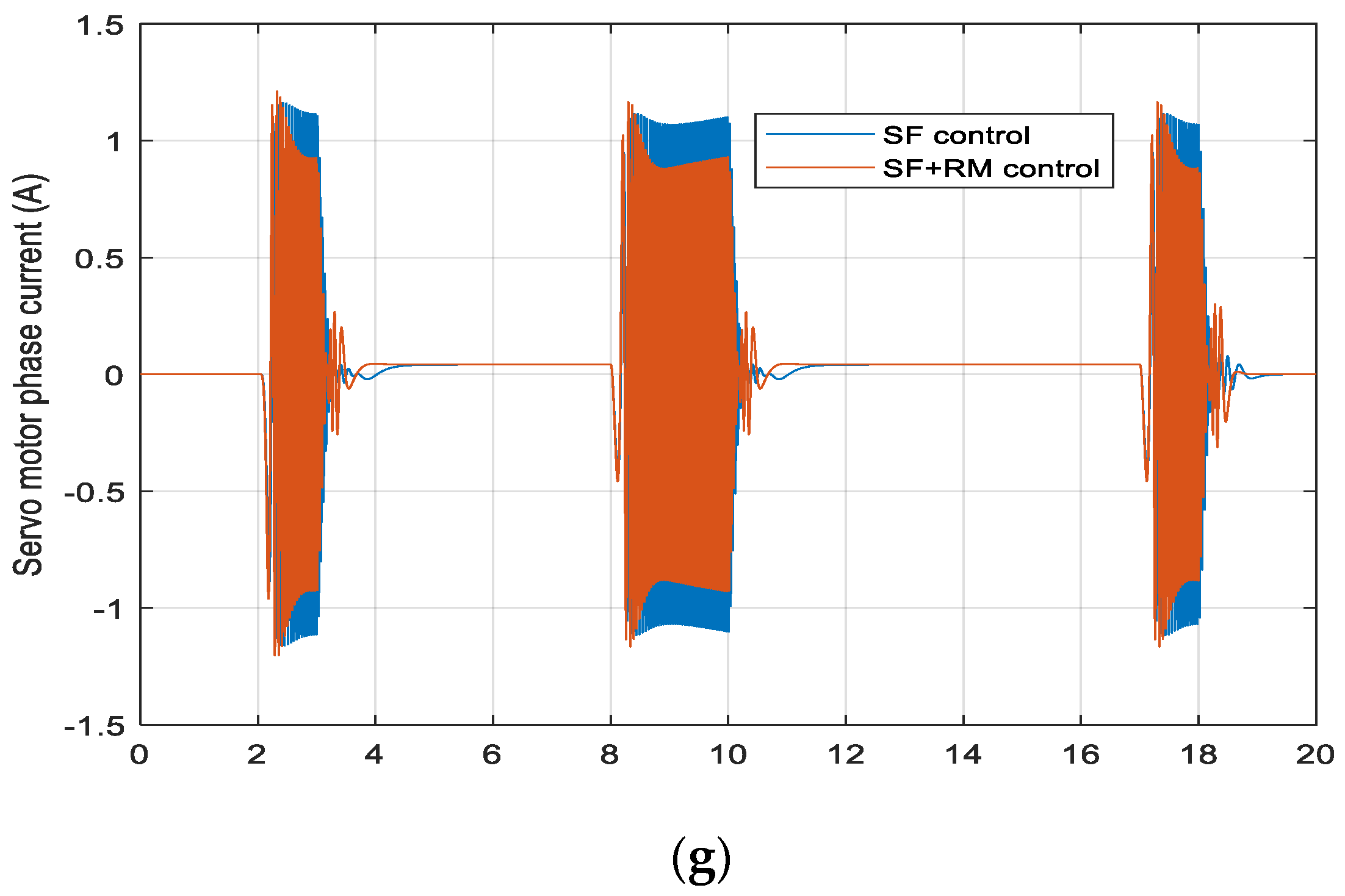
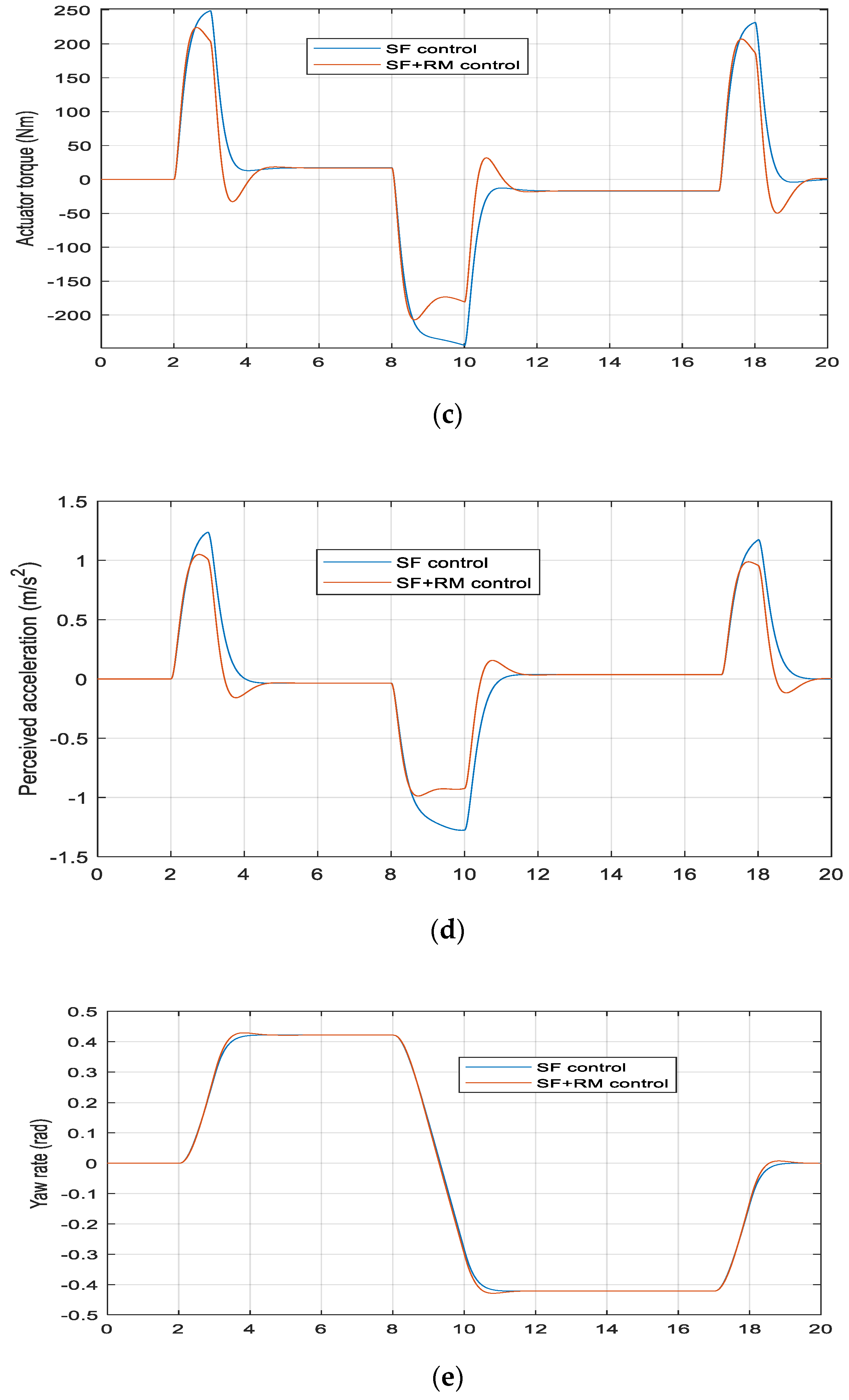
3.2.1. Simulation Results
4. Experimental Results
4.1. Software Development
- ▪
- Software development in SCU based on Simulink models;
- ▪
- Creation of CAN 2.0 .dbc files for CAN messages;
- ▪
- Code generation in SCU.
- ▪
- PLC program development for protocol conversions and matching of messages;
- ▪
- Configuration of gateway modules for each CAN message;
- ▪
- Protocol conversion for SMC is implemented from Profinet to CAN 2.0;
- ▪
- Protocol conversion for absolute encoder measuring the steering position is implemented from Profinet to CAN 2.0;
- ▪
- For IMU sensor: from CANopen to Profinet and from Profinet to CAN 2.0.
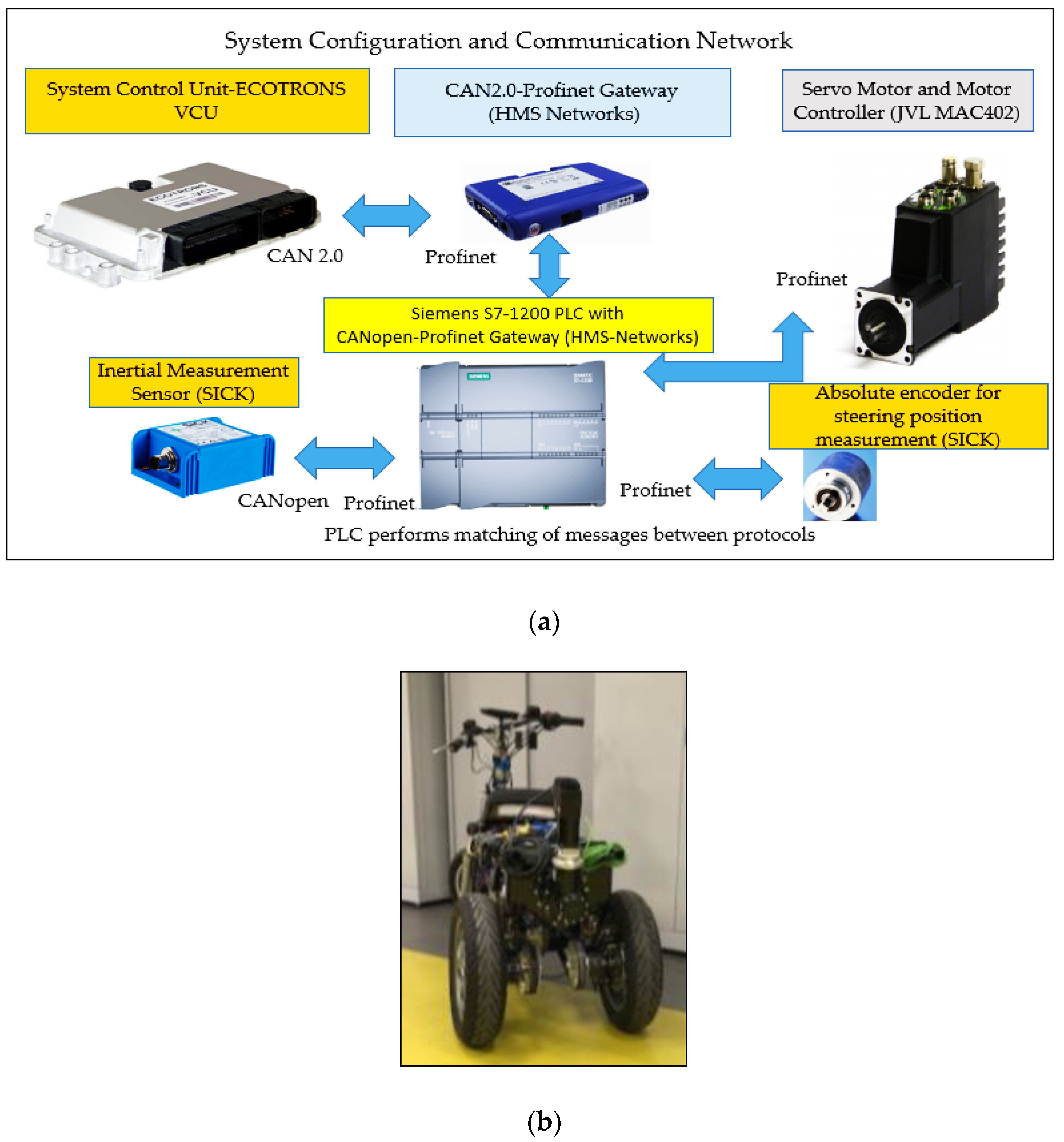
4.2. Configuration of Test Equipments
4.3. Experiments
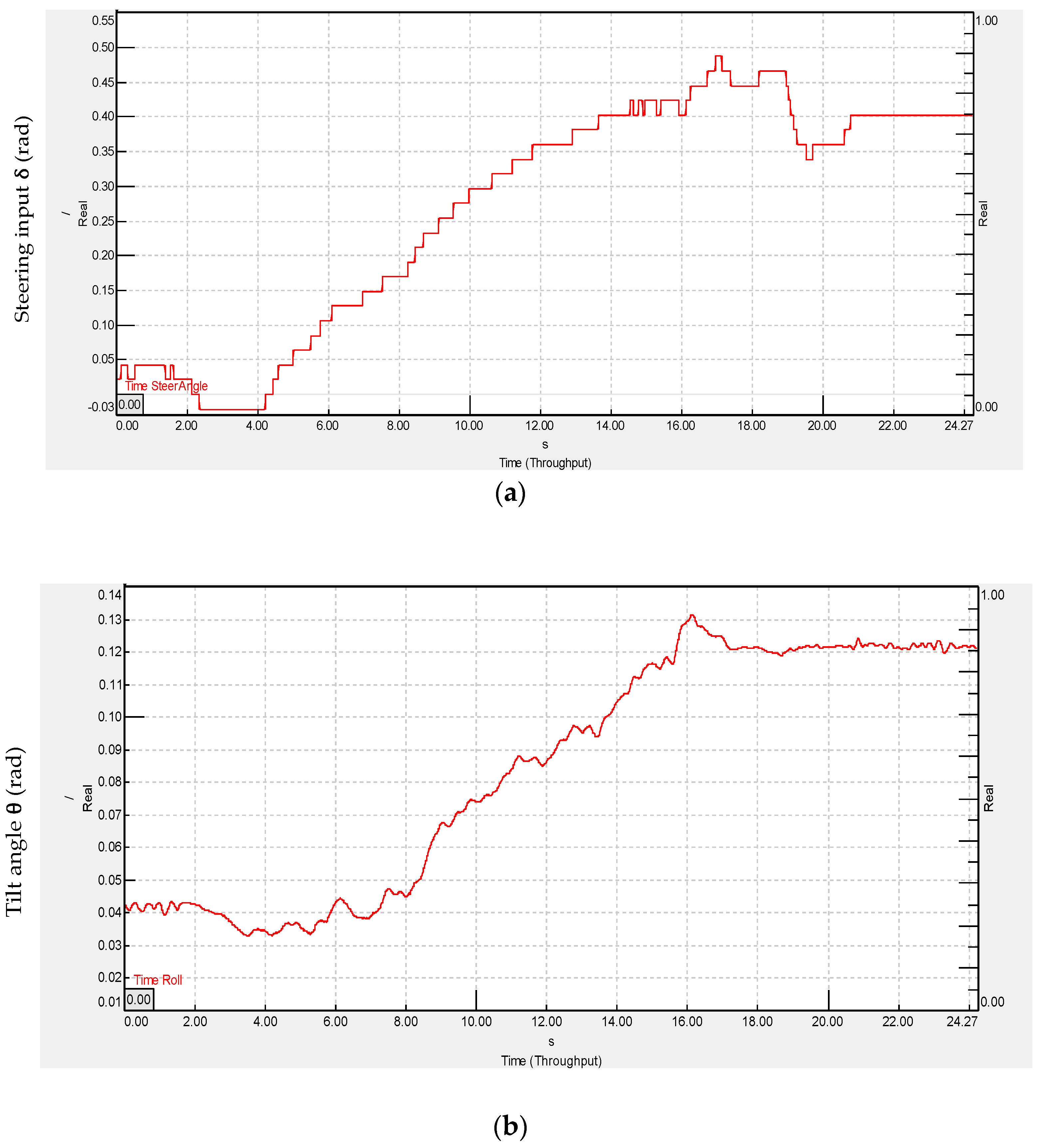
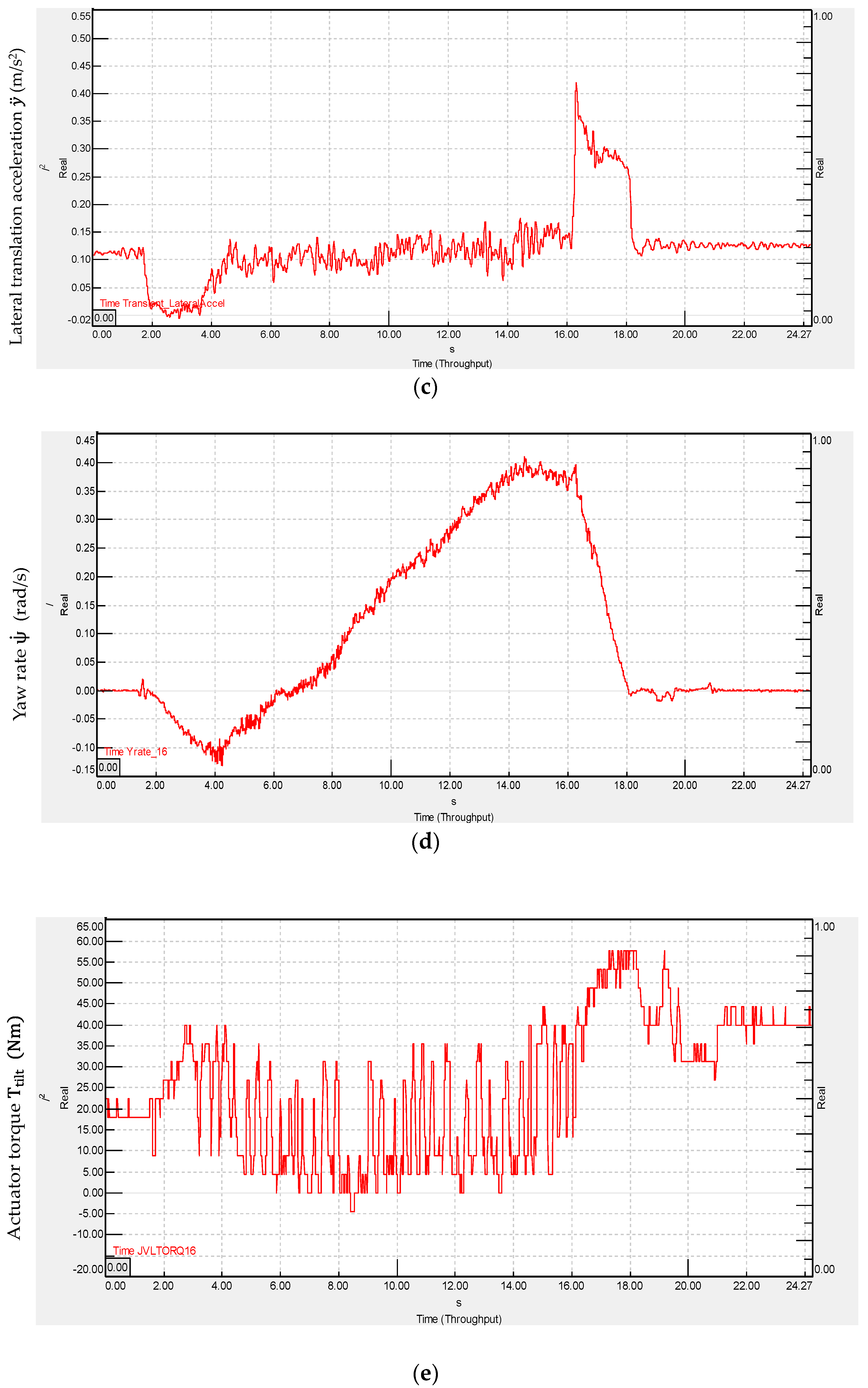
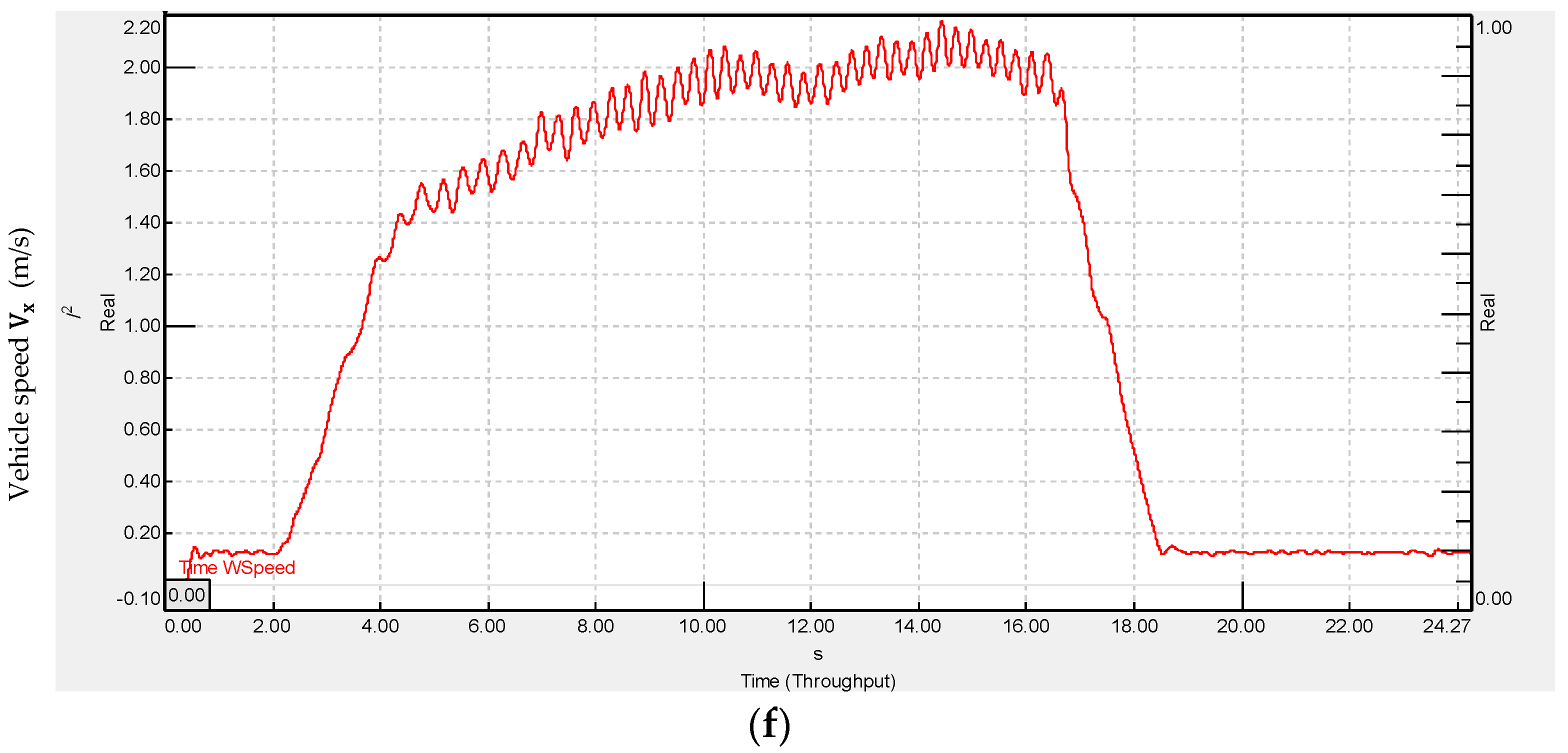
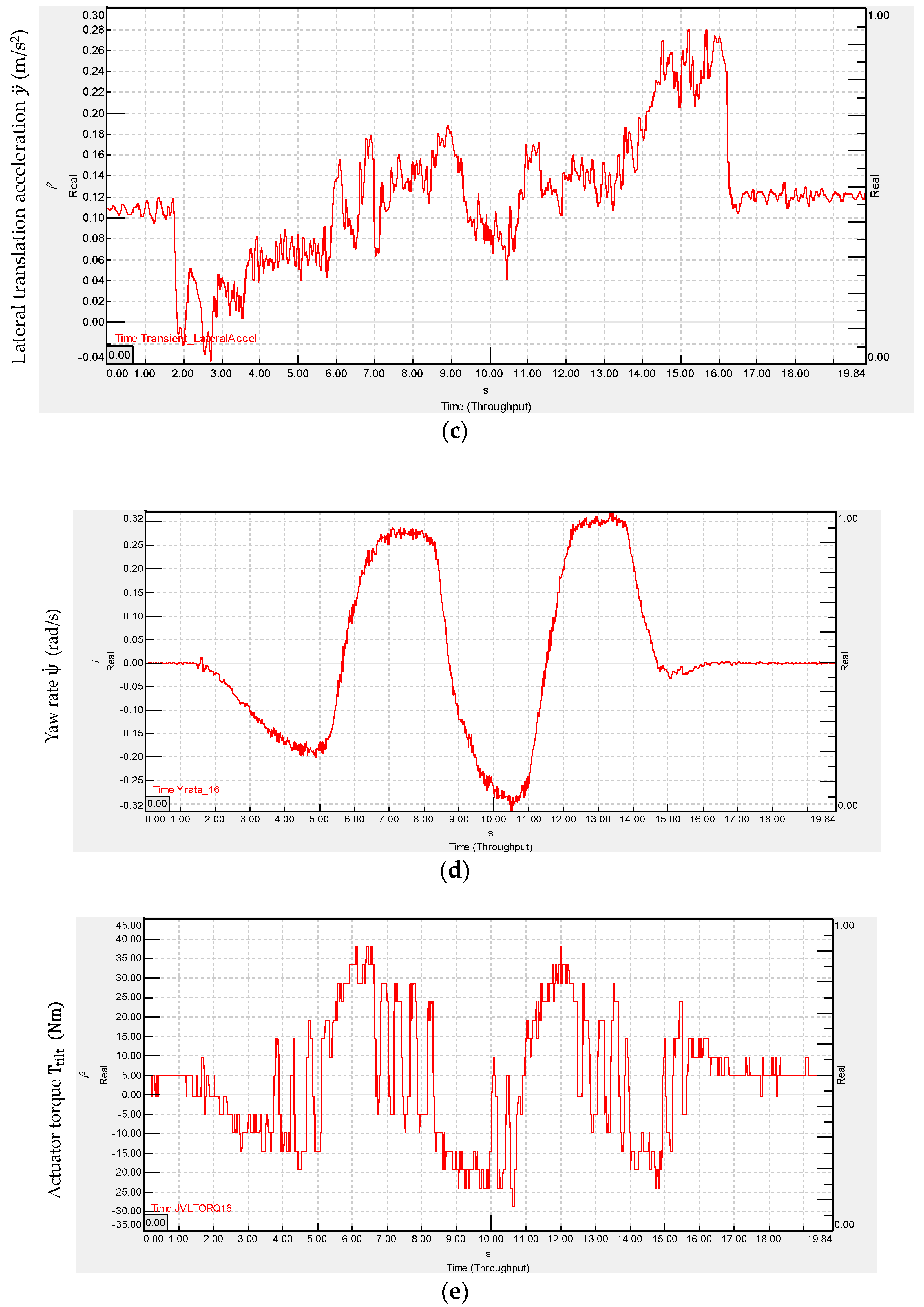
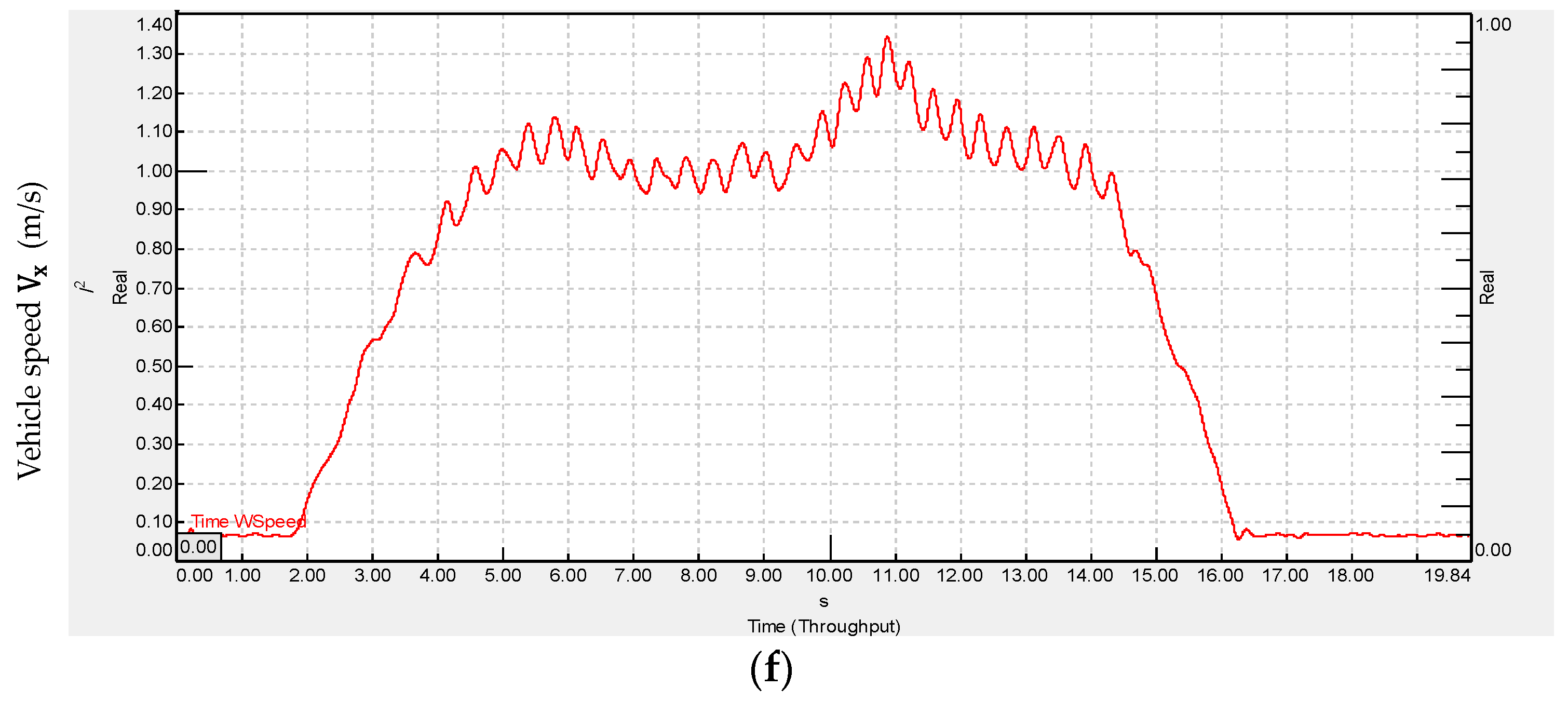
4.3.1. Cornering Test at 2 m/s Vehicle Speed
4.3.2. Slalom Test
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| θtilt_ref | Tilt control reference (rad) |
| A | State matrix in state space equation |
| B | Input matrix in state space equation |
| Input matrix for steering input | |
| Input matrix for actuator torque input | |
| Total vehicle mass including driver (290 kg) | |
| Longitudinal vehicle speed (m/s) | |
| Height of center of gravity (0.65 m) | |
| Coefficient representing one front wheel in Equation (2) (0.5) | |
| λf1 | Front wheel camber stiffness (1500 N/rad) |
| Front wheel camber stiffness applied in Equation (2) (750 N/rad) | |
| λr | Rear wheel camber stiffness (1000 N/rad) |
| Front wheel cornering stiffness (8000 N/rad) | |
| = | Front wheel cornering stiffness applied in Equation (2) (4000 N/rad) |
| Rear wheel cornering stiffness (10.000 N/rad) | |
| lf | Distance from center of gravity to front wheel (0.65 m) |
| Distance from center of gravity to rear wheels (0.75 m) | |
| Ix | Tilt moment of inertia (75 kg∙m2) |
| Yaw moment of inertia (140 kg∙m2) | |
| g | Gravity of earth (9.81 m/s2) |
| Lateral speed of vehicle (m/s) | |
| Lateral translation acceleration of vehicle (m/s2) | |
| Yaw rate (rad/s) | |
| Actual tilt angle (rad) | |
| Actual tilt speed (rad/s) | |
| Driver steering input (rad) | |
| Tilt actuator torque (Nm) | |
| θsmref | Position reference of SMC (rad) |
| Actual position of SMC (rad) | |
| Speed reference of SMC (rad/s) | |
| Speed actual value of SMC (rad/s) | |
| SMC torque reference (Nm) | |
| Total moment of inertia reflected on servo motor shaft (kg∙m2) | |
| Moment of inertia of servo motor (kg∙m2) | |
| Gear ratio of gearbox (330:1) | |
| Position controller gain of SMC | |
| Speed controller gain of SMC | |
| State feedback gain of lateral speed | |
| State feedback gain of yaw rate | |
| State feedback gain of tilt angle | |
| State feedback gain of tilt speed | |
| Gain of reference model | |
| prf | Pole of reference model |
| Perceived acceleration (m/s2) |
References
- So, S.-G.; Karnopp, D. Active Dual Mode Tilt Control for Narrow Ground Vehicles. Veh. Syst. Dyn. 1997, 27, 19–36. [Google Scholar] [CrossRef]
- So, S.-G.; Karnopp, D. Switching Strategies for Narrow Ground Vehicles with Dual Mode Automatic Tilt Control. Int. J. Veh. Des. 1997, 18, 518–532. [Google Scholar]
- Gohl, J.; Rajamani, R.; Alexander, L.; Starr, P. The Development of Tilt-Controlled Narrow Ground Vehicles. In Proceedings of the American Control Conference, Anchorage, AK, USA, 8–10 May 2002. [Google Scholar]
- Rajamani, R.; Gohl, J.; Alexander, L.; Starr, P. Dynamics of narrow tilting vehicles. Math. Comput. Model. Dyn. Syst. 2003, 9, 209–231. [Google Scholar] [CrossRef]
- Gohl, J.; Rajamani, R.; Alexander, L.; Starr, P. Active Roll Mode Control Implementation on a Narrow Tilting Vehicle. Veh. Syst. Dyn. 2004, 42, 347–372. [Google Scholar] [CrossRef]
- Piyabongkarn, D.; Keviczky, T.; Rajamani, R. Active Direct Tilt Control For Stability Enhancement Of A Narrow Commuter Vehicle. Int. J. Automot. Technol. 2004, 5, 77–88. [Google Scholar]
- Drew, B.W. Development of Active Tilt Control for a Three-Wheeled Vehicle. Ph.D. Thesis, University of Bath, Bath, UK, 2006. [Google Scholar]
- Snell, A. An Active Roll-Moment Control Strategy for Narrow Tilting Commuter Vehicles. Veh. Syst. Dyn. 1998, 29, 277–307. [Google Scholar] [CrossRef]
- Kidane, S.; Alexander, L.; Rajamani, R.; Starr, P.; Donath, M. A fundamental investigation of tilt control systems for narrow commuter vehicles. Veh. Syst. Dyn. Int. J. Veh. Mech. Mobil. 2008, 46, 295–322. [Google Scholar] [CrossRef]
- Chiou, J.C.; Lin, C.Y.; Chen, C.L.; Chien, C.P. Tilting motion control in narrow tilting vehicle using double-loop PID controller. In Proceedings of the 7th Asian Control Conference, Hong Kong, China, 27–29 August 2009. [Google Scholar]
- Kidane, S.; Rajamani, R.; Alexander, L.; Starr, P.; Donath, M. Development and experimental evaluation of a tilt stability control system for narrow commuter Vehicles. IEEE Trans. Control. Syst. Technol. 2010, 18, 1266–1279. [Google Scholar] [CrossRef]
- Berote, J. Dynamics and Control of a Tilting Three Wheeled Vehicle. Ph.D. Thesis, University of Bath, Bath, UK, 2010. [Google Scholar]
- Cabrera, L.D.S. Active Tilt and Steer Control for a Narrow Tilting Vehicle. Ph.D. Thesis, Politecnico di Torino, Torino, Italy, 2010. [Google Scholar]
- Poelgeest, A.V. The Dynamics and Control of a Three-Wheeled Tilting Vehicle. Ph.D. Thesis, University of Bath, Bath, UK, 2011. [Google Scholar]
- Mourad, L.; Claveau, F.; Chevrel, P. A Lateral Control Strategy for Narrow Tilting Commuter Vehicle Based on the Perceived Lateral Acceleration. In Proceedings of the 18th World Congress The International Federation of Automatic Control, Milano, Italy, 28 August–2 September 2011. [Google Scholar]
- Mourad, L. Contrôle actif de l’accélération latérale perçue d’un véhicule automobile étroit et inclinable. In Automatique/Robotique; Ecole des Mines de Nantes: Nantes, France, 2012. [Google Scholar]
- Robertson, J. Active Control of Narrow Tilting Vehicle Dynamics. Ph.D. Thesis, University of Bath, Bath, UK, 2014. [Google Scholar]
- Claveau, F.; Chevrel, P.; Mourad, L. Non-linear control of a narrow vehicles, tilting vehicle. In Proceedings of the 2014 IEEE International Conference on Systems, Man, and Cybernetics, San Diego, CA, USA, 5–8 October 2014. [Google Scholar]
- Mourad, L.; Claveau, F.; Chevrel, P. Direct and Steering Tilt Robust Control of Narrow Vehicles. IEEE Trans. Intell. Transp. Syst. 2014, 15, 1206–1215. [Google Scholar] [CrossRef]
- Sindha, J.; Chakraborty, B.; Chakravarty, D. Automatic stability control of three-wheeler vehicles-recent developments and concerns towards a sustainable technology. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2018, 232, 418–434. [Google Scholar] [CrossRef]
- Furuichi, H.; Huang, J.; Fukuda, T. Switching dynamic modelling and driving stability analysis of three-wheeled narrow tilting vehicle. IEEE/ASME Trans. Mechatron. 2014, 19, 1309–1322. [Google Scholar] [CrossRef]
- Ataei, M. Reconfigurable Integrated Control for Urban Vehicles with Different Types of Control Actuation. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 2017. [Google Scholar]
- Ren, Y.; Dinh, T.Q.; Marco, J.; Greenwood, D.; Hessar, C. Nonlinearity Compensation based Tilting Controller for Electric Narrow Tilting Vehicles. In Proceedings of the 5th International Conference on Control, Decision and Information Technologies (CoDIT’18), Thessaloniki, Greece, 10–13 April 2018. [Google Scholar]
- Tang, C. Narrow Urban Vehicles with an Integrated Suspension Tilting System. Design, Modeling, and Control. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 2018. [Google Scholar]
- Docquier, Q. Dynamic Analysis and Control of Narrow Track Vehicles via a Multibody Modeling Approach. Ph.D. Thesis, Catholique University of Leuven, Ottignies-Louvain-la-Neuve, Belgium, 2020. [Google Scholar]
- Nguyen, A.T.; Chevrel, P.; Claveau, F. LPV Static Output Feedback for Constrained Direct Tilt Control of Narrow Tilting Vehicles. IEEE Trans. Control. Syst. Technol. 2018, 28, 661–670. [Google Scholar] [CrossRef]
- Choi, Y.; Lee, W.; Kim, J.; Yoo, J. A Variable-Sampling Time Model Predictive Control Algorithm for Improving Path-Tracking Performance of a Vehicle. Sensors 2021, 21, 6845. [Google Scholar] [CrossRef] [PubMed]
- Rohten, J.A.; Muñoz, J.E.; Pulido, E.S.; Silva, J.J.; Villarroel, F.A.; Espinoza, J.R. Very Low Sampling Frequency Model Predictive Control for Power Converters in the Medium and High-Power Range Applications. Energies 2021, 14, 199. [Google Scholar] [CrossRef]
- Jardin, P.; Esser, A.; Givone, S.; Eichenlaub, T.; Schleiffer, J.-E.; Rinderknecht, S. The Sensitivity in Consumption of Different Vehicle Drivetrain Concepts Under Varying Operating Conditions: A Simulative Data Driven Approach. Vehicles 2019, 1, 69–87. [Google Scholar] [CrossRef]
- Simchon, L.; Rabinovici, R. Real-Time Implementation of Green Light Optimal Speed Advisory for Electric Vehicles. Vehicles 2020, 2, 35–54. [Google Scholar] [CrossRef]
- Krah, J.-O.; Holtz, J. High-performance current regulation and efficient PWM implementation for low-inductance servo motors. IEEE Trans. Ind. Appl. 1999, 35, 1039–1049. [Google Scholar] [CrossRef]
- Gross, H.; Hamann, J.; Wiegaertner, G. Electrical Feed Drives in Automation: Basics, Computation and Dimensioning, 1st ed.; Publicis: Erlangen, Germany; Munich, Germany, 2001. [Google Scholar]
- Enomoto, M.; Kamoshita, S.; Kamiyama, M.; Sasaki, K.; Hamada, T.; Kazato, A. Development of Tilt Control System Using Electro-Hydraulic Actuators. Q. Rep. RTRI 2005, 46, 219–224. [Google Scholar] [CrossRef][Green Version]
- Available online: https://www.baumueller.com/en/insights/basics/what-is-the-cogging-torque (accessed on 30 December 2021).
- Ellis, G.; Lorentz, R.D. Comparison of Motion Control Loops for Industrial Applications. In Proceedings of the 1999 IEEE Industry Applications Conference. Thirty-Forth IAS Annual Meeting, Phoenix, AZ, USA, 3–7 October 1999. [Google Scholar]
- Amann, N.; Bocker, J.; Prenner, F. Active damping of drive train oscillations for an electrically driven vehicle. IEEE/ASME Trans. Mechatron. 2004, 9, 697–700. [Google Scholar] [CrossRef]
- Available online: www.jvl.dk (accessed on 30 December 2021).
- Available online: https://us.mitsubishielectric.com/fa/en/support/technical-support/knowledge-base/getdocument/?docid=3E26SJWH3ZZR-41-13086 (accessed on 30 December 2021).
- Ritari, A.; Vepsäläinen, J.; Kivekäs, K.; Tammi, K.; Laitinen, H. Energy Consumption and Lifecycle Cost Analysis of Electric City Buses with Multispeed Gearboxes. Energies 2020, 13, 2117. [Google Scholar] [CrossRef]
- Eberleh, B.; Hartkopf, T. A high speed induction machine with two speed transmission as drive for electric vehicles. In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Taormina, Italy, 23–26 May 2006. [Google Scholar]
- Weihua, J.; Hao, W. Analysis on Servo Control of High-quality Servo System. In Proceedings of the International Conference on Digital Manufacturing & Automation, Changsha, China, 18–20 December 2010. [Google Scholar]
- Available online: https://www.a-m-c.com/what-is-dual-loop-position-control-and-where-is-it-needed/ (accessed on 30 December 2021).
- Available online: https://www.ecotrons.com/vcu-2/ (accessed on 30 December 2021).
- Ogata, K. Modern Control Engineering; Prentice Hall: Hoboken, NJ, USA, 2010. [Google Scholar]
- Slotine, E.J.-J.; Li, W. Applied Non-Linear Control; Prentice Hall: Hoboken, NJ, USA, 1991. [Google Scholar]
- Ellis, G. Control System Design Guide a Practical Guide; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Pettersson, P. Vehicle Lateral Speed Estimation. Master’s Thesis, Lund University, Lund, Sweden, 2008. [Google Scholar]
- Vas, P. Sensorless Vector and Direct Torque Control; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Ong, C.-M. Dynamic Simulation of Electric Machinery; Prentice Hall: Hoboken, NJ, USA, 1998. [Google Scholar]
- Haidekker, M.A. Linear Feedback Controls: The Essentials, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Yao, B.; Jiang, C. Advanced Motion Control: From Classical PID to Nonlinear Adaptive Robust Control. In Proceedings of the 11th IEEE International Workshop on Advanced Motion Control, Nagaoka, Japan, 21–24 March 2010. [Google Scholar]
- Available online: https://www.sick.com/tr/en/ (accessed on 30 December 2021).
- Available online: https://www.hms-networks.com/ (accessed on 30 December 2021).
- Available online: https://new.siemens.com/global/en/products/automation/systems.html (accessed on 30 December 2021).



| Vx (m/s) | Open Loop Poles | Closed Loop Poles with SF |
|---|---|---|
| 1 | 3.02; −3.08; −70.89; −287.82 | −7.29; −26.58; −120.02; −390.73 |
| 2 | 2.99; −3.11; −35.91; −143.35 | −9.97 + j1.7; −9.97 − j1.7; −93.86; −251.99 |
| 3 | 2.96; −3.14; −24.48; −94.93 | −6.79 + j3.65; −6.79 − j3.65; −83.34; −208.52 |
| 4 | 2.93; −3.16; −18.94; −70.52 | −5.31 + j3.59; −5.31 − j3.59; −76.79; −188.15 |
| 5 | 2.90; −3.18; −15.78; −55.70 | −4.43 + j3.30; −4.43 − j3.30; −72.14; −176.61 |
| 6 | 2.88; −3.19; −13.83; −45.65 | −3.86 + j3.0; −3.86 − j3.0; −68.64; −169.30 |
| 7 | 2.85; −3.19; −12.59; −38.31 | −3.47 + j2.73; −3.47 − j2.73; −65.90; −164.28 |
| 8 | 2.83; −3.18; −11.84; −32.64 | −3.19 + j2.50; −3.19 − j2.50; −63.68; −160.65 |
| State Feedback Controller | SMC | Reference Model |
|---|---|---|
| = 0 | ||
| = 6.82 at 8 m/s | = 1.2 | = 15 |
| = 1.7 at 2 m/s | = 26.4 | = 10 |
| = −7.6 | ||
| = −0.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karamuk, M.; Alankus, O.B. Development and Experimental Implementation of Active Tilt Control System Using a Servo Motor Actuator for Narrow Tilting Electric Vehicle. Energies 2022, 15, 1996. https://doi.org/10.3390/en15061996
Karamuk M, Alankus OB. Development and Experimental Implementation of Active Tilt Control System Using a Servo Motor Actuator for Narrow Tilting Electric Vehicle. Energies. 2022; 15(6):1996. https://doi.org/10.3390/en15061996
Chicago/Turabian StyleKaramuk, Mustafa, and Orhan Behic Alankus. 2022. "Development and Experimental Implementation of Active Tilt Control System Using a Servo Motor Actuator for Narrow Tilting Electric Vehicle" Energies 15, no. 6: 1996. https://doi.org/10.3390/en15061996
APA StyleKaramuk, M., & Alankus, O. B. (2022). Development and Experimental Implementation of Active Tilt Control System Using a Servo Motor Actuator for Narrow Tilting Electric Vehicle. Energies, 15(6), 1996. https://doi.org/10.3390/en15061996






