A Study of the Vibration Characteristics of Flexible Mechanical Arms for Pipe String Transportation in Oilfields
Abstract
1. Introduction
2. Methodology
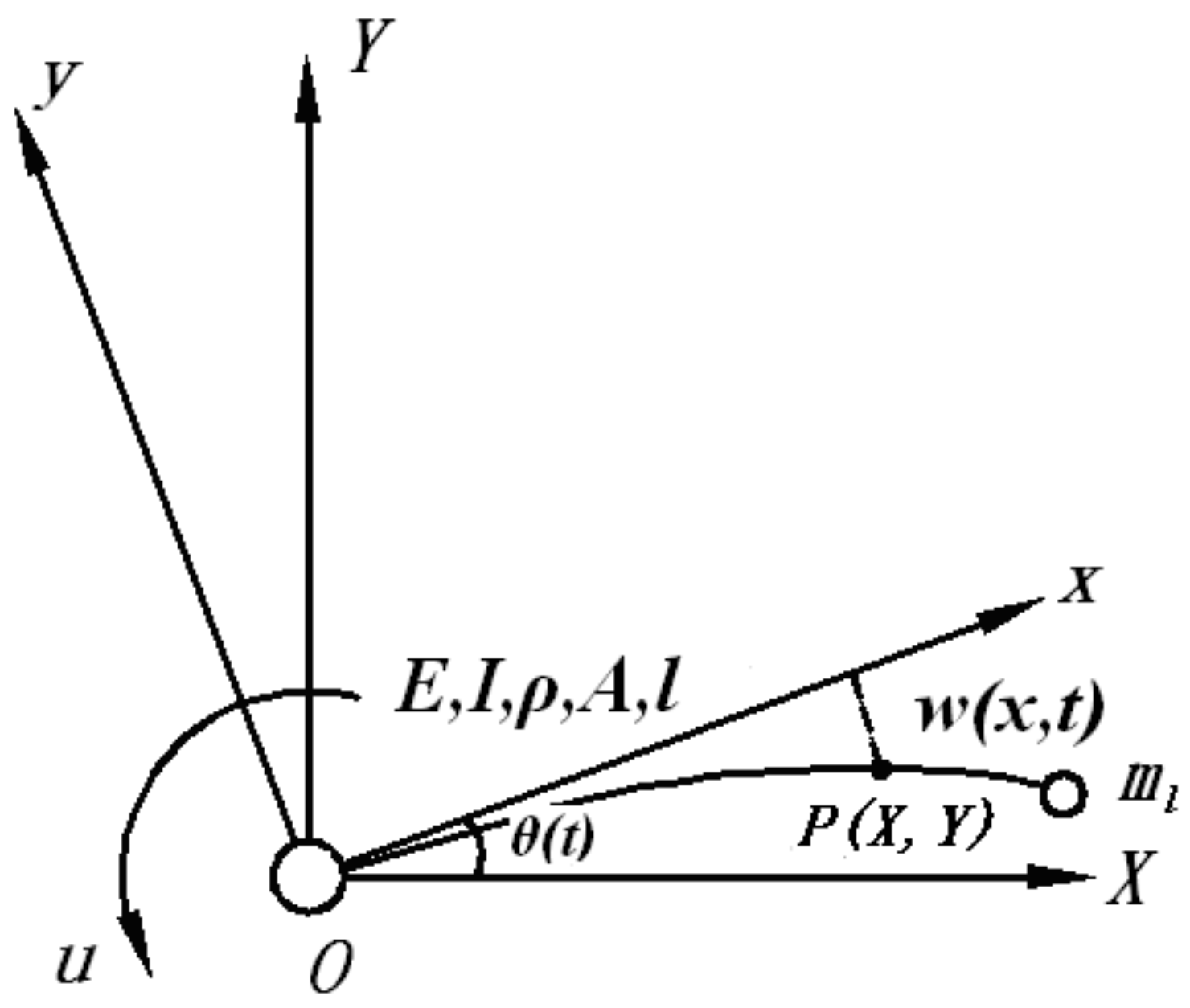
2.1. Kinematics Equation of a Mechanical Arm
- (1)
- On the premise of small deformation, the influence of shear deformation and the rotational inertia of the section about the neutral axis was ignored;
- (2)
- The radius of the rotating shaft was ignored;
- (3)
- The rotating shaft was rigid, and the joint between the beam and the rotating shaft was the hinge support boundary condition;
- (4)
- The size of the end manipulator was ignored and considered a particle.
2.2. Dynamic Equation of a Mechanical Arm
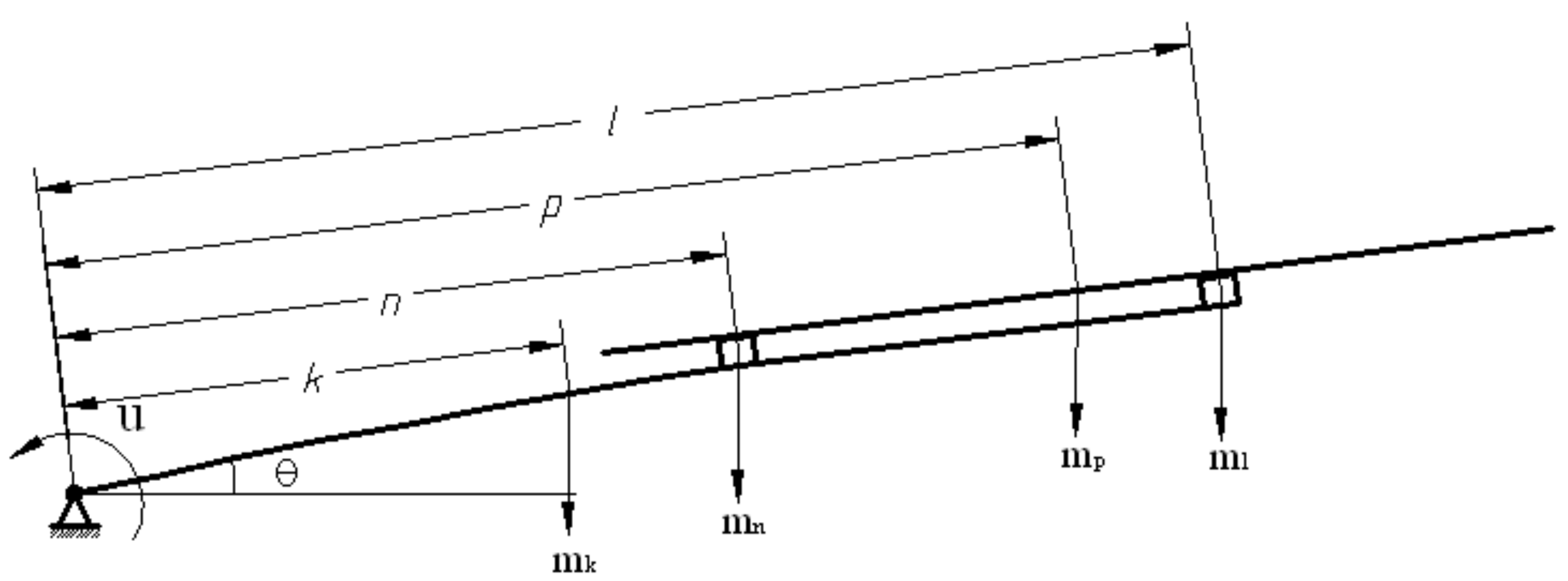
2.2.1. External Load of the Flexible Arm
- 1.
- Single-point force and torque
- 2.
- Distributed load
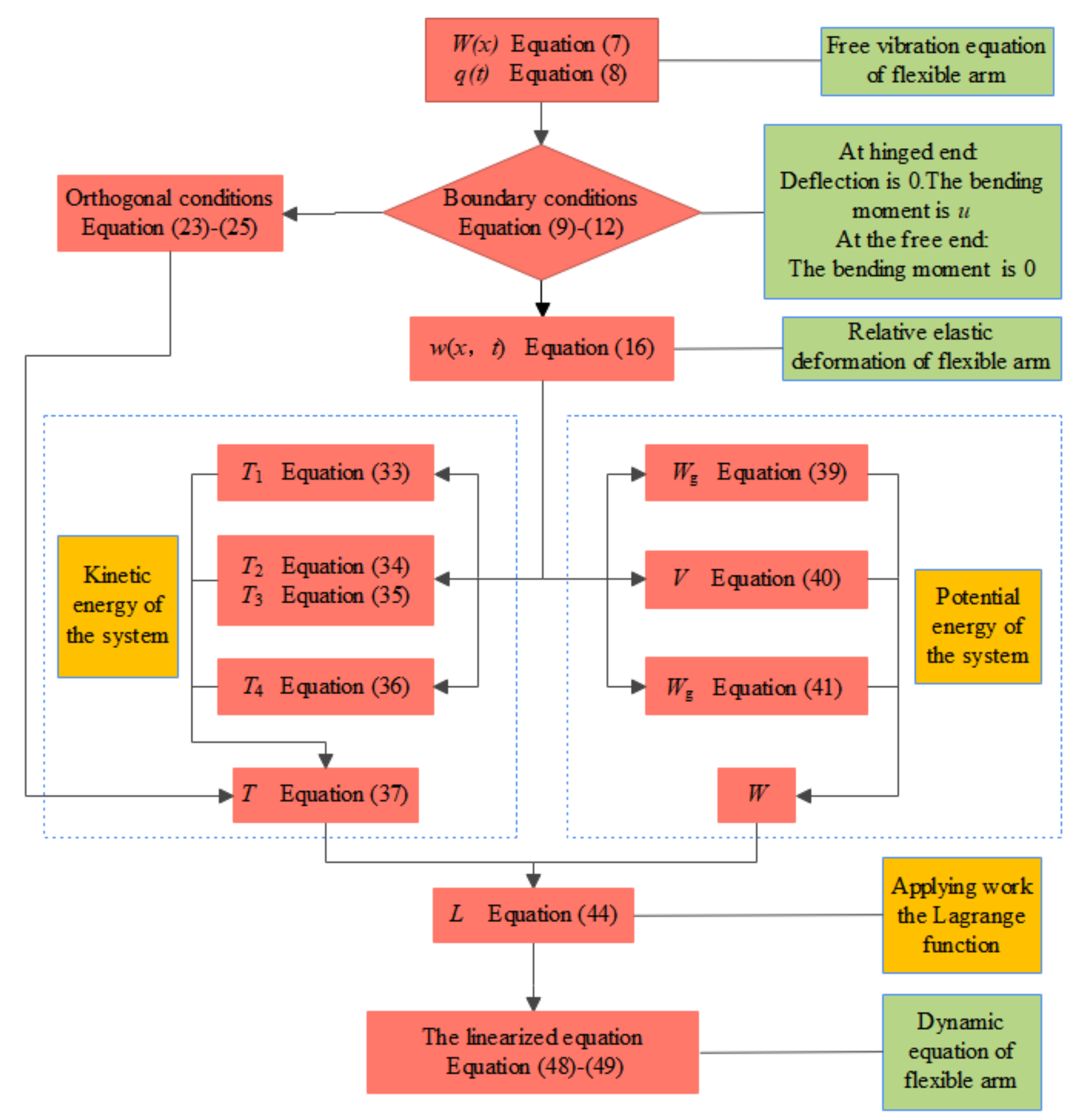
2.2.2. Energy of the System
- 1.
- Kinetic energy of the system
- 2.
- Potential energy of the system
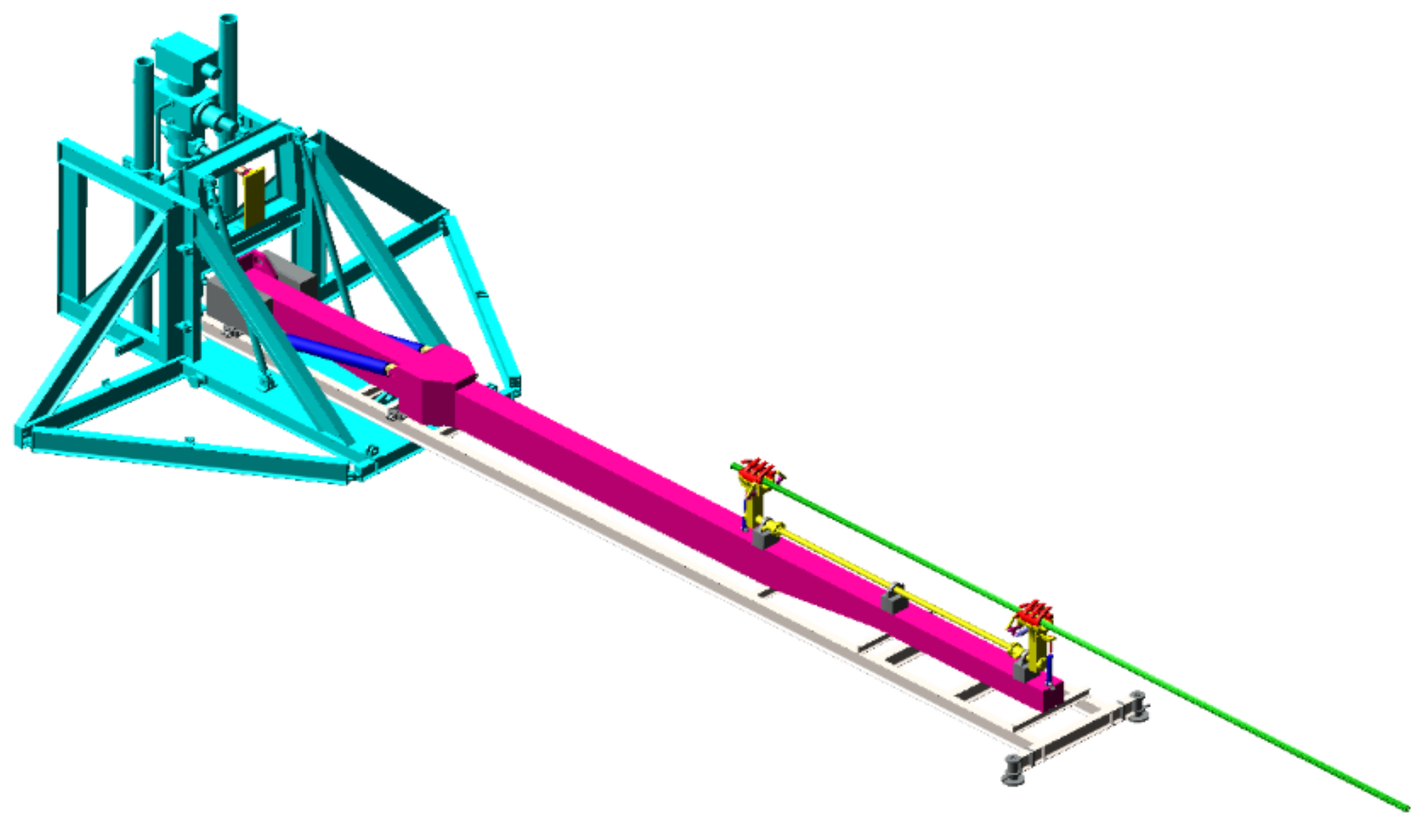
3. Modeling and Simulation of a Rigid–Flexible Coupling Mechanical Arm
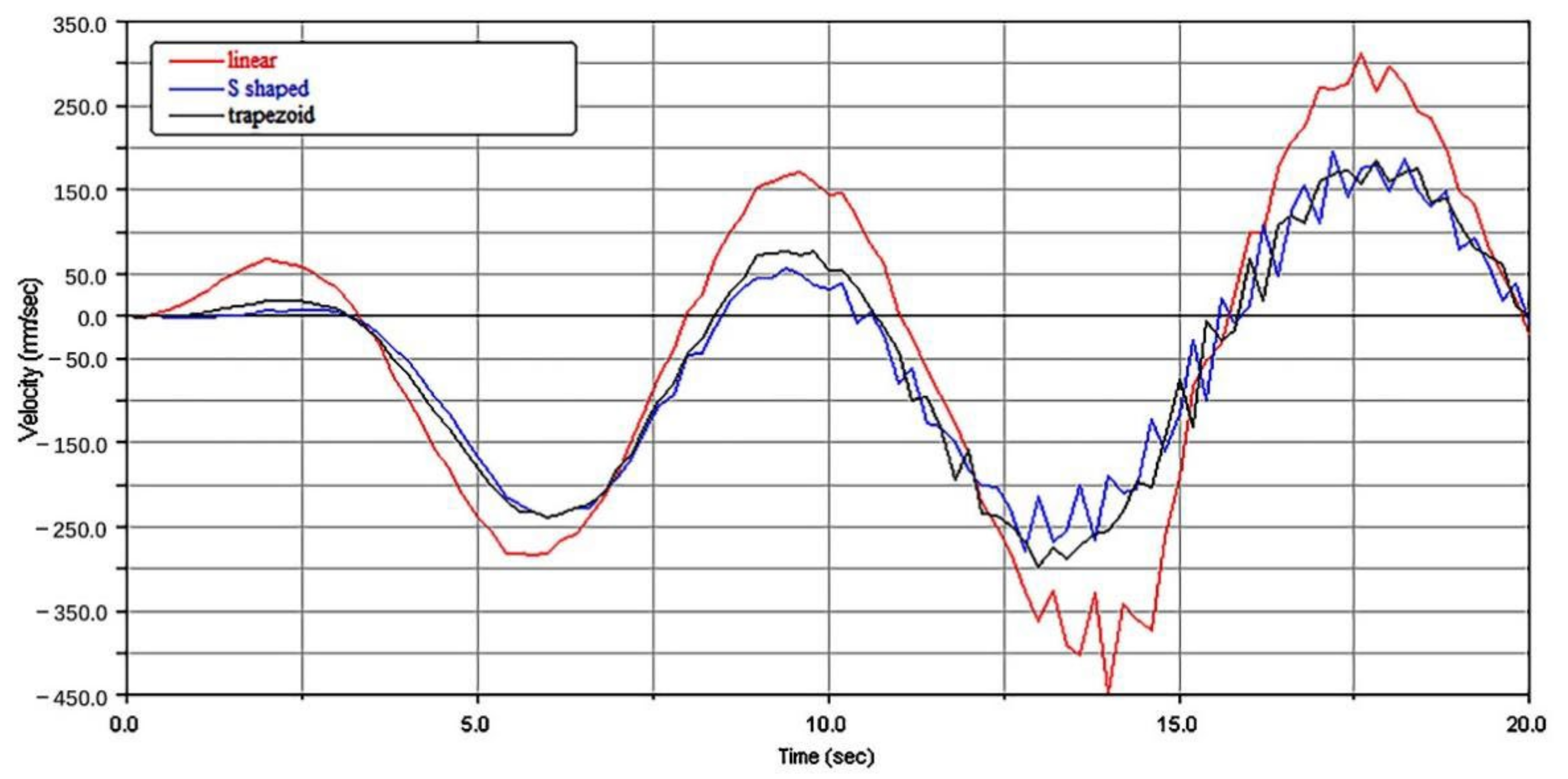
3.1. Simulation Experiment with Different Drive Types
3.1.1. Lifting Characteristics with Different Drive Types
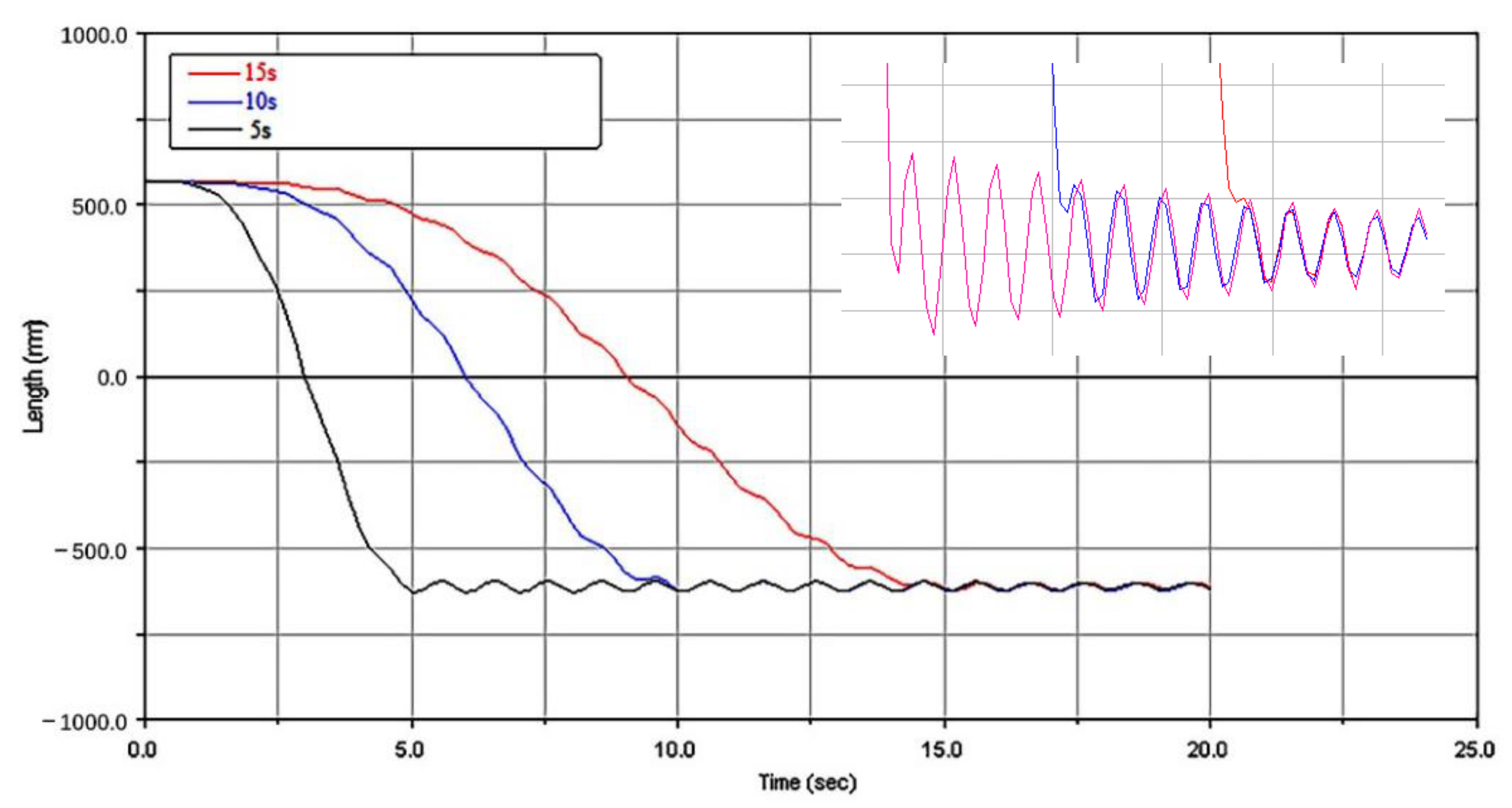
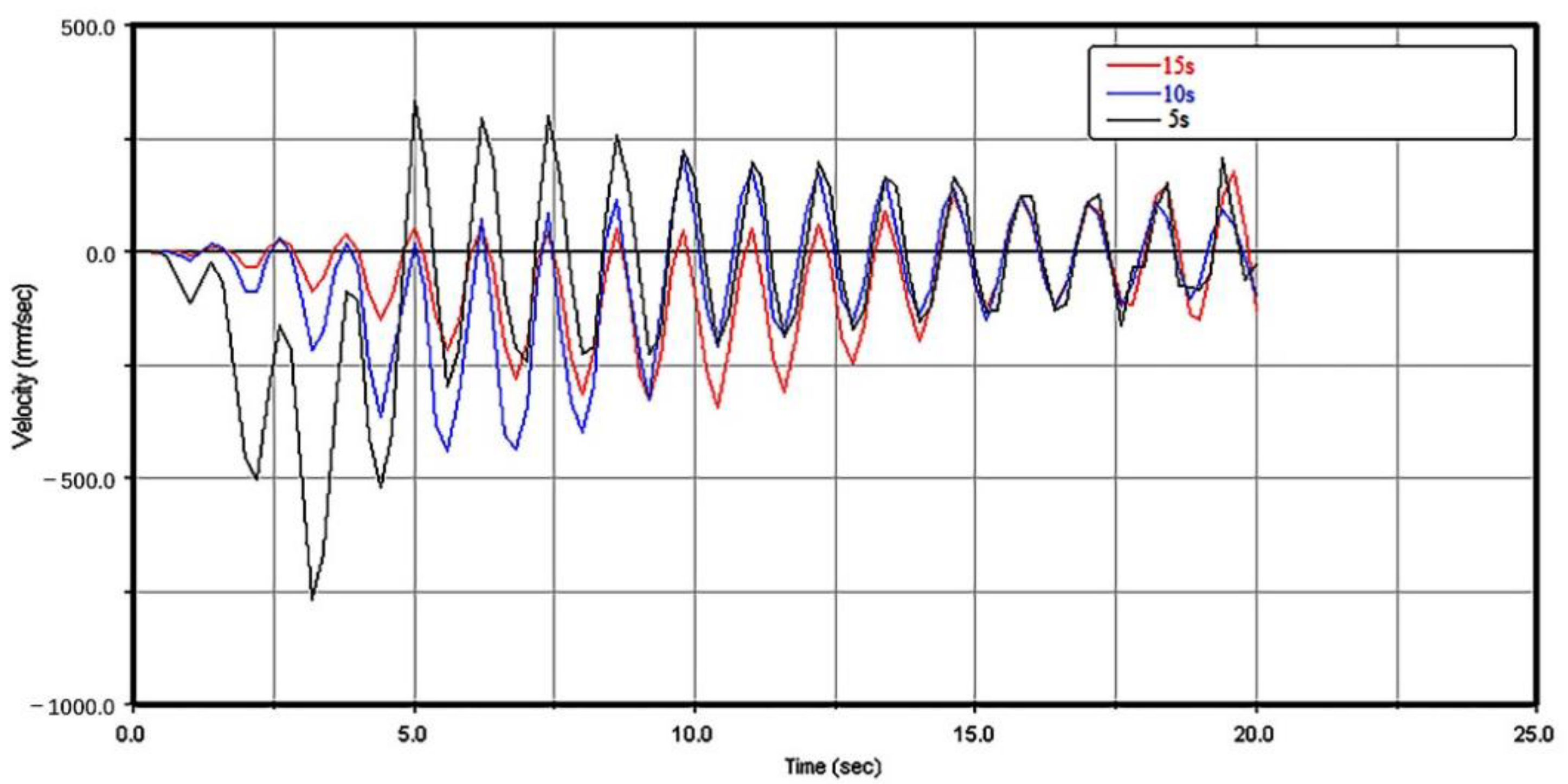
3.1.2. Lifting Characteristics with Different Drive Speeds
3.2. Simulation Experiment with Different Structure Parameters
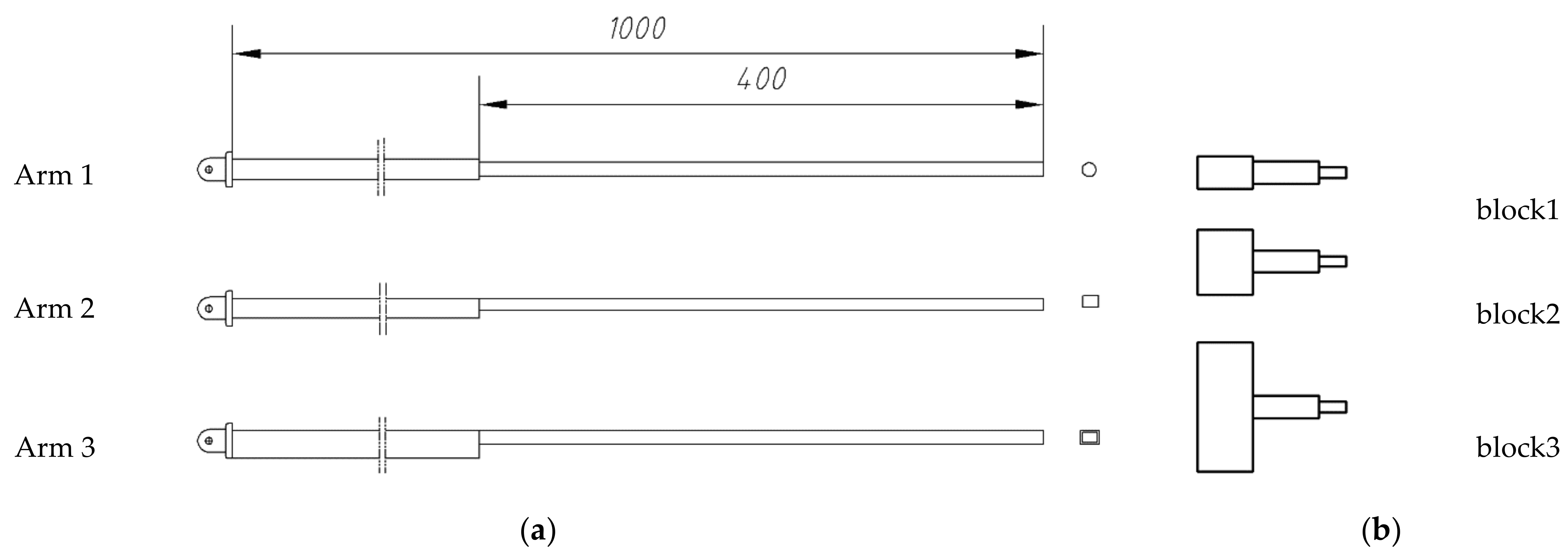
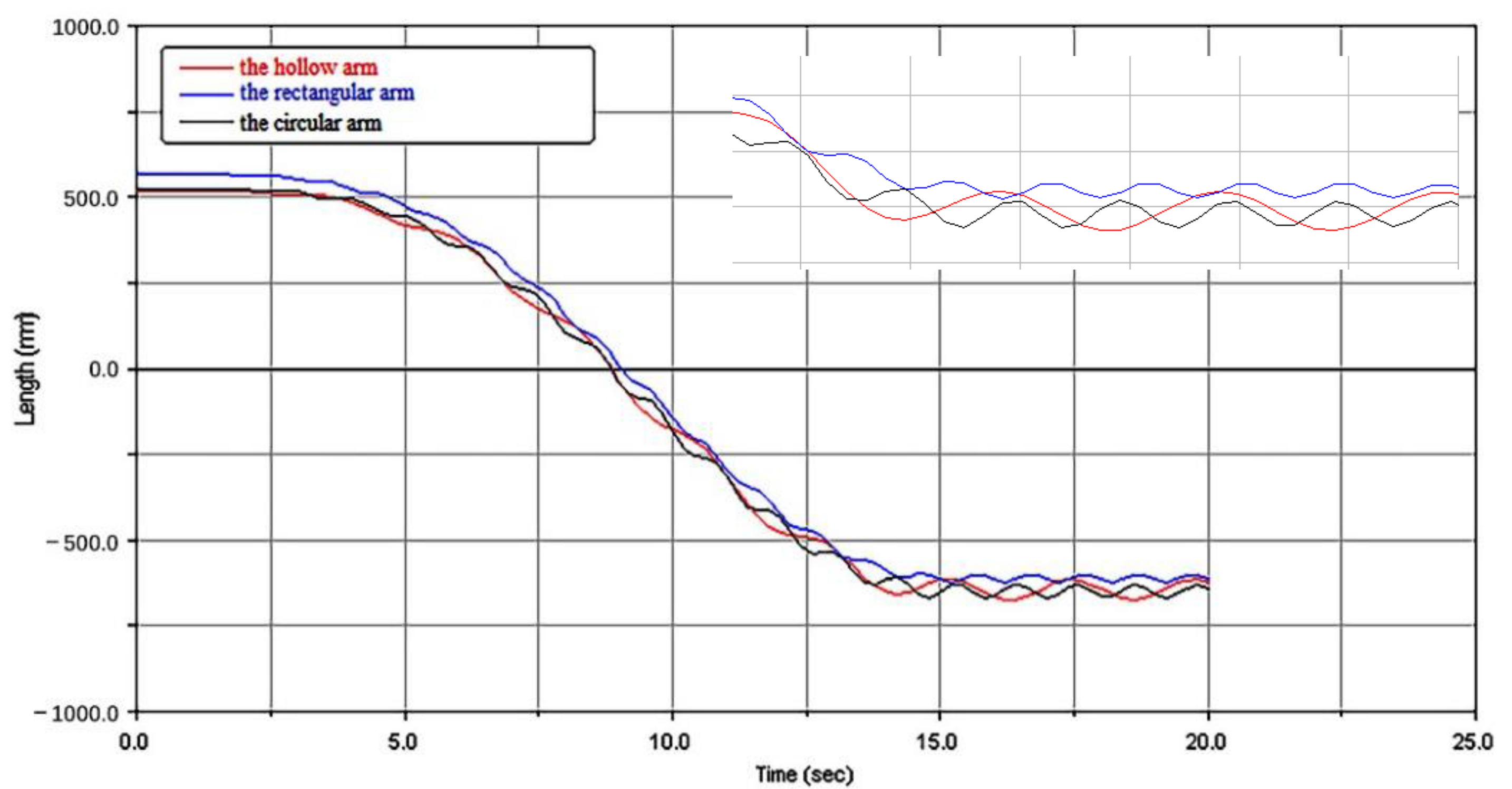
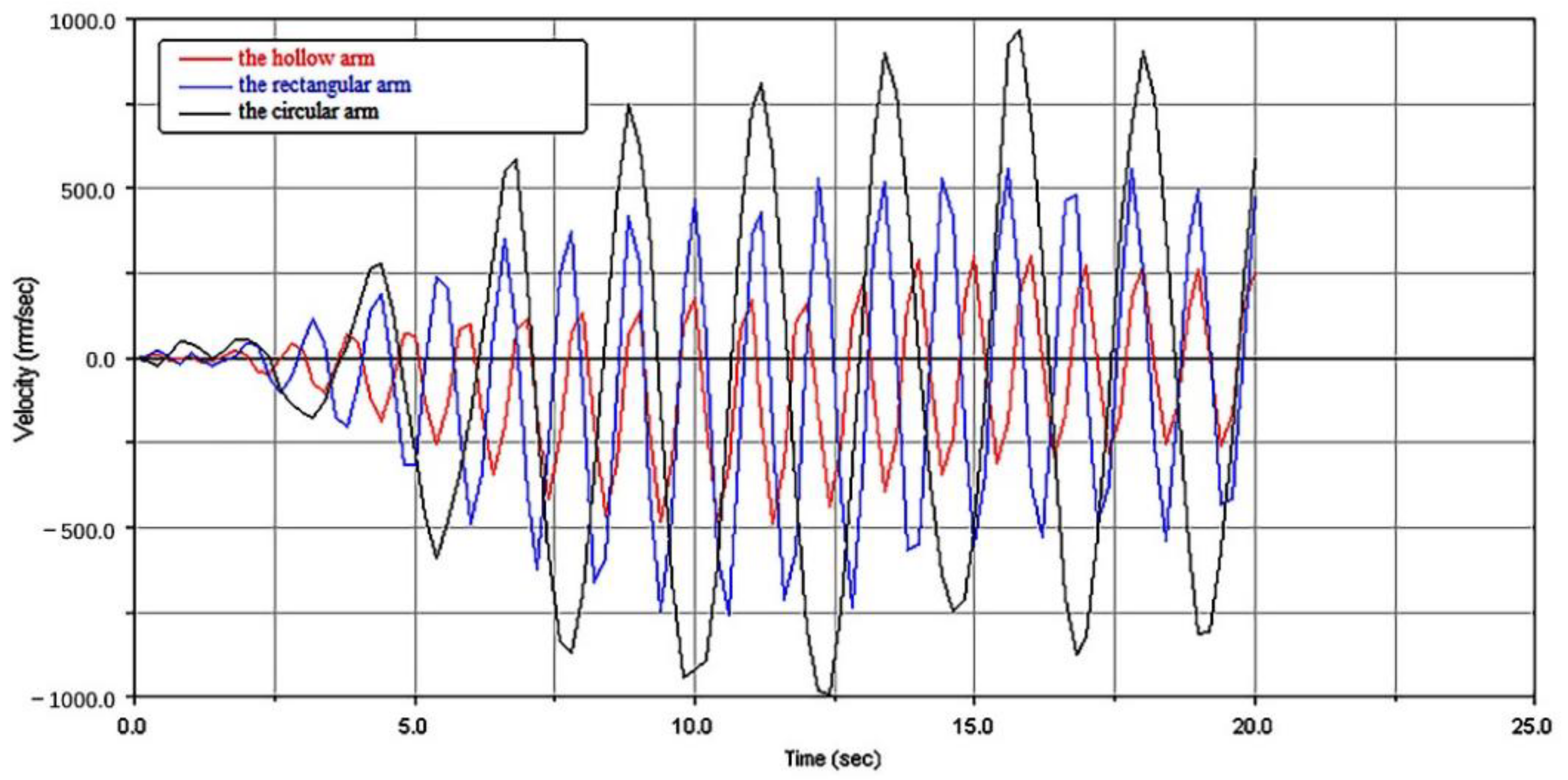
3.2.1. Lifting Characteristics with Different Section Structures
3.2.2. Lifting Characteristics with Different Loads
3.3. Simulation Experiment with Hold Strings and Different-Sized Strings
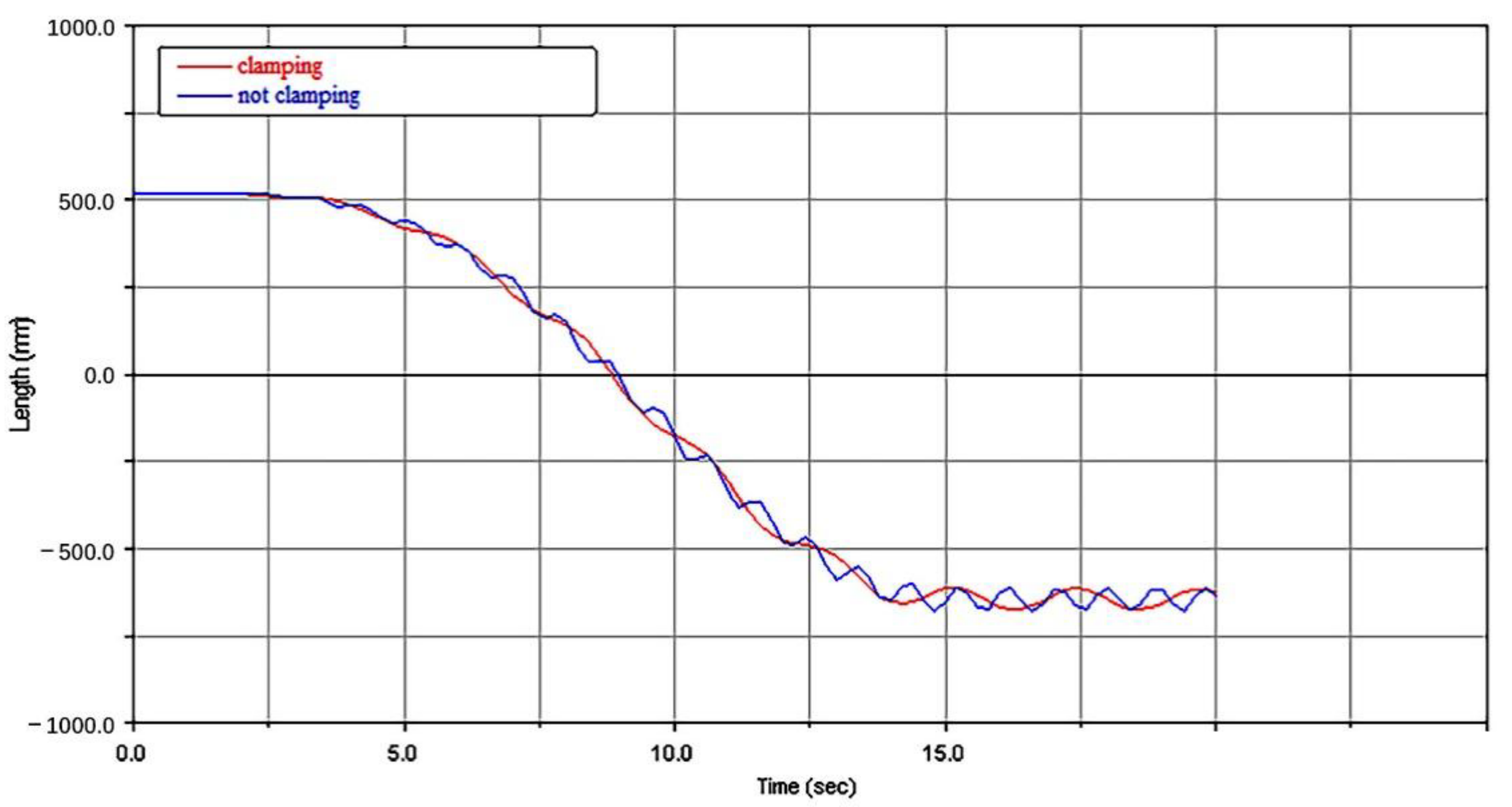
3.3.1. Lifting Characteristics with Clamp String
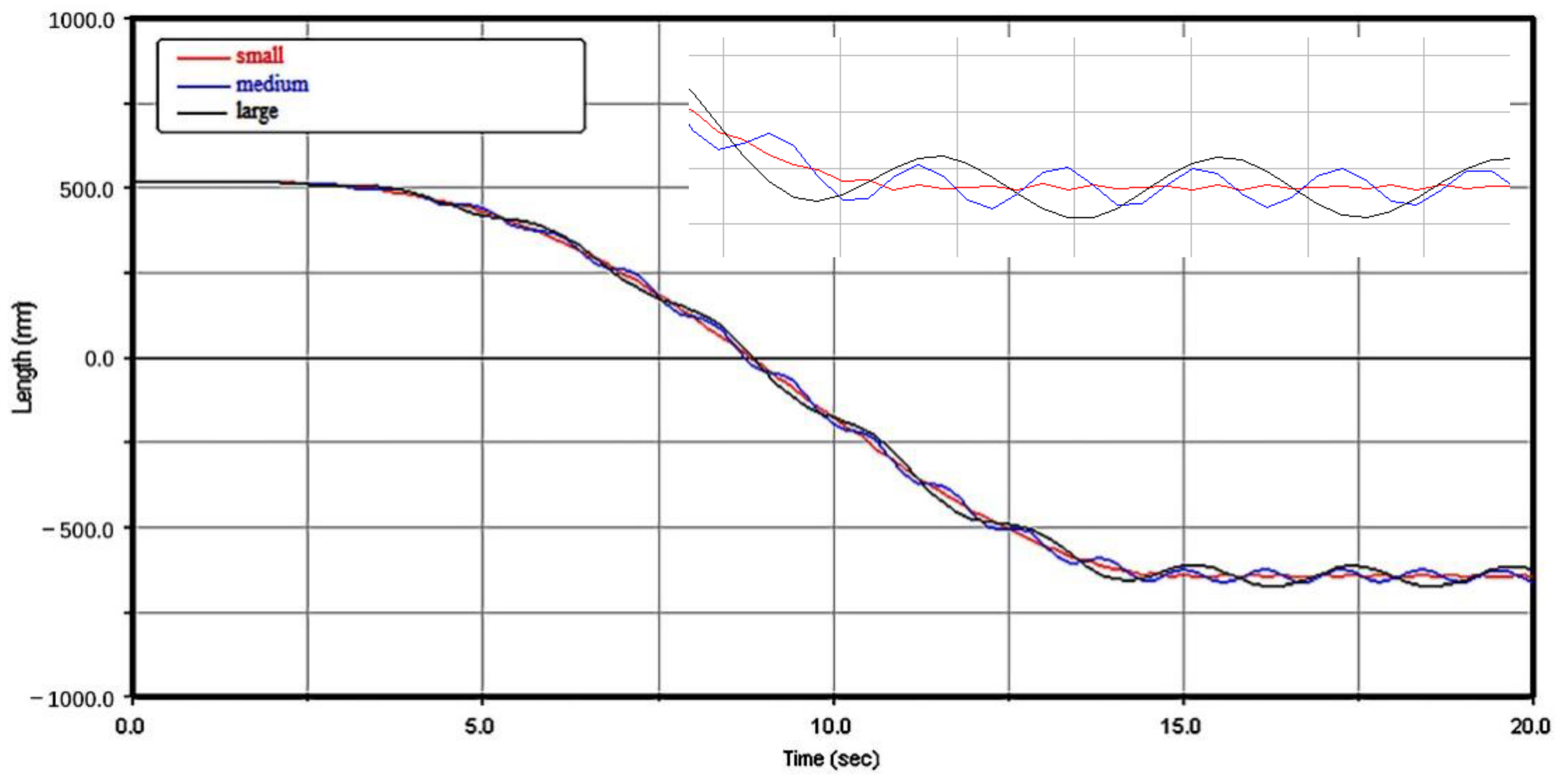
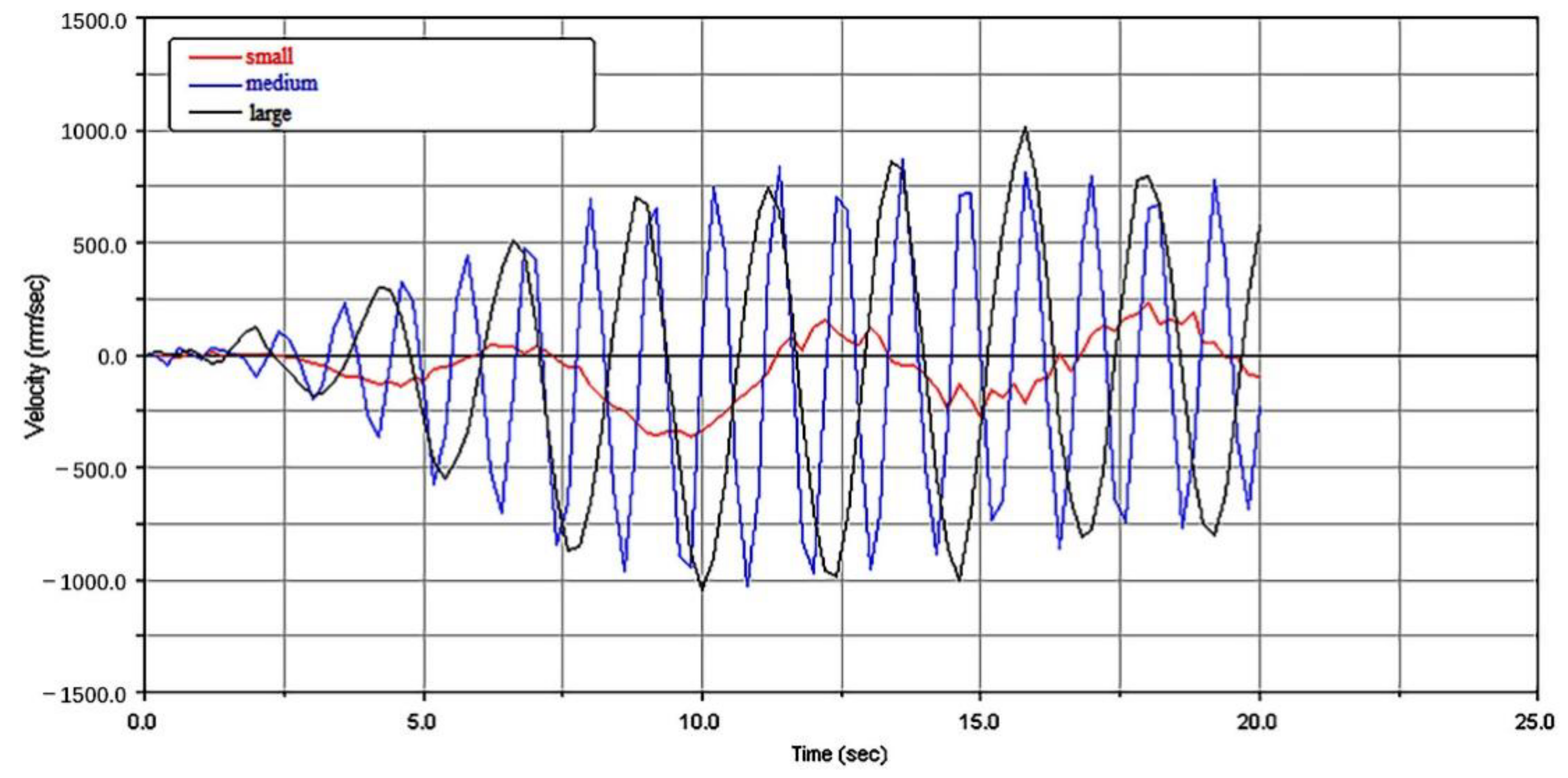
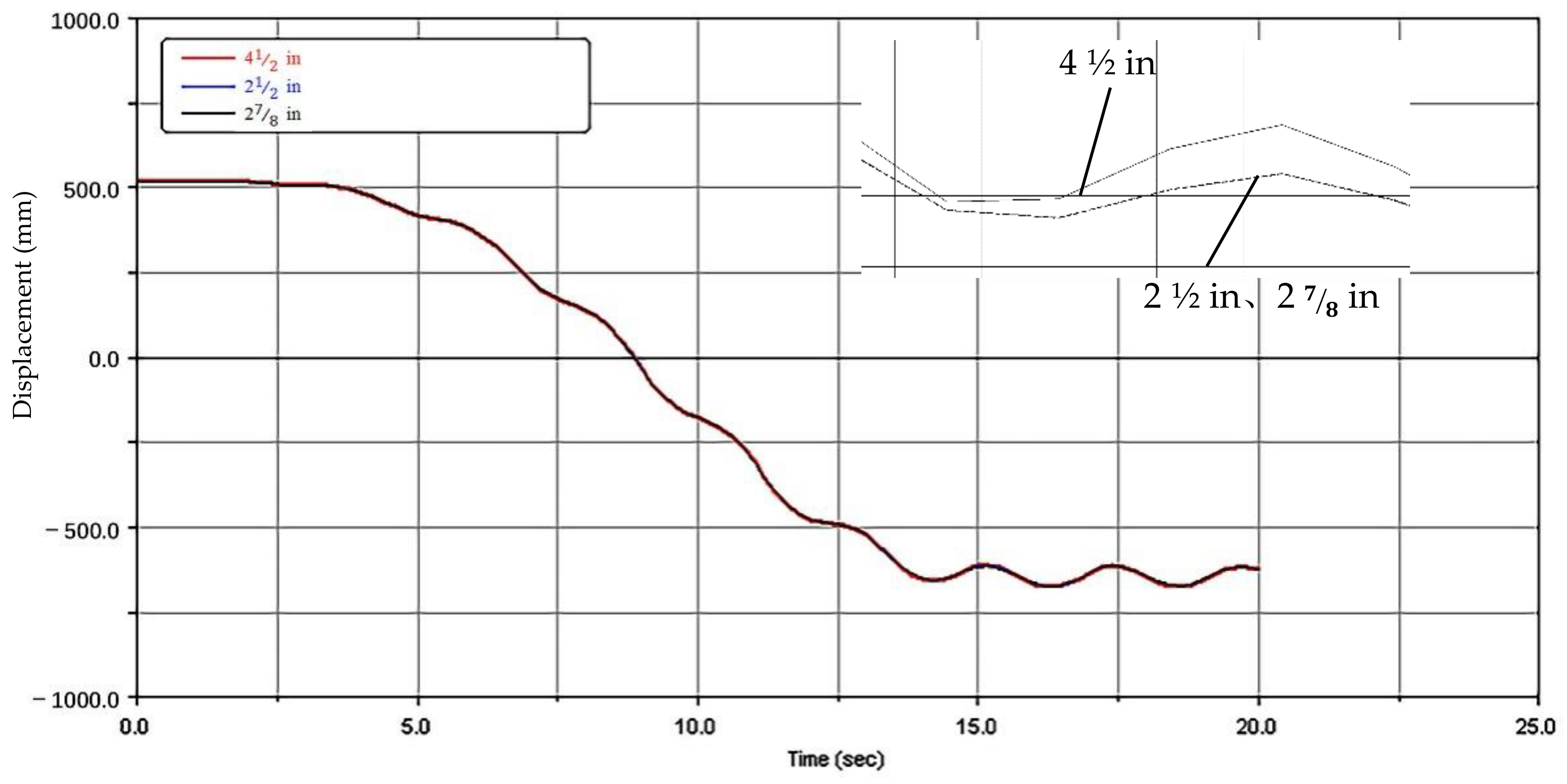
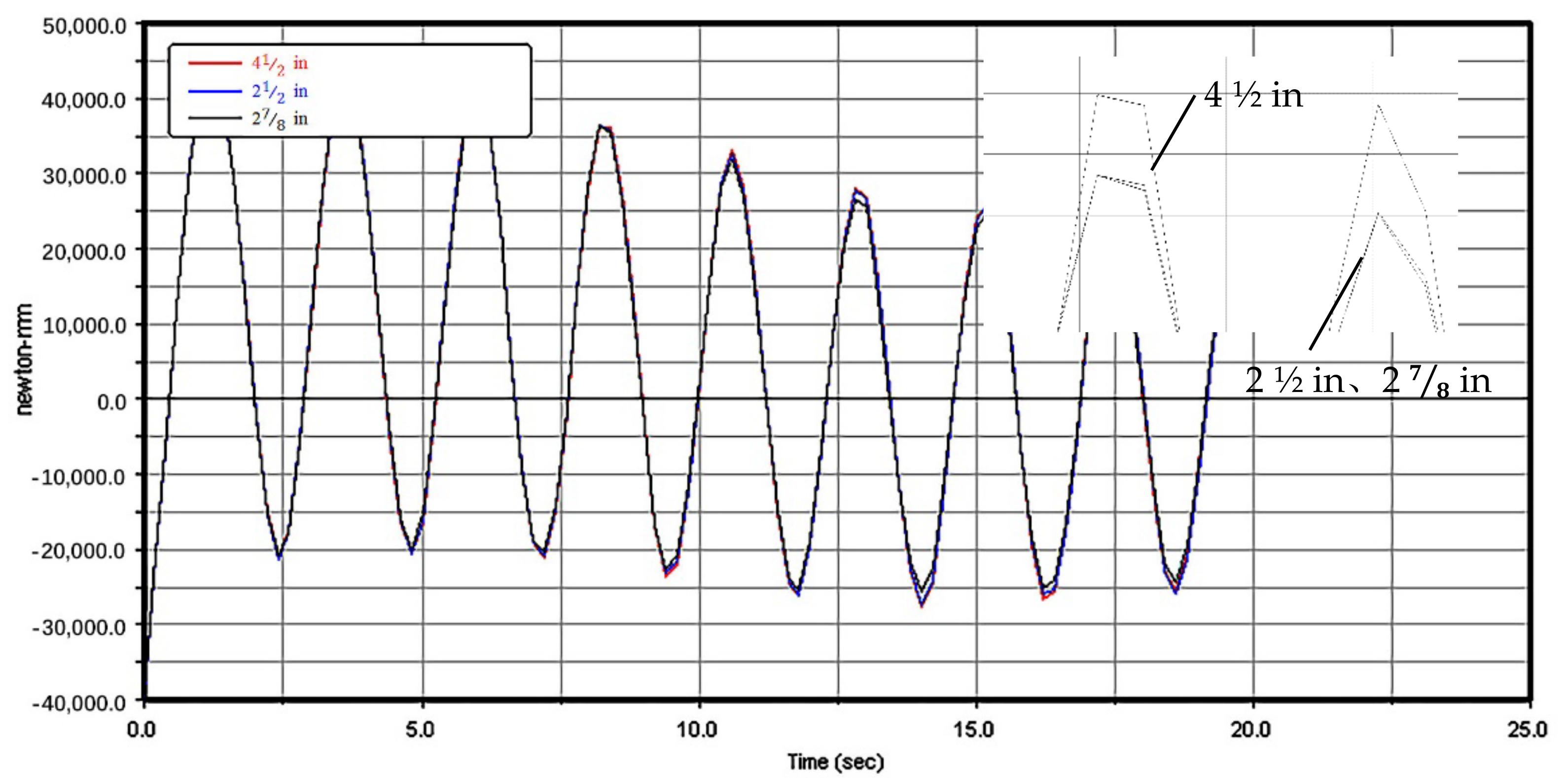
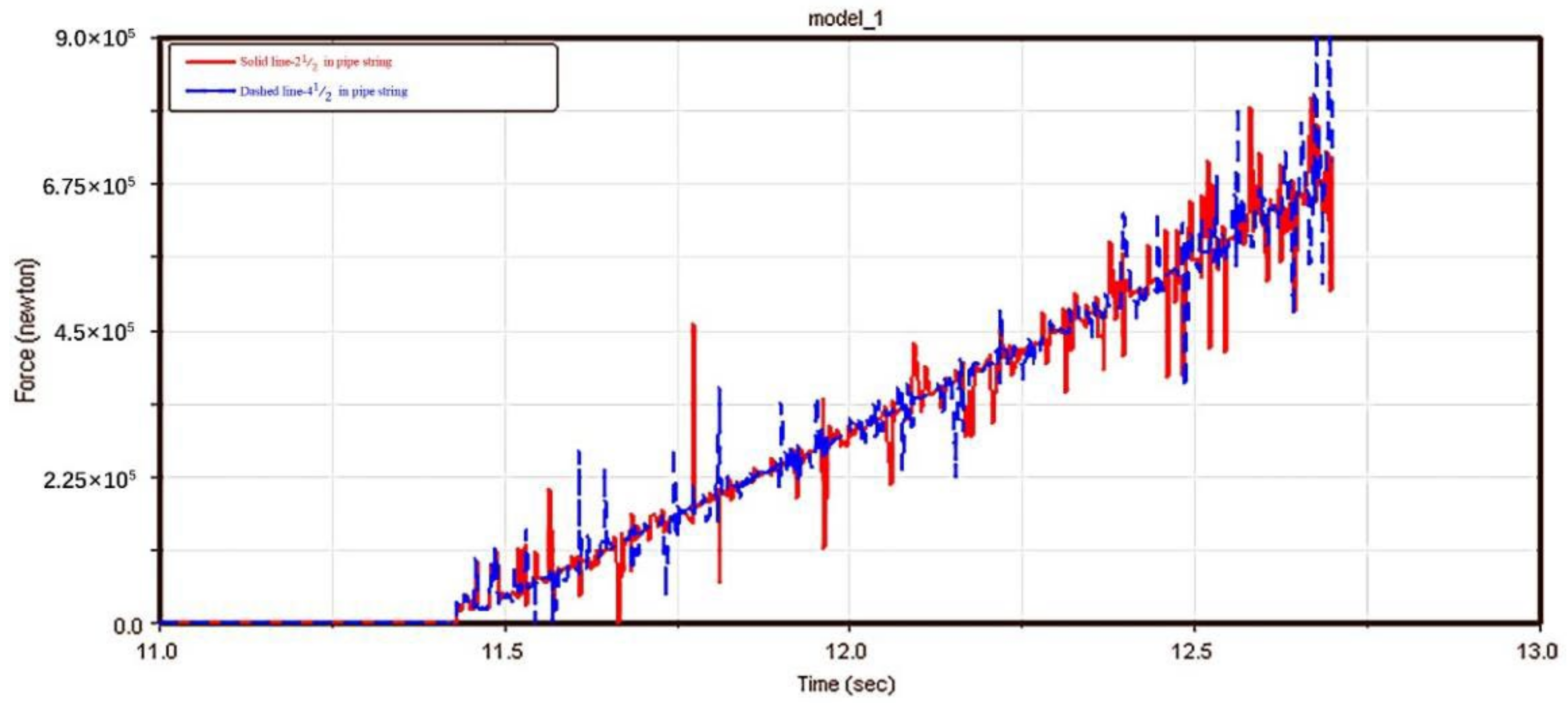
3.3.2. Lifting Characteristics with Different-Sized Strings
3.4. Contact Collision with Different-Sized Strings
4. Discussion
5. Conclusions
- Based on the theory of flexible dynamics modeling, the orthogonality condition of the natural vibration mode of the mechanical arm with a concentrated mass block at its end was deduced. Then, a numerical calculation model of the rigid–flexible coupling system was established based on the Lagrangian equation.
- ADAMS and Ansys were used to carry out the finite element analysis of a rigid–flexible coupling system, and a rigid–flexible hybrid model was established. The lifting process of a mechanical arm was numerically simulated to investigate the lifting characteristics of the flexible arm and the effects of lifting speeds, arm section, and driving modes. The target position and stability of a moving pipe string were calculated. It was concluded that the simulation of flexible parts was close to the reality, and the rigid–flexible coupling analysis was able to reveal the essence of the system.
- The simulation results showed that the weight of the string had little influence on the vibration characteristics. The following considerations should be considered in the design of the mechanism. ① Design parameters such as the weight of the end mass and the structure of the arm have more significant effects on the system than operation parameters. The design of a mechanical arm should first focus on the structure and then optimize the operation parameters of the mechanical arm. ② A flexible arm is characterized by reciprocating vibration lifting, and the vibration amplitude at the end is less than 2% of the total length of the arm. The effect of pipe string transportation and target position were not significant, and compensation from the mechanical hand is unnecessary. ③ The stability problem caused by the vibration of the flexible arm can be greatly reduced with a reasonable shock absorber design and material selection, and an appropriate control method can also quickly attenuate the vibration.
- According to the simulation results, when the design parameter [w/l] of a single-flexible mechanical arm is between 1/650 and 1/1000, the mechanical arm can be modeled as a rigid body. When [w/l] is between 1/400 and 1/650, the rigid–flexible coupling model should be considered for the system. When [w/l] is between 1/250 and 1/400, flexible body modeling should be used for the mechanical arm and the coupling effect of control parameters should be considered.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lee, H.W. The Study of Mechanical Arm and Intelligent Robot. IEEE Access 2020, 8, 119624–119634. [Google Scholar] [CrossRef]
- Sun, L.N.; Dong, W.; Du, Z.J. Research status and key technologies of macro / micro dual-driven robot system. China Mech. Eng. 2005, 16, 89–93. [Google Scholar]
- Sipos, A.A.; Varkonyi, P.L. The longest soft robotic arm. Int. J. Non-Linear Mech. 2020, 119, 103354. [Google Scholar] [CrossRef]
- Tarnita, D.; Marghitu, D.B. Analysis of a hand arm system. Robot. Comput.-Integr. Manuf. 2013, 29, 493–501. [Google Scholar] [CrossRef]
- Zhu, Y.; Qiu, J.H.; Tani, J. Simultaneous optimization of a flexible robot arm. JSME Int. J. Ser. C-Mech. Syst. Mach. Elem. Manuf. 2000, 43, 32–37. [Google Scholar] [CrossRef][Green Version]
- Chen, L.P.; Zhang, Y.Q.; Ren, W.Q.; Qin, G. The Mechanical System Dynamics Analysis and the ADAMS Application Tutorial; Tsinghua University Press: Beijing, China, 2005. [Google Scholar]
- Hong, J.Z.; Jiang, L.Z. Flexible multibody dynamics with coupled rigid and deformation motions. Adv. Mech. 2000, 30, 15–20. [Google Scholar]
- Hong, J.Z.; Jiang, L.Z. Dynamic stiffening and multibody dynamics with coupled rigid and deformation motions. Chin. J. Comput. Mech. 1999, 16, 295–301. [Google Scholar]
- Kane, T.R.; Ryan, R.R.; Banerjee, A.K. Dynamics of a cantilever beam attached to a moving base. J. Guid. Control. Dyn. 1987, 10, 139–151. [Google Scholar] [CrossRef]
- Liu, J.Y.; Hong, J.Z. Dynamic modeling and modal truncation approach for a high-speed rotating elastic beam. Arch. Appl. Mech. 2002, 72, 554–563. [Google Scholar] [CrossRef]
- Yan, G.H.; Hong, J.Z.; Yu, Z.Y. Dynamics modeling of a flexible hub-beam system with a tip mass. J. Sound Vib. 2003, 266, 759–774. [Google Scholar]
- Naganathan, G.; Soni, A.H. An analytical and experimental investigation of flexible manipulator performance. In Proceedings of the IEEE International Conference on Robotics and Automation, Raleigh, NC, USA, 31 March–3 April 1987; pp. 767–773. [Google Scholar]
- Luca, A.; Sicilano, B. Closed-form dynamic model of planar multilink light weight robots. IEEE Trans. Syst. Man Cybern. 1991, 21, 826–839. [Google Scholar] [CrossRef]
- My, C.A.; Bien, D.X.; Le, C.H.; Packianather, M. An efficient finite element formulation of dynamics for a flexible robot with different type of joints. Mech. Mach. Theory 2018, 134, 267–288. [Google Scholar] [CrossRef]
- My, C.A.; Bien, D.X. New development of the dynamic modeling and the inverse dynamic analysis for flexible robot. Int. J. Adv. Robot. Syst. 2020, 17, 1–12. [Google Scholar] [CrossRef]
- Chu, A.M.; Nguyen, C.D.; Duong, X.B.; Nguyen, A.V.; Nguyen, T.A.; Le, C.H.; Packianather, M. A novel mathematical approach for finite element formulation of flexible robot dynamics. Mech. Based Des. Struct. Mach. 2020, 1–21. [Google Scholar] [CrossRef]
- Korayem, M.H.; Shafei, A.M.; Dehkordi, S.F. Systematic modeling of a chain of N-flexible link manipulators connected by revolute–prismatic joints using recursive Gibbs-Appell formulation. Arch. Appl. Mech. 2014, 84, 187–206. [Google Scholar] [CrossRef]
- Theodore, R.J.; Ghosal, A. Comparison of the Assumed Modes and Finite Element Models for Flexible Multilink Manipulators. Int. J. Robot. Res. 1995, 14, 91–111. [Google Scholar] [CrossRef]
- Huston, R.L. Multi-body dynamics: Modeling and analysis methods. Appl. Mech. Rev. 1991, 44, 109–117. [Google Scholar] [CrossRef]
- Shabana, A.A. Flexible multi-body dynamics: Review of past and recent developments. Multi-Body Syst. Dyn. 1997, 1, 189–222. [Google Scholar] [CrossRef]
- Schiehlen, W. Multi-body system dynamics: Roots and perspectives. Multi-Body Syst. Dyn. 1997, 1, 149–188. [Google Scholar] [CrossRef]
- Zhang, Y.; Hao, H.Y.; Sun, Z.Q. Esearchon continuous trajectory tracing control of flexible macro-micro space manipulator system. J. Mech. Eng. 2005, 41, 125–131. [Google Scholar] [CrossRef]
- Li, J.T.; Deng, H. Vibration suppression of rotating long flexible mechanical arms based on harmonic input signals. J. Sound Vib. 2018, 436, 253–261. [Google Scholar] [CrossRef]
- He, B.Y.; Wang, S.X. Study on the dynamic model and simulation of a flexible mechanical arm considering its random parameters. J. Mech. Sci. Technol. 2005, 19, 265–271. [Google Scholar] [CrossRef]
- Cai, G.P.; Hong, J.Z. Assumed mode method of a rotating flexible beam. Acta Mech. Sin. 2005, 37, 48–56. [Google Scholar]
- Wang, F.Y.; Gao, Y.Q. Modeling Design Control and Applications: Advanced Studies of Flexible Robotic Manipulators; World Scientific Publishing Co. Pte. Ltd.: London, UK, 2003. [Google Scholar]
- Kang, X.W.; Zhang, Y.; Jiang, L.H.; Han, L.; Chu, H.Q.; Zhu, Q. Study of vibration characteristic of phononic crystals flexible mechanical arms. Optoelectron. Adv. Mater.-Rapid Commun. 2014, 8, 964–967. [Google Scholar]
- Ahmed, A.; Shabana, A. Dynamics of Multibody Systems; The United States of America by Cambridge University Press: New York, NY, USA, 2005. [Google Scholar]
- Liu, Z.Y. Study on Modeling Theory and Simulation Technique for Rigid-Flexible Coupling Systems Dynamics; Shanghai Jiao Tong University: Shanghai, China, 2008. [Google Scholar]
- Song, Y.M.; Yu, Y.Q.; Zhang, C.; Ma, J.S. Summary on the study of dynamics analysis and vibration control of flexible robots. J. Mach. Des. 2003, 20, 1–5. [Google Scholar]
- Liu, S.Z.; Yu, Y.Q.; Du, Z.C.; Liu, Q.B. A summary of the dynamics analysis and control strategy of flexible manipulators. Ind. Instrum. Autom. 2008, 2, 18–24. [Google Scholar]
- Zhang, Y.; Kang, X.W.; Jiang, L.H.; Han, L.; Chu, H.Q.; Zhu, Q. Vibration attenuation in two-link flexible mechanical arms with periodic composite materials. Adv. Mech. Eng. 2015, 7, 1–8. [Google Scholar] [CrossRef]
- Li, J.; Wang, Y.; Zhang, K.; Wang, Z.Q.; Lu, J.X. Design and analysis of demolition robot arm based on finite element method. Adv. Mech. Eng. 2019, 11, 1–9. [Google Scholar] [CrossRef]
- Cheng, D.X.; Wang, D.F.; Liu, S.C.; Ji, K.S.; Han, X.S.; Yu, M.S.; Gao, S.Z.; Ke, R.Z.; Yang, Q.; Liu, Z.J.; et al. Mechanical Design Manual; Chemical Industry Press House: Beijing, China, 2004. [Google Scholar]
- Deng, Z.C.; Wang, X.R.; Zhao, Y.L. Precise control for vibration of rigid-flexible mechanical arm. Mech. Res. Commun. 2003, 30, 135–141. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Lu, S.; Gao, S.; Ren, Y.; Zhang, R. A Study of the Vibration Characteristics of Flexible Mechanical Arms for Pipe String Transportation in Oilfields. Energies 2022, 15, 2030. https://doi.org/10.3390/en15062030
Wang Y, Lu S, Gao S, Ren Y, Zhang R. A Study of the Vibration Characteristics of Flexible Mechanical Arms for Pipe String Transportation in Oilfields. Energies. 2022; 15(6):2030. https://doi.org/10.3390/en15062030
Chicago/Turabian StyleWang, Yan, Shuwen Lu, Sheng Gao, Yongliang Ren, and Ruijie Zhang. 2022. "A Study of the Vibration Characteristics of Flexible Mechanical Arms for Pipe String Transportation in Oilfields" Energies 15, no. 6: 2030. https://doi.org/10.3390/en15062030
APA StyleWang, Y., Lu, S., Gao, S., Ren, Y., & Zhang, R. (2022). A Study of the Vibration Characteristics of Flexible Mechanical Arms for Pipe String Transportation in Oilfields. Energies, 15(6), 2030. https://doi.org/10.3390/en15062030




