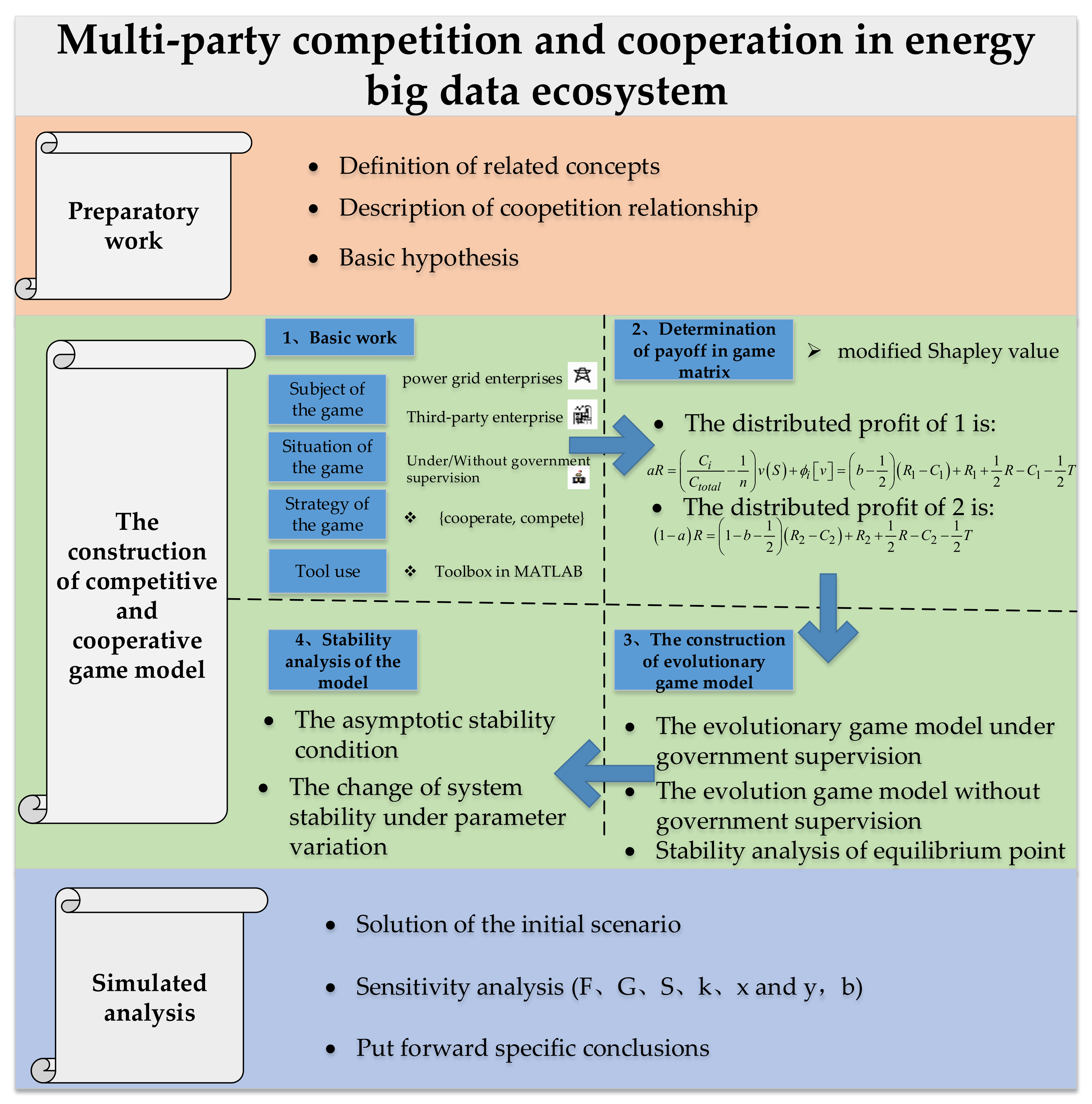
In this section, model analysis and simulation analysis are carried out. The model analysis part takes the relevant parameters as the benchmark research object and analyzes the system stability under the parameter settings. In the simulation analysis part, the parameters in the model are reasonably assigned, and the results verify the rationality of our model construction and give corresponding suggestions.
4.1. Model Analysis
In the system replication dynamic equation, under the four selection strategies, the revenue of the power grid company is simplified as
Ui,
I = 1, 2, 3, 4, and that of the third-party company is simplified as
uj,
j = 1, 2, 3, 4. According to Friedman’s discriminant method, when the Jacobian matrix satisfies the value of determinant greater than zero and traces less than zero, the local equilibrium point is the stable strategy of the system [
58].
By solving eigenvalues of different stable points, the determinant value and trace of the matrix under different stable points are obtained, and the final evolution strategy is obtained by judging whether the point is stable. When u1 > u2, U1 > U3—that is, when the grid company chooses the cooperative strategy, and the third-party enterprise chooses the competitive strategy, the profit is less than the cooperative strategy.
In the case that the third-party enterprises choose the cooperative strategy, and the grid enterprises choose the competitive strategy, the benefits are less than the cooperative strategy, both sides will prefer the cooperative strategy, and there are five stable points,
E1 (0, 0),
E2 (0, 1),
E3 (1, 0),
E4 (1, 1),
E5 (
x*,
y*). When there are five stability points, the stability of different stability points can be judged, as shown in
Table 6.
In this case,
E1 (0, 0) and
E5 (
x*,
y*) are selected, regardless of the initial state—that is, both sides choose a competitive strategy or both sides choose a cooperative strategy. The evolution process under different initial states is shown in
Figure 2.
From the above analysis, it can be seen that the final strategy selection of each entity in the energy big data ecosystem may tend to be the evolutionarily stable strategy {compete, compete}, or the evolutionarily stable strategy {cooperate, cooperate}.
The relevant parameters in the payment matrix will closely affect the evolution path of the co-competition relationship between the main players in the energy big data ecosystem. This study takes the case of government supervision as an example to analyze the influence of different parameter settings in the model on the evolution stability strategy.
In
Figure 2,
E1 E3 E5 E2 and
E3 E4 E2 E5 together form the area of the square
E1 E2 E3 E4. The sum of the total areas is 1. Let
S (
E1 E3 E5 E2) be
S. Then, the area of
E3 E4 E2 E5 is 1-
S, (
S, 1-
S) ∈ [0, 1] × [0, 1]. 1-
S can represent the probability that the principal policy evolves to
E4. The smaller
S value is, the greater the probability that the policy eventually evolves to {cooperate, cooperate} and the higher the probability that {cooperate, cooperate} becomes ESS [
59]. Therefore, to realize the final state of the energy big data ecosystem, the government should effectively design relevant parameters of supervision in addition to the personal will of each participant in the system, to maximize the probability of the evolution of the system to {cooperate, cooperate}.
Under the condition of government supervision, the area of region
S (
E1 E3 E5 E2) can be expressed as:
Let
S (
E1 E3 E5 E2) take the derivative of government’s financial support
G to obtain:
The value of (∂S (E1 E3 E5 E2))/∂G is less than zero, and with the increase of G, (∂S (E1 E3 E5 E2)))/∂G increases. S (E1 E3 E5 E2) is the minus function of G, reducing the area of the area will be reduced gradually with the increase of G, It tends to evolve to the lower left, which eventually increases the area on the line and finally increases the probability that the co-opetition relationship of the energy big data ecosystem converges to the evolutionarily stable strategy {cooperate, cooperate}.
Let
S (
E1 E3 E5 E2) take the derivative of the government’s supervision punishment
F to obtain:
When such a situation exists, K is the speculative benefit of collaborative innovation, F is the supervision penalty of the government. With the increase of F, (∂S (E1 E3 E5 E2))/∂F becomes larger, S (E1 E3 E5 E2) is the minus function of F, and the area of the region will gradually decrease with the increase of F. This tends to evolve to the lower left, which eventually increases the area on the line and finally increases the probability that the co-opetition relationship of the energy big data ecosystem converges to the evolutionarily stable strategy {cooperate, cooperate}.
In the process of F increasing, K − F + (1 − b) T > 0 is still greater than zero. At this point, for the player that does not participate in the collaboration, since the other party pays the cost of the collaboration but does not pay the cost of the collaboration and gains the free-rider benefit, the synergy cost paid by the other party can be counted as part of the benefit. K + (1 − b) T represents the benefits gained in the free-riding behavior, and F is the punishment obtained in the free-riding behavior. Therefore, although the value of F keeps increasing, K − F + (1 − b) T > 0. The non-participation in the synergy can create more benefits for the player; however, with the increase of F, the benefits will decrease. Therefore, the probability of selecting competition will become increasingly smaller. System stability tends to choose the cooperative strategy.
By analyzing the eigenvalues and stability of different scenarios, the evolution paths of different players in the energy big data ecosystem under different conditions, and the evolution strategies finally achieved can be obtained. At the beginning of the ecological system to establish great energy data, under the government-led system, the player realizes orderly participation of data services. At this point, the government can—through relevant macro policy or incentives to improve—improve the competition game model to realize the related parameters and the stability of the ecosystem to achieve the ultimate state of evolution and achieve the ultimate state of orderly cooperation strategy.
After the great energy data ecosystem development matures, participation in the main body of the data service can be solved through its own related game model parameter is set judgment system eventually reaching a steady state, orderly coordinated system. To achieve the ultimate state, the player can adjust the associated state to achieve the ultimate collaborative strategy and to achieve orderly synergies in the energy big data ecosystem.
4.2. Simulation Analysis
In the process of dynamic evolution simulation of the game system using MATLAB, the parameters are set as follows: C1 = 100, C2 = 90, R1 = 140, R2 = 125, R = 35, T = 25, b = 0.6, S = 5, G = 3.5, F = 8, and K = 5. The initial probabilities are set to x = 0.4 and y = 0.6.
- 1.
Sharpe profit return solution
According to the initial correlation parameter hypothesis, we obtain the income of each subject under the calculation of the cost correction Shapley value.
The distributed profit of 1 is:
Similarly, the distributed profit of 2 is:
- 2.
Cooperative competition strategy solution
Based on the calculated initial distribution income of each subject, combined with the constructed evolutionary game payment matrix, we obtain the payment matrix of both parties as shown in
Table 7.
The probability evolution diagram of different participant selection strategies can be obtained through MATLAB simulation. As shown in
Figure 3, under government control measures, the initial synergy probability of power grid enterprises is 0.4, and that of third-party enterprises is 0.6. However, regardless of the initial willingness of different participants to choose coordination, the final strategy is stable and tends to be the coordination strategy. The initial strategy selection probability obtained through evolution has a short time to reach the final steady-state, which proves that under the control of the government, reasonable parameter setting can make all the subjects in the energy data ecosystem achieve a better cooperative operation state.
As can be seen from the evolution path of energy ecological big data system, the final state of the system is that each player is in an equal position, each player carries out free co-opetition, and the government no longer performs supervision functions. When the government no longer performs the function of government supervision, the power grid company and the third-party enterprise continue the previous revenue model in the initial stage and carry on the co-opetition game.
Figure 4 shows the evolution path of the selection strategies of each player under anarchic supervision. It can be seen from the figure that, in the simulation process, the final evolution strategies of both power grid enterprises and third-party enterprises tend to be collaborative. However, compared with the government supervision, it can be seen from the figure that it takes a longer time for power grid enterprises and third-party enterprises to evolve to the collaborative strategy.
Among these, the probability evolution rate of power grid enterprises is more obvious than that of third-party enterprises. When the government retires from its regulatory function, it should adjust its parameters to reasonably allocate the costs and expenses in the energy big data ecosystem. These measures will enhance the initiative of each body to participate in collaborative development and realize the collaborative development of different bodies in different evolutionary stages.