Moisture Transfer Characteristics and Kinetics Determination for Insulated Paperboard in Hot-Pressing Process
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials Preparation
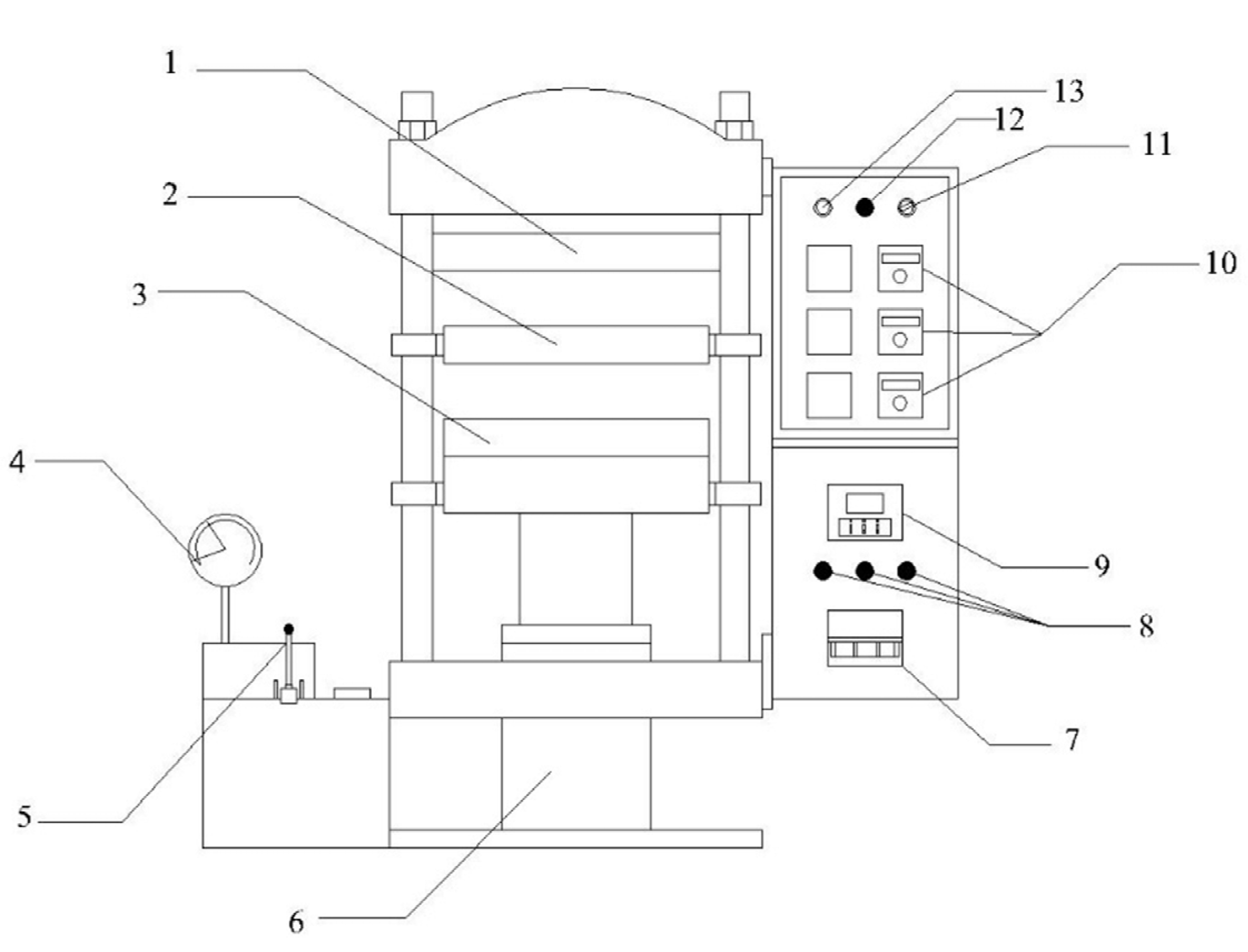
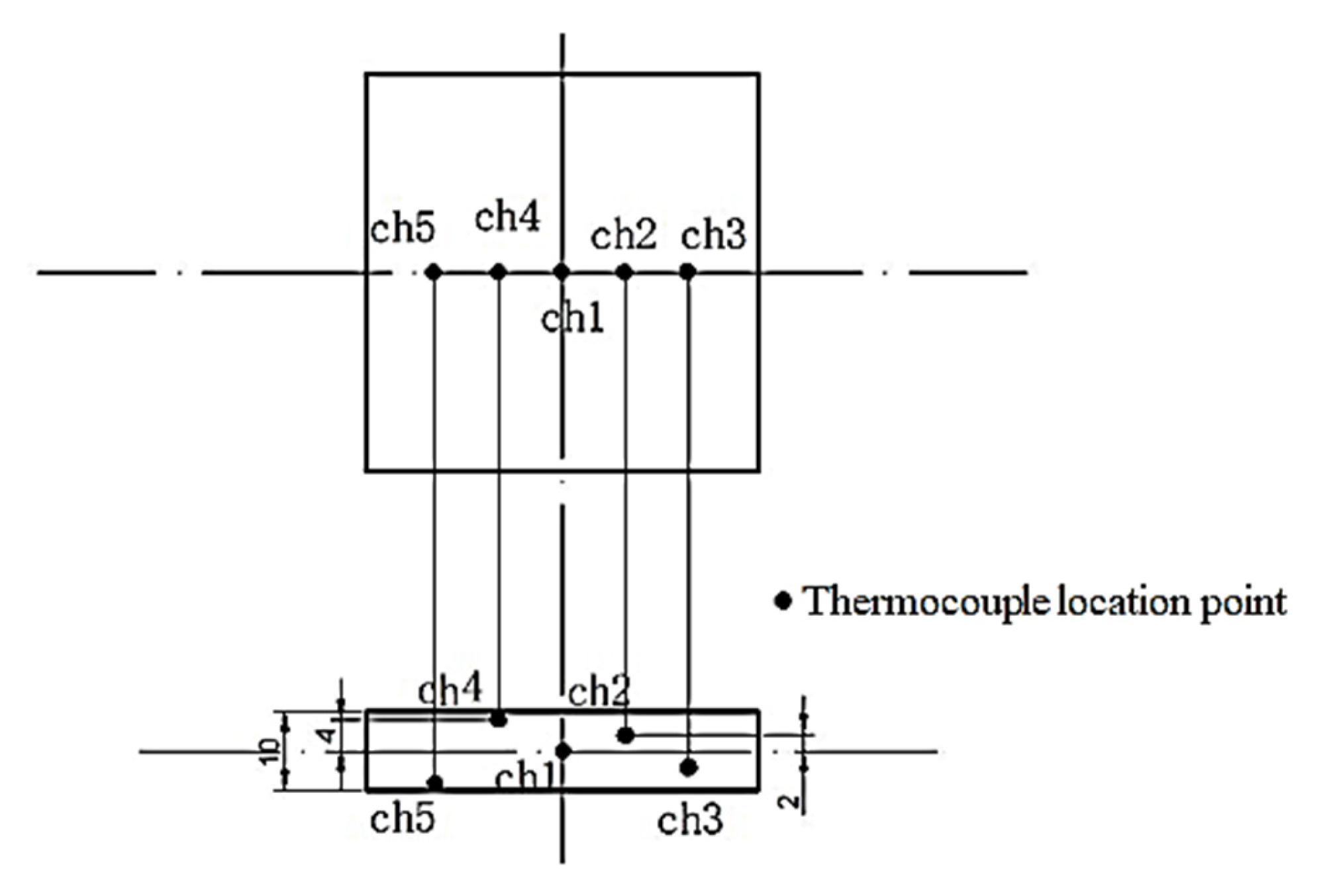
2.2. Experimental Equipment and Methods
2.3. Moisture Transfer Characteristics Calculation
3. Results and Discussions
3.1. The Morphological Changes of the Insulated Paperboard
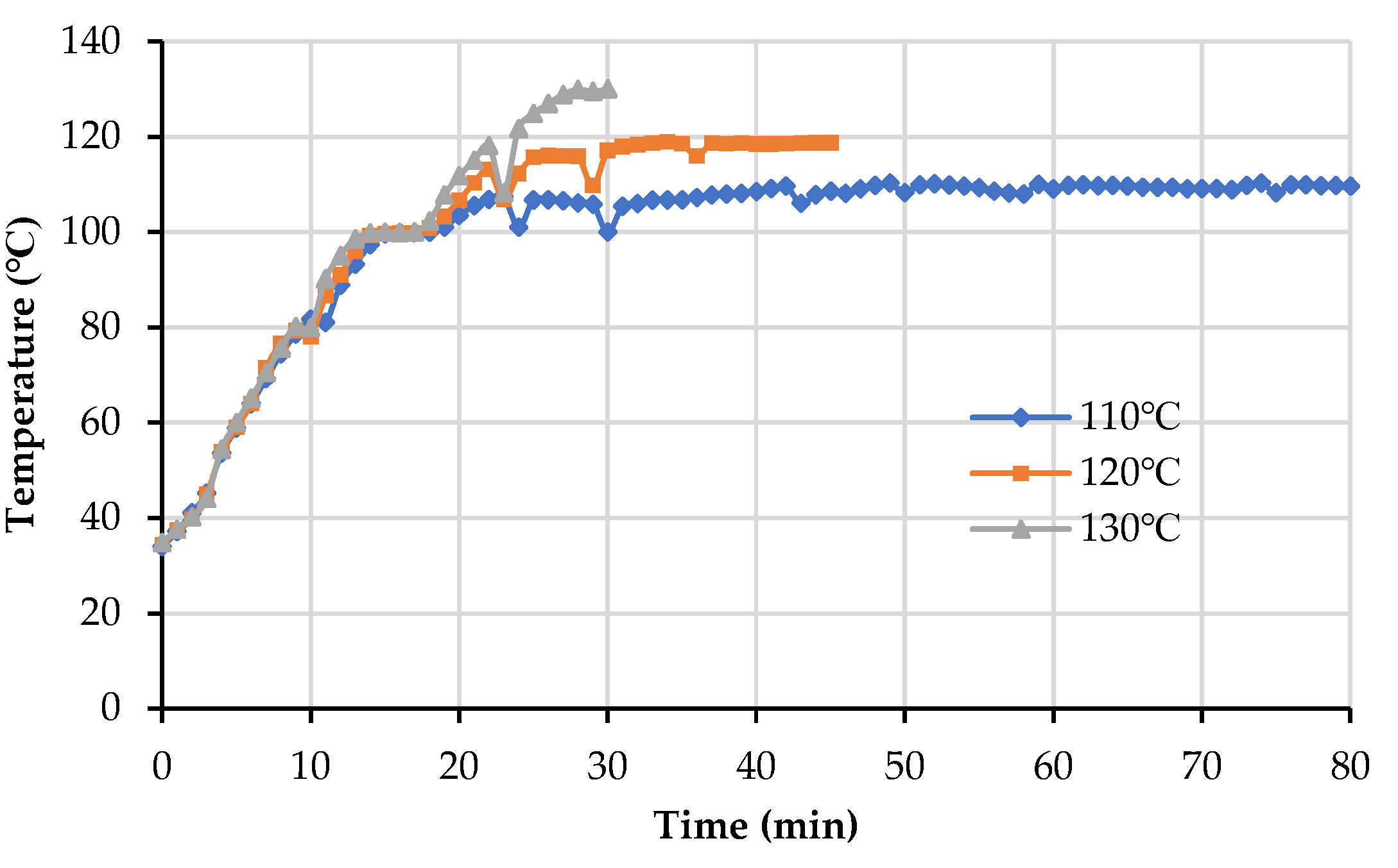
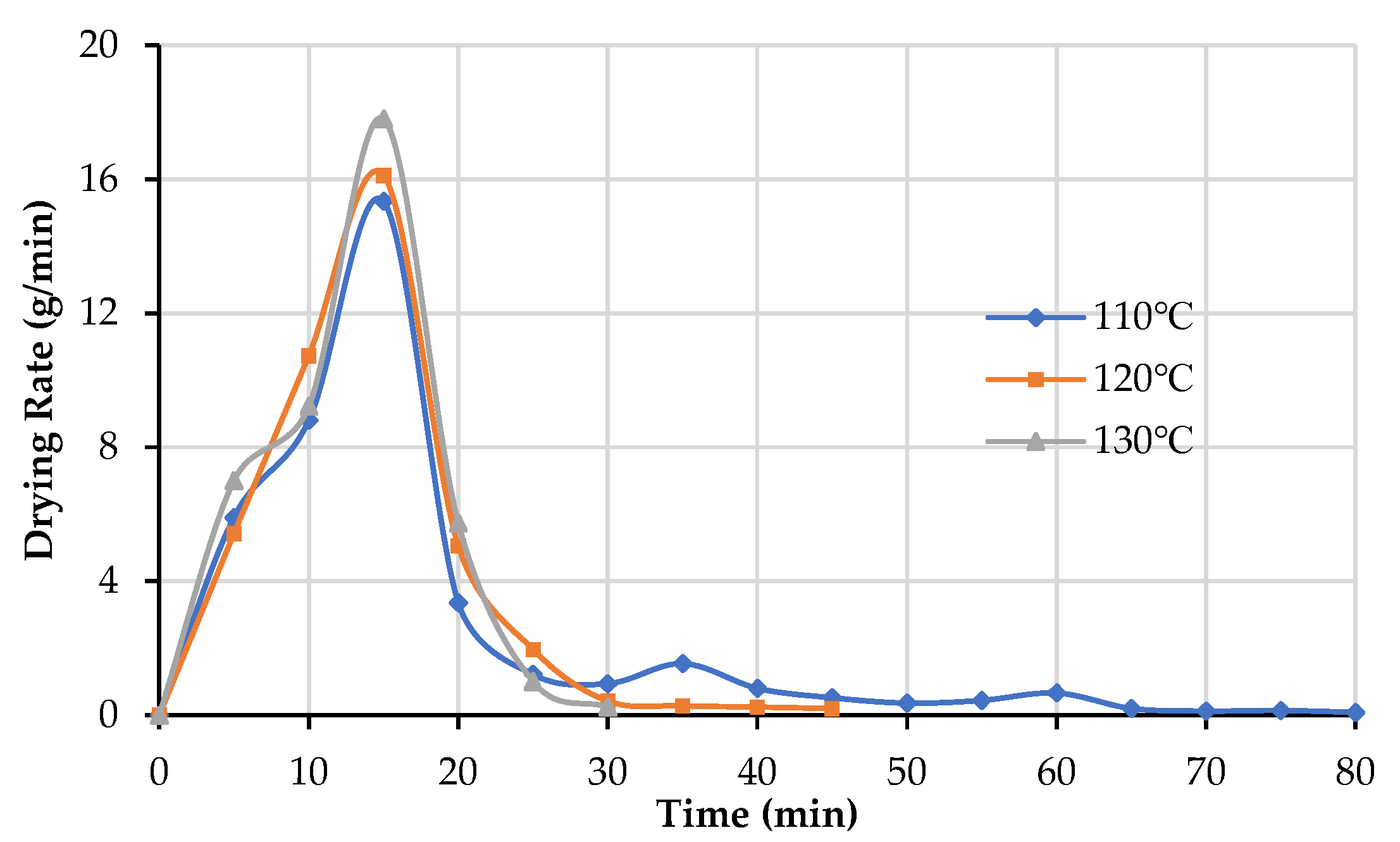
3.2. Moisture Transfer Characteristics of the Insulated Paperboard
3.3. Effects of Temperature on Moisture Transfer Characteristics
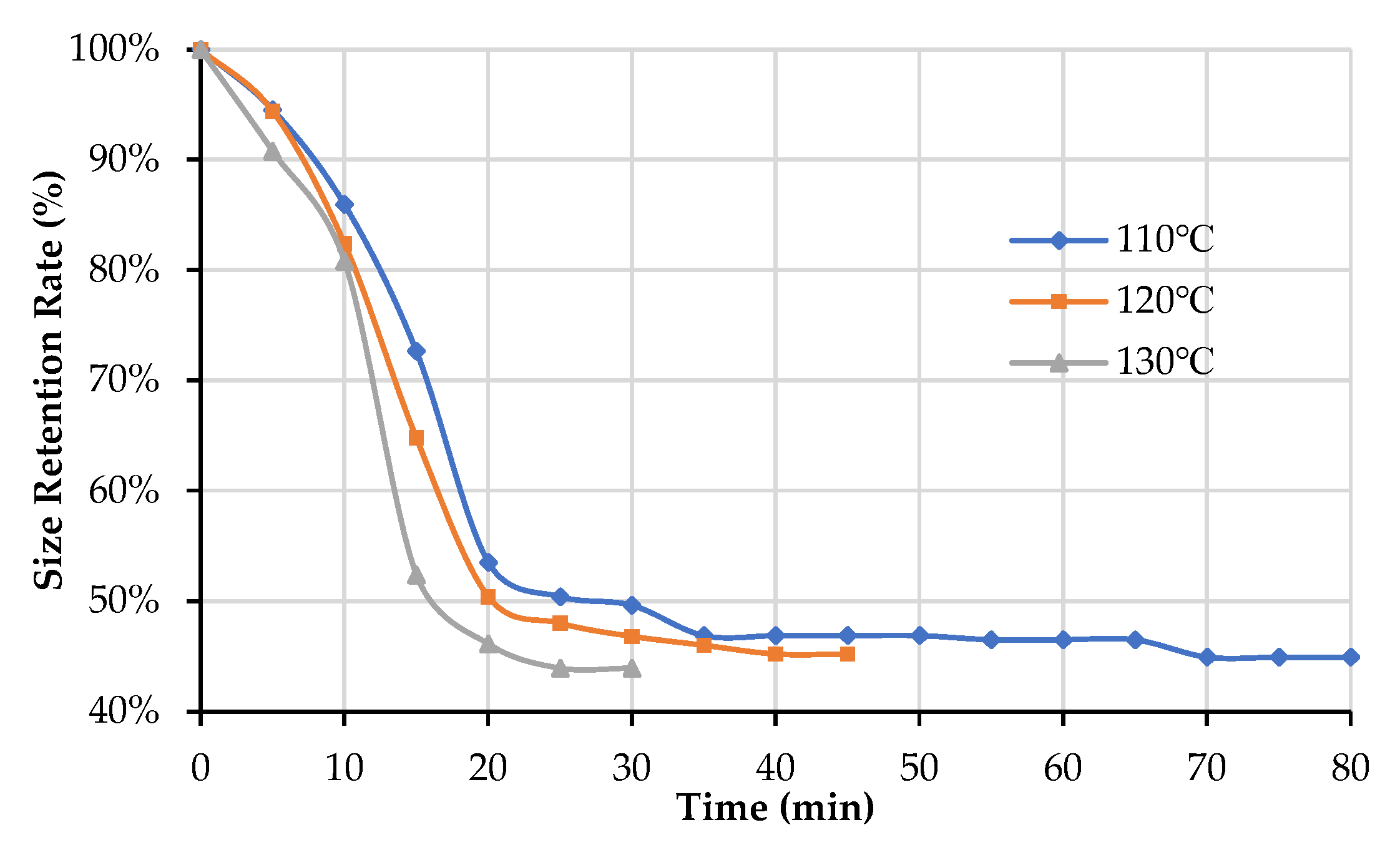
3.4. Effects of Temperature on Size Retention Rate and Relative Porosity
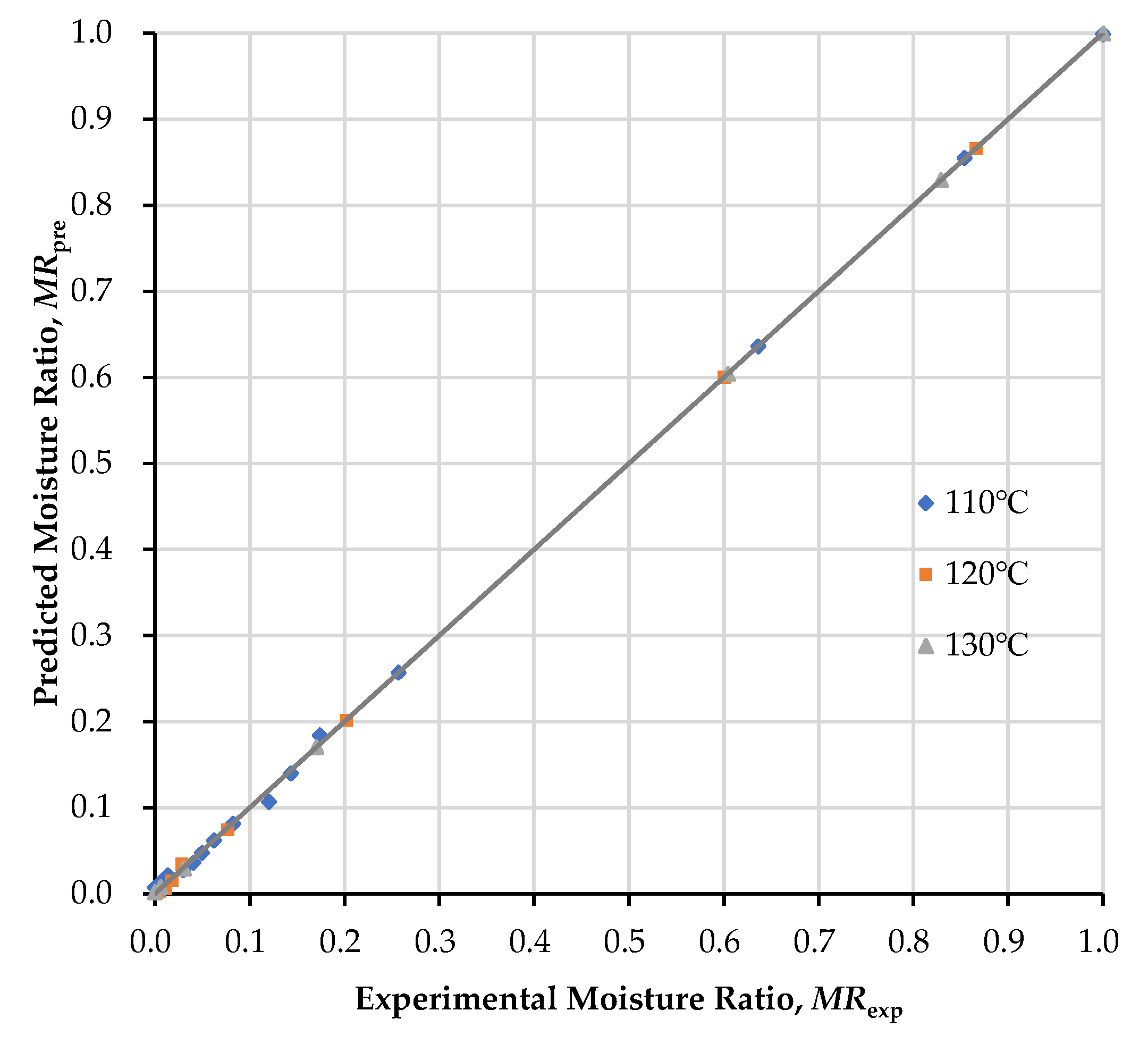
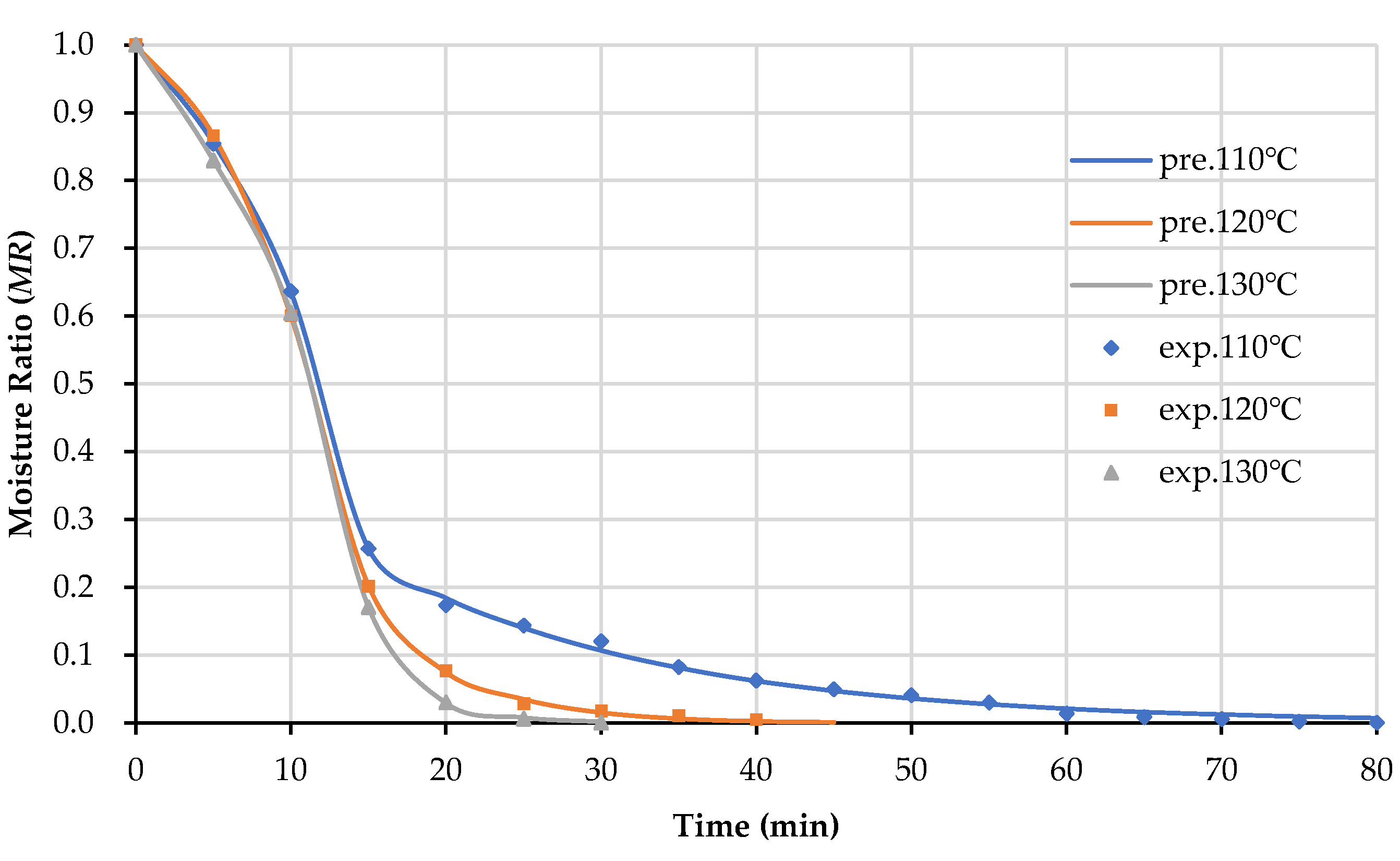
3.5. Moisture Transfer Kinetics Determination
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- El-Saied, H.; El-Meligy, M.G.; Mohamed, S.H.; El-Mongy, S.A. Electrical insulated paper from cotton linter. Carbohydr. Polym. 2021, 90, 147–151. [Google Scholar] [CrossRef] [PubMed]
- Fahmy, T.Y.A.; Mobarak, F.; El-Meligy, M.G. Introducing undeinked old newsprint as a new resource of electrical purposes paper. Wood Sci. Technol. 2008, 42, 691–698. [Google Scholar] [CrossRef]
- Schaible, M. Electrical insulating papers-An overview. IEEE Electr. Insul. Mag. 1987, 3, 8–12. [Google Scholar] [CrossRef]
- Prevost, T.A.; Oommen, T.V. Cellulose insulation in oil-filled power transformers: Part I-history and development. IEEE Electr. Insul. Mag. 2006, 22, 28–35. [Google Scholar] [CrossRef]
- Fernández, I.; Delgado, F.; Ortiz, F.; Ortiz, A.; Fernández, C.; Renedo, C.J.; Santisteban, A. Thermal degradation assessment of Kraft paper in power transformers insulated with natural esters. Appl. Therm. Eng. 2016, 104, 129–138. [Google Scholar] [CrossRef] [Green Version]
- Wu, G.F.; Jiang, Y.F.; Ping, Q.; Lang, Q.; Pu, J. Effect of chemical modification and hot-press drying on poplar wood. Bioresources 2010, 5, 2581–2590. [Google Scholar]
- Emsley, A.M.; Stevens, G.C. Kinetics and mechanisms of the low-temperature degradation of cellulose. Cellulose 1994, 1, 26–56. [Google Scholar] [CrossRef]
- Ribeiro, H.A.; Costa, C. Modeling and simulation of the hot-pressing process in paper production: A heat- and mass-transfer analysis. Ind. Eng. Chem. Res. 2007, 46, 8205–8219. [Google Scholar] [CrossRef]
- Hou, J.; Yi, S.; Zhou, Y.; Pan, B. Moisture state variety in poplar lumber with moisture content above fibre saturation point during hot-press drying. J. Wood Sci. 2018, 64, 730–737. [Google Scholar] [CrossRef] [Green Version]
- Tang, Y.; Pearson, R.G.; Hart, C.A.; Simpson, W.T. A numerical model for heat transfer and moisture evaporation processes in hot-press drying-an integral approach. Wood Fiber Sci. 1994, 26, 78–90. [Google Scholar]
- Han, C.J.; Xu, J.M.; Jiang, J.L.; Jiang, J.H.; Lv, J.X. Moisture content distribution of multiple eucalyptus veneers during hot-press-drying. Wood Res. 2014, 59, 351–358. [Google Scholar]
- Ribeiro, D.P.; Vilela, A.P.; Silva, D.W.; Napoli, A.; Mendes, R.F. Effect of Heat Treatment on the Properties of Sugarcane Bagasse Medium Density Particleboard (MDP) Panels. Waste Biomass Valorization 2019, 11, 6429–6441. [Google Scholar] [CrossRef]
- Kong, L.; Yang, X.; Hou, Z.; Dong, J. Mathematical modeling of drying kinetics for pulp sheet based on Fick’s second law of diffusion. J. Korea Tech. Assoc. Pulp Pap. Ind. 2020, 52, 23–31. [Google Scholar] [CrossRef]
- Zhao, P.; Ge, S.; Ma, D.; Areeprasert, C.; Yoshikawa, K. Effect of hydrothermal pretreatment on convective drying characteristics of paper sludge. ACS Sustain. Chem. Eng. 2014, 2, 665–671. [Google Scholar] [CrossRef]
- Doymaz, İ. Evaluation of some thin-layer drying models of persimmon slices (Diospyros kaki L.). Energy Convers. Manag. 2012, 56, 199–205. [Google Scholar] [CrossRef]
- Han, C. Heat and Mass Transfer of Multiple Veneers Hot-Press Drying and Its Process Optimization. Ph.D. Thesis, Chinese Academy of Forestry, Beijing, China, 27 June 2014. (In Chinese). [Google Scholar]
- Liu, Y. Study on Heat-Conduction of Fiberboard and Plywood in the Hot-Pressing Process. Ph.D. Thesis, Nanjing Forestry University, Nanjing, China, 18 June 2013. (In Chinese). [Google Scholar]
- Wang, H.; Lu, T.; Jiang, P. Experimental investigation on carrot drying characteristics by hot air. J. Therm. Sci. Technol. 2015, 14, 456–461. [Google Scholar]
- Hii, C.L.; Law, C.L.; Cloke, M. Modeling using a new thin layer drying model and product quality of cocoa. J. Food Eng. 2009, 90, 191–198. [Google Scholar] [CrossRef]
- Gómez-de la Cruz, F.J.; Casanova-Peláez, P.J.; López-García, R.; Cruz-Peragón, F. Review of the drying kinetics of olive oil mill wastes: Biomass recovery. Bioresources 2015, 10, 5777–5802. [Google Scholar] [CrossRef] [Green Version]
- Henderson, S.M.; Pabis, S. Grain drying theory: I. Temperature effect on drying coefficient. J. Agric. Eng. Res. 1961, 6, 169–174. [Google Scholar]
- Henderson, S.M. Progress in developing the thin layer drying equation. Trans. Am. Soc. Agric. Eng. 1974, 17, 1167–1172. [Google Scholar] [CrossRef]
- Lewis, W.K. The rate of drying of solid materials. J. Ind. Eng. Chem. 1921, 13, 427–432. [Google Scholar] [CrossRef]
- Page, G.E. Factors Influencing the Maximum Rate of Air Drying Shelled Corn in Thin-Layers. Master’s Thesis, Purdue University, West Lafayette, IN, USA, 1949. [Google Scholar]
- Omolola, A.O.; Kapila, P.F.; Silungwe, H.M. Mathematical modeling of drying characteristics of Jew’s mallow (Corchorus olitorius) leaves. Inf. Processing Agric. 2019, 6, 109–115. [Google Scholar] [CrossRef]
- Midilli, A.; Kucuk, H.; Yapar, Z. A new model for single-layer drying. Dry. Technol. 2002, 20, 1503–1513. [Google Scholar] [CrossRef]
- Ertekin, C.; Firat, M.Z. A comprehensive review of thin-layer drying models used in agricultural products. Crit. Rev. Food Sci. Nutr. 2015, 57, 701–717. [Google Scholar] [CrossRef]
- Cai, Z.L.; Ma, X.Q.; Qing, X.; Yu, S. Drying kinetics and characteristics of sewage sludge/rice straw mixture. Dry. Technol. 2015, 33, 1500–1509. [Google Scholar] [CrossRef]




| Model Name | Model Equation | Reference |
|---|---|---|
| Henderson and Pabis model | MR = aexp(−kt) | [21] |
| Two-term model | MR = aexp(−k1t) + bexp(−k2t) | [22] |
| Lewis model | MR = exp(−kt) | [23] |
| Page model | MR = exp(−ktn) | [24] |
| Logarithmic model | MR =aexp(−kt) + b | [25] |
| Midilli model | MR = aexp(−ktn) + bt | [26] |
| Weibull distribution | MR = exp(−(t/a)n) | [27] |
| Hii et al. model | MR = aexp(−ktn) + bexp(−gtn) | [19] |
| New model | MR = aexp(−ktn) + bexp(−gtm) | This article |
| Model Name | Drying Temp. (℃) | R2 | χ2 | RMSE |
|---|---|---|---|---|
| Henderson and Pabis model | 110 | 0.96888 | 0.00326 | 0.05361 |
| 120 | 0.93314 | 0.01145 | 0.09572 | |
| 130 | 0.90496 | 0.02067 | 0.12150 | |
| Two-term model | 110 | 0.96977 | 0.00365 | 0.05284 |
| 120 | 0.95180 | 0.01101 | 0.08128 | |
| 130 | 0.94917 | 0.01842 | 0.08886 | |
| Lewis model | 110 | 0.96394 | 0.00354 | 0.05771 |
| 120 | 0.92209 | 0.01186 | 0.10333 | |
| 130 | 0.89347 | 0.01930 | 0.12863 | |
| Page model | 110 | 0.97959 | 0.00214 | 0.04341 |
| 120 | 0.99710 | 0.00050 | 0.01995 | |
| 130 | 0.99232 | 0.00167 | 0.03454 | |
| Logarithmic model | 110 | 0.96897 | 0.00348 | 0.05353 |
| 120 | 0.94724 | 0.01033 | 0.08503 | |
| 130 | 0.94721 | 0.01435 | 0.09055 | |
| Midilli model | 110 | 0.98280 | 0.00208 | 0.03985 |
| 120 | 0.99752 | 0.00057 | 0.01844 | |
| 130 | 0.99363 | 0.00231 | 0.03144 | |
| Weibull distribution | 110 | 0.97959 | 0.00214 | 0.04341 |
| 120 | 0.99710 | 0.00050 | 0.01995 | |
| 130 | 0.99232 | 0.00167 | 0.03454 | |
| Hii et al. model | 110 | 0.99644 | 0.00047 | 0.01813 |
| 120 | 0.99805 | 0.00053 | 0.01634 | |
| 130 | 0.99362 | 0.00347 | 0.03146 | |
| New model | 110 | 0.99961 | 0.00005 | 0.00599 |
| 120 | 0.99994 | 0.00002 | 0.00283 | |
| 130 | 0.99999 | 0.00001 | 0.00120 |
| Drying Temp. (°C) | MR =aexp(−ktn) + bexp(−gtm) | |||||
|---|---|---|---|---|---|---|
| a | k | n | b | g | m | |
| 110 | 0.43340 | 0.00000 | 5.87493 | 0.56562 | 0.05954 | 0.97990 |
| 120 | 0.45233 | 0.00000 | 4.86347 | 0.54772 | 0.02646 | 1.44339 |
| 130 | 0.61253 | 0.02439 | 1.61096 | 0.38738 | 0.00000 | 10.27563 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, L.; Zhao, J.; Li, J.; Yuan, Y. Moisture Transfer Characteristics and Kinetics Determination for Insulated Paperboard in Hot-Pressing Process. Energies 2022, 15, 2069. https://doi.org/10.3390/en15062069
Kong L, Zhao J, Li J, Yuan Y. Moisture Transfer Characteristics and Kinetics Determination for Insulated Paperboard in Hot-Pressing Process. Energies. 2022; 15(6):2069. https://doi.org/10.3390/en15062069
Chicago/Turabian StyleKong, Lingbo, Jingyi Zhao, Jiahao Li, and Yuejin Yuan. 2022. "Moisture Transfer Characteristics and Kinetics Determination for Insulated Paperboard in Hot-Pressing Process" Energies 15, no. 6: 2069. https://doi.org/10.3390/en15062069
APA StyleKong, L., Zhao, J., Li, J., & Yuan, Y. (2022). Moisture Transfer Characteristics and Kinetics Determination for Insulated Paperboard in Hot-Pressing Process. Energies, 15(6), 2069. https://doi.org/10.3390/en15062069





