A Critical Review of State-of-the-Art Optimal PMU Placement Techniques
Abstract
:1. Introduction
1.1. SCADA versus PMU
1.2. Existing Surveys in OPP
- A comprehensive review of state-of-the-art optimal PMU placement techniques is presented.
- We have outlined the strengths and weaknesses of research efforts in the PMU placement problem. Critical discussion is also made on the previously published review articles in optimal PMU placement.
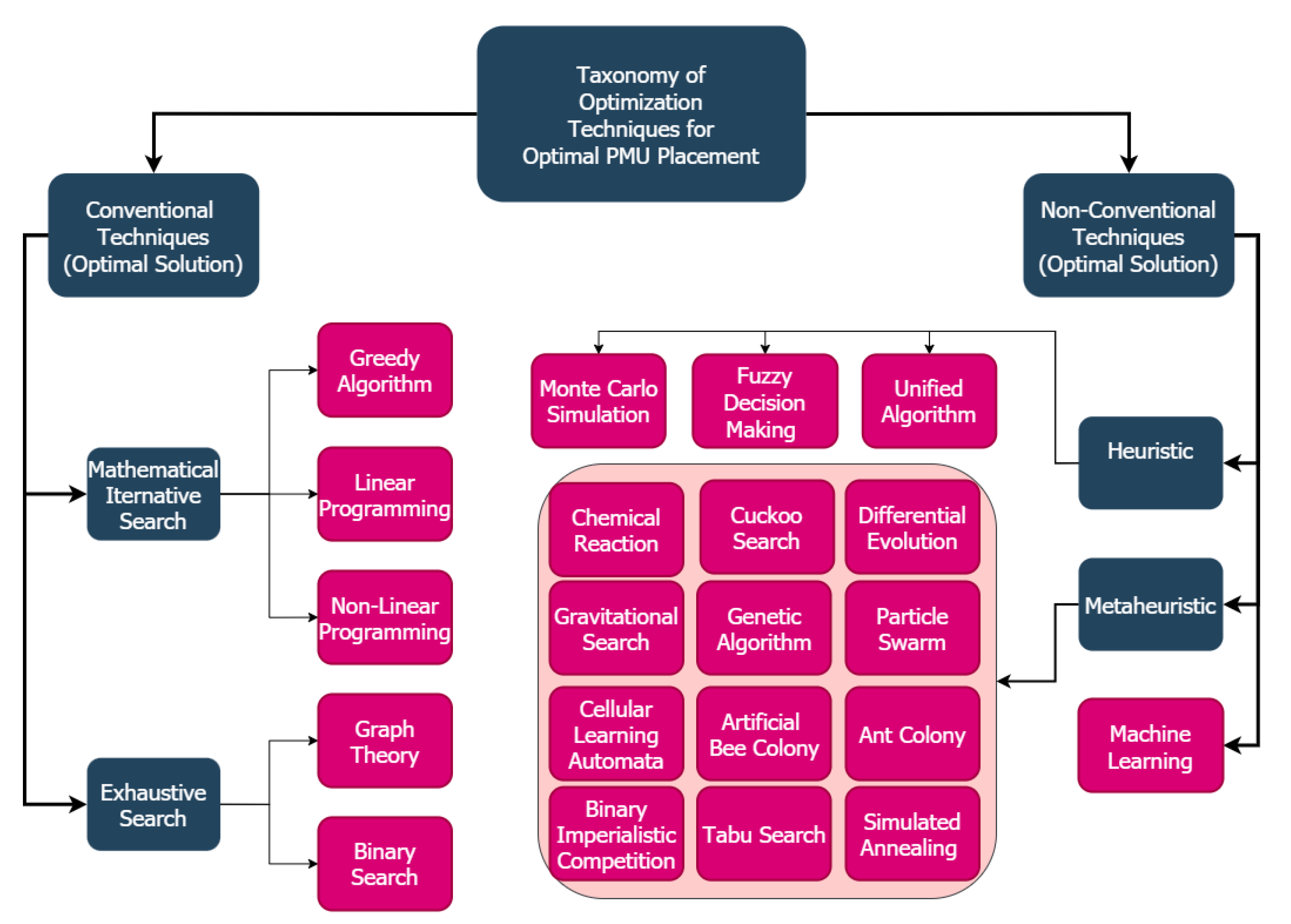
- A taxonomy of optimization techniques, used in optimal PMU placement, is presented that gives a framework for grouping different optimization algorithms. The literature discussed in this paper follows the same taxonomy.
- A summary of commonly used techniques like linear programming, genetic algorithm, and particle swarm optimization is presented. A comparative analysis of common algorithms used in the PMU placement problem is also provided in tables.
- Comprehensive discussion on testbed systems, optimization solvers, and pros and cons of different techniques in the literature of optimal PMU placement is provided.
- An extensive list of references covering the work of the last two decades is provided. Important missing gaps in this field of research are also discussed in detail.
2. Optimal PMU Placement
2.1. Fundamental Statement of Objective Function
2.2. Fundamental Statement of Observability Constraint
3. OPP Using Conventional Optimization
3.1. Mathematical Iterative Algorithms
3.1.1. Greedy Algorithm Based OPP
3.1.2. Linear Programming (LP) Based OPP
3.1.3. Non-Linear Programming (NLP) Based OPP
3.2. Exhaustive Search
3.2.1. Graph Theory-Based OPP
3.2.2. Binary Search-Based OPP
4. OPP Using Non-Conventional Optimization
4.1. Heuristic Techniques
4.1.1. Unified Algorithm Based OPP
4.1.2. Fuzzy Decision Based OPP
4.1.3. Monte Carlo Simulation Based OPP
4.2. Metaheuristic Techniques
4.2.1. Chemical Reaction Based OPP
4.2.2. Cuckoo Search Based OPP
4.2.3. Differential Evolution Based OPP
4.2.4. Gravitational Search-Based OPP
4.2.5. Genetic Algorithm (GA) Based OPP
4.2.6. Particle Swarm Optimization (PSO) Based OPP
4.2.7. Cellular Learning Automata (CLA) Based OPP
4.2.8. Artificial Bee Colony Based (ABC) OPP
4.2.9. Ant Colony (AC) Based OPP
4.2.10. Binary Imperialistic Competition Algorithm (BICA) Based OPP
4.2.11. Tabu Search (TS) Based OPP
4.2.12. Simulated Annealing Based OPP
4.3. Machine Learning (ML) Based OPP
5. Discussion and Future Work
5.1. Testbed Systems
5.2. Optimization Solvers
5.3. Pros and Cons
5.4. Future Scope
5.4.1. Application Based Planning
5.4.2. Node-Breaker Model
5.4.3. Hybrid Optimization Algorithm
5.4.4. Performance Evaluators
5.4.5. PMU Placement
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Saly, S.; Signer, K.; Sullivan, A. Power System Monitoring. IFAC Proc. Vol. 1980, 13, 189–198. [Google Scholar] [CrossRef]
- Sefid, M.; Rihan, M. Optimal PMU placement in a smart grid: An updated review. Int. J. Smart Grid Clean Energy 2019, 8, 59–69. [Google Scholar] [CrossRef]
- Dusabimana, E.; Yoon, S.G. A survey on the micro-phasor measurement unit in distribution networks. Electronics 2020, 9, 305. [Google Scholar] [CrossRef] [Green Version]
- Madani, V.; Parashar, M.; Giri, J.; Durbha, S.; Rahmatian, F.; Day, D.; Adamiak, M.; Sheble, G. PMU placement considerations - A roadmap for optimal PMU placement. In Proceedings of the 2011 IEEE/PES Power Systems Conference and Exposition, Phoenix, AZ, USA, 20–23 March 2011; pp. 1–7. [Google Scholar]
- Virginia, D.; Kyle, P.; Gardner, M.; Energy, D.; Bradberry, T. Using Synchrophasor Data for Phase Angle Monitoring NASPI Control Room Solutions Task Team Paper. pp. 1–54. Available online: https://www.naspi.org/sites/default/files/reference_documents/0.pdf (accessed on 14 May 2016).
- Moxley, R.; Anderson, C.; Laboratories, S.E. Uses and Limitations of Advanced Analog Quantities. 2003, pp. 1–7. Available online: https://cdn.selinc.com/assets/Literature/Publications/Technical%20Papers/6234_UsesLimitations_RM_20060303.pdf (accessed on 14 August 2003).
- Phadke, A.G. Synchronized phasor measurements: A historical overview. Proc. IEEE Power Eng. Soc. Transm. Distrib. Conf. 2002, 1, 476–479. [Google Scholar]
- Mohanta, D.K.; Murthy, C.; Sinha Roy, D. A Brief Review of Phasor Measurement Units as Sensors for Smart Grid. Electr. Power Components Syst. 2016, 44, 411–425. [Google Scholar] [CrossRef]
- Hojabri, M.; Dersch, U.; Papaemmanouil, A.; Bosshart, P. A comprehensive survey on phasor measurement unit applications in distribution systems. Energies 2019, 12, 4552. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Wu, L.; Li, J. D-PMU based applications for emerging active distribution systems: A review. Electr. Power Syst. Res. 2020, 179, 106063. [Google Scholar] [CrossRef]
- Kerdphol, T.; Matsukawa, Y.; Watanabe, M.; Mitani, Y. Application of PMUs to monitor large-scale PV penetration infeed on frequency of 60 Hz Japan power system: A case study from Kyushu Island. Electr. Power Syst. Res. 2020, 185, 106393. [Google Scholar] [CrossRef]
- Pal, A.; Chatterjee, P.; Thorp, J.S.; Centeno, V.A. Online Calibration of Voltage Transformers Using Synchrophasor Measurements. IEEE Trans. Power Deliv. 2016, 31, 370–380. [Google Scholar] [CrossRef]
- Ahmed, M.; Imran, K. An Optimal PMU Placement Against N-1 Contingency of PMU Using Integer Linear Programming Approach. In Proceedings of the 2019 International Conference on Applied and Engineering Mathematics, Taxila, Pakistan, 27–29 August 2019. [Google Scholar]
- Tao, W.; Ma, M.; Ding, M.; Xie, W.; Fang, C. A priority-based synchronous phasor transmission protocol extension method for the active distribution network. Appl. Sci. 2019, 9, 2135. [Google Scholar] [CrossRef] [Green Version]
- Nanda, P.; Panigrahi, C.K.; Dasgupta, A. Phasor Estimation and Modelling Techniques of PMU—A Review. Energy Procedia 2017, 109, 64–77. [Google Scholar] [CrossRef]
- Dubey, R.; Popov, M.; Muro, J.d.J.C. Cost Effective Wide Area Measurement Systems for Smart Power Network. IEEE Power Energy Technol. Syst. J. 2018, 5, 85–93. [Google Scholar] [CrossRef]
- Yuill, W.; Edwards, A.; Chowdhury, S.; Chowdhury, S.P. Optimal PMU placement: A comprehensive literature review. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–8. [Google Scholar]
- Manousakis, N.M.; Korres, G.N.; Georgilakis, P.S. Taxonomy of PMU placement methodologies. IEEE Trans. Power Syst. 2012, 27, 1070–1077. [Google Scholar] [CrossRef]
- Synchrophasor Measurement Technology in Power Systems: Panorama and State-of-the-Art. IEEE Access 2014, 2, 1607–1628. [CrossRef]
- Negash, K.; Khan, B.; Yohannes, E. Artificial Intelligence Versus Conventional Mathematical Techniques: A Review for Optimal Placement of Phasor Measurement Units. Technol. Econ. Smart Grids Sustain. Energy 2016, 1, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Baba, M.; Nor, N.B.; Ibrahim, T.B.; Sheikh, M.A. A comprehensive review for optimal placement of phasor measurement unit for network observability. Indones. J. Electr. Eng. Comput. Sci. 2020, 19, 301–308. [Google Scholar] [CrossRef]
- Johnson, T.; Moger, T. A critical review of methods for optimal placement of phasor measurement units. Int. Trans. Electr. Energy Syst. 2020, 31, e12698. [Google Scholar] [CrossRef]
- Abdulkareem, A.; Ogbe, D.; Somefun, T. Review of different methods for optimal placement of phasor measurement unit on the power system network. Adv. Sci. Technol. Eng. Syst. 2021, 5, 1071–1081. [Google Scholar] [CrossRef]
- Kallrath, J.; Molone, E. Brief Review of Mathematical Optimization; Springer: Berlin, Germany, 2009; pp. 351–427. [Google Scholar]
- Adibhatla, S.; Leigh, D.C. A comparison of optimization methods for engineering system optimization. Eng. Optim. 1987, 12, 13–23. [Google Scholar] [CrossRef]
- Lee, J.Y.; Hwang, S.N. A high-gain boost converter using voltage-stacking cell. Trans. Korean Inst. Electr. Eng. 2008, 57, 982–984. [Google Scholar]
- Sodhi, R.; Srivastava, S.C.; Singh, S.N. Optimal PMU placement method for complete topological and numerical observability of power system. Electr. Power Syst. Res. 2010, 80, 1154–1159. [Google Scholar] [CrossRef]
- Lukomski, R.; Wilkosz, K. Power network observability for state estimation review of the methods. In Proceedings of the 9th International Scientific Conference Electric Power Engineering 2008, EPE 2008, Brno, Czech Republic, 13–15 May 2008; pp. 183–190. [Google Scholar]
- Crainic, E.D.; Do, X.D.; Mukhedkar, D.; Horisberger, H.P. Power network observability: The assessement of the measurement system strength. IEEE Trans. Power Syst. 1990, 5, 1267–1285. [Google Scholar] [CrossRef]
- Dehghani, M.; Goel, L.; Li, W. PMU based observability reliability evaluation in electric power systems. Electr. Power Syst. Res. 2014, 116, 347–354. [Google Scholar] [CrossRef]
- Chen, X.; Tseng, K.J.; Amaratunga, G. State estimation for distribution systems using micro-synchrophasors. In Proceedings of the Asia-Pacific Power and Energy Engineering Conference, Suzhou, China, 15–17 April 2016. [Google Scholar]
- Resende, M.G.; Ribeiro, C.C. Optimization by GRASP; Springer Science + Business Media: New York, NY, USA, 2016. [Google Scholar]
- Li, Q.; Cui, T.; Weng, Y.; Negi, R.; Franchetti, F.; Ilic, M.D. An information-theoretic approach to PMU placement in electric power systems. IEEE Trans. Smart Grid 2013, 4, 446–456. [Google Scholar] [CrossRef] [Green Version]
- Yang, P.; Tan, Z.; Wiesel, A.; Nehorai, A. Placement of PMUs Considering Measurement Phase-Angle Mismatch. IEEE Trans. Power Deliv. 2015, 30, 914–922. [Google Scholar] [CrossRef]
- Islam, S.M.S.; Mohammad, H.; Science, D. Linear Programming; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 2018. [Google Scholar]
- Abbasy, N.H.; Ismail, H.M. A unified approach for the optimal PMU location for power system state estimation. IEEE Trans. Power Syst. 2009, 24, 806–813. [Google Scholar] [CrossRef]
- Enshaee, A.; Hooshmand, R.A.; Fesharaki, F.H. A new method for optimal placement of phasor measurement units to maintain full network observability under various contingencies. Electr. Power Syst. Res. 2012, 89, 1–10. [Google Scholar] [CrossRef]
- Amare, K.; Centeno, V.A.; Pal, A. Unified PMU Placement Algorithm for Power Systems. In Proceedings of the 2015 North American Power Symposium (NAPS), Charlotte, NC, USA, 4–6 October 2015; p. 6. [Google Scholar]
- Rezaeian Koochi, M.H.; Esmaeili, S.; Ledwich, G. Locating minimum number of PMUs for pre- and post-disturbance monitoring of power systems. IET Gener. Transm. Distrib. 2019, 13, 127–136. [Google Scholar] [CrossRef]
- Mahaei, S.M.; Hagh, M.T. Minimizing the number of PMUs and their optimal placement in power systems. Electr. Power Syst. Res. 2012, 83, 66–72. [Google Scholar] [CrossRef]
- Bei, X.; Yoon, Y.J.; Abur, A. Optimal Placement and Utilization of Phasor Measurements for State Estimation; PSERC Publication: Tempe, AZ, USA, 2005; pp. 1–6. [Google Scholar]
- Sarailoo, M.; Wu, N.E. Cost-Effective Upgrade of PMU Networks for Fault-Tolerant Sensing. IEEE Trans. Power Syst. 2018, 33, 3052–3063. [Google Scholar] [CrossRef]
- Gou, B. Generalized integer linear programming formulation for optimal PMU placement. IEEE Trans. Power Syst. 2008, 23, 1099–1104. [Google Scholar] [CrossRef]
- Kavasseri, R.; Srinivasan, S. Joint placement of phasor and conventional power flow measurements for fault observability of power systems. IET Gener. Transm. Distrib. 2011, 5, 1019. [Google Scholar] [CrossRef]
- Sodhi, R.; Srivastava, S.; Singh, S. Multi-criteria decision-making approach for multi-stage optimal placement of phasor measurement units. IET Gener. Transm. Distrib. 2011, 5, 181. [Google Scholar] [CrossRef]
- Dobakhshari, A.S.; Member, S. Optimal integration of phasor measurement units in power systems considering conventional measurements. IEEE Trans. Smart Grid 2013, 4, 1113–1121. [Google Scholar]
- Gou, B.; Kavasseri, R.G. Uni fi ed PMU Placement for Observability and Bad Data Detection in State Estimation. IEEE Trans. Power Syst. 2014, 29, 2573–2580. [Google Scholar] [CrossRef]
- Pal, A.; Vullikanti, A.K.S.; Ravi, S.S. A PMU Placement Scheme Considering Realistic Costs and Modern Trends in Relaying. IEEE Trans. Power Syst. 2017, 32, 552–561. [Google Scholar] [CrossRef]
- Khajeh, K.G.; Bashar, E.; Rad, A.M.; Gharehpetian, G.B. Integrated Model Considering Effects of Zero Injection Buses and Conventional Measurements on Optimal PMU Placement. IEEE Trans. Smart Grid 2017, 8, 1006–1013. [Google Scholar]
- Singh, S.P.; Thakur, A.K.; Singh, S.P. PMU Placement for Maximum Observability of Power System under Different Contingencies. Energy Procedia 2017, 117, 893–900. [Google Scholar] [CrossRef]
- Gou, B. Optimal Placement of PMUs by Integer Linear Programming. IEEE Trans. Power Syst. 2008, 23, 1525–1526. [Google Scholar] [CrossRef]
- Pal, A.; Mishra, C.; Vullikanti, A.K.S.; Ravi, S. General optimal substation coverage algorithm for phasor measurement unit placement in practical systems. IET Gener. Transm. Distrib. 2017, 11, 347–353. [Google Scholar] [CrossRef] [Green Version]
- Rashidi, M.; Farjah, E. Lyapunov exponent-based optimal PMU placement approach with application to transient stability assessment. IET Sci. Meas. Technol. 2016, 10, 492–497. [Google Scholar] [CrossRef]
- Rakpenthai, C.; Premrudeepreechacharn, S.; Uatrongjit, S.; Watson, N.R. An optimal PMU placement method against measurement loss and branch outage. IEEE Trans. Power Deliv. 2007, 22, 101–107. [Google Scholar] [CrossRef]
- Emami, R.; Abur, A. Robust measurement design by placing synchronized phasor measurements on network branches. IEEE Trans. Power Syst. 2010, 25, 38–43. [Google Scholar] [CrossRef]
- Huang, L.; Sun, Y.; Xu, J.; Gao, W.; Zhang, J.; Wu, Z. Optimal PMU placement considering controlled islanding of power system. IEEE Trans. Power Syst. 2014, 29, 742–755. [Google Scholar] [CrossRef]
- Tesfay, T.T.; Le Boudec, J.Y.; Svensson, O. Optimal software patching plan for PMUs. IEEE Trans. Smart Grid 2018, 9, 6500–6510. [Google Scholar] [CrossRef]
- Mousavian, S.; Valenzuela, J.; Wang, J. A two-phase investment model for optimal allocation of phasor measurement units considering transmission switching. Electr. Power Syst. Res. 2015, 119, 492–498. [Google Scholar] [CrossRef]
- Huang, J.; Wu, N.E.; Ruschmann, M.C. Data-availability-constrained placement of PMUs and communication links in a power system. IEEE Syst. J. 2014, 8, 483–492. [Google Scholar] [CrossRef]
- Kekatos, V.; Giannakis, G.B.; Wollenberg, B. Optimal placement of phasor measurement units via convex relaxation. IEEE Trans. Power Syst. 2012, 27, 1521–1530. [Google Scholar] [CrossRef]
- Bae, J. Cost-Effective placement of phasor measurement units to defend against false data injection attacks on power grid. Energies 2020, 13, 3862. [Google Scholar] [CrossRef]
- Chen, X.; Wei, F.; Cao, S.; Soh, C.B.; Tseng, K.J. PMU Placement for Measurement Redundancy Distribution Considering Zero Injection Bus and Contingencies. IEEE Syst. J. 2020, 14, 5396–5406. [Google Scholar] [CrossRef]
- Rezaeian Koochi, M.H.; Dehghanian, P.; Esmaeili, S. PMU Placement with Channel Limitation for Faulty Line Detection in Transmission Systems. IEEE Trans. Power Deliv. 2020, 35, 819–827. [Google Scholar] [CrossRef]
- Hyacinth, L.R.; Gomathi, V. Optimal pmu placement technique to maximize measurement redundancy based on closed neighbourhood search. Energies 2021, 14, 4782. [Google Scholar] [CrossRef]
- Baba, M.; Nor, N.B.; Sheikh, M.A.; Baba, A.M.; Irfan, M.; Glowacz, A.; Kozik, J.; Kumar, A. Optimization of phasor measurement unit placement using several proposed case factors for power network monitoring. Energies 2021, 14, 5596. [Google Scholar] [CrossRef]
- Elimam, M.; Isbeih, Y.J.; Moursi, M.S.E.; Elbassioni, K.; Hosani, K.H.A. Novel Optimal PMU Placement Approach Based on the Network Parameters for Enhanced System Observability and Wide Area Damping Control Capability. IEEE Trans. Power Syst. 2021, 36, 5345–5358. [Google Scholar] [CrossRef]
- Aminifar, F.; Fotuhi-Firuzabad, M.; Shahidehpour, M.; Khodaei, A. Probabilistic multistage PMU placement in electric power systems. IEEE Trans. Power Deliv. 2011, 26, 841–849. [Google Scholar] [CrossRef]
- Aminifar, F.; Fotuhi-firuzabad, M.; Safdarian, A. Optimal PMU Placement Based on Probabilistic Cost/Bene fi t Analysis. IEEE Trans. Power Syst. 2013, 28, 566–567. [Google Scholar] [CrossRef]
- Esmaili, M.; Gharani, K.; Shayanfar, H.A. Redundant observability PMU placement in the presence of flow measurements considering contingencies. IEEE Trans. Power Syst. 2013, 28, 3765–3773. [Google Scholar] [CrossRef]
- Nikkhah, S.; Aghaei, J.; Safarinejadian, B.; Norouzi, M.A. Contingency constrained phasor measurement units placement with n-k redundancy criterion: A robust optimisation approach. IET Sci. Meas. Technol. 2018, 12, 151–160. [Google Scholar] [CrossRef]
- Aminifar, F.; Fotuhi-firuzabad, M.; Member, S. Observability of Hybrid AC/DC Power Systems With Variable-Cost PMUs. IEEE Trans. Power Deliv. 2014, 29, 345–352. [Google Scholar] [CrossRef]
- Ruben, C.; Dhulipala, S.C.; Bretas, A.S.; Guan, Y.; Bretas, N.G. Multi-objective MILP model for PMU allocation considering enhanced gross error detection: A weighted goal programming framework. Electr. Power Syst. Res. 2020, 182, 106235. [Google Scholar] [CrossRef]
- Zhu, X.; Wen, M.H.; Li, V.O.; Leung, K.C. Optimal PMU-Communication Link Placement for Smart Grid Wide-Area Measurement Systems. IEEE Trans. Smart Grid 2019, 10, 4446–4456. [Google Scholar] [CrossRef]
- Azizi, S.; Dobakhshari, A.S.; Nezam Sarmadi, S.A.; Ranjbar, A.M. Optimal PMU placement by an equivalent linear formulation for exhaustive search. IEEE Trans. Smart Grid 2012, 3, 174–182. [Google Scholar] [CrossRef]
- Manousakis, N.M.; Korres, G.N. AWeighted Least Squares Algorithm for Optimal PMU Placement. IEEE Trans. Power Syst. 2013, 28, 3499–3500. [Google Scholar] [CrossRef]
- Chakrabarti, S.; Kyriakides, E.; Eliades, D.G. Placement of synchronized measurements for power system observability. IEEE Trans. Power Deliv. 2009, 24, 12–19. [Google Scholar] [CrossRef] [Green Version]
- Qi, J.; Sun, K.; Kang, W. Optimal PMU Placement for Power System Dynamic State Estimation by Using Empirical Observability Gramian. IEEE Trans. Power Syst. 2015, 30, 2041–2054. [Google Scholar] [CrossRef] [Green Version]
- Löfberg, J.; Manousakis, N.M.; Korres, G.N.; Xygkis, T.C. Optimal phasor measurement unit placement for numerical observability in the presence of conventional measurements using semi-definite programming. IET Gener. Transm. Distrib. 2015, 9, 2427–2436. [Google Scholar]
- Manousakis, N.M.; Korres, G.N. Optimal PMU Placement for Numerical Observability Considering Fixed Channel Capacity-A Semidefinite Programming Approach. IEEE Trans. Power Syst. 2016, 31, 3328–3329. [Google Scholar] [CrossRef]
- Li, X.; Scaglione, A.; Chang, T.H. A framework for phasor measurement placement in hybrid state estimation via Gauss-Newton. IEEE Trans. Power Syst. 2014, 29, 824–832. [Google Scholar] [CrossRef] [Green Version]
- Shi, Y.; Tuan, H.D.; Duong, T.Q.; Poor, H.V.; Savkin, A.V. PMU Placement Optimization for Efficient State Estimation in Smart Grid. IEEE J. Sel. Areas Commun. 2020, 38, 71–83. [Google Scholar] [CrossRef]
- Ghosh, P.K.; Chatterjee, S.; Saha Roy, B.K. Optimal PMU placement solution: Graph theory and MCDM-based approach. IET Gener. Transm. Distrib. 2017, 11, 3371–3380. [Google Scholar] [CrossRef]
- Xie, N.; Torelli, F.; Bompard, E.; Vaccaro, A. A graph theory based methodology for optimal PMUs placement and multiarea power system state estimation. Electr. Power Syst. Res. 2015, 119, 25–33. [Google Scholar] [CrossRef]
- Chakrabarti, S.; Kyriakides, E. Optimal placement of phasor measurement units for power system observability. IEEE Trans. Power Syst. 2008, 23, 1433–1440. [Google Scholar] [CrossRef]
- Lu, C.; Wang, Z.; Ma, M.; Shen, R.; Yu, Y.; Member, S. An Optimal PMU Placement With Reliable Zero Injection Observation. IEEE Access 2018, 6, 54417–54426. [Google Scholar] [CrossRef]
- Aghaei, J.; Baharvandi, A.; Rabiee, A.; Akbari, M.A. Probabilistic PMU Placement in Electric Power Networks: An MILP-Based Multiobjective Model. IEEE Trans. Ind. Inform. 2015, 11, 332–341. [Google Scholar] [CrossRef]
- Esmaili, M.; Ghamsari-Yazdel, M. Voltage Stability-Constrained Optimal Simultaneous Placement of PMUs and Channels Enhancing Measurement Reliability and Redundancy. IEEE Power Energy Technol. Syst. J. 2017, 4, 32–39. [Google Scholar] [CrossRef]
- Lu, C.; Wang, Z.; Yu, Y. Optimal PMU placement for pessimistic dynamic vulnerability assessment. IET Gener. Transm. Distrib. 2018, 12, 2231–2237. [Google Scholar] [CrossRef]
- Wen, M.H.; Xu, J.; Li, V.O. Optimal multistage PMU placement for wide-area monitoring. IEEE Trans. Power Syst. 2013, 28, 4134–4143. [Google Scholar] [CrossRef]
- Kazemi Karegar, H.; Dalali, M. Optimal PMU placement for full observability of the power network with maximum redundancy using modified binary cuckoo optimisation algorithm. IET Gener. Transm. Distrib. 2016, 10, 2817–2824. [Google Scholar]
- Singh, S.P.; Singh, S.P. Optimal cost wide area measurement system incorporating communication infrastructure. IET Gener. Transm. Distrib. 2017, 11, 2814–2821. [Google Scholar] [CrossRef]
- A Multi-objective PMU Placement Method in Power System via Binary Gravitational Search Algorithm. Electr. Power Components Syst. 2017, 45, 1832–1845. [CrossRef]
- Alzohairy, A.M. Darwin’s Theory Of Evolution. J. Genet. Univ. Zagagig 2014, 1, 1–23. [Google Scholar] [CrossRef]
- Immanuel, S.D.; Chakraborty, U.K. Genetic Algorithm: An Approach on Optimization. In Proceedings of the 4th International Conference on Communication and Electronics Systems, ICCES 2019, Coimbatore, India, 17–19 July 2019; pp. 701–708. [Google Scholar]
- Castro, C.A.; Müller, H.H. Genetic algorithm-based phasor measurement unit placement method considering observability and security criteria. IET Gener. Transm. Distrib. 2016, 10, 270–280. [Google Scholar]
- Satish Kumar, K.; Sydulu, M. Optimal PMU Placement Techniques for the Topological Observability of a Partial Network of the Southern Grid of India; IFAC: Prague, Czech Republic, 2014; Volume 3, pp. 1044–1048. [Google Scholar]
- Marin, F.; Garcia-Lagos, F.; Joya, G.; Sandoval, F. Genetic algorithms for optimal placement of phasor measurement units in electrical networks. Electron. Lett. 2003, 39, 1403–1405. [Google Scholar] [CrossRef] [Green Version]
- Kumar, S.; Tyagi, B.; Kumar, V.; Chohan, S. Incremental PMU placement considering reliability of power system network using analytical hierarchical process. IET Gener. Transm. Distrib. 2018, 12, 3900–3909. [Google Scholar] [CrossRef]
- Appasani, B.; Mohanta, D.K. Co-optimal placement of PMUs and their communication infrastructure for minimization of propagation delay in the WAMS. IEEE Trans. Ind. Inform. 2018, 14, 2120–2132. [Google Scholar] [CrossRef]
- Almasabi, S.; Mitra, J. Multistage Optimal PMU Placement Considering Substation Infrastructure. IEEE Trans. Ind. Appl. 2018, 54, 6519–6528. [Google Scholar] [CrossRef]
- Milosevic, B.; Begovic, M. Nondominated sorting genetic algorithm for optimal phasor measurement placement. IEEE Trans. Power Syst. 2003, 18, 69–75. [Google Scholar] [CrossRef]
- Aminifar, F.; Lucas, C.; Khodaei, A.; Fotuhi-Firuzabad, M. Optimal placement of phasor measurement units using immunity genetic algorithm. IEEE Trans. Power Deliv. 2009, 24, 1014–1020. [Google Scholar] [CrossRef]
- Asgari, A.; Firouzjah, K.G. Optimal PMU placement for power system observability considering network expansion and N-1 contingencies. IET Gener. Transm. Distrib. 2018, 12, 4216–4224. [Google Scholar] [CrossRef]
- Miljanić, Z.; Djurović, I.; Vujošević, I. Optimal placement of PMUs with limited number of channels. Electr. Power Syst. Res. 2012, 90, 93–98. [Google Scholar] [CrossRef]
- Parsopoulos, K.E.; Vrahatis, M.N. Particle Swarm Optimization and Intelligence; IGI Global: Hershey, PA, USA, 2010; Volume 270, pp. 373–394. [Google Scholar]
- Clerc, M. Discrete Particle Swarm Optimization, Illustrated by the Traveling Salesman Problem; Springer: Berlin/Heidelberg, Germany, 2004; pp. 219–239. [Google Scholar]
- Saleh, A.A.; Adail, A.S.; Wadoud, A.A. Optimal phasor measurement units placement for full observability of power system using improved particle swarm optimisation. IET Gener. Transm. Distrib. 2017, 11, 1794–1800. [Google Scholar] [CrossRef]
- Rather, Z.H.; Chen, Z.; Thogersen, P.; Lund, P.; Kirby, B. Realistic approach for phasor measurement unit placement: Consideration of practical hidden costs. IEEE Trans. Power Deliv. 2015, 30, 3–15. [Google Scholar] [CrossRef]
- Pal, A.; Jones, K.D.; Mishra, C.; Centeno, V.A. Binary particle swarm optimisation-based optimal substation coverage algorithm for phasor measurement unit installations in practical systems. IET Gener. Transm. Distrib. 2016, 10, 555–562. [Google Scholar]
- Rahman, N.H.A.; Zobaa, A.F. Integrated Mutation Strategy with Modified Binary PSO Algorithm for Optimal PMUs Placement. IEEE Trans. Ind. Inform. 2017, 13, 3124–3133. [Google Scholar] [CrossRef]
- Maji, T.K.; Acharjee, P. Multiple Solutions of Optimal PMU Placement Using Exponential Binary PSO Algorithm for Smart Grid Applications. IEEE Trans. Ind. Appl. 2017, 53, 2550–2559. [Google Scholar] [CrossRef]
- Mazhari, S.M.; Monsef, H.; Lesani, H.; Fereidunian, A. A multi-objective PMU placement method considering measurement redundancy and observability value under contingencies. IEEE Trans. Power Syst. 2013, 28, 2136–2146. [Google Scholar] [CrossRef]
- Arul Jeyaraj, K.; Rajasekaran, V.; Nandha Kumar, S.K.; Chandrasekaran, K. A multi-objective placement of phasor measurement units using fuzzified artificial bee colony algorithm, considering system observability and voltage stability. J. Exp. Theor. Artif. Intell. 2016, 28, 113–136. [Google Scholar] [CrossRef]
- Mouwafi, M.T.; El-Sehiemy, R.A.; Abou El-Ela, A.A.; Kinawy, A.M. Optimal placement of phasor measurement units with minimum availability of measuring channels in smart power systems. Electr. Power Syst. Res. 2016, 141, 421–431. [Google Scholar] [CrossRef]
- Hosseini, S.; Al Khaled, A. A survey on the Imperialist Competitive Algorithm metaheuristic: Implementation in engineering domain and directions for future research. Appl. Soft Comput. 2014, 24, 1078–1094. [Google Scholar] [CrossRef]
- Mohammadi, M.B.; Hooshmand, R.A.; Fesharaki, F.H. A new approach for optimal placement of PMUs and their required communication infrastructure in order to minimize the cost of the WAMS. IEEE Trans. Smart Grid 2016, 7, 84–93. [Google Scholar] [CrossRef]
- Mahari, A.; Seyedi, H. Optimal PMU placement for power system observability using BICA, considering measurement redundancy. Electr. Power Syst. Res. 2013, 103, 78–85. [Google Scholar] [CrossRef]
- Korres, G.N.; Georgilakis, P.S.; Koutsoukis, N.C.; Manousakis, N.M. Numerical observability method for optimal phasor measurement units placement using recursive Tabu search method. IET Gener. Transm. Distrib. 2013, 7, 347–356. [Google Scholar]
- Nuqui, R.F.; Phadke, A.G. Phasor measurement unit placement techniques for complete and incomplete observability. IEEE Trans. Power Deliv. 2005, 20, 2381–2388. [Google Scholar] [CrossRef]
- Ghosh, S.; Ghosh, D.; Kumar Mohanta, D. Multi-Level Reliability Allocation of Phasor Measurement Unit Using Bayesian Networks. Electr. Power Components Syst. 2018, 46, 1756–1768. [Google Scholar] [CrossRef]
- Kim, T.; Wright, S.J. PMU placement for line outage identification via multinomial logistic regression. IEEE Trans. Smart Grid 2018, 9, 122–131. [Google Scholar] [CrossRef]
- NERC. Node-Breaker Modeling Representation; Technical Report By NERC: North American Electric Reliability Corporation; NERC: Atlanta, GA, USA, 2016. [Google Scholar]
- Ramanathan, R.; Tuck, B. Contingency analysis using node/breaker model for operation studies. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015. [Google Scholar]
- Park, B.; Demarco, C.L. Optimal Network Topology for Node-Breaker Representations with AC Power Flow Constraints. IEEE Access 2020, 8, 64347–64355. [Google Scholar] [CrossRef]
- Celik, M.K.; Management, D.G. Mixed Node/Breaker and Bus/Branch Models Using CIM Exponentially Increasing Challenges for the Grid; Nexant, Inc.: San Francisco, CA, USA, 2015. [Google Scholar]
- Koenig, M.; Sagareli, S.; Vaiman, M.; Vaiman, M. Node-breaker topology representation of Con Edison’s Stations for planning studies. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015. [Google Scholar]
- Alam, M.N.; Das, B.; Pant, V. Protection scheme for reconfigurable radial distribution networks in presence of distributed generation. Electr. Power Syst. Res. 2021, 192, 106973. [Google Scholar] [CrossRef]
- Lee, L.A.; Centeno, V. Comparison of μPMU and PMU. In Proceedings of the Clemson University Power Systems Conference (PSC), Clemson, SC, USA, 4–7 September 2019. [Google Scholar]
- Von Meier, A.; Arghandeh, R. Every Moment Counts: Synchrophasors for Distribution Networks with Variable Resources; Jones, L.E., Ed.; Academic Press: Cambridge, MA, USA, 2017; pp. 435–444. [Google Scholar]
- Ghalei Monfared Zanjani, M.; Mazlumi, K.; Kamwa, I. Combined analysis of distribution-level PMU data with transmission-level PMU for early detection of long-term voltage instability. IET Gener. Transm. Distrib. 2019, 13, 3634–3641. [Google Scholar] [CrossRef]
- Samantaray, S.R.; Kamwa, I.; Joos, G. Phasor measurement unit based wide-area monitoring and information sharing between micro-grids. IET Gener. Transm. Distrib. 2017, 11, 1293–1302. [Google Scholar] [CrossRef]
- Von Meier, A.; Stewart, E.; McEachern, A.; Andersen, M.; Mehrmanesh, L. Precision Micro-Synchrophasors for Distribution Systems: A Summary of Applications. IEEE Trans. Smart Grid 2017, 8, 2926–2936. [Google Scholar] [CrossRef]
- Arghandeh, R.; Gahr, M.; Von Meier, A.; Cavraro, G.; Ruh, M.; Andersson, G. Topology detection in microgrids with micro-synchrophasors. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015. [Google Scholar]
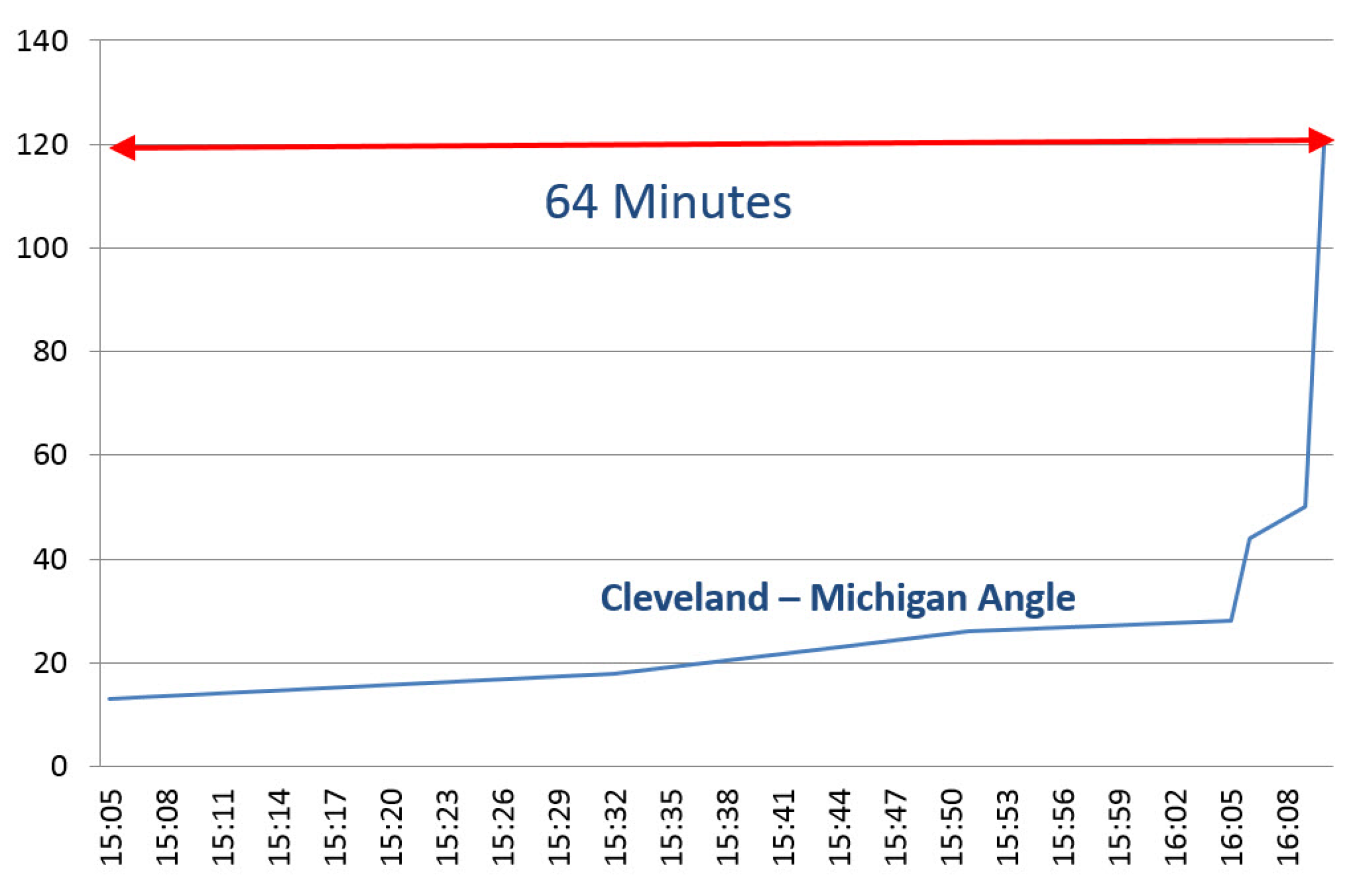
| Attribute | SCADA | PMU |
|---|---|---|
| Universal time synchronization | ✗ | ✓ |
| Local estimation of phase angles | ✗ | ✓ |
| Reporting rate | Once in (4 to 6) s | (10/12/15/20/30/60 frames)/s |
| Data flow latency | High | Negligible |
| State view of power system | Steady | Dynamic |
| Total input/output channels | 100+ Analog and digital | 10 Phasors, 32+ analog and digital |
| Communication method | Serial communication | Network communication |
| Ref. | Technique | Objective Function | Constraints | ||
|---|---|---|---|---|---|
| Observability | Contingency | Installation Scheme | |||
| [42] | BILP | Min. no. of PMUs, Min. no. of Data links | Pseudo observability | , measurements and communication | 3-stage installation of PMUs |
| [43] | BILP | Min. no. of PMUs | CNO and INO | – | Effect of ZIB and CMs |
| [44] | BILP | Min. no. of PMUs and flow measurements | CNO and observability in case of faults | – | Effect of CMs |
| [45] | BILP | Min. no. of PMUs, Max. System observability | CNO | Multistage installation of PMUs | |
| [46] | BILP | Min. no. of PMUs | CNO, | and measurements | Effect of CMs, flow measurements, Channel limitation, and measured injection buses |
| [47] | BILP | Min. no. of PMUs | CNO | Measurements | Effect of CMs, converting CMs to non-CMs |
| [48] | BILP | Min. Substation disruption, Max. bus observability using DULRs | – | Handling relays synchrophasors, critical buses, prohibited substations, existing PMUs, unknown transformer tap ratio, ZIB, and channel limitation | |
| [49] | BILP | Min. no. of PMUs | CNO | Effect of CMs and ZIB | |
| [50] | BILP | Min. no. of PMUs, Max. System observability | – | Effect of ZIB | |
| [51] | BILP | Min. no. of PMUs | CNO | – | Effect of CMs and old power flows |
| [52] | BILP | Min. Substation disruption | – | Handling Channel capacity, prohibited substation, preinstalled PMUs, ZIB, relays synchrophasors, Redundancy in critical measurements, estimating unknown tap setting and tap ratios of transformer | |
| [53] | BILP | Min. no. of PMUs | CNO | Redundancy in critical measurements | |
| [54] | BILP | Min. no. of PMUs | CNO | – | |
| [55] | BILP | Min. no. of PMUs for branch monitoring | CNO | and transformer | Improved redundancy |
| [56] | BILP | Min. no. of PMUs | CNO | Effect of ZIB and controlled islanding | |
| [58] | BILP | Min. no. of PMUs | CNO | Effect of line switching | |
| [59] | BILP | Min. no. of PMUs, communication links, and operation cost | – | Limitation on communication infrastructure | |
| [36] | BILP | Min. no. of PMUs, Max. system observability | – | Effect of CMs and ZIB | |
| [37] | BILP | Min. no. of PMUs | CNO with maximum redundancy | Effect of channel limitation and ZIB | |
| [39] | BILP | Min. no. of PMUs | CNO | – | Effect of post-disturbance coherency of the buses |
| [40] | BILP | Min. no. of PMUs, Max. measurement redundancy | CNO with two adjacent injection measurements | Effect of CMs and PMUs multistage installation | |
| [61] | BILP | Min. no. of PMUs | CNO | – | Effect of CMs and cyberattack |
| [62] | BILP | Min. no. of PMUs, Max. measurement redundancy, | CNO | Effect of Channel limitation, CMs and ZIB | |
| [63] | BILP | Min. no. of PMUs | CNO | – | Effect of Channel limitation and backup faults protection |
| [64] | BILP | Min. no. of PMUs | CNO | – | based on three attributes DOV, the ANDOV, and BOI |
| [65] | BILP | Min. no. of PMUs | CNO | Effect of channel limitation and ZIB | |
| [66] | BILP | Min. no. of PMUs | CNO | Effect of channel limitation, ZIB, network impedences, and small signal stability of network | |
| [67] | MILP | Min. no. of PMUs, max system observability | – | Probability of power system components outage | Financial and physical constraints, PMUs Multistage installation |
| [69] | MILP | Min. no. of PMUs, Max. redundancy | CNO | – | |
| [70] | MILP | Min. no. of PMUs | CNO | Effect of ZIB | |
| [71] | MILP | Min. no. of PMUs | CNO | Variable cost PMUs and ZIB | |
| [72] | MILP | Min. no. of PMUs | CNO | – | Budgeted PMUs allocation |
| [73] | MILP | Min. no. of PMUs, Min. no. of communication channel, | CNO | Effect of ZIB and data transmission bandwidth | |
| [74] | EILP | Min. no. of PMUs | – | Effect of communication infrastructure, CMs and ZIB | |
| Ref. | Technique | Objective Function | Constraints | ||
|---|---|---|---|---|---|
| Observability | Contingency | Installation Scheme | |||
| [95] | GA | Min. no. of PMUs, Max. measurement Redundancy | CNO | Pre-installed PMUs | |
| [88] | GA | Min. no. of PMU, Max. vulnerability index | CNO | – | |
| [96] | GA | Min. no. of PMUs | CNO | – | – |
| [97] | GA | Min. no. of PMUs based on current phasor measurements | CNO | – | – |
| [98] | GA | Min. no. of PMUs | CNO | – | Multistage installation |
| [99] | GA | Min. no. of PMUs, Min. Propagation delay | CNO | – | – |
| [100] | BGA | Min. no. of PMUs, Min. cost of communication infrastructure | CNO | Multistage installation | |
| [101] | NS-GA | Min. no. of PMUs, Max. measurement Redundancy | CNO | – | |
| [102] | IGA | Min. no. of PMUs, Min. no. of unobserved buses | CNO | – | – |
| [104] | CGA | Min. no. of PMUs | CNO | Channel and communication limitation | |
| Ref. | Technique | Objective Function | Constraints | ||
|---|---|---|---|---|---|
| Observability | Contingency | Installation Scheme | |||
| [107] | BPSO | Min. no. of PMUs | Numerical CNO | – | – |
| [108] | BPSO | Min. total realistic cost | CNO | – | |
| [109] | BPSO | min. no. of substations | CNO | – | Prioritize critical elements. Prohibited substation installation and digital relays as relays synchrophasors |
| [110] | BPSO | Min. no. of PMUs, Max. Measurement redundancy, Max. System observability | CNO | channel limitation | |
| [111] | BPSO | Min. no. of PMUs | CNO | Multistage | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, M.M.; Amjad, M.; Qureshi, M.A.; Imran, K.; Haider, Z.M.; Khan, M.O. A Critical Review of State-of-the-Art Optimal PMU Placement Techniques. Energies 2022, 15, 2125. https://doi.org/10.3390/en15062125
Ahmed MM, Amjad M, Qureshi MA, Imran K, Haider ZM, Khan MO. A Critical Review of State-of-the-Art Optimal PMU Placement Techniques. Energies. 2022; 15(6):2125. https://doi.org/10.3390/en15062125
Chicago/Turabian StyleAhmed, Muhammad Musadiq, Muhammad Amjad, Muhammad Ali Qureshi, Kashif Imran, Zunaib Maqsood Haider, and Muhammad Omer Khan. 2022. "A Critical Review of State-of-the-Art Optimal PMU Placement Techniques" Energies 15, no. 6: 2125. https://doi.org/10.3390/en15062125
APA StyleAhmed, M. M., Amjad, M., Qureshi, M. A., Imran, K., Haider, Z. M., & Khan, M. O. (2022). A Critical Review of State-of-the-Art Optimal PMU Placement Techniques. Energies, 15(6), 2125. https://doi.org/10.3390/en15062125







