Development of a Trajectory Period Folding Method for Burnup Calculations
Abstract
:1. Introduction
2. Transition Matrix of a Folded Period
- i is the index of the nuclide family corresponding to the index of the transmuting nuclide;
- k is the trajectory index of i-th family, which contains mi trajectories;
- l(k) represents the index of the final isotope in k-th trajectory;
- j is the index of the descendant nuclide.
- i is the initial nuclide index (or the family index);
- is the initial contribution of i-th nuclide;
- is the transition vector obtained from the i-th column of total transition matrix.
3. Transition Trajectories Period Folding
- is the number of trajectories for the first period;
- is the number of trajectories for the second period.
4. Implementation Procedure
- i, i1 and i2 are the indices of nuclide family from folded, first and second periods, respectively;
- k, k1 and k2 and are the trajectory indices of i-th, i1-th and i2-th nuclide families, each containing m, and trajectories, respectively;
- j(k), j1(k1) and j2(k2) are the indices of last nuclide in trajectory k, k1 and k2, respectively.
5. Passage Trajectory Period Folding
- i is the index of the ancestor nuclide (the first in the transmutation chain);
- k is the trajectory index;
- j is the index of the descendant nuclide resulting in the transmutation chain;
- j(k) is the indices of the last nuclide in the trajectory k;
- and is the activity of the considered trajectory,
6. Trajectory Period Folding Case Study
7. Discussion
- (a)
- The first dependency considers the use of folded trajectories to trace the evolution of individual nuclide masses, as described in the previous sections. As a reminder, it is expressed as follows:The sum of all trajectories that start and end with the same pair of nuclides corresponds to the matrix element describing the relation between the initial and the derived nuclide for the transmutation period [20].
- (b)
- The second dependency, which can be obtained from linear chains, concerns the importance of a specific reaction or reaction sequence. The reactions occurring in a chain are summed up and multiplied by the transition value. The selection of reactions can be performed in various configurations. Depending on the interest, reactions can be counted for a single family or selected trajectories between specific nuclides. For instance, this approach can be used to find a reaction with higher importance in the simulated system or as an alternative method of calculating the conversion (breeding) ratio [21]. A sample relation can be written as:where is a nuclear reaction or a sequence of reactions between nuclides a and b occurring in the sequence of transmutation reactions that conditions the trajectories. Trajectories are calculated for family, i, which contains mi trajectories in total, where k is the trajectory index. The reaction is counted when it appears in the considered trajectory sequence.
- (c)
- The third dependency considers burnup modelling, where calculations need to be performed in many burnable zones over the reactor core to find axial and radial distributions of defined isotopes [22]. The material-mixing procedure can be applied, whereas the following material (fuel) batches have to be composed. In this case, it may be accompanied by the trajectory-averaging procedure. The trajectory-averaging procedure can be performed together with mixing of the materials and represents the defined material batch. Thus, the period-folding procedure can be performed for each calculated burnable zone over all irradiation and cooling periods. Thus, the user can indicate which group of burnable zones to trace as a single batch for a specific period of time. The average value of the transition is calculated automatically during the simulation using the following relation:where:S—number of burnable zones,—mass of the nuclide i-th in the p-th zone.
- (d)
- The fourth dependency is related to numerical error propagation in folding procedure. As mentioned in the previous sections, numerical error is connected with the residual passage determined by the cut-off parameter. Residual passage, , is defined as the total numerical error in the considered family. It is calculated for each computational single period as a sum of passages for trajectories that have not yet been extended. Therefore, cumulative residual passage of a folded period represents a cumulative truncation error of folded trajectories in the same way as residual passages for a single period [23,24].
- (e)
- The last dependency considers trajectory sensitivity in the nuclide cross sections [25,26]. The formed trajectories may be purposely influenced by the introduced changed in nuclide cross sections, which further affects the formation of the nuclides for the second time step. The obtained sensitivity coefficients and resultant uncertainties can be presented as a function of time. The analysis of those coefficients allows us to identify the most sensitive trajectories and thus reaction-rate sensitivities, which lead to the production of, e.g., safety-related actinides. Therefore, the most important reaction rates can be identified in order to be assessed and to reduce their uncertainties [27]. This kind of information may be useful in qualification and experimental verification of neutronic calculations. However, a sensitivity and uncertainty formalism accompanied by the presented methods demands development. Some trials were performed using perturbation theory, but the task is quite complicated and foreseen for further studies.
8. Summary
9. Conclusions
- The developed numerical method of transmutation trajectory folding might be applied for the analysis of any subcritical or critical nuclear system with an arbitrary number of successive cooling and irradiation intervals.
- The standard transmutation trajectory analysis solution of Bateman equations for successive time intervals could be applied to characterize the joined isotope mass balance for the whole irradiation period with multiple-cycle reloading.
- The detection of significant trajectories preceding the formation of TRU elements is important for the understanding of the notably radioactive isotope-formation mechanism, which might help to optimize treatment of discharged nuclear fuel before its final disposal or reprocessing.
- The trajectory period folding method may reveal reactions that appear more often than others in the production of crucial nuclides from the safety point of view.
- The developed method can help to understand how different minor actinides from LWRs waste may influence the build-up of some isotope mass peaks in multi-cycle reloading schemas, e.g., in fast spectrum reactors, before reaching equilibrium levels.
- The method can help in determination of total neutron generation rate through defined transmutation paths.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hanbook of Nuclear Engineering; Lead-Cooled Fast Reactor; Cacuci, D.G. (Ed.) Springer: Berlin/Heidelberg, Germany, 2010; ISBN 978-0-387-98149-9. [Google Scholar]
- Stanisz, P.; Oettingen, M.; Cetnar, J. Monte Carlo modeling of Lead-Cooled Fast Reactor in adiabatic equilibrium state. Nucl. Eng. Des. 2016, 301, 341–352. [Google Scholar] [CrossRef]
- Artioli, C.; Grasso, G.; Petrovich, C. A new paradigm for core design aimed at the sustainability of nuclear energy: The solution of the extended equilibrium state. Ann. Nuclear Energy 2010, 37, 915–922. [Google Scholar] [CrossRef]
- Isotalo, A.E.; Aarnio, P.A. Comparison of depletion algorithms for large systems of nuclides. Ann. Nuclear Energy 2011, 38, 261–268. [Google Scholar] [CrossRef]
- Pusa, M.; JLeppänen, J. Computing the Matrix Exponential in Burnup Calculations. Nuclear Sci. Eng. 2010, 164, 140–150. [Google Scholar] [CrossRef]
- Moler, C.; van Loan, C. Nineteen Dubious Ways to Compute the Exponential of a Matrix, Twenty-Five Years Later. SIAM Rev. 2003, 45, 3–49. [Google Scholar] [CrossRef]
- Cetnar, J. General solution of bateman equations for nuclear transmutations. Ann. Nucl. Energy 2006, 33, 640–645. [Google Scholar] [CrossRef]
- Pusa, M. Numerical Methods for Nuclear Fuel Burnup Calculations. Ph.D. Thesis, VTT Technical Research Centre of Finland, Espoo, Finland, 2013. [Google Scholar]
- Huang, K.; Wu, H.; Cao, L.; Li, Y.; Shen, W. Improvements to the Transmutation Trajectory Analysis of depletion evaluation. Ann. Nuclear Energy 2016, 87, 637–647. [Google Scholar] [CrossRef]
- Cetnar, J.; Stanisz, P.; Oettingen, M. Linear Chain Method for Numerical Modelling of Burnup Systems. Energies 2021, 14, 1520. [Google Scholar] [CrossRef]
- Oettingen, M.; Cetnar, J.; Mirowski, T. The MCB code for numerical modelling of fourth generation nuclear reactors. Comput. Sci. 2015, 16, 329–350. [Google Scholar] [CrossRef] [Green Version]
- Oettingen, M.; Cetnar, J. Validation of gadolinium burnout using PWR benchmark specification. Nuclear Eng. Des. 2014, 273, 359–366. [Google Scholar] [CrossRef]
- Oettingen, M.; Cetnar, J. Comparative analysis between measured and calculated concentrations of major actinides using destructive assay data from Ohi-2 PWR. Nukleonika 2015, 60, 571–580. [Google Scholar] [CrossRef] [Green Version]
- Oettingen, M. Validation of Fuel Burnup Modelling with MCB Monte Carlo System Using Destructive Assay Data from Ohi-2 PWR; Wydawnictwa AGH: Krakow, Poland, 2016; p. 174. [Google Scholar]
- Stanisz, P.; Malicki, M.; Kopeć, M. Validation of VHTRC calculation benchmark of critical experiment using the MCB code. E3S Web Conf. 2016, 10, 123. [Google Scholar] [CrossRef] [Green Version]
- X5-Team: MCNP—A General Monte Carlo N-Particle Transport Code, 5th ed.; Volume I: Overview and Theory; Los Alamos National Laboratory: Los Alamos, NM, USA, 2008.
- Isotalo, A. Computational Methods for Burnup Calculations with Monte Carlo Neutronics. Ph.D. Thesis, Aalto University, Espoo, Finland, 2013. [Google Scholar]
- Takeda, T.; Hazama, T.; Fujimura, K.; Sawada, S. Method Development and Reactor Physics Data Evaluation for Improving Prediction Accuracy of Fast Reactors’ Minor Actinides Transmutation Performance. In Proceedings of the PHYSOR2014 International Conference, Kyoto, Japan, 28 September–3 October 2014. [Google Scholar]
- Takeda, T. Minor actinides transmutation performance in a fast reactor. Ann. Nuclear Energy 2016, 95, 48–53. [Google Scholar] [CrossRef]
- Stanisz, P.J.; Cetnar, J.; Oettingen, M. Radionuclide neutron source trajectories in the closed nuclear fuel cycle. Nukleonika 2019, 64, 3–9. [Google Scholar] [CrossRef] [Green Version]
- Salvatores, M.; Palmiotti, G. Radioactive waste partitioning and transmutation within advanced fuel cycles: Achievements and challenges. Prog. Part. Nuclear Phys. 2011, 66, 144–166. [Google Scholar] [CrossRef]
- Górkiewicz, M.; Cetnar, J. Flattening of the Power Distribution in the HTGR Core with Structured Control Rods. Energies 2021, 14, 7377. [Google Scholar] [CrossRef]
- Kępisty, G.; Oettingen, M.; Stanisz, P.; Cetnar, J. Statistical error propagation in HTR burnup model. Ann. Nuclear Energy 2017, 105, 355–360. [Google Scholar] [CrossRef]
- Tohjoh, M.; Endob, T.; Watanabe, M.; Yamamoto, A. Effect of error propagation of nuclide number densities on Monte Carlo burnup calculations. Ann. Nuclear Energy 2006, 33, 1424–1436. [Google Scholar] [CrossRef]
- Cacuci, D.G. High-Order Deterministic Sensitivity Analysis and Uncertainty Quantification: Review and New Developments. Energies 2021, 14, 6715. [Google Scholar] [CrossRef]
- Tadepalli, S.C.; Subhash, P. Simplified recursive relations for the derivatives of Bateman linear chain solution and their application to sensitivity and multi-point analysis. Ann. Nuclear Energy 2018, 121, 479–486. [Google Scholar] [CrossRef]
- Frosio, T.; Bonaccorsi, T.; Blaise, P. Nuclear data uncertainties propagation methods in Boltzmann/Bateman coupled problems: Application to reactivity in MTR. Ann. Nuclear Energy 2016, 90, 303–317. [Google Scholar] [CrossRef] [Green Version]
- Oettingen, M. Assessment of the Radiotoxicity of Spent Nuclear Fuel from a Fleet of PWR Reactors. Energies 2021, 14, 3094. [Google Scholar] [CrossRef]
- Neuber, J.C. Specification for Phase II-E Benchmark: Study on the Impact of Changes in the Isotopic Inventory Due to Control Rod Insertions in PWR UO2 Fuel Assemblies during Irradiation on the End Effect, 1st ed.; OECD Nuclear Energy Agency: Paris, France, 2006. [Google Scholar]


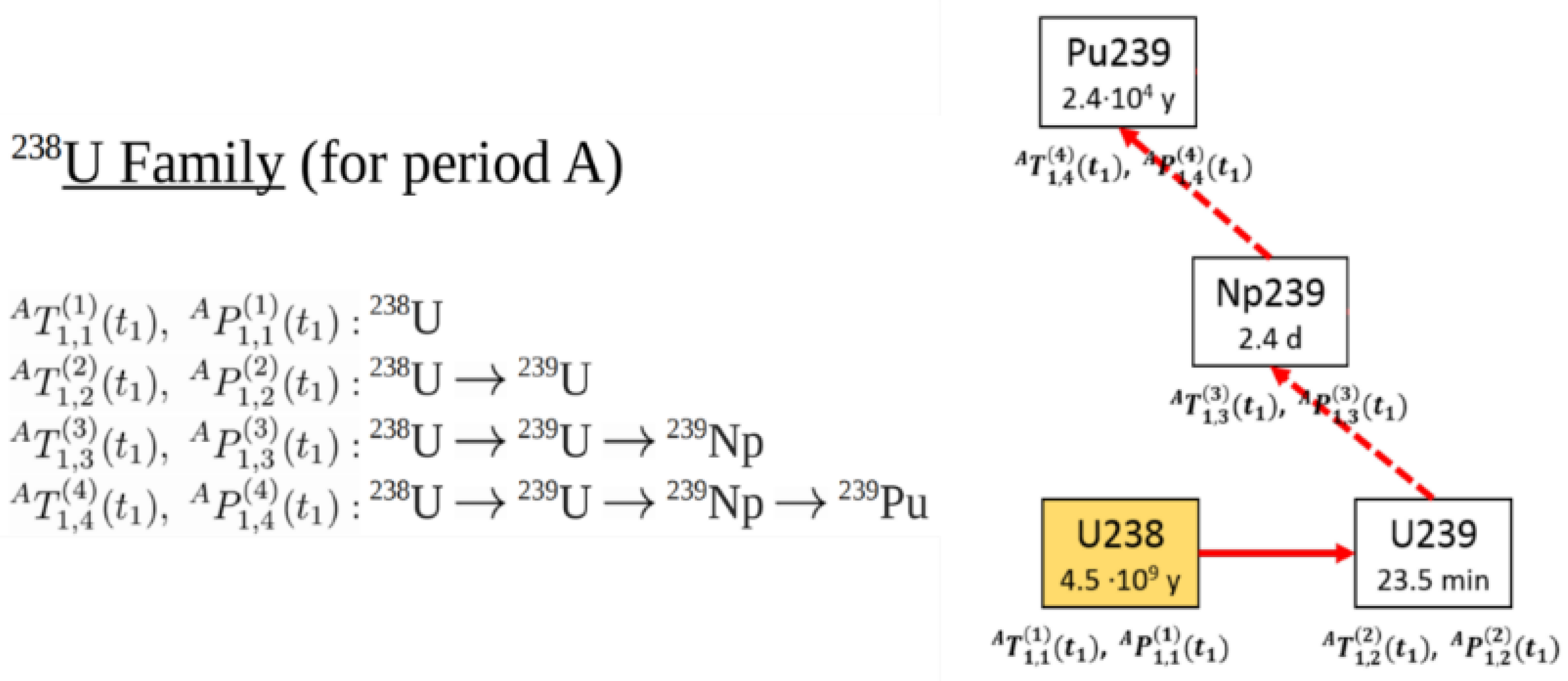




| Chain transmutation pattern: 238U (survival) | ||
| A: 238U | B: 238U | |
| Chain transmutation pattern: 238U→239U | ||
| A: 238U | B: 238U→239U | |
| A: 238U→239U | B: 239U | |
| Chain transmutation pattern: 238U→239U→239Np | ||
| A: 238U | B: 238U→239U→239Np | |
| A: 238U→239U | B: 239U→239Np | |
| A: 238U→239U→239Np | B: 239Np | |
| Chain transmutation pattern: 238U→239U→239Np→239Pu | ||
| A: 238U | B: 238U→239U→239Np→239Pu | |
| A: 238U→239U | B: 239U→239Np→239Pu | |
| A: 238U→239U→239Np | B: 239Np→239Pu | |
| A: 238U→239U→239Np→239Pu | B: 239Pu | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stanisz, P.; Oettingen, M.; Cetnar, J. Development of a Trajectory Period Folding Method for Burnup Calculations. Energies 2022, 15, 2245. https://doi.org/10.3390/en15062245
Stanisz P, Oettingen M, Cetnar J. Development of a Trajectory Period Folding Method for Burnup Calculations. Energies. 2022; 15(6):2245. https://doi.org/10.3390/en15062245
Chicago/Turabian StyleStanisz, Przemysław, Mikołaj Oettingen, and Jerzy Cetnar. 2022. "Development of a Trajectory Period Folding Method for Burnup Calculations" Energies 15, no. 6: 2245. https://doi.org/10.3390/en15062245






