Stray Load Loss Valuation in Electrical Transformers: A Review
Abstract
:1. Introduction
2. Stray Load Loss Components
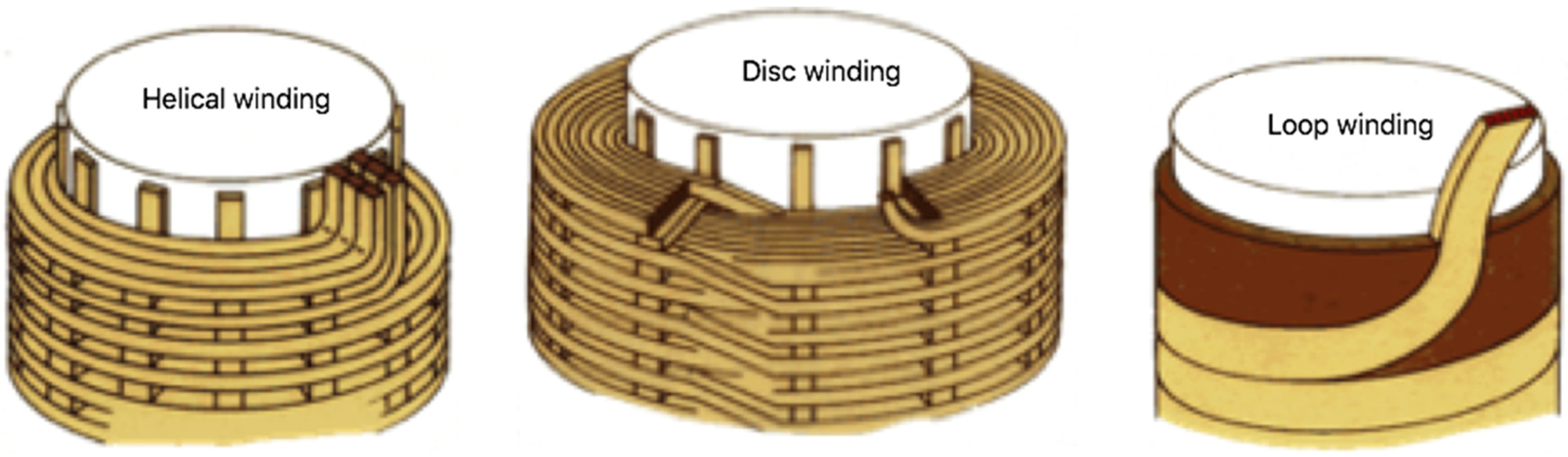
2.1. Winding Eddy Losses
2.2. Winding Circulating Current
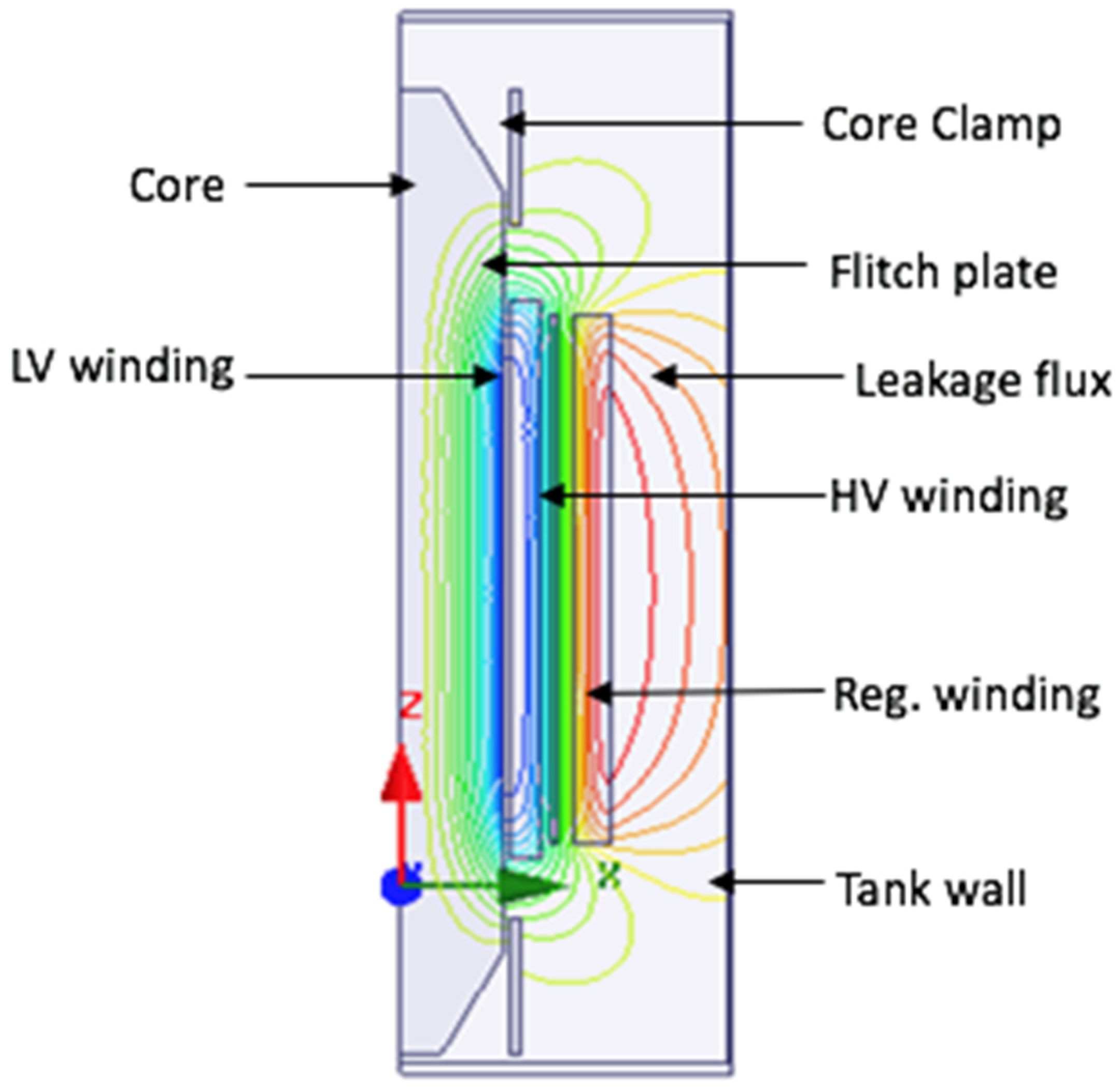
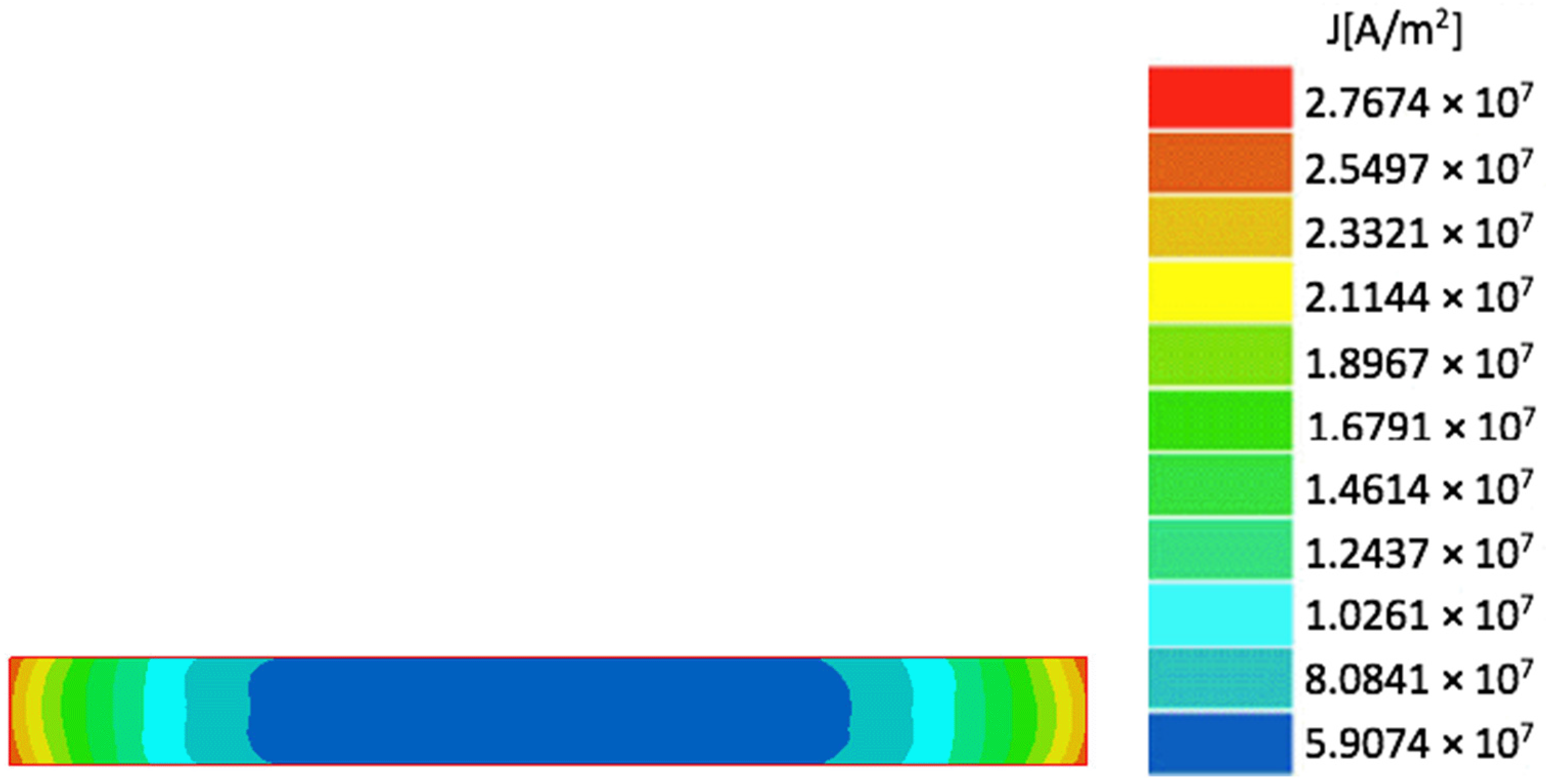
2.3. Stray Loss in Other Structural Parts
3. Theoretical Foundation of Eddy Currents
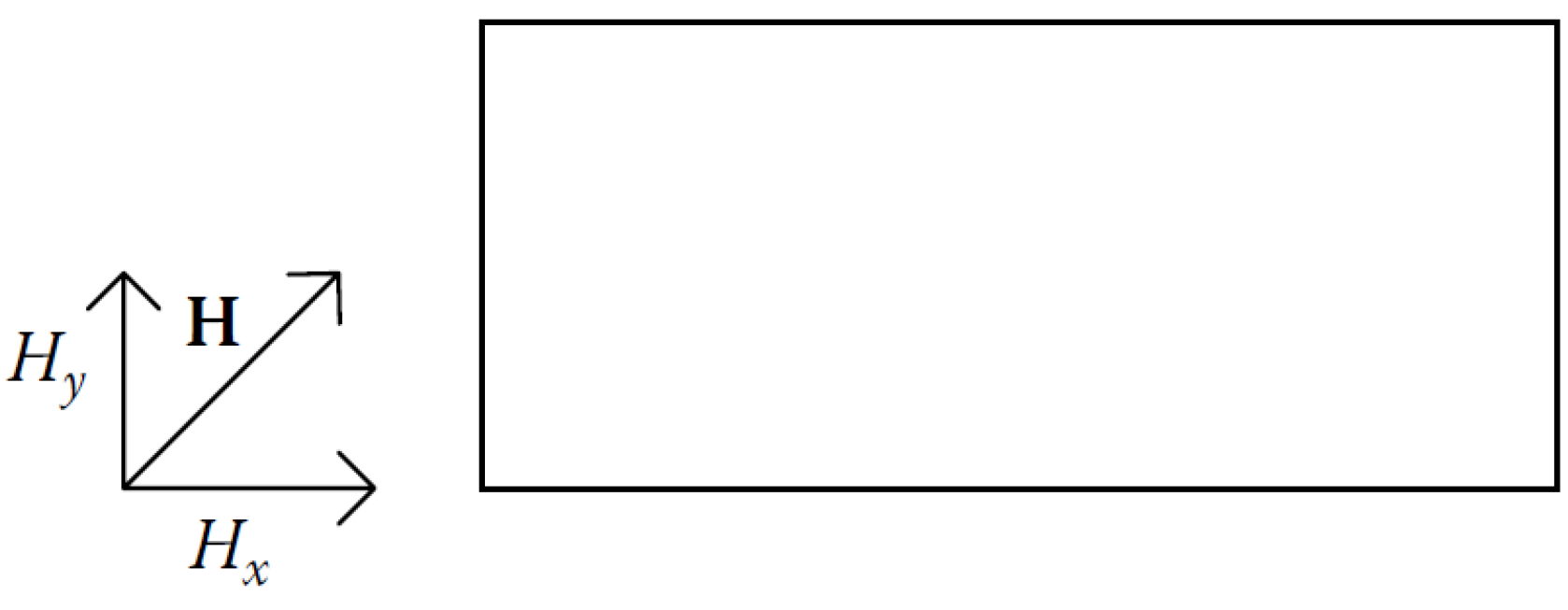
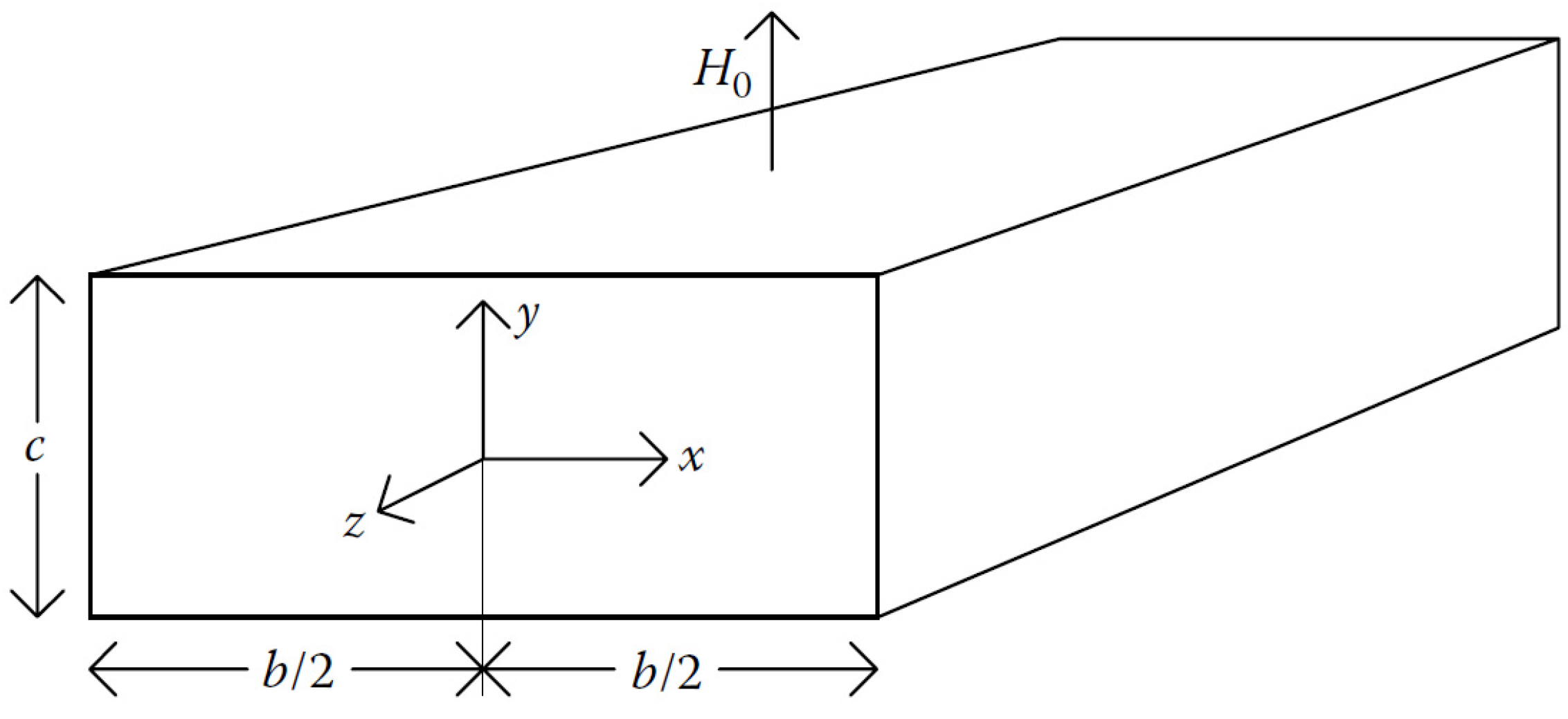
3.1. Generation of Electromagnetic Fields in Conductors
3.2. Eddy Current Loss Formulation in Time-Varying Fields
- Electric field strength ()
- Flux density ()
- Permeability of material ()
- Magnetic field strength ()
- Current density ()
- conductivity ()
- resistivity of a conductor ().
4. Electric Transformer Losses
- Load loss (in kW)
- No-load loss (in kW)
- Copper loss (in kW)
- Winding Eddy loss (in kW)
- Other Stray loss (in kW)
4.1. Copper Loss under Harmonic Conditions
- Copper loss under harmonic conditions
- Copper loss at rated conditions
- Harmonic order
- Harmonic load current
4.2. Winding Eddy Loss under Harmonic Conditions
4.3. Other Stray Loss under Harmonic Conditions
4.4. Transformer Maximum Loading Capacity
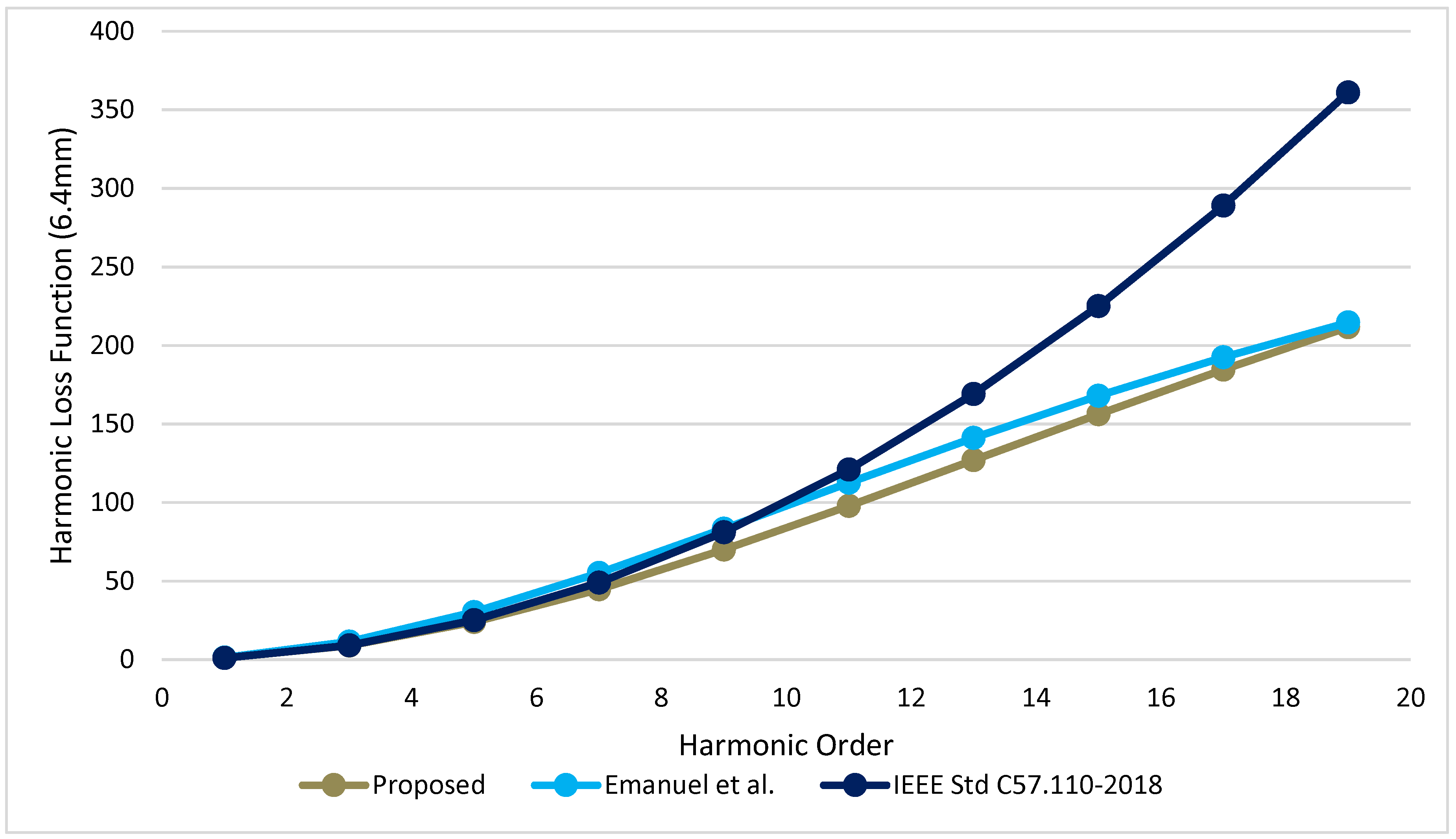
4.5. Winding Eddy Loss Corrective Functions
4.6. Emanuel et al. Winding Eddy Loss Correction Function
- Frequency of the sinusoidal magnetic field
- Specific conductor conductivity
- Width and height of the conductor
- Local induction axial and radial components
- Ratio of width and height of the conductor
- Winding Eddy loss correction function
4.7. Thango et al. Winding Eddy Loss Correction Function
- Conductor skin depth in relation to the conductor thickness
- Conductor thickness
- Winding conductor skin depth
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- GreenCape. Utility-Scale Renewable Energy-Market Intelligence Report; GreenCape: Cape Town, South Africa, 2019. [Google Scholar]
- The World Bank. Solar Resource Data: Solargis; The World Bank: Washington, WA, USA, 2017. [Google Scholar]
- SolarPower Europe. Global Market Outlook; SolarPower Europe: Brussels, Europe, 2018–2022. [Google Scholar]
- Utility-Scale Photovoltaic Procedures and Interconnection Requirements. Available online: https://digital.library.unt.edu/ark:/67531/metadc828656/m2/1/high_res_d/1051725.pdf (accessed on 27 January 2022).
- Mantosh, D. Investigation of High-Frequency Switching Transients on Wind Turbine Step-Up Transformers. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2015. [Google Scholar]
- Gurleyen, H. Analysis of Magnetic Coupling Between Armature and Field Windings of VFRM. In Proceedings of the 2021 IEEE International Magnetic Conference (INTERMAG), Lyon, France, 26–30 April 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Khanali, M. Effects of Distorted Voltages on the Performance of Renewable Energy Plant Transformers; Semantic Scholar: Waterloo, ON, Canada, 2017. [Google Scholar]
- Liang, S.; Hu, Q.; Lee, W. A survey of harmonic emissions of a commercial operated wind farm. In Proceedings of the IEEE Industrial and Commercial Power Systems Technical Conference, Tallahassee, FL, USA, 9–13 May 2010. [Google Scholar]
- Tentzerakis, S.; Papathanassiou, S.; Papadopoulos, P.; Foussekis, D.; Vionis, P. Evaluation of wind farm harmonic current emissions. In Proceedings of the European Wind Energy Conference (EWEC), Milan, Italy, 7–10 May 2007. [Google Scholar]
- Overett, J.S. Assessment of the Harmonic Behavior of a Utility-Scale Photovoltaic Plant. Ph.D. Thesis, Stellenbosch University, Stellenbosch, South Africa, 2017. [Google Scholar]
- Sokolov, V.V. Transformer is Gassing—What to Do; Scientific and Engineering Center ZTZ-Service Company: Zaporozhye, Ukraine, 2013. [Google Scholar]
- Zhao, C.; Huang, Q.; Li, D.; Bai, H.; Cheng, Y. The statistical distribution of the DGA data of transformers and its application. In Proceedings of the 2016 IEEE International Conference on Dielectrics (ICD), Montpellier, France, 3–7 July 2016; pp. 497–500. [Google Scholar] [CrossRef]
- Hohlein, B.; Hohlein, I.A. Unusual Cases of Gassing in Transformers in Service. IEEE Electr. Insul. Mag. 2006, 22, 24–27. [Google Scholar] [CrossRef]
- Upadhyay, G.; Singh, A.; Seth, S.K.; Jarial, R.K. FEM based no-load loss calculation of triangular wound core transformer. In Proceedings of the 2016 IEEE 1st International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 4–6 July 2016; pp. 1–4. [Google Scholar] [CrossRef]
- C57.110-2018. IEEE Recommended Practice for Establishing Liquid-Immersed and Dry-Type Power and Distribution Transformer Capability When Supplying Nonsinusoidal Load Currents. Available online: https://ieeexplore.ieee.org/document/8511103 (accessed on 22 January 2022).
- Makarov, S.N.; Emanuel, A.E. Correction harmonic loss factor for transformers supplying nonsinusoidal load currents. In Proceedings of the 9th International Conference on Harmonics and Quality of Power, Orlando, FL, USA, 1–4 October 2000. [Google Scholar]
- Elmoudi, A.; Lehtonen, M.; Nordman, H. Correction Winding Eddy-Current Harmonic Loss Factor for Transformers Subject to Nonsinusoidal Load Currents. In Proceedings of the 2005 IEEE Russia Power Tech, St. Petersburg, Russia, 27–30 June 2005. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, D.; Li, Z.; Huang, Q.; Li, B.; Li, M.; Liu, J. Calculation method of winding eddy-current losses for high-voltage direct current converter transformers. IET Electr. Power Appl. 2016, 10, 488–497. [Google Scholar] [CrossRef]
- Taher, M.A.; Kamel, S.; Ali, Z.M. K-Factor and transformer losses calculations under harmonics. In Proceedings of the 18th International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 27–29 December 2016. [Google Scholar]
- Thango, B.A.; Jordaan, J.A.; Nnachi, A.F. A Weighting Factor for Estimating the Winding Eddy Loss in Transformers for High Frequencies. In Proceedings of the 2020 6th IEEE International Energy Conference (ENERGYCon), Gammarth, Tunisia, 28 September–1 October 2020; pp. 489–493. [Google Scholar] [CrossRef]
- Rad, M.S.; Kazeroomi, M.K.; Ghorbani, J.; Mokhtari, H. Analysis of the grid harmonics and their impacts on distribution transformers. In Proceedings of the IEEE Power and Energy Conference, Champaign, IL, USA, 24–25 February 2012. [Google Scholar]
- Liu, Z.; Zhu, J.; Zhu, L. Accurate Calculation of Eddy Current Loss in Litz-Wired High-Frequency Transformer Windings. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar] [CrossRef]
- Chatzipetros, D.; Pilgrim, J.A. Impact of Proximity Effects on Sheath Losses in Trefoil Cable Arrangements. IEEE Trans. Power Deliv. 2020, 35, 455–463. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, G.; Qiu, R.; Liu, Z.; Yao, N. Distribution Correction Model of Urban Rail Return System Considering Rail Skin Effect. IEEE Trans. Transp. Electrif. 2021, 7, 883–891. [Google Scholar] [CrossRef]
- PC57.110/D6. Sept 2017—IEEE Draft Recommended Practice for Establishing Liquid-Immersed and Dry-Type Power and Distribution Transformer Capability When Supplying Nonsinusoidal Load Currents. Available online: https://ieeexplore.ieee.org/document/8048766 (accessed on 22 January 2022).
- C57.110-2008. IEEE Recommended Practice for Establishing Liquid-Filled and Dry-Type Power and Distribution Transformer Capability When Supplying Nonsinusoidal Load Currents. Available online: https://ieeexplore.ieee.org/servlet/opac?punumber=4601579 (accessed on 22 January 2022).
- Collins, M.; Martins, C.A. Evaluation of a Novel Capacitor Charging Structure for Flicker Mitigation in High-Power Long-Pulse Modulators. IEEE Trans. Plasma Sci. 2019, 47, 985–993. [Google Scholar] [CrossRef]
- Thango, B.A.; Jordaan, J.A.; Nnachi, A.F. Step-Up Transformers for PV Plants: Load Loss Estimation under Harmonic Conditions. In Proceedings of the 2020 19th International Conference on Harmonics and Quality of Power (ICHQP), Dubai, United Arab Emirates, 6–7 July 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Yildirim, D.; Fuchs, E.F. Measured Transformer De-Rating Comparison with Harmonic Loss Factor (FHL) Approach. IEEE Trans. Power Deliv. 2000, 15, 166–191. [Google Scholar]
- Cheng, K.W.E.; Kwok, K.F.; Ho, S.L.; Ho, Y.L. Calculation of winding losses using matrix modelling of high frequency transformer. Int. J. Comput. Math. Electr. Electron. Eng. 2002, 21, 573–580. [Google Scholar] [CrossRef]
- Kulkarni, S.V.; Khaparde, S.A. Transformer Engineering: Design and Practice; Marcel Dekker: New York, NY, USA, 2004. [Google Scholar]
- Bachinger, F.; Langer, U.; Schoberl, J. Numerical Analysis of Nonlinear Multiharmonic Eddy Current Problems. Numer. Math. 2005, 100, 593–616. [Google Scholar] [CrossRef] [Green Version]
- Da Silva, J.R.; Paganoto, S.P.; Graeff, R.; Da Rocha, C.M.; Bernartt, M.L.; Dos Santos, C.W. Analysis of Methods Eddy Current Loss Estimation in Power Transformer Windings with Multiphysical Consideration (Electromagnetic and Fluid Dynamic). In Proceedings of the 2020 IEEE 19th Biennial Conference on Electromagnetic Field Computation (CEFC), Pisa, Italy, 16–18 November 2020. [Google Scholar] [CrossRef]
- Van den Bossche, A.; Valchev, V.C.; Barudov, S.T. Practical Wide Frequency Approach for Calculating Eddy Current Losses in Transformer Windings. In Proceedings of the IEEE ISIE 2006, Montreal, QC, Canada, 9–12 July 2006. [Google Scholar]
- Frelin, W.; Berthet, L.; Petit, M.; Vannier, J.C. Transformer Winding Losses Evaluation when Supplying Non-Linear Load. In Proceedings of the 44th International Universities Power Engineering Conference (UPEC), Glasgow, UK, 1–4 September 2009. [Google Scholar]
- Zhilichev, Y. Analysis of Eddy Currents in Rectangular Coils by Integral Equation Method in Sub-Domains. IEEE Trans. Magn. 2014, 50, 1–10. [Google Scholar] [CrossRef]
- Larsson, L. On Integral Equation Methods of Solution to Eddy Current Interaction Problems. Ph.D. Thesis, Chalmers University of Technology, Goteborg, Sweden, 2014. [Google Scholar]
- Del Vecchio, R.M.; Poulin, B.P.; Feghali, P.T.; Shah, D.M.; Ahuja, R. Transformer Design Principles; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Yin, Z.; Wei, W. Distortion Characteristics and Experimental Research on Transformer Windings under Harmonic Condition. In Proceedings of the 3rd Asia Conference on Power and Electrical Engineering, Kitakyushu, Japan, 22–24 March 2018. [Google Scholar]
- Sikhosana, L.S.; Akuru, U.B.; Thango, B.A. Analysis and Harmonic Mitigation in Distribution Transformers for Renewable Energy Applications. In Proceedings of the 2021 Southern African Universities Power Engineering Conference/Robotics and Mechatronics/Pattern Recognition Association of South Africa (SAUPEC/RobMech/PRASA), Potchefstroom, South Africa, 27–29 January 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Xia, B.; Jeong, G.; Koh, C. Co-Kriging Assisted PSO Algorithm and Its Application to Optimal Transposition Design of Power Transformer Windings for the Reduction of Circulating Current Loss. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- Stadler, A.; Gulden, C. The calculation of eddy current losses in tube wound high current transformer windings. In Proceedings of the 14th International Power Electronics and Motion Control Conference EPE-PEMC 2010, Ohrid, Macedonia, 6–8 September 2010. [Google Scholar] [CrossRef]
- Motalleb, M.; Vakilian, M.; Abbaspour, A. Calculation of eddy current losses caused by leads and other current sources in high current power transformers. In Proceedings of the 2008 Australasian Universities Power Engineering Conference, Sydney, Australia, 14–17 December 2008. [Google Scholar]
- Del Vecchio, R.M. Eddy-Current Losses in a Conducting Plate Due to a Collection of Bus Bars Carrying Currents of Different Magnitudes and Phases. IEEE Trans. Magn. 2003, 39, 549–552. [Google Scholar] [CrossRef]
- Olivares, J.C.; Escarela-Perez, R.; Kulkarni, S.V.; de León, F.; Venegas-Vega, M.A. 2D finite-element determination of tank wall losses in pad-mounted transformers. Electr. Power Syst. Res. 2004, 71, 179–185. [Google Scholar] [CrossRef]
- Olivares, J.C.; Escarela-Perez, R.; Kulkarni, S.V.; de León, F.; Venegas-Vega, M.A. Improved Insert Geometry for Reducing Tank-Wall Losses in Pad-Mounted Transformers. IEEE Trans. Power Deliv. 2004, 19, 1120–1126. [Google Scholar] [CrossRef]
- Ho, S.L.; Li, Y.; Tang, R.Y.; Cheng, K.W.E.; Yang, S.Y. Calculation of Eddy Current Field in the Ascending Flange for the Bushings and Tank Wall of a Large Power Transformer. IEEE Trans. Magn. 2008, 44, 1522–1525. [Google Scholar] [CrossRef] [Green Version]
- Da Luz, M.V.F.; Dular, P.; Dang, Q.V.; Kuo-Peng, P. Evaluation of Eddy Losses Due to High Current Leads in Transformers Using a Sub Problem Method. In Proceedings of the ISEF 2011-XV International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering Funchal, Madeira, Portugal, 1–3 September 2011. [Google Scholar]
- Predicting Stray Losses in Power Transformers and Optimization of Tank Shielding using FEM. Available online: https://library.e.abb.com/public/9eb08c572459433e996a97df264d1df6/51-56%204m6053_EN_72dpi.pdf (accessed on 22 January 2022).
- Kralj, L.; Miljavec, D. Stray Losses in Power Transformer Tank Walls and Construction Parts. Available online: https://www.researchgate.net/publication/224184598.2009 (accessed on 22 January 2022).
- Cedrat Group. User’s Guide Flux 3d, Version 10.3; Cedrat Technologies: Meylan, France, 2009. [Google Scholar]
- Najafi, A.; Ozgonenel, O.; Kurt, U. Reduction stray loss on transformer tank wall with optimized widthwise electromagnetic shunts. In Proceedings of the 2017 10th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 30 November–2 December 2017; pp. 6–10. [Google Scholar]
- Wiak, S.; Drzymala, P.; Welfle, H. Nonlinear phenomena in tank of transformer and power losses computations. Przegląd Elektrotechniczny 2013, 89, 230–232. [Google Scholar]
- Li, Y.; Li, L.; Jing, Y.; Zhang, B. 3D Finite Element Analysis of the Stray Loss in Power Transformer Structure Parts. Energy Power Eng. 2013, 5, 1089–1092. [Google Scholar] [CrossRef]
- Li, Y.; Eerhemubayaer; Sun, X.; Jing, Y.; Li, J. Calculation and analysis of 3-D nonlinear eddy current field and structure losses in transformer. In Proceedings of the 2011 International Conference on Electrical Machines and Systems, Beijing, China, 20–23 August 2011; pp. 1–4. [Google Scholar] [CrossRef]
- Krasl, M.; Jiricková, J.; Vlk, R. Stray Losses in Transformer Tank; Faculty of Electrical Engineering: Cheb, Czech Republic, 2009. [Google Scholar]
- Yan, X.; Yu, X.; Shen, M.; Xie, D.; Bai, B.; Wang, Y. Calculation of Stray Losses in Power Transformer Structural Parts Using Finite Element Method Combined with Analytical Method. In Proceedings of the 18th International Conference on Electrical Machines and Systems (ICEMS), Pattaya, Thailand, 25–28 October 2015. [Google Scholar]
- Yan, X.; Yu, X.; Shen, M.; Xie, D.; Bai, B. Research on Calculating Eddy-Current Losses in Power Transformer Tank Walls Using Finite-Element Method Combined with Analytical Method. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- Moghaddami, M.; Sarwat, A.I.; de Leon, F. Reduction of Stray Loss in Power Transformers Using Horizontal Magnetic Wall Shunts. IEEE Trans. Magn. 2017, 53, 1–7. [Google Scholar] [CrossRef]
- Thango, B.A.; Jordaan, J.A.; Nnachi, A.F. A Novel Approach for Evaluating Eddy Current Loss in Wind Turbine Generator Step-Up Transformers. Adv. Sci. Technol. Eng. Syst. J. 2021, 6, 488–498. [Google Scholar] [CrossRef]
- Thango, B.A.; Akumu, A.O.; Sikhosana, L.S.; Nnachi, A.F.; Jordaan, J.A. Preventive Maintenance of Transformer Health Index Through Stray Gassing: A Case Study. In Proceedings of the 2021 IEEE PES/IAS PowerAfrica, Nairobi, Kenya, 23–27 August 2021. [Google Scholar] [CrossRef]
- Thango, B.A.; Jordaan, J.A.; Nnachi, A.F. Analyzing Harmonic Current Effect on Distributed Photovoltaic Power Generation System Transformers. In Proceedings of the 2021 IEEE PES/IAS PowerAfrica, Nairobi, Kenya, 23–27 August 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Emanuel, A.E.; Wang, X. Estimation of Loss of Life of Power Transformers Supplying Nonlinear Loads. IEEE Trans. Power Appar. Syst. 1985, PAS-104, 628–636. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thango, B.A.; Bokoro, P.N. Stray Load Loss Valuation in Electrical Transformers: A Review. Energies 2022, 15, 2333. https://doi.org/10.3390/en15072333
Thango BA, Bokoro PN. Stray Load Loss Valuation in Electrical Transformers: A Review. Energies. 2022; 15(7):2333. https://doi.org/10.3390/en15072333
Chicago/Turabian StyleThango, Bonginkosi A., and Pitshou N. Bokoro. 2022. "Stray Load Loss Valuation in Electrical Transformers: A Review" Energies 15, no. 7: 2333. https://doi.org/10.3390/en15072333
APA StyleThango, B. A., & Bokoro, P. N. (2022). Stray Load Loss Valuation in Electrical Transformers: A Review. Energies, 15(7), 2333. https://doi.org/10.3390/en15072333





