Effect of Shear-Thinning Property on the Energy Performance and Flow Field of an Axial Flow Pump
Abstract
:1. Introduction
2. Experimental Setup and Numerical Methods
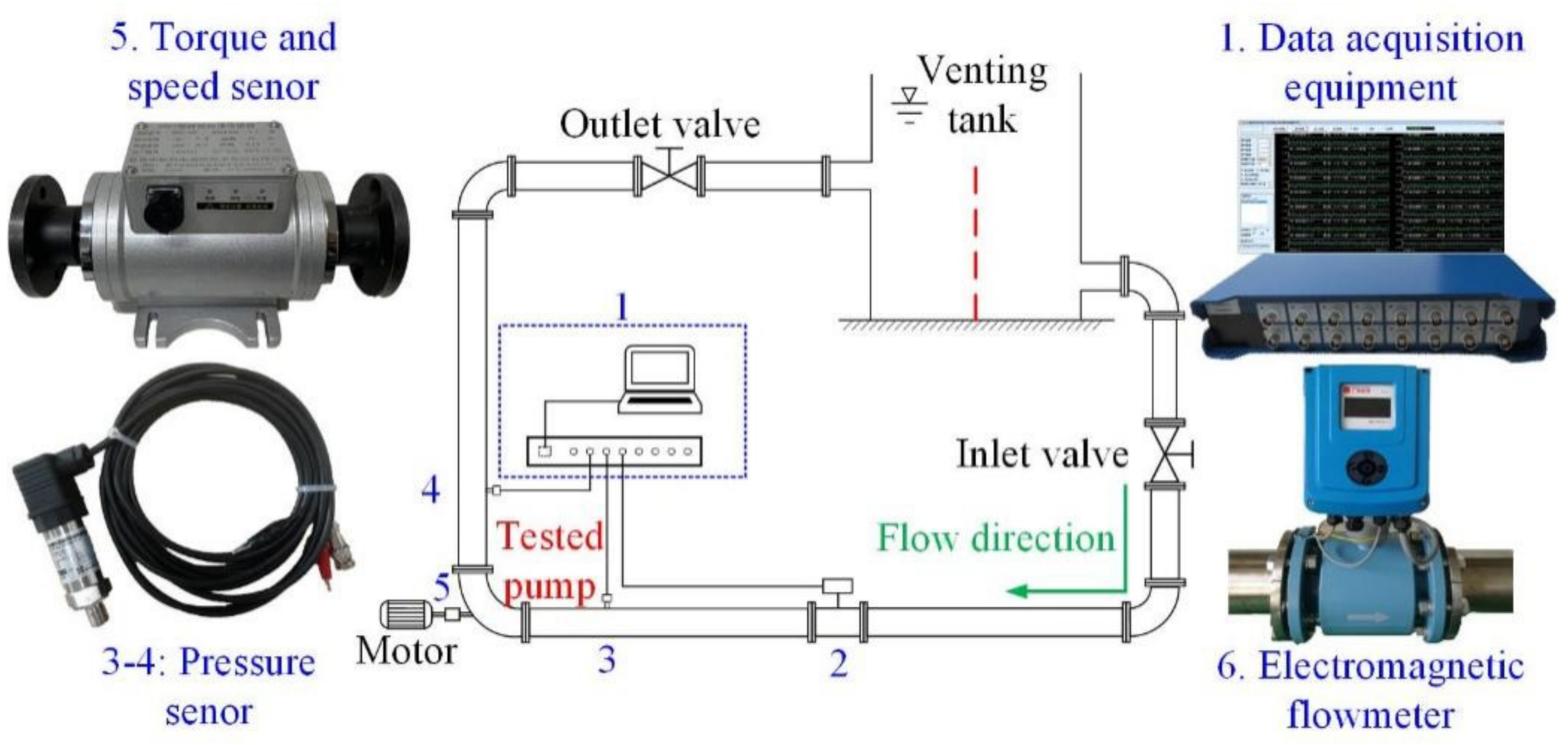
2.1. Experimental Setup
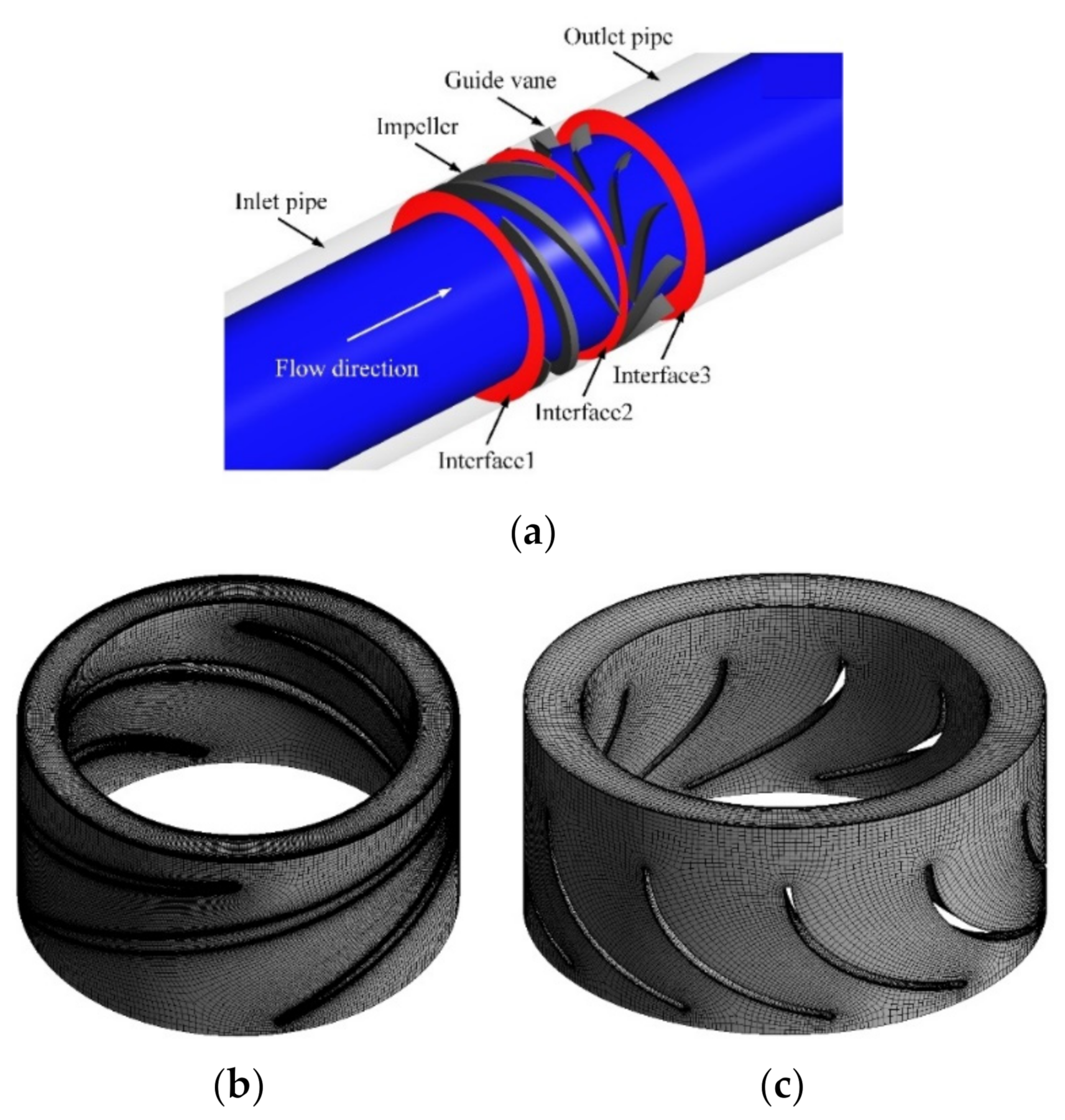
2.2. Numerical Method
3. Results and Discussion
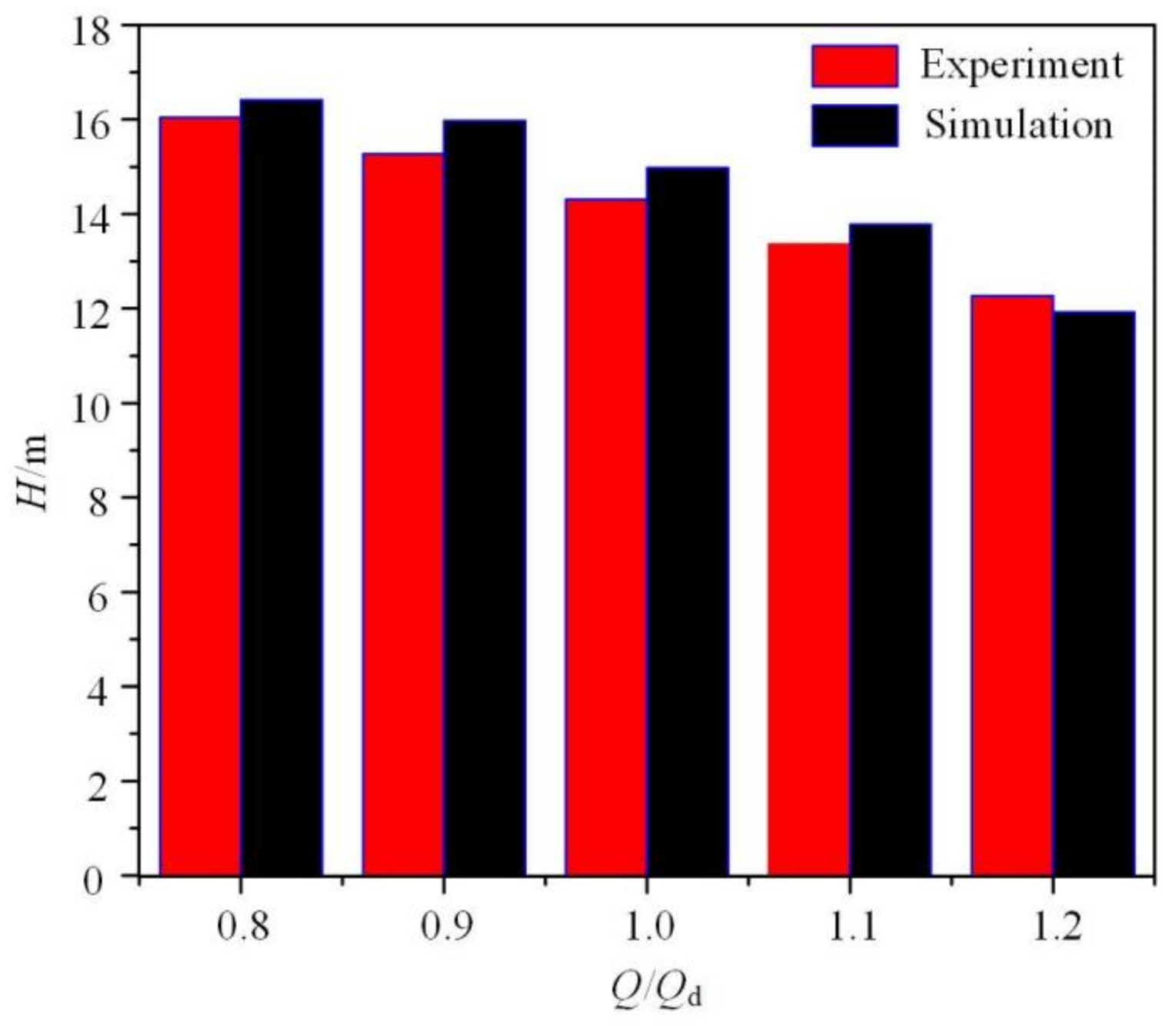
3.1. Validation of Calculation
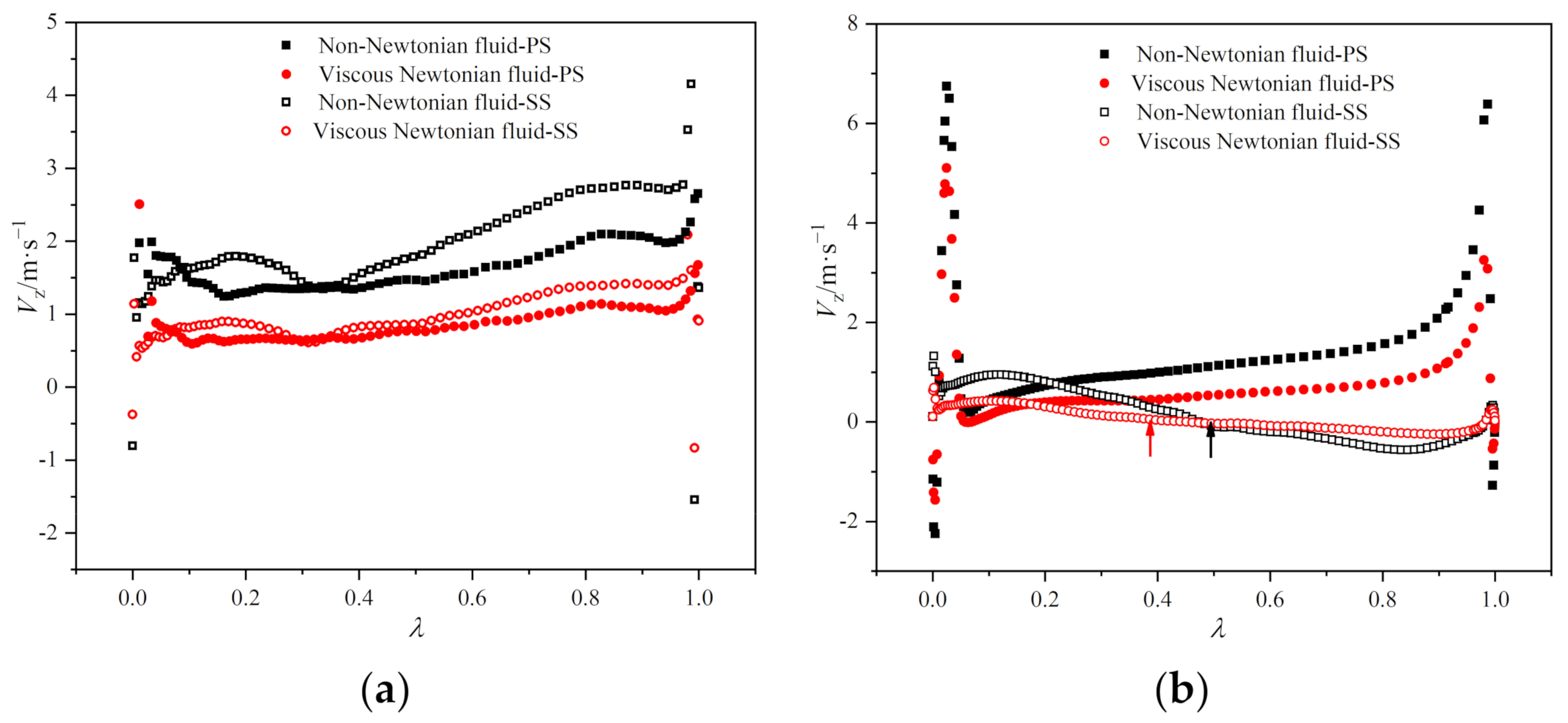
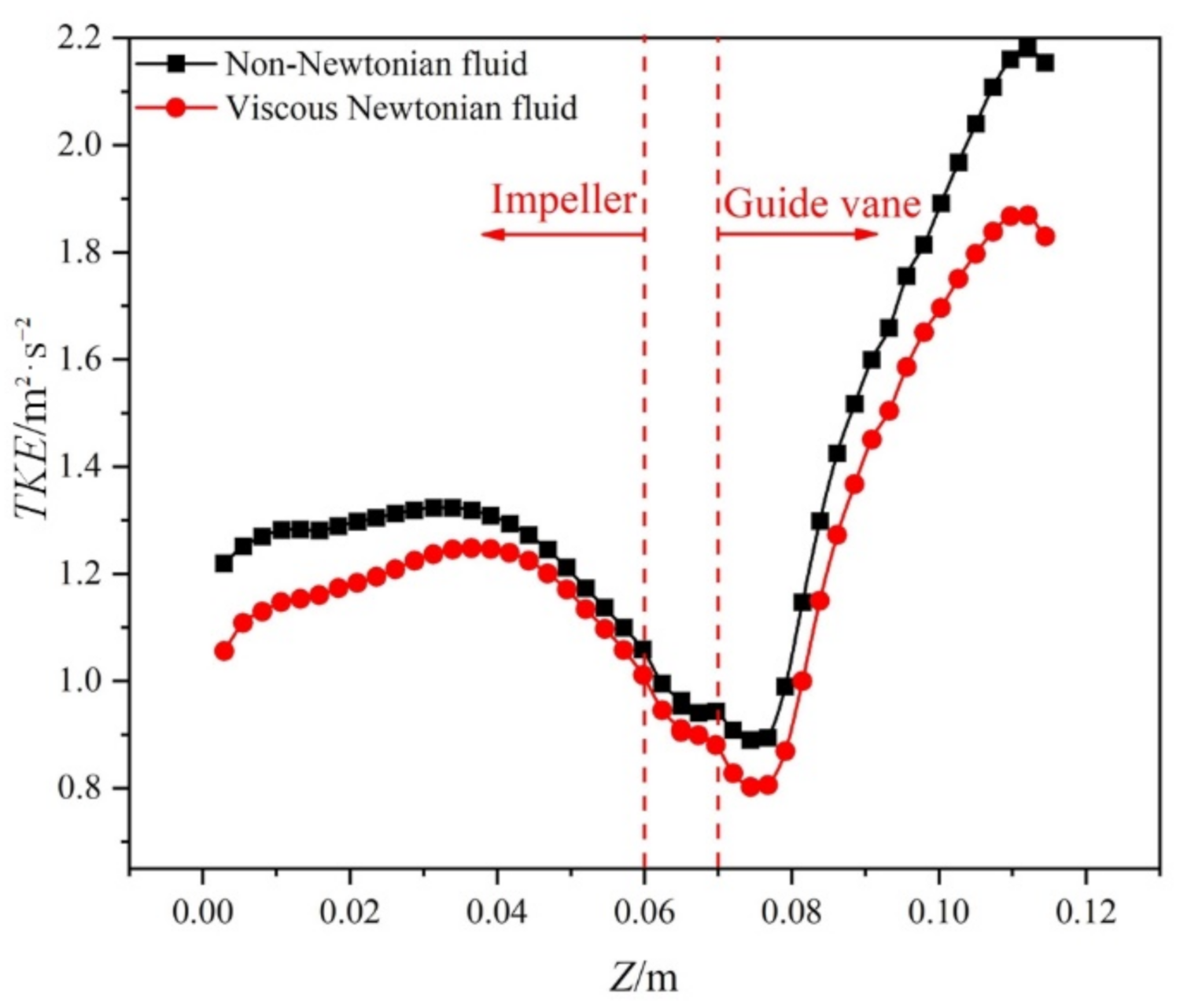
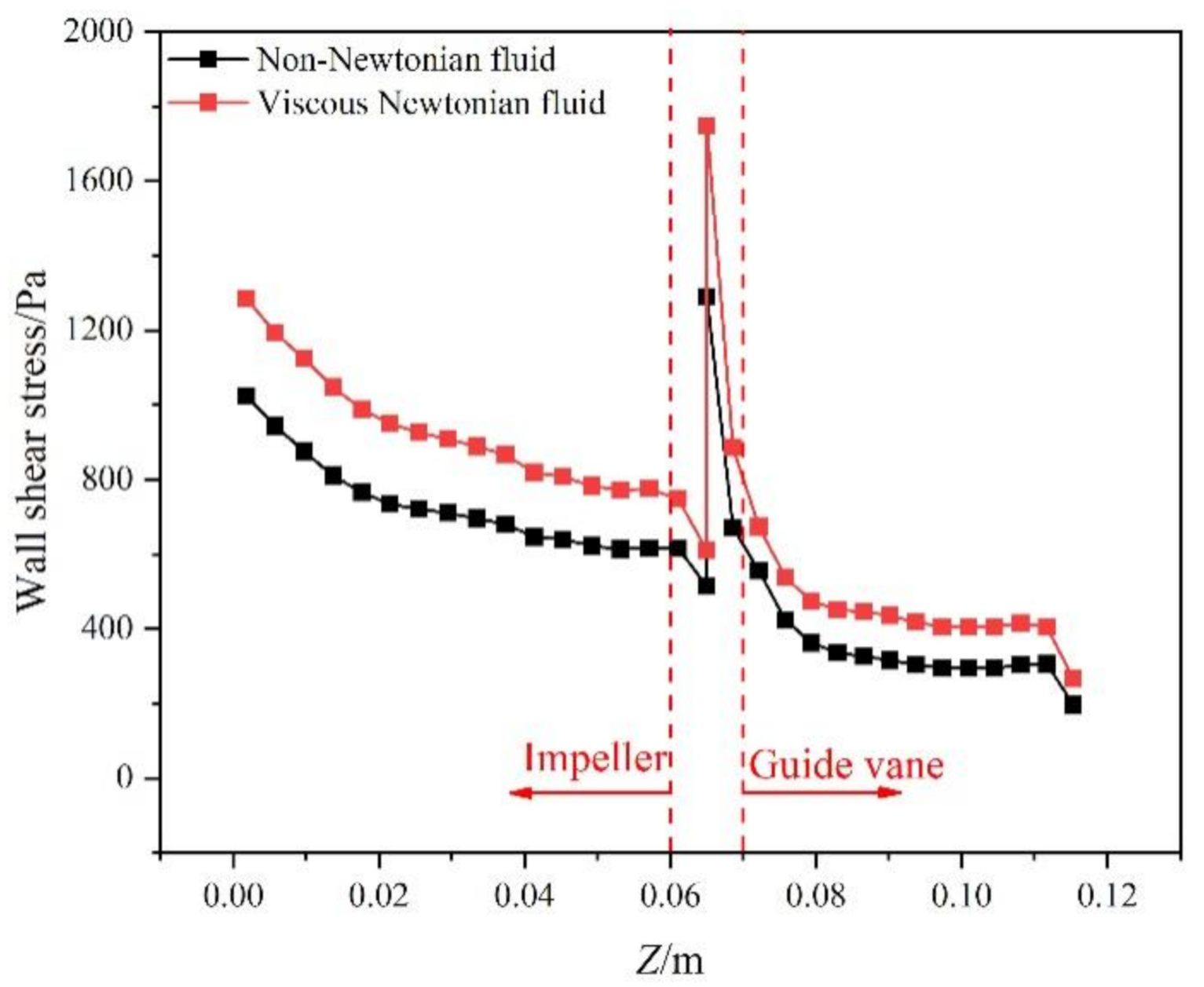
3.2. Discussion on Flow Fields
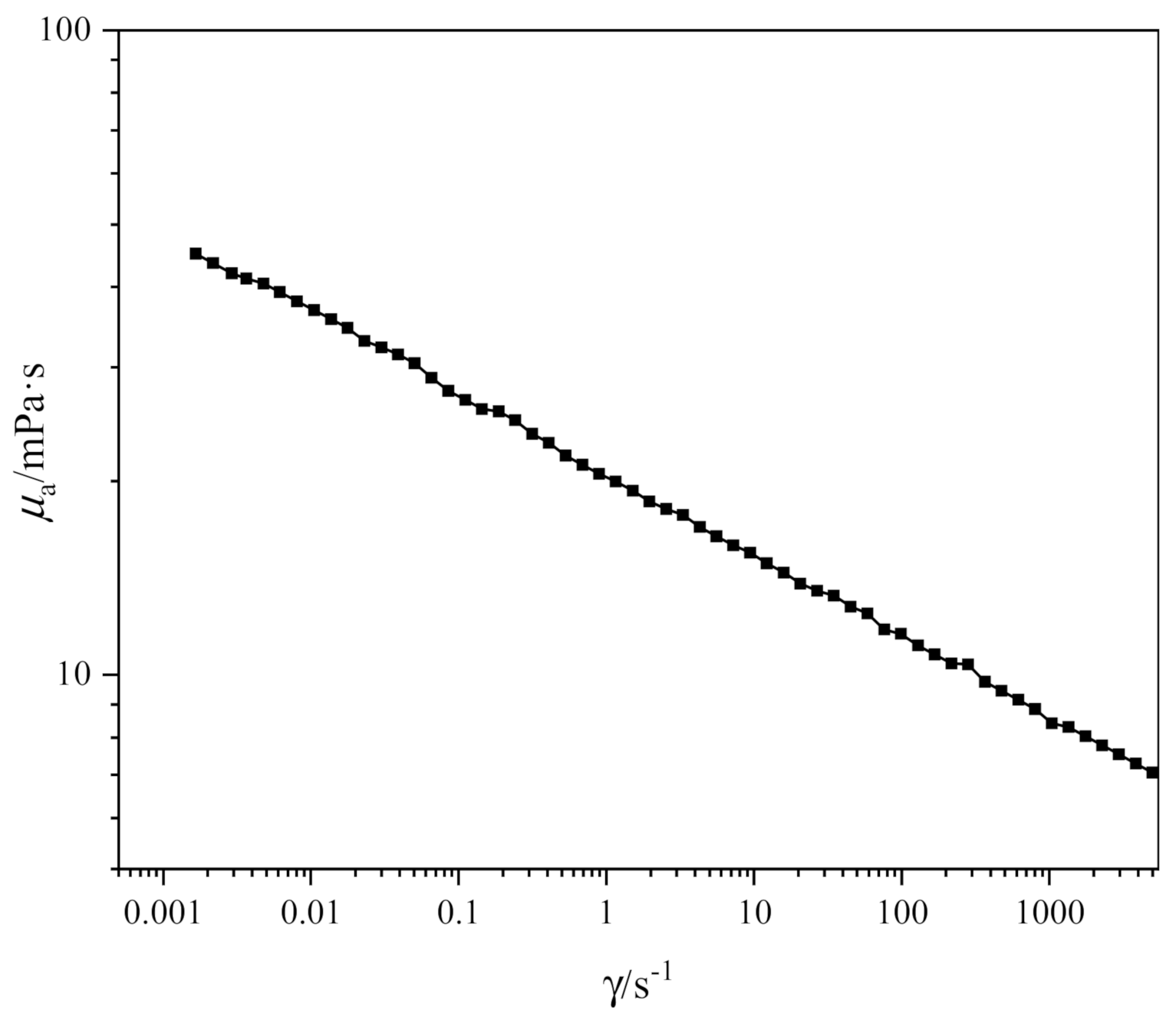
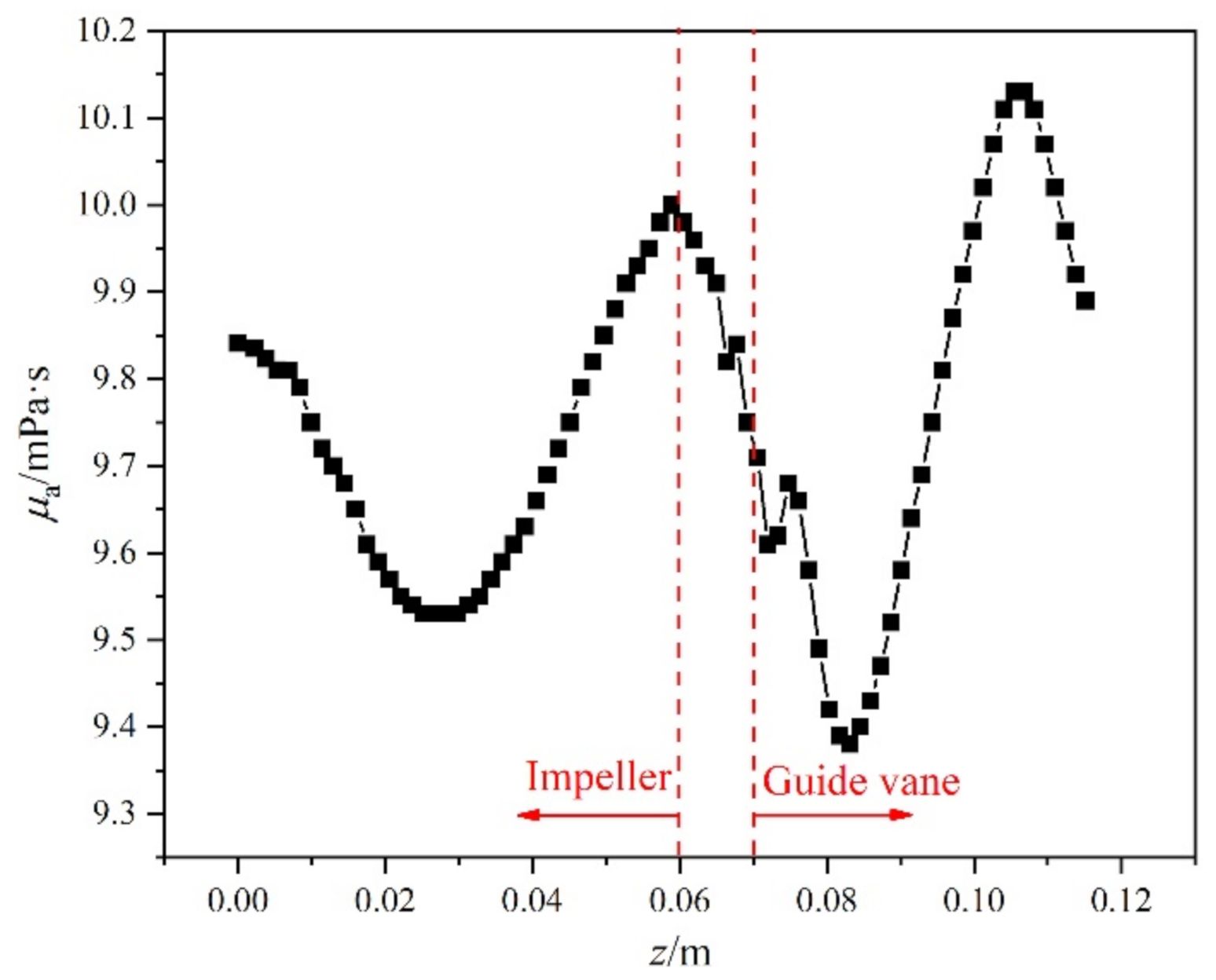
3.2.1. Variation of Apparent Viscosity
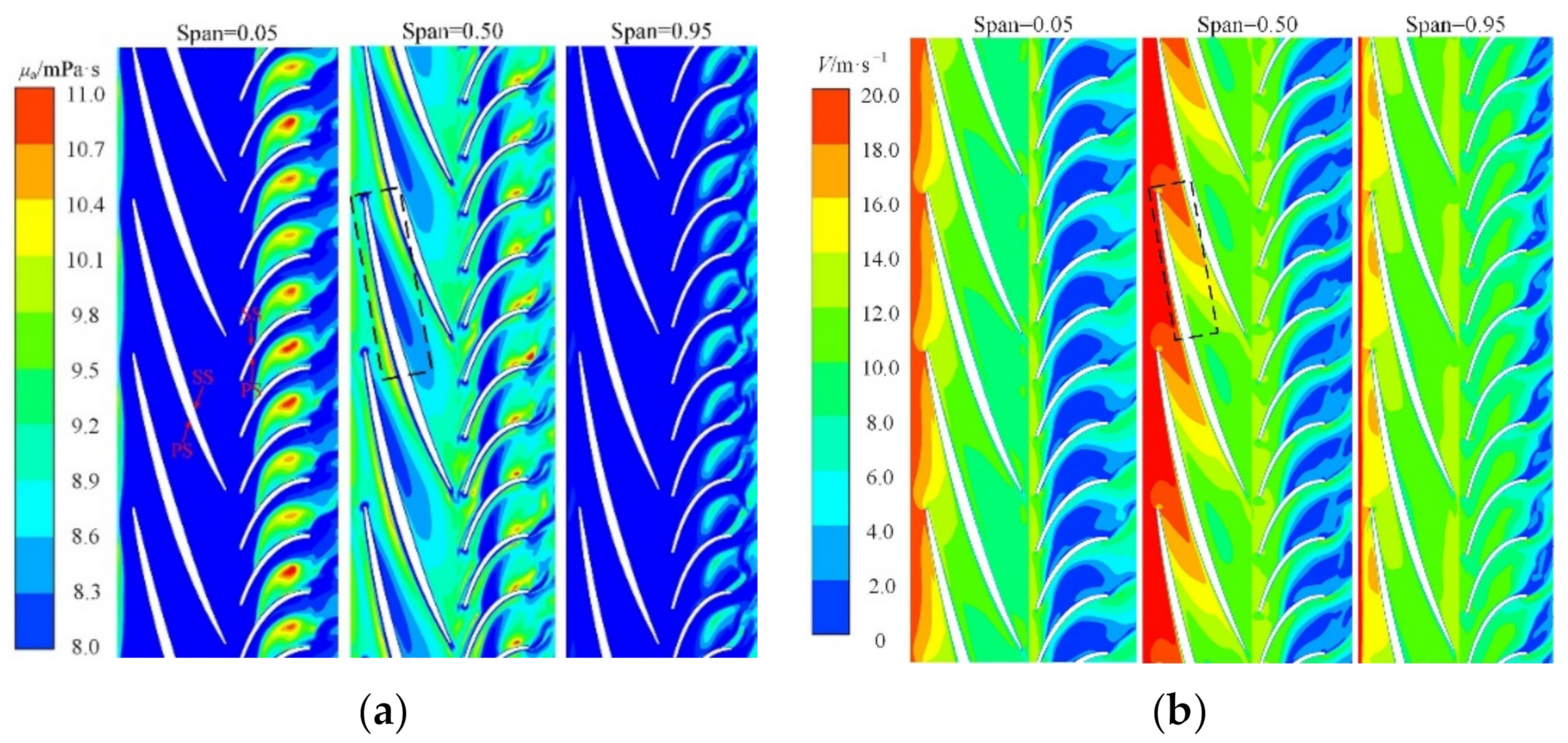
3.2.2. Influence of Shear-Thinning Properties
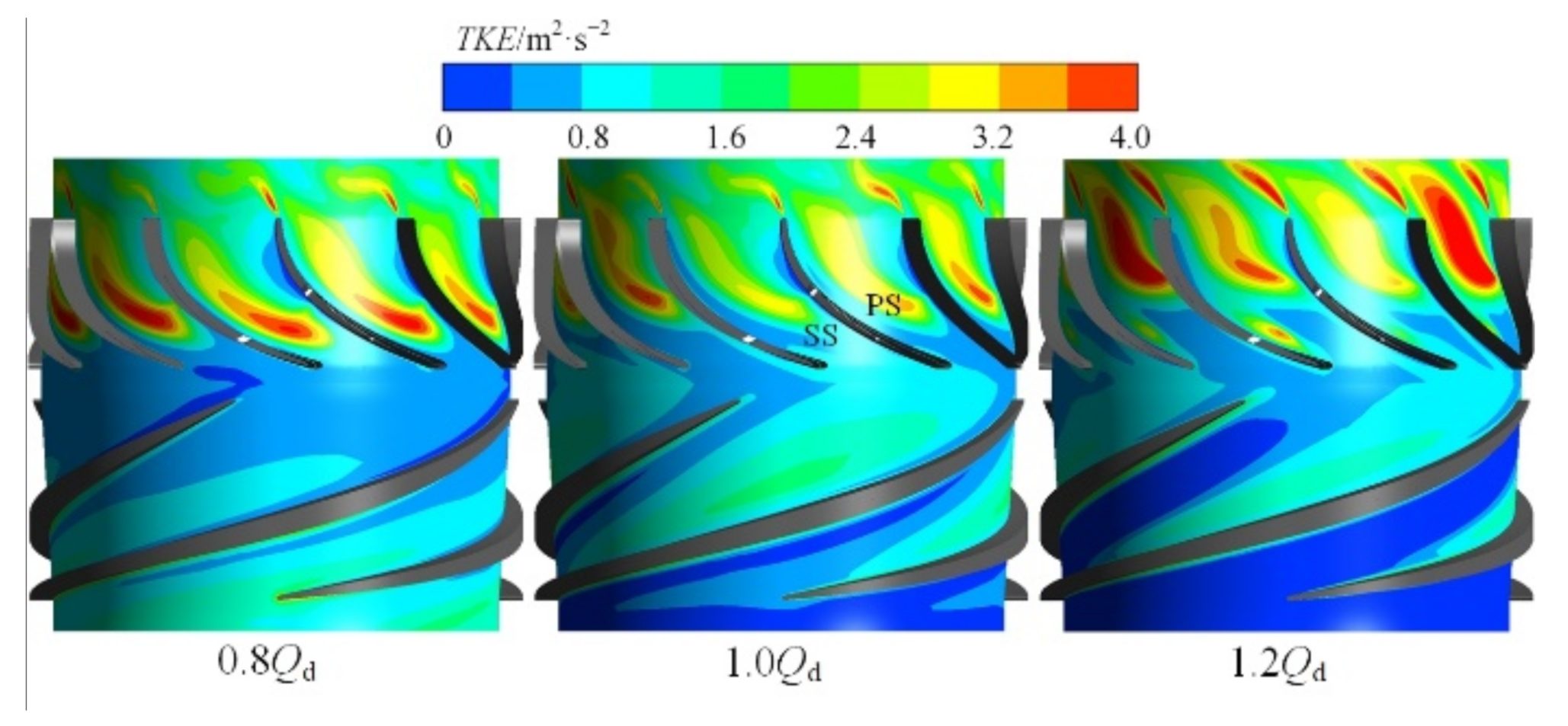
3.2.3. Influence of Flow Rate
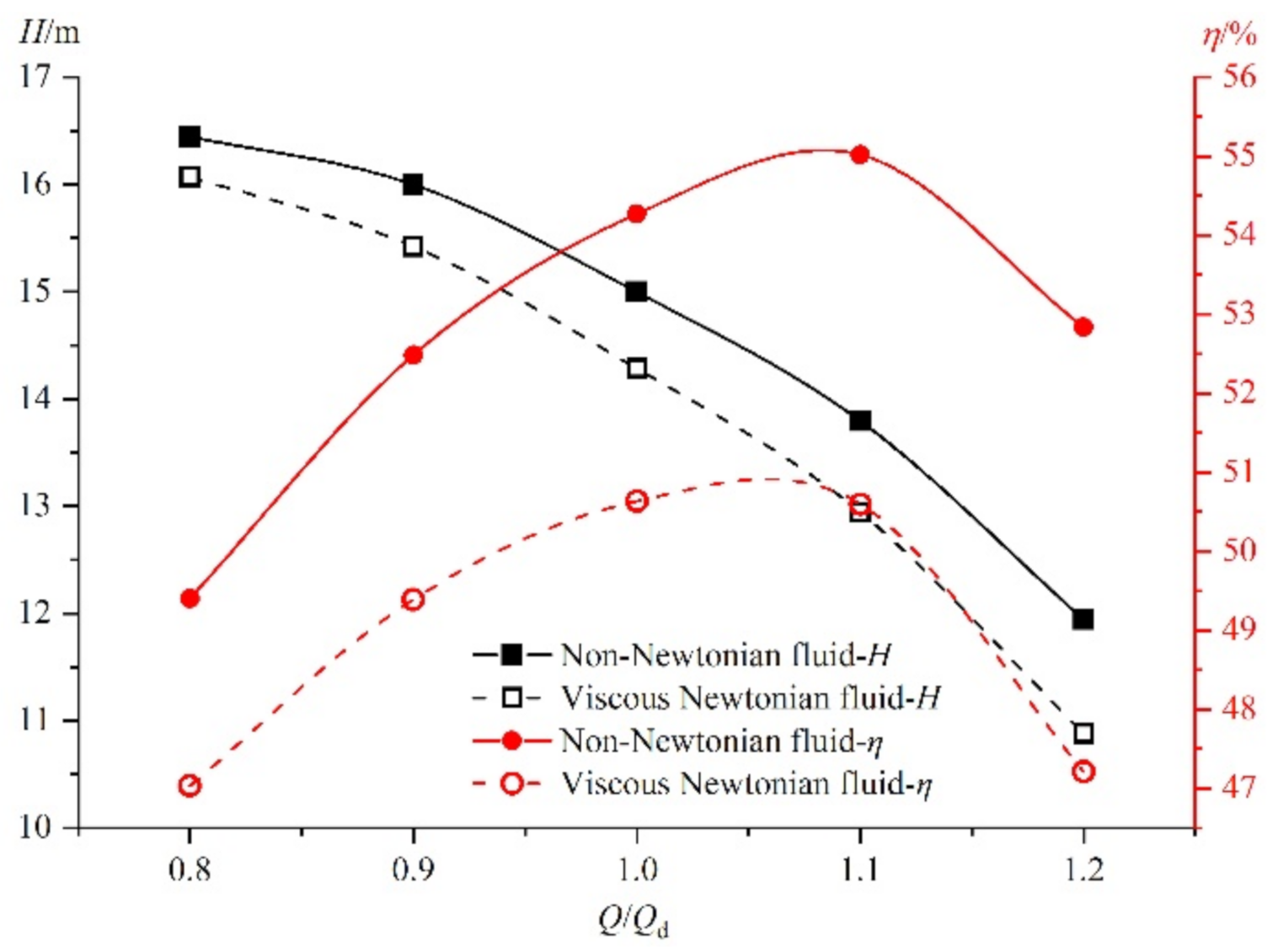
3.3. Pump Performance
4. Conclusions
- (1)
- For the shear-thinning non-Newtonian fluid, the reduction of apparent viscosity occurs mainly in the region of the impeller and guide vane inlets, vaneless area, guide vane outlet, and the near-wall region. In addition, a large velocity gradient is a common feature in these regions.
- (2)
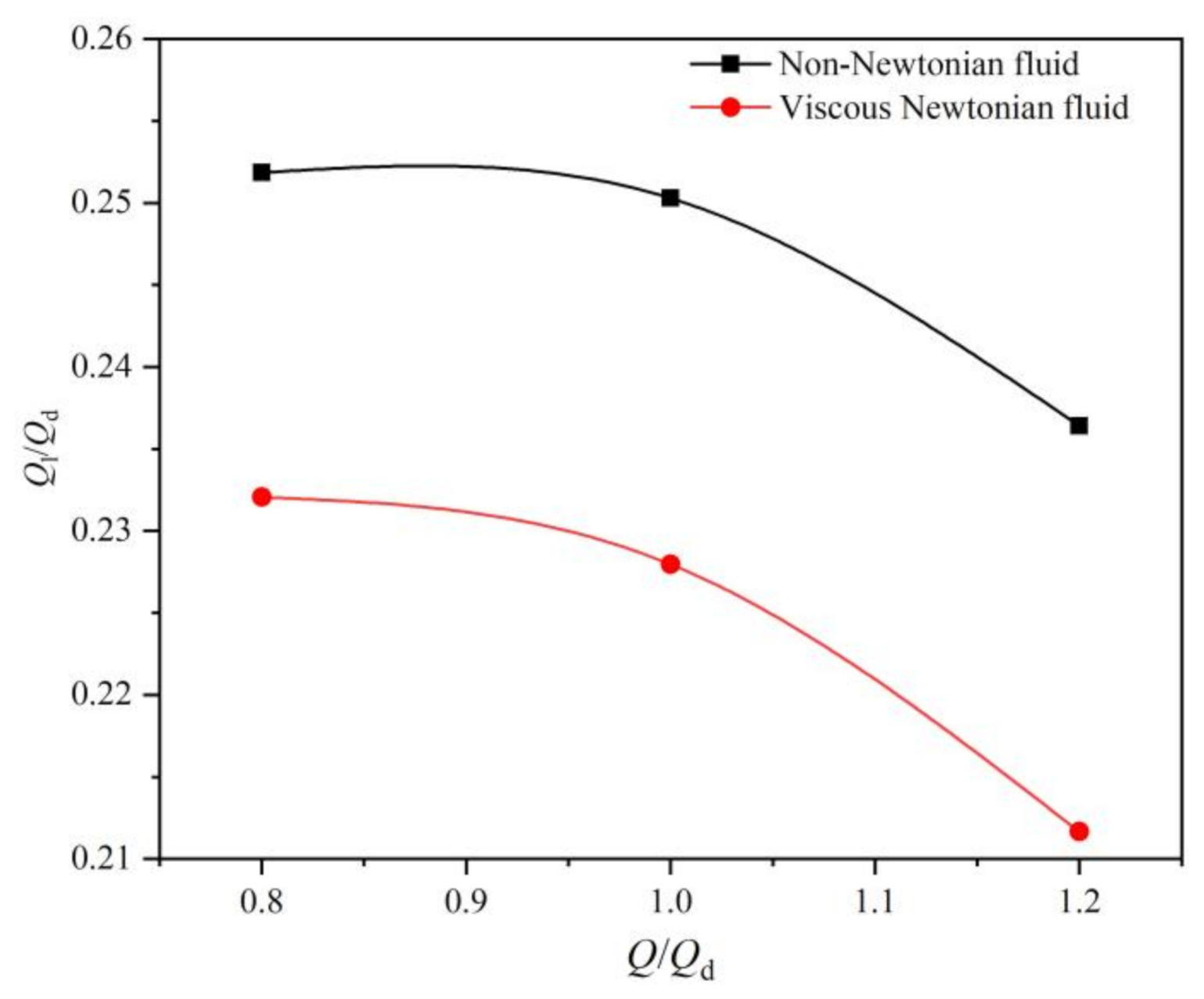
- Shear-thinning properties lead to a higher flow loss and volume loss, but the friction loss is significantly reduced. In addition, friction loss is the main part of the total loss under shear-thinning solution conditions, which is the same with viscous Newtonian fluid conditions.
- (3)
- As the flow rate increases, the low apparent viscosity area near the leading edge of the suction side gradually expands, which is caused by the intensified solution shock. Due to the intensified flow separation, the low apparent viscosity area in the pressure side also shows an increasing trend.
- (4)
- Compared to the viscous Newtonian fluid, the pump head and efficiency could decrease sharply while the shear-thinning non-Newtonian fluid is handled. In addition, the reduction of efficiency is more obvious as the flow rate increases. It is noteworthy to mention that the shear-thinning properties lead to a relatively small flow rate range with high efficiency.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Li, Y.J.; Yu, Z.Y. Distribution and motion characteristics of bubbles in a multiphase rotodynamic pump based on modified non-uniform bubble model. J. Petrol. Sci. Eng. 2020, 195, 107569. [Google Scholar] [CrossRef]
- Zhang, J.S.; Tan, L. Energy performance and pressure fluctuation of a multiphase pump with different gas volume fractions. Energies 2018, 11, 1216. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.; Tan, L.; Xu, Y.; Cao, S.L. Optimization design method of multi-stage multiphase pump based on Oseen vortex. J. Petrol. Sci. Eng. 2020, 184, 106532. [Google Scholar] [CrossRef]
- Kim, J.H.; Lee, H.C.; Kim, J.W.; Choi, Y.S.; Yoon, J.; Yoo, I.; Choi, W. Improvement of hydrodynamic performance of a multiphase pump using design of experiment techniques. J. Fluid Eng.-ASME 2015, 137, 081301. [Google Scholar] [CrossRef]
- Suh, J.W.; Kim, J.W.; Choi, Y.S.; Kim, J.H.; Joo, W.G.; Lee, K.Y. Development of numerical Eulerian-Eulerian models for simulating multiphase pumps. J. Petrol. Sci. Eng. 2018, 162, 588–601. [Google Scholar] [CrossRef]
- Liu, M.; Tan, L.; Cao, S.L. Design method of controllable blade angle and orthogonal optimization of pressure rise for a multiphase pump. Energies 2018, 11, 1048. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Cao, S.L.; Sano, T.; Wakai, T.; Reclari, M. Experimental investigation on transient pressure characteristics in a helico-axial multiphase pump. Energies 2019, 12, 461. [Google Scholar] [CrossRef] [Green Version]
- Liu, N.; Wang, Y.; Zhang, G. The Pump Models Test of the South-to-North Water Diversion Project; China Water & Power Press: Beijing, China, 2006; p. 53. [Google Scholar]
- Bilal, S.; Rehman, M.; Noeiaghdam, S.; Ahmad, H.; Akgül, A. Numerical analysis of natural convection driven flow of a non-Newtonian power-law fluid in a trapezoidal enclosure with a U-Shaped constructal. Energies 2021, 14, 5355. [Google Scholar] [CrossRef]
- Xin, X.K.; Li, Y.Q.; Yu, G.M.; Wang, W.Y.; Zhang, Z.Z.; Zhang, M.L.; Ke, W.L.; Kong, D.B.; Wu, K.L.; Chen, Z.X. Non-Newtonian flow characteristics of heavy oil in the Bohai Bay oilfield: Experimental and simulation studies. Energies 2017, 10, 1698. [Google Scholar] [CrossRef]
- Anastasiou, A.D.; Passos, A.D.; Mouza, A.A. Bubble columns with fine pore sparger and non-Newtonian liquid phase: Prediction of gas holdup. Chem. Eng. Sci. 2013, 98, 331–338. [Google Scholar] [CrossRef]
- Buwa, V.V.; Ranade, V.V. Characterization of dynamics of gas-liquid flows in rectangular bubble columns. Aiche J. 2004, 50, 2394–2407. [Google Scholar] [CrossRef]
- Fan, W.Y.; Li, S.C.; Li, L.X.; Zhang, X.; Du, M.Q.; Yin, X.H. Hydrodynamics of gas/shear-thinning liquid two-phase flow in a co-flow mini-channel: Flow pattern and bubble length. Phys. Fluids 2020, 32, 092004. [Google Scholar] [CrossRef]
- Van Wyk, S.; Prahl Wittberg, L.; Bulusu, K.V.; Fuchs, L.; Plesniak, M.W. Non-Newtonian perspectives on pulsatile blood-analog flows in a 180° curved artery model. Phys. Fluids 2015, 27, 071901. [Google Scholar] [CrossRef]
- Picchi, D.; Correra, S.; Poesio, P. Flow pattern transition, pressure gradient, hold-up predictions in gas/non-Newtonian power-law fluid stratified flow. Int. J. Multiph. Flow 2014, 63, 105–115. [Google Scholar] [CrossRef]
- Gabelle, J.C.; Morchain, J.; Anne-Archard, D.; Augier, F.; Liné, A. Experimental determination of the shear rate in a stirred tank with a non-newtonian fluid: Carbopol. Aiche J. 2013, 59, 2251–2266. [Google Scholar] [CrossRef]
- Story, A.; Jaworski, Z.; Simmons, M.J.; Nowak, E. Comparative PIV and LDA studies of Newtonian and non-Newtonian flows in an agitated tank. Chem. Pap. 2018, 72, 593–602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cortada-Garcia, M.; Dore, V.; Mazzei, L.; Angeli, P. Experimental and CFD studies of power consumption in the agitation of highly viscous shear thinning fluids. Chem. Eng. Res. Des. 2017, 119, 171–182. [Google Scholar] [CrossRef]
- Wang, X.; Feng, X.; Yang, C.; Mao, Z.S. Energy Dissipation rates of Newtonian and Non-Newtonian fluids in a stirred vessel. Chem. Eng. Technol. 2014, 37, 1575–1582. [Google Scholar] [CrossRef]
- Torres, M.D.; Gadala-Maria, F.; Wilson, D.I. Comparison of the rheology of bubbly liquids prepared by whisking air into a viscous liquid (honey) and a shear-thinning liquid (guar gum solutions). J. Food Eng. 2013, 118, 213–228. [Google Scholar] [CrossRef]
- Sun, W.H.; Tan, L. Cavitation-vortex-pressure fluctuation interaction in a centrifugal pump using bubble rotation modified cavitation model under partial load. J. Fluids Eng.-ASME 2020, 142, 051206. [Google Scholar] [CrossRef]
- Li, Y.J.; Yu, Z.Y.; Sun, W.H. Drag coefficient modification for turbulent gas-liquid two-phase flow in a rotodynamic pump. Chem. Eng. J. 2021, 417, 128570. [Google Scholar] [CrossRef]
- Zhang, W.W.; Zhu, B.S.; Yu, Z.Y. Characteristics of bubble motion and distribution in a multiphase rotodynamic pump. J. Petrol. Sci. Eng. 2020, 193, 107435. [Google Scholar] [CrossRef]
- Aldi, N.; Buratto, C.; Pinelli, M.; Spina, P.R.; Suman, A.; Casari, N. CFD analysis of a non-Newtonian fluids processing pump. Energy Procedia 2016, 101, 742–749. [Google Scholar] [CrossRef]
- Donmez, M.; Yemenici, O. A numerical study on centrifugal pump performance with the influence of non-Newtonian fluids. Int. J. Sci. 2019, 8, 39–45. [Google Scholar] [CrossRef]
- Shi, Y.; Zhu, J.J.; Wang, H.Y.; Zhu, H.W.; Zhang, J.C.; Zhang, H.Q. Experiments and mechanistic modeling of viscosity effect on a multistage ESP performance under viscous fluid flow. Proc. Inst. Mech. Eng. Part A J. Power Energy 2021, 235, 1976–1991. [Google Scholar] [CrossRef]
- Li, W. Effects of viscosity of fluids on centrifugal pump performance and flow pattern in the impeller. Int. J. Heat Fluid Flow 2000, 21, 207–212. [Google Scholar] [CrossRef]
- Ofuchi, E.M.; Stel, H.; Sirino, T.; Vieira, T.S.; Ponce, F.J.; Chiva, S.; Morales, R.E.M. Numerical investigation of the effect of viscosity in a multistage electric submersible pump. Eng. Appl. Comp. Fluid 2017, 11, 258–272. [Google Scholar] [CrossRef] [Green Version]
- Valdés, J.P.; Becerra, D.; Rozo, D.; Cediel, A.; Torres, F.; Asuaje, M.; Ratko-vich, N. Comparative analysis of an electrical submersible pump’s performance handling viscous Newtonian and non-Newtonian fluids through experimental and CFD approaches. J. Petrol. Sci. Eng. 2020, 187, 106749. [Google Scholar] [CrossRef]
- Sun, W.H.; Yu, Z.Y.; Zhang, K.; Liu, Z. Analysis of tip clearance effect on the transportation characteristics of a multiphase rotodynamic pump based on the non-uniform bubble model. Fluids 2022, 7, 58. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Hajmohammadi, M.R.; Salman Nourazar, S.; Campo, A. Analytical solution for two-phase flow between two rotating cylinders filled with power law liquid and a micro layer of gas. J. Mech. Sci. Technol. 2014, 28, 1849–1854. [Google Scholar] [CrossRef]
- Liu, Y.B.; Tan, L. Theoretical prediction model of tip leakage vortex in a mixed flow pump with tip clearance. J. Fluid Eng.-ASME 2020, 142, 021203. [Google Scholar] [CrossRef]
- Yu, Z.Y.; Zhang, W.W.; Zhu, B.S.; Li, Y.J. Numerical analysis for the effect of tip clearance in a low specific speed mixed-flow pump. Adv. Mech. Eng. 2019, 11, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.; Tan, L.; Cao, S.L. Influence of viscosity on energy performance and flow field of a multiphase pump. Renew. Energy 2020, 162, 1151–1160. [Google Scholar] [CrossRef]
- Simão, M.; Pérez-Sánchez, M.; Carravetta, A.; Ramos, H. Flow conditions for PATs operating in parallel: Experimental and numerical analyses. Energies 2019, 12, 901. [Google Scholar] [CrossRef] [Green Version]





| Parameter | Value |
|---|---|
| Number of impeller blades | 4 |
| Number of guide vane blades | 11 |
| Specific speed ns | 166 |
| Rotating speed n (r/min) | 2950 |
| Design head H (m) | 15 |
| Design flow rate Qd (m3/h) | 50 |
| Rotational frequency fi (Hz) | 49.2 |
| Equipment | Manufacturers | Model | Details |
|---|---|---|---|
| Axial Pump | Shandong Deep Design Pump Technology Co., Ltd. Zibo, China. | Self-designed | Shown in Table 1 |
| Want Tank | - | - | Capacity: 1.2 m3 |
| Variable Frequency Motor | Shanghai Yaqi Motor Co., Ltd. Shanghai, China. | YP-50-7.5-2 | Power: 7.5 KW Speed: 0~3000 rpm |
| Pressure Sensor | Nanjing Aire Sensor Technology Co., Ltd. Nanjing, China | AE-T | Pressure Range: −100~300 kPa Precision: ± 0.1% |
| Electromagnetic Flowmeter | Shanghai Kent Instrument Co., Ltd. Shanghai, China. | KEFA | Flowrate Range: 0~300 m3/h Precision: ± 0.2% |
| Speed and Torque Sensor | Beijing AvIC Electrical Measurement and Control Technology Co., Ltd. Beijing, China. | ZH07-100 | Speed and Torque Range: 0~6000 rpm 0~100 N·m Precision: ± 0.2% |
| Rheometer | Anton Paar Co., Ltd. Graz, Austria. | MCR | Shear Rate Range: 0.001~5000 s−1 |
| Data Acquisition Equipment | Beijing Yiyang Vibration Testing Technology Co., Ltd. Beijing, China. | YSV8016 | Frequency Range: 0~40 kHz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, W.; Yu, Z.; Zhang, W. Effect of Shear-Thinning Property on the Energy Performance and Flow Field of an Axial Flow Pump. Energies 2022, 15, 2341. https://doi.org/10.3390/en15072341
Sun W, Yu Z, Zhang W. Effect of Shear-Thinning Property on the Energy Performance and Flow Field of an Axial Flow Pump. Energies. 2022; 15(7):2341. https://doi.org/10.3390/en15072341
Chicago/Turabian StyleSun, Weihua, Zhiyi Yu, and Wenwu Zhang. 2022. "Effect of Shear-Thinning Property on the Energy Performance and Flow Field of an Axial Flow Pump" Energies 15, no. 7: 2341. https://doi.org/10.3390/en15072341
APA StyleSun, W., Yu, Z., & Zhang, W. (2022). Effect of Shear-Thinning Property on the Energy Performance and Flow Field of an Axial Flow Pump. Energies, 15(7), 2341. https://doi.org/10.3390/en15072341







