A Comparison of Multi-Criteria Decision Analysis Methods for Sustainability Assessment of District Heating Systems
Abstract
:1. Introduction
2. Materials and Methods
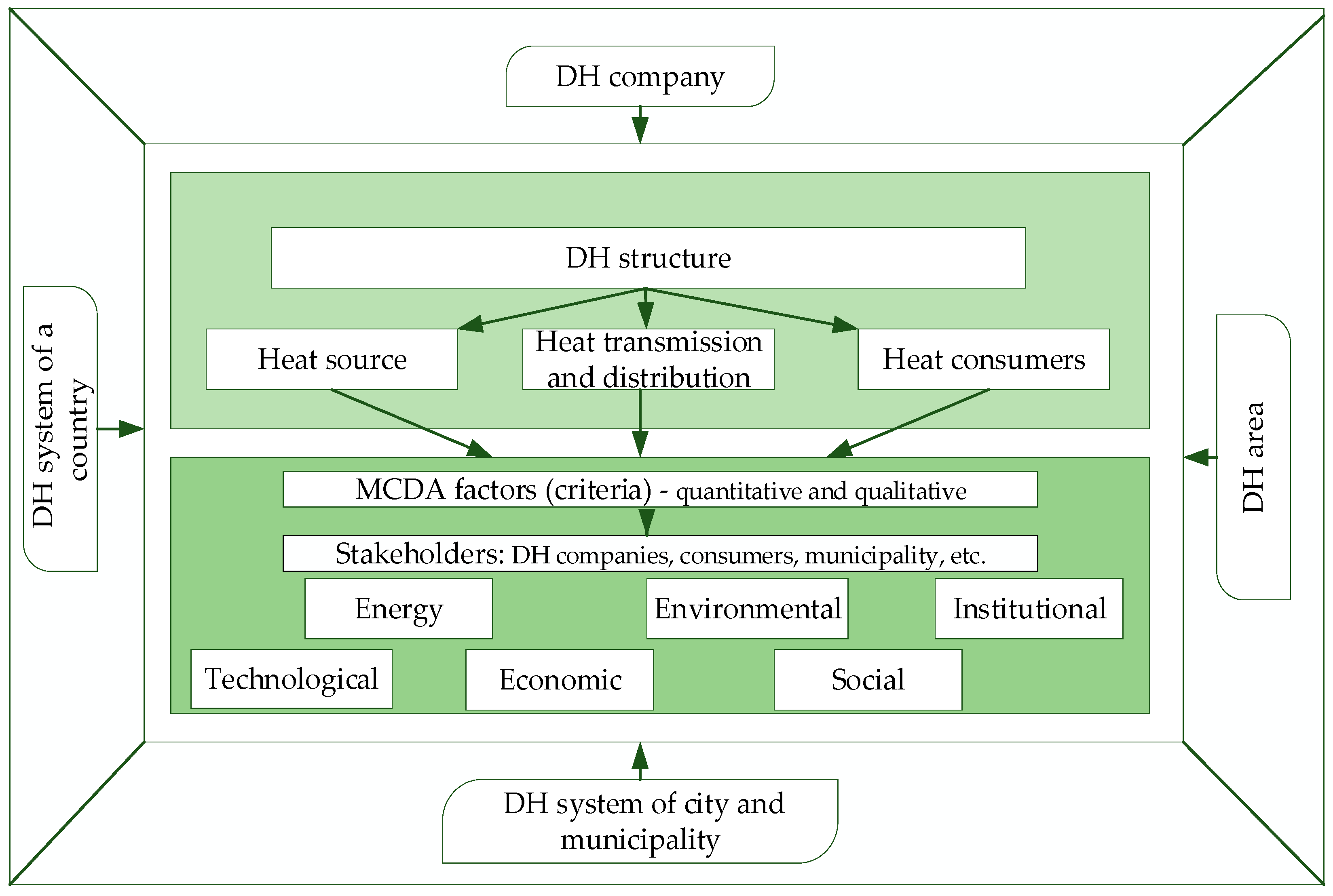
2.1. Criteria Selection
2.2. Criteria Weighting
2.3. Data Normalization
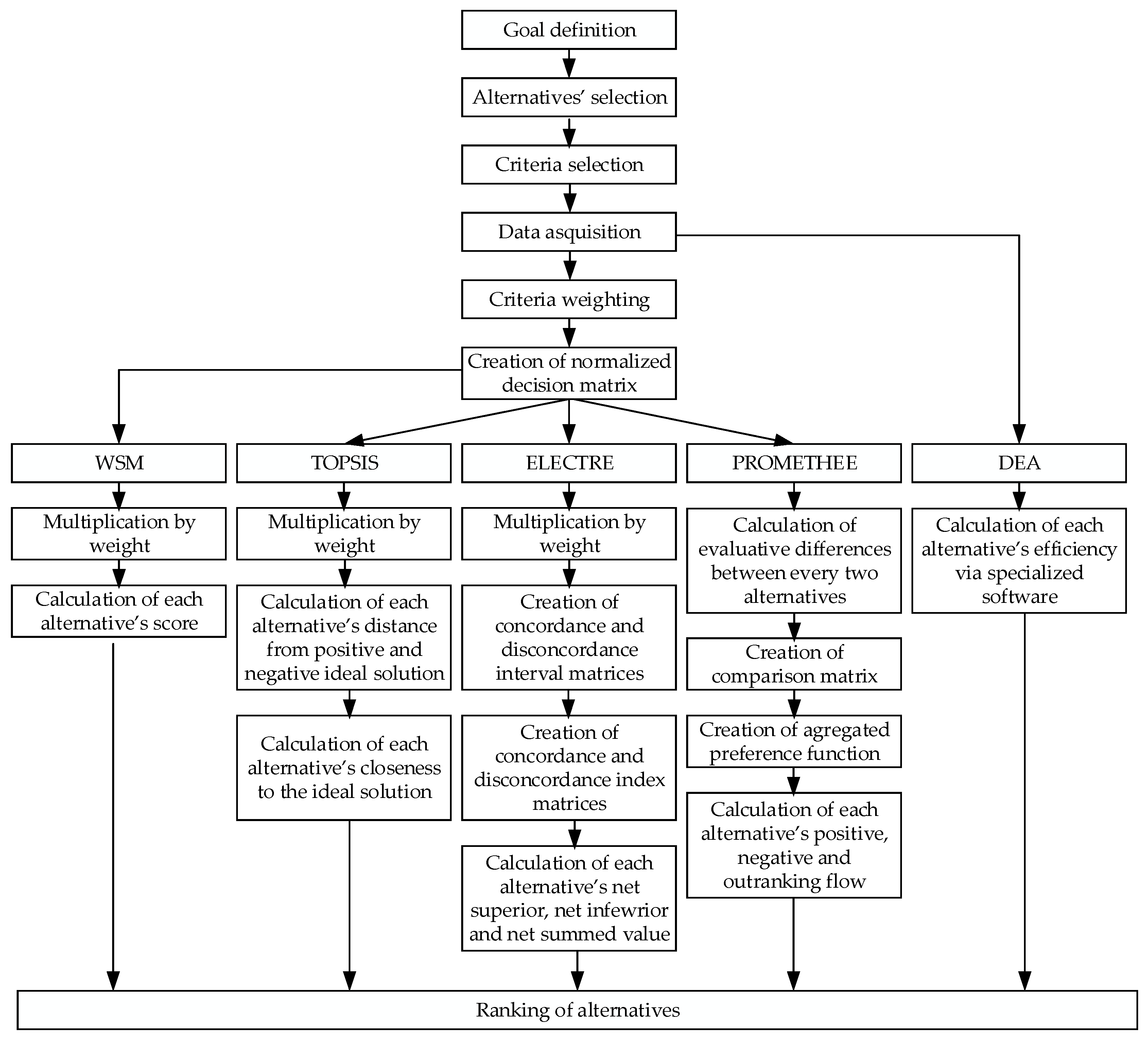
2.4. Ranking of Alternatives
2.4.1. WSM
2.4.2. TOPSIS
2.4.3. ELECTRE
2.4.4. PROMETHEE
2.4.5. DEA
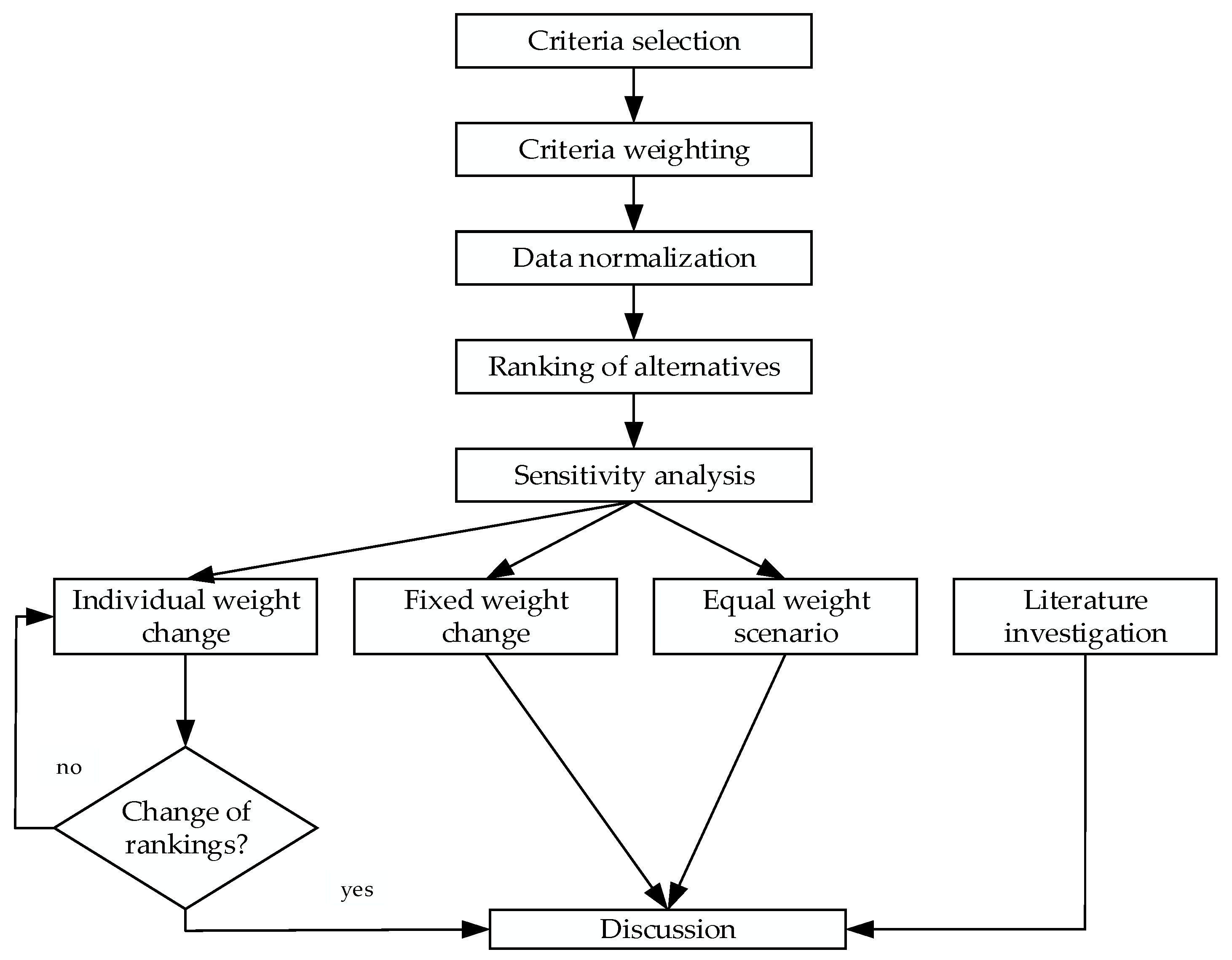
2.5. Sensitivity Analysis
2.5.1. Individual Weight Change
2.5.2. Fixed Weight Change
2.5.3. Equal Weight Method
3. Results and Discussion
3.1. The Ranking Results
3.2. Results of Sensitivity Analysis
3.2.1. Individual Weight Change
3.2.2. Fixed Weight Change
3.2.3. Equal Weight Method
3.3. Results of MCDA Methods’ Comparative Assessment
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- United Nation. Transforming Our World: The 2030 Agenda for Sustainable Development. Available online: https://sdgs.un.org/publications/transforming-our-world-2030-agenda-sustainable-development-17981 (accessed on 18 March 2022).
- Wang, J.J.; Jing, Y.Y.; Zhang, C.F.; Zhao, J.H. Review on multi-criteria decision analysis aid in sustainable energy decision-making. Renew. Sustain. Energy Rev. 2009, 13, 2263–2278. [Google Scholar] [CrossRef]
- Mart, M.; Dias, L.C.; Quinteiro, P.; Freire, F.; Cl, A. Multi-Criteria and Life Cycle Assessment of Wood-Based Bioenergy Alternatives for Residential Heating: A Sustainability Analysis. Energies 2019, 12, 4391. [Google Scholar] [CrossRef] [Green Version]
- Kolios, A.; Mytilinou, V.; Lozano-Minguez, E. A Comparative Study of Multiple-Criteria Decision-Making Methods under Stochastic Inputs. Energies 2016, 9, 566. [Google Scholar] [CrossRef] [Green Version]
- Marguerite, C.; Andresen, G.B.; Dahl, M. Multi-criteria analysis of storages integration and operation solutions into the district heating network of Aarhus—A simulation case study. Energy 2018, 158, 81–88. [Google Scholar] [CrossRef]
- Ziemele, J.; Talcis, N.; Osis, U.; Dace, E. A methodology for selecting a sustainable development strategy for connecting low heat density consumers to a district heating system by cascading of heat carriers. Energy 2021, 230, 120776. [Google Scholar] [CrossRef]
- Ziemele, J.; Pakere, I.; Talcis, N.; Blumberga, D. Multi-criteria Analysis of District Heating Systems in Baltic States. Energy Procedia 2014, 61, 2172–2175. [Google Scholar] [CrossRef] [Green Version]
- Vasić, G. Application of multi criteria analysis in the design of energy policy: Space and water heating in households—City Novi Sad, Serbia. Energy Policy 2018, 113, 410–419. [Google Scholar] [CrossRef]
- Siksnelyte-Butkiene, I.; Streimikiene, D.; Balezentis, T. Multi-criteria analysis of heating sector sustainability in selected North European countries. Sustain. Cities Soc. 2021, 69, 102826. [Google Scholar] [CrossRef]
- EC Smart Cities. Available online: https://ec.europa.eu/info/eu-regional-and-urban-development/topics/cities-and-urban-development/city-initiatives/smart-cities_en (accessed on 18 March 2022).
- Hiltunen, P.; Syri, S. Low-temperature waste heat enabling abandoning coal in Espoo district heating system. Energy 2021, 231, 120916. [Google Scholar] [CrossRef]
- Andrés, M.; Regidor, M.; Macía, A.; Vasallo, A.; Lygnerud, K. Assessment methodology for urban excess heat recovery solutions in energy-efficient District Heating Networks. Energy Procedia 2018, 149, 39–48. [Google Scholar] [CrossRef]
- European Smart Cities. Available online: http://www.smart-cities.eu/ (accessed on 15 March 2022).
- Lund, H.; Werner, S.; Wiltshire, R.; Svendsen, S.; Thorsen, J.E.; Hvelplund, F.; Mathiesen, B.V. 4th Generation District Heating (4GDH): Integrating smart thermal grids into future sustainable energy systems. Energy 2014, 68, 1–11. [Google Scholar] [CrossRef]
- Buffa, S.; Cozzini, M.; D’Antoni, M.; Baratieri, M.; Fedrizzi, R. 5th generation district heating and cooling systems: A review of existing cases in Europe. Renew. Sustain. Energy Rev. 2019, 104, 504–522. [Google Scholar] [CrossRef]
- Kinelski, G.; Stęchły, J.; Sienicki, A.; Czornik, K.; Borkowski, P. Application of Smart Technologies in Metropolis GZM to Reduce Harmful Emissions in District Heating Systems. Energies 2021, 14, 7665. [Google Scholar] [CrossRef]
- Wu, Z.; You, S.; Zhang, H.; Wang, Y.; Jiang, Y.; Liu, Z.; Sha, L.; Wei, S. Experimental investigations and multi-objective optimization of an air-source absorption heat pump for residential district heating. Energy Convers. Manag. 2021, 240, 114267. [Google Scholar] [CrossRef]
- Kandakoglu, A.; Frini, A.; Ben Amor, S. Multicriteria decision making for sustainable development: A systematic review. J. Multi-Criteria Decis. Anal. 2019, 26, 202–251. [Google Scholar] [CrossRef]
- Rigo, P.D.; Rediske, G.; Rosa, C.B.; Gastaldo, N.G.; Michels, L.; Júnior, A.L.N.; Siluk, J.C.M. Renewable energy problems: Ex-ploring the methods to support the decision-making process. Sustainability 2020, 12, 195. [Google Scholar] [CrossRef]
- DorotiĆ, H.; Pukšec, T.; Duić, N. Economical, environmental and exergetic multi-objective optimization of district heating systems on hourly level for a whole year. Appl. Energy 2019, 251, 113394. [Google Scholar] [CrossRef]
- Di Somma, M.; Graditi, G.; Mongibello, L.; Bertini, I.; Puglisi, G. Trade-Off Solutions between Economy and CO2 Emissions for the Daily Operation of a Distributed Energy System: A Real Case Study in Italy. In Proceedings of the 2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Palermo, Italy, 12–15 June 2018. [Google Scholar] [CrossRef]
- Arslan, A.E.; Arslan, O.; Kandemir, S.Y. AHP–TOPSIS hybrid decision-making analysis: Simav integrated system case study. J. Therm. Anal. Calorim. 2021, 145, 1191–1202. [Google Scholar] [CrossRef]
- Zhao, J.; Li, Y.; Li, J.; Li, Z. Operation Characteristic Analysis and Parameter Optimization of District Heating Network with Double Heat Sources. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2021; Volume 772, p. 012077. [Google Scholar] [CrossRef]
- Laktuka, K.; Pakere, I.; Lauka, D.; Blumberga, D.; Volkova, A. Long-term policy recommendations for improving the efficiency of heating and cooling. Environ. Clim. Technol. 2021, 25, 392–404. [Google Scholar] [CrossRef]
- Stennikov, V.; Postnikov, I.; Edeleva, O. Methodology of indicative analysis to determine the municipal units for implementation of the energy-saving strategy. Environ. Clim. Technol. 2020, 24, 115–123. [Google Scholar] [CrossRef]
- Pakere, I.; Blumberga, D. Solar power or solar heat: What will upraise the efficiency of district heating? Multi-criteria analyses approach. Energy 2020, 198, 117291. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, Y.; You, S.; Zhang, H.; Zheng, X.; Guo, J.; Wei, S. Thermo-economic analysis of composite district heating substation with absorption heat pump. Appl. Therm. Eng. 2020, 166, 114659. [Google Scholar] [CrossRef]
- Polikarpova, I.; Lauka, D.; Blumberga, D.; Vigants, E. Multi-Criteria Analysis to Select Renewable Energy Solution for District Heating System. Environ. Clim. Technol. 2019, 23, 101–109. [Google Scholar] [CrossRef] [Green Version]
- Prodanuks, T.; Blumberga, D. Methodology of municipal energy plans. Priorities for sustainability. Energy Procedia 2018, 147, 594–599. [Google Scholar] [CrossRef]
- Ziemele, J.; Pakere, I.; Blumberga, D. The future competitiveness of the non-Emissions Trading Scheme district heating systems in the Baltic States q. Appl. Energy 2016, 162, 1579–1585. [Google Scholar] [CrossRef]
- Ziemele, J.; Vigants, G.; Vitolins, V.; Blumberga, D.; Veidenbergs, I. District heating systems performance analyses. Heat energy tariff. Environ. Clim. Technol. 2014, 13, 32–43. [Google Scholar] [CrossRef]
- Boran, F.E. A Multidimensional Analysis to Evaluate District Heating Systems. Energy Sources Part B Econ. Plan. Policy 2013, 8, 122–129. [Google Scholar] [CrossRef]
- Grujić, M.; Ivezić, D.; Živković, M. Application of multi-criteria decision-making model for choice of the optimal solution for meeting heat demand in the centralized supply system in Belgrade. Energy 2014, 67, 341–350. [Google Scholar] [CrossRef]
- Fang, F.; Wang, N. Optimal hierarchical decision-making for heat source selection of district heating systems. Math. Probl. Eng. 2014, 2014, 594862. [Google Scholar] [CrossRef] [Green Version]
- Ghafghazi, S.; Sowlati, T.; Sokhansanj, S.; Melin, S. A multicriteria approach to evaluate district heating system options. Appl. Energy 2010, 87, 1134–1140. [Google Scholar] [CrossRef]
- Ziemele, J.; Gravelsins, A.; Blumberga, A.; Blumberga, D. Sustainability of heat energy tariff in district heating system: Statistic and dynamic methodologies. Energy 2017, 137, 834–845. [Google Scholar] [CrossRef]
- Agrell, P.J.; Bogetoft, P. Endogenous Common Weights as a Collusive Instrument in Frontier-Based Regulation. Int. Ser. Oper. Res. Manag. Sci. 2016, 249, 181–194. [Google Scholar] [CrossRef]
- Hatami-Marbini, A.; Rostamy-Malkhalifeh, M.; Agrell, P.J.; Tavana, M.; Mohammadi, F. Extended symmetric and asymmetric weight assignment methods in data envelopment analysis. Comput. Ind. Eng. 2015, 87, 621–631. [Google Scholar] [CrossRef]
- Saati, S.; Hatami-Marbini, A.; Agrell, P.J.; Tavana, M. A common set of weight approach using an ideal decision making unit in data envelopment analysis. J. Ind. Manag. Optim. 2012, 8, 623–637. [Google Scholar] [CrossRef]
- Lygnerud, K.; Peltola-Ojala, P. Factors impacting district heating companies’ decision to provide small house customers with heat. Appl. Energy 2010, 87, 185–190. [Google Scholar] [CrossRef]
- Munksgaard, J.; Pade, L.L.; Fristrup, P. Efficiency gains in Danish district heating. Is there anything to learn from benchmarking? Energy Policy 2005, 33, 1986–1997. [Google Scholar] [CrossRef]
- Wen, Q.; Liu, G.; Wu, W.; Liao, S. Multicriteria comprehensive evaluation framework for industrial park-level distributed energy system considering weights uncertainties. J. Clean. Prod. 2021, 282, 124530. [Google Scholar] [CrossRef]
- Wen, Q.; Yan, Q.; Qu, J.; Liu, Y. Fuzzy Ensemble of Multi-Criteria Decision Making Methods for Heating Energy Transition in Danish Households. Mathematics 2021, 9, 2420. [Google Scholar] [CrossRef]
- Abokersh, M.H.; Gangwar, S.; Spiekman, M.; Vallès, M.; Jiménez, L.; Boer, D. Sustainability insights on emerging solar district heating technologies to boost the nearly zero energy building concept. Renew. Energy 2021, 180, 893–913. [Google Scholar] [CrossRef]
- Dénarié, A.; Muscherà, M.; Calderoni, M.; Motta, M. Industrial excess heat recovery in district heating: Data assessment methodology and application to a real case study in Milano, Italy. Energy 2019, 166, 170–182. [Google Scholar] [CrossRef]
- Fitó, J.; Ramousse, J.; Hodencq, S.; Wurtz, F. Energy, exergy, economic and exergoeconomic (4E) multicriteria analysis of an industrial waste heat valorization system through district heating. Sustain. Energy Technol. Assess. 2020, 42, 100894. [Google Scholar] [CrossRef]
- Hirsch, P.; Grochowski, M.; Duzinkiewicz, K. Decision support system for design of long distance heat transportation system. Energy Build. 2018, 173, 378–388. [Google Scholar] [CrossRef]
- Kirppu, H.; Lahdelma, R.; Salminen, P. Multicriteria evaluation of carbon-neutral heat-only production technologies for district heating. Appl. Therm. Eng. 2018, 130, 466–476. [Google Scholar] [CrossRef] [Green Version]
- Lipošćak, M.; Afgan, N.H.; Duić, N.; da Graça Carvalho, M. Sustainability assessment of cogeneration sector development in Croatia. Energy 2006, 31, 2276–2284. [Google Scholar] [CrossRef]
- Loikkanen, O.; Lahdelma, R.; Salminen, P. Multicriteria evaluation of sustainable energy solutions for Colosseum. Sustain. Cities Soc. 2017, 35, 289–297. [Google Scholar] [CrossRef]
- Mabrouk, M.T.; Haurant, P.; Dessarthe, V.; Meyer, P.; Lacarrière, B. Combining a dynamic simulation tool and a multi-criteria decision aiding algorithm for improving existing District Heating. Energy Procedia 2018, 149, 266–275. [Google Scholar] [CrossRef]
- Marinakis, V.; Doukas, H.; Xidonas, P.; Zopounidis, C. Multicriteria decision support in local energy planning: An evaluation of alternative scenarios for the Sustainable Energy Action Plan. Omega 2017, 69, 1–16. [Google Scholar] [CrossRef]
- Özdemir, E.D.; Härdtlein, M.; Jenssen, T.; Zech, D.; Eltrop, L. A confusion of tongues or the art of aggregating indicators—Reflections on four projective methodologies on sustainability measurement. Renew. Sustain. Energy Rev. 2011, 15, 2385–2396. [Google Scholar] [CrossRef]
- Pinto, G.; Abdollahi, E.; Capozzoli, A.; Savoldi, L.; Lahdelma, R. Optimization and Multicriteria Evaluation of Carbon-neutral Technologies for District Heating. Energies 2019, 12, 1653. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Duanmu, L.; Lahdelma, R.; Li, X. A fuzzy-grey multicriteria decision making model for district heating system. Appl. Therm. Eng. 2018, 128, 1051–1061. [Google Scholar] [CrossRef]
- Wang, H.; Duanmu, L.; Lahdelma, R.; Li, X. Developing a multicriteria decision support framework for CHP based combined district heating systems. Appl. Energy 2017, 205, 345–368. [Google Scholar] [CrossRef]
- Selvakkumaran, S.; Axelsson, L.; Svensson, I.-L. Drivers and barriers for prosumer integration in the Swedish district heating sector. Energy Rep. 2021, 7, 193–202. [Google Scholar] [CrossRef]
- Krumm, A.; Süsser, D.; Blechinger, P. Modelling social aspects of the energy transition: What is the current representation of social factors in energy models? Energy 2022, 239, 121706. [Google Scholar] [CrossRef]
- Socorro García-Cascales, M.; Teresa Lamata, M.; Miguel Sánchez-Lozano, J. Evaluation of photovoltaic cells in a multi-criteria decision making process. Ann. Oper. Res. 2012, 199, 373–391. [Google Scholar] [CrossRef]
- Xu, B.; Nayak, A.; Gray, D.; Ouenniche, J. Assessing energy business cases implemented in the North Sea Region and strategy recommendations. Appl. Energy 2016, 172, 360–371. [Google Scholar] [CrossRef]
- Murry, J.W.; Hammons, J.O. Delphi: A Versatile Methodology for Conducting Qualitative Research. Rev. High. Educ. 1995, 18, 423–436. [Google Scholar] [CrossRef]
- Dace, E.; Blumberga, D. How do 28 European Union Member States perform in agricultural greenhouse gas emissions? It depends on what we look at: Application of the multi-criteria analysis. Ecol. Indic. 2016, 71, 352–358. [Google Scholar] [CrossRef]
- European Parliament, Council of the European Union. EC Directive 2012/27/EU of the European Parliament and of the Council of 25 October 2012 on energy efficiency, amending Directives 2009/125/EC and 2010/30/EU and repealing Directives 2004/8/EC and 2006/32/EC. Off. J. Eur. Union 2012, L315, 1–56. [Google Scholar]
- Rita, M.; Assumpc, P. Techniques to model uncertain input data of multi-criteria decision-making problems: A literature review Techniques to model uncertain input data of multi-criteria decision-making problems: A literature review. Int. Trans. Oper. Res. 2018, 28, 523–559. [Google Scholar] [CrossRef]
- Saaty, T.L. Analytic Hierarchy Process. In Encyclopedia of Biostatistics; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2005. [Google Scholar] [CrossRef]
- Goepel, K.D. Implementation of an Online Software Tool for the Analytic Hierarchy Process-Challenges and Practical Experiences. Int. J. Anal. Hierarchy Process 2017, 10, 469–487. [Google Scholar]
- Behzadian, M.; Khanmohammadi Otaghsara, S.; Yazdani, M.; Ignatius, J. A state-of the-art survey of TOPSIS applications. Expert Syst. Appl. 2012, 39, 13051–13069. [Google Scholar] [CrossRef]
- Vafaei, N.; Ribeiro, R.A.; Camarinha-Matos, L.M. Data normalisation techniques in decision making: Case study with TOPSIS method. Int. J. Inf. Decis. Sci. 2018, 10, 19–38. [Google Scholar] [CrossRef]
- Sałabun, W.; Watróbski, J.; Shekhovtsov, A. Are MCDA methods benchmarkable? A comparative study of TOPSIS, VIKOR, COPRAS, and PROMETHEE II methods. Symmetry 2020, 12, 1549. [Google Scholar] [CrossRef]
- Chakraborty, S.; Yeh, C.H. A simulation comparison of normalization procedures for TOPSIS. In Proceedings of the 2009 International Conference on Computers & Industrial Engineering, Troyes, France, 6–9 July 2009; pp. 1815–1820. [Google Scholar] [CrossRef]
- Chakraborty, S. A Simulation Based Comparative Study of Normalization Procedures in Multiattribute Decision Making. In Proceedings of the 6th WSEAS International Conference on Artificial Intelligence, Knowledge Engineering and Data Bases, Corfu Island, Greece, 16–19 February 2007; pp. 102–109. [Google Scholar]
- Sałabun, W. The mean error estimation of TOPSIS method using a fuzzy reference models. J. Theor. Appl. Comput. Sci. 2013, 7, 40–50. [Google Scholar]
- Dace, E.; Blumberga, D. Selecting a Catalyst for Methanation Process: Technical and Economic Performance Based TOPSIS Analysis. In Proceedings of the 27th International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems, Turku, Finland, 15–19 June 2014. [Google Scholar]
- Lee, H.C.; Chang, C. Ter Comparative analysis of MCDM methods for ranking renewable energy sources in Taiwan. Renew. Sustain. Energy Rev. 2018, 92, 883–896. [Google Scholar] [CrossRef]
- He, L.; Shen, J.; Zhang, Y. Ecological vulnerability assessment for ecological conservation and environmental management. J. Environ. Manag. 2018, 206, 1115–1125. [Google Scholar] [CrossRef]
- Omran, I.I.; Al-Saati, N.H.; Al-Saati, H.H.; Hashim, K.S.; Al-Saati, Z.N. Sustainability assessment of wastewater treatment techniques in urban areas of iraq using multi-criteria decision analysis (Mcda). Water Pract. Technol. 2021, 16, 648–660. [Google Scholar] [CrossRef]
- Velasquez, M.; Hester, P. An analysis of multi-criteria decision making methods. Int. J. Oper. Res. 2013, 10, 56–66. [Google Scholar]
- Pang, J.; Zhang, G.; Chen, G. ELECTRE I decision model of reliability design scheme for computer numerical control machine. J. Softw. 2011, 6, 894–900. [Google Scholar] [CrossRef]
- Chatterjee, P.; Athawale, V.M.; Chakraborty, S. Selection of industrial robots using compromise ranking and outranking methods. Robot. Comput. Integr. Manuf. 2010, 26, 483–489. [Google Scholar] [CrossRef]
- Behzadian, M.; Kazemzadeh, R.B.; Albadvi, A.; Aghdasi, M. PROMETHEE: A comprehensive literature review on methodologies and applications. Eur. J. Oper. Res. 2010, 200, 198–215. [Google Scholar] [CrossRef]
- Scheel, H. Efficiency Measurement System Users Manual; Version 1.3; Universität D. EMS: Dortmund, Germany, 2000. [Google Scholar]
- Li, P.; Qian, H.; Wu, J.; Chen, J. Sensitivity analysis of TOPSIS method in water quality assessment: I. Sensitivity to the parameter weights. Environ. Monit. Assess. 2013, 185, 2453–2461. [Google Scholar] [CrossRef] [PubMed]
- Yatsalo, B.; Didenko, V.; Gritsyuk, S.; Sullivan, T. Decerns: A Framework for Multi-Criteria Decision Analysis. Int. J. Comput. Intell. Syst. 2015, 8, 467–489. [Google Scholar] [CrossRef] [Green Version]
- Ros, C.J.; Mateu, A.V.; Isern, L.M. Introduction to Decision Deck-Diviz: Examples and User Guide. Available online: https://www.diviz.org/_static/ReportDecisionDeck-DEIM-URV.pdf (accessed on 18 March 2022).
- Brans, J.P.; De Smet, Y. PROMETHEE methods. Int. Ser. Oper. Res. Manag. Sci. 2016, 233, 187–219. [Google Scholar] [CrossRef]
- Zanakis, S.H.; Solomon, A.; Wishart, N.; Dublish, S. Multi-attribute decision making: A simulation comparison of select methods. Eur. J. Oper. Res. 1998, 107, 507–529. [Google Scholar] [CrossRef]
- Triantaphyllou, E.; Baig, K. The impact of aggregating benefit and cost criteria in four MCDA methods. IEEE Trans. Eng. Manag. 2005, 52, 213–226. [Google Scholar] [CrossRef]
- Cinelli, M.; Coles, S.R.; Kirwan, K. Analysis of the potentials of multi criteria decision analysis methods to conduct sustainability assessment. Ecol. Indic. 2014, 46, 138–148. [Google Scholar] [CrossRef] [Green Version]





| Criterion | Environmental | Economic | Technological | Institutional | ||||
|---|---|---|---|---|---|---|---|---|
| CO2 Emissions, kgCO2/MWh | Share of RES, % | Heat Tariff, €/MWh | Installed Capacity Utilization Rate, % | Heat Losses, % | Average Supply Water Temperature, °C | Produced Heat in Cogene-Ration, % | Heat Consumption of Buildings, kWh/m2 | |
| Criterion Type | min | max | min | max | min | min | max | min |
| DHC 1 | 223.71 | 0.04 | 52.14 | 21.74 | 17.14 | 120.00 | 22.39 | 189.02 |
| DHC 2 | 209.32 | 1.44 | 50.53 | 10.23 | 16.46 | 120.00 | 27.84 | 176.28 |
| DHC 3 | 181.82 | 0.13 | 58.94 | 15.58 | 10.00 | 90.00 | 21.41 | 168.97 |
| DHC 4 | 144.33 | 30.83 | 44.39 | 16.66 | 9.55 | 120.00 | 18.65 | 162.34 |
| DHC 5 | 84.88 | 61.97 | 54.95 | 15.18 | 15.92 | 90.00 | 46.62 | 136.00 |
| DHC 6 | 44.41 | 79.38 | 60.70 | 4.85 | 14.40 | 100.00 | 1.36 | 151.40 |
| DHC 7 | 55.08 | 80.00 | 55.24 | 23.73 | 8.76 | 63.68 | 0.00 | 156.85 |
| DHC 8 | 45.86 | 80.04 | 51.73 | 28.27 | 16.83 | 75.95 | 97.37 | 143.79 |
| DHC 9 | 49.25 | 87.10 | 54.90 | 19.91 | 9.20 | 90.00 | 5.70 | 120.18 |
| DHC 10 | 3.13 | 99.00 | 49.80 | 30.48 | 18.54 | 100.00 | 49.09 | 129.03 |
| DHC 11 | 0.00 | 100.00 | 61.55 | 93.88 | 13.09 | 90.00 | 0.00 | 162.47 |
| DHC 12 | 0.00 | 100.00 | 53.49 | 92.59 | 24.78 | 90.00 | 100.00 | 168.87 |
| Criterion weight, % | 14.54 | 11.59 | 17.06 | 14.12 | 16.90 | 7.18 | 6.00 | 12.60 |
| WSM | DHC 10 > DHC 9 > DHC 8 > DHC 12 > DHC 11 > DHC 7 | >DHC 5 > DHC 4 > DHC 6 > DHC 3 > DHC 2 > DHC 1 |
| TOPSIS | DHC 10 > DHC 9 > DHC 8 > DHC 7 > DHC 11 > DHC 12 | >DHC 4 > DHC 5 > DHC 6 > DHC 3 > DHC 2 > DHC 1 |
| ELECTRE | DHC 9 > DHC 10 > DHC 8 > DHC 11 > DHC 7 > DHC 12 | >DHC 4 > DHC 5 > DHC 6 > DHC 3 > DHC 2 > DHC 1 |
| PROMETHEE | DHC 10 > DHC 9 > DHC 8 > DHC 12 > DHC 11 > DHC 7 | >DHC 5 > DHC 4 > DHC 6 > DHC 3 > DHC 2 > DHC 1 |
| DEA | DHC 12 > DHC 11 > DHC 8 > DHC 10 > DHC 9 > DHC 7 | >DHC 6 > DHC 5 > DHC 4 > DHC 3 > DHC 1 > DHC 2 |
| MCDA Method | WSM | TOPSIS | ELECTRE | PROMETHEE | DEA | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| MCDA Result | Score | % | Closeness Value | % | Net Value | % | Phi Value | % | Efficiency | % |
| DHC 1 | 0.21 | 0 | 0.30 | 0 | −11.78 | 0 | −0.31 | 0 | 33 | 1 |
| DHC 2 | 0.26 | 10 | 0.34 | 12 | −8.73 | 15 | −0.26 | 10 | 31 | 0 |
| DHC 3 | 0.31 | 23 | 0.38 | 26 | −8.02 | 19 | −0.20 | 23 | 48 | 4 |
| DHC 4 | 0.50 | 66 | 0.54 | 78 | 2.22 | 70 | 0.00 | 66 | 53 | 5 |
| DHC 5 | 0.50 | 66 | 0.49 | 62 | −2.65 | 46 | 0.01 | 66 | 71 | 9 |
| DHC 6 | 0.42 | 48 | 0.45 | 47 | −7.11 | 23 | −0.08 | 48 | 77 | 11 |
| DHC 7 | 0.59 | 88 | 0.58 | 88 | 4.97 | 84 | 0.11 | 88 | 116 | 20 |
| DHC 8 | 0.62 | 95 | 0.58 | 91 | 5.75 | 88 | 0.14 | 95 | 143 | 26 |
| DHC 9 | 0.64 | 98 | 0.61 | 99 | 8.10 | 100 | 0.15 | 98 | 124 | 22 |
| DHC 10 | 0.65 | 100 | 0.61 | 100 | 5.92 | 89 | 0.17 | 100 | 126 | 22 |
| DHC 11 | 0.61 | 92 | 0.57 | 86 | 5.48 | 87 | 0.13 | 92 | 192 | 38 |
| DHC 12 | 0.62 | 93 | 0.55 | 79 | 2.66 | 73 | 0.13 | 93 | 460 | 100 |
| WSM | TOPSIS | ELECTRE | PROMETHEE | ||||
|---|---|---|---|---|---|---|---|
| Equal Weights | AHP Weights | Equal Weights | AHP Weights | Equal Weights | AHP Weights | Equal Weights | AHP Weights |
| DHC 12 | DHC 12 | DHC 12 | DHC 12 | DHC 12 | DHC 12 | DHC 12 | DHC 12 |
| DHC 11 | DHC 11 | DHC 11 | DHC 11 | DHC 11 | DHC 11 | DHC 11 | DHC 11 |
| DHC 10 | DHC 10 | DHC 10 | DHC 10 | DHC 10 | DHC 10 | DHC 10 | DHC 10 |
| DHC 8 | DHC 8 | DHC 8 | DHC 7 | DHC 7 | DHC 7 | DHC 8 | DHC 8 |
| DHC 7 | DHC 7 | DHC 7 | DHC 8 | DHC 8 | DHC 8 | DHC 7 | DHC 7 |
| DHC 9 | DHC 9 | DHC 9 | DHC 9 | DHC 9 | DHC 9 | DHC 9 | DHC 9 |
| DHC 6 | DHC 6 | DHC 5 | DHC 4 | DHC 6 | DHC 5 | DHC 6 | DHC 6 |
| DHC 1 | DHC 3 | DHC 1 | DHC 3 | DHC 1 | DHC 3 | DHC 1 | DHC 3 |
| DHC 4 | DHC 2 | DHC 4 | DHC 2 | DHC 4 | DHC 1 | DHC 4 | DHC 2 |
| DHC 3 | DHC 1 | DHC 3 | DHC 1 | DHC 2 | DHC 2 | DHC 3 | DHC 1 |
| DHC 5 | DHC 5 | DHC 6 | DHC 5 | DHC 5 | DHC 4 | DHC 5 | DHC 5 |
| DHC 2 | DHC 4 | DHC 2 | DHC 6 | DHC 3 | DHC 6 | DHC 2 | DHC 4 |
| WSM | TOPSIS | ELECTRE | PROMETHEE | DEA | |
|---|---|---|---|---|---|
| Simplicity of calculations | |||||
| Weighting | Required | Required | Required | Required | Not required |
| Normalization | Required | Required | Required | Required | Not required |
| Number of steps | 3 | 4 | 11 | 8 | Not assessed |
| Ease of automation for sensitivity analysis | Easy | Easy | High difficulty | Medium difficulty | High difficulty |
| Overall simplicity | Very easy | Easy | High difficulty | Medium difficulty | High difficulty |
| Results | |||||
| Result interpretation difficulty | High difficulty | High difficulty | Easy (negative and positive values) | Easy (negative and positive values) | High difficulty |
| Robustness | |||||
| Can ranks reverse if an alternative is deleted? | No, by design | No, by design | Yes, by design | Yes, by design | Yes, by design |
| Relationship between low and high criteria values | |||||
| Does a low criteria value get compensated by a high criteria value? | Yes, by increasing the alternatives’ final value | Yes, by increasing the alternatives’ final value | Yes, by outranking principles | Yes, by outranking principles | Yes, by increasing the alternatives’ final value |
| Can an alternative with one lowest criterion value be the leader? | Yes | Yes | No | No | Yes |
| Availability of free and documented software | Not needed | Yes (e.g., DecernsMCDA [83]) | Yes (e.g., Decision Deck [84]) | Yes (e.g., Visual PROMETHEE [85]) | Yes (e.g., EMS [81]) |
| Popularity | |||||
| In the field of DH (number of papers) | Not widely used (2) | Most popular (12) | Least popular (1) | Not widely used (3) | Fairly popular (7) |
| Additional properties | Rank reversals when the number of criteria is low [86] | Rank reversals when the number of criteria is high [86]; arbitrary definition of threshold values | Different preference functions can lead to different outcomes; arbitrary definition of threshold values | Does not fare well with imprecise data | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Daugavietis, J.E.; Soloha, R.; Dace, E.; Ziemele, J. A Comparison of Multi-Criteria Decision Analysis Methods for Sustainability Assessment of District Heating Systems. Energies 2022, 15, 2411. https://doi.org/10.3390/en15072411
Daugavietis JE, Soloha R, Dace E, Ziemele J. A Comparison of Multi-Criteria Decision Analysis Methods for Sustainability Assessment of District Heating Systems. Energies. 2022; 15(7):2411. https://doi.org/10.3390/en15072411
Chicago/Turabian StyleDaugavietis, Janis Edmunds, Raimonda Soloha, Elina Dace, and Jelena Ziemele. 2022. "A Comparison of Multi-Criteria Decision Analysis Methods for Sustainability Assessment of District Heating Systems" Energies 15, no. 7: 2411. https://doi.org/10.3390/en15072411
APA StyleDaugavietis, J. E., Soloha, R., Dace, E., & Ziemele, J. (2022). A Comparison of Multi-Criteria Decision Analysis Methods for Sustainability Assessment of District Heating Systems. Energies, 15(7), 2411. https://doi.org/10.3390/en15072411








