Spatial-Temporal Pattern and Driving Factors of Carbon Efficiency in China: Evidence from Panel Data of Urban Governance
Abstract
:1. Introduction
2. Methods
2.1. Environmental Production Technology
2.2. Super-Efficiency SBM Model
2.3. ESDA Method
2.4. Dynamic Spatial Dubin Model
3. Data Sources and Variable Selection
3.1. Input–Output Variables
3.2. Driving Factors of CE
- (1)
- Economic development () is measured using the logarithm of per capita GDP. According to environmental Kuznets curve (EKC) hypothesis, there is an inverted U-shaped relationship between income and environmental pollution. An increasing number of studies have verified the nonlinear relationship between economic growth and CE [61]. Therefore, the per capita GDP and its square term () are both introduced to the model.
- (2)
- Foreign trade () is expressed as the proportion of total imports and exports to GDP. A large number of studies have shown that foreign trade is conducive to improving productivity and energy utilization and reducing the negative impact on the environment [42,62,63,64,65]. However, many studies have also verified the hypothesis of “pollution paradise” [66,67,68].
- (3)
- Environmental regulation (). Following the method of Ren et al. [69], we build a comprehensive environmental regulation index based on five indicators: sulfur dioxide removal rate, soot removal rate, comprehensive utilization rate of industrial solid waste, domestic sewage treatment rate, and harmless treatment of domestic waste. According to the “green paradox” [70], strengthening environmental regulation is not conducive to the improvement in CE. A number of studies have also proved this conclusion [71,72,73]. However, the continuous improvement in environmental regulation will increase the production cost of enterprises, and then force enterprises to improve energy utilization, which will lead to the growth of CE [74,75,76,77,78].
- (4)
- Industrial structure () is measured using the proportion of secondary industry output value to GDP. Compared with the primary and tertiary industries, the energy consumption of secondary industry is higher and will, thus, lead to higher CO2 emissions.
- (5)
- Industrial structure upgrading (). To alleviate the negative impact of industrial structure on environmental efficiency, industrial structure upgrading is vital. Existing studies generally believe in the positive effect of industrial structure upgrading on environmental efficiency [79,80,81]. Referring to Wu [82], we adopt the ratio of tertiary industry output value to secondary industry output value to measure the industrial structure upgrading.
- (6)
- Population density () is expressed as the logarithm of the average number of residents per square kilometer of urban area. Higher population density may increase energy consumption and worsen environmental quality [83]; however, it is also conducive to the realization of the scale effect through the sharing of public infrastructure to reduce per capita carbon emissions [84,85].
- (7)
- (8)
- Technological progress (). Technological progress is conducive to improving the productivity and clean technology level to improve the CE. The significant positive effects of technological progress on environmental efficiency have been extensively studied [43,90,91,92]. Considering that patents are important output of innovation and R&D activities, we adopt the number of patents authorized to express technological progress.
- (9)
- Financial development () is measured using the ratio of the balance of deposits and loans of financial institutions to GDP. Some believe that financial development improves environmental quality by promoting enterprises to develop environmental protection technologies and strengthen corporate governance [93,94]. Others believe that financial development is conducive to promoting economic growth; thus, leading to the growth of energy consumption and carbon emissions [95,96].
- (10)
- Government intervention (). Government intervention reflects the government’s resource allocation and indirectly affects pollution emissions. Yan et al. [97] determined the inhibitory effect of environmental intervention plans on pollution. The significant effects of China’s government expenditure on CO2 emissions have been examined [98,99]. Following the practice of Fan et al. [100], we adopt the ratio of government general public budget expenditure to GDP to measure the government intervention.
4. Results and Analysis
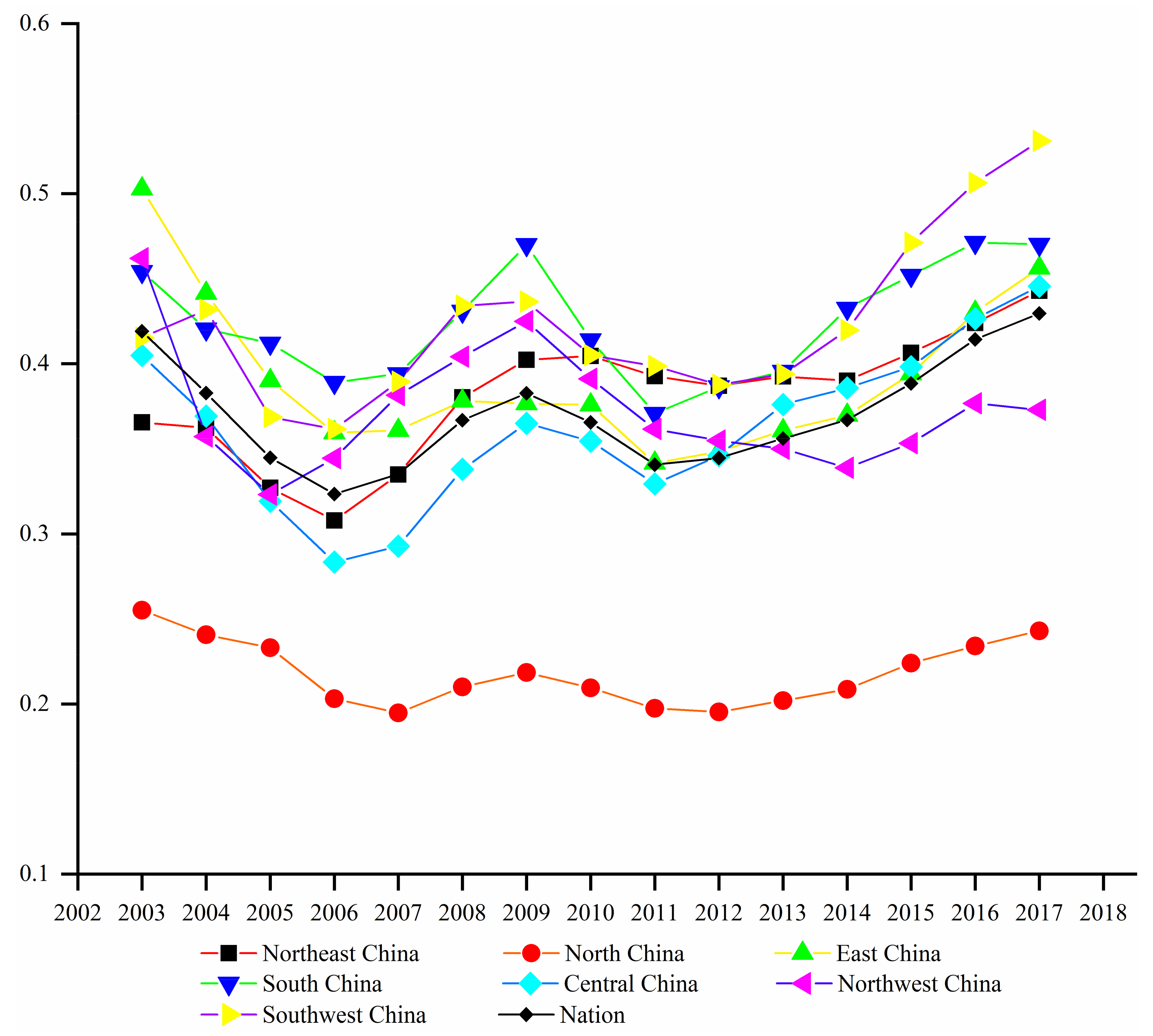
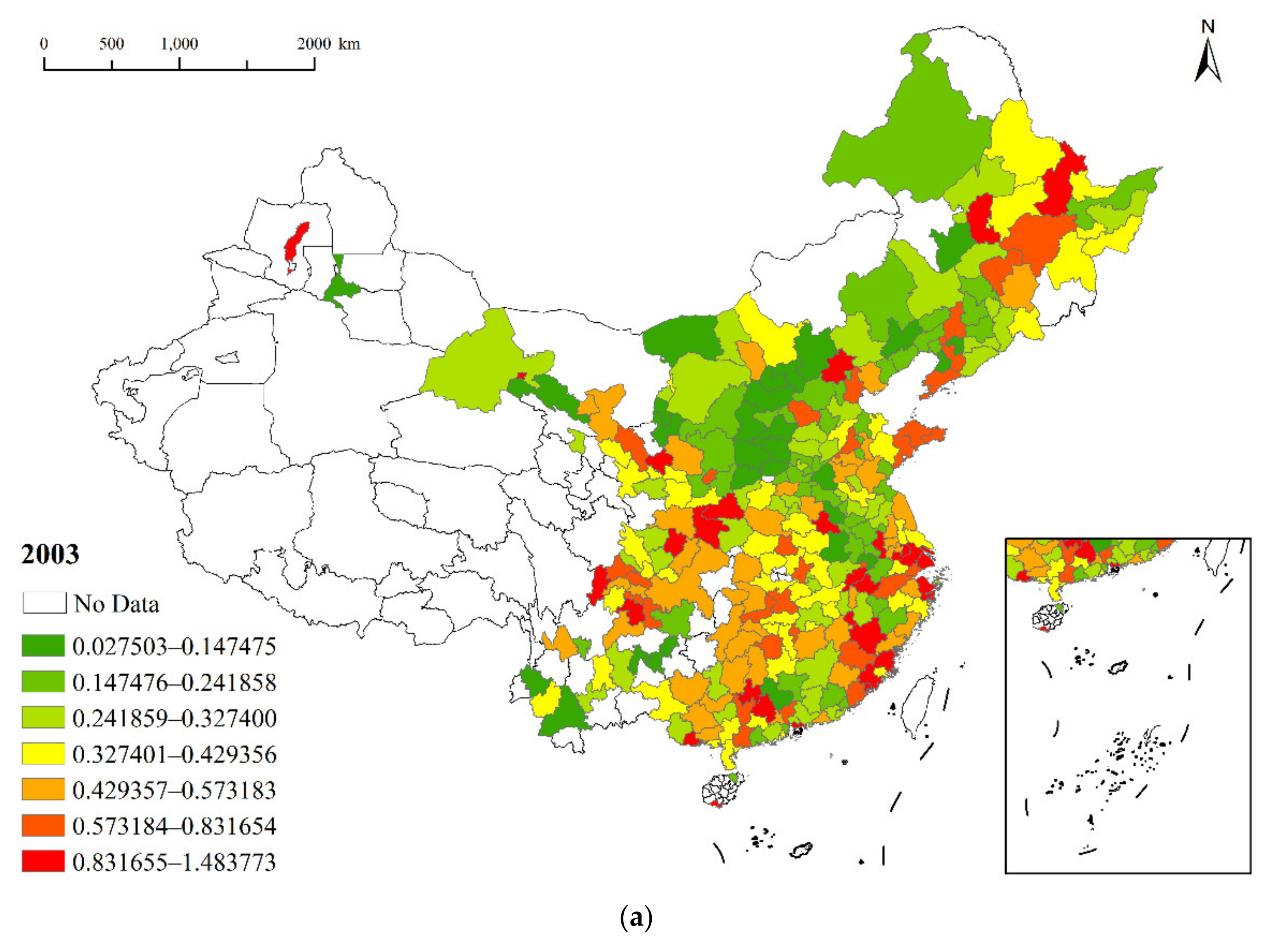
4.1. Spatio-Temporal Patterns of City-Level CE
4.2. Spatial Correlation Tests
4.3. Estimation Results
4.4. Short- and Long-Term Marginal Effects
5. Conclusions and Policy Recommendations
- (1)
- Overall, the average city-level CE from 2003 to 2017 showed a “W”-type growth trend. There were significant spatial heterogeneity characteristics of city-level CE. In 2003, city-level CE was low in the north and high in the south. In 2010, North China, North Central China, and South China formed a continuous low-value area. In 2017, the high-value area of CE expanded significantly.
- (2)
- There is a significant spatial dependency of city-level CE. Cities belonging to L-L clusters are mainly located throughout the territory of Shanxi and Northern Shaanxi, and gradually expand to Inner Mongolia, Gansu, Ningxia, Hebei, and other regions. The H-H clusters are mainly located in the southeast coastal cities and central and eastern Sichuan, and new H-H clusters emerged in Northeast China in 2010.
- (3)
- The empirical results of the dynamic spatial econometric model show that the spatial dependence characteristics of city-level CE co-exist with path dependence on time. There is a significant “U” relationship between economic development and CE. Factors such as industrial structure upgrading and environmental regulation have significant improvement effects on city-level CE, while technological progress, financial development, energy intensity, and government intervention can significantly inhibit city-level CE.
- (4)
- The long-term effect of driving factors on city-level CE is greater than the short-term effect, and the short-term indirect effect is greater than the direct effect. Factors such as economic development, foreign trade, technological progress, financial development, energy intensity, government intervention, and environmental regulation generate significant spatial spillover effects on city-level CE.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- I.E.A. CO2 Emissions from Fuel Combustion, Highlights. 2012. Available online: https://www.osti.gov/etdeweb/servlets/purl/21589332 (accessed on 1 February 2022).
- Lu, Y.; Liu, Y.; Zhou, M. Rebound effect of improved energy efficiency for different energy types: A general equilibrium analysis for China. Energy Econ. 2017, 62, 248–256. [Google Scholar] [CrossRef] [Green Version]
- Poluzzi, A.; Guandalini, G.; Romano, M.C. “Potential carbon efficiency” as a new index to track the performance of biofuels production processes. Biomass Bioenergy 2020, 142, 105618. [Google Scholar] [CrossRef]
- Wilson, C.; Pettifor, H.; Cassar, E.; Kerr, L.; Wilson, M. The potential contribution of disruptive low-carbon innovations to 1.5 °C climate mitigation. Energy Effic. 2019, 12, 423–440. [Google Scholar] [CrossRef] [Green Version]
- I.E.A. World Energy Outlook 2007: China and India Insights. 2007. Available online: https://www.iea.org/reports/world-energy-outlook-2007 (accessed on 1 February 2022).
- Gouldson, A.; Colenbrander, S.; Sudmant, A.; Papargyropoulou, E.; Kerr, N.; McAnulla, F.; Hall, S. Cities and climate change mitigation: Economic opportunities and governance challenges in Asia. Cities 2016, 54, 11–19. [Google Scholar] [CrossRef] [Green Version]
- Rosenzweig, C.; Solecki, W.; Hammer, S.A.; Mehrotra, S. Cities lead the way in climate-change action. Nature 2010, 467, 909–911. [Google Scholar] [CrossRef]
- Zhang, Y. Interregional Supply-driven Carbon Emission Spillover-feedback Effects. J. China Populat. Resourc. Environ. 2016, 26, 55–62. [Google Scholar]
- Sun, L.; Wang, Q.; Zhou, P.; Cheng, F. Effects of carbon emission transfer on economic spillover and carbon emission reduction in China. J. Clean. Prod. 2016, 112, 1432–1442. [Google Scholar] [CrossRef]
- Kaya, Y.; Yokobori, K. Environment, Energy, and Economy: Strategies for Sustainability; United Nations University Press: Tokyo, Japan, 1997. [Google Scholar]
- Mielnik, O.; Goldemberg, J. The evolution of the “carbonization index” in developing countries. Energy Policy 1999, 27, 307–308. [Google Scholar] [CrossRef]
- Sun, J.W. The decrease of CO2 emission intensity is decarbonization at national and global levels. Energy Policy 2005, 33, 975–978. [Google Scholar] [CrossRef]
- Ramanathan, R. Combining indicators of energy consumption and CO2 emissions: A cross-country comparison. Int. J. Glob. Energy Issues 2002, 17, 214–227. [Google Scholar] [CrossRef]
- Ramanathan, R. A multi-factor efficiency perspective to the relationships among world GDP, energy consumption and carbon dioxide emissions. Technol. Forecast. Soc. Change 2006, 73, 483–494. [Google Scholar] [CrossRef]
- Molinos-Senante, M.; Sala-Garrido, R.; Hernandez-Sancho, F. Development and application of the Hicks-Moorsteen productivity index for the total factor productivity assessment of wastewater treatment plants. J. Clean. Prod. 2016, 112, 3116–3123. [Google Scholar] [CrossRef]
- Song, M.; An, Q.; Zhang, W.; Wang, Z.; Wu, J. Environmental efficiency evaluation based on data envelopment analysis: A review. Renew. Sustain. Energy Rev. 2012, 16, 4465–4469. [Google Scholar] [CrossRef]
- Meng, F.; Su, B.; Thomson, E.; Zhou, D.; Zhou, P. Measuring China’s regional energy and carbon emission efficiency with DEA models: A survey. Appl. Energy 2016, 183, 1–21. [Google Scholar] [CrossRef]
- Shang, Y.; Liu, H.; Lv, Y. Total factor energy efficiency in regions of China: An empirical analysis on SBM-DEA model with undesired generation. J. King Saud Univ.-Sci. 2020, 32, 1925–1931. [Google Scholar] [CrossRef]
- Cecchini, L.; Venanzi, S.; Pierri, A.; Chiorri, M. Environmental efficiency analysis and estimation of CO2 abatement costs in dairy cattle farms in Umbria (Italy): A SBM-DEA model with undesirable output. J. Clean. Prod. 2018, 197, 895–907. [Google Scholar] [CrossRef]
- Iftikhar, Y.; Wang, Z.; Zhang, B.; Wang, B. Energy and CO2 emissions efficiency of major economies: A network DEA approach. Energy 2018, 147, 197–207. [Google Scholar] [CrossRef]
- Färe, R.; Grosskopf, S.; Lovell, C.A.K.; Pasurka, C. Multilateral productivity comparisons when some outputs are undesirable: A nonparametric approach. Rev. Econ. Stat. 1989, 71, 90–98. [Google Scholar] [CrossRef]
- Färe, R.; Grosskopf, S.; Pasurka, C.A. Environmental production functions and environmental directional distance functions. Energy 2007, 32, 1055–1066. [Google Scholar] [CrossRef]
- Färe, R.; Grosskopf, S. Directional distance functions and slacks-based measures of efficiency. Eur. J. Oper. Res. 2010, 200, 320–322. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, G.; Zhao, Y. An analysis of Chinese provincial carbon dioxide emission efficiencies based on energy consumption structure. Energy Policy 2016, 96, 524–533. [Google Scholar] [CrossRef]
- Wang, G.; Deng, X.; Wang, J.; Zhang, F.; Liang, S. Carbon emission efficiency in China: A spatial panel data analysis. China Econ. Rev. 2019, 56, 101313. [Google Scholar] [CrossRef]
- Li, J.; Cheng, Z. Study on total-factor carbon emission efficiency of China’s manufacturing industry when considering technology heterogeneity. J. Clean. Prod. 2020, 260, 121021. [Google Scholar] [CrossRef]
- Yan, D.; Lei, Y.; Li, L.; Song, W. Carbon emission efficiency and spatial clustering analyses in China’s thermal power industry: Evidence from the provincial level. J. Clean. Prod. 2017, 156, 518–527. [Google Scholar] [CrossRef]
- Zhu, R.; Zhao, R.; Sun, J.; Xiao, L.; Jiao, S.; Chuai, X.; Zhang, L.; Yang, Q. Temporospatial pattern of carbon emission efficiency of China’s energy-intensive industries and its policy implications. J. Clean. Prod. 2021, 286, 125507. [Google Scholar] [CrossRef]
- Cheng, Z.; Li, L.; Liu, J.; Zhang, H. Total-factor carbon emission efficiency of China’s provincial industrial sector and its dynamic evolution. Renew. Sustain. Energy Rev. 2018, 94, 330–339. [Google Scholar] [CrossRef]
- Yao, X.; Zhou, H.; Zhang, A.; Li, A. Regional energy efficiency, carbon emission performance and technology gaps in China: A meta-frontier non-radial directional distance function analysis. Energy Policy 2015, 84, 142–154. [Google Scholar] [CrossRef]
- Yao, X.; Guo, C.; Shao, S.; Jiang, Z. Total-factor CO2 emission performance of China’s provincial industrial sector: A meta-frontier non-radial Malmquist index approach. Appl. Energy 2016, 184, 1142–1153. [Google Scholar] [CrossRef]
- Zhang, W.; Tang, X.; Yang, G.; Zha, D. Decomposition of CO2 emission intensity in Chinese MIs through a development mode extended LMDI method combined with a production-theoretical approach. Sci. Total Environ. 2020, 702, 134787. [Google Scholar] [CrossRef]
- Fan, M.; Shao, S.; Yang, L. Combining global Malmquist-Luenberger index and generalized method of moments to investigate industrial total factor CO2 emission performance: A case of Shanghai (China). Energy Policy 2015, 79, 189–201. [Google Scholar] [CrossRef]
- Du, K.; Li, J. Towards a green world: How do green technology innovations affect total-factor carbon productivity. Energy Policy 2019, 131, 240–250. [Google Scholar] [CrossRef]
- Tan, X.; Choi, Y.; Wang, B.; Huang, X. Does China’s carbon regulatory policy improve total factor carbon efficiency? A fixed-effect panel stochastic frontier analysis. Technol. Forecast. Soc. Change 2020, 160, 120222. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, W.; Lv, X.; Chen, X.; Shen, M. Investigating interior driving factors and cross-industrial linkages of carbon emission efficiency in China’s construction industry: Based on Super-SBM DEA and GVAR model. J. Clean. Prod. 2019, 241, 118322. [Google Scholar] [CrossRef]
- Zeng, L.; Lu, H.; Liu, Y.; Zhou, Y.; Hu, H. Analysis of regional differences and influencing factors on China’s carbon emission efficiency in 2005–2015. Energies 2019, 12, 3081. [Google Scholar] [CrossRef] [Green Version]
- Marbuah, G.; Amuakwa-Mensah, F. Spatial analysis of emissions in Sweden. Energy Econ. 2017, 68, 383–394. [Google Scholar] [CrossRef] [Green Version]
- Zhou, H.; Jiang, M.; Huang, Y.; Wang, Q. Directional spatial spillover effects and driving factors of haze pollution in North China Plain. Resour. Conserv. Recycl. 2021, 169, 105475. [Google Scholar] [CrossRef]
- Ning, Y.; Miao, L.; Ding, T.; Zhang, B. Carbon emission spillover and feedback effects in China based on a multiregional input-output model. Resour. Conserv. Recycl. 2019, 141, 211–218. [Google Scholar] [CrossRef]
- Chu, X.; Geng, H.; Guo, W. How does energy misallocation affect carbon emission efficiency in China? An empirical study based on the spatial econometric model. Sustainability 2019, 11, 2115. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Xiong, L.; Cheng, B.; Yu, C. How does foreign trade influence China’s carbon productivity? Based on panel spatial lag model analysis. Struct. Change Econ. Dyn. 2018, 47, 171–179. [Google Scholar] [CrossRef]
- Xie, Z.; Wu, R.; Wang, S. How technological progress affects the carbon emission efficiency? Evidence from national panel quantile regression. J. Clean. Prod. 2021, 307, 127133. [Google Scholar] [CrossRef]
- Sun, W.; Huang, C. How does urbanization affect carbon emission efficiency? Evidence from China. J. Clean. Prod. 2020, 272, 122828. [Google Scholar] [CrossRef]
- Wang, K.; Wu, M.; Sun, Y.; Shi, X.; Sun, A.; Zhang, P. Resource abundance, industrial structure, and regional carbon emissions efficiency in China. Resour. Policy 2019, 60, 203–214. [Google Scholar] [CrossRef]
- Andersen, P.; Petersen, N.C. A Procedure for Ranking Efficient Units in Data Envelopment Analysis. Manag. Sci. 1993, 39, 1261–1264. [Google Scholar] [CrossRef]
- Tone, K. A slacks-based measure of super-efficiency in data envelopment analysis. Eur. J. Oper. Res. 2002, 143, 32–41. [Google Scholar] [CrossRef] [Green Version]
- Zhao, P.; Zeng, L.; Lu, H.; Zhou, Y.; Hu, H.; Wei, X.-Y. Green economic efficiency and its influencing factors in China from 2008 to 2017: Based on the super-SBM model with undesirable outputs and spatial Dubin model. Sci. Total Environ. 2020, 741, 140026. [Google Scholar] [CrossRef]
- Zhang, J.; Zeng, W.; Wang, J.; Yang, F.; Jiang, H. Regional low-carbon economy efficiency in China: Analysis based on the Super-SBM model with CO2 emissions. J. Clean. Prod. 2017, 163, 202–211. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, X.; Mao, Y.; Shuai, C.; Jiao, L.; Wu, Y. Analysis of resource allocation and PM2.5 pollution control efficiency: Evidence from 112 Chinese cities. Ecol. Indic. 2021, 127, 107705. [Google Scholar] [CrossRef]
- Bian, J.; Zhang, Y.; Shuai, C.; Shen, L.; Ren, H.; Wang, Y. Have cities effectively improved ecological well-being performance? Empirical analysis of 278 Chinese cities. J. Clean. Prod. 2020, 245, 118913. [Google Scholar] [CrossRef]
- Acheampong, A.O. Economic growth, CO2 emissions and energy consumption: What causes what and where? Energy Econ. 2018, 74, 677–692. [Google Scholar] [CrossRef]
- Abid, M. Does economic, financial and institutional developments matter for environmental quality? A comparative analysis of EU and MEA countries. J. Environ. Manag. 2017, 188, 183–194. [Google Scholar] [CrossRef]
- Chen, Y.; Guo, F.; Wang, J.; Cai, W.; Wang, C.; Wang, K. Provincial and gridded population projection for China under shared socioeconomic pathways from 2010 to 2100. Sci. Data 2020, 7, 83. [Google Scholar] [CrossRef] [Green Version]
- Zhou, P.; Ang, B.W.; Wang, H. Energy and CO2 emission performance in electricity generation: A non-radial directional distance function approach. Eur. J. Oper. Res. 2012, 221, 625–635. [Google Scholar] [CrossRef]
- Elhorst, J.P. Spatial Econometrics: From Cross Sectional Data to Spatial Panels; Springer: Berlin/Heidelberg, Germany, 2014; ISBN 978-1-4200-7287-7. [Google Scholar]
- Shao, S.; Yang, L.; Yu, M.; Yu, M. Estimation, characteristics, and determinants of energy-related industrial CO2 emissions in Shanghai (China), 1994–2009. Energy Policy 2011, 39, 6476–6494. [Google Scholar] [CrossRef]
- Changqing, L.; Lei, L.; Ping, W. Measurement of capital stock of cities at prefecture level and above in China. Urban Probl. 2017, 0, 67–72. [Google Scholar]
- Su, Y.; Chen, X.; Li, Y.; Liao, J.; Ye, Y.; Zhang, H.; Huang, N.; Kuang, Y. China’s 19-year city-level carbon emissions of energy consumptions, driving forces and regionalized mitigation guidelines. Renew. Sustain. Energy Rev. 2014, 35, 231–243. [Google Scholar] [CrossRef]
- Wang, Y.; Li, G. Mapping urban CO2 emissions using DMSP/OLS ‘city lights’ satellite data in China. Environ. Plan. A 2017, 49, 248–251. [Google Scholar] [CrossRef] [Green Version]
- Sheng, P.; Li, J.; Zhai, M.; Huang, S. Coupling of economic growth and reduction in carbon emissions at the efficiency level: Evidence from China. Energy 2020, 213, 118747. [Google Scholar] [CrossRef]
- Antweiler, W.; Copeland, B.R.; Taylor, M.S. Is free trade good for the environment? Am. Econ. Rev. 2001, 91, 877–908. [Google Scholar] [CrossRef] [Green Version]
- Almodóvar, P.; Saiz-Briones, J.; Silverman, B.S. Learning through foreign market participation: The relative benefits of exporting, importing, and foreign direct investment. J. Technol. Transf. 2014, 39, 915–944. [Google Scholar] [CrossRef]
- Zhao, H.; Lin, B. Impact of foreign trade on energy efficiency in China’s textile industry. J. Clean. Prod. 2020, 245, 118878. [Google Scholar] [CrossRef]
- Danish; Ud-Din Khan, S.; Ahmad, A. Testing the pollution haven hypothesis on the pathway of sustainable development: Accounting the role of nuclear energy consumption. Nucl. Eng. Technol. 2021, 53, 2746–2752. [Google Scholar] [CrossRef]
- Lin, B.; Xu, M. Does China become the “pollution heaven” in South-South trade? Evidence from Sino-Russian trade. Sci. Total Environ. 2019, 666, 964–974. [Google Scholar] [CrossRef] [PubMed]
- Duan, Y.; Jiang, X. Pollution haven or pollution halo? A Re-evaluation on the role of multinational enterprises in global CO2 emissions. Energy Econ. 2021, 97, 105181. [Google Scholar] [CrossRef]
- Duan, Y.; Yan, B. Economic gains and environmental losses from international trade: A decomposition of pollution intensity in China’s value-added trade. Energy Econ. 2019, 83, 540–554. [Google Scholar] [CrossRef]
- Ren, S.; Li, X.; Yuan, B.; Li, D.; Chen, X. The effects of three types of environmental regulation on eco-efficiency: A cross-region analysis in China. J. Clean. Prod. 2018, 173, 245–255. [Google Scholar] [CrossRef]
- Sinn, H.-W. Public policies against global warming: A supply side approach. Int. Tax Public Financ. 2008, 15, 360–394. [Google Scholar] [CrossRef]
- Van Der Werf, E.; Di Maria, C. Imperfect environmental policy and polluting emissions: The green paradox and beyond. Int. Rev. Environ. Resour. Econ. 2012, 6, 153–194. [Google Scholar] [CrossRef] [Green Version]
- Smulders, S.; Tsur, Y.; Zemel, A. Announcing climate policy: Can a green paradox arise without scarcity? J. Environ. Econ. Manag. 2012, 64, 364–376. [Google Scholar] [CrossRef] [Green Version]
- Lanoie, P.; Laurent-Lucchetti, J.; Johnstone, N.; Ambec, S. Environmental policy, innovation and performance: New insights on the porter hypothesis. J. Econ. Manag. Strateg. 2011, 20, 803–842. [Google Scholar] [CrossRef] [Green Version]
- Floros, N.; Vlachou, A. Energy demand and energy-related CO2 emissions in Greek manufacturing: Assessing the impact of a carbon tax. Energy Econ. 2005, 27, 387–413. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, Y. Environmental regulations, energy and environment efficiency of China’s metal industries: A provincial panel data analysis. J. Clean. Prod. 2021, 280, 124437. [Google Scholar] [CrossRef]
- Pei, Y.; Zhu, Y.; Liu, S.; Wang, X.; Cao, J. Environmental regulation and carbon emission: The mediation effect of technical efficiency. J. Clean. Prod. 2019, 236, 117599. [Google Scholar] [CrossRef]
- Yasmeen, H.; Tan, Q.; Zameer, H.; Tan, J.; Nawaz, K. Exploring the impact of technological innovation, environmental regulations and urbanization on ecological efficiency of China in the context of COP21. J. Environ. Manag. 2020, 274, 111210. [Google Scholar] [CrossRef]
- Hu, W.; Wang, D. How does environmental regulation influence China’s carbon productivity? An empirical analysis based on the spatial spillover effect. J. Clean. Prod. 2020, 257, 120484. [Google Scholar] [CrossRef]
- Zhou, Y.; Kong, Y.; Sha, J.; Wang, H. The role of industrial structure upgrades in eco-efficiency evolution: Spatial correlation and spillover effects. Sci. Total Environ. 2019, 687, 1327–1336. [Google Scholar] [CrossRef]
- Han, Y.; Zhang, F.; Huang, L.; Peng, K.; Wang, X. Does industrial upgrading promote eco-efficiency?—A panel space estimation based on Chinese evidence. Energy Policy 2021, 154, 112286. [Google Scholar] [CrossRef]
- Zhou, X.-Y.; Lei, K.; Meng, W.; Khu, S.-T. Industrial structural upgrading and spatial optimization based on water environment carrying capacity. J. Clean. Prod. 2017, 165, 1462–1472. [Google Scholar] [CrossRef]
- Wu, J. The Choice of China’s Growth Model; Shanghai Far East Publishers: Shanghai, China, 2013. [Google Scholar]
- Borck, R.; Schrauth, P. Population density and urban air quality. Reg. Sci. Urban Econ. 2021, 86, 103596. [Google Scholar] [CrossRef]
- Clark, T.A. Metropolitan density, energy efficiency and carbon emissions: Multi-attribute tradeoffs and their policy implications. Energy Policy 2013, 53, 413–428. [Google Scholar] [CrossRef]
- Liu, S.; Xia, X.H.; Tao, F.; Chen, X.Y. Assessing urban carbon emission efficiency in China: Based on the global data envelopment analysis. Energy Procedia 2018, 152, 762–767. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, S. Why does China’s carbon intensity decline and India’s carbon intensity rise? A decomposition analysis on the sectors. J. Clean. Prod. 2020, 265, 121569. [Google Scholar] [CrossRef]
- Liu, N.; Ma, Z.; Kang, J. Changes in carbon intensity in China’s industrial sector: Decomposition and attribution analysis. Energy Policy 2015, 87, 28–38. [Google Scholar] [CrossRef]
- Su, B.; Ang, B.W. Demand contributors and driving factors of Singapore’s aggregate carbon intensities. Energy Policy 2020, 146, 111817. [Google Scholar] [CrossRef]
- Song, M.; Wu, J.; Song, M.; Zhang, L.; Zhu, Y. Spatiotemporal regularity and spillover effects of carbon emission intensity in China’s Bohai Economic Rim. Sci. Total Environ. 2020, 740, 140184. [Google Scholar] [CrossRef]
- Zhang, F.; Deng, X.; Phillips, F.; Fang, C.; Wang, C. Impacts of industrial structure and technical progress on carbon emission intensity: Evidence from 281 cities in China. Technol. Forecast. Soc. Change 2020, 154, 119949. [Google Scholar] [CrossRef]
- Cheng, Z.; Li, L.; Liu, J. Industrial structure, technical progress and carbon intensity in China’s provinces. Renew. Sustain. Energy Rev. 2018, 81, 2935–2946. [Google Scholar] [CrossRef]
- Dong, F.; Yu, B.; Hadachin, T.; Dai, Y.; Wang, Y.; Zhang, S.; Long, R. Drivers of carbon emission intensity change in China. Resour. Conserv. Recycl. 2018, 129, 187–201. [Google Scholar] [CrossRef]
- Tamazian, A.; Rao, B.B. Do economic, financial and institutional developments matter for environmental degradation? Evidence from transitional economies. Energy Econ. 2010, 32, 137–145. [Google Scholar] [CrossRef] [Green Version]
- Zagorchev, A.; Vasconcellos, G.; Bae, Y. Financial development, technology, growth and performance: Evidence from the accession to the EU. J. Int. Financ. Mark. Inst. Money 2011, 21, 743–759. [Google Scholar] [CrossRef]
- Acheampong, A.O.; Amponsah, M.; Boateng, E. Does financial development mitigate carbon emissions? Evidence from heterogeneous financial economies. Energy Econ. 2020, 88, 104768. [Google Scholar] [CrossRef]
- Sadorsky, P. Financial development and energy consumption in Central and Eastern European frontier economies. Energy Policy 2011, 39, 999–1006. [Google Scholar] [CrossRef]
- Yan, B.; Wu, L.; Wang, X.H.; Wu, J. How can environmental intervention work during rapid urbanization? Examining the moderating effect of environmental performance-based accountability in China. Environ. Impact Assess. Rev. 2021, 86, 106476. [Google Scholar] [CrossRef]
- Cheng, S.; Fan, W.; Chen, J.; Meng, F.; Liu, G.; Song, M.; Yang, Z. The impact of fiscal decentralization on CO2 emissions in China. Energy 2020, 192, 116685. [Google Scholar] [CrossRef]
- Krajewski, P.; Mackiewicz, M. The role of capital and labour in shaping the environmental effects of fiscal stimulus. J. Clean. Prod. 2019, 216, 323–332. [Google Scholar] [CrossRef]
- Fan, W.; Li, L.; Wang, F.; Li, D. Driving factors of CO2 emission inequality in China: The role of government expenditure. China Econ. Rev. 2020, 64, 101545. [Google Scholar] [CrossRef]
- Zhang, K.-Y.; Wang, Y.-Z.; Peng, Z.Y.S. The Evolution, Causes and Influencing Factors of South-North Differentiation within the Western China Zhang. Economist 2021, 3, 51–62. [Google Scholar] [CrossRef]
- Huang, J.; Chen, X.; Yu, K.; Cai, X. Effect of technological progress on carbon emissions: New evidence from a decomposition and spatiotemporal perspective in China. J. Environ. Manag. 2020, 274, 110953. [Google Scholar] [CrossRef]
- Wang, S.; Zeng, J.; Liu, X. Examining the multiple impacts of technological progress on CO2 emissions in China: A panel quantile regression approach. Renew. Sustain. Energy Rev. 2019, 103, 140–150. [Google Scholar] [CrossRef]
- Chen, S.; Sun, Z.; Tang, S.; Wu, D. Government intervention and investment efficiency: Evidence from China. J. Corp. Financ. 2011, 17, 259–271. [Google Scholar] [CrossRef]
- National Energy Administration. The 13th Five-Year Plan for Coal Industry Development. Available online: http://www.gov.cn/zhengce/content/2017-02/03/content_5164865.htm (accessed on 12 January 2017).
- Lin, B.; Tian, P. The energy rebound effect in China’s light industry: A translog cost function approach. J. Clean. Prod. 2016, 112, 2793–2801. [Google Scholar] [CrossRef]
- Binswanger, M. Technological progress and sustainable development: What about the rebound effect? Ecol. Econ. 2001, 36, 119–132. [Google Scholar] [CrossRef]
- Chen, J.; Gao, M.; Shahbaz, M.; Cheng, S.; Song, M. An improved decomposition approach toward energy rebound effects in China: Review since 1992. Renew. Sustain. Energy Rev. 2021, 145, 111141. [Google Scholar] [CrossRef]





| Variable | Mean | Std. Dev. | Min | Max |
|---|---|---|---|---|
| GDP | 1275.856 | 1912.396 | 31.446 | 23,402.05 |
| Capital | 2544.254 | 4025.465 | 17.32 | 52,548.78 |
| Labor | 260.1852 | 612.287 | 9.17 | 38,230 |
| Energy | 1292.399 | 1299.467 | 26.248 | 11,858.96 |
| CO2 emission | 34.1974 | 35.583 | 0.546 | 265.208 |
| Carbon efficiency | 0.371 | 0.225 | 0.028 | 1.484 |
| Economic development | 9.91 | 0.852 | 7.244 | 12.698 |
| Industrial structure | 0.484 | 0.111 | 0.09 | 0.91 |
| Industrial structure upgrading | 0.868 | 0.511 | 0.094 | 10.766 |
| Population density | 5.729 | 0.908 | 1.547 | 7.886 |
| Technological progress | 6.163 | 1.845 | 0.693 | 11.578 |
| Financial development | 2.315 | 1.504 | 0.142 | 31.586 |
| Foreign trade | 0.253 | 0.476 | 0.00002 | 7.018 |
| Energy intensity | 1.515 | 1.211 | 0.121 | 14.842 |
| Government intervention | 0.208 | 0.152 | 0.031 | 2.422 |
| Environmental regulation | 0.659 | 0.158 | 0.1639 | 0.978 |
| Year | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
| I | 0.088 | 0.085 | 0.108 | 0.1 | 0.104 | 0.119 | 0.125 | 0.103 |
| Z(I) | 4.912 | 4.744 | 6.008 | 5.593 | 5.803 | 6.58 | 6.888 | 5.739 |
| p-value | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Year | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | |
| I | 0.098 | 0.093 | 0.115 | 0.132 | 0.156 | 0.174 | 0.165 | |
| Z(I) | 5.477 | 5.173 | 6.39 | 7.288 | 8.537 | 9.518 | 9.004 | |
| p-value | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Model A | Model B | Model C | Model D | |
|---|---|---|---|---|
| w.ce | 0.38 *** (9.52) | 0.59 *** (8.25) | ||
| l.ce | 0.71 *** (7.44) | 0.407 *** (5.81) | ||
| pgdp | 0.176 *** (3.01) | 0.235 *** (3.43) | −0.52 *** (−3.54) | −0.347 *** (−2.42) |
| pgdp 2 | −0.007 *** (−2.63) | −0.009** (−2.9) | 0.027 *** (3.69) | 0.02 *** (2.83) |
| is | −0.088 ** (−2.14) | −0.037 (−0.82) | −0.014 (0.28) | −0.22 (0.98) |
| isa | 0.016 *** (2.77) | 0.007 * (1.42) | 0.01 * (1.52) | 0.07 * (1.25) |
| pd | −0.022 (−1.55) | −0.01 (−0.77) | −0.008 (−1.53) | −0.002 (0.2) |
| tp | −0.008 ** (−2.29) | −0.008 ** (−1.85) | −0.004 (−0.91) | −0.007 * (−1.17) |
| fd | −0.007 *** (−3.99) | −0.007 *** (−4.25) | −0.007 *** (−3.07) | −0.01 ** (−2) |
| ft | −0.021 *** (−2.42) | 0.001 (0.14) | −0.013 (−1.5) | −0.004 (−0.22) |
| ei | −0.016 *** (−4.6) | −0.018 *** (−4.59) | −0.017 ** (−2.19) | −0.04 *** (−3.58) |
| gi | −0.068 *** (−2.97) | −0.071 *** (−3.31) | −0.006 *** (−0.31) | −0.005 *** (0.14) |
| er | 0.054 *** (3.32) | 0.008 (0.52) | 0.103 *** (4.47) | 0.069 *** (−2.43) |
| α | −0.407 (−1.36) | 0.007 *** (0.1) | 2.63 *** (3.51) | −0.62 (−0.35) |
| AR (1) | 0.028 | 0.026 | ||
| AR (2) | 0.334 | 0.332 | ||
| Hansen Over-identification | 0.107 | 0.165 |
| Short-Term Effects | Long-Term Effects | |||||
|---|---|---|---|---|---|---|
| Direct | Indirect | Total | Direct | Indirect | Total | |
| pgdp | −0.1521 *** (−3.01) | 0.2727 * (1.5) | 0.1206 (0.7) | −0.4827 (−0.65) | −1.6483 (−0.08) | −2.167 (−0.11) |
| pgdp 2 | 0.0085 *** (3.63) | −0.0129 * (−1.47) | −0.0045 (−0.53) | 0.0265 (0.59) | 0.0647 (0.08) | 0.0912 (0.11) |
| is | 0.0563 (1.84) | −0.0716 (−0.6) | −0.0153 (−0.13) | 0.1545 (0.21) | −0.813 (−0.05) | −0.0685 (−0.04) |
| isa | 0.0031 (0.86) | 0.0161 (0.79) | 0.0192 (0.92) | 0.0012 (0.01) | −0.4625 (−0.19) | −0.4613 (−0.19) |
| pd | −0.0008 (−0.08) | −0.0201 (−0.43) | −0.0209 (−0.46) | −0.0057 (−0.03) | −0.294 (−0.02) | −0.2997 (−0.02) |
| tp | 0.0004 (0.14) | 0.0207 ** (2.11) | 0.0211 *** (2.3) | −0.0025 (−0.02) | −0.2422 (−0.06) | −0.2447 (−0.07) |
| fd | −0.0039 ** (−2.27) | −0.0416 *** (−4.09) | −0.0455 *** (−4.45) | −0.0031 (−0.01) | 0.4196 (0.05) | 0.4166 (0.05) |
| ft | 0.0031 (0.54) | 0.0476 * (1.65) | 0.0507 * (1.74) | 0.0057 (0.02) | −0.5668 (−0.09) | −0.5611 (−0.09) |
| ei | −0.0041 * (−1.34) | 0.0222 ** (1.83) | 0.0181 * (1.62) | −0.019 (−0.11) | −0.2324 (−0.13) | −0.2514 (−0.14) |
| gi | −0.00007 * (−0.00) | −0.1145 * (−1.23) | −0.1146 * (−1.22) | 0.0393 (0.04) | 2.2759 (0.15) | 2.3151 (0.15) |
| er | 0.003 3* (0.27) | 0.1956 *** (4.55) | 0.1989 *** (4.71) | −0.0403 (−0.03) | −2.1032 (−0.06) | −2.1434 (−0.07) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, J.; Song, X.; Zhang, J. Spatial-Temporal Pattern and Driving Factors of Carbon Efficiency in China: Evidence from Panel Data of Urban Governance. Energies 2022, 15, 2536. https://doi.org/10.3390/en15072536
Tian J, Song X, Zhang J. Spatial-Temporal Pattern and Driving Factors of Carbon Efficiency in China: Evidence from Panel Data of Urban Governance. Energies. 2022; 15(7):2536. https://doi.org/10.3390/en15072536
Chicago/Turabian StyleTian, Juanjuan, Xiaoqian Song, and Jinsuo Zhang. 2022. "Spatial-Temporal Pattern and Driving Factors of Carbon Efficiency in China: Evidence from Panel Data of Urban Governance" Energies 15, no. 7: 2536. https://doi.org/10.3390/en15072536
APA StyleTian, J., Song, X., & Zhang, J. (2022). Spatial-Temporal Pattern and Driving Factors of Carbon Efficiency in China: Evidence from Panel Data of Urban Governance. Energies, 15(7), 2536. https://doi.org/10.3390/en15072536







