An Analytical Heat Transfer Model in Oil Reservoir during Long-Term Production
Abstract
:1. Introduction
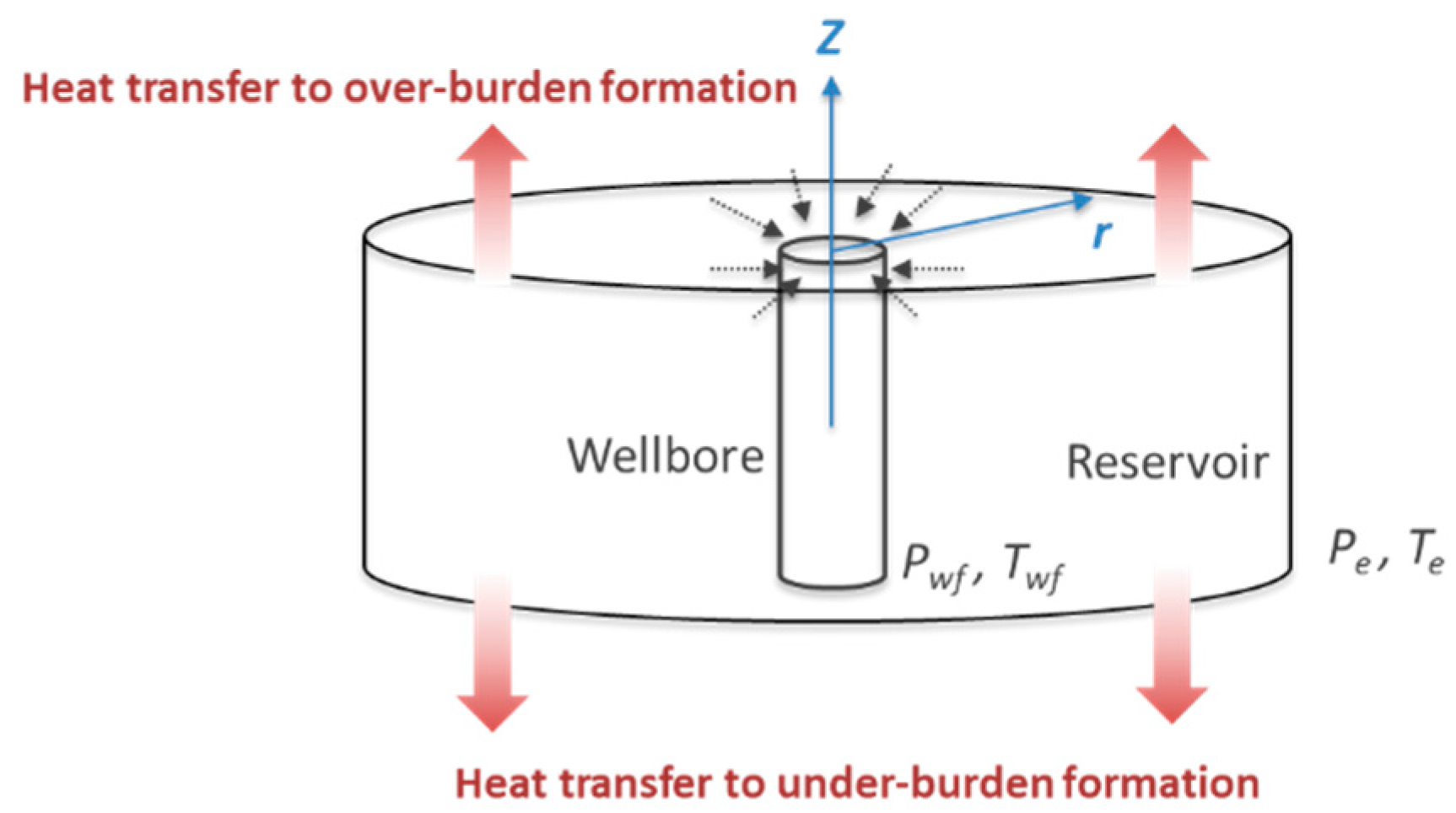
2. Mathematical Models
2.1. Analytical Steady-State Model without System Heat Transfer
2.2. Analytical Steady-State Model without System Heat Transfer and Conduction
2.3. Analytical Steady-State Model with System Heat Transfer
3. Results
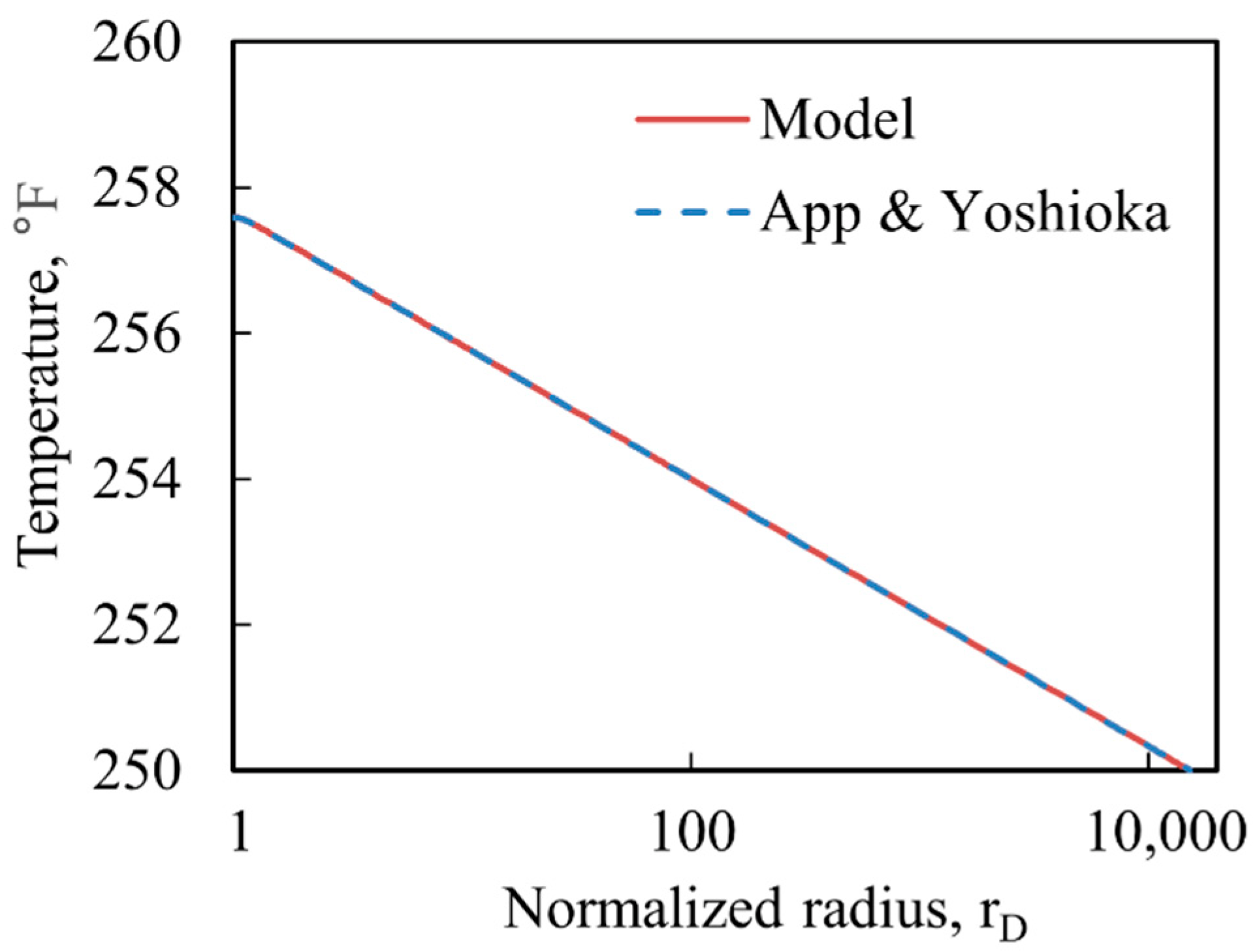
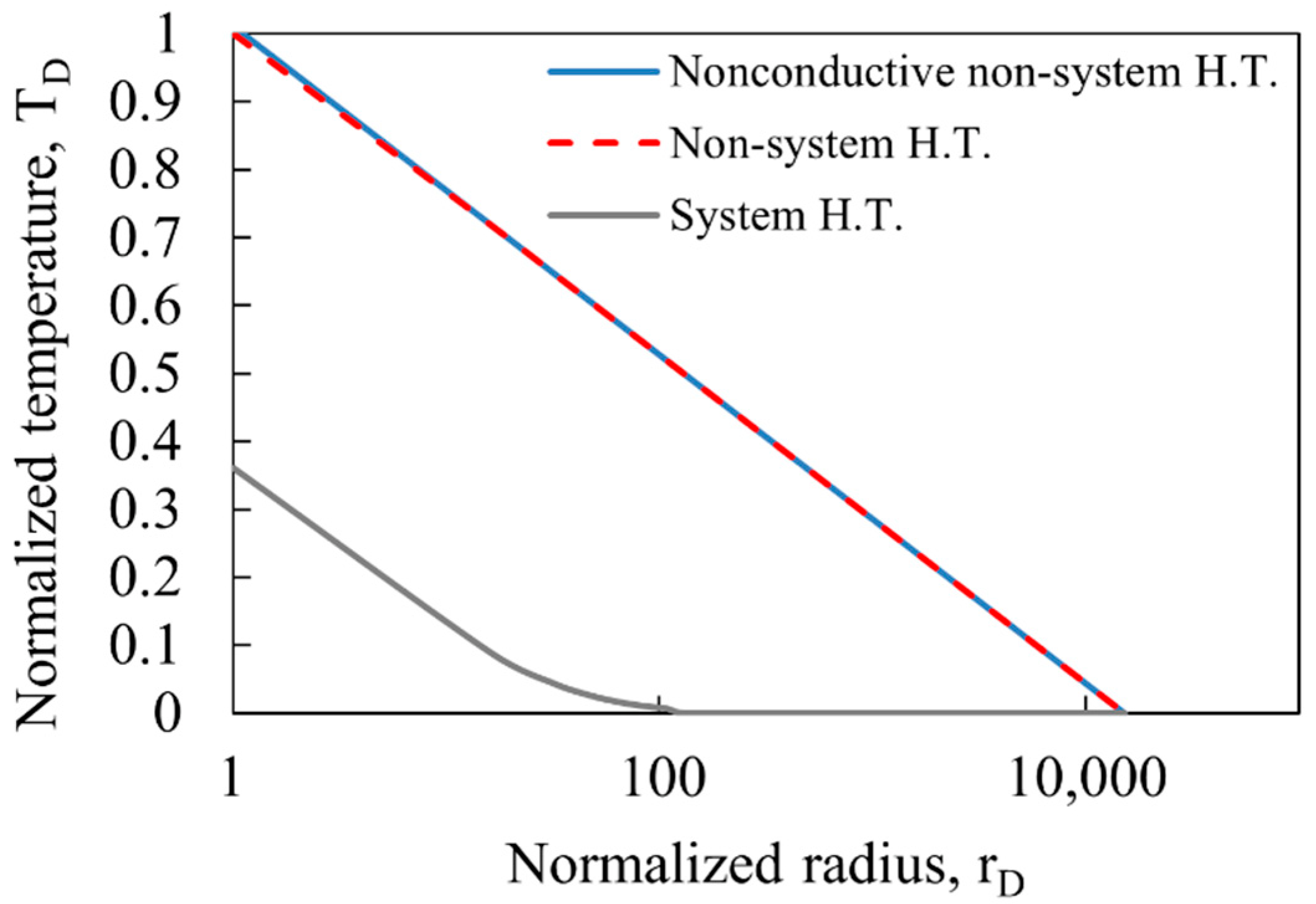
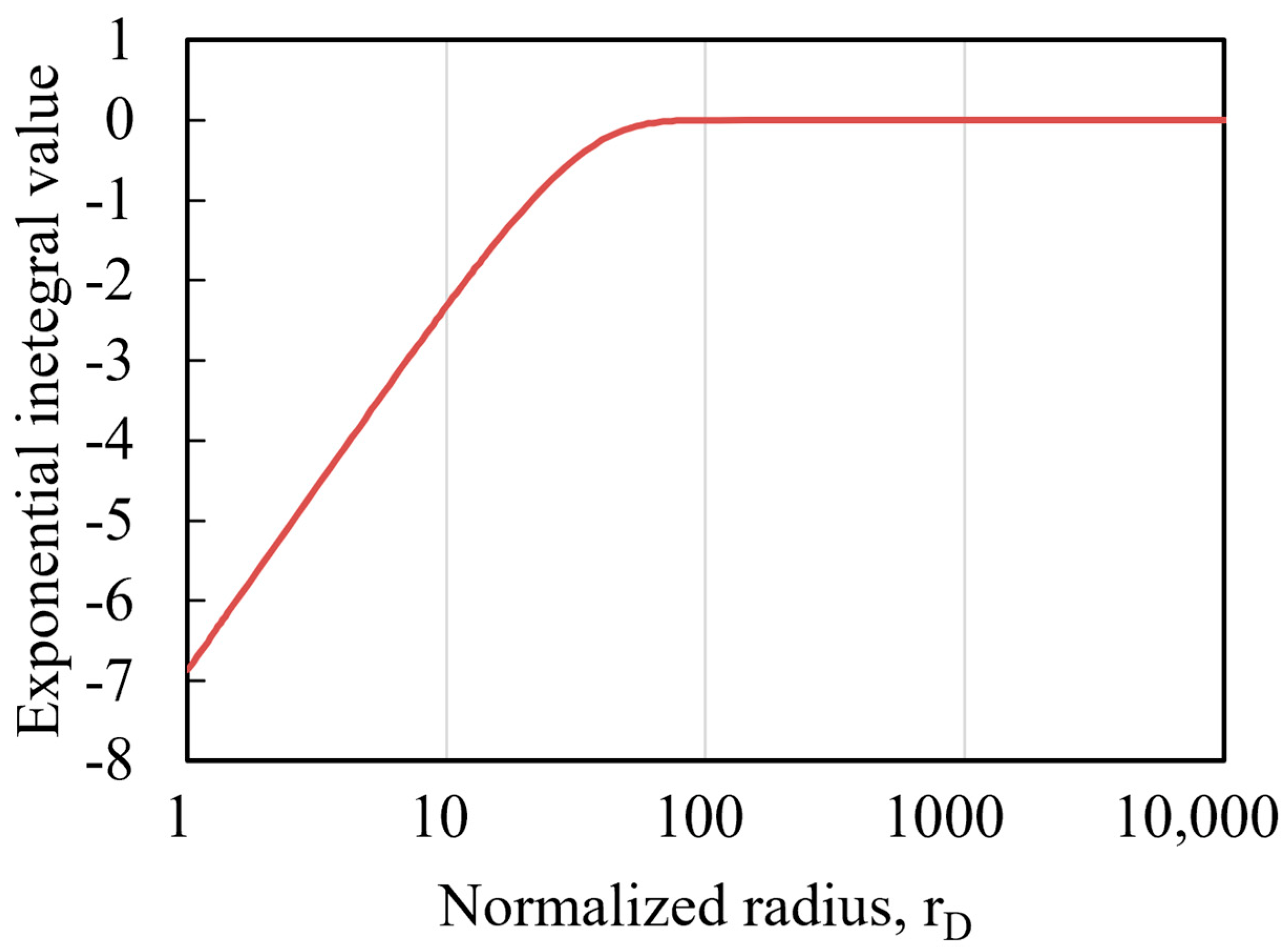
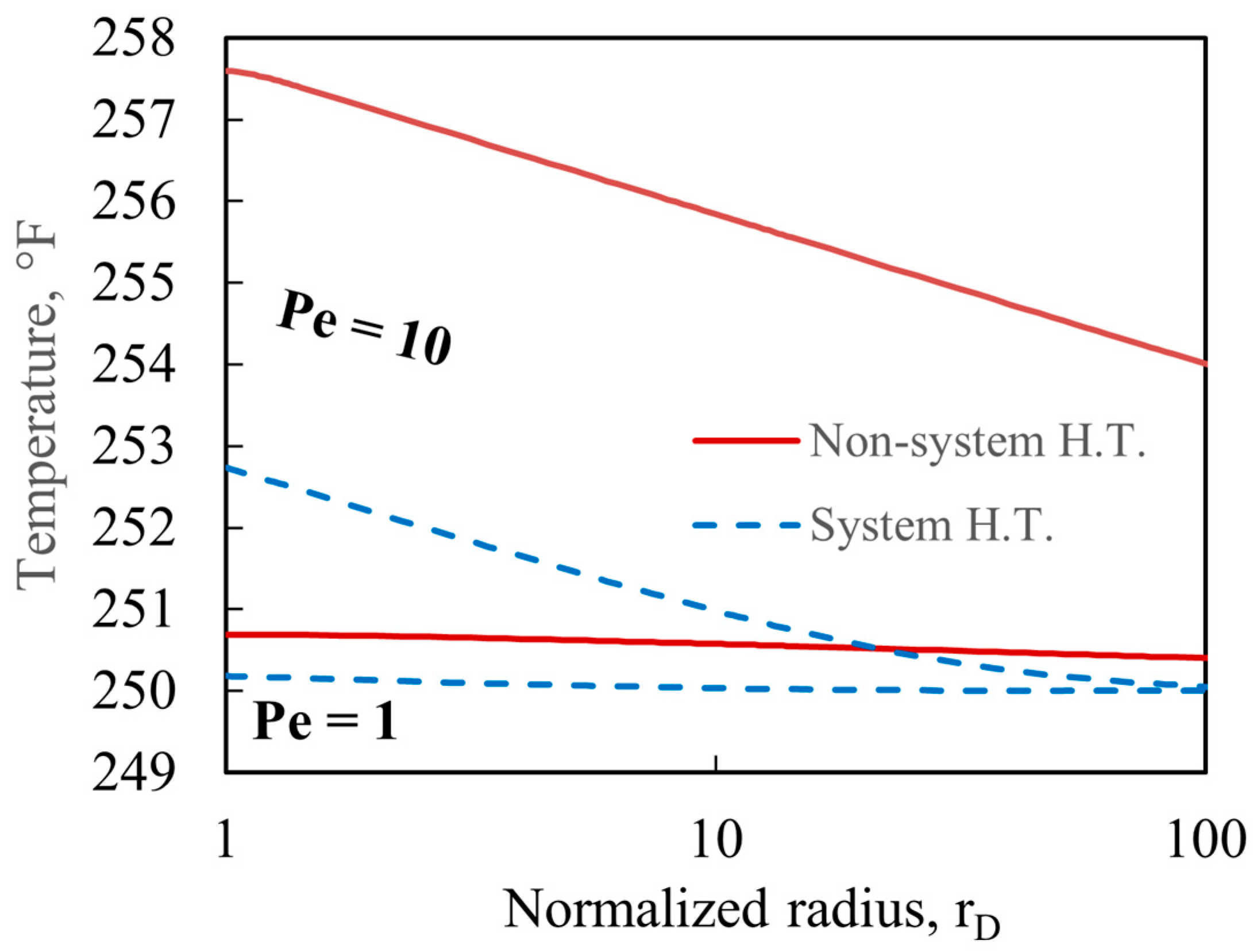
3.1. Identification of System Heat Transfer Effect
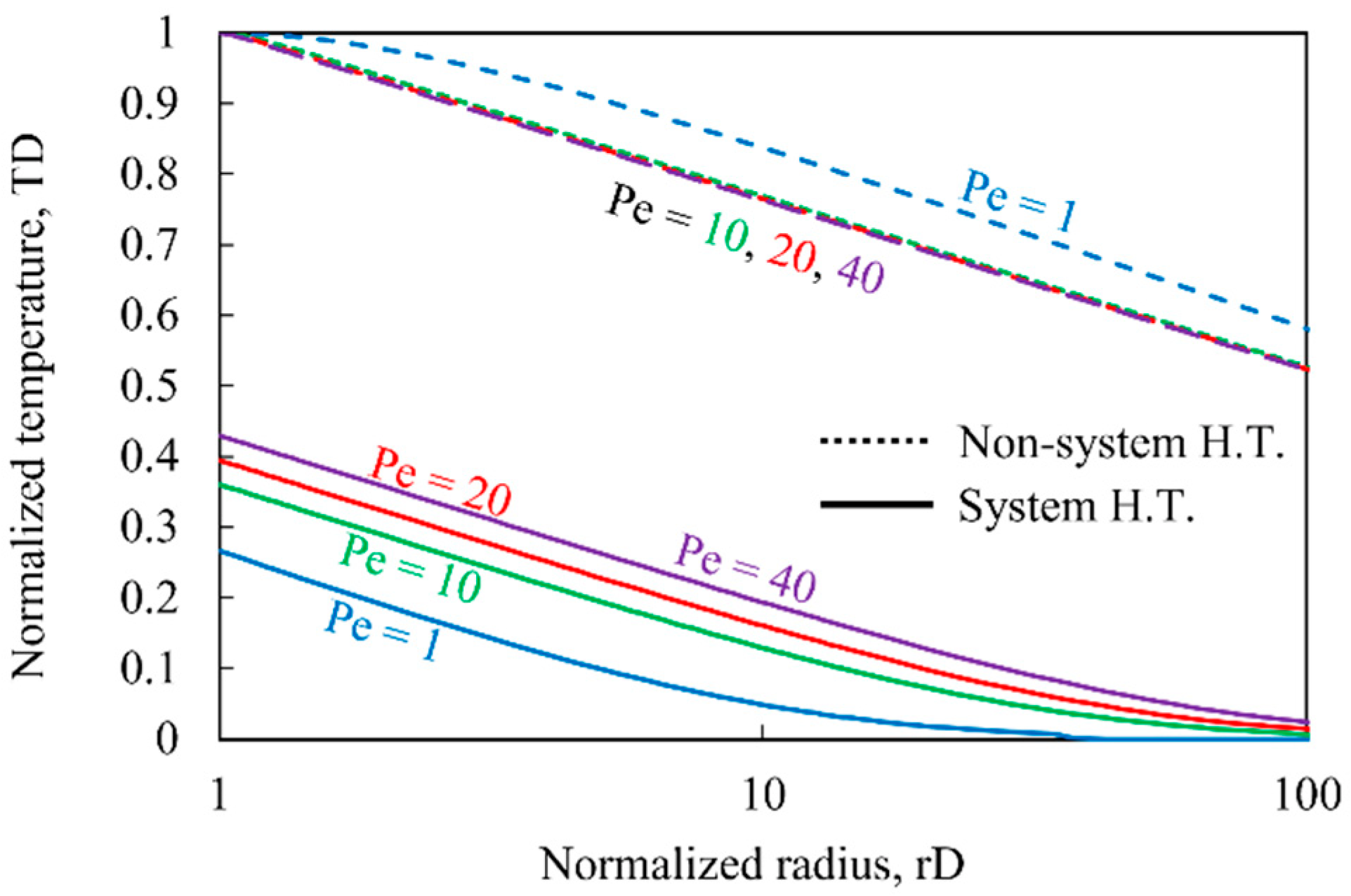
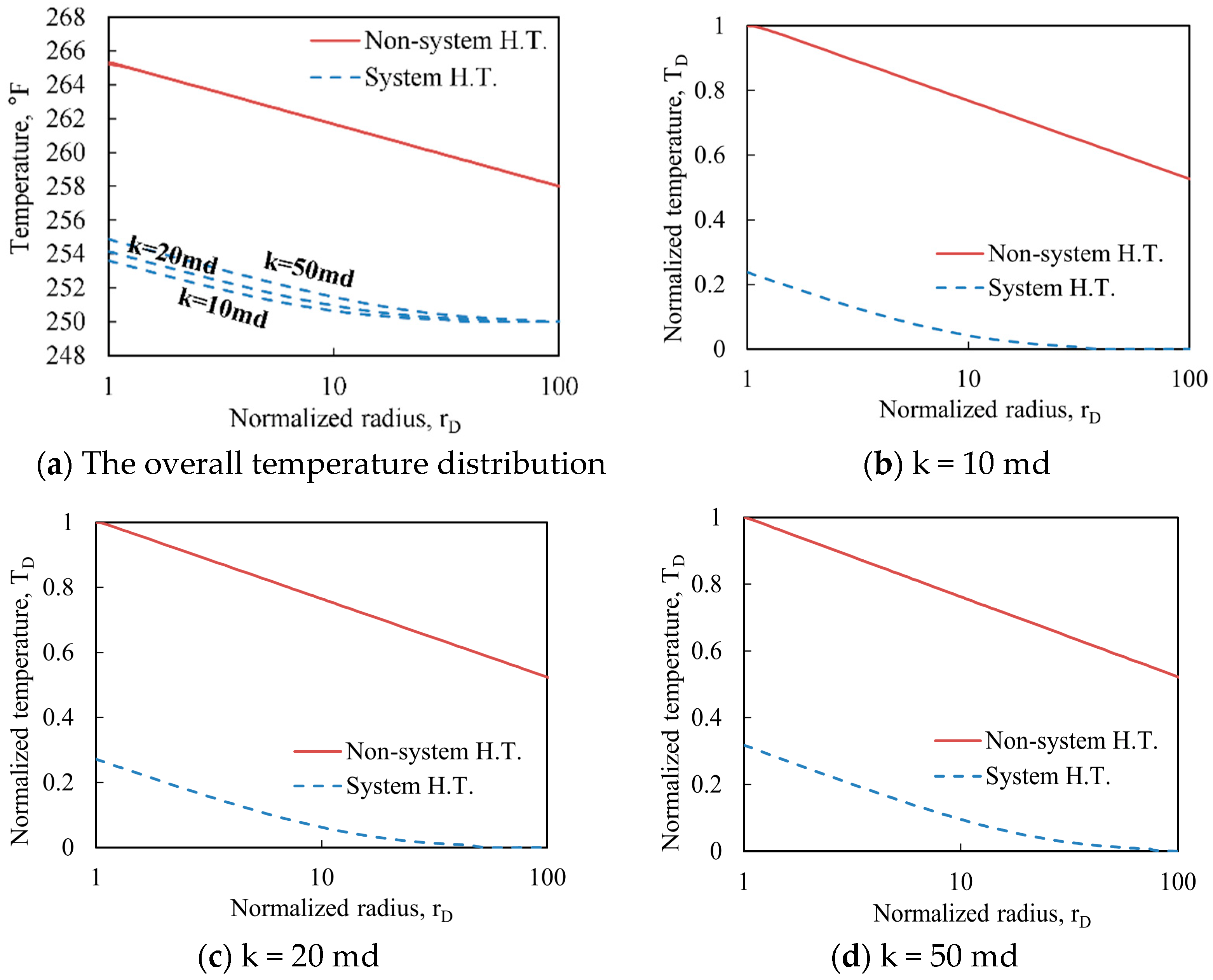
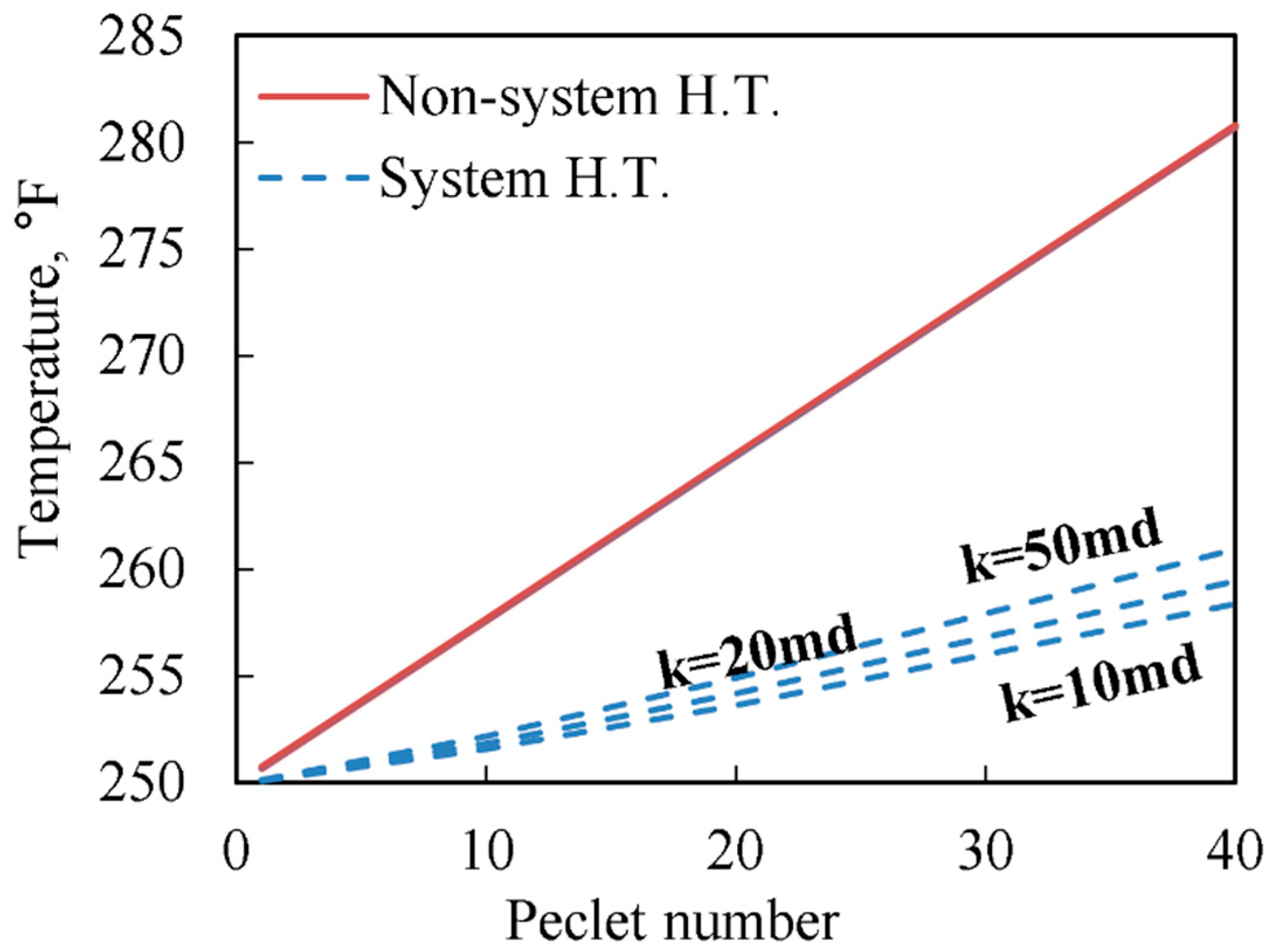
3.2. Sensitivity Analysis
4. Discussion
5. Conclusions
- After long-term production and reaching a steady-state, a straight line is observed in the semi-log graph of radius and temperature.
- The system heat transfer induces a cooling effect on radial temperature in the oil reservoir, reducing some of the temperature rises due to J–T heating.
- As the Peclet number increases, the cooling effect of system heat transfer increases. However, its relative influence diminishes compared to J–T heating.
- Higher permeability causes the convection-dominating phase, which reduces the cooling effect of the system heat transfer.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| J–T | Joule–Thomson |
| Pe | Peclet number |
| H.T. | heat transfer |
| STB | Barrel at the standard condition |
| A | cross-sectional area, |
| Formation volume factor, bbl/STB | |
| fluid specific heat capacity, Btu/(lbm·°F) | |
| h | pay-zone height, ft |
| heat transfer coefficient, Btu/(h··°F) | |
| permeability, md | |
| pressure, psi | |
| net heat transfer between reservoirs, Btu/(h·) | |
| q | volumetric well flow rate, STB/day |
| radius, ft | |
| saturation | |
| temperature, °F | |
| time, day | |
| fluid velocity, ft/day | |
| thermal diffusivity, /h | |
| fluid thermal conductivity, Btu/(h·ft·°F) | |
| viscosity, cp | |
| fluid density, lbm/ | |
| Joule-Thomson throttling coefficient, Btu/(lbm·psi) | |
| porosity | |
| Subscript | |
| D | dimensionless variable |
| earth (formation) | |
| f | fluid |
| o | oil |
| s | surrounding |
| w | well |
| wat | water |
| wellbore wall fluid |
References
- Xu, B. Modeling and Applications of Heat Transfer in Wellbore and Its Surrounding Formation. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 2018. [Google Scholar]
- Lauwerier, H.A. The Transport of Heat in an Oil Layer Caused by the Injection of Hot Fluid. Appl. Sci. Res. 1955, 5, 145–150. [Google Scholar] [CrossRef]
- Rubinshtein, L.I. The Total Heat Losses in Injection of a Hot Liquid into a Stratum. Neft’i Gaz 1959, 2, 41–48. [Google Scholar]
- Spillette, A.G. Heat Transfer during Hot Fluid Injection into an Oil Reservoir. J. Can. Pet. Technol. 1965, 4, 213–218. [Google Scholar] [CrossRef]
- Satman, A.; Brigham, W.E.; Zolotukhin, A.B. A New Approach for Predicting the Thermal Behavior in Porous Media during Fluid Injection. Trans. Geotherm. Resour. Counc. 1979, 3, 621–624. [Google Scholar]
- Sweet, M.L.; Sumpter, L.T. Genesis field, Gulf of Mexico: Recognizing Reservoir Compartments on Geologic and Production Time Scales in Deep-water Reservoirs. AAPG Bull. 2007, 91, 1701–1729. [Google Scholar] [CrossRef]
- Duan, S.; Lach, J.R.; Beadall, K.K.; Li, X. Water Injection in Deepwater, Over-Pressured Turbidites in the Gulf of Mexico: Past, Present, and Future. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 6–9 May 2013. [Google Scholar] [CrossRef]
- Dastkhan, Y.; Kazemi, A. The Impact of Isothermal Flow Assumption on Accuracy of Pressure Transient Analysis Results. Can. J. Chem. Eng. 2021, 1. [Google Scholar] [CrossRef]
- Steffensen, R.J.; Smith, R.C. The Importance of Joule-Thomson Heating (or Cooling) in Temperature Log Interpretation. In Proceedings of the Fall Meeting of the Society of Petroleum Engineers of AIME, Las Vegas, NV, USA, 30 September–3 October 1973. [Google Scholar] [CrossRef]
- Hermanrud, C.; Lerche, I.; Meisingset, K.K. Determination of Virgin Rock Temperature from Drillstem Tests. J. Pet. Technol. 1991, 43, 1126–1131. [Google Scholar] [CrossRef]
- Kortekaas, W.G.; Peters, C.J.; de Swaan Arons, J. Joule-Thomson Expansion of High-Pressure-High-Temperature Gas Condensates. Fluid Phase Equilib. 1997, 139, 205–218. [Google Scholar] [CrossRef]
- App, J.F. Field Cases: Nonisothermal Behavior Due to Joule-Thomson and Transient Fluid Expansion/Compression Effects. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 4–7 October 2009. [Google Scholar] [CrossRef]
- Naccache, P.F. A Fully-Implicit Thermal Reservoir. In Proceedings of the SPE Reservoir Simulation Symposium, Dallas, TX, USA, 8–11 June 1997. [Google Scholar] [CrossRef]
- Pao, W.K.S.; Lewis, R.W.; Masters, I. A Fully Coupled Hydro-Thermo-Poro-Mechanical Model for Black Oil Reservoir Simulation. Int. J. Numer. Anal. Meth. Geomech. 2001, 25, 1229–1256. [Google Scholar] [CrossRef]
- Yan, C.; Jiao, Y.; Yang, S. A 2D Coupled Hydro-Thermal Model for the Combined Finite-Discrete Element Method. Acta Geotech. 2019, 14, 403–416. [Google Scholar] [CrossRef]
- App, J.F. Nonisothermal and Productivity Behavior of High-Pressure Reservoirs. SPE J. 2010, 15, 50–63. [Google Scholar] [CrossRef]
- Ramazanov, A.S.; Nagimov, V.M.; Akhmetov, R.K. Analytical Model of Temperature Prediction for a Given Production History. Oil Gas Bus. 2013, 1, 537–546. [Google Scholar]
- Onur, M.; Çinar, M. Temperature Transient Analysis of Slightly Compressible, Single-Phase Reservoirs. In Proceedings of the 78th EAGE Conference and Exhibition, Vienna, Austria, 30 May–2 June 2016. [Google Scholar] [CrossRef]
- Onur, M.; Çinar, M. Analysis of Sandface-Temperature-Transient Data for Slightly Compressible, Single-Phase Reservoirs. SPE J. 2017, 22, 1134–1155. [Google Scholar] [CrossRef]
- Mao, Y.; Zeidouni, M. Accounting for Fluid-Property Variations in Temperature-Transient Analysis. SPE J. 2017, 23, 868–884. [Google Scholar] [CrossRef]
- Mao, Y.; Zeidouni, M. Analytical Solutions for Temperature Transient Analysis and Near Wellbore Damaged Zone Characterization. In Proceedings of the SPE Reservoir Characterisation and Simulation Conference and Exhibition, Abu Dhabi, United Arab Emirates, 8–10 May 2017. [Google Scholar] [CrossRef]
- Mao, Y.; Zeidouni, M. Transient and Boundary Dominated Flow Temperature Analysis under Variable Rate Conditions. In Proceedings of the SPE Trinidad and Tobago Section Energy Resources Conference, Port of Spain, Trinidad and Tobago, 25–26 June 2018. [Google Scholar] [CrossRef]
- Galvao, M.S.; Carvalho, M.S.; Barreto, A.B. A Coupled Transient Wellbore/Reservoir-Temperature Analytical Model. SPE J. 2019, 24, 2335–2361. [Google Scholar] [CrossRef]
- Panini, F.; Onur, M.; Viberti, D. An Analytical Solution and Nonlinear Regression Analysis for Sandface Temperature Transient Data in the Presence of a Near-Wellbore Damaged Zone. Transp. Porous Med. 2019, 129, 779–810. [Google Scholar] [CrossRef]
- Mathias, S.A.; Gluyas, J.G.; Oldenburg, C.M.; Tsang, C. Analytical Solution for Joule–Thomson Cooling during CO2 Geo-Sequestration in Depleted Oil and Gas Reservoirs. Int. J. Greenh. Gas Control. 2010, 4, 806–810. [Google Scholar] [CrossRef] [Green Version]
- Chevarunotai, N. Analytical Models for Flowing-Fluid Temperature Distribution in Single-phase Oil Reservoirs Accounting for Joule-Thomson Effect. Master’s Thesis, Texas A&M University, College Station, TX, USA, 2014. [Google Scholar]
- Hashish, R.G.; Zeidouni, M. Analytical Approach for Injection Profiling through Warm-Back Analysis in Multilayer Reservoirs. J. Pet. Sci. Eng. 2019, 182, 106274. [Google Scholar] [CrossRef]
- App, J.F.; Yoshioka, K. Impact of Reservoir Permeability on Flowing Sandface Temperatures: Dimensionless Analysis. SPE J. 2013, 18, 685–694. [Google Scholar] [CrossRef]
- App, J.F. Influence of Flow Geometry on Sandface Temperatures during Single-Phase Oil Production: Dimensionless Analysis. SPE J. 2016, 21, 928–937. [Google Scholar] [CrossRef]
- Anees, A.; Zhong, S.W.; Ashraf, U.; Abbas, A. Development of A Computer Program for Zoeppritz Energy Partition Equations and Their Various Approximations to Affirm Presence of Hydrocarbon in Missakeswal Area. Geosciences 2017, 7, 55–67. [Google Scholar] [CrossRef]
- Ashraf, U.; Zhang, H.; Anees, A.; Mangi, H.N.; Ali, M.; Zhang, X.; Imraz, M.; Abbasi, S.S.; Abbas, A.; Ullah, Z.; et al. A Core Logging, Machine Learning and Geostatistical Modeling Interactive Approach for Subsurface Imaging of Lenticular Geobodies in a Clastic Depositional System, SE Pakistan. Nat. Resour. Res. 2021, 30, 2807–2830. [Google Scholar] [CrossRef]
- Jiang, R.; Zhao, L.; Xu, A.; Ashraf, U.; Yin, J.; Song, H.; Su, N.; Du, B.; Anees, A. Sweet Spots Prediction through Fracture Genesis Using Multi-Scale Geological and Geophysical Data in the Karst Reservoirs of Cambrian Longwangmiao Carbonate Formation, Moxi-Gaoshiti Area in Sichuan Basin, South China. J. Petrol. Explor. Prod. Technol. 2021. [Google Scholar] [CrossRef]
- Ullah, J.; Luo, M.; Ashraf, U.; Pan, H.; Anees, A.; Li, D.; Ali, M.; Ali, J. Evaluation of the Geothermal Parameters to Decipher the Thermal Structure of the Upper Crust of the Longmenshan Fault Zone Derived from Borehole Data. Geothermics 2022, 98, 102268. [Google Scholar] [CrossRef]
- Palabiyik, Y.; Onur, M.; Tureyen, O.I.; Cinar, M. Transient Temperature Behavior and Analysis of Single-Phase Liquid-Water Geothermal Reservoirs during Drawdown and Buildup Tests: Part I. Theory, New Analytical and Approximate Solutions. J. Pet. Sci. Eng. 2016, 146, 637–656. [Google Scholar] [CrossRef]

| Transient State | Steady-State | |
|---|---|---|
| App (2010) [16] | J–T, AE, System H.T. | |
| Mathias et al. (2010) [25] | J–T | |
| Ramazanov (2013) [17] | J–T, Radial conduction | |
| App and Yoshioka (2013) [28] | J–T, Radial conduction | |
| Chevarunotai et al. (2014) [26] | J–T, System H.T. | |
| Onur and Cinar (2016) [18,19] | J–T, AE | |
| Mao and Zeidouni (2017) [20,21,22] | J–T, AE | |
| Hashish and Zeidouni (2019) [27] | AE, System H.T. | |
| Our proposed model | J–T, System H.T. |
| Parameters | Value |
|---|---|
| , ft | 5325 |
| , ft | 0.35 |
| Pay-zone height, h, ft | 10 |
| 0.18 | |
| Permeability, k, md | 20 |
| , Btu/(h·°F·ft) | 1.93 |
| , lbm/ft3 | 51.19 |
| , Btu/(lbm·°F) | 0.53 |
| , cp | 1 |
| , Btu/(lbm·psi) | 0.00313 |
| , bbl/STB | 1.05 |
| Well flow rate, q, STB/day | 181.95 |
| , °F | 250 |
| , psi | 10,000 |
| ·°F) [26] | 0.92 |
| Radius, ft | rD | Temperature, °F Nonconductive Non-System H.T. | Temperature, °F Non-System H.T. | Temperature, °F System H.T. |
|---|---|---|---|---|
| 0.35 (=rw) | 1 | 257.72 | 257.64 | 252.76 |
| 3.5 | 10 | 255.87 | 255.84 | 250.99 |
| 35 | 100 | 254.03 | 254.03 | 250.06 |
| 350 | 1000 | 252.18 | 252.18 | 250.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jang, M.; Chun, T.S.; An, J. An Analytical Heat Transfer Model in Oil Reservoir during Long-Term Production. Energies 2022, 15, 2544. https://doi.org/10.3390/en15072544
Jang M, Chun TS, An J. An Analytical Heat Transfer Model in Oil Reservoir during Long-Term Production. Energies. 2022; 15(7):2544. https://doi.org/10.3390/en15072544
Chicago/Turabian StyleJang, Minsoo, Troy S. Chun, and Jaewoo An. 2022. "An Analytical Heat Transfer Model in Oil Reservoir during Long-Term Production" Energies 15, no. 7: 2544. https://doi.org/10.3390/en15072544
APA StyleJang, M., Chun, T. S., & An, J. (2022). An Analytical Heat Transfer Model in Oil Reservoir during Long-Term Production. Energies, 15(7), 2544. https://doi.org/10.3390/en15072544






