Direct Participation of Dynamic Virtual Power Plants in Secondary Frequency Control
Abstract
:1. Introduction
2. Problem Formulation and Framework of the Approach
2.1. Classic SFC
- Frequency deviation of each SFC area i should go to zero:
- The deviation of each tie-lines power exchange between areas should go to zero: .
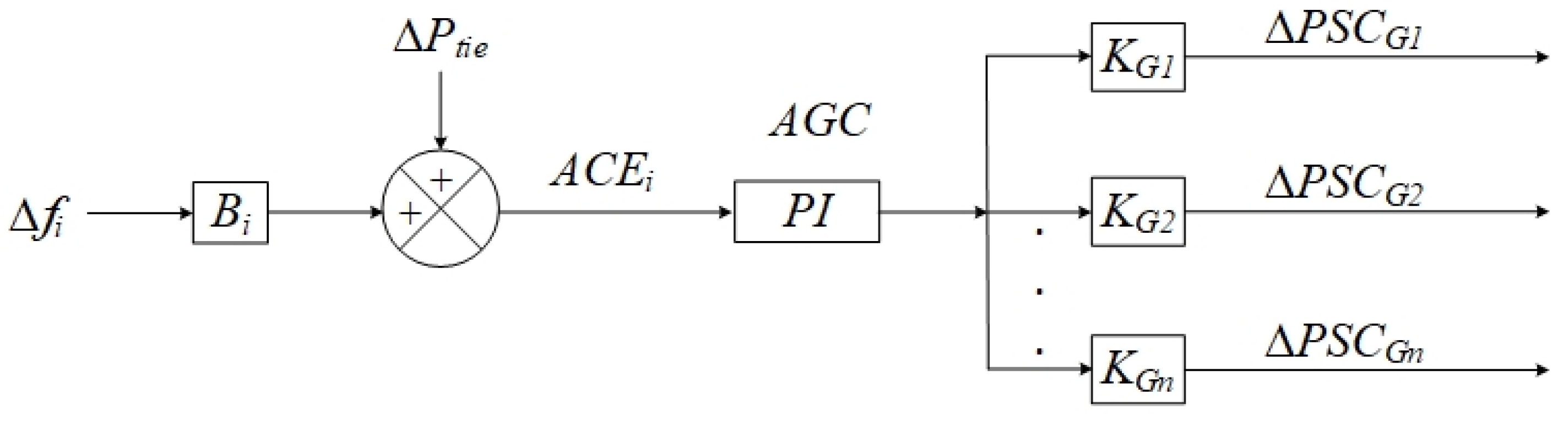
2.2. Indirect Participation of DVPP to Classic SFC
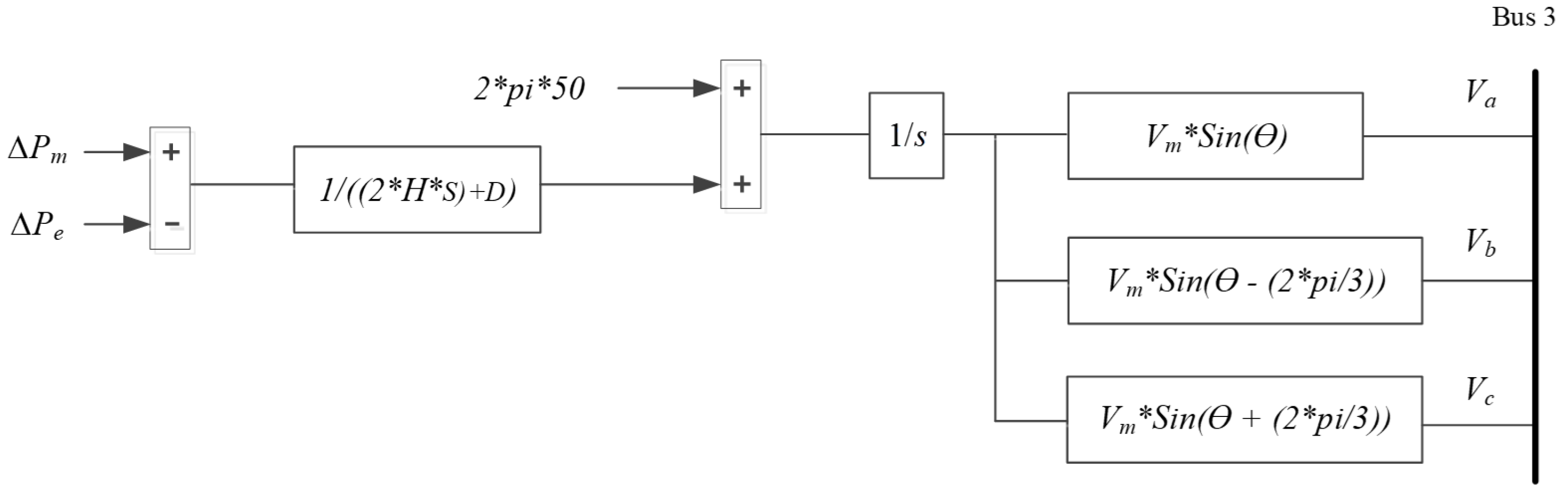
2.3. New Model for Simulation and Control
3. New Control for Direct Participation of the DVPP to the SFC
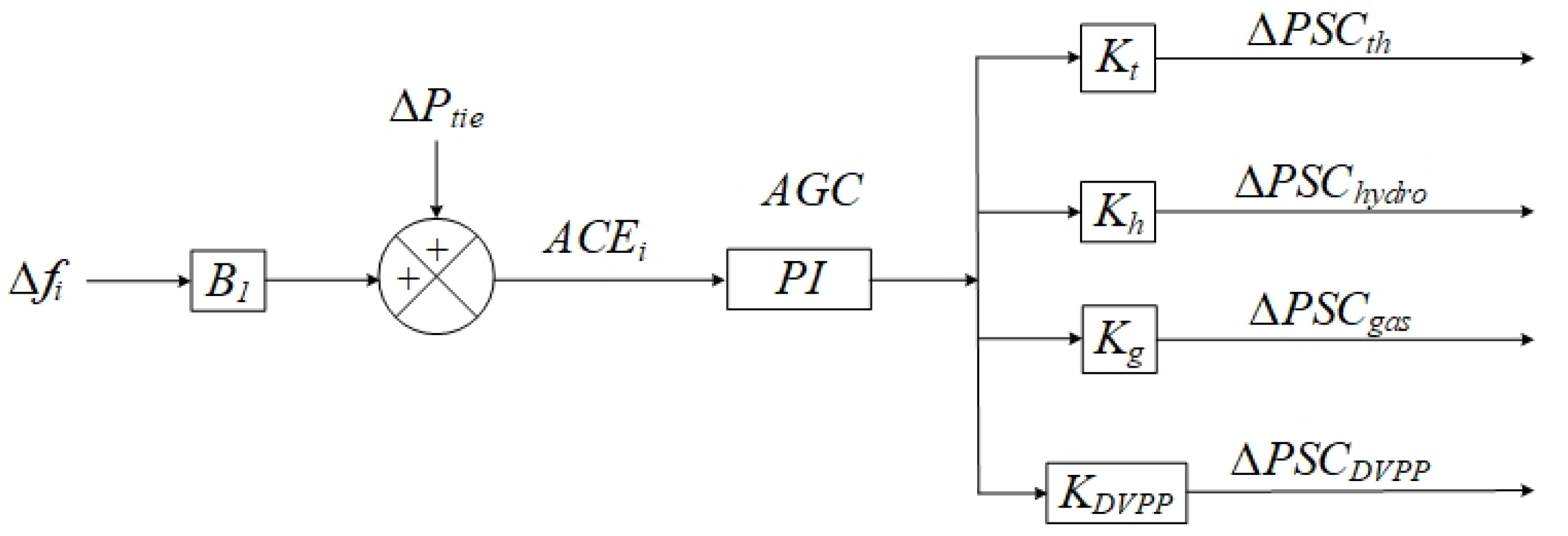
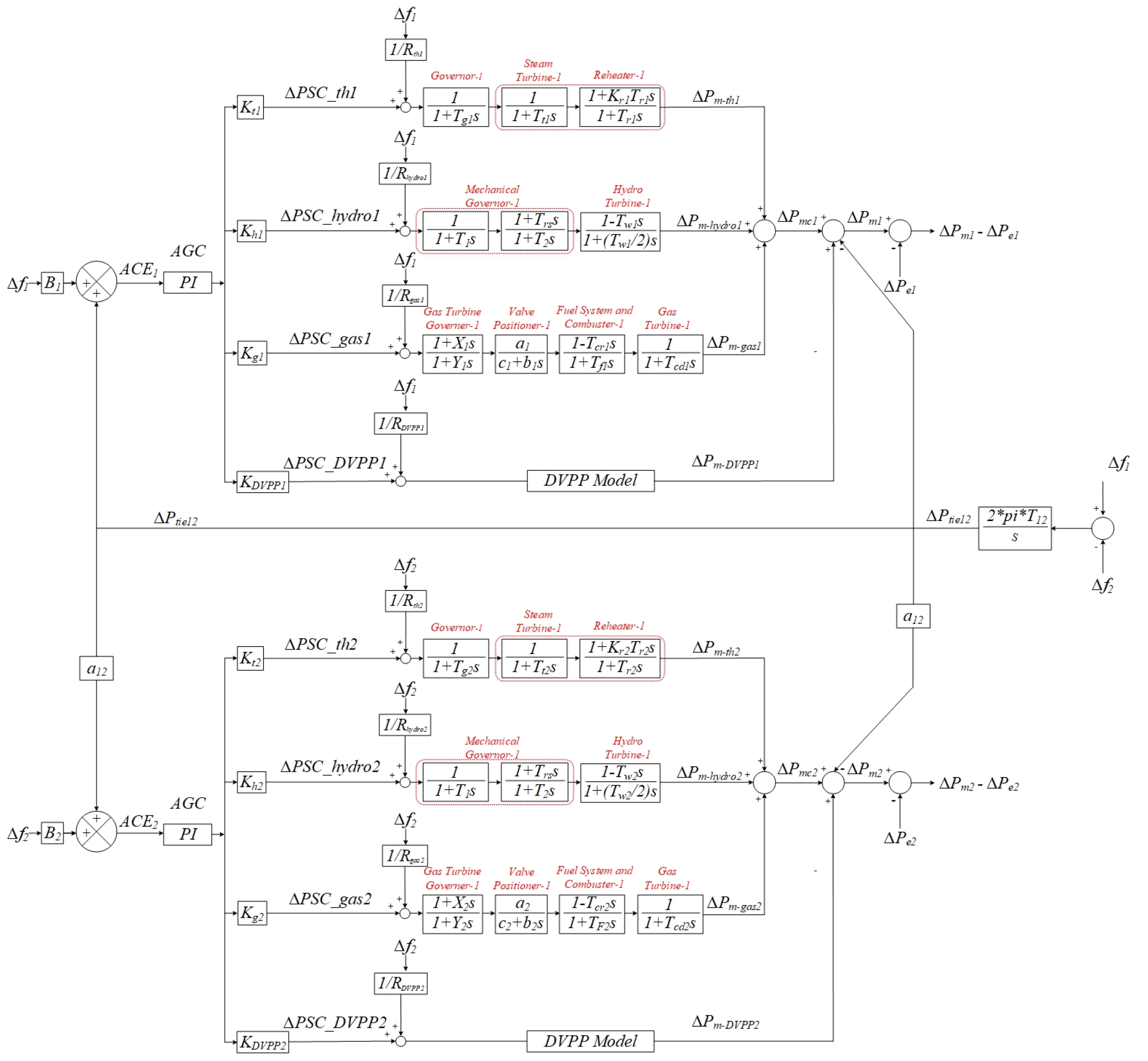
3.1. Direct Participation of the DVPP to the SFC
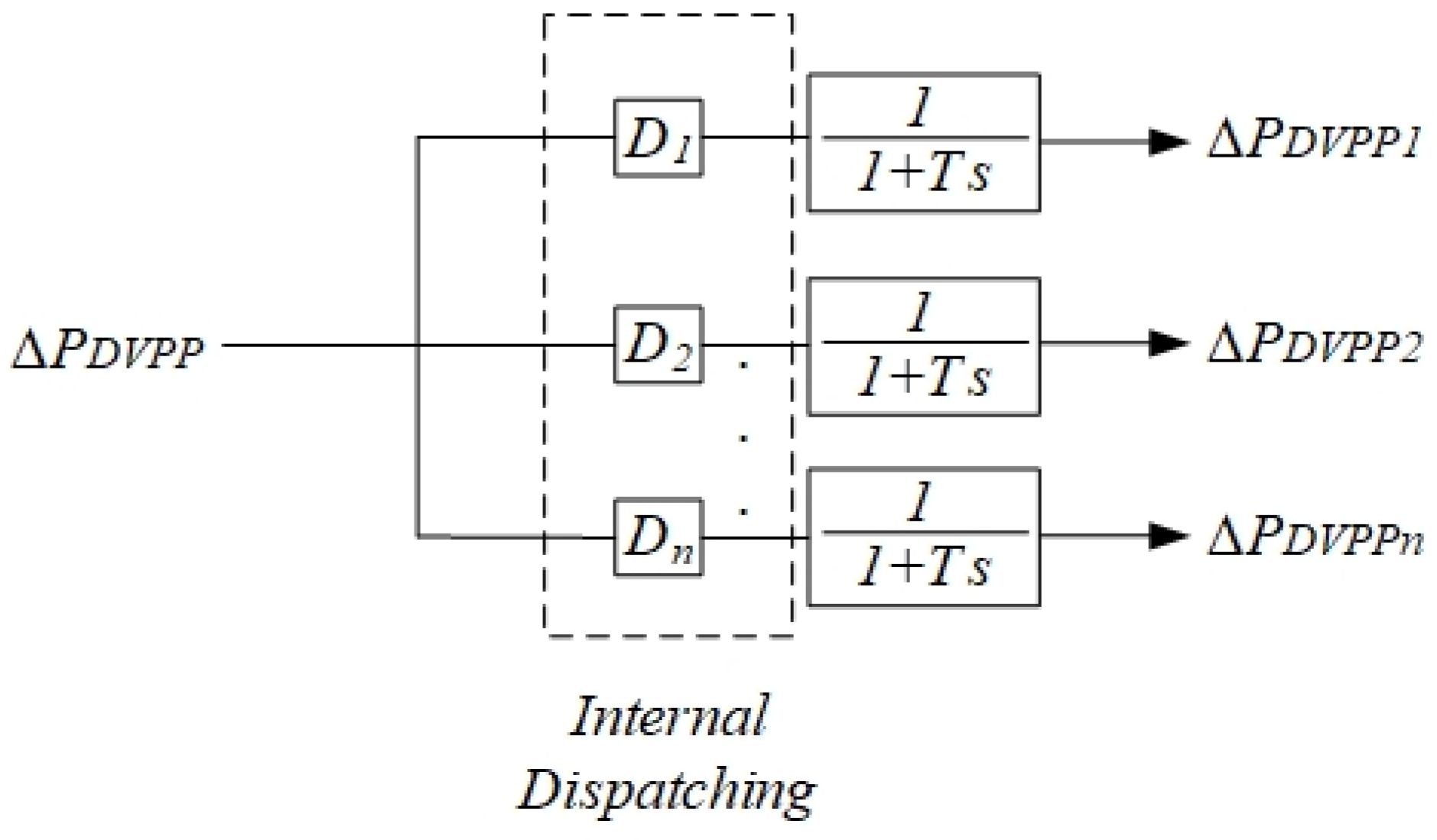
3.2. Internal DVPP Redispatch
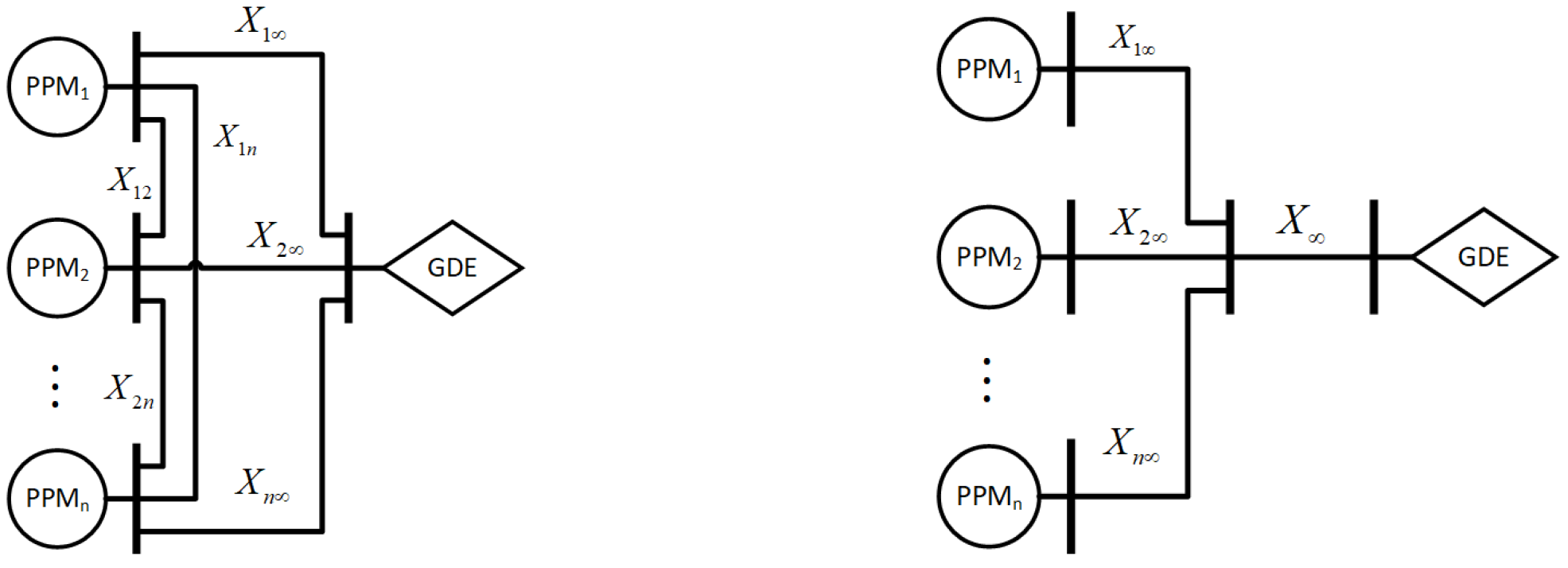
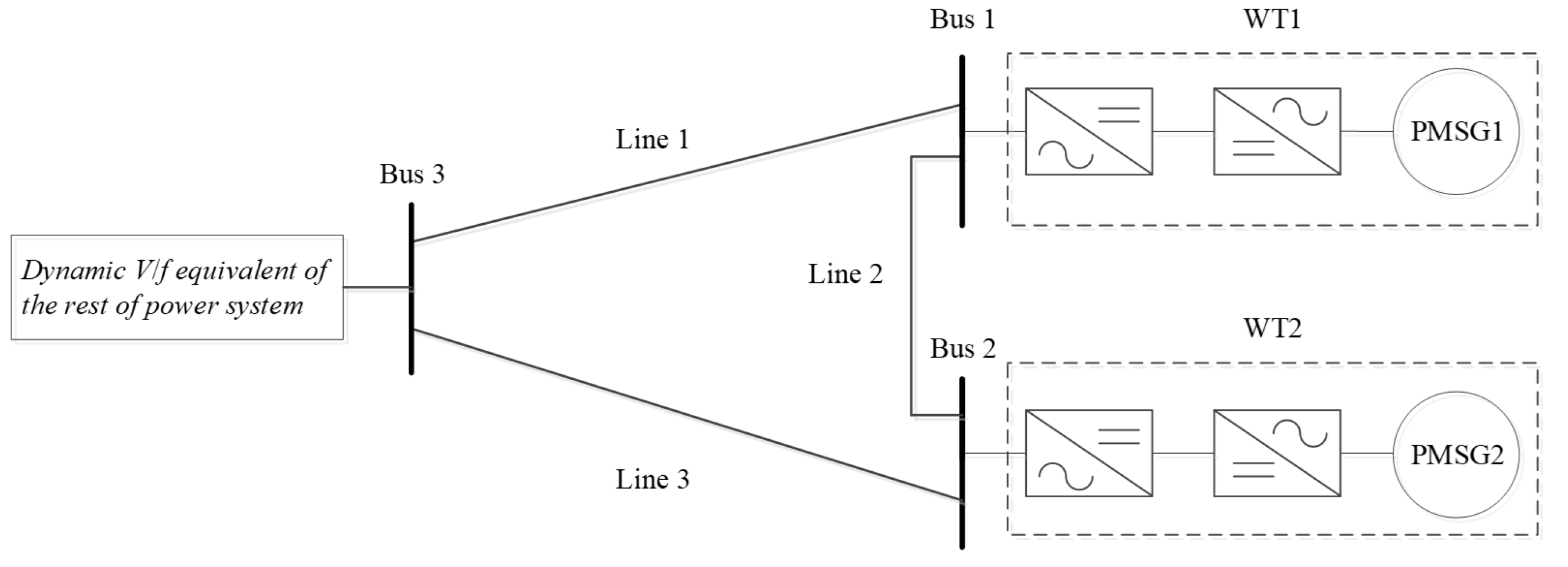
3.3. Simulation Benchmark and Control Strategy for Direct Participation of the DVPP to the SFC
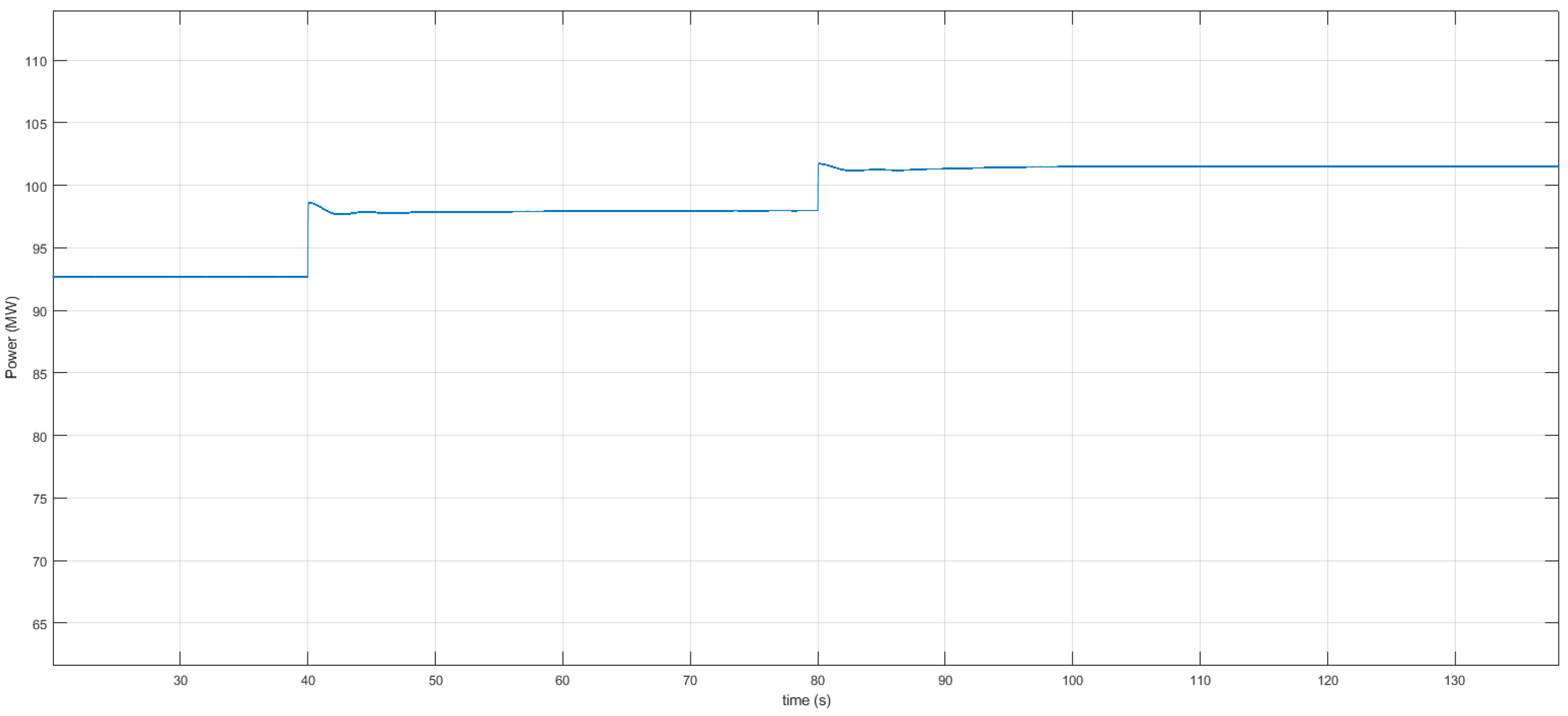
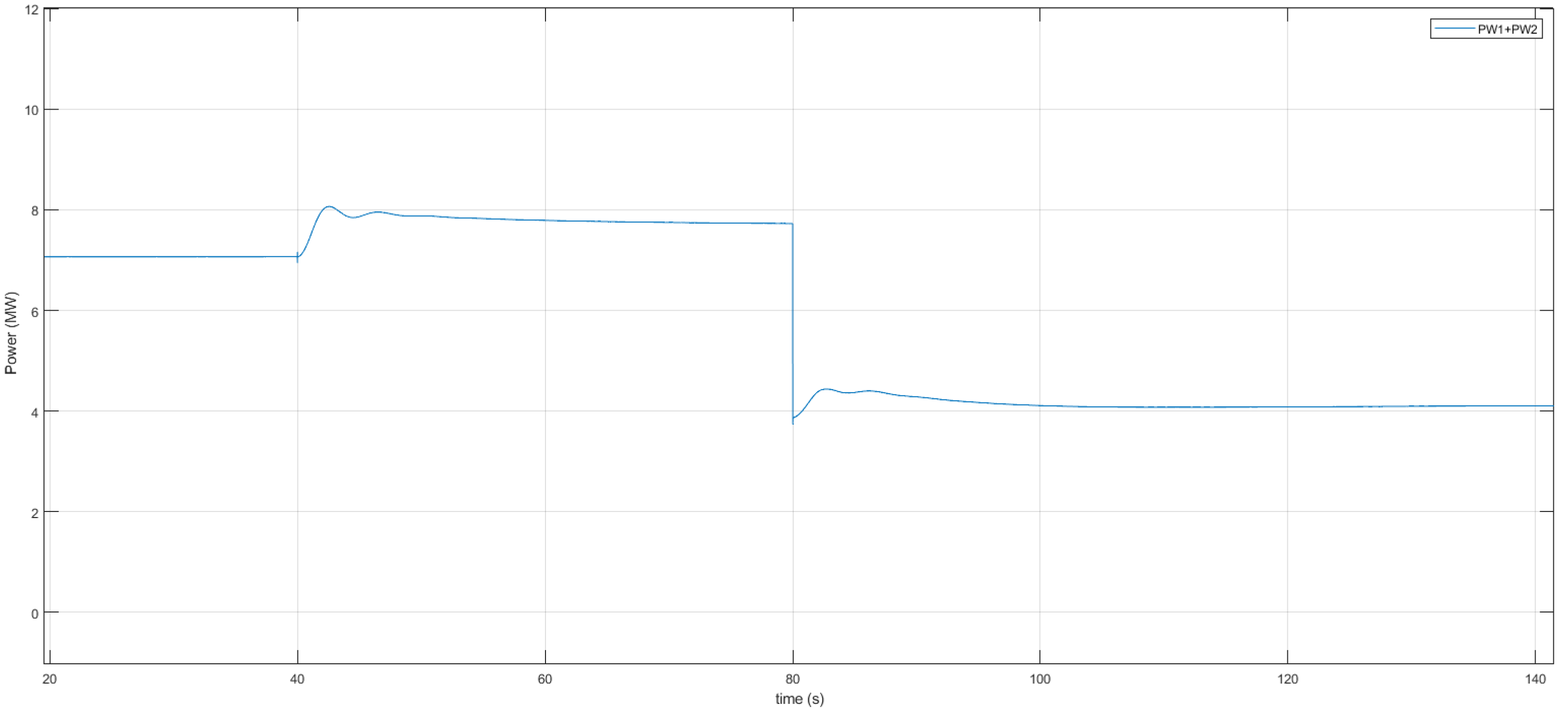
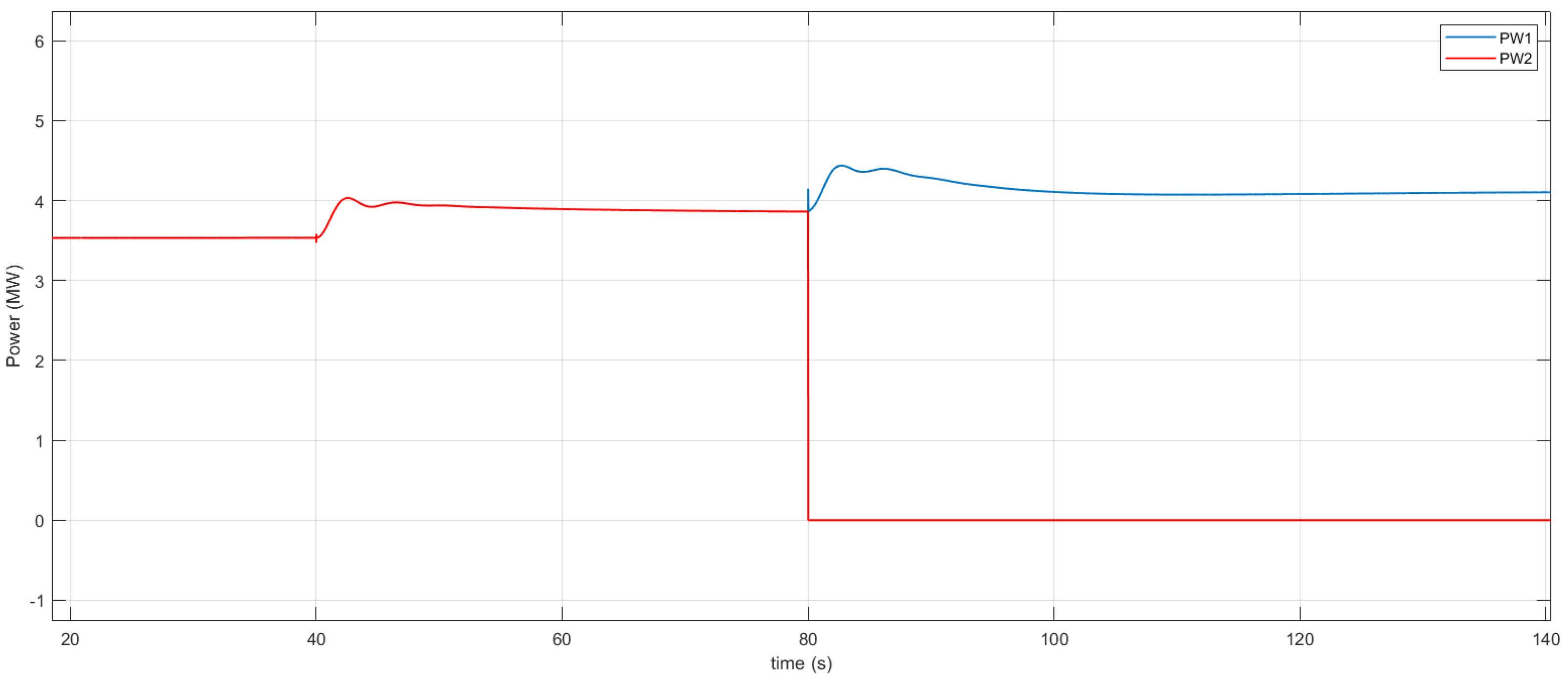
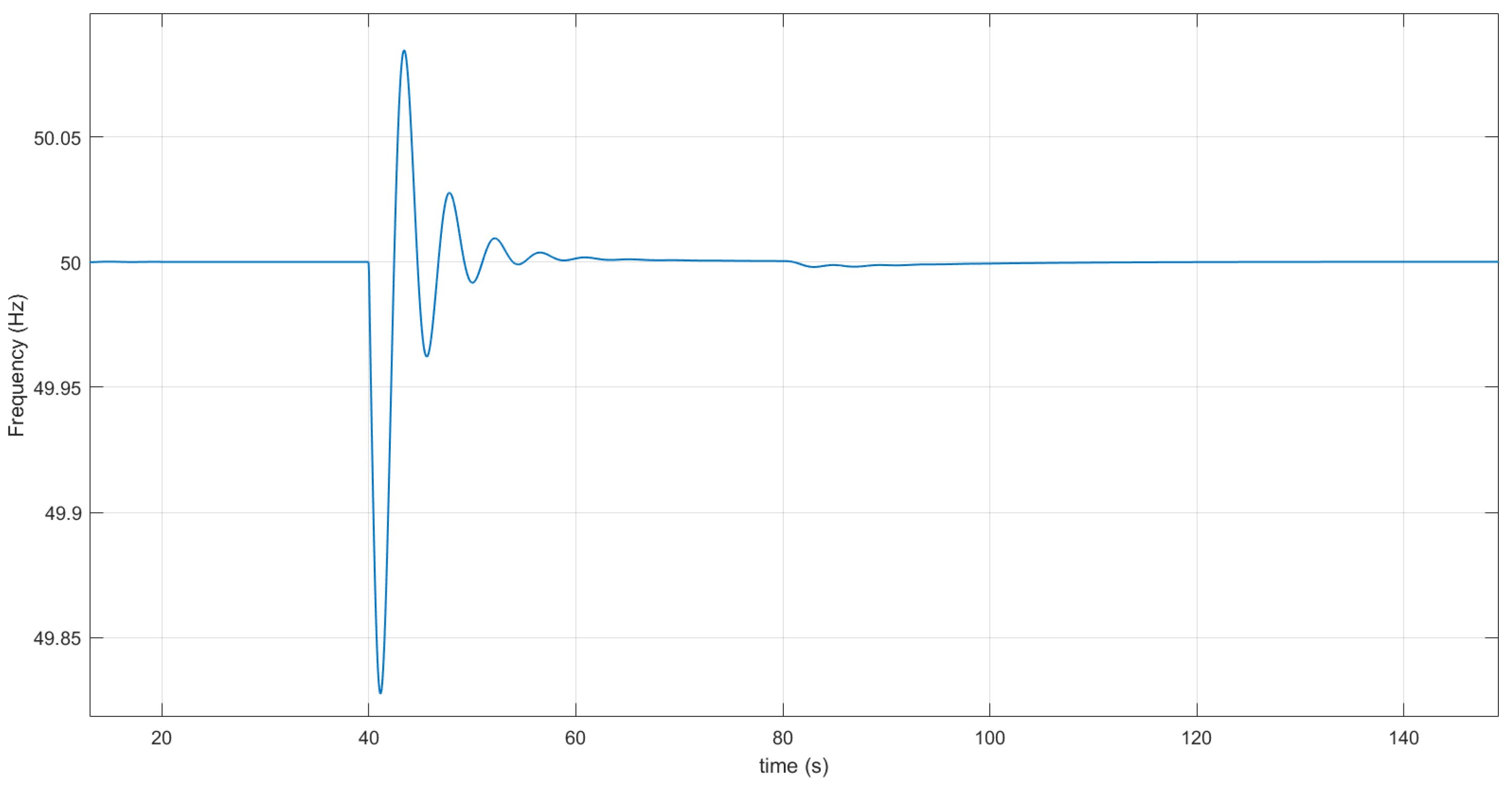
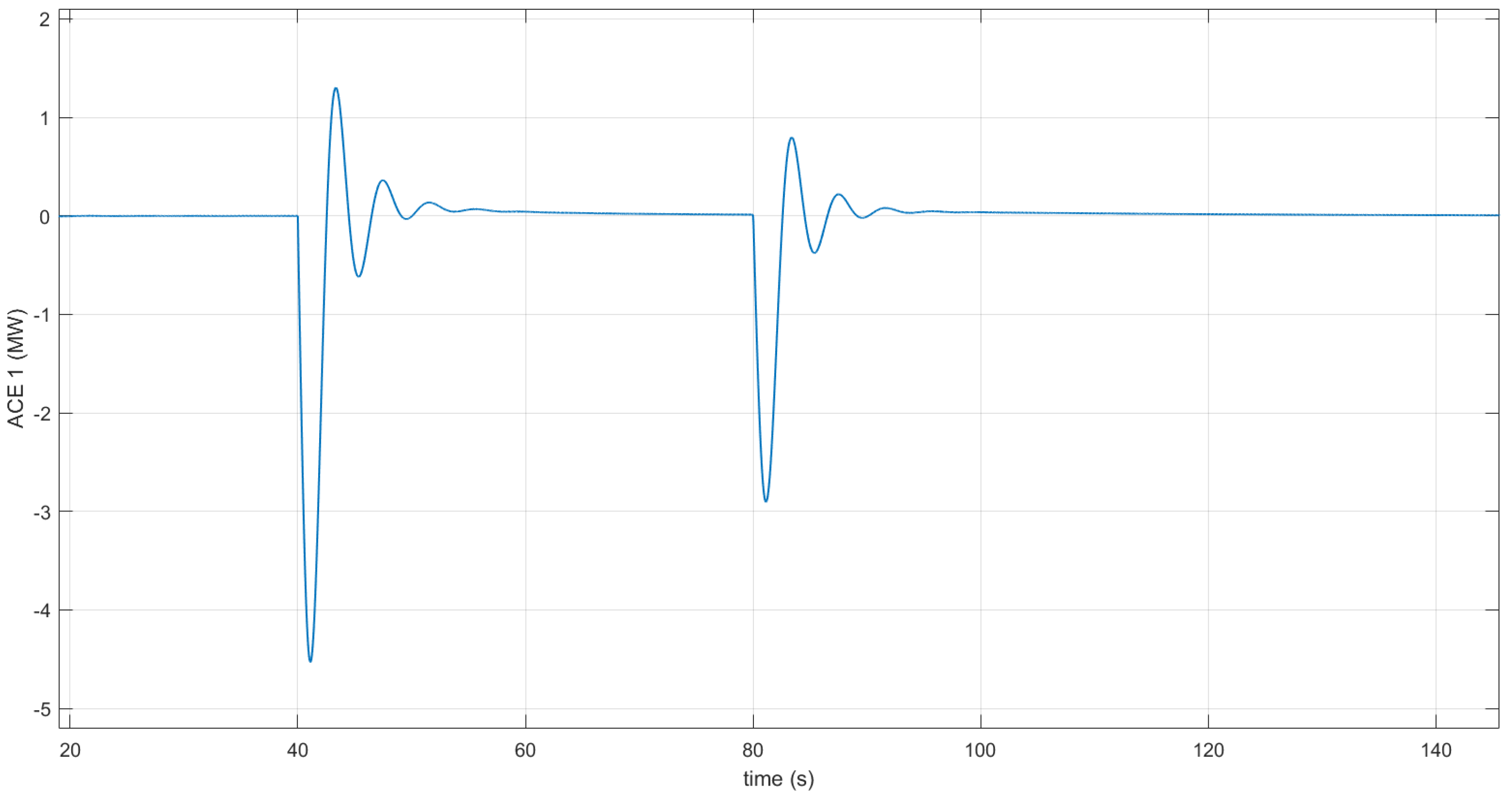
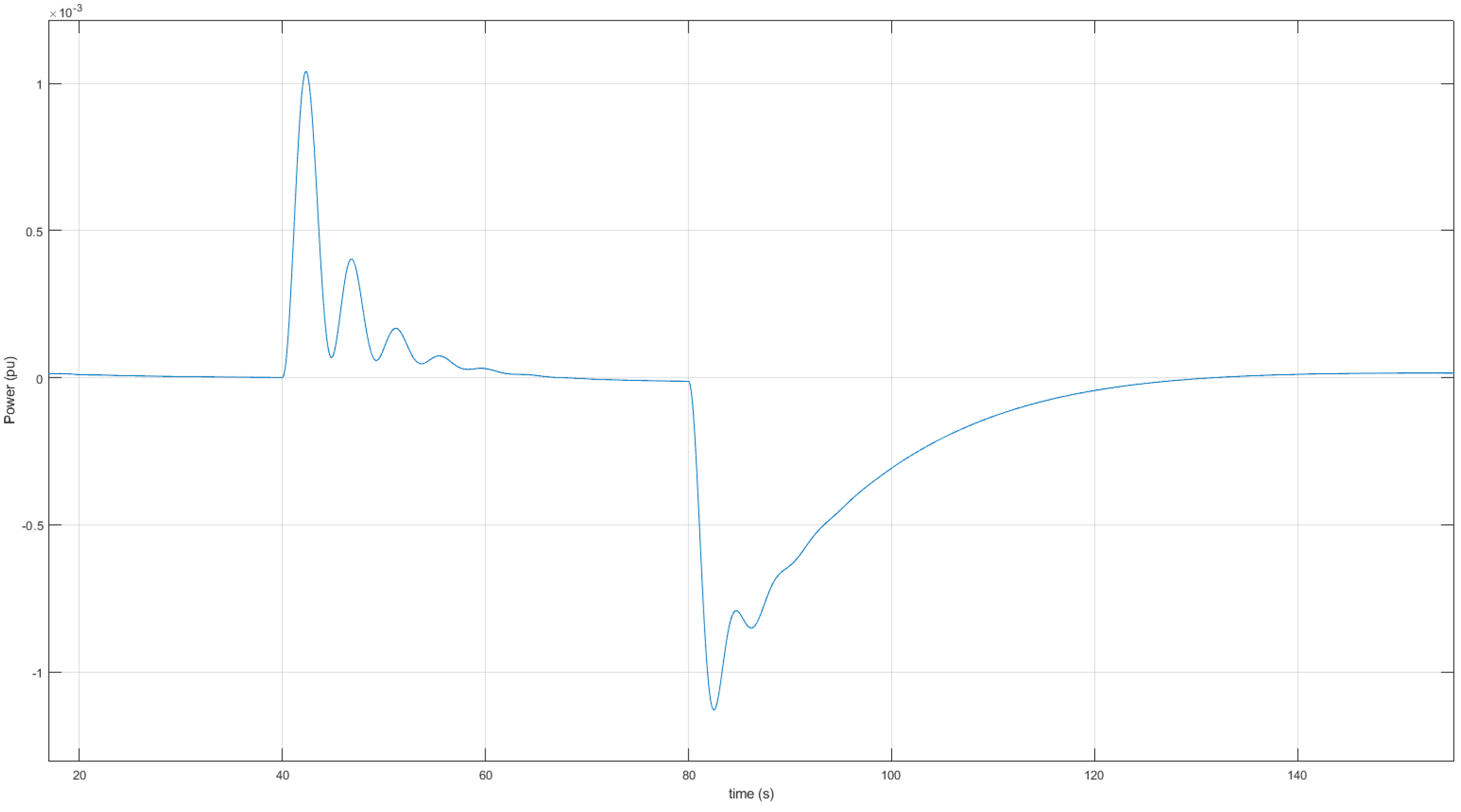
4. Simulation Results
4.1. Nominal Scenarios
4.2. Behavior in Case of Disturbances
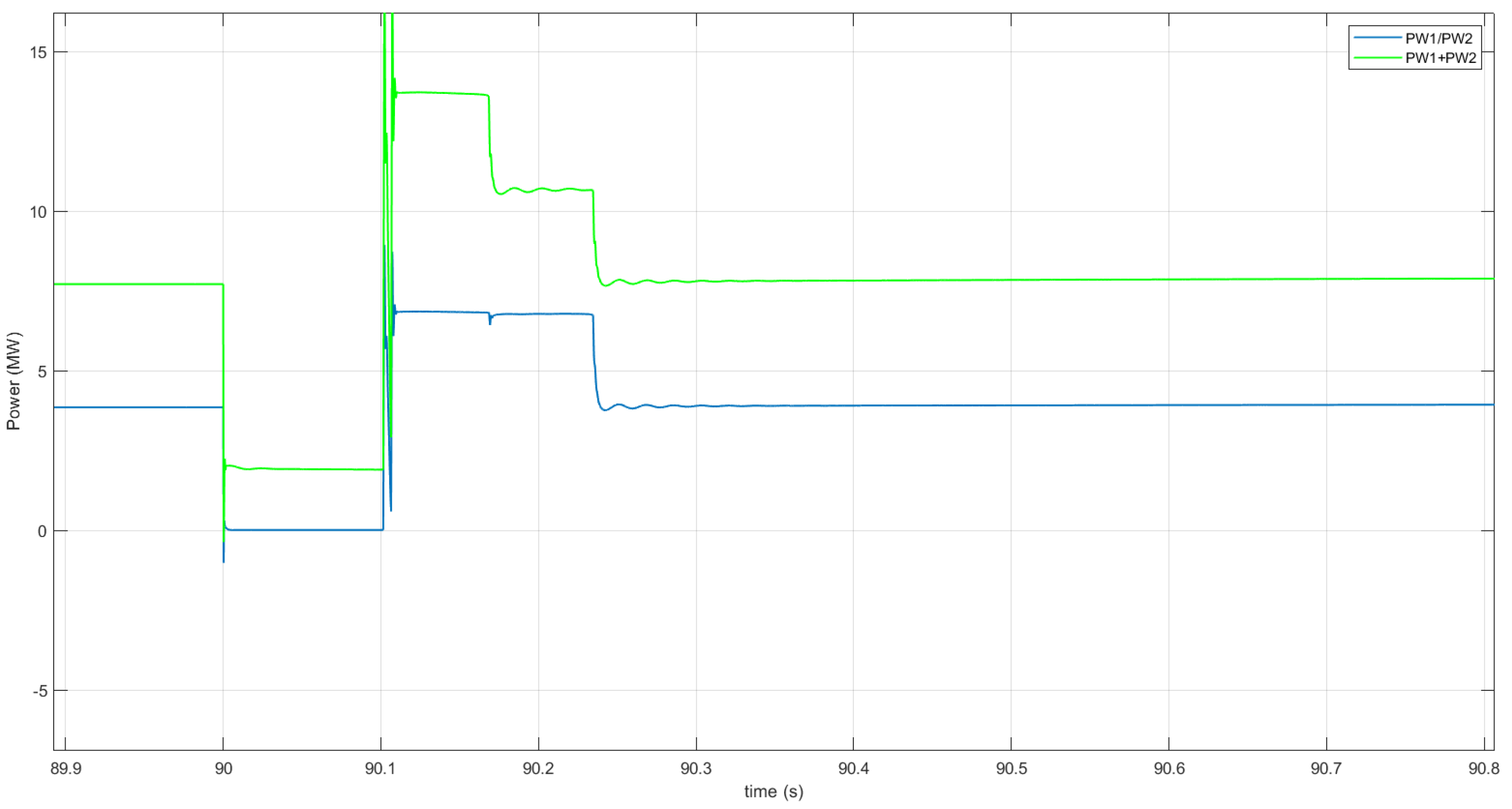
4.2.1. Influence of Internal Redispatch
4.2.2. Interaction between SFC Zones
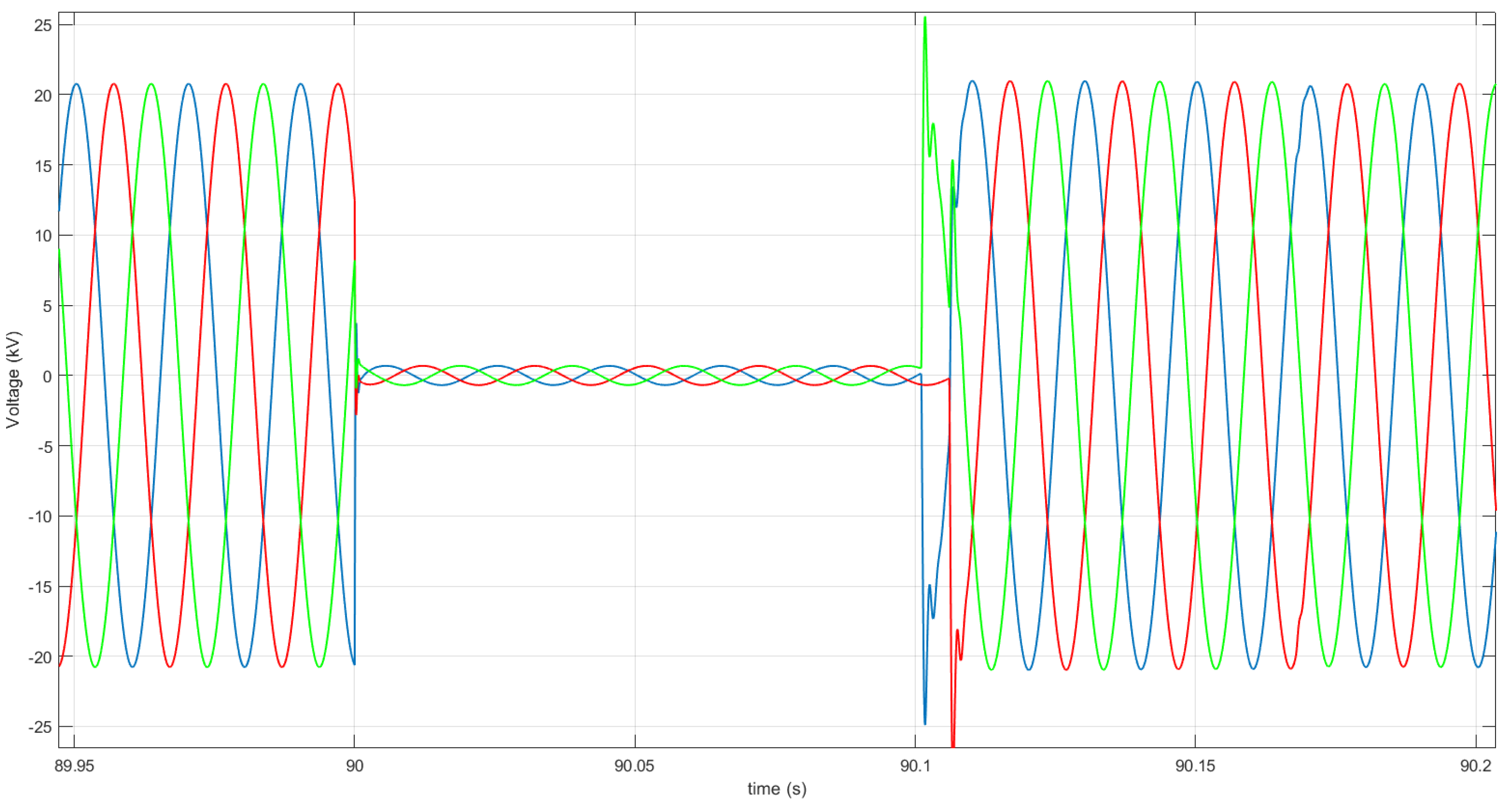
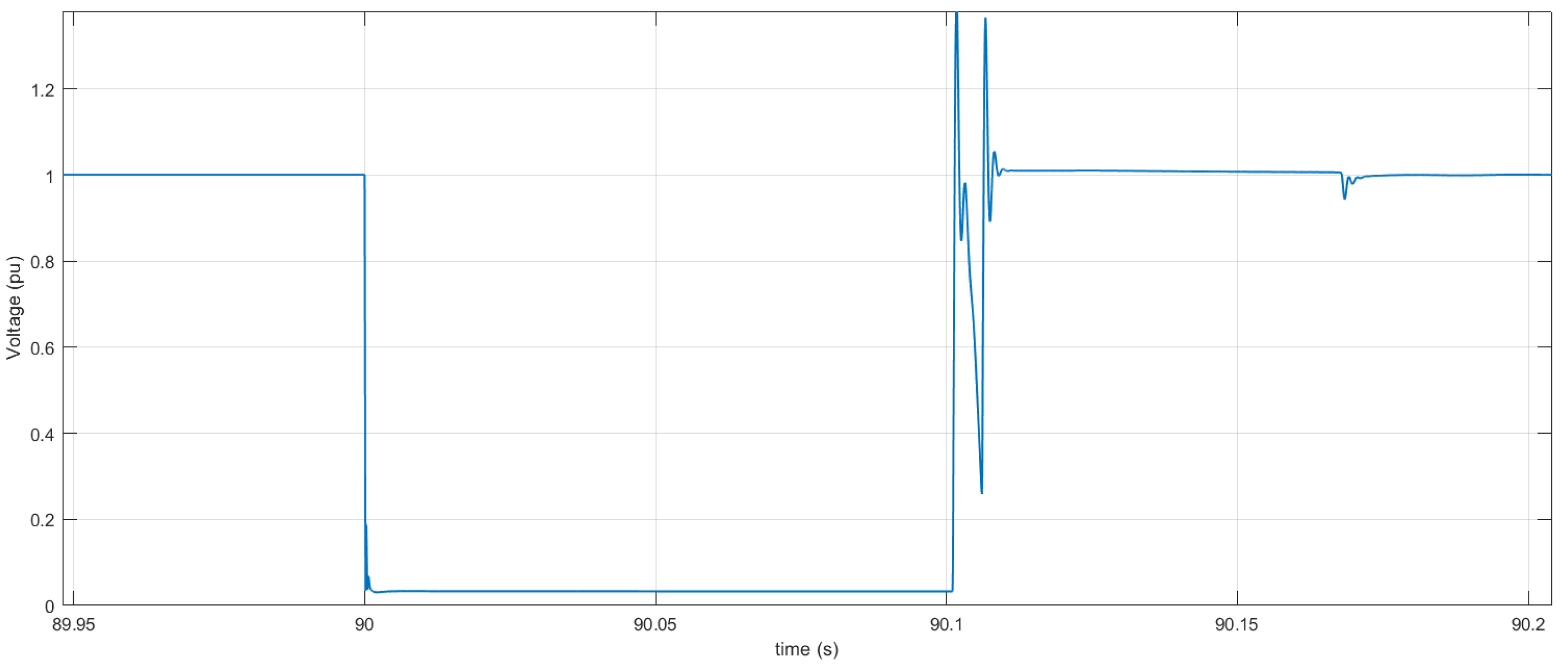
4.2.3. Short-Circuit Test
5. Conclusions
- They consider a detailed model of the DVPP generators (PMSG machines in the example treated here);
- The grid dynamics model integrates both voltage and frequency dynamics;
- Two SFC zones are considered to incorporate the tie-lines power exchange regulation and to consider dynamic interactions at all levels (frequency/time-domains) between the SFC zones.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, S.; Tomsovic, K. A Novel Active Power Control Framework for Wind Turbine Generators to Improve Frequency Response. IEEE Trans. Power Syst. 2018, 33, 6579–6589. [Google Scholar] [CrossRef]
- Díaz-González, F.; Hau, M.; Sumper, A.; Gomis-Bellmunt, O. Participation of wind power plants in system frequency control: Review of grid code requirements and control methods. Renew. Sustain. Energy Rev. 2014, 34, 551–564. [Google Scholar] [CrossRef]
- Miller, N.W.; Clark, K.; Shao, M. Frequency responsive wind plant controls: Impacts on grid performance. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011. [Google Scholar]
- Singhvi, V.; Pourbeik, P.; Bhatt, N.; Brooks, D.; Zhang, Y.; Gevorgian, V.; Ela, E.; Clark, K. Impact of Wind Active Power Control Strategies on Frequency Response of an Interconnection. In Proceedings of the IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013. [Google Scholar]
- Murali, S.; Shankar, R. Optimal CC-2DOF(PI)-PDF controller for LFC of restructured multi-area power system with IES-based modified HVDC tie-line and electric vehicles. Eng. Sci. Technol. Int. J. 2022, 32, 101058. [Google Scholar] [CrossRef]
- Sharma, P.; Mishra, A.; Saxena, A.; Shankar, R. A Novel Hybridized Fuzzy PI-LADRC Based Improved Frequency Regulation for Restructured Power System Integrating Renewable Energy and Electric Vehicles. IEEE Access 2021, 9, 7597–7617. [Google Scholar] [CrossRef]
- Murali, S.; Shankar, R. Impact of Inertia Emulation Based Modified HVDC Tie-Line for AGC Using Novel Cascaded Fractional Order Controller in Deregulated Hybrid Power System. J. Electr. Eng. Technol. 2021, 16, 1219–1239. [Google Scholar] [CrossRef]
- Rebours, Y.G.; Kirschen, D.S.; Trotignon, M.; Rossignol, S. Survey of Frequency and Voltage Control Ancillary Services—Part I: Technical Features. IEEE Trans. Power Syst. 2007, 22, 350–357. [Google Scholar] [CrossRef]
- Marinescu, B.; Gomis-Bellmunt, O.; Dörfler, F.; Schulte, H.; Sigrist, L. Dynamic Virtual Power Plant: A New Concept for Grid Integration of Renewable Energy Sources. arXiv 2021, arXiv:2108.00153. [Google Scholar]
- Zhang, X.; Chen, Y.; Wang, Y.; Zha, X.; Yue, S.; Cheng, X.; Gao, L. Deloading power coordinated distribution method for frequency regulation by wind farms considering wind speed differences. IEEE Access 2019, 7, 122573–122582. [Google Scholar] [CrossRef]
- Oshnoei, A.; Khezri, R.; Muyeen, S.M.; Blaabjerg, F. On the Contribution of Wind Farms in Automatic Generation Control: Review and New Control Approach. Appl. Sci. 2018, 8, 1848. [Google Scholar] [CrossRef] [Green Version]
- Bevrani, H.; Golpîra, H.; Messina, A.R.; Hatziargyriou, N.; Milano, F.; Ise, T. Power system frequency control: An updated review of current solutions and new challenges. Electr. Power Syst. Res. 2021, 194, 107114. [Google Scholar] [CrossRef]
- Liu, Y.; Jiang, L.; Wu, Q.H.; Zhou, X. Frequency control of DFIG-based wind power penetrated power systems using switching angle controller and AGC. IEEE Trans. Power Syst. 2017, 32, 1553–1567. [Google Scholar] [CrossRef] [Green Version]
- Pradhan, C.; Bhende, C.N. Frequency sensitivity analysis of load damping coefficient in wind farm-integrated power system. IEEE Trans. Power Syst. 2017, 32, 1016–1029. [Google Scholar]
- Zhang, Y.; Liu, X.; Yan, Y. Model predictive control for load frequency control with wind turbines. J. Control. Sci. Eng. 2015, 2015, 49. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Qu, B. Distributed model predictive load frequency control of multi-area power system with DFIGs. IEEE/CAA J. Autom. Sin. 2017, 4, 125–135. [Google Scholar] [CrossRef]
- Nguyen Duc, H.; Nguyen Hong, N. Optimal Reserve and Energy Scheduling for a Virtual Power Plant Considering Reserve Activation Probability. Appl. Sci. 2021, 11, 9717. [Google Scholar] [CrossRef]
- Iria, J.; Soares, F. Real-time provision of multiple electricity market products by an aggregator of prosumers. Appl. Energy 2019, 255, 113792. [Google Scholar] [CrossRef]
- Nguyen-Duc, H.; Nguyen-Hong, N. A study on the bidding strategy of the Virtual Power Plant in energy and reserve market. Energy Rep. 2020, 6 (Suppl. 2), 622–626. [Google Scholar] [CrossRef]
- Iria, J.; Soares, F.; Matos, M. Optimal bidding strategy for an aggregator of prosumers in energy and secondary reserve markets. Appl. Energy 2019, 238, 1361–1372. [Google Scholar] [CrossRef]
- Oladimeji, O.; Ortega, A.; Sigrist, L.; Sanchez-Martin, P.; Lobato, E.; Rouco, L. Modeling Demand Flexibility of RES-based Virtual Power Plants. arXiv 2021, arXiv:2112.03261. [Google Scholar]
- Oladimeji, O.; Ortega, A.; Sigrist, L.; Sanchez-Martin, P.; Lobato, E.; Rouco, L. Optimal Participation of Heterogeneous, RES-based Virtual Power Plants in Energy Markets. arXiv 2021, arXiv:2112.02200. [Google Scholar]
- Marinescu, B.; Kamal, E.; Ngo, H.-T. A System Model-Based Approach for the Control of Power Park Modules for Grid Voltage and Frequency Services. arXiv 2021, arXiv:2107.02000. [Google Scholar]
- Alhelou, H.H.; Hamedani-Golshan, M.E.; Zamani, R.; Heydarian-Forushani, E.; Siano, P. Challenges and Opportunities of Load Frequency Control in Conventional, Modern and Future Smart Power Systems: A Comprehensive Review. Energies 2018, 11, 2497. [Google Scholar] [CrossRef] [Green Version]
- Kundur, P. Power Systems Stability and Control; EPRI: Washington, DC, USA, 1994. [Google Scholar]
- Xiong, X.; Ouyang, J.; Jin, J. Calculation of steady-state short-circuit current of wind turbines with doubly fed induction generator. In Proceedings of the IEEE International Conference on Advanced Power System Automation and Protection, Beijing, China, 16–20 October 2011; Volume 3, pp. 1782–1788. [Google Scholar]
- Pathak, N.; Bhatti, T.S.; Verma, A. Accurate modelling of discrete AGC controllers for interconnected power systems. IET Gener. Transm. Distrib. 2017, 11, 2102–2114. [Google Scholar] [CrossRef]

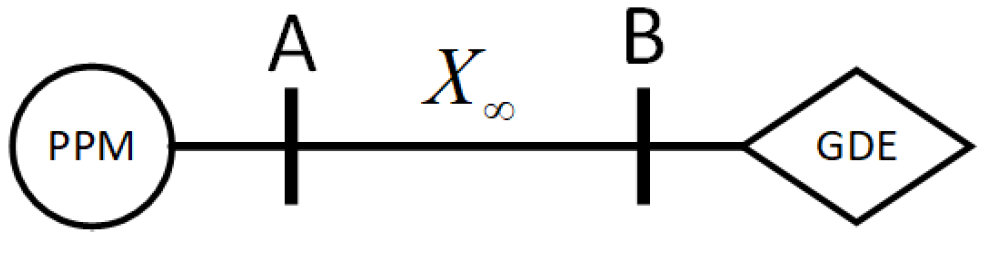


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adabi, M.E.; Marinescu, B. Direct Participation of Dynamic Virtual Power Plants in Secondary Frequency Control. Energies 2022, 15, 2775. https://doi.org/10.3390/en15082775
Adabi ME, Marinescu B. Direct Participation of Dynamic Virtual Power Plants in Secondary Frequency Control. Energies. 2022; 15(8):2775. https://doi.org/10.3390/en15082775
Chicago/Turabian StyleAdabi, M. Ebrahim, and Bogdan Marinescu. 2022. "Direct Participation of Dynamic Virtual Power Plants in Secondary Frequency Control" Energies 15, no. 8: 2775. https://doi.org/10.3390/en15082775
APA StyleAdabi, M. E., & Marinescu, B. (2022). Direct Participation of Dynamic Virtual Power Plants in Secondary Frequency Control. Energies, 15(8), 2775. https://doi.org/10.3390/en15082775





